Abstract
Background and Purpose
Contrast agent extravasation through a disrupted blood-brain barrier potentiates inaccurate DSC-MRI estimation of rCBV. We explored whether incorporation of interstitial washout rate in a leakage correction model for single-echo, gradient-echo DSC-MRI improves rCBV estimates in high-grade gliomas.
Materials and Methods
We modified the traditional model-based post-processing leakage correction algorithm assuming unidirectional contrast agent extravasation (Boxerman-Weisskoff model, BW-model) to account for bidirectional contrast agent exchange between intra- and extravascular spaces (Bidirectional model, Bidir-model). For both models, we compared goodness of fit to parent leakage-contaminated relaxation rate curves using Akaike Information Criterion (AIC) and difference between modeled interstitial relaxation rate curves and DCE-MRI using Euclidean distance (ED) in 21 patients with GBMs.
Results
The Bidir-model had improved AIC versus the BW-model in >50% of enhancing tumor voxels in all 21 GBMs (77%±9%; p<0.0001), and reduced ED in >50% of enhancing tumor voxels for 17/21 GBMs (62%±17%; p=0.0041). The Bidir-model- and DCE-derived kep demonstrates a strong correlation (r = 0.74±0.13). On average, enhancing tumor rCBV for the BW-model exceeded that for the Bidir-model by 16.6±14.0%.
Conclusion
Inclusion of bidirectional exchange in leakage correction models for single-echo DSC-MRI improves the model fit to leakage-contaminated DSC-MRI data and significantly improves estimation of rCBV in high-grade gliomas.
Keywords: dynamic susceptibility contrast MRI, high-grade glioma, contrast agent extravasation, leakage correction, relative cerebral blood volume
INTRODUCTION
The most common DSC-MRI metric in neuro-oncology is rCBV,1 which has been used for grading gliomas,2,3 predicting low-grade to high-grade transformation,4,5 distinguishing recurrent tumor from pseudoprogression6,7, differentiating tumor regression from pseudoresponse,8 and assessing overall treatment response.9,10 Relative CBV is typically calculated by integrating the dynamic first-pass change in transverse relaxation rate (ΔR2*) resulting from bolus injection of gadolinium-based contrast agent, which transiently causes a dose-dependent change in magnetic susceptibility of the blood.11 This technique mimics classic indicator-dilution theory,12 which assumes intravascular compartmentalization of injected contrast agent “tracer”. However, common gadolinium-based contrast agents extravasate in lesions with blood-brain barrier disruption,13 including malignant gliomas. The exchange of contrast agent between the intravascular and the extravascular, extracellular space, which is the objective measurement in dynamic contrast enhanced (DCE)-MRI,14–16 contaminates the desired DSC-MRI signal, depending on pulse sequence parameters and underlying tumor biology.17
A popular model-based DSC-MRI leakage correction method proposed by Weisskoff and Boxerman2,18,19 linearly fits measured ΔR2*(t) to two constant functions derived from average relaxation rate in non-enhancing tissue, one of which is permeability-weighted. Deviation from the reference function is used to derive corrected rCBV for each voxel. A limiting assumption of this approach is that contrast agent reflux from the interstitial space back to blood plasma is negligible within the time frame of DSC-MRI signal acquisition (~2 minutes). However, standard models quantifying contrast agent exchange between blood plasma and interstitium (i.e. DCE-MRI14) use two-compartment pharmacokinetics to account for bidirectional transport of contrast agent. We hypothesized that incorporating bidirectional contrast agent transport into the original DSC-MRI signal model improves rCBV estimates in brain tumors. To test this hypothesis, we compared model-based DSC-MRI leakage correction methods with and without consideration of bidirectional transport using simulations and clinical application to high-grade gliomas.
METHODS
Patients
A total of 24 sequential GBM patients with histologically proven GBM treated with maximal surgical resection followed by radiotherapy and concurrent temozolomide and both DSC-MRI and DCE-MRI performed at initial tumor progression were studied. Of these patients, two patients illustrated no bolus of contrast during DSC acquisition and one DSC dataset was corrupted by significant motion. Thus, a total of 21 patients (15 men; mean age 54 years, range 30–73) were included in the final cohort. Progression was defined prospectively by the treating neuro-oncologists if subsequent scans showed more than 2 sequential months of increasing contrast enhancement and worsening mass effect or evidence of neurologic decline. Specifically, progression was defined as ≥ 25% increase in the sum of enhancing lesion volumes, new enhancing lesions > 1 cm maximum dimension, an unequivocal qualitative increase in non-enhancing tumor, or an unequivocal new area of non-contrast enhancing tumor. Additionally, progression must have occurred more than 3 months following completion of radiation therapy. All participants gave informed written consent to have both DSC-MRI and DCE-MRI data collected. All procedures complied with the principles of the Declaration of Helsinki and were approved by the Institutional Review Board at our institution.
DSC-MRI and DCE-MRI
We retrospectively reviewed DSC-MRI and DCE-MRI scans (3T, Siemens Trio or Skyra, Siemens Healthcare, Erlangen, Germany) acquired in the same scan session in all 21 patients. T1 maps were generated from 5 pre-contrast T1–weighted images (flip angle=5°, 10°, 15°, 20°, 30°) prior to DCE-MRI (3D spoiled gradient echo sequence, 16 slices, 130 time points, 5 s time resolution, TE/TR=1.87/5ms, 25° flip angle, 3 mm slice thickness, 256×192 matrix, 24 cm FOV). The DCE-MRI was acquired for ~10 minutes, which is the waiting time between preload and DSC contrast injections for this study. Contrast agent bolus (0.1 mmol/kg) (Magnevist, Bayer HealthCare) was injected after 10–13 baseline images, serving as pre-load13 for DSC-MRI (gradient echo EPI, TE/TR=32/1840ms, 35° flip angle, 120 time points, bolus injection after 20–25 baseline images, 9–20 slices, 5mm slice thickness, 128×128 matrix size, 24cm FOV). The same amount of contrast agent was used for the DSC-MRI studies. Conventional post-contrast T1-weighted imaging was subsequently performed. Patients were excluded if DCE-MRI or DSC-MRI was corrupted by motion or technical error.
Image Registration and ROI Selection
All conventional and DCE-MRI images for each subject were registered to baseline DSC-MRI images using 12-degree of freedom affine transformation with a mutual information cost function (FSL; http://www.fmrib.ox.ac.uk/fsl). If required, manual alignment was subsequently performed (tkregister2, Freesurfer; surfer.nmr.mgh.harvard.edu). Contrast enhancing tumor regions of interest (ROIs) were defined in three dimensions using custom scripts (AFNI; http://afni.nimh.nih.gov/afni), excluding hemorrhage, large vessels, and central necrosis, followed by manual editing to exclude non-lesion voxels.20 Tumor sizes ranged from 2.8 to 106.6 mL, with an average enhancing volume of 40.1 ± 28.4 mL (s.d.). Spherical ROIs of 1.6 mL were also selected in normal-appearing, contralateral white matter for rCBV normalization.
Computation of DSC-MRI rCBV
All simulations and calculations were performed in MATLAB using custom scripts. Uncorrected rCBV was calculated from trapezoidal integration of the original DSC-MRI relaxation rate-time curve, . The whole-brain average relaxation rate for non-enhancing voxels (Eqs. 3–4) was used for both the original Boxerman-Weisskoff model19 (BW-model) and the new bidirectional exchange model (Bidir-model). Linear least squares optimization was used to determine the free parameters for both the Bidir-model (via Eq. 7) and the BW-model (Eq. 5, with kep = 0) algorithms, and corrected rCBV was computed from Eq. 8. The average runtime per patient in MATLAB was 19.5±6.7s for the Bidir-model and 18.3±6.2s for the BW-model (3.2 GHz Intel Core i5, 32 GB RAM). Tumor rCBV for each method was subsequently normalized to median rCBV within the normal appearing white matter ROI.
Simulation of DSC-MRI rCBV
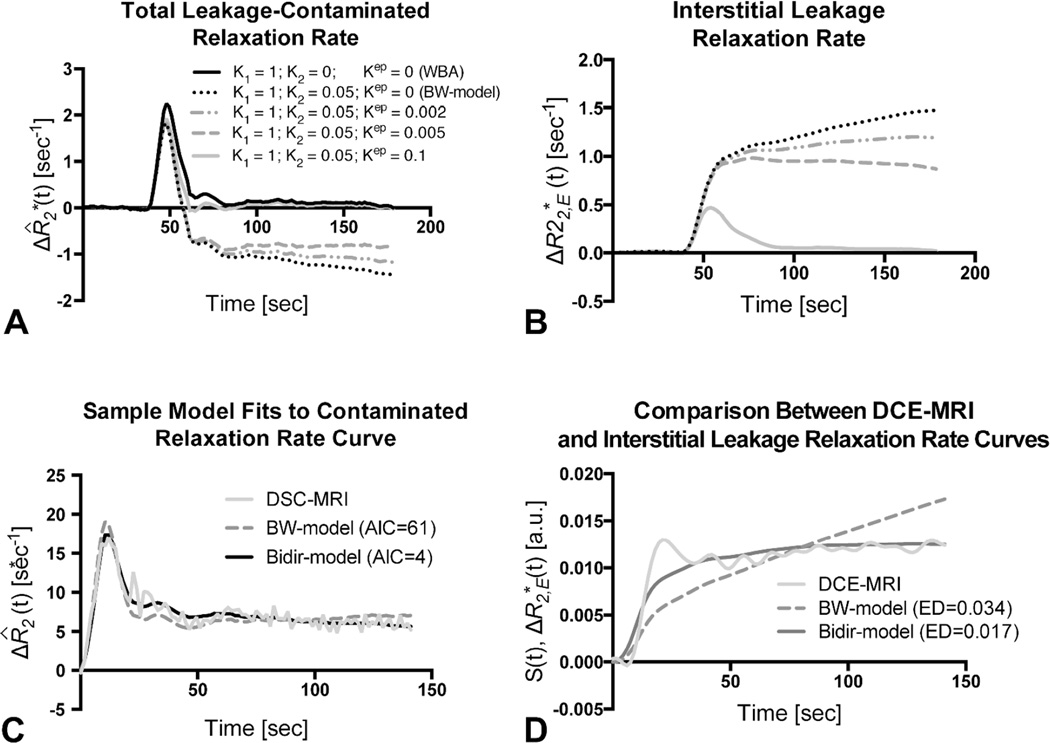
Whole-brain average relaxation rate, , was chosen from a sample patient and corresponds to the curve with K1=1, K2=0, and kep=0. K2=0.05 (adding T1-dominant leakage), with kep=0 was set to simulate the BW-model. A nonzero kep (0.002 or 0.005) was used to simulate the Bidir-model of . For kep=0.1, the simulation is reflective of the correction of relaxation rate curves at “artery-like” voxels.
Goodness of Fit Analysis
For each enhancing tumor voxel for all patients, we computed the Akaike Information Criterion (AIC) between leakage-contaminated relaxation rate (Eq. 1) and its model fit (Eq. 5) for the BW-model and Bidir-model:
| 9) |
where n is the number of fitted time points (injection to end of DSC-MRI acquisition), RSS is the sum of the squared residuals, and p is the number of free parameters (2 for the BW-model, 3 for the Bidir-model).21 Differences in the BW-model and Bidir-model AIC were calculated for all voxels where kep>0.
We also computed Euclidean distance (square root of the sum of the squared differences) between the interstitial leakage relaxation rate curves, , generated by the BW-model and Bidir-model corrections and DCE-MRI signal, where the DCE-MRI signal was up-sampled from a 5-second resolution to a 1.8-second resolution to match that of the DSC-MRI data via linear interpolation using the MATLAB function “resample”. Because interstitial leakage relaxation rate curves and DCE-MRI signal have units of 1/sec and mM, respectively, both were standardized to an area under the curve equal to unity and vectorized for computation of Euclidean distance. Higher AIC and ED imply worse fits. Two-sample t-tests were used to compare whether the AIC and ED measurements were significantly different between the two leakage correction methods.
Post-processing of DCE-MRI
DCE-MRI imaging biomarkers – kep and Ktrans – were derived via a fit to the Tofts model14. As described above, the temporal resolution of the DCE-MRI data was up-sampled to match the DSC-MRI data. For the DCE-MRI analysis, the “whole brain average” served as the arterial input function (AIF) for the DCE model fit. This was done to mirror the DSC Bidir-model analysis, in which the “whole brain average” effectively serves as the AIF Voxels with highly fluctuating time courses in either the DSC or DCE images were eliminated from the analysis.
Correlation between DSC- and DCE-derived Imaging Biomarkers
DSC-MRI imaging biomarkers – kep and rCBV – were derived as described in the Appendix. Voxel-wise Pearson correlation coefficients between the DSC- and DCE-derived parameters were performed in MATLAB within contrast-enhancing tumor only for each patient independently. In this study, we report means and standard deviations of the correlation coefficients from all 21 patients.
RESULTS
Simulation of the Bidir-model
Figure 1 compares simulated total leakage contaminated relaxation rate, , (Fig. 1A) and the component from interstitial leakage, , (Fig. 1B) for various conditions according to the Tofts model14 assuming T1-dominant leakage-associated relaxation enhancement. For the BW-model, rises over time in the absence of washout. For nonzero kep, there is less rise in and closer approximation of the tail of to , reflecting tumors with different contrast agent pharmacokinetics. For kep=0.1, the tail of approaches zero, but because the first-pass of differs from that of , correction of relaxation rate curves at “artery-like” voxels using K1 and K2 is still required to achieve accurate rCBV estimates.
Figure 1.
Sample simulated model results for all GBM patients. (A) Total leakage contaminated relaxation rate and the component from interstitial leakage (B) for T1-dominant leakage-associated relaxation enhancement. Whole-brain average relaxation rate (WBA) is simulated with K2=0 and kep=0. Kep=0 with non-zero K2 simulates the BW-model. Inclusion of a washout term (non-zero kep) in the Bidir-model yields less rise in and closer approximation of the tail of to WBA. (C) The Bidir-model fit to sample leakage-contaminated relaxation rate curve has substantially improved AIC compared to BW-model for T2*-dominant leakage-associated relaxation enhancement in a GBM patient. (D) Standardized interstitial leakage relaxation rate from the Bidir-model better tracks standardized DCE-MRI signal than the BW-model for the tumor voxel used in (C) with substantially improved Euclidean distance.
Figure 1C plots sample , with T2*-dominant leakage-associated relaxation enhancement for a representative patient, with superimposed BW-model and Bidir-model fit relaxation rate curves. In this example, the BW-model overestimates the first-pass curve, underestimates the second and third passes, and overestimates the tail. The Bidir-model better approximates over all time points, visually, and has substantially improved AIC, quantitating an improved fit to the total leakage contaminated relaxation rate curve.
Figure 1D plots standardized DCE-MRI signal for the tumor voxel used in Figure 1C, with superimposed standardized interstitial leakage relaxation rate curves, , from the BW-model and Bidir-model. The standardized interstitial leakage relaxation rate continually rises over time for the BW-model, whereas it better tracks standardized DCE-MRI for Bidir-model with substantially improved Euclidean distance.
Goodness of Fit Analysis
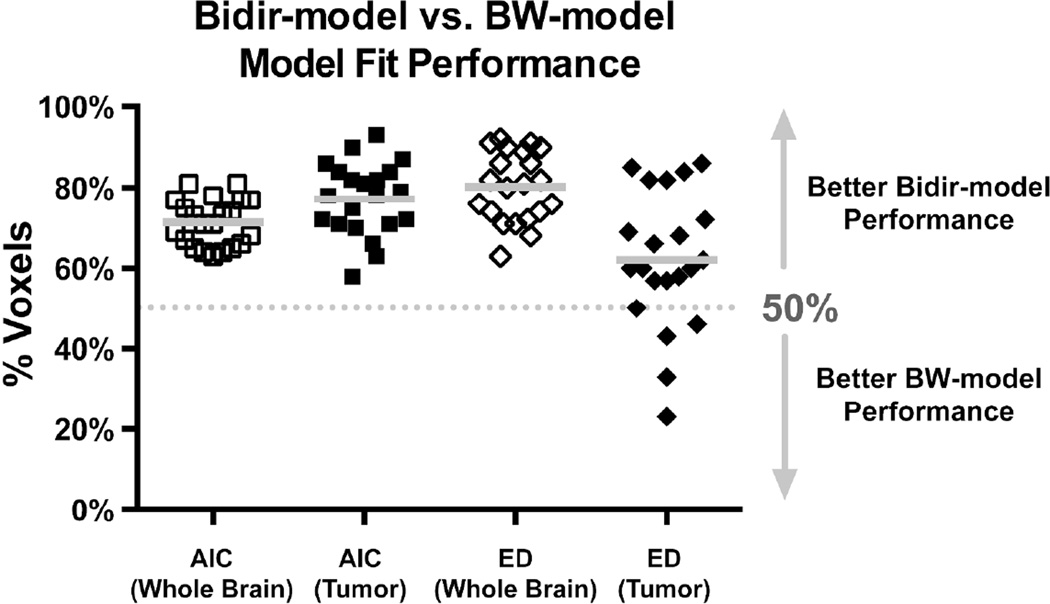
Figure 2 plots the percentage of voxels where the Bidir-model outperformed BW-model for AIC and Euclidean distance metrics in whole brain and tumor for the 21 GBM patients. The Bidir-model had better AIC performance than BW-model in greater than 50% of whole-brain (mean±standard deviation = 71%±6%, p<0.0001) and tumor (77%±9%, p<0.0001) voxels in all patients, and better Euclidean distance performance in greater than 50% of whole-brain voxels (80%±9%, p<0.0001) for all patients, and tumor voxels (62%±17%, p=0.0041) for 17 of the 21 patients. All were statistically significant for a one-sample t-test with null hypothesis of 50%.
Figure 2.
Percentage of voxels (with mean and standard deviation) where the Bidir-model outperformed BW-model on Akaike Information Criterion (AIC) and Euclidean distance (ED) metrics within whole brain and tumor for all 21 GBM patients. Gray line represents the group mean percentage of voxels.
Correlation between DSC-derived and DCE-derived imaging biomarkers
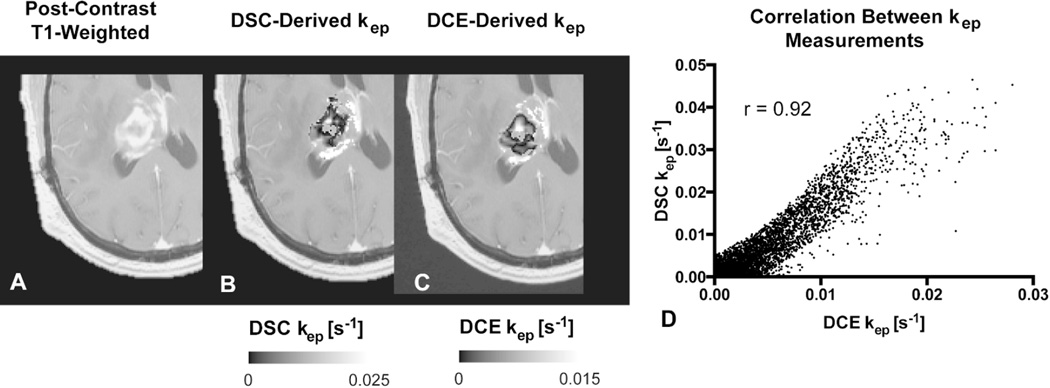
We then performed a voxel-wise correlation between the DSC-derived imaging biomarkers from the bidirectional leakage correction algorithm (kep and rCBV) with the DCE-derived imaging biomarkers (kep and Ktrans). Across the 21 patients, the Pearson correlation coefficient between the two kep measurements was 0.74±0.13 across the 21 patients, with a weak correlation between the Pearson’s correlation coefficient and tumor size (r = 0.11). Figure 3 demonstrates an example of the correlation between DSC- and DCE-derived kep. A correlation test was performed between the bidirectional model-derived rCBV and DCE-derived Ktrans, with a moderate correlation of 0.49±0.22. A moderate correlation was also found between rCBV and vp at 0.54±0.12. Finally, the correlation between the same rCBV and kep was r = 0.29±0.26. The average Ktrans value was 0.0015±0.0018 s−1 (0.09±0.11 min−1), DCE-Kep was 0.0050±0.0023 s−1 (0.30±0.14 min−1), DSC-kep was 0.0057±0.0042 s−1 (0.34±0.25 min−1), vp was 0.01±0.01, and rCBV was 1.98±1.24.
Figure 3.
Comparison between DSC- and DCE-derived kep measurements within tumor. A) Example of anatomical MRI of a patient with recurrent glioblastoma. B) DSC-derived kep measurements within tumor. C) Corresponding DCE-derived kep measurements. D) Scatter plot between (B) and (C) demonstrate high correlation (r = 0.92) for this tumor. Note that areas of low kep are similar in both DSC- and DCE-derived maps.
Difference in rCBV between the Bidir-model and BW-model
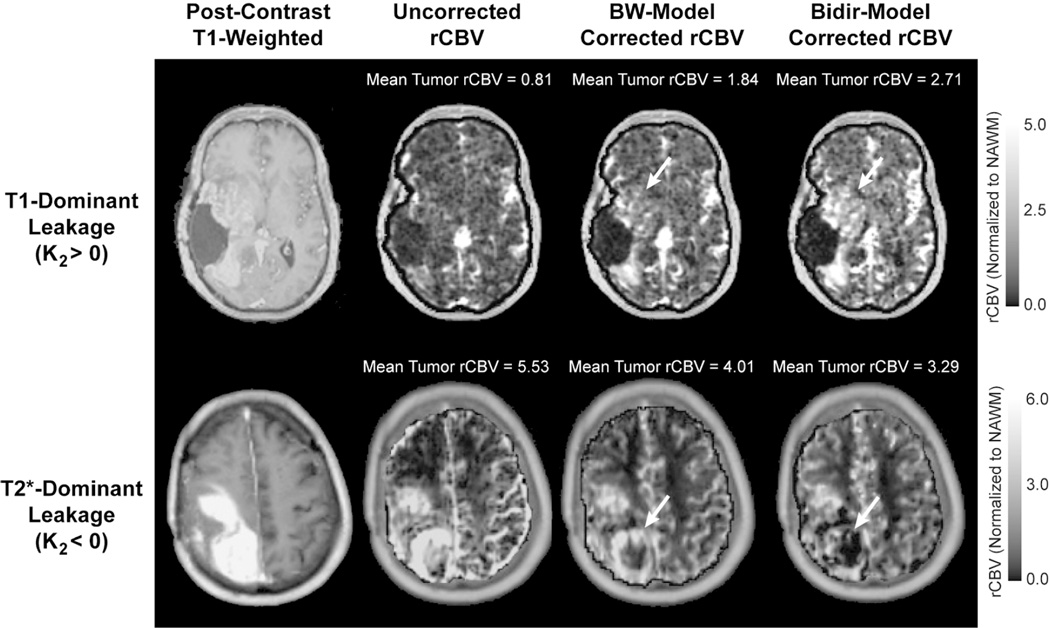
Figure 4 compares rCBV maps processed without leakage correction, and with the BW-model or Bidir-model, in two different GBM patients, one with T1-dominant leakage (K2>0) on average in contrast enhancing tumor voxels and the other with T2*-dominant leakage (K2<0). For all patients, average uncorrected rCBV was 1.98±1.24, average BW-model corrected rCBV was 1.59 ± 0.89, and average Bidir-model corrected rCBV was 1.35±0.80. The average difference between BW-model corrected and Bidir-model corrected rCBV was 16.6±14.0%. A closer inspection of the T2*-dominant versus T1-dominant voxels (as defined by a negative or positive K2, respectively) revealed that the difference between the two correction methods in T2*-dominant voxels was 37.7±42.6%, while the same metric for T1-dominant voxels was 5.8±3.4%.
Figure 4.
Comparison of uncorrected, BW-model corrected, and Bidir-model corrected rCBV in a GBM with T1-dominant leakage on average in contrast enhancing voxels (first row) and a GBM with T2*-dominant leakage (second row). For T1-dominant leakage, mean tumor rCBV is underestimated using the BW-model compared with the Bidir-model, with the converse true for T2*-dominant leakage. Arrows depict regions of the tumor with large changes in estimated rCBV between leakage correction models.
DISCUSSION
By incorporating the Tofts model into the single-echo DSC-MRI relaxation rate equation, we developed an improved post-processing leakage correction method accounting for bidirectional contrast agent transport between the intravascular and interstitial spaces that commonly occurs in angiogenic high-grade gliomas. Our results demonstrate the importance of considering the interstitial washout term, even when modeling the relaxation rate changes during short image acquisitions. For instance, in the simulation, we observed differences between the Bidir-model and BW-model model fits to relaxation rate data in high-grade gliomas in the first-pass curve (as early as 10–20 seconds after injection). Furthermore, by including a washout term, the Bidir-model alleviates the error in relaxation rate estimates for arteries and normal brain introduced by conventional models constrained to increasing contrast agent concentration over time in all tissues.
Our results suggest that the conventional BW-model undercorrects rCBV, with insufficiently increased and decreased rCBV compared to uncorrected rCBV in T1-dominant and T2*-dominant leakage scenarios, respectively. Furthermore, since the low flip angle DSC-MRI protocol was largely T2*-dominant, and the largest discrepancies between Bidir-model and BW-model estimates of rCBV existed for T2* dominant voxels, our results suggest that the Bidir-model may be particularly advantageous over the BW-model for correcting the residual T2* effects frequently encountered in dual-echo gradient-echo acquisitions. It is also important to note that this algorithm can be performed without a substantial increase in post-processing computation time over the unidirectional model; therefore, the bidirectional model can simply replace the previous model in routine clinical work as well as for evaluating tumor grade, distinguishing pseudoprogression from true progression, and evaluating treatment response.
Several post-processing leakage correction techniques have previously been proposed.22,23 The method by Weisskoff and Boxerman2,18,19 (BW-model), which linearly fits measured to two constant functions derived from average relaxation rate in non-enhancing tissue, can be applied quickly to conventional single-echo (spin echo or gradient echo) acquisitions and contrast agent injection schemes. Improved correlation of rCBV with glioma grade compared to uncorrected rCBV19 provides anecdotal evidence of the benefit of the BW-model, which has also been shown to improve correlation of gadolinium-based rCBV measures to those obtained using intravascular MION agent as a gold standard.24
Bjornerud et al.25 proposed a method that reduces the sensitivity of rCBV correction to mean transit time that could be combined with the Bidir-model scheme. Interestingly, Schmiedeskamp et al.23 employed a multi-echo gradient echo and spin echo acquisition scheme to correct for T1 and T2* leakage using a backflow term; however, results were highly dependent on literature values for and , the T2* relaxation effects of gadolinium in the extravascular space and plasma, respectively, which can vary quite substantially depending on the literature source. Additionally, Quarles et al.17 suggested these values could vary from tumor to tumor, depending on physiologic factors such as interstitial, vascular, and cell volume fractions and vessel and cell size. An advantage of the Bidir-model correction method is the lack of assumptions for and . It is also important to note that all of these leakage correction algorithms aim to isolate the relaxation rate due to the residual intravascular contrast agent by eliminating the T1- and T2*-related contributions to relaxation rate from the extravasated contrast agent. They do not “add back” T2* relaxation that would have been realized had the extravasated contrast agent not left the plasma space, and so “corrected rCBV” may still differ from that computed for a tumor with no vascular permeability, all other parameters (including true blood volume) being equal.
One potential limitation to this study is its retrospective design, which may have yielded a selection bias in the sample. Specifically, all patients were chosen because they failed standard therapy. Another potential limitation is the lack of correlation with a gold standard, such as histology or with CBV estimates using intravascular agents such as iron oxide contrast agents. Moreover, AIC is a unitless quantity that can compare relative goodness of fit between models, but does not have a direct test to determine if one model is significantly better than the other. Finally, the current study only included patients with glioblastoma, therefore we were unable to recommend a threshold between low-grade and high-grade gliomas using the new leakage correction algorithm.
In summary, the Bidir-model more accurately corrects for the T1 or T2* enhancement arising from contrast agent extravasation due to blood-brain barrier disruption in high-grade gliomas by incorporating interstitial washout rates into the DSC-MRI relaxation rate model. To this end, the Bidir-model may potentially improve patient diagnosis and evaluation of treatment response by more accurately estimating rCBV in DSC-MRI.
Acknowledgments
Research Support: American Cancer Society (ACS) Research Scholar Grant RSG-15-003-01-CCE (BME); NIH/NCI R21CA167354 (BME); UCLA Jonsson Comprehensive Cancer Center Seed Grant (BME); National Brain Tumor Society Research Grant (BME); Siemens Healthcare Research Grant (BME); Art of the Brain (TFC); Ziering Family Foundation in memory of Sigi Ziering (TFC); Singleton Family Foundation (TFC); Clarance Klein Fund for Neuro-Oncology (TFC); National Institute of Health National Institute of General Medical Sciences training grant, GM08042 (KL) and the University of California Los Angeles Medical Scientist Training Program (KL)
Abbreviations
- DCE-MRI
dynamic contrast enhanced MRI
- DSC-MRI
dynamic susceptibility contrast MRI
- rCBV
relative cerebral blood volume
APPENDIX
Following Eq. A6 of Boxerman et al.,19 the leakage-contaminated DSC-MRI relaxation rate-time curve, , equals intravascular contrast-driven transverse relaxation rate change, , plus , a tissue leakage term describing the simultaneous T1 and T2* relaxation effects resulting from gadolinium extravasation:
| 1) |
where E1 = e−TR/T1o, T1o is the pre-contrast tissue T1, r1 is the T1 relaxivity of gadolinium, CE(t) is the concentration of gadolinium in the extravascular, extracellular space, and represents the T2* relaxation effects of gadolinium extravasation, as described by Quarles17 and Schmiedeskamp.23 From the original Tofts model describing bidirectional contrast agent flux between the intravascular and extravascular compartments,14
| 2) |
where ktrans and kep are the transfer coefficients for intra- to extravascular and extra- to intravascular contrast flux, respectively, and Cp(t) is the plasma contrast concentration. Cp(t) and ΔR2*(t) can be defined as scaled versions of the whole-brain average relaxation rate in non-enhancing voxels, :19
| 3) |
| 4) |
| 5) |
where
| 6) |
K1, K2, and kep (units of sec−1) are the free parameters of Eq. 5. In general, K1 depends on CBV, vessel size, and other physiologic factors, while K2 is related to vascular permeability. Substituting kep=0, which occurs with no backflow of extravasated contrast agent, yields the original Weisskoff-Boxerman leakage correction algorithm, where K1 and K2 are solved by linear least squares fit to .19 For the Bidir-model correction method, a linear least squares fit to K1, K2, and kep can be employed using the methodology of Murase,26 as described by the following equation:
| 7) |
Integrating the corrected relaxation rate-time curve yields leakage-corrected rCBV:
| 8) |
REFERENCES
- 1.Cha S, Knopp EA, Johnson G, et al. Intracranial mass lesions: dynamic contrast-enhanced susceptibility-weighted echo-planar perfusion MR imaging. Radiology. 2002;223:11–29. doi: 10.1148/radiol.2231010594. [DOI] [PubMed] [Google Scholar]
- 2.Aronen HJ, Gazit IE, Louis DN, et al. Cerebral blood volume maps of gliomas: comparison with tumor grade and histologic findings. Radiology. 1994;191:41–51. doi: 10.1148/radiology.191.1.8134596. [DOI] [PubMed] [Google Scholar]
- 3.Law M, Yang S, Wang H, et al. Glioma grading: sensitivity, specificity, and predictive values of perfusion MR imaging and proton MR spectroscopic imaging compared with conventional MR imaging. AJNR Am J Neuroradiol. 2003;24:1989–1998. [PMC free article] [PubMed] [Google Scholar]
- 4.Law M, Oh S, Babb JS, et al. Low-grade gliomas: dynamic susceptibility-weighted contrast-enhanced perfusion MR imaging--prediction of patient clinical response. Radiology. 2006;238:658–667. doi: 10.1148/radiol.2382042180. [DOI] [PubMed] [Google Scholar]
- 5.Danchaivijitr N, Waldman AD, Tozer DJ, et al. Low-grade gliomas: do changes in rCBV measurements at longitudinal perfusion-weighted MR imaging predict malignant transformation? Radiology. 2008;247:170–178. doi: 10.1148/radiol.2471062089. [DOI] [PubMed] [Google Scholar]
- 6.Boxerman JL, Ellingson BM, Jeyapalan S, et al. Longitudinal DSC-MRI for Distinguishing Tumor Recurrence From Pseudoprogression in Patients With a High-grade Glioma. Am J Clin Oncol. 2014 doi: 10.1097/COC.0000000000000156. [DOI] [PubMed] [Google Scholar]
- 7.Gahramanov S, Varallyay C, Tyson RM, et al. Diagnosis of pseudoprogression using MRI perfusion in patients with glioblastoma multiforme may predict improved survival. CNS Oncol. 2014;3:389–400. doi: 10.2217/cns.14.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schmainda KM, Zhang Z, Prah M, et al. Dynamic susceptibility contrast MRI measures of relative cerebral blood volume as a prognostic marker for overall survival in recurrent glioblastoma: results from the ACRIN 6677/RTOG 0625 multicenter trial. Neuro Oncol. 2015 doi: 10.1093/neuonc/nou364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leu K, Enzmann DR, Woodworth DC, et al. Hypervascular tumor volume estimated by comparison to a large-scale cerebral blood volume radiographic atlas predicts survival in recurrent glioblastoma treated with bevacizumab. Cancer Imaging. 2014;14:31. doi: 10.1186/s40644-014-0031-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.LaViolette PS, Cohen AD, Prah MA, et al. Vascular change measured with independent component analysis of dynamic susceptibility contrast MRI predicts bevacizumab response in high-grade glioma. Neuro Oncol. 2013;15:442–450. doi: 10.1093/neuonc/nos323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Villringer A, Rosen BR, Belliveau JW, et al. Dynamic imaging with lanthanide chelates in normal brain: contrast due to magnetic susceptibility effects. Magn Reson Med. 1988;6:164–174. doi: 10.1002/mrm.1910060205. [DOI] [PubMed] [Google Scholar]
- 12.Meier P, Zierler KL. On the theory of the indicator-dilution method for measurement of blood flow and volume. J Appl Physiol. 1954;6:731–744. doi: 10.1152/jappl.1954.6.12.731. [DOI] [PubMed] [Google Scholar]
- 13.Paulson ES, Schmainda KM. Comparison of dynamic susceptibility-weighted contrast-enhanced MR methods: recommendations for measuring relative cerebral blood volume in brain tumors. Radiology. 2008;249:601–613. doi: 10.1148/radiol.2492071659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tofts PS, Kermode AG. Measurement of the blood-brain barrier permeability and leakage space using dynamic MR imaging. 1. Fundamental concepts. Magn Reson Med. 1991;17:357–367. doi: 10.1002/mrm.1910170208. [DOI] [PubMed] [Google Scholar]
- 15.Roberts HC, Roberts TPL, Brasch RC, et al. Quantitative measurement of microvascular permeability in human brain tumors achieved using dynamic contrast-enhanced MR imaging: Correlation with histologic grade. AJNR Am J Neuroradiol. 2000;21:891–899. [PMC free article] [PubMed] [Google Scholar]
- 16.Ludemann L, Wurm R, Zimmer C. Pharmacokinetic modeling of Gd-DTPA extravasation in brain tumors. Invest Radiol. 2002;37:562–570. doi: 10.1097/00004424-200210000-00005. [DOI] [PubMed] [Google Scholar]
- 17.Quarles CC, Gochberg DF, Gore JC, et al. A theoretical framework to model DSC-MRI data acquired in the presence of contrast agent extravasation. Phys Med Biol. 2009;54:5749–5766. doi: 10.1088/0031-9155/54/19/006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Donahue KM, Krouwer HG, Rand SD, et al. Utility of simultaneously acquired gradient-echo and spin-echo cerebral blood volume and morphology maps in brain tumor patients. Magn Reson Med. 2000;43:845–853. doi: 10.1002/1522-2594(200006)43:6<845::aid-mrm10>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- 19.Boxerman JL, Schmainda KM, Weisskoff RM. Relative cerebral blood volume maps corrected for contrast agent extravasation significantly correlate with glioma tumor grade, whereas uncorrected maps do not. AJNR Am J Neuroradiol. 2006;27:859–867. [PMC free article] [PubMed] [Google Scholar]
- 20.Ellingson BM, Cloughesy TF, Lai A, et al. Quantitative volumetric analysis of conventional MRI response in recurrent glioblastoma treated with bevacizumab. Neuro Oncol. 2011;13:401–409. doi: 10.1093/neuonc/noq206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Burnham KPaDRA. Model Selection and Inference. NY: Springer-Verlag; 1998. [Google Scholar]
- 22.Quarles CC, Ward BD, Schmainda KM. Improving the reliability of obtaining tumor hemodynamic parameters in the presence of contrast agent extravasation. Magn Reson Med. 2005;53:1307–1316. doi: 10.1002/mrm.20497. [DOI] [PubMed] [Google Scholar]
- 23.Schmiedeskamp H, Andre JB, Straka M, et al. Simultaneous perfusion and permeability measurements using combined spin- and gradient-echo MRI. J Cereb Blood Flow Metab. 2013;33:732–743. doi: 10.1038/jcbfm.2013.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Boxerman JL, Prah DE, Paulson ES, et al. The Role of preload and leakage correction in gadolinium-based cerebral blood volume estimation determined by comparison with MION as a criterion standard. AJNR American journal of neuroradiology. 2012;33:1081–1087. doi: 10.3174/ajnr.A2934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bjornerud A, Sorensen AG, Mouridsen K, et al. T1- and T2*-dominant extravasation correction in DSC-MRI: part I--theoretical considerations and implications for assessment of tumor hemodynamic properties. J Cereb Blood Flow Metab. 2011;31:2041–2053. doi: 10.1038/jcbfm.2011.52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Murase K. Efficient method for calculating kinetic parameters using T-1-weighted dynamic contrast-enhanced magnetic resonance imaging. Magnet Reson Med. 2004;51:858–862. doi: 10.1002/mrm.20022. [DOI] [PubMed] [Google Scholar]