Molecular Mechanisms and Design Principles for Promiscuous Inhibitors to Avoid Drug Resistance: Lessons Learned from HIV-1 Protease Inhibition

Abstract

Molecular recognition is central to biology and ranges from highly selective to broadly promiscuous. The ability to modulate specificity is particularly important for drug development, and discovery of mechanisms contributing to binding specificity is crucial for our basic understanding of biology and for applications in health care. In this study we used computational molecular design to create a large data set of diverse small molecules with a range of binding specificities. We then performed structural, energetic, and statistical analysis to the data set in order to study molecular mechanisms of achieving specificity goals. The work was done in the context of HIV-1 protease inhibition and the molecular designs targeted a panel of wild-type and drug-resistant mutant HIV-1 protease structures. The analysis focused on mechanisms for promiscuous binding to bind robustly even to resistance mutants. Broadly binding inhibitors tended to be smaller in size, more flexible in chemical structure, and more hydrophobic in nature compared to highly selective ones. Furthermore, structural and energetic analyses illustrated mechanisms by which flexible inhibitors achieved binding; we found ligand conformational adaptation near mutation sites and structural plasticity in targets through torsional flips of asymmetric functional groups to form alternative, compensatory packing interactions or hydrogen bonds. As no inhibitor bound to all variants, we designed small cocktails of inhibitors to do so and discovered that they often jointly covered the target set through mechanistic complementarity. Furthermore, utilizing structural plasticity observed in experiments and simulations could be a viable means of designing adaptive inhibitors bind promiscuously.

INTRODUCTION

Molecular recognition plays a central role in biological systems. In a cellular environment of various molecular contents, a molecule may bind to some molecular identities (cognate partners or intended targets) with a non-trivial affinity level but not to others (non-partners or off-targets). This phenomenon is termed specificity. Different binding processes exhibit a range of specificity from narrow (or selective) to broad (or promiscuous) for which the range (also termed “coverage” later) in this study is measured by the number of cognate partners or intended targets that a molecule can bind and does not involve undesired off-target binding. Binding specificity has direct implications for biological function¹. It remains a fundamental challenge to understand molecular mechanisms leading to different specificities of binding and to modulate binding specificity robustly through design^2–5. To intervene effectively in complex disease pathways –– particularly for cancer and infectious disease, in which molecular evolution can play a crucial role –– it is becoming increasingly important to develop therapeutic compounds with carefully tailored specificity profiles. The emerging paradigm of polypharmacology focuses on multiple objectives across targets and decoys (also called off-targets) and on balancing binding selectivity and promiscuity, jointly improving potency, reducing resistance, and minimizing side effects^6–8.

Some examples, drawn from a recent review⁵, are discussed here. Theoretical and experimental studies have identified candidate molecular mechanisms possibly contributing to observed binding specificity patterns. Drug selectivity can often be achieved by utilizing shape, polarity, charge, or flexibility differences between decoy and target molecules to provide differential shape complementarity, electrostatic complementarity, or conformational change for targets over decoys. In one example, an inhibitor binds to COX-2 over 13,000 fold tighter than it does to COX-1 apparently because it packs well with a valine at position 523 of COX-2 but has a steric clash with a bulkier isoleucine at the same position of COX-1⁹. Another example shows a highly selective compound for PTP1B designed by using the fact that other PTPs all have uncharged asparagines at position 48 instead of the negatively charged aspartic acid found in PTP1B¹⁰. In the third example, some TNF-α converting enzyme (TACE) inhibitors achieved high selectivity against other, similar matrix metalloproteinases that lack the additional flexibility of a loop allowed by smaller residues in TACE¹¹ . Other factors not covered by the examples above include the difference in the cost of re-locating interfacial water molecules and effects of allosteric conformational change⁵. On the other hand, broadly speaking, promiscuity can derive from taking advantage of and interacting with properties common among targets but not shared with decoys. These principles are gaining support due to their conceptual attractiveness and slowly accumulating experimental evidence, but a greater number of implemented cases would more firmly establish and develop them. Moreover, implementation of these principles into design protocols for molecules of desired binding specificity profiles is far from trivial. Examples include energy-minimization based conformational search and interface redesign for altered specificity^12–16, charge optimization theory for narrow or broad electrostatic specificity^{17– 19}, the substrate-envelope hypothesis for binding promiscuity of target variants (broad specificity) ^20–22, and sequence-based co-variation analysis for specificity switching²³.

In this study we aim to understand molecular mechanisms by which small molecules can exhibit binding promiscuity and to develop scoring functions to evaluate or design strategies to implement such promiscuity. The promiscuity under study refers to the desired binding to target variants (specifically arising from drug-resistant mutations here) and does not involve undesired off-target binding. We chose the inhibition of HIV-1 protease as the prototype of the study to obtain generalizable insights because robust HIV-1 protease inhibition in the face of an evolving viral population remains a tremendous challenge, yet significant structural, inhibitory, and evolutionary data exist upon which to base our investigation.

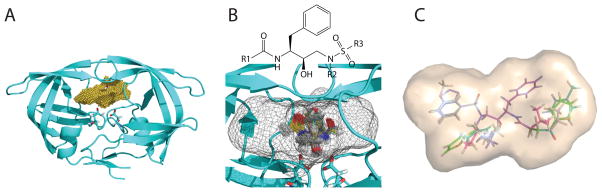
The approach taken was to construct a large-scale inhibitor library for a set of wild-type and drug-resistant mutant HIV-1 proteases using computational inhibitor design and then to analyze the library for property differences between selective binders and promiscuous ones. Specifically, for each protease variant, a set of tightest small-molecule binders sharing the same scaffold (see its 2D structure in Figure 1B) and differing in functional group combinations was first predicted with their lowest-energy conformations and binding affinities. The computational design approach was first introduced by Altman et al.²² and is illustrated in Figure 1. Each set is derived from an efficient combinatorial optimization approach that guarantees the coverage of the tightest binders statistically. All such sets for all target variants pooled together gave a library of small molecules with predicted number of binding targets and thus classified promiscuous or selective. Promiscuous small molecules were then analyzed statistically, structurally, and energetically against selective ones to lead to distinguishing physico-chemical properties and underlying molecular mechanisms. Furthermore, optimal small-molecule cocktails with the smallest number of molecules were computed by solving a set cover problem with an integer programming approach²⁴ and analyzed for mechanistic insights.

Figure 1.

Illustration of our computational approach for inhibitor design. (A) Grid generation: the binding pocket of each target structure (cyan cartoon) is partitioned into grids (in yellow) on which van der waals energies and continuum electrostatic potentials are calculated. (B) Scaffold placing: conformational choices of a scaffold are first determined by assessing discretized translational, rotational, and conformational rotamers on grids (the envelope of the grids is now in a mesh representation). (C) Functional group placing: combinations of functional-group rotamers are pruned efficiently for each scaffold conformation retained in Step B. Subsequently, the energetically most favorable ensemble of structures for each target structure is reranked with more accurate energy models hierarchically.

In the Methods section, we provide details of the computational inhibitor design approach, the statistical, structural, and energetic analysis protocols, and the optimal inhibitor cocktail construction. In the Results and Discussion section, we describe the statistical, structural, and energetic analyses of the designed inhibitor library; we also describe molecular mechanisms underlying several physicochemical properties associated with promiscuous inhibitors, as well as optimal inhibitor cocktails that jointly cover the target set of HIV-1 proteases. To our knowledge, our results present the largest-scale computational study probing the substrate-envelope hypothesis, which suggests that inhibitors with promiscuous binding to drug-resistant mutants can be designed by mimicking the natural substrates and staying inside an envelope that encloses their shared volume^{20, 21}. The substrate-envelope hypothesis has proven useful but incomplete; when a collection of inhibitors was designed, synthesized, and characterized that all obeyed the substrate-envelope hypothesis, only a relatively small fraction had promiscuous binding profiles^{22, 25}. Thus, there is a need for understanding additional factors beyond the current substrate-envelope hypothesis for enhancing binding promiscuity. The results of the work presented here show additional factors beyond satisfying the substrate-envelope hypothesis that contribute to binding promiscuity, including inhibitor flexibility, hydrophobicity, and hydrogen-bond satisfaction. In particular, flexible inhibitors, often with asymmetric functional groups, were able to compensate for lost van der Waals or hydrogen-bonding interactions due to mutations.

Taken together, this report provides analysis of several factors leading to binding promiscuity in HIV-1 protease that are likely to generalize to other systems. In addition, procedures are suggested to select inhibitor candidates that have a greater likelihood of being promiscuous binders. In cases for which one inhibitor cannot target all mutants, an optimal cocktail of a few inhibitors can be designed to do so, and we found that joint coverage could be achieved with complementary mechanisms. Moreover, when structural or sequence information for all target forms is not available, structural diversity in known structures, such as multiple wild-type conformations, was useful in designing promiscuous inhibitors to other targets whose structures were not included explicitly in the design.

METHODS

Target Selection

Clinically-relevant drug-resistance mutations were obtained from the Stanford HIV drug resistance database²⁶ and a recent report from the International AIDS Society²⁷, and cross-referenced with the Protein Data Bank²⁸. A representative set of crystal structures was selected to include a diversity of resistance profiles to FDA-approved drugs (multi- or specific-drug resistance), point and co-evolved mutations, and mutations at various sites (active-site, flap-region, and distal). Only complexes with darunavir²⁹ or a compound from the MIT-2 library²² bound were considered, which might be more representative of what an early- or mid-stage drug design project would face (MIT-2 library compounds, as well as inhibitors designed in this study, share a common scaffold that resembles that of darunavir²²). These considerations resulted in 10 mutant structures in the target set, each of which corresponded to a drug-resistance mutant sequence. Eight of the ten are multi-drug resistant (some to darunavir and others not) and the remaining two are each resistant to a specific drug (Table I). In addition, 4 structures of wild-type proteases were included in the target set, including two sequences co-crystallized with darunavir (WT1 and WT2, PDB codes 1T3R and 2IEN) and two with MIT-2 compounds MIT-2-AD-93 and MIT-2-KC-08 (WT3 and WT4, PDB codes 2QI4 and 2QI5, respectively). WT2 contains a slightly different wild-type protein sequence than WT1, WT3, and WT4, which all share the same sequence. These targets were also referred to as Target 1 through Target 14 and were indexed in the row order of Table I, with Targets 1–4 corresponding to wild type and the remainder to drug-resistant mutants.

Table I.

Target panel of HIV-1 protease structures.

Index	Protease Sequencea	Bound Ligand	Drug Resistanceb	PDB Code
	Wild types
1	Reference wild type	darunavir	None	1T3R29
2	R14K, L33I, N37S, K41R, P63I, V64I, C67A, C95A	darunavir	None	2IEN64
3	V64I	MIT-2-AD- 93	None	2QI422
4	V64I	MIT-2-KC- 08	None	2QI522
	Multi-drug resistance mutants
5	R14K, L33I, N37S, K41R, I50V, P63I, V64I, C67A, C95A	darunavir	darunavir, amprenavir, lopinavir	2F8G65
6	R14K, L33I, N37S, K41R, P63I,	darunavir	atazanavir, darunavir, amprenavir,	2IEO64
	V64I, C67A, I84V, C95A		indinavir, lopinavir, nelfinavir, saquinavir, tipranavir
7	K41R, V64I, V82T, I84V (ACT)	darunavir	atazanavir, darunavir, amprenavir, indinavir, lopinavir, nelfinavir, saquinavir, tipranavir66	1T7I29
8	R14K, L33I, N37S, K41R, G48V, P63I, V64I, C67A, C95A	darunavir	atazanavir, lopinavir, nelfinavir, saquinavir	3CYW67
9	R14K, L33I, N37S, K41R, I54V, P63I, V64I, C67A, C95A	darunavir	atazanavir, amprenavir, indinavir, lopinavir, nelfinavir, saquinavir, tipranavir	3D2067
10	R14K, L33I, N37S, K41R, P63I, V64I, C67A, V82A, C95A	darunavir	atazanavir, amprenavir, indinavir, lopinavir, nelfinavir, saquinavir	2IDW64
11	R14K, L33I, N37S, K41R, P63I, V64I, C67A, L90M, C95A	darunavir	atazanavir, amprenavir, indinavir, lopinavir, nelfinavir, saquinavir	2F8165
12	L10I, G48V, I54V, V64I, V82A (M1)	darunavir	atazanavir, indinavir, lopinavir, nelfinavir, saquinavir, tipranavir25	3EKT66
	Signature drug-resistance mutants
13	R14K, D30N, L33I, N37S, K41R, P63I, V64I, C67A, C95A	darunavir	nelfinavir	2F8065
14	I50L, A71V (M4)	darunavir	atazanavir	3EM668

^aMutant sequences are defined as relative to the wild-type sequence for PDB entry1T3R. Marked in bold fonts are major resistance mutations defined in an HIV drug resistance database from Stanford (http://hivdb.stanford.edu/DR/PIResiNote.html).

^bDrug resistance profiles, unless provided with references elsewhere, are taken from the Stanford database .

Structure Preparation

All protein structures were downloaded from the Protein Data Bank (PDB accession codes listed in Table I). The coordinates for the proteases were extracted. One of the two catalytic residues was protonated; specifically, Asp25(A) was protonated at OD1 to form a hydrogen bond with deprotonated Asp25(B). All histidine residues were singly protonated at the ε-position. Torsional angles of asparagine (χ₂), glutamine (χ₃), and histidine (χ₂) residues were incremented by 180^° when doing so would improve local hydrogen-bonding. Crystallographic water molecules were retained if their B-factor values were less than 30 and they formed three hydrogen-bond contacts with the protease, as judged by a distance cutoff of 3.3 Å. The flap water in the active site was also retained for each protease structure. Missing heavy-atom positions were added with standard geometry as defined in the CHARMm22³⁰ parameter set with the molecular simulation software CHARMM^{31, 32}, and all hydrogen atoms were placed using the HBUILD module³³ of CHARMM.

Computational Inhibitor Design

To enumerate inhibitors whose calculated binding free energy values are within 10 kcal/mol of the tightest binder (the global optimum) for each chosen target structure of HIV-1 protease, a computational inhibitor design approach²² developed earlier by our research group, was adapted. In this approach, designed inhibitors consisted of a scaffold and three attached functional groups. The chemical identities of the scaffold and the three variable groups were limited to the MIT-2 library²², including an (R)-(hydroxyethylamino)sulfon-amide scaffold derived from darunavir and amprenavir as well as three position-specific sets of functional groups derived from the ZINC database³⁴ and commercial catalogues. The conformations of the scaffold and the functional groups, including internal torsions and external translations and rotations, were discretized onto uniform grids. The resulting discrete chemical and conformational space was searched using a hierarchy of energy functions of increasing accuracy together with the dead-end elimination and A* search techniques, as described by Altman et al.²².

Scaffold Library

For each target, conformations of the (R)-(hydroxyethylamino)sulfon-amide scaffold were enumerated as described below. To evaluate energetics during enumeration, the scaffold was assigned CHARMm22 atom-types with an in-house automated program and parameterized with the CHARMm22 molecular mechanics parameters³⁰. For continuum electrostatics, their atomic radii were parameterized with PARSE parameters³⁵ and partial atomic charges were derived from quantum-mechanical calculations using Gaussian 03³⁶. The starting structure of the scaffold was constructed by removing three functional groups (R1 through R3) from a co-crystallized inhibitor (darunavir, MIT-2-AD-93, or MIT-2-KC-08) and replacing them with hydrogen atoms that acted as attachment points in later designs. This scaffold structure was geometry optimized at the restricted Hartree-Fock (RHF) 6-31G* level, and partial atomic charges were calculated for the optimized geometry by restrained electrostatic potential (RESP)^{37, 38} fitting to RHF/6-31G* potentials. A conformational ensemble of scaffold poses for each protein was generated by enumerating the discretized conformational space as detailed below (“Combinatorial Search with DEE/A*”).

Functional Group Library

A version of the MIT-2 functional group library of Altman et al²² was used here. It included 1105 carboxylic acids for R1, 161 aliphatic amines for R2, and 126 sulfonyl chlorides for R3, all taken from the ZINC database and Sigma-Aldrich catalog. LIGPREP³⁹ was used with default settings to construct functional group library members, and their 3D structures were geometry optimized using quantum-mechanical calculations at the RHF/6-31G* level; conformational ensembles were generated by enumerating torsional angles around each rotatable bond at 30° increments (except sp²–sp², which was sampled at 45° increments). Self-interacting and identical conformations were removed from the ensemble. CHARMm22 molecular mechanics parameters were assigned, and PARSE atomic radii were used for continuum electrostatics calculations with partial atomic charges calculated from RESP fitting to quantum-mechanical potentials as was done previously by Altman et al.²²

Combinatorial Search with DEE/A*

An inverse image of the binding site, known as the “maximal envelope”, was generated and used to define the maximum outer extent for any designed inhibitor. The volume inside the envelope was partitioned with a cubic lattice for calculations of energies and potentials in the presence of a protein structure. The binding energy model includes van der Waals, solvent-screened electrostatics, and desolvation penalties. Our previous study indicates that this energy model predicted binding affinities with good correlation (R² = 0.8) to experimentally measured binding affinities for a set of over 50 designed HIV-1 protease inhibitors and two drugs (amprenavir and darunavir).²² The inclusion of internal energies (molecular mechanics terms related to bonds, angles, torsions, and other internal deformations) was not found to improve the correlation and was not considered here. A cubic lattice of 0.2 Å-grid spacing was used to calculate on-grid van der Waals energy values for all CHARMm22 atom types using the CHARMm22 force field. A cubic lattice of 0.75 Å-grid spacing was used to calculate on-grid electrostatic interaction and desolvation potentials. The electrostatic potentials were calculated by placing a unit charge at each grid point in turn while leaving the other grid points neutral and protein atoms at parameterized values, and then solving the linearized Poisson–Boltzmann (LPB) equation with a locally modified version of the DelPhi program⁴⁰. The LPB calculations involved a 129×129×129 grid-resolution, successive focusing values of 23%, 92%, and 184% fill, a dielectric constant of 4 for the molecular interior and 80 for the solvent, and an ionic strength of 0.145 M with a 2.0-Å Stern layer surrounding all molecules. The major approximation for calculating electrostatic potentials was that the molecular shape of any designed inhibitor would be well approximated by the maximal envelope, and this approximation was corrected in further steps of the hierarchy of energy functions.

The scaffold conformational ensemble was generated by enumerating discretized conformational space with geometric and energetic filters. The starting coordinates of the scaffold taken from each co-crystallized inhibitor were treated as the origin of the conformational space that was later partitioned into grids. Specifically, external degrees of freedom were enumerated every 0.25 Å in each Cartesian direction and every 0.5 Å in arc length for rotations of the vector connecting the scaffold geometric center and the atom furthest from the center. For the internal degrees of freedom, bond lengths and angles were fixed and torsional angles around rotatable bonds were enumerated every 30° (except sp²–sp² hybridization, for which every 45° was used). A conformation was removed from the ensemble library if it resulted in one or more atom centers being placed outside the maximal envelope; likewise, ligand self-collisions, unfavorable interactions with the protein based on the van der Waals energy values, or unsatisfied hydrogen-bonding groups (including those with the flap water molecule and catalytic residues in the protein) based on van der Waals radii-based distance criteria resulted in exclusion from the library. Thus, designed inhibitors were required to maintain conserved interactions between scaffold and protease observed in co-crystal structures. Additionally, an RMSD cutoff of 0.5 Å of the scaffold from the observed co-crystal conformation was also imposed to limit the search to scaffold conformations and placements close to those previously observed.

Top solutions for placing functional groups in the context of each scaffold conformation and pose were obtained by first pruning the vast space of chemical and conformational choices with dead-end elimination (DEE) and then enumerating all solutions within 30 kcal/mol from the global minimum of calculated binding affinity with A*⁴¹. Discrete functional group ensembles (from the functional group library plus extra adjacent rotamers differing by 10° in one or more torsional angles) were placed at corresponding attachment atoms for any given scaffold conformation and hierarchically screened. First, a functional group conformation was excluded from further consideration if any atom center extended beyond the maximal envelope, collided with the scaffold (with an unfavorable van der Waals interaction when the van der Waals radii were scaled to 75% of the CHARMm22-parameterized values), or had an unsatisfied hydrogen-bonding group. Next, all non-intersecting pairs of functional groups were placed on the scaffold and their desolvation contributions were considered. In this way, combinations of self- and pairwise energies added up to the total binding free energy. Such additivity in the binding free energy model allowed for the efficient, guaranteed search scheme of DEE/A* that produced the global minimum of the combinatorial optimization problem as well as an ordered, gapless list of near-optimal solutions. Namely, for each scaffold conformation, all solutions within 25 kcal/mol of the global minimum were retained. Such solutions for all scaffold conformations were retained if within 30 kcal/mol of the best solution.

Hierarchical Rescoring and Statistical Correlation

The ordered list obtained with DEE/A* contained up to a million solutions. Because they were generated with approximations in the binding free energy model, they were re-evaluated hierarchically with two, increasingly accurate models. First, in the medium-resolution binding free energy model (as opposed to the low-resolution model described above), the actual molecular shapes of designed inhibitors were used in approximate continuum calculations, rather than using the maximal inhibitor envelope as the inhibitor shape. For each designed inhibitor, a correction to the previously computed low-resolution continuum electrostatic contribution to binding was calculated by integrating the dielectric constant-scaled low-resolution energy densities over the volume that was inside the maximal envelope but not occupied by the inhibitor. Moreover, van der Waals interactions between the protein and the inhibitor were calculated at an all-atom level instead of the grid-based one. After the medium-resolution rescoring, the top 15 kcal/mol portion of the re-ordered list was re-evaluated again with a high-resolution model, in which electrostatics were calculated by solving the linearized Poisson–Boltzmann equation with point charges placed at atom centers and using the true dielectric boundaries, a 129×129×129 grid, and a successive focusing scheme of 23%, 92%, and 184% fill. The hierarchical scoring scheme was adopted to balance solution accuracy and computational cost. As each lower-resolution binding free energy model strongly correlated to its next-level counterpart, a strong statistical guarantee of the top solutions in the highest-resolution model was achieved. In the systems studied, it was noted that the top 25 kcal/mol of solutions obtained in the low-resolution search statistically guaranteed the coverage of the top 15 kcal/mol of solutions in the medium-resolution model, and the latter statistically guaranteed the coverage of the top 10 kcal/mol solutions in the high-resolution model. More rigorous performance analysis of the hierarchical method in a statistical framework can be found in work by Green⁴².

Inhibitor Library Characterization

Compounds resulting from the hierarchical search and energy evaluation procedure were ordered by their high-resolution energy, and the highest affinity conformation was retained for each compound if its binding affinity was computed to be within 10 kcal/mol of the global optimum for that target. Across all 14 targets there was a total of 17,906 unique inhibitors in 28,795 bound conformations. The coverage of an inhibitor was defined as the number of targets for which it was calculated to bind within this 10 kcal/mol set. There were a large number of inhibitors with coverage 1, and the largest observed coverage was 12 of a possible 14.

Each inhibitor was characterized by properties including size (number of non-hydrogen atoms), flexibility (number of rotatable torsions, normalized by size), number of hydrogen-bonding groups, hydrophobicity (high-resolution continuum electrostatic desolvation penalty, averaged over covered targets), and adherence to the substrate-envelope hypothesis. A torsion was regarded as non-rotatable if it was terminal (hence, methyl rotations were excluded), a double or triple bond, or was contained in a ring structure. Amide bonds and their comparatives (thiocarbonyl or nitrocarbonyl amides) were considered non-rotatable as well.

Each of these measures gave one value for each of the 17,906 inhibitors, whereas the measure for the satisfiability of the substrate-envelope hypothesis was evaluated for each of the 28,795 conformations. First, a substrate envelope was constructed as in Altman et al²². Five protease–substrate complex structures were simultaneously aligned on all Cα atoms using the program PROFIT⁴³. A set of spheres with 1.5 Å-radii on a cubic lattice of 0.5 Å-grid spacing was then generated to include the superimposed substrates, and grid points were retained only if they were within 1 Å of non-hydrogen atom centers from at least three substrates or within 3.5 Å of any side-chain atom center of the inactivated catalytic residues Asn25. Second, the substrate envelope was fit into the darunavir-bound HIV-1 protease structure (PDB code 1T3R, our Target 1) by maintaining the relative orientation of the substrate envelope to the five substrate-bound protease structures and aligning one of them (as in PDB code 1KJG²⁰) to the target structure on Cα atoms. Third, similar to the last step, all inhibitor conformations were fit into the substrate envelope by maintaining their relative orientations to corresponding target proteases and aligning these targets to Target 1 on Cα atoms. Finally, for each inhibitor conformation the total number of non-hydrogen atoms whose center was outside the substrate envelope was used as a measure of the extent of substrate-envelope hypothesis violation. The distributions of all the physicochemical measures described above were plotted for inhibitors across coverage bins 1 through 12 using the program MATLAB⁴⁴.

Structural and Energetic Analyses

All inhibitor conformations were superimposed along with the pairwise alignment of corresponding targets to Target 1 (WT1, PDB code 1T3R²⁹). Structures of target proteins and inhibitors were visualized with the program PyMol⁴⁵. Van der Waals interaction energies and their decompositions were calculated with CHARMm22 parameters using the molecular modeling program CHARMM³² (version 36a1). Statistical analyses were performed using computer program MATLAB⁴⁴ (version 2008a).

Optimum Inhibitor Cocktail Design

A binary 14×17,906 coverage-matrix was first constructed so that elements were all zeros except (i ,j) if Target i was covered by Inhibitor j. The 28,795 target–inhibitor pairs produced 28,795 ones in the matrix. To find the smallest inhibitor cocktail to cover all 14 targets, a set cover problem was formulated as Formulation IP 1.1 in Radhakrishnan et al²⁴ with the coverage matrix (denoted by A in IP 1.1). The corresponding integer programming problem was solved by the optimization solver CPLEX 9.0⁴⁶ provided through the GAMS⁴⁷ platform. After the size of the optimal inhibitor cocktail was known, the optimal configuration was chosen to optimize the average binding affinity for the optimal ensemble. This was again formulated as an integer programming problem as Formulation IP 1.3 in Radhakrishnan et al²⁴ and solved by CPLEX. To this end, a 14×17,906 binding-free-energy matrix (denoted by E in IP 1.3) was constructed, where element (i, j) was the calculated binding affinity for the pair of Target i and Inhibitor j.

RESULTS AND DISCUSSION

Designed Library of Small-Molecule Inhibitors

A panel of 14 HIV-1 protease complex structures with a variety of sequences and drug-resistance profiles was chosen to represent a range of binding sites. Computational ligand design was used to evaluate a very large set of small-molecule inhibitors against each of the 14 targets in the panel.

Panel of wild-type and mutant HIV-1 protease structures to serve as targets

A panel of four wild-type and ten drug-resistant mutant HIV-1 protease structures, each in complex with an inhibitor, was constructed from the Protein Data Bank²⁸ (see Table I). The four wild-type structures included two slightly different protein sequences (Q7K and L63P versus Q7K, L33I, L63I, C67A, and C95A) and protein structures extracted from complexes with three different inhibitors (darunavir²⁹ and two MIT-2 compounds developed previously by us²²). Eight of the mutant structures were of clinically derived multi-drug resistant enzymes in complex with darunavir; the two remaining mutants were also in complex with darunavir but were enzymes resistant to a single drug and containing its signature resistance pattern^{26, 27}. Further information regarding the panel is given in Table I. It should be noted that the three different inhibitors present across the set of structures share a very similar core. This choice was made purposely to increase the number of compounds that could bind to multiple structures in the panel and reflects the adaptation different sequences can make to bind a similar ligand.

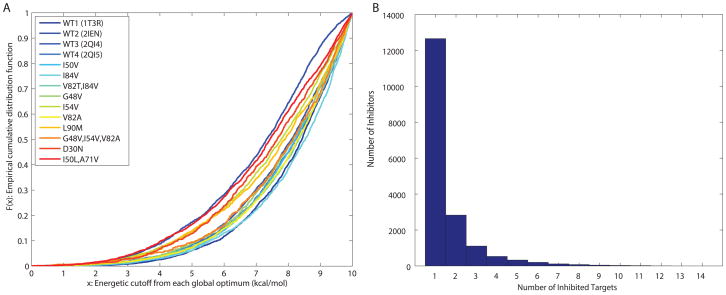
For each target, all inhibitors with computed binding affinity within 10 kcal/mol of the global optimum were enumerated. We refer to their relative binding energy, which we define as their binding energy relative to that of the global optimum for that target. In total, 17,906 unique inhibitors (a total of 28,795 conformations) were collected across all 14 targets. The number of inhibitors with computed binding affinity in range for each target grew in an exponential-like fashion with increasing relative energy from the global optimum (Figure 2A). Interestingly, each of the structures and mutants appears to have a similar distribution profile. The energetic cutoff of 10 kcal/mol was chosen to account for the use of a rigid protein. Low-energy protein deformations are capable of relieving binding strain on this order of magnitude. Moreover, the statistical trends observed here were not strongly sensitive to the value of this cutoff.

Figure 2.

The designed inhibitor library represented as (A) a cumulative distribution function of the predicted binding affinity for each target (in kcal/mol), and (B) a histogram of predicted binding specificity measured by number of targets covered.

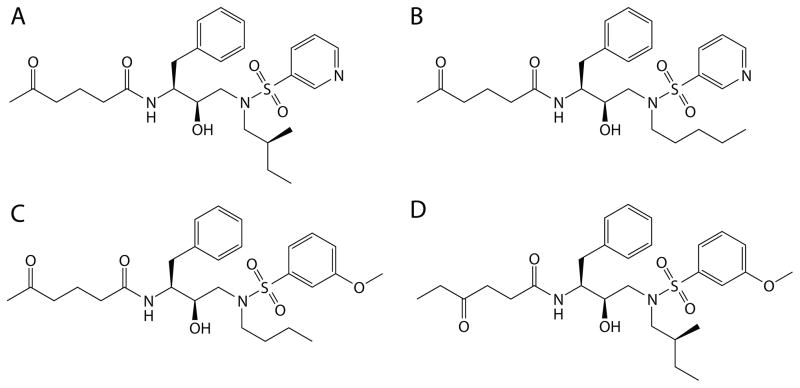
The resulting designed library of inhibitors contained a wide range of binding promiscuity profiles. As a measure of binding promiscuity, the number of targets that an inhibitor was computed to bind within the 10 kcal/mol range was termed its coverage. Thus, low coverage indicates selective binding, and high coverage indicates promiscuity. The distribution of coverages obtained falls off rapidly with increasing coverage (Figure 2B). Specifically, 12,650 inhibitors (over 70% of the library) covered only a single target, whereas only 91 inhibitors (0.5% of the library) covered at least 9 targets, which we consider the most promiscuous set. None were computed to bind 13 or all 14 targets, but four inhibitors covered 12 targets (see Figure 3). Limiting the set of relative binding energies to less than 7 kcal/mol (rather than 10 kcal/mol) resulted in 6,426 inhibitors including just 5 that covered 9 or 10 targets and none that covered more. Thus, binding promiscuity is a relatively rare property among binders to this family of active sites for this set of compounds. Because our ligand design scheme uses a rigid protein active site, we chose what otherwise might seem like a generous cutoff of 10 kcal/mol to account for relaxation that could occur. Surprising, we still find promiscuity a relatively rare property. The general trends that we report here were also found when we used a smaller cutoff, albeit with lower statistical power; we therefore report results using the 10-kcal/mol cutoff.

Figure 3.

2D structures of the four most promiscuous inhibitors designed to cover 12 of the 14 targets.

Likewise, the library contained a rich diversity of chemical properties, as will be shown below. In the following subsections we first analyze the compound collection to understand better the behavior of binding selectivity and promiscuity among the set. We describe a physicochemical characterization with a focus on size, flexibility, hydrophobicity, hydrogen bonding, and resemblance to natural substrates. Next, we analyze results further to probe molecular mechanisms that contribute to binding promiscuity and propose how the strategies found could be deployed as design strategies for promiscuous small-molecule inhibitors that are robust to drug-resistance mutations.

Physicochemical Properties of Promiscuous Small-Molecule Inhibitors

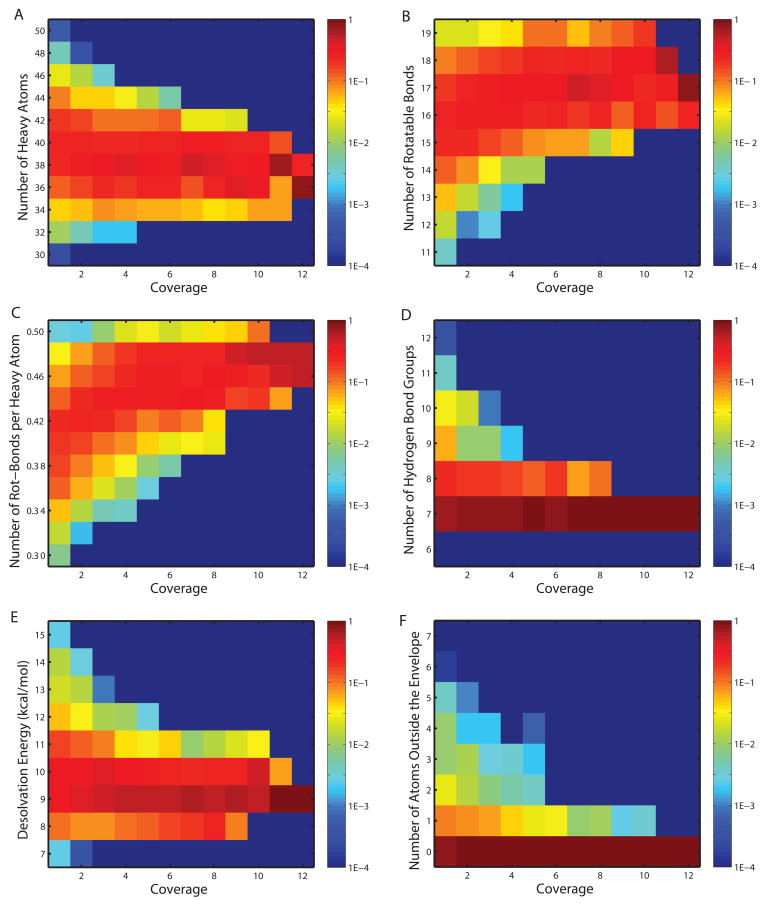
The inhibitor library was partitioned into 12 bins based on the number of targets covered (from one to twelve). In separate experiments, inhibitors were further categorized by a second dimension into equal-sized intervals corresponding to ranges of some physicochemical measure (i.e., number of heavy atoms [size], number of rotatable bonds per heavy atom [flexibility], desolvation penalty [related to relative hydrophobicity], number of hydrogen bond donors or acceptors [hydrogen-bonding capacity], number of non-hydrogen inhibitor atoms violating the substrate envelope [a shape measure giving one view of resemblance to natural substrates]). Distributions of inhibitors for these five properties are shown in Figure 4. (The Figure also includes the distribution for the number of rotatable bonds not normalized by the number of heavy atoms for completeness, but it is not emphasized because the normalized version is a better representation of flexibility independent of size.) Promiscuous inhibitors (covering at least 9 targets) had property distributions distinct from selective inhibitors (coverage no more than 4). Promiscuous inhibitors had narrower ranges for all properties considered in comparison to selective ones. Promiscuous inhibitors were consistently similar to each other in terms of size, flexibility, hydrophobicity, hydrogen-bonding capacity, and substrate similarity; by contrast, selective inhibitors showed a much greater diversity for each of these properties, as if there are multiple ways of being specific but fewer ways of being promiscuous. Note that the distributions are normalized for each coverage bin; thus, even though there are more selective inhibitors than promiscuous inhibitors, this does not affect the vertical range of the distributions in Figure 4. The same point is made by pairwise marginal distributions that also show increasingly promiscuous inhibitors occupied decreasing regions of physicochemical space (Figure S1). By tracking the most likely physicochemical patterns (shown in the warmest colors in Figure 4) for inhibitors of increasing coverage, one sees that promiscuous inhibitors tended to be smaller in size, more flexible in chemical connectivity, more hydrophobic in structure, and more respectful of the substrate envelope compared to selective ones. These conclusions (used as alternative hypotheses against the null hypothesis that the two types of inhibitors share the same distributions) were supported by single-sided Kolmogorov–Smirnov tests (with p-values of 2.5×10^–8, 1.4×10^–48, 2.3×10^–17, 2.9×10^–11, 7.2×10^–7, and 3.2×10^–11) for the observed trends in size, flexibility, number of rotatable bonds, hydrophobicity, hydrogen-bonding, and substrate envelope, respectively.

Figure 4.

Distributions of physicochemical measures for designed inhibitors across coverage bins. Colors in each block (x, y) represent the frequencies for inhibitors in coverage bin x to fall in the physicochemical range y.

We also computed the Jensen–Shannon divergence (JSD)⁴⁸, which measures the strength of the trends directly (that is, the magnitude of the difference between two distributions, rather than the statistical likelihood that they are different). The Jensen–Shannon divergence gives the square of a distance metric^{49, 50} with a value between 0 (for identical distributions) and 1, and it directly measures the dissimilarity between two probability distributions (see applications of JSD^{51, 52}). For our purposes, JSD tells how much the selective and the promiscuous inhibitors are separated in physicochemical distributions. Based on the probability distributions given in Figure 5, JSD values between the selective and the promiscuous inhibitors were calculated to be 0.15, 0.55, 0.24, 0.12, 0.15, and 0.06, respectively for the observed trends in size, flexibility, number of rotatable bonds, hydrophobicity, hydrogen-bonding capacity, and substrate envelope. Flexibility again stood out with the highest JSD value of 0.55, consistent with its smallest p-value reported earlier. The JSD values for size, hydrogen bonding groups, and hydrophobicity were all comparatively lower. The JSD value for the substrate-envelope hypothesis appears disproportionally small compared to its low p-value, although the latter could be due to its larger sample size (28,795 versus 17,906), as all bound conformations of each inhibitor were considered in determining how much the substrate envelope was violated, but only the 2D structure for each inhibitor was used to calculate the other quantities. These data provide the very encouraging result that a number of properties beyond the substrate envelope appear to contribute strongly to the computed binding promiscuity of compounds developed in this study to a panel of drug resistant HIV-1 protease structures. We are strongly motivated both to understand how these properties lead to promiscuity and to develop strategies for generalizing them to other binding sites. The goal is to then augment the substrate envelope approach with additional criteria that together lead to resistance-defying inhibitors with greater frequency.

Figure 5.

Histograms of physicochemical properties for selective and promiscuous inhibitor sets.

Molecular Mechanisms that Contribute to Binding Promiscuity

The analysis described above establishes the statistical significance of five ligand properties being related to relative binding selectivity or promiscuity to HIV-1 protease variant structures. Here we investigate each property to understand the mechanism by which it operates and affects binding promiscuity.

Flexibility

Flexibility was the strongest determinant of binding promiscuity, with more promiscuous inhibitors tending to have more rotatable bonds per heavy atom. The flexibility results could reflect the ability to make small, subtle conformational adjustments within a fixed rotamer state, or they could indicate ligand rotameric changes in response to enzyme mutations. By manually inspecting modeled complex structures of promiscuous inhibitors and individual targets, we found a pattern of conformational change contributing to binding promiscuity — asymmetric functional groups flip into a different rotameric conformation in response to mutation of an adjacent protein residue, which at least partially compensates for interactions lost upon mutation. Specifically, 87% of the promiscuous inhibitors with an asymmetric R2 group flipped from their wild-type conformation (WT1, PDB code 1T3R) when bound to the L10I, G48V, I54V, V64I, V82A (M1, PDB code 3EKT) mutant structure. The conformational change resulted in branched hydrophobic R2 functional groups rotating away from position 82 and being directed into a different subpocket of the binding site (Figure 6A,B), consistent with the notion that the valine-to-alanine (larger-to-smaller mutation) caused a loss of packing interactions that was at least partially compensated in the new subpocket. Energetic analysis of inhibitor–mutant complexes indicated that, on average, the conformational flip cost 0.2 kcal/mol in van der Waals interactions with A82 (and 0.3 kcal/mol with L23) but improved interactions with I84 and I50 in the new subpocket by 0.3 and 0.7 kcal/mol, respectively (Figure 6C). Interestingly, this compensatory strategy was not observed when the original loss in van der Waals interactions was smaller or when a second mutation made the gain in new interactions insufficient to compensate for the loss in original interactions. In the case of mutant K41R, V64I, V82T, I84V, over 90% of the promiscuous inhibitors with an asymmetric R2 group did not flip from their wild-type R2 conformation. Similar energetic analysis indicated that the binding affinity loss due to the V82T mutation would not be compensated by flipping to the new subpocket with I84V mutation. Moreover, the strategy of trading a new interaction for a lost one through a conformational flip was not limited to compensating packing interactions. For instance, 91% of the promiscuous inhibitors with an asymmetric R3 group flipped from their wild-type R3 conformation when interacting with a D30N mutant protease. In this case, the inhibitors formed new, compensating hydrogen-bonding interactions with their R3 group (Figure 6D,E). We note that the conformational-change strategy observed here is reminiscent of ideas introduced by Freire, Arnold, and their co-workers^53–55. Taken together, these results suggest that the use of asymmetric functional groups in the design of inhibitors could provide more versatility in responding to mutations than symmetric groups and could be one way of making conformationally-adaptive inhibitors that avoid acquired drug-resistance mutations. In this context it is interesting to note that substrates tend to place more symmetric residues at the corresponding position for R2 (P1/P1’ site) (Val or Phe, for instance), which suggests that this may not be a major strategy used by substrates.

Figure 6.

Flexibility was observed as a mechanism to achieve binding promiscuity. (A,B) Asymmetric functional group R2 flipped away from V82A mutation site to form compensating van der Waals interactions. (C) Box plot of binding affinity difference for promiscuous inhibitors with asymmetric R2 that flipped away from a wild-type (WT1) conformation when binding to mutant M1. (D,E) Asymmetric functional group R3 flipped toward D30N mutation site when no longer repelled to form alternative hydrogen bond. Proteases are shown in wheat cartoons with lines representing residues that are mutated or form alternative contacts. Ligands are shown in cyan sticks. Carbon atoms are magenta for proteases and cyan for ligands. The other elements follow the same color code: red for oxygen, blue for nitrogen, white for hydrogen, yellow for sulfur, and pale cyan for fluorine. Red bars and black asterisks in the box plot correspond to median and mean values correspondingly.

The approximate binding free energy computations used here neglected conformational entropy loss due to frozen torsions in both the proteins and the inhibitors. To ascertain whether this could have a significant effect on the results obtained, we carried out a comparative study in which a commonly-used entropic term of 0.4 kcal/mol per rotatable bond^{56, 57} for the inhibitor was added to approximate the loss of entropy upon binding; it was assumed that all inhibitor torsions were free in the unbound state and became frozen upon binding. Results for the distributions of inhibitors across coverage bins are given for all physicochemical measures in Figures S2 and S3. For each measure, the same trend was observed for promiscuous inhibitors as in the case neglecting conformational entropy change. In particular, the increased flexibility previously observed for more promiscuous inhibitors was still observed, and this trend was statistically significant with a p-value of 3.7×10^–38. Other p-values were 4.3×10^–9, 1.0×10^–11, 1.8×10^–5, 1.0×10^–10, and 1.1×10^–8 for size, number of rotatable bonds, hydrogen-bonding groups, hydrophobicity, and substrate envelope respectively. All panels of Figures S2 and S3 are very similar to the corresponding panel of Figure 4 or 5, which indicates very little difference in the distributions due to including an entropy correction.

A series of higher penalties for torsional entropies have also been tested with 1.0, 1.5, 2.0 kcal/mol per rotatable bond which are in the range usually considered. In general, the resulting inhibitors became more selective, with the maximum coverage being 12, 11, and 10 respectively. This can be seen from the resulting distributions in flexibility for inhibitors of various coverages (Figure S4). Even though the higher penalty acts more against flexible inhibitors, the trend of promiscuous inhibitors being more flexible in general was found to be robust with p-values being 1.5×10^–21, 2.8×10^–8, and 1.3×10^–2 for the parameters considered, respectively. Clearly, a larger penalty diminished but did not remove the trend when the parameter for torsional entropy falls within or even above the range usually adopted in literature⁵⁷.

Size

Promiscuous inhibitors showed a narrow distribution of size, biased slightly towards smaller compounds on average, compared to their more selective counterparts (Figures 4A and 5A show statistics on the number of inhibitor heavy atoms). The narrow size range occupied by promiscuous inhibitors (34 to 41 heavy atoms) was a subset of the broader range occupied by selective ones; whereas 100% of the promiscuous inhibitors occupied this range, only 80% of the selective ones did. On average promiscuous inhibitors were smaller by 1 to 2 heavy atoms.

To investigate the reason why extra-large and extra-small inhibitors bound more specifically, on average, than medium-sized ones, a random set of small and large inhibitors was selected and subjected to additional conformational search for binding to all fourteen targets, including their off-targets. Of 350 extra-small and 2531 extra-large inhibitors that were predicted to be extremely selective (binding to just one target), 10 were randomly chosen from each set and labeled XS-i or XL-i (i=1, …, 10). For the pair of each chosen inhibitor and each target, successive conformational searches were performed to examine three possible explanations for missed coverage: weak relative binding affinity (beyond 10 kcal/mol but still below 25 kcal/mol), steric clashes with the active site, and unsatisfied hydrogen-bond groups. These searches were performed with similar strategies as in the inhibitor design, as elaborated earlier in the Methods section. For each inhibitor, the binding affinity with each missed target was compared to its binding affinity with its covered target, and the binding-affinity loss was decomposed into a packing contribution (van der Waals and the surface-area term of solvation energy) and an electrostatic contribution (electrostatic interactions between the target and the inhibitor as well as their individual desolvation energies). The fraction of the total loss between a target on the horizontal axis and an inhibitor on the vertical axis due to the electrostatic contribution, truncated to the range 0–100%, is reported in Figure 7; warmer colors indicate a greater electrostatic contribution. Additionally, the color white indicates an inhibitor paired with its selective target, black indicates a geometric clash, deep red indicates an unsatisfied hydrogen bond (an extreme electrostatic contribution), and deep blue indicates a van der Waals clash (an extreme packing contribution).

Figure 7.

Fraction of electrostatic contributions to relative binding affinity losses for randomly chosen, mono-specific compounds that were extra small (A), extra large (B), and extra polar (C). Each block represents a pair of protein (on the x-axis) and inhibitor (on the y-axis). Warmer color represents more contribution from electrostatics. The deepest red color indicates that hydrogen-bond groups on corresponding inhibitors could not be all satisfied. The black color indicates that corresponding compounds do not fit in the binding site geometrically. The white color indicates that the compound binds the corresponding target.

For the 10 extra-small, extra-selective inhibitors, no steric clashes were observed with the targets they failed to bind (Figure 7A), consistent with their small size. Of the 130 pairs of an inhibitor and a missed target, 100 cases were due to weak binding affinities and 30 cases were due to burying a hydrogen-bonding group without forming a hydrogen bond with the target. For the 100 cases with weak binding affinities, the majority was caused by a dominant packing contribution (van der Waals interactions) with more than 90% relative contribution to the binding-affinity loss.

The 10 extra-large, extra-selective inhibitors told a somewhat different story (Figure 7B). Of the 130 cases of an extra-large inhibitor and its missed target, only 19 (mostly with Target 5 [mutant I50V] and Target 8 [mutant G48V]) were due to steric clashes. This is a relatively small fraction of the cases, which indicates that these inhibitors, although extra large, did not fail to cover most targets simply because of sterics. Rather, the cases were dominated by unsatisfied hydrogen-bonding groups (30 cases) and weak binding affinity (81 cases, 50 of which were dominated by packing, 6 by electrostatics, and 25 by a balance of both).

Hydrogen-Bonding

Interestingly, all promiscuous inhibitors had exactly 7 hydrogen-bonding groups (5 on the scaffold and 1 on each of R1 and R3; choices at R2 were limited to aliphatic groups as suggested in an earlier structure–function analysis²²). All 330 inhibitors with more than 7 hydrogen-bonding groups, high selectivity (coverage no more than 4), and bound to at least one wild-type structure (WT1, PDB code 1T3R) were examined to understand how more hydrogen bonding groups led to increased selectivity. The extra hydrogen bonds in these inhibitors came from having more than one hydrogen-bonding group at R1, R3, or both.

In binding to the wild-type protease 1T3R, 198 R1 dual-hydrogen-bonding-groups (one acceptor and one donor) of the 330 selective inhibitors simultaneously formed hydrogen bonds with the carbonyl oxygen atom of Gly48(A) and the backbone hydrogen atom of Asp29(A) or Asp30(A). The positions of these hydrogen bond donors on Asp29 and Asp30 were well conserved across the set of bound protease structures considered. However, Gly48 lies in the flexible flap region, and its carbonyl atom moved up to 1.3 Å relative to its position in WT1. Furthermore, Gly48 was mutated to valine in two of the targets considered, which also results in positional changes for backbone atoms. The result of this movement is that all 198 compounds with R1 dual-hydrogen-bonding groups that bound selectively to 1T3R did so because they failed to make at least one hydrogen bond to each of their missed targets (which eliminates them from further consideration). Similar results held for 53 dual-hydrogen-bond-donor R1 that simultaneously formed hydrogen bonds with a carboxyl oxygen atom on the backbone of Gly27(A) and a charged oxygen atom on the side chain of Asp29(A). The backbone conformation of Gly27(A) was well conserved across all structures in the target set, and the carbonyl atom on Gly27(A) was also the hydrogen-bond acceptor for a hydroxyl hydrogen atom on the scaffold. However, the side chain of Asp29(A) was highly variable with movement of the hydrogen-bond acceptor by up to 1 to 2 Å relative to its position in WT1. Therefore, in both cases described above rigid connectivity between inhibitor hydrogen-bonding groups limited the ability of both to be satisfied simultaneously in mutant proteases with altered relationship between hydrogen-bond partners, which resulted in the selective binding patterns for these inhibitors. Note that in these cases it is less true that a greater number of inhibitor hydrogen-bonding groups promoted binding selectivity; rather, it was a greater number of hydrogen bonds formed with positionally variable protease partners that did. For example, over 72% of the 290 selective inhibitors with multiple hydrogen-bonding groups on R1 formed a hydrogen bond with Gly48(A), whereas the ratio was only 11% for all promiscuous inhibitors.

A separate group of selective inhibitors had only a single polar group at each position (R1 and R3; 70% of the selective inhibitors and 100% of the promiscuous ones had this property, each set with 7 total hydrogen-bonding groups). To investigate what differentiated the two sets, we identified differences between the distributions of protein hydrogen-bonding partners. The largest two differences were that the selective set made more interactions with the positionally variable Gly48(A) in the wild-type protease WT1 than did the promiscuous set (25% versus 11%). Similarly, the selective set made fewer interactions with the positionally conserved backbone hydrogen atom of Asp29(A) than the promiscuous set (50% versus 84%).

Thus, a significant difference between selective and promiscuous binders is the extent to which they make interactions with positionally variable or conserved partners in the binding site. In some cases examined here they are two-pronged hydrogen-bonding interactions in which selectivity derives from one prong being to a conserved and the other to a variable position; in other cases they are one-pronged interactions in which selectivity derives from the interaction frequently being to a variable position. Both cases support a mechanism of selectivity deriving from reduced binding to missed targets due to the inability to simultaneously make multiple interactions because some of the interaction sites move relative to others in the binding site. In the case of the two-prong interactions, at least one of the anchoring interactions is likely to be the other prong; for one-prong interactions, the anchoring can come to other interactions and conformational constraints.

Hydrophobicity

Figures 4E and 5E give the distribution of inhibitor desolvation penalties as a function of binding promiscuity (represented by coverage). Promiscuous inhibitors paid lower desolvation penalties on average compared to selective ones, yet there was still significant overlap of the distributions. The most polar inhibitors (with a desolvation penalty over 11 kcal/mol) accounted for about 30% of selective inhibitors but only about 2% of promiscuous ones. Similar to the procedure for the extra-small or extra-large selective inhibitors, a series of conformational searches was done for these extra-polar selective inhibitors (named XP-1 through XP-10) to discover why they missed other targets. The contribution of the binding energy loss was reported in Figure 7C with the same color code as in Figures 7A and 7B. Of the 130 cases of an especially polar, selective inhibitor and its missed target, the majority are excluded by weak affinity (73%; 52% due to poorer packing alone, less than 1% due to weakened electrostatics alone, and 20% due to both). Of the remainder, 21% don’t bind due to unsatisfied hydrogen bonds and 10% due to steric clashes (the sum adds up to slightly more than 100% due to 4 cases that produce a steric clash and an unsatisfied hydrogen bond). Interestingly, although these inhibitors show a correlation between greater polarity and greater selectivity, the data suggest that only some of this might be causality and much of it is probably correlation. In particular, 52% of the non-binding pairs that lead to selectivity are due to poor packing interactions alone and 10% due to steric clashes, both of which could be due to the inhibitors being larger rather than more polar (but the two are partially correlated). Size is not likely to explain the whole effect, as the 21% of lost interactions due to unsatisfied hydrogen-bonding groups and 21% due at least partially to weakened electrostatics are related to polarity.

Substrate-Envelope Hypothesis

The substrate-envelope hypothesis was previously proposed and suggests that inhibitors designed to mimic geometrical features of natural substrates should be more likely to avoid resistance; mutations that would interfere with inhibitor binding would also interfere with substrate binding, and thus not be tolerated. The hypothesis is supported by structures of inhibitors with more and less susceptibility to resistance^{21, 25, 58, 59} and led to the successful design of inhibitors that maintained high-affinity to drug-resistant HIV-1 protease mutants²². In the current study the hypothesis was further tested against the designed library of small-molecule inhibitors. Specifically, for each predicted bound conformation of an inhibitor with a covered target, the number of non-hydrogen atoms on the inhibitor that extended outside of the substrate envelope (as defined in Altman et al.²²) was used to represent the extent that the substrate-envelope hypothesis was violated. The violation measure and the binding promiscuity measure (coverage) of all inhibitor conformations are reported as distributions in Figures 4F and 5F. More selective inhibitors tended to violate the substrate envelope to a greater extent. Whereas selective inhibitors could have up to 7 non-hydrogen atoms beyond the substrate envelope, promiscuous inhibitors had at most 1 such atom. In fact, for the most promiscuous inhibitors that covered at least 11 targets, none of their conformations ever extended beyond the substrate envelope. Of the selective inhibitors that violate the substrate envelope, structural analysis indicated that they extended beyond the substrate envelope near the mutation-rich P2–P2’ site and the deformable flap region.

A striking result was that, although selective inhibitors were more likely to violate the substrate envelope than promiscuous ones, over 80% of the selective complexes still remained within the substrate envelope. This makes the point very strongly that respecting the substrate envelope is a contributory but not sufficient property for promiscuous binding. This observation is consistent with our previous study, in which some designed inhibitors that respect the substrate envelope still lost significant binding affinity in complex with some drug-resistant mutants^{22, 25}.

In seeking inhibitor properties that when combined with the substrate-envelope hypothesis could better distinguish promiscuous from specific binders, we performed the single-sided Kolmogorov–Smirnov (KS) test and JSD calculations for promiscuous inhibitors and selective inhibitors that did not violate the substrate envelope, as in the subsection “Physicochemical Properties of Promiscuous Small-Molecule Inhibitors”. Trends similar to those observed previously were observed for promiscuous inhibitors relative to substrate-envelope-respecting selective ones. Specifically, the KS p-values were calculated to be 6.9×10^–3, 2.0×10^–40, 6.3×10^–9, and 9.3×10^–6 for the observed trends in size, flexibility, hydrophobicity, and hydrogen-bonding, respectively. These values are still statistically significant but somewhat larger than the counterparts reported in the physicochemical properties subsection comparing promiscuous inhibitors and all selective inhibitors irrespective of the substrate envelope; this reduction in statistical significance when substrate-envelope differences are removed indicates that it does contribute significance. Similar to our previous results, the JSD values were computed to be 0.08, 0.48, 0.14, and 0.11, respectively. Even though all these properties can complement the substrate-envelope hypothesis, the high JSD value (0.48) for flexibility indicates that the ability to adapt conformations to target mutations contributes the most to complement the substrate-envelope hypothesis. Conversely, the low JSD value (0.08) for size distributions in particular suggests a partial overlap between our size measure and the measure for substrate-envelope violation.

Inhibitors with Experimentally Characterized Binding Profiles

We constructed a test set of 21 HIV-1 protease inhibitors that included 14 designed by us previously (AD-86, AD-93, AD-94, KB-83, KB-98, and KC-08²²; AG-23, AF-72, AF-69, AF-71, AF-68, AF-77, AF-78, and AF-80⁶⁰), 5 designed by our collaborators (KB-60, KB-62, AD-78, KB-79, and AD-81⁶¹), and 2 FDA-approved drugs (amprenavir and darunavir). These inhibitors’ K_i values were previously collected against a panel of both wild-type and 4 drug-resistant HIV proteases^{25, 60}. Similar to our previous definition, an inhibitor is regarded to bind (or cover) a protease variant if its relative K_i loss (fold-loss compared to the best K_i for this variant) is no more than 100-fold; an inhibitor is regarded promiscuous if its coverage is at least 60% of the size of the panel or selective if its coverage is no more than 40% of that. Similar to our previous treatment, those compounds in the “gray zone” with a coverage of 3 were removed to create enough separation between selective and promiscuous inhibitors. The threshold in relative Ki was chosen among 10, 100, and 1000 to create balanced sets of selective and promiscuous inhibitors. In the end, 5 inhibitors were classified selective and 8 promiscuous.

The distributions of physicochemical properties for selective and promiscuous inhibitors are compared, as shown in Figure 8. As all the inhibitors were experimentally assessed for substrate-envelope satisfiability previously^{25, 60}, and so was not considered here. As p-values are no longer meaningful for the small sample set, we only give JSD values to show how much the two distributions differ from each other and mean values to reflect the trends. Consistent with what we observed in the computational study, promiscuous inhibitors are smaller (by 1 to 2 non-hydrogen atoms on average), yet have more rotatable bonds (by about 1 on average), and are thus more flexible compared to selective inhibitors. Flexibility is again the most distinguishing property for promiscuous inhibitors as the corresponding JSD value of 0.69 is the highest among all. For the distribution in the number of hydrogen bond, the mean for promiscuous inhibitors is somewhat larger than selective inhibitors, which is opposite to the trend observed in the computational library. However, the small JSD value (0.09) indicates that the two distributions are not that distinguishable. This is consistent with our earlier analysis that promiscuous inhibitors in our computational library did not achieve binding promiscuity due to the number of hydrogen bond but rather the more frequent pattern of forming hydrogen-bonds with sequentially or structurally conserved partners on HIV-1 protease.

Figure 8.

Histograms of physicochemical properties for experimentally-determined selective and promiscuous HIV-1 protease inhibitors indicate similar trends observed in the computationally constructed inhibitor library.

Design of Optimal Small-Molecule Inhibitor Cocktails

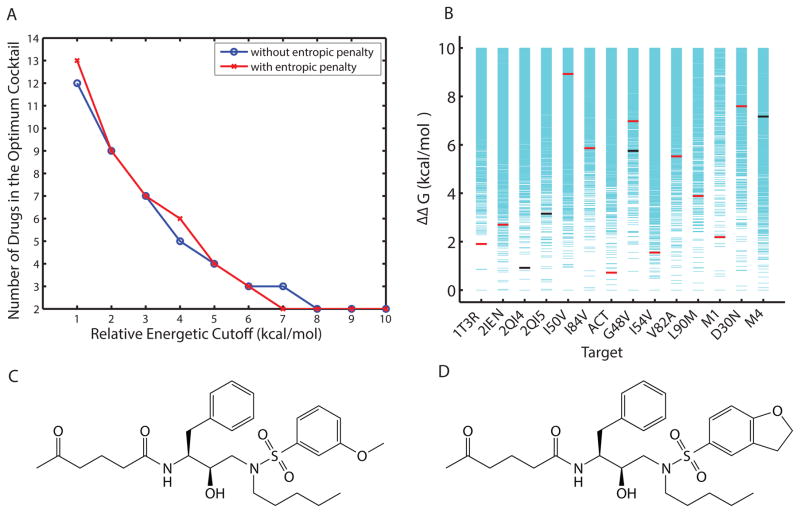
The most promiscuous inhibitors designed were calculated to cover 12 targets, whereas there are 14 targets in the set considered. When there is no single inhibitor found that binds well to all targets, a natural strategy is to design a cocktail of inhibitors that together cover all targets. To decrease the chance of interference and the cost of administration for these inhibitors, it is desired to have a cocktail with a minimum number of inhibitors. Radhakrishnan and Tidor showed that such an optimal inhibitor cocktail can be designed by solving a set cover problem, a classical question in computer science, with integer programming²⁴. Adopting the same methodology, we calculated size and composition of the optimal inhibitor cocktail for the target set of 14 HIV-1 protease variants. Among inhibitor cocktails with the same minimum number of members, the one with the highest average binding affinity was chosen as the optimum. When multiple inhibitors in a cocktail bound the same target, only the inhibitor with the highest binding affinity was considered to cover the target effectively. As shown in Figure 9A, when allowing for inhibitors of weaker and weaker binding affinities through the incremental increase of a relative binding affinity cutoff, fewer and fewer inhibitors were required to cover all targets as an optimal cocktail. This held true in both cases where the configurational entropy of the inhibitor was included or excluded, as in the earlier subsection “Molecular Mechanisms that Contribute to Binding Promiscuity”. When inhibitors with the top 6 (or 10) kcal/mol of binding affinity for each target were allowed, only three (or two) inhibitors were needed. The compositions of the optimal inhibitor cocktails at various levels of relative binding affinity cutoffs are reported in Table II.

Figure 9.

(A) Size of the optimal inhibitor cocktail as a function of relative binding affinity cutoff. (B) A two-inhibitor optimum cocktail (compound 607 in red and 10300 in black): individual coverages and relative binding affinities. The two included inhibitors (C) compound 607 and (D) compound 10300 only differ in functional group R3.

Table II.

The size and composition of designed optimal inhibitor cocktails as a function of relative binding affinity cutoff (member inhibitor indices are represented in distinctive colors; calculations neglect inhibitor configurational entropy).

Cutoff (kcal/mol)	1	2	3	4	5	6	7	8	9	10
Cocktail Size	12	9	7	5	4	3	3	2	2	2
WT1	17220	17220	17138	7961	15170	4689	4689	13967	607	607
WT2	6898	6898	7961	7961	7961	7063	7063	13967	607	607
WT3	103	17138	17138	385	385	851	851	10300	10300	10300
WT4	8162	8162	8162	385	385	7063	7063	10300	10300	10300
I50V	8318	8318	5201	5201	851	851	851	13967	607	607
I84V	6547	6547	11091	7961	7961	4689	4689	13967	607	607
V82T,I84V	5355	17220	7961	7961	7961	4689	4689	13967	607	607
G48V	9003	9003	9003	385	385	7063	7063	10300	10300	10300
I54V	17220	17220	7961	7961	7961	4689	4689	13967	607	607
V82A	11091	6898	11091	5441	7961	4689	4689	13967	607	607
L90M	10627	10627	5201	5201	15170	4689	4689	13967	607	607
M1	6898	6898	7961	7961	7961	7063	7063	13967	607	607
D30N	4179	4179	4179	4179	15170	4689	4689	13967	607	607
M4	11288	17138	17138	5441	851	851	851	10300	10300	10300

The 2-inhibitor cocktail consists of inhibitors 10300 and 607, with effective coverages of 4 and 10, respectively. The targets they each cover and the relative binding affinity values are shown in Figure 9B, together with the binding energy spectrum for all inhibitors binding each target. Interestingly, neither of them belonged to the set of four inhibitors that covered 12 targets: inhibitor 607 alone covered 11 targets and inhibitor 10300 was selective in our classification (with a coverage of 4). These two inhibitors do not differ significantly in their physicochemical properties: inhibitor 607 (10300) had 37 (38) heavy atoms, 18 (17) rotatable bonds, flexibility score of 0.486 (0.447), 7 (7) hydrogen-bonding groups, and a desolvation penalty of 8.7 (9.4) kcal/mol. Chemically, they share the same functional groups at R1 and R2, and they only differ in R3 (Figure 9C,D). Note that both R1 and R2 were structurally asymmetric, flexible groups (with 4 rotatable bonds for each when disregarding rotation of terminal methyl groups) that are capable of adopting the conformational-change strategy described earlier in the molecular mechanisms subsection. Moreover, conformational changes were observed for R1 and R2 of both inhibitors in their predicted structures bound to different targets. 607 had an R3 with 2 rotatable bonds. It also adopted the conformational-change strategy when bound to different targets, where the ether oxygen atom (a hydrogen-bond acceptor) moved up to 3.4 Å and changed its hydrogen-bonding partner between a backbone hydrogen atom of Asp29 (or 30) and that of Gly48. In contrast, 10300 had an R3 with only 1 rotatable, attachment bond to the scaffold, which did not change its conformation significantly and remained hydrogen bonding with a backbone hydrogen atom of Asp29 (or Asp30) for all 4 targets to which it bound. Therefore, 10300 did not complement 607 by offering more hydrogen-bonding groups or more ways of forming a hydrogen bond. It did not seem to improve hydrogen-bond quality judging from distances and orientations. We suggest that the additional carbon atom at R3 of 10300 potentially offered more van der Waals contacts compared to that of 607, thus complementing it in nonpolar interactions in jointly covering all targets considered.

Leveraging Information from Known Structures to Unknown Structures

In the optimal-inhibitor-cocktail approach described above, structural knowledge about all targets was assumed. However, nearly 70% of the HIV-1 protease residues can mutate and many of their combinations emerge under the pressure of antiviral therapy⁶². Therefore, design of inhibitors that can target mutants without structural or even sequence information is highly desirable in practice. In an earlier subsection (“Molecular Mechanisms that Contribute to Binding Promiscuity”) we identified molecular mechanisms that could enable small-molecule inhibitors to adapt to structural changes due to resistance mutations represented in our panel. Here we explore the specific question of whether the structural diversity present in the wild-type structures alone are sufficiently representative so that compounds designed to bind them as a set of targets would effectively bind drug-resistant mutants; this question was motivated by a study that correlated inherent flexibility and structural changes of HIV-1 proteases⁶³.

We split the 14-target set into two subsets, a training set of 4 wild-type structures and a testing set of 10 drug-resistant mutants. We first investigated inhibitors that bind only one of the four wild-type structures and found that they covered on average 1.78 of the mutants (Table III). We then investigated compounds that bound multiple wild-type structures and examined the number of structures they covered. The results show that increasing coverage of wild-type structures led to increased mutant coverage. For example, inhibitors that bound to three wild-type structures covered on average 3.21 mutants, and those that bound to four wild-type structures covered on average 4.67 mutants (Table 3). These results stress the risk of single-structure-based drug designs in the context of a rapidly mutating target, and they suggest that multiple wild-type structures can serve as a complex target set to find compounds that bind somewhat more robustly to a mutant panel. However, the results presented here are rather modest. For example, of the compounds computed to bind to four wild-type structures, the maximum number of mutants covered was just five. A larger panel of wild-type structures, produced either from X-ray crystallography or perhaps from a molecular dynamics simulation, could lead to even more robust binding across panels of mutants.

Table III.

Binding specificity profiles toward 10 drug-resistant HIV-1 protease mutants for the inhibitors that target wild types.

Coverage of Wild-Type Panel	Average Coverage of Mutant Panel	Abundance
1	1.78	8,836
2	2.77	1,725
3	3.21	140
4	4.67	3
≥2	2.80	1,869

CONCLUSION

This study explores molecular mechanisms responsible for binding specificity (selectivity versus promiscuity) for small-molecule inhibitors, which we anticipate could provide a set of design principles to facilitate programming of the desired level of specificity. Using HIV-1 protease as a model system, a set of 14 wild-type and clinically-relevant drug-resistant mutant structures was chosen as the target set and a computational inhibitor design approach was applied for each target to generate combinatorially small-molecule inhibitors with a common scaffold but various functional-group combinations. The resulting inhibitor library contained rich data of diverse structures and binding specificity profiles whose analysis revealed statistically significant differences in properties for selective and promiscuous inhibitors.

This analysis provides large-scale, systematic support for the substrate-envelope hypothesis; whereas no promiscuous inhibitors violated the substrate envelope, selective inhibitors tended to do so. Meanwhile, the identified molecular mechanisms provided valuable insight and potential additions to the substrate-envelope hypothesis; the results show a substantial number of inhibitors that reside wholly within the substrate envelope but were calculated to be selective. In other words, it is not sufficient for a small-molecule inhibitor to resemble the consensus substrate volume in order to be adaptive to drug-resistant mutations. Interestingly, we found that promiscuous inhibitors tended to display a narrower range of physicochemical properties (molecular size, flexibility, hydrophobicity, and number of hydrogen-bonding groups) than their selective counterparts. In particular, promiscuous inhibitors tended to be smaller in size, more flexible in structure, less polar, and of a conserved number of hydrogen-bond groups compared to their selective peers. Intuitively, a larger, more rigid inhibitor whose shape is optimized for complementarity to certain targets could lose binding affinity to other targets with deformed binding sites that impair shape complementarity and binding affinity. By contrast, smaller, more flexible inhibitors could fit in and adapt to a wider variety of active-site shapes. These trends in physicochemical properties for promiscuous inhibitors relative to selective ones that did not violate the substrate envelope still held. Again, structural flexibility stood out as the most distinguishing property among all considered. Even though these trends were derived from computationally designed and characterized inhibitors, they were also observed in our follow-up study on a small set of experimentally characterized HIV-1 protease inhibitors.

Mechanistically, we observed the torsional flipping of asymmetric functional groups to a different local minimum to compensate lost or weakened interactions in different active sites. The feasibility of compensatory torsional adjustments was limited by tight geometrical constraints due to large size, rigid connectivity, and even multiple hydrogen-bonding groups to satisfy simultaneously. In principle, it is desirable to introduce flexible functional groups that can locally adapt to amino-acid mutations and structural plasticity, while a well-constructed scaffold maintains its contacts with requisite conserved regions. It remains a practical challenge to determine how and where functional-group flexibility should be introduced to enable a small-molecule inhibitor to recognize a mutating target adaptively. The ability to fully answer this question is limited by factors that include accurate calculation of entropic contributions (we used a rotatable-bond-dependent approximation scheme) and complete treatment of protein flexibility (we treated it as a set of structures that could approximate a thermodynamic ensemble but did not introduce flexibility for each structure) in efficient ways. It is conceivable that our treatment of these factors could have an impact on the physicochemical distributions observed. Meanwhile, as these factors would challenge both promiscuous and selective inhibitors, the general trends for promiscuous inhibitors relative to selective ones could be maintained even though the exact extent of these trends may differ.”

While a single “magic bullet” able to cover the entire “moving target” of a quickly evolving viral population is highly challenging, a more conservative approach would involve a cocktail of inhibitors that together jointly cover all forms of the target (essentially a “shot gun” approach). Constructing a minimum cocktail can be formulated as a set cover problem, and we found that two or three small-molecule inhibitors together could cover all 14 targets even though no single molecule did. Complementarity in target coverage can sometimes be achieved by complementarity in molecular mechanisms. In one example of the optimum, a two-inhibitor cocktail differed in only a single functional group (R3); one member had a more rigid but bulkier R3 to avoid van der Waals loss and the other had a smaller, more flexible R3 to form hydrogen bonds adaptively. Finally, because structural information is not readily available for all mutant forms in practice, we validated the idea that structural diversity among wild-type (or more generally, all existing) structures can facilitate the design of adaptive inhibitors for mutant (or more generally, unknown) protease structures. One can also extend the idea to utilize structural plasticity reflected in dynamics simulations of known protease structures as well.