The Impact of Pial Collaterals on Infarct Growth Rate in Experimental Acute Ischemic Stroke

Abstract

Background and Purpose

This work sought to mathematically model infarct growth and determine if infarct volume growth can be predicted by angiographic assessment of pial collateral recruitment in an experimental Middle Cerebral Artery Occlusion (MCAO) animal model.

Materials and Methods

Pial collateral recruitment was quantified using DSA, acquired 15 minutes following permanent MCAO in six canines based on a scoring system (Pc) and arterial arrival time (AAT). MRI based infarct volumes were measured 1,1.5,2,3,4 and 24 hours following MCAO and parameterized in terms of growth rate index (G) and final infarct volume (V_Final) as V(t) = V_Final (1−e ^(−G*t)). Correlations of G and V_Final to Pc and AAT were assessed by linear bivariate analysis. Correlations were used to generate asymptotic models of infarct growth for Pc or AAT values. Pc and AAT based models were assessed by F-test and residual errors.

Results

Evaluation of pial collateral recruitment at 15 minutes post occlusion were strongly correlated with 24-hour infarct volumes (Pc: r²=0.96, p<0.003; AAT: r²=0.86, p<0.008). Infarct growth, G, had strong and moderate linear relationships to Pc (r² = 0.89; p<0.0033) and AAT (r² = 0.69; p<0.0419), respectively. V_Final and G were algebraically replaced by angiographically based collateral assessments to model infarct growth. F-test, demonstrated no statistical advantage to using Pc- over AAT-based predictive models despite lower residual error in the Pc-based mode (p<0.03).

Conclusion

In an experimental permanent MCAO model, assessment of pial collaterals correlates with infarct growth rate index and has the potential to predict asymptotic infarct volume growth.

INTRODUCTION

Reperfusion treatment in acute ischemic stroke due to major vessel occlusion aims to rescue brain at risk for ischemic injury. Compromise in cellular function, during the early phases of cerebral ischemia, precedes but does not consistently predict irreversible dysfunction or infarction. Based on the premise that discrepancies exist between tissue with irreversible damage and tissue with reversible functional compromise, reversible functional compromise could be operationally defined as a component of the diffusion-perfusion mismatch profile derived from MRI [1–3]. Tissue infarction is known to depend on both the degree to which blood flow is compromised and the duration of compromise (time from onset of ischemia) [4]. In the setting of major vessel occlusion, blood flow via pial collateral vessels sustains tissue at risk such that an effective measure of the collaterals may approximate the tissue state as indicated by perfusion-diffusion mismatch. Furthermore, given the identical cerebrovascular occlusion site, victims of acute cerebrovascular occlusion with the same degree and time of reperfusion can vary in their final irreversible tissue damage or infarct volume [5]. Final infarct volumes in patients with prolonged occlusion of the middle cerebral artery (MCA), for example, vary depending on the degree of sustained pial collateral recruitment and depend on the degree to which the cerebral tissue type at risk is able to withstand permanent ischemic damage [5,6]. A better understanding of infarct growth rate has the potential to lead to a more personalized treatment plan based on tissue rather than time selection alone and improve the effectiveness of reperfusion therapy in the current era of precision medicine.

With respect to the mathematical modeling of cerebral infarct volume growth within the first 24 hours of ictus, growth rate decreases as infarct volume increases indicating that infarct volume evolves in a non-linear fashion; thus non-linear growth models more accurately reflect true infarct volume growth relative to a linear model. Non-linear models can be divided into asymptotic (those that level off after time) and non-asymptotic models (those that grow indefinitely). Because infarct volume does not enlarge indefinitely but rather approaches a point in time after which any growth is negligible or cannot be measured, an asymptotic model makes more sense. This work sought to mathematically model infarct growth rate as a non-linear asymptotic function of time and hypothesize that the infarct growth rate can be predicted by pial collateral recruitment in a setting of acute and permanent MCA occlusion (MCAO) in a canine model.

MATERIALS AND METHODS

Animal care guidelines of the University of Chicago were followed. Six mongrel dogs (20–30 kg) underwent four vessel cerebral angiography and permanent endovascular MCA at its origin at the carotid terminus, M1 segment occlusion (MCAO) using previously described endovascular techniques [7,8]. Briefly, following induction, animals were anesthetized (1.5–2.0% isoflurane) and ventilated. Cardiac rhythm, end-tidal CO₂, glucose, body temperature, hematocrit and arterial pressure were maintained within physiologic range. The MCA was accessed from the posterior circulation via the circle of Willis using a microcatheter (Echelon 10, EV3, Plymouth, MN) and occluded using embolic coils (Axium, EV3, Plymouth, MN) [7]. DSA images were acquired (OEC9800, General Electric, OEC Medical Systems, Inc, Salt Lake City, UT) to confirm occlusion and quantify pial collateral blood supply by selective injection of the contralateral internal carotid artery and the vertebral artery 15 minutes following MCAO.

MRI Scan Protocol

All MRI images were acquired on a 3 Tesla human magnet (Achieva, Philips Healthcare, Best, Netherlands). Animals were placed in the head first, prone position within a 32 channel transmit-receive head coil. Diffusion Weighted MRI (DWI) (field of view (FOV)=140×140mm, matrix = 128×128, number of excitations (NEX)=1, repetition time(TR)/echo time (TE) 192–2131/71, B-values= 0,1000 s/mm², Slice thickness (ST)=3 mm) was acquired 1, 1.5, 2, 3, and 4 hours post MCAO and T2 weighted Fluid Attenuated Inversion Recovery (T2 FLAIR) MRI (FOV= 160 mm, matrix=512×512, NEX=1, TR/TE/inversion time(TI)=11000/125/2800, ST=3 mm, scan time~8 minutes) was acquired at 24 hours to quantify final infarct volume. Susceptibility weighted imaging (FOV= 160mm, matrix=148×148, NEX=1, TR/TE=14.89/21.00, flip angle=10, ST=0.5mm) was acquired after the 1 hour, 2 hour and 4 hour DWI scans and at 24 hours”.

Quantification of Pial Collateral Arterial Recruitment (P_C)

Two interventional neuroradiologists (GAC, SA) semi-quantitatively assessed pial collateral recruitment (Pc), using a previously published scoring method [7]. The results of the two observers were averaged. Briefly, this 11-point scoring system compares post-occlusion to pre-occlusion arteriographic images to assess extent of reconstitution of the occluded MCA territory and transit time relative to jugular vein opacification. Extent is evaluated within each of 3 sections of the MCA territory (anterior, middle and posterior). For each section, one point is assigned if only the medial part of the MCA distal branches were reconstituted and two points if the lateral part of the MCA branches were reconstituted within that section. Up to two additional points were added if there was reconstitution of the distal and proximal M2 segments within the operculum. Transit time was assigned up to one point for each section of the MCA territory (anterior, middle and posterior) if contrast arrived in MCA branches along the lateral aspect of each section before contrast arrived to the jugular bulb. Bland-Altman statistic for this pial collateral scoring system between two observers has been reported at 22.6% (95% of scores within 1.3 points of each other) and the mean difference of 0.23 between observers [7]. Pial scores were averaged and treated as a continuous variable in all statistical analyses. Agreement of P_c between the two observers in this study was assessed using a Bland-Altman analysis.

Arterial Arrival Time (AAT)

Pial collateral recruitment was also quantitatively assessed by arterial arrival time (AAT). Signal versus time curves were extracted from time-resolved angiograms using a combination of Amira software (Pro Medicus, San Diego) and MATLAB (v2012b, Mathworks, Nantik, MA) which measured contrast density over time within Regions of Interest (ROI). The AAT was defined as the time interval between contrast arrival at the normal M1 segment and contrast arrival at the reconstituted M3/4 junction on hemisphere distal to the permanent MCAO (See Figure 1).

Figure 1.

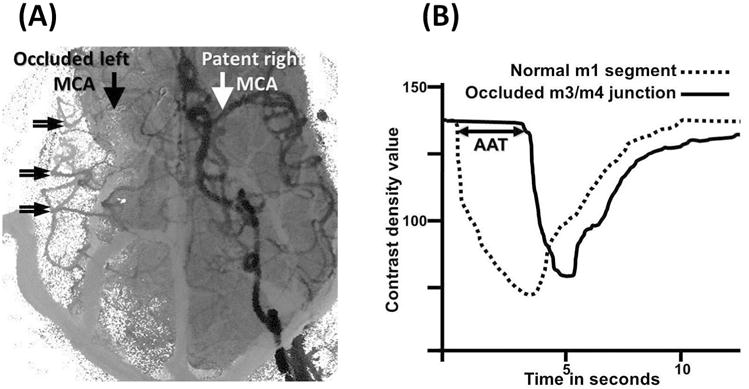
Arterial arrival times (AAT) were measured from angiographic time-density curves. Regions of interest (ROIs) within normal MCA proximal M1 segment (white arrow, 1A) and from collateralized MCA branches (double arrows, 1A) are identified on composite angiographic images. ROIs were used to calculate time density curves (1B). AAT (in seconds) was defined as the time interval between contrast arrival at the normal M1 segment (interrupted curve, b) and the average of three ROIs at the M3/4 junction of the MCA corresponding to the occluded MCA (continuous curve, b). AAT is graphically depicted by the horizontal double arrow line.

Quantification of Infarct Volume

The evolution of the infarct was determined from parametric images of mean diffusivity (MD) and T2 FLAIR images independently by two trained observers. A previously described semi-automated infarct segmentation algorithm was used to quantify infarct volumes through time [7]. Briefly, infarct volumes by MD maps and FLAIR MRI were estimated using a quantitative voxel-wise threshold by setting a threshold of 1.5 standard deviations relative to normal values based on an ROI drawn to cover the entire contra-lateral normal hemisphere inclusive of gray and white matter but exclusive of ventricles on a slice-by-slice basis. Total infarct volume was defined as the number of voxels that were 1.5 standard deviations greater than the mean value of normal tissue multiplied by voxel volume. Volumes were calculated using Image J (NIH, open source). Previous results by Bland-Altman statistic indicate that there is good reproducibility of infarct volume estimations using the MD maps (15.9%) acquired between 0 and 240 minutes post MCAO and FLAIR images (13.3%) acquired at 24 hours [7]. Therefore a combination of early (i.e. 0–240 minutes) MD (V(t)) and 24 hour T2 FLAIR (V_Final) images were used to determine the evolution of the infarcted volume over time.

Predicting 24-hour Infarct Volume from Angiography

Least squares regression analysis was performed to test the hypothesis that angiographic assessment of pial collateral arterial reconstitution (i.e. P_c and AAT) can predict final infarct volumes. Both Pc and AAT were compared using a correlation analysis to determine the level of agreement between both Pc and AAT and V_Final. It is important to note that cytotoxic, ionic and vasogenic edema were not differentially accounted when deriving this representative asymptotic function.

Modelling Infarct Growth

Asymptotic infarct growth was mathematically modelled by an asymptotic function. Infarct growth was parameterized as:

$$V\mathit{\left(}t\mathit{\right)}=V_{\mathit{Fit}}\ast \mathit{\left(}\mathit{1}-e^{\mathit{\left(}-G\ast \mathit{time}\mathit{\right)}}\right),$$ Equation 1

where V(t) was infarct volume at time t, with G (Growth Rate) and V_Fit (Fitted final infarct volume) were free parameters in the fit. For this analysis, infarct over time data collected at over the acute phase of the stroke, t = [0, 240 min] was combined with 24 hour (t=1440 min) infarct volume, V_Final. Leveburg-Marquart fits were performed to extract G and V_Fit for each experiment separately. The goodness of fit was then reported as the coefficient of determination, r². Growth rates and V_Fit values resulting from the fits were then subject to a linear regression analysis to derive an expression that would allow the modelling of infarct growth rate as a function of pial collateral recruitment (Pc and AAT). The modelling of infarct growth using Pc and AAT were compared. The slope intercept of the correlation plots and correlation coefficients of P_c and AAT were compared to determine which more closely follows a linear model.

Parameterizing Infarct Growth From Collateralization

Expressions for infarct volume and infarct growth rate were back substituted into the Equation 1 to yield infarct vs time curves as a function of P_C and AAT, i.e. angiographic measures acquired 15 minutes post-occlusion. A two-sided Wilcoxon Signed-Rank test determined the difference (if any) between the measured and model-predicted volume of the lesion size at all time points. Since P_C and AAT derived models utilized a similar number of parameters, we applied an F-test with the following formula for measuring the F-statistic, F = SSE_AAT/SSE_Pc. SSE_AAT and SSE_Pc are the sum square of the errors (SSE) between the AAT- and Pc-modeled lesion volumes and the 24 hours post-occlusion FLAIR-measured volumes. Subsequently, comparison of the F-statistic with an F– distribution was used to assess the P_C and AAT derived models for goodness of fit to the measured data. In addition, mean absolute error of both models were compared at each time point using a Wilcoxon Signed rank to determine if the errors from each model were significantly different. Statistical significance was defined at the 5% level.

RESULTS

All experiments were successful and all six dogs survived to the 24-hour time point. None of the animals showed evidence of hemorrhagic conversion or herniation on the 24-hour MRI exams. Bland-Altman Statistic for Pc determination between the two observers in this investigation was 22.4% (95% of scores within 1.5 points of each other) and the mean difference was 0.17 between observers. This is similar to previously described reproducibility (7). Raw data for each experiment (infarct volumes by time, Pc and AAT) are shown in Table 1.

Table 1.

Raw data

Experiment No.	1	2	3	4	5	6
<PC>	9.00	7.00	10.50	5.50	4.00	3.50
AAT, s	1.344	3.469	1.812	4.938	4.656	4.156
V(60 min),mm3	3533	8960	3575	9842	14947	15074
V(90 min),mm3	3976	9221	4009	10310	15428	16464
V(120 min),mm3	3922	9174	4430	14493	16805	18134
V(180 min),mm3	5492	13043	5312	16811	18034	20694
V(240 min),mm3	5058	14800	6461	17419	19257	22197
V(24 hour),mm3	9612	17987	9668	20946	24479	25419

<PC> = Average Pial Collateral Score evaluated 15 minutes post occlusion

AAT = Average Arterial Arrival Time evaluated 15 minutes post occlusion

V(time) = infarct volume at “time” evaluated with DWI MRI

V(24 hour) = final infarct volume from FLAIR MRI

Predicting 24-hour Infarct Volume from Angiography

Strong linear relations were observed between baseline pial collateral score, Pc, and final infarct volume (V_Final) (V_Final= −1483.6*Pc+20578; r²= 0.96, p<0.003) as well as AAT and final infarct volume (V_Final = 2596.3*AAT +1994.4; r²=0.86; p<0.008) (See Figure 2 A and Figure 2 B, respectively). A secondary analysis showed that a strong correlation exists between pail collateral score and ATT (ATT= −0.4754*Pc+ 6.52; r²=0.78, p<0.02) as might be expected from simply physiologic arguments, i.e., robust collaterals provide earlier contrast agent arrival distal to an occlusion. It is noteworthy that pial collateral score is a semi-quantitative assessment, whereas AAT is a continuous quantitative measure of pial collateral recruitment.

Figure 2.

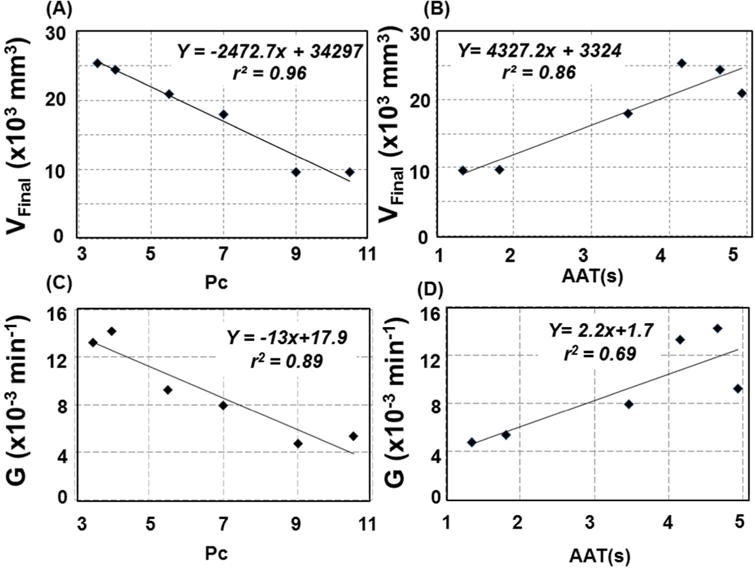
Final infarct volumes by T2 FLAIR images acquired 24 hours post MCA occlusion were compared to baseline (i.e. 15 minutes post occlusion) angiographic measures of pial collateral recruitment. (A) Angiographic scoring of pial collateral score, Pc and (B) Arterial Arrival Time (AAT) both strongly correlated with final infarct volume. Both (C) pial collateral score, Pc, and (D) AAT are predictive the infract growth rate index, G (derived from the fits shown in Figure 3B) based on a linear function.

Modelling Infarct Growth

A representative image for early (Figure 3 A top), and Final (24 hour, Figure 3 A, bottom) infarcts are shown along with the results of the semi-automated infarct volume algorithm. In all cases, infarct volumes were observed to increase asymptotically over time until reaching a final infarct volume V_Final, (See Figure 3 B). Levenberg-Marquart fits to Equation 1 converged with r² values exceeding 0.92 in all cases (See Table 2). The growth rate index, G, extracted from the fits of the full time course (combined MD for 0–240 minutes and 24-hour FLAIR) exhibited a strong linear relation to Pc (G = −0.0013*Pc + 0.0179; r² = 0.89; p<0.003) and a moderate linear relation with AAT (G = 0.0022*AAT+0.0017; r² = 0.69; p<0.04). See Figure 2 C and Figure 2 D, respectively.

Figure 3.

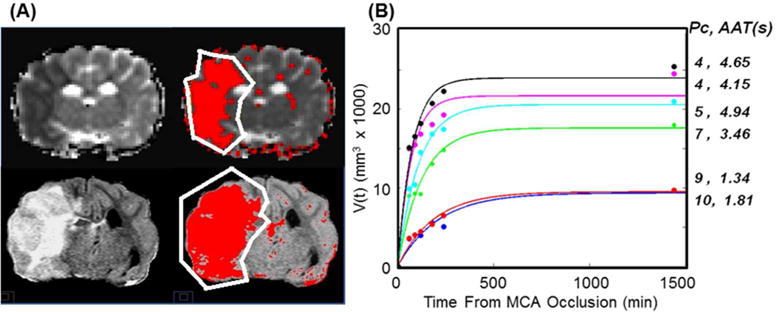
(A) Single slice 120 minute mean diffusivity (top) and 24 hour FLAIR (bottom) images (A) were used to estimate and plot the growth of the infarct volume over time (B). A semi-automated algorithm was used to estimate the volume of the infarct based on signal intensity within the affected hemisphere (outlined) varying 1.5 times the standard deviation from the mean of the signal in the contralateral normal appearing tissue (red area). (B) Infarct volume growth over time follows a predicable trend. Each curve corresponds to one experiment. The pial collateral scores, Pc and AAT, measured immediately after occlusion (i.e. at t = 15 min) for each curve are listed on the right.

Table 2.

Growth Rate index and Final infarct volumes

Experiment	G(C.I.) ×(10−3)1/min	Vfit(C.I.) ×1000 mm3	r2
1	4.765 (2.37, 7.16)	9.31 (7.08, 11.55)	0.92
2	7.951 (4.65, 11.25)	17.58 (14.52, 20.63)	0.96
3	5.337 (3.629, 7.05)	9.467 (8.04, 10.89)	0.97
4	9.23 (6.79, 11.67)	20.54 (18.41, 22.67)	0.98
5	14.20 (5.64, 22.75)	21.65(17.64, 25.66)	0.94
6	13.22 (8.79, 17.67)	23.95 (21.36, 26.54)	0.98

G = Growth Rate Index from Fit

Vfit = final infarct volume from fit

C.I. = 95% Confidence Interval

r² = coefficient of determination of fit.

Parameterizing Infarct Growth From Collateralization

Because the experimental data were well described by a linear model to V_Final, G to P_c and AAT, a parameterization of infarct volume based solely angiographic observables determined 15 minutes post occlusion, was derived through simple algebraic back substitution of V_Fit and G to obtain:

$$V\mathit{\left(}t\mathit{\right)}=\mathit{\left(}A\mathit{1}\ast P_{c+}B\mathit{1}\mathit{\right)}\ast \mathit{\left(}\mathit{1}-e^{\mathit{\left(}C\mathit{1}\ast Pc+D\mathit{1}\mathit{)}\ast t\mathit{\right)}}\mathit{\right)}$$ Equation 2

with: A1=−1483; B1 = 20578, C1 = −0.0013 and D1= 0.0179). The equivalent expression for AAT was:

$$V\mathit{\left(}t\mathit{\right)}=\mathit{\left(}A\mathit{2}\ast \mathit{AAT}+B\mathit{2}\mathit{\right)}\ast \mathit{\left(}\mathit{1}-e^{\mathit{\left(}C\mathit{2}\ast \mathit{AAT}+D\mathit{2}\mathit{)}\ast t\mathit{\right)}}\mathit{\right)}$$ Equation 3

with: A2=2596, B2 = 1994, C2 =0.0022 and D2 = 0.0017. The resulting curves are displayed on Figure 4 for a range of P_C and AAT values. The sum square of the error (SSE) of the AAT-based models were 3.99, 4.06, 1.93, 1.57, 1.31, and 3.98 times greater than the correspond Pc-based model SSEs at the 60, 90, 120, 180, 240 min, and 24 hour time points. Congruently, the F-test did not demonstrate a significant difference between the P_C or AAT-based model of infarct volume growth at any time point with respective p-values 0.10, 0.10, 0.3, 0.3, 0.40, 0.1. However, a comparison of the mean absolute error showed significantly better agreement between the Pc-based infarct growth modelling (ε = −0.66+/− 0.22) than that of the AAT (ε =1.49 +/− 2.08) based on a two-sided Wilcoxon signed rank test (p<0.03).

Figure 4.

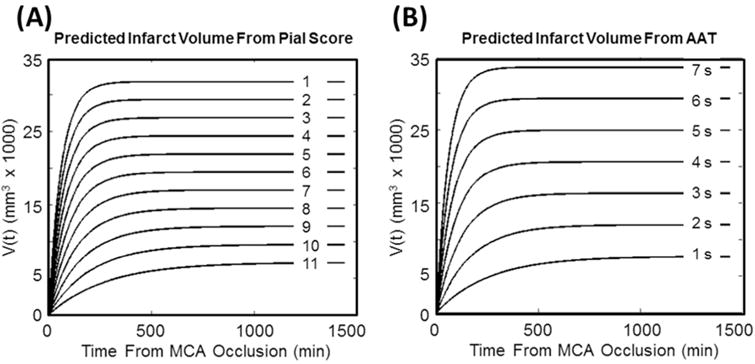
Families of curves for predicting infarct volume over 24 hours predicted by pial collateral score (Pc) and Arterial Arrival Time (AAT).

DISCUSSION

Our experimental results indicate that infarct growth in a permanent MCAO canine model can be mathematically modeled based on an angiographic assessment of pial collateral recruitment. Reperfusion during the evolution of acute ischemia to cerebral infarction has the potential to either salvage brain at risk leading to improved clinical outcomes or cause reperfusion injury/hemorrhage leading to poorer clinical outcomes. As such, the ability to assess salvageable ischemic tissue during the early phases of an acute ischemic stroke may impact treatment decisions [1–3]. Patients with acute ischemic stroke with large vessel occlusion are potential candidates for embolectomy and undergo angiography prior to embolectomy. This circumstance lends itself to angiographic evaluation of pial collateral recruitment and may help in the assessment for embolectomy. Additionally, a clear understanding of the infarct volume growth rate as it relates to specific parameters can assist in estimating residual brain at risk and available time for intervention.

This work demonstrates that infarct growth after permanent occlusion of the MCA follows a predictable trend that can be mathematically modeled with respect to the degree of collateral blood supply distal to the occluded artery. During the early phases of cerebral ischemia after MCAO in mongrel canines, infarct volume measured by MRI diffusion restriction can be approximated by an asymptotic function of time. Based on this function, infarct growth rate decreases with time and a growth rate index can be derived from this function. If the growth rate index is known, predictors of the final infarct volume can be used to define the evolution of cerebral infarction during MCAO. Final infarct volume and growth rate index can be linearly fitted to pial collateral score based on results derived in this study. Even if a linear relationship does not truly exist, an assessment of pial collateral recruitment can be used to estimate the final infarct volume as well as the infarct growth rate index. Ultimately in a controlled animal model with a specific occlusion site, such as the proximal middle cerebral artery, a set of estimated infarct growth curves can be generated for each pial collateral score and for various arterial arrival times (Figure 4). Using these curves one may be able to estimate the salvageable brain tissue at risk. Given that the assessment of pial collaterals is reflective of the cerebral perfusion during acute ischemic infarction, cross-sectional perfusion imaging may also be predictive of infarct growth index and final infarct volume.

Previous studies have assessed infarct growth over time and have determined that the growth of infarct volume changes in the early hours and reaches a maximum volume after which it decreases [9–15]. There is tremendous intraspecies and interspecies variation in the time course of cerebral infarct volume growth. Indeed, in humans, the mean time for maximal infarct volume for anterior circulation infarction appears to be around 70 hours [9]. Comparing Wistar rats to Sprague Dawley rats, the time it takes to reach maximum infarct volume appears to be 2 and 4 hours respectively [10]. In Macaque monkeys, MCA infarction appears to reach a maximum at 24 or 48 hours [11]. Furthermore, the growth rate is suddenly altered if and when reperfusion occurs. Vasogenic edema appears to be more profound if reperfusion occurs later in the time course of infarction [12]. Finally, most studies which employ MRI to assess infarct volume appear to suggest that a maximal infarct volume is reached based on a logarithmic growth function [11, 13, 14]. After the maximal volume is reached, infarct volume decreases in size. Based on observations from this study as well as prior studies, it seems reasonable to suggest that given similar occlusion sites, the growth rate and the maximum infarct volume within each species vary to a large degree depending on the degree of pial collateral recruitment [5, 16]. This assumes that significantly less variability in the susceptibility of the cerebral tissues to ischemia exists within each species. The current study did not account for change in MRI based infarct growth rate as a result of reperfusion which would represent an additive function likely depending on the degree of blood brain barrier break down (i.e. V(t) = Vf (1−e^(−Gt)) + B(t) where B(t) represents this additive function).

There are limitations associated with this study. It is quite possible that a similar asymptotic function predictive of infarct volume may be found in humans, but our results may not be readily translatable across species. Unlike controlled experiments, physiologic parameters, occlusion site, age and time of onset relative to MRI acquisition time are highly variable in the clinical setting. The current study was performed in a homogeneous population of canines with controlled physiologic conditions, permanent MCAO at a known occlusion site, and with precisely known times of onset and imaging times. Varying metabolic, physiologic and vascular events during cerebral infarction may directly and indirectly influence pial collateral recruitment under typical clinical circumstances. Additionally, the relative contributions of vasogenic, cytotoxic and ionic edema were not differentially incorporated into the derived mathematical function. Cytotoxic and ionic edema are thought to have an immediate influence on infarct volume measured by diffusion weighted imaging, whereas vasogenic edema would be expected to have a delayed and more prolonged impact [17]. Additionally, vasogenic edema due to reperfusion would be expected to have an additive influence at the time of reperfusion as mentioned earlier. Finally, the confined space of the calvarium may influence infarct growth rate depending on the baseline difference in cerebral volume relative to calvarial volume which increases with age. Further refinements of this mathematical function would need to consider the relative contributions of reperfusion, and potential variability of pial collateral recruitment over time. Despite these limitations, the observation that the degree of pial collateral recruitment can estimate infarct volume growth can be incorporated in clinical decision making. The findings of final infarct volume being dependent on pial collateral recruitment, indicates that a variable peripheral zone of benign oligemia also exists in acute ischemic stroke. Finally, the observation that infarct growth rates depends on time and extent of pial collaterals suggests that the window for potential interventional benefit may be significantly longer in patients with good collaterals versus those with poor collaterals.

CONCLUSIONS

MRI derived cerebral infarct volumes from an experimental MCAO canine model can be mathematically modeled using an asymptotic function of time governed by final infarct volume and growth rate index. Because both final infarct volume and growth rate index can be linearly fitted to pial collateral recruitment, pial collateral assessment may be used to estimate potential infarct growth in the early stages of experimental cerebral ischemia due to MCAO.