Applications of nonlocal means algorithm in low-dose X-ray CT image processing and reconstruction: a review

Abstract

Low-dose X-ray computed tomography (LDCT) imaging is highly recommended for use in the clinic because of growing concerns over excessive radiation exposure. However, the CT images reconstructed by the conventional filtered back-projection (FBP) method from low-dose acquisitions may be severely degraded with noise and streak artifacts due to excessive X-ray quantum noise, or with view-aliasing artifacts due to insufficient angular sampling. In 2005, the nonlocal means (NLM) algorithm was introduced as a non-iterative edge-preserving filter to denoise natural images corrupted by additive Gaussian noise, and showed superior performance. It has since been adapted and applied to many other image types and various inverse problems. This paper specifically reviews the applications of the NLM algorithm in LDCT image processing and reconstruction, and explicitly demonstrates its improving effects on the reconstructed CT image quality from low-dose acquisitions. The effectiveness of these applications on LDCT and their relative performance are described in detail.

1. Introduction

X-ray computed tomography (CT) is widely used in the clinic for diagnosis, screening, image-guided radiotherapy, and image-guided surgeries. CT scan is a radiation-intensive procedure ¹, and its potential harmful effects including genetic and cancerous diseases have raised growing concerns in the medical physics community ². Hence, many strategies have been proposed for dose reduction in CT scan to decrease radiation-associated risks ^3–5. In addition to hardware improvements in CT systems, two additional cost-effective strategies have also been widely explored: (1) lowering the X-ray tube current and exposure time (milliampere-second (mAs)) or the X-ray tube voltage (kilovoltage peak (kVp)) settings to reduce the X-ray flux toward the patient (i.e., low-flux acquisition); (2) reducing the number of projection views per rotation (i.e., sparse-view acquisition). The first strategy would inevitably increase the projection data noise, and the resulting image by the conventional filtered back-projection (FBP) method (equipped on most of commercial CT systems) may be degraded with excessive noise and streak artifacts due to X-ray quantum noise. The second strategy would produce undersampled projection data and the image reconstructed by the FBP method usually suffers from view-aliasing artifacts due to insufficient angular sampling. The two strategies may be combined, leading to both noisy and undersampled projection data and further degrading the corresponding CT image reconstructed by the FBP method.

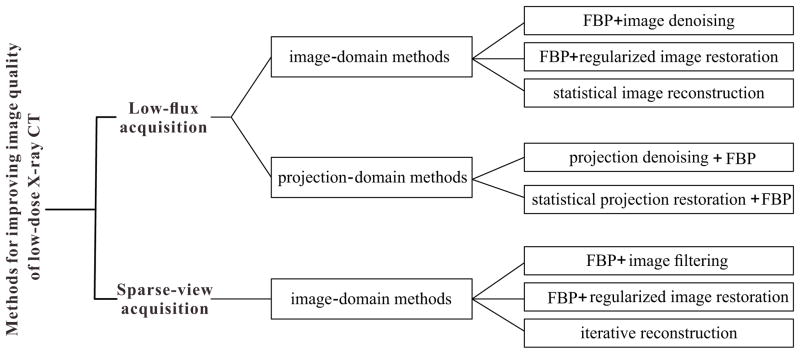
Numerous methods have been proposed to improve CT image quality from low-dose acquisitions, as illustrated in Fig. 1. For low-flux scanned data, the methods can work in either the image domain or the projection domain. One category of the image domain methods is the application of edge-preserving filter directly to the FBP reconstructed image ^6–11. However, because noise and streak artifacts in the CT image are typically non-stationary and unable to be modeled with a general distribution, it is difficult to effectively suppress them while fruitfully preserving fine structures and details. Another category includes regularized image restoration methods, which restore the FBP reconstructed image by optimizing an objective function consisting of a quadratic data-fidelity term and a regularization term ^{12, 13}. The third category includes statistical image reconstruction (SIR) methods, which reconstruct the CT image by optimizing a penalized maximum likelihood (pML) criterion or penalized weighted least-squares (PWLS) criterion in the image domain ^{14, 15}. The projection domain methods can either denoise the projection data with edge-preserving filter ^16–21 or estimate the ideal noiseless projection data by optimizing a pML/PWLS criterion in the projection domain ^22–25. The denoised/restored projection data can then be reconstructed with the analytical FBP method. For sparse-view scanned data, the methods generally work in the image domain. The first method category attempts to suppress view-aliasing artifacts in the FBP reconstructed image with an edge-preserving filter, but is relatively ineffective when the view-aliasing artifacts are severe ^{26, 27}. The second category includes regularized image restoration methods that are exactly the same as those of low-flux scanned data. The third category includes iterative reconstruction methods that typically exploit the compressed sensing or other sparse representations as prior knowledge to reconstruct CT image ^28–30.

Fig. 1.

Overview of the methods proposed to improve CT image quality from low-dose acquisitions. It is noted that statistical image reconstruction for low-flux CT and iterative reconstruction for sparse-view CT are grouped into image-domain methods herein, because their objective function is typically a function of the reconstructed image. But strictly speaking, they should be considered as combined image-domain and projection-domain methods.

The nonlocal means (NLM) algorithm was originally proposed as a non-iterative edge-preserving filter to denoise natural images corrupted by additive white Gaussian noise ^{31, 32}. Essentially, it is one of the neighborhood filters which denoise each pixel with a weighted average of its neighboring pixels according to similarity. However, differently from previous neighborhood filters, the NLM filter calculates the similarity based on patches instead of pixels. The patch of a pixel can be defined as a squared region centered at that pixel. Using patch strengthens the NLM filter because the intensity of a single pixel can be very noisy. The authors compared the performance of the NLM filter with an array of denoising algorithms including the Gaussian filter, anisotropic filter, total variation (TV), Yaroslavsky neighborhood filter, and observed noticeable improvements over them. Motivated by this success, NLM-based regularization models ^33–35 were also proposed and applied to various inverse problems including image denoising, image deblurring, image inpainting, image reconstruction, and image super-resolution reconstruction. Inspired by its success in natural image scenarios, researchers also extended its use to medical images including MRI ^36–40, ultrasound ^{41, 42}, PET ^43–46, SPECT ⁴⁷, and X-ray CT. Because noise distribution and other degradations may vary for different image types, special adaptation may be needed for each one of them. We specifically review the applications and adaptations of the NLM algorithm in low-dose X-ray CT (LDCT), and demonstrate how it improves the reconstructed CT image quality from low-dose acquisitions.

The remainder of this paper is presented as follows. In Section 2, we provide an overview of the NLM algorithm as a filter or regularization model. In Section 3, we explicitly illustrate different applications of the NLM algorithm in LDCT from low-flux or sparse-view acquisitions, for both three-dimensional and four-dimensional scans. After discussing several issues, we provide conclusions in Section 4.

2. Overview of the NLM algorithm

2.A. NLM filter

The NLM filter was originally proposed to denoise the natural images corrupted by additive white Gaussian noise ^{31, 32}. The filter exploits the high degree of redundancy that typically exists in an image, and reduces image noise by replacing the intensity of each pixel with a weighted average of its neighbors according to similarity. Although the similarity comparison can be performed between any two pixels within the entire image, in practice, this is typically limited to a fixed neighboring window area (called search-window (SW), e.g., 17×17 in two-dimensional (2D) case) of a target pixel for computational efficiency. Mathematically, the NLM filter can be described as:

$$\mathit{NLM}({\widehat{u}}_j)=\sum _{k\in S{W}_j}{w}_{jk}(\widehat{\mathbf{u}})•{\widehat{u}}_k$$ (1)

where the vector û represents the noisy image to be smoothed, k denotes the pixel index within the SW of pixel j, w_jk(û) is the weighting coefficient and satisfies the conditions 0≤w_jk(û)≤1 and Σ_k∈SWj w_jk (û) = 1, and NLM(û_j) denotes the intensity of pixel j after the NLM filtering.

However, differently from previous neighborhood filters, the NLM filter calculates similarity based on patches instead of pixels. The patch of a pixel can be defined as a squared region centered at that pixel (called patch-window (PW), e.g., 5×5 in 2D case). Let P(û_j) denote the patch centered at pixel j and P(û_k) denote the patch centered at pixel k. The similarity between pixels j and k depends on the weighted Euclidean distance of their patches, ${\Vert \mathbf{P}({\widehat{u}}_j)-\mathbf{P}({\widehat{u}}_k)\Vert }_{2,a}^2$, computed as the distance between two intensity vectors in high dimensional space with a Gaussian kernel (a>0 is the standard deviation of the Gaussian kernel) to weight the contribution to each dimension. The exponential function converts the distance to the weighting coefficient that indicates the interaction degree between two pixels. The normalized weighting coefficient is given as:

$$w_{jk}(\widehat{\mathbf{u}})=\frac{exp\left(-{\Vert \mathbf{P}({\widehat{u}}_j)-\mathbf{P}({\widehat{u}}_k)\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\widehat{u}}_j)-\mathbf{P}({\widehat{u}}_k)\Vert }_{2,a}^2/h^2\right)}$$ (2)

where h is the filtering parameter that controls the exponential function decay and the weighting coefficient. When h is small, the image tends to be weakly smoothed; when h is large, the image tends to be strongly smoothed. As previously reported ^{31, 32}, the filtering parameter h is a function of the standard deviation of Gaussian noise in the image. And if we further consider the size of the patch-window, the filtering parameter h can be given as ⁴⁰:

$$h^2=\tau {\sigma }^2=2\eta {\sigma }^2\left|PW\right|$$ (3)

where τ and η are free scalar parameters, σ is the standard deviation of Gaussian noise, and |PW| denotes the size of the patch-window.

2.B. NLM-based regularization models

Motivated by the success of the NLM filter, several NLM-based regularization models were also proposed for various inverse problems including image denoising, deblurring, and reconstruction. The first regularization model takes a general form as ³³:

$$U(\mathbf{u})=\sum _j\sum _{k\in S{W}_j}{w}_{jk}(\stackrel{\sim }{\mathbf{u}})•\varphi (u_j-u_k)$$ (4)

where ϕ denotes a positive potential function and one common choice is ϕ(Δ) = Δ²/2, and ũ ∈ ℝ ^J×1 represents a reference image. The weighting coefficient w_jk(ũ) is computed on the reference image and given as:

$$w_{jk}(\stackrel{\sim }{\mathbf{u}})=\frac{exp\left(-{\Vert \mathbf{P}({\stackrel{\sim }{u}}_j)-\mathbf{P}({\stackrel{\sim }{u}}_k)\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\stackrel{\sim }{u}}_j)-\mathbf{P}({\stackrel{\sim }{u}}_k)\Vert }_{2,a}^2/h^2\right)}$$ (5)

The regularization in Eq. (4) is similar to the Markov random field (MRF) model-based regularization ⁴⁸, but a different method is used to calculate the weighting coefficient. In this regularization, the weighting coefficient is smaller when the patch distance of pixel j and pixel k is larger, and vice versa. By this way, the sharp edges in the image can be better preserved.

Another general form of the NLM-based regularization is given as ³⁴:

$$U(\mathbf{u})=\sum _j\varphi \left(u_j-\sum _{k\in S{W}_j}{w}_{jk}(\stackrel{\sim }{\mathbf{u}})•u_k\right)$$ (6)

This regularization model is similar to that in Eq.(4), but the idea varies slightly. This model assumes that the intensity of each pixel can be approximated by a weighted average of its neighbors according to similarity, which is also the original thought of the NLM filter.

The third general form for the NLM-based regularization is described as ³⁵:

$$U(\mathbf{u})=\frac{1}{p}\sum _j{\left(\sum _{k\in S{W}_j}{w}_{jk}(\stackrel{\sim }{\mathbf{u}})•{(u_j-u_k)}^2\right)}^{p/2},0<p<2$$ (7)

This regularization model is inspired by both the NLM filter and the compressed sensing theory. With p=1, the regularization in Eq. (7) becomes the nonlocal TV regularization ⁴⁹.

The weighting coefficients w_jk(ũ) in Eqs. (4), (6), and (7) are calculated from reference image ũ. For the image denoising or deblurring problem, the current noisy or blurred image could be used as the reference image, and for tomographic image reconstruction, the FBP reconstructed image was explored to serve as the reference image ⁴⁹. However, because the quality of the reference image is generally low, the resulting regularization may lead to a suboptimal solution.

Alternatively, investigators modified the above regularization models by replacing w_jk(ũ) with w_jk(u), described as ^{43, 50}:

$$w_{jk}(\mathbf{u})=\frac{exp\left(-{\Vert \mathbf{P}(u_j)-\mathbf{P}(u_k)\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}(u_j)-\mathbf{P}(u_k)\Vert }_{2,a}^2/h^2\right)}$$ (8)

This way, the regularization models eliminate the need for a specific reference image, and the weighting coefficients are computed on the unknown image u. However, direct optimization of the resulting objective function can be complicated. In practice, an empirical one-step-late implementation is usually employed in an iterative approach to obtain the solution. In this implementation, the weighting coefficients are computed on current image estimate, and are considered constants when the image is updated ^{43, 50}. Although this strategy would inevitably increase the computational load, it may produce a more accurate solution as compared with the use of a low quality reference image.

3. Applications of the NLM algorithm in LDCT

The pixel intensity of a CT image reflects the X-ray attenuation coefficient for the scanned object or patient. Therefore, the conventional notation μ will be used instead of u which representing a general image. In this section, we explicitly review the various applications of the NLM algorithm in LDCT, for both three-dimensional and four-dimensional CT scanning.

3.A. Three-dimensional CT scanning

Three-dimensional CT scanning refers to both fan-beam CT and cone-beam CT scanning (either in axial or helical acquisition mode) commonly used in the clinic to produce tomographic images of specific patient volumes.

1. NLM-based image filtering

(1) Simple image filtering

The NLM filter can be directly applied to the FBP reconstructed low-flux CT images ^6–11, which are typically degraded with noise and streak artifacts, as shown in Fig. 2(b). However, because noise and streak artifacts are non-stationary and cannot be modeled with a general distribution, it is difficult to determine the standard deviation σ in Eq. (3). The filtering parameter h is usually set as a global constant for the entire image, although this setting may lead to a suboptimal filtering result, because a spatially-invariant filtering may be too strong for some regions (blurring much) but too weak for others (filtering little) across the image ¹⁰. Recently, Li et al analytically derived a local noise level estimation method for low-flux CT images by considering noise propagation from the projection data to the FBP reconstructed images ¹⁰. Based on the estimated noise map, the filtering parameter h employed for each pixel can be adjusted proportionally to the local noise level:

$$h_j^2=\tau {\sigma }_j^2=2\eta {\sigma }_j^2\left|P{W}_j\right|$$ (9)

where σ_j denotes the estimated noise level of pixel j. This is one way to introduce spatial adaptivity into traditional NLM filtering, and this spatially-variant NLM filtering has demonstrated improved performance for low-contrast objects ¹⁰. Thaipanich and Kuo suggested to adaptively adjust the SW according to the local structure information as follows: a large SW in the smooth regions, a small SW in strong edge/texture regions, and a medium window for the other regions ⁵¹. This may be another way to introduce spatial adaptivity into NLM filtering, but the discrimination of the three different regions may be time-consuming and technically challenging, especially when the CT images are severely degraded. The third way to incorporate spatial adaptivity is to employ a fixed SW but exclude some patches that are very different from the patch of the central pixel. The selection process can be expressed as ^{40, 52}:

$$w_{jk}({\mathbf{\mu }}^{LD})=\{\begin{array}{ll}\frac{exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-\mathbf{P}({\mu }_k^{LD})\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-\mathbf{P}({\mu }_k^{LD})\Vert }_{2,a}^2/h^2\right)},\hfill & \text{if}\lambda <\frac{E(\mathbf{P}({\mu }_j^{LD}))}{E(\mathbf{P}({\mu }_k^{LD}))}<\frac{1}{\lambda }\text{and}{\nu }^2<\frac{var(\mathbf{P}({\mu }_j^{LD}))}{var(\mathbf{P}({\mu }_k^{LD}))}<\frac{1}{{\nu }^2}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (10)

where μ^LD ∈ ℝ^J×1 represents the FBP reconstructed LDCT image, and J is the number of pixels in the image; $E(\mathbf{P}({\mu }_j^{LD}))$ and $var(\mathbf{P}({\mu }_j^{LD}))$ represent the mean and the variance, respectively, for the patch of pixel ${\mu }_j^{LD}$; the parameters 0 < λ < 1 and 0 < ν < 1 can be chosen as, for example, λ = 0.5 and ν = 0.5. The rationale behind the adaptive SW and patch selection strategies is that increasing the number of patches tends to improve filtering in the smooth regions because they contain many similar patches; meanwhile it tends to either blur or remove details in the edge/texture regions that contain fewer similar patches. Therefore, both ways can make the NLM filtering be adaptive and improve the overall performance. Besides, Zheng et al explored the point-wise fractal dimension (PWFD) to achieve spatial adaptivity for NLM filtering of low-flux CT images ¹¹. The PWFD can provide local structure information, that is, the pixels in the smooth regions exhibit PWFDs close to zero and pixels near the edge regions have relatively large PWFDs. They designed a new weighting coefficient for NLM filtering by considering both the traditional patch distance and the new PWFD difference.

Fig. 2.

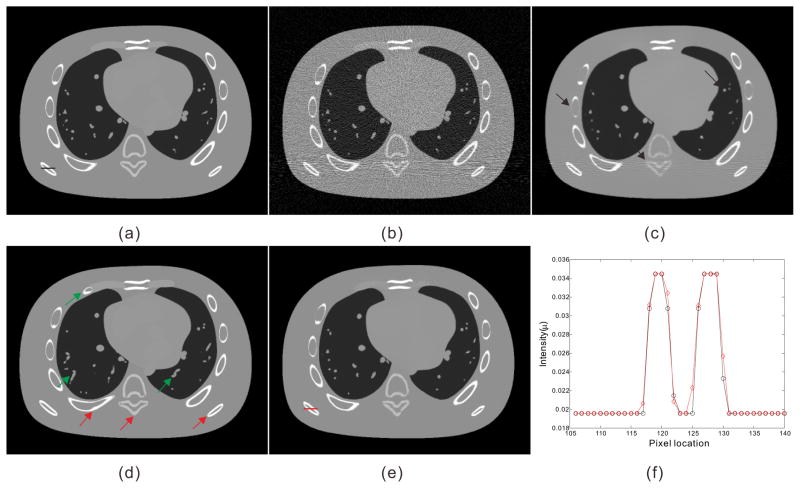
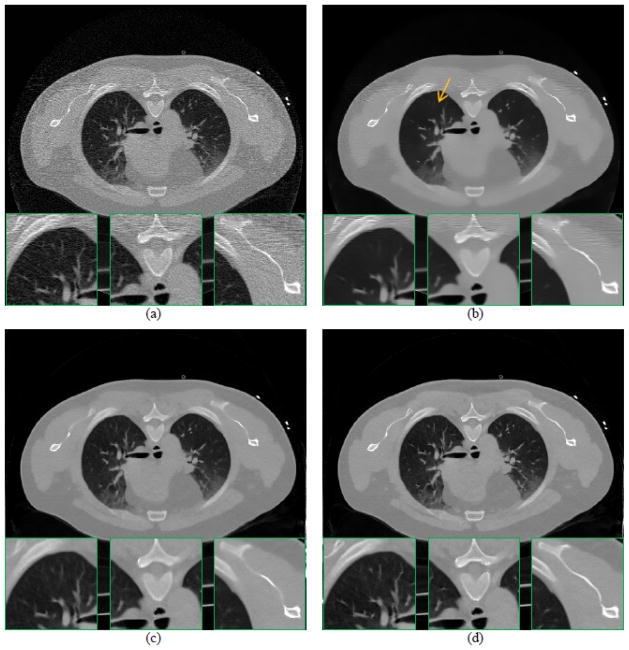
Illustration of the preHQ-guided NLM image filtering for low-flux CT: (a) one transverse slice of the NCAT phantom; (b) FBP reconstruction from simulated noisy projection data; (c) traditional NLM filtering of low-dose image in Fig. 2(b), SW=33², PW=5², h=0.015; (d) another transverse slice of the NCAT phantom serving as the prior image for preHQ-guided NLM filtering of low-dose image in Fig. 2(b); (e) corresponding preHQ-guided NLM filtering result, SW=33², PW=5², h=0.007; (f) profile comparison between the ground truth Fig. 2(a) and the filtering result Fig. 2(e).

While NLM filtering may suppress noise to a large extent, it is not as effective in removing the streak artifacts in low-flux CT images resulting from photon starvation, as demonstrated in Fig. 2(c). The streak artifacts are typically along the high-attenuation paths and appear as directional patterns. To solve this issue, Chen et al applied a directional one-dimensional nonlinear diffusion in the stationary wavelet domain to suppress the streak artifacts first, followed by a NLM filtering step to reduce the noise ⁹. This approach showed advantages in streak artifacts suppression over simple NLM filtering.

The CT images reconstructed by the FBP method from sparse-view acquisition typically suffer from view-aliasing artifacts, as shown in Fig. 3(b). The view-aliasing artifacts in the images are also non-stationary, and the conventional NLM filtering generally cannot remove them without sacrifice of image details ^{26, 27}.

Fig. 3.

Illustration of the preHQ-guided NLM image filtering for sparse-view CT: (a) one transverse CT image of a patient; (b) FBP reconstruction from sparse-view projection data; (c) conventional NLM filtering of low-dose image in (b); (d) a deformed version of (a) serving as the prior image for preHQ-guided NLM filtering; (e) prior image registered to (a); (f) registered prior image with simulated view-alising artifacts; (g) the corresponding preHQ-guided NLM filtering result with Eq. (11); (h) corresponding preHQ-guided NLM filtering result with Eq. (13). (Figure reprinted from the work of Xu and Mueller ²⁶)

(2) Previous high quality scan (preHQ)-guided image filtering

Repeated CT scans are required in clinical applications such as disease monitoring, longitudinal studies, and image-guided radiotherapy. To optimize radiation dose utility, high quality scanning can be first performed to set up the reference, followed by a series of low-dose scans (e.g., low-flux or sparse-view acquisitions). In these applications, the previous high quality scan can be exploited as prior information because of the anatomical similarity between the reconstructed image series of the scans. Using previous high quality image to improve low-dose scan reconstruction has recently drawn great interest ^{26, 53–60}, some of which are based on the NLM algorithm. Because scans are acquired sequentially rather than simultaneously, misalignment or deformation may occur among the image series, so registration is usually needed to align the different scans. Fortunately, the NLM-based methods do not heavily depend on registration accuracy because of the patch-based search mechanism. A rough registration might be adequate in practice, although a more accurate one can reduce the computational load by allowing the use of a smaller SW.

Ma et al proposed a preHQ-guided NLM filtering method for CT image from low-flux acquisition, described as ⁶¹:

$$\mathit{guidedNLM}({\mu }_j^{LD})=\sum _{k\in S{W}_j}{w}_{jk}({\mathbf{\mu }}^{LD},{\mathbf{\mu }}^{\mathit{preHQ}\mathit{registered}})•{\mu }_k^{\mathit{preHQ}\mathit{registered}}$$ (11)

where μ^LD ∈ℝ ^J×1 represents the FBP reconstructed low-dose image, μ^{preHQ registered} ∈ℝ^J×1 represents the previous high quality image registered to current low-dose image, w_jk (μ^LD, μ^{preHQ registered}) denotes the weighting coefficient, and $\mathit{guidedNLM}({\mu }_j^{LD})$ denotes the intensity of pixel j after filtering. Specifically, the weighting coefficient was given as ⁶¹:

$$w_{jk}({\mathbf{\mu }}^{LD},{\mathbf{\mu }}^{\mathit{preHQ}\mathit{registered}})=\frac{exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}})\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}})\Vert }_{2,a}^2/h^2\right)}$$ (12)

One concern with this method is whether the registration accuracy may affect the filtering result. The red arrows in Fig. 2(d) indicate some structure deformations between Fig. 2(b) and Fig. 2(d). Without any registration between two images, the preHQ-guided NLM filtering result (as shown in Fig. 2(e)) of Fig. 2(b) using Fig. 2(d) as prior image still retains good image quality, revealing that image registration accuracy may not be an obstacle. After comparing Fig. 2(c) with Fig. 2(e), we observed that preHQ-guided NLM filtering reduces noise and streak artifacts better than traditional NLM filtering.

Xu and Muller used a similar approach to explore the preHQ-guided NLM filtering method for sparse-view CT ²⁶. But they found that using an artifact-free image μ^{preHQ registered} and a low-dose image μ^LD with severe view-aliasing artifacts to calculate the weighting coefficient as in Eq. (12) may yield inferior filtering result, because of the challenge to perform patch matching. Thus, they proposed to transform μ^{preHQ registered} into a tandem-image μ^{preHQ registered + degraded} with view-aliasing artifacts resembling those in μ^LD, and then employed μ^{preHQ registered + degraded} and μ^LD for patch matching. The preHQ-guided NLM filtering method for sparse-view CT with artifact-matched scheme can be described as ²⁶:

$$\mathit{guidedNLM}({\mu }_j^{LD})\frac{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}+\mathit{degraded}})\Vert }_{2,a}^2/h^2\right)•{\mu }_k^{\mathit{preHQ}\mathit{registered}}}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}+\mathit{degraded}})\Vert }_{2,a}^2/h^2\right)}$$ (13)

In Eq. (13), the high quality image μ^{preHQ registered} is still used to determine the pixel estimates although the degraded image μ^{preHQ registered + degraded} is employed to calculate the weight coefficients. Fig. 3 illustrates that the filtering method in Eq. (13) is better than that in Eq. (11) for sparse-view CT image.

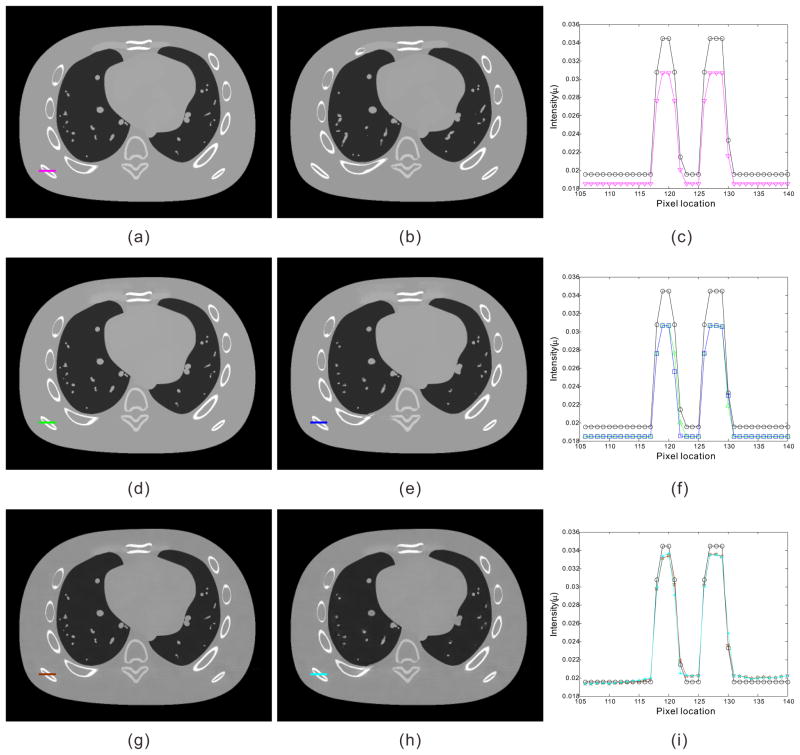
One potential drawback of the preHQ-guided NLM filtering method is that the pixel intensity of filtering result may resemble that of prior image when there are attenuation difference (e.g., due to kVp mismatch, detector difference, etc.) between the current low-dose image and prior image. Fig. 4(a) and Fig. 4(b) illustrate the same transverse slices of the NCAT phantom as Fig. 2(a) and Fig. 2(d) except for different kVp settings. Because the attenuation coefficient of the X-ray in materials is energy-dependent, the pixel intensity of Fig. 2(a) and Fig. 4(a) at the same location is different, as indicated by the profiles in Fig. 4(c). The preHQ-guided NLM filtering results of Fig. 2(b), using Fig. 4(a) and Fig. 4(b) as prior image, are shown in Fig. 4(d) and Fig. 4(e). It is observed that the pixel intensity of Fig. 4(d) and Fig. 4(e) are closer to the prior image in Fig. 4(a), rather than that of the ground truth image in Fig. 2(a). To mitigate this issue, a modified preHQ-guided NLM filtering method accounting for changes in pixel intensity was given as ⁶¹:

$$\mathit{guidedNLM}({\mu }_j^{LD})=\frac{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-C_{jk}•\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}})\Vert }_{2,a}^2/h^2\right)•C_{jk}•{\mu }_k^{\mathit{preHQ}\mathit{registered}}}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-C_{jk}•\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}})\Vert }_{2,a}^2/h^2\right)}$$ (14)

where $C_{jk}=E(\mathbf{P}({\mu }_j^{LD}))/E(\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}}))$ is a local adjusting factor used to account for changes in pixel intensity due to different kVp settings. This strategy was also applied in perfusion CT imaging ^{54, 61}, where the pixel intensity of different scans can change due to contrast enhancement. However, a large PW size may be desired to strengthen C_jk, because a small PW may lead to an imprecise estimation of $E(\mathbf{P}({\mu }_j^{LD}))$. Using Eq. (14) and a large PW, the filtering results in Fig. 4(g) and Fig. 4(h) demonstrate higher intensity accuracy than those in Fig. 4(d) and Fig. 4(e), as indicated by the profiles. Meanwhile, we also observed that this strategy may still induce small pixel intensity inaccuracies, especially for relatively non-uniform regions. More sophisticated approaches may be required to further improve its performance.

Fig. 4.

Illustration of the preHQ-guided NLM image filtering for low-flux CT: (a) the same transverse slice of NCAT phantom as Fig. 2(a) except for different kVp setting; (b) the same transverse slice of NCAT phantom as Fig. 2(d) except for different kVp setting; (c) profile comparison between Fig. 2(a) and Fig. 4(a); (d) preHQ-guided NLM filtering of Fig. 2(b) using Eq. (11) with Fig. 4(a) as prior image, SW=33², PW=13², h=0.007; (e) preHQ-guided NLM filtering of Fig. 2(b) using Eq. (11) with Fig. 4(b) as prior image, SW=33², PW=13², h=0.007; (f) profile comparison between Fig. 2(a) and the filtering results in Fig. 4(d) and Fig. 4(e); (g) preHQ-guided NLM filtering of Fig. 2(b) using Eq. (14) with Fig. 4(a) as prior image, SW=33², PW=13², h=0.007; (h) preHQ-guided NLM filtering of Fig. 2(b) using Eq. (14) with Fig. 4(b) as prior image, SW=33², PW=13², h=0.007; (i) profile comparison between Fig. 2(a) and the filtering results in Fig. 4(g) and Fig. 4(h).

Finally, we observed that the low-contrast objects and subtle structures in Fig. 2(e), Fig. 3(g)(h) and Fig. 4(g)(h) are not as well-preserved as the high-contrast objects. One reason for this observation is that a fixed SW size and constant filtering parameter h were used for both cases, resulting in adequate filtering for high-contrast objects but excessive filtering for other regions. By using the adaptive filtering strategies illustrated in Section 3.A.1(1), the preHQ-guided filtering results may be further improved, especially for low-contrast objects and subtle structures.

(3) Database-assisted image filtering

Because previous high quality image of the same patient may not always be available for some clinical applications, Xu et al extended to utilize a database of high quality CT images from other patients, for guided NLM image filtering ⁶². However, the CT images from other patients are typically less similar to the current low-dose image than those from the same patient. Therefore, the authors first picked a set of images from the database with similar anatomical structures to the current low-dose image, and registered them to the current low-dose image to construct the set of database priors. Then, they subdivided current low-dose image and database priors into blocks (e.g., 129×129), and then performed block registration and guided NLM filtering in a blockwise fashion using Eq. (11). The reason for constructing a set of database priors rather than a single one is to considerably improve the ultimate filtering result, because one database prior unlikely matches the target image from a different patient. In their study, the authors found that three database priors are sufficient to faithfully restore all the features, for either low-flux or sparse-view CT images ⁶².

To avoid the need for error-prone image registration and massive image storage, Ha and Mueller also proposed to replace the high-quality image database with a database of high-quality small patches (e.g., 7×7). Two types of patch database were investigated for NLM filtering of low-flux CT image ⁶³, a localized patch database with anatomical region tags (e.g., lung, heart, spine) and a global patch database with no tags. For each pixel j in the low-flux CT image, the patch is first extracted and matched with the database patches to find a certain number of most similar patches. Then, the patch database assisted NLM image filtering was expressed as ⁶³:

$$\mathit{assistedNLM}({\mu }_j^{LD})\frac{{\displaystyle \sum _{l\in S{P}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-\mathbf{P}({\mu }_l^{SP})\Vert }_{2,a}^2/h^2\right)•{\mu }_l^{SP}}{{\displaystyle \sum _{l\in S{P}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{LD})-\mathbf{P}({\mu }_l^{SP})\Vert }_{2,a}^2/h^2\right)}$$ (15)

where SP_j denotes the selected patches from the database for pixel j, l indexes the selected patches, and ${\mu }_l^{SP}$ denotes the central pixel intensity of the lth selected patch. This method was validated on low-flux CT images, and demonstrated better recovery of the image features than the conventional NLM filtering. Also, the global patch database assisted filtering removed a lower amount of structural information than the localized patch database, because of a larger patch variety ⁶³. Nevertheless, it is still unknown whether the method works on sparse-view CT images, which are degraded with severe view-aliasing artifacts and may jeopardize the search for matched patches from the database.

2. NLM-regularized image restoration

(1) Generic NLM-regularized image restoration

In addition to applying the filter directly to a FBP reconstructed LDCT image, the low-dose image can also be restored by solving the following problem:

$${\mathbf{\mu }}^{\ast }=argmin\{{\Vert \mathbf{\mu }-{\mathbf{\mu }}^{LD}\Vert }_2^2+\beta U(\mathbf{\mu })\}$$ (16)

where μ^LD represents the FBP reconstructed low-dose image, as defined above. The first term in Eq. (16) is a data-fidelity term, the second term is a regularization term, and β > 0 is a scalar control parameter that balances the two terms. Too small β may not eliminate noise/streaks in LDCT image, while too large β may remove valuable image features.

The NLM-based regularization models illustrated in Section 2.B can be employed in Eq. (16) for the restoration of FBP reconstructed LDCT images. Hashemi et al explored the nonlocal TV regularization for low-flux CT image restoration with promising results ¹². For sparse-view CT, while μ^LD is severely degraded with view-aliasing artifacts and some structures are hardly resolved, the resulting image restoration may only yield inferior image quality because of the challenge to find similar patches within the image.

(2) preHQ-regularized image restoration

As discussed in Section 3.A.1(2), if a previous high quality CT image of the same patient is available, the prior image can be formulated into the NLM-based regularization models in Section 2.B, to generate the preHQ-induced NLM regularization models, which are given as ^{54, 58}:

$$U(\mathbf{\mu })=\sum _j\sum _{k\in S{W}_j}{w}_{jk}(\mathbf{\mu },{\mathbf{\mu }}^{\mathit{preHQ}\mathit{registered}})•\varphi ({\mu }_j-{\mu }_k^{\mathit{preHQ}\mathit{registered}})$$ (17)

$$U(\mathbf{\mu })=\sum _j\varphi \left({\mu }_j-\sum _{k\in S{W}_j}{w}_{jk}(\mathbf{\mu },{\mathbf{\mu }}^{\mathit{preHQ}\mathit{registered}})•{\mu }_k^{\mathit{preHQ}\mathit{registered}}\right)$$ (18)

$$U(\mathbf{\mu })=\frac{1}{p}\sum _j{\left(\sum _{k\in S{W}_j}{w}_{jk}(\mathbf{\mu },{\mathbf{\mu }}^{\mathit{preHQ}\mathit{registered}})•{({\mu }_j-{\mu }_k^{\mathit{preHQ}\mathit{registered}})}^2\right)}^{p/2},0<p<2$$ (19)

where

$$w_{jk}(\mathbf{\mu },{\mathbf{\mu }}^{\mathit{preHQ}\mathit{registered}})=\frac{exp\left(-{\Vert \mathbf{P}({\mu }_j)-\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}})\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j)-\mathbf{P}({\mu }_k^{\mathit{preHQ}\mathit{registered}})\Vert }_{2,a}^2/h^2\right)}$$ (20)

The preHQ-induced NLM regularizations in Eqs. (17)–(19) can all potentially be employed in Eq. (16) for the restoration of FBP reconstructed LDCT images. The prior image contains similar anatomical structures and provides excellent correspondence to a current low-dose image, further improving image restoration over the use of generic regularizations.

3. NLM-regularized image reconstruction

(1) Generic NLM-regularized image reconstruction

The NLM-based regularization models in Section 2.B can be also employed for statistical image reconstruction (SIR) of LDCT image. In practice, the SIR method either uses calibrated transmitted photons (before log-transform) with the pML criterion or calibrated line integrals (after log-transform) with the PWLS criterion ⁶⁴. Because of its computational advantage, the PWLS criterion is a common choice and is described as:

$${\mathbf{\mu }}^{\ast }=\underset{\mu \ge 0}{argmin}\{{(\mathbf{y}-\mathbf{A}\mathbf{\mu })}^T{\mathbf{\sum }}^{-1}(\mathbf{y}-\mathbf{A}\mathbf{\mu })+\beta U(\mathbf{\mu })\}$$ (21)

where y ∈ℝ^I×1 is the vector of the measured line integrals, and I is the total number of line integral measurements; μ ∈ℝ^J×1 is the vector of attenuation coefficients of the object to be reconstructed, and J is the number of image pixels; A ∈ℝ^I×J is the system or projection matrix; Σ ∈ℝ^I×I is the covariance matrix, and because the measurement among different detector bins are assumed to be independent, the covariance matrix is diagonal and expressed as $\mathbf{\sum }=\text{diag}\{{\sigma }_{y_i}^2\}$⁶⁴; the symbols T and -1 indicate transpose and inverse operators, respectively. The first term in Eq. (21) is a data-fidelity term that models the statistics of projection measurements, while the second term can be the NLM-based regularization demonstrated in Section 2.B.

Chen et al first explored the NLM-based regularization for Bayesian reconstruction of emission tomography ⁴³ and X-ray CT ⁶⁵, and impressive reconstruction results were observed in noise suppression and tissue feature preservation. Later, they also applied a joint estimation strategy to solve the convergence problem caused by the weight update in iterations ⁶⁶. Zhang et al compared the performance of NLM-based regularization with traditional MRF model-based regularizations for SIR of LDCT, and found the NLM-based regularization can provide better noise reduction and resolution preservation for both phantoms and patient data ^{50, 67, 68}.

Similarly to NLM filtering, the use of locally adaptive filtering parameter h in NLM-based regularization can also improve the image quality of the resulting reconstruction ⁶⁸. While the local noise level in the SIR reconstructed image is difficult to estimate, an empirical approach to determine locally adaptive filtering parameter was given as ⁶⁸:

$$h_j^2=s•\mathit{mean}\left\{{\Vert \mathbf{P}({\mu }_j)-\mathbf{P}({\mu }_k)\Vert }_{2,a},k\in S{W}_j\right\}+t$$ (22)

where s and t are two constants. The rationale behind this mathematical expression is that the value of h should depend on the similarity between the patch of the target pixel and the patches within the corresponding SW. When SW contains many patches similar to P(μ_j), h needs to be decreased to reduce the influence of the other patches. Conversely, when very few similar patches exist in SW for P(μ_j), h needs to be increased to relax the selection ⁶⁹.

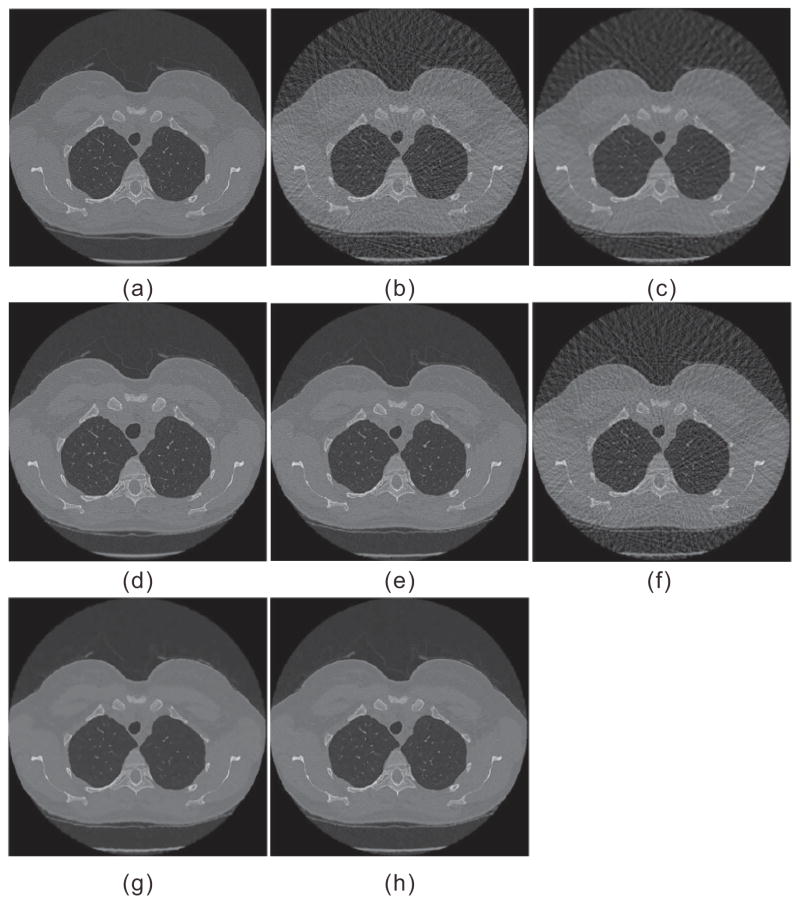
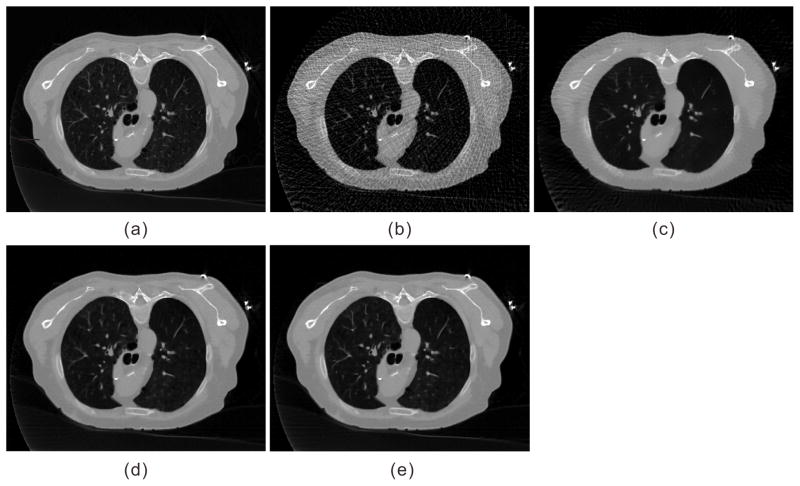
Fig. 5 shows the reconstructed images from the low-dose projection data (20mAs, 120kVp) of a patient by the following methods: the FBP method, the FBP reconstruction followed by NLM filtering (referred to as FBP+NLM filtering), the NLM-regularized SIR using constant filtering parameter (referred to as PWLS-NLM), and the NLM-regularized SIR using adaptive filtering parameters in Eq. (22) (referred to as PWLS-adaptiveNLM). The FBP+NLM filtering method cannot eliminate the streak artifacts within the image, but the two NLM-regularized SIR methods do not have such problem because of the statistical modeling of the projection data. As observed in the zoom-in views of three detailed regions, the PWLS-adaptiveNLM outperforms the PWLS-NLM on the reconstruction of subtle structures, demonstrating the need to introduce spatial adaptivity into NLM-based regularization. Nevertheless, besides adjusting the filtering parameter h, other approaches may be used to make the NLM-based regularization adaptive, such as those mentioned in Section 3.A.1(1).

Fig. 5.

One reconstructed slice of a patient from low-flux projection data: (a) FBP reconstruction; (b) FBP reconstruction followed by NLM filtering (SW=17², PW=5², h=0.012); (c) PWLS-NLM reconstruction (SW=17², PW=5², h=0.008); (d) PWLS-adaptiveNLM reconstruction (SW=17², PW=5², s=1×10⁻³, t=4×10⁻⁶). All images are displayed with the same window. (Figure reprinted from the work of Zhang et al ⁶⁸)

The NLM-regularized image reconstruction for sparse-view CT ²⁷ can also be formulated as Eq. (21). While a penalized least-squares criterion (i.e., the covariance matrix Σ is set to be identity matrix) may be adequate in relatively high flux imaging application, a more accurate modeling of the projection measurements would be important for a limited number of X-ray photons in each detector bin ⁷⁰. Thus, the PWLS criterion in Eq. (21) can be a better choice to account for the credibility of each measurement in both sparse-view and low-flux cases.

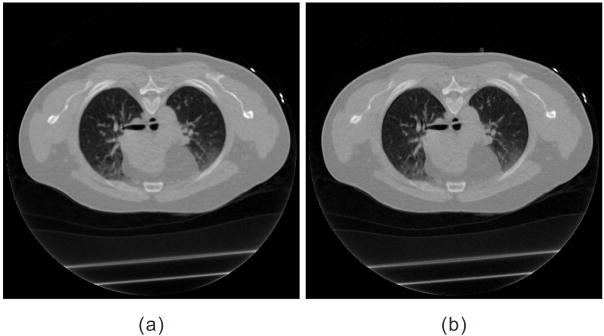
Fig. 6(a) illustrates one transverse CT image of a patient, which is reconstructed from 1160 full projection views with the FBP method and serves as the ground truth for reference. Fig. 6(b)–(e) shows the reconstructed images by the FBP method, FBP+NLM filtering, PWLS-NLM and PWLS-adaptiveNLM, from 145 projection views which were evenly extracted from the 1160 projection views. The NLM-regularized image reconstructions can suppress the view-aliasing artifacts more effectively than the FBP and FBP+NLM filtering methods while retaining good image quality. Also, the PWLS-adaptiveNLM is superior to the PWLS-NLM in preserving the subtle structures within the lung region, which may be of great importance for diagnosis.

Fig. 6.

A reconstructed slice of one patient dataset: (a) FBP reconstruction from the full 1160 projection views; (b) FBP reconstruction from 145 projection views; (c) FBP+NLM filtering from 145 projection views (SW=17², PW=5², h=0.01); (d) PWLS-NLM reconstruction from 145 projection views (SW=17², PW=5², h=0.006); (e) PWLS-adaptiveNLM reconstruction from 145 projection views (SW=17², PW=5², s=1×10⁻³, t=4×10⁻⁶). All the images are displayed with the same window.

(2) preHQ-regularized image reconstruction

The preHQ-induced NLM regularizations described in Section 3.A.2(2) were also used for low-flux and sparse-view CT image reconstruction as in Eq. (21) with promising reconstruction results ^{58, 71, 72}. It was also demonstrated that they may outperform the generic NLM-based regularizations in terms of reconstructed image quality, or potentially yield good images from lower dose acquisition, because of the introduction of a previous high quality image ^58,71,72. Finally, because optimization of the criterion in Eq. (21) is routinely performed by an iterative algorithm and the reconstructed image is updated after each iteration, the artifact-matched scheme may not be needed as in Section 3.A.1(2).

4. NLM-based projection data denoising

The NLM filter can also be applied to CT projection data before image reconstruction ¹⁶. The accessible projection data are commonly calibrated transmitted photons (before log-transform) or calibrated line integrals (after log-transform) ⁶⁴. The calibrated transmitted photons can be described by a Poisson distribution or ‘Poisson+Gaussian’ distribution with consideration of the electronic noise, while the calibrated line integrals can be approximated by a Gaussian distribution with a nonlinear signal-dependent variance ⁶⁴. Therefore, the local noise level of the projection data can be easily determined. Taking the calibrated line integrals as an example, the variance of each measurement can be given as ^73–75:

$${\sigma }_{y_i}^2=\frac{1}{{\overline{N}}_{0i}}exp({\overline{y}}_i),\text{or}{\sigma }_{y_i}^2=\frac{1}{{\overline{N}}_{0i}}exp({\overline{y}}_i)\left(1+\frac{{\sigma }_e^2}{{\overline{N}}_{0i}}exp({\overline{y}}_i)\right)$$ (23)

where y_i represents the line integral measurement along the ith X-ray path, ȳ_i and ${\sigma }_{y_i}^2$ are the mean and variance of y_i, N̄_0i denotes the mean number of incident photons, and ${\sigma }_e^2$ denotes the variance of electronic noise. As a result, the filtering parameter h employed for each projection measurement can be adjusted adaptively as $h_i^2=\epsilon {\sigma }_{y_i}^2=2\gamma {\sigma }_{y_i}^2\mid P{W}_i\mid$, which is similar to Eq. (3) but defined in the projection domain. The NLM-based projection data denoising can then be performed similarly as that in Eq. (1).

If the projection data of previous high quality scan and current LDCT scan are both available, the same strategy as that of the image domain in Eq. (11) can be potentially used to perform preHQ-guided projection data denoising. However, registration of the projection data can be more challenging than that of the images, which may impede its practical application.

The denoisied projection data can then be reconstructed by the FBP method. The CT projection data denoising is advantageous because noise is removed early in the pipeline preventing its propagation into the reconstruction process ¹⁷. However, the edges in the projection domain are usually not well defined as compared to those in the image domain, which may result in edge sharpness loss in the ultimate reconstructed image, as shown in Fig. 7(a).

Fig. 7.

One reconstructed slice from the same low-flux projection data as Fig. 5: (a) NLM-based projection data denoising followed by FBP reconstruction (SW=5², PW=3², ε=15); (b) NLM-regularized statistical projection restoration followed by FBP reconstruction (SW=5², PW=3², ε=3).

5. NLM-regularized statistical projection restoration

NLM-based regularizations can also be used for statistical projection restoration of low-flux CT. Similar to the SIR methods, statistical projection restoration can optimize either the pML or PWLS criterion in the projection domain to estimate the ideal noiseless projection data from the acquired noisy ones ^22–25. For instance, the PWLS criterion in the projection domain is given as:

$${\mathbf{q}}^{\ast }=argmin\{{(\mathbf{y}-\mathbf{q})}^T{\mathbf{\sum }}^{-1}(\mathbf{y}-\mathbf{q})+\beta U(\mathbf{q})\}$$ (24)

where q∈ℝ^I×1 is the vector of ideal noiseless line integrals to be estimated, and U (q) denotes a penalty term in the projection domain. Although this projection restoration is also typically optimized by an iterative algorithm, the computational speed is far more rapid than that of the SIR.

Similar to the regularization model of Eq. (4) in the image domain, the corresponding NLM-based regularization in the projection domain can be described as:

$$U(\mathbf{q})=\sum _i\sum _{m\in S{W}_i}{\omega }_{im}(\mathbf{q})•\varphi (q_i-q_m)$$ (25)

where the weighting coefficient is also computed as:

$${\omega }_{im}(\mathbf{q})=\frac{exp\left(-{\Vert \mathbf{P}(q_i)-\mathbf{P}(q_m)\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{m\in S{W}_i}}\left[exp\left(-{\Vert \mathbf{P}(q_i)-\mathbf{P}(q_m)\Vert }_{2,a}^2/h^2\right)\right]}$$ (26)

Also, similar to the preHQ-induced NLM regularization model of Eq. (17) in the image domain, the corresponding regularization in the projection domain can be described as:

$$U(\mathbf{q})=\sum _i\sum _{m\in S{W}_i}{\omega }_{im}(\mathbf{q},{\mathbf{y}}^{\mathit{preHQ}\mathit{registered}})•\varphi (q_i-y_m^{\mathit{preHQ}\mathit{registered}})$$ (27)

where y^{preHQ registered} ∈ℝ ^I×1 represents the projection data of previous high quality scan registered to the projection data of current low-dose scan, and the weighting coefficient is given as:

$${\omega }_{im}(\mathbf{q},{\mathbf{y}}^{\mathit{preHQ}\mathit{registered}})=\frac{exp\left(-{\Vert \mathbf{P}(q_i)-\mathbf{P}(y_m^{\mathit{preHQ}\mathit{registered}})\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{m\in S{W}_i}}\left[exp\left(-{\Vert \mathbf{P}(q_i)-\mathbf{P}(y_m^{\mathit{preHQ}\mathit{registered}})\Vert }_{2,a}^2/h^2\right)\right]}$$ (28)

The other NLM-based regularization models can also be adapted from the image domain to the projection domain. And all regularization models can potentially be used for the statistical projection restoration of low-dose projection data with Eq. (24).

The restored projection data is then reconstructed by the analytical FBP method. The NLM-regularized statistical projection restoration may have similar drawbacks to the NLM-based projection data denoising, that is, the ultimate FBP reconstructed image may lose edge sharpness, as illustrated in Fig. 7(b).

3.B. Four-dimensional CT scanning

For imaging respiratory motion-involved sites such as the thoracic and upper abdominal regions, four-dimensional CT (4D-CT) and four-dimensional cone-beam CT (4D-CBCT) have been widely used to resolve organ motions and reduce motion artifacts ^{13, 76, 77}. To achieve low-dose imaging, the same strategies (i.e., low-flux or sparse-view acquisition) can be employed as in three-dimensional CT scanning. In 4D-CT and 4D-CBCT, the projection data can be sorted into different groups corresponding to different breathing phases. After phase binning, each phase image can be reconstructed independently with either analytical (e.g., FBP, FDK) or iterative reconstruction methods. Each phase image can also be improved with the methods presented in Section 3.A. However, these methods neglect the highly temporal correlation between the images at successive phases, which could potentially improve the image quality of each phase. The same anatomical features may exist in successive phases, with slight motion and deformation. Therefore, Li et al developed a partial temporal nonlocal means filter for 4D-CT, which uses a partial temporal profile to determine the similarity between pixels and exploits redundant information in both temporal and spatial domains to achieve noise reduction ⁷⁸. In addition, a temporal NLM (TNLM) method was proposed for image enhancement and reconstruction of 4D-CT and 4D-CBCT, to exploit the temporal redundancy among images at successive phases ^{13, 76, 77}.

Let us divide a respiratory cycle into N phases labeled by n=1,2,...,N. The image of phase n is denoted by μ⁽ⁿ⁾ ∈ℝ^J×1, and a periodic boundary condition along the temporal direction is assumed, i.e., μ^{N+1} = μ^{1}. The TNLM regularization model is described as^{13, 76, 77}:

$$U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})=\sum _j\sum _{k\in S{W}_j}{w}_{jk}({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})•\varphi ({\mu }_j^{\{n\}}-{\mu }_k^{\{n+1\}})$$ (29)

where

$$w_{jk}({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})=\frac{exp\left(-{\Vert \mathbf{P}({\mu }_j^{\{n\}})-\mathbf{P}({\mu }_k^{\{n+1\}})\Vert }_{2,a}^2/h^2\right)}{{\displaystyle \sum _{k\in S{W}_j}}exp\left(-{\Vert \mathbf{P}({\mu }_j^{\{n\}})-\mathbf{P}({\mu }_k^{\{n+1\}})\Vert }_{2,a}^2/h^2\right)}$$ (30)

And according to Section 2.B, the TNLM regularization model can also be given as:

$$U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})=\sum _j\varphi \left({\mu }_j^{\{n\}}-\sum _{k\in S{W}_j}{w}_{jk}({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})•{\mu }_k^{(n+1)}\right)$$ (31)

$$U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})=\frac{1}{p}\sum _j{\left(\sum _{k\in S{W}_j}{w}_{jk}({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})•{({\mu }_j^{\{n\}}-{\mu }_k^{\{n+1\}})}^2\right)}^{p/2},0<p<2$$ (32)

It can be seen that the TNLM regularization models are very similar to those described in Section 3.A.2(2), although they exploit neighboring phases instead of a previous high quality image.

1. TNLM-regularized image restoration

Let g^{n} ∈ℝ^J×1 denote the reconstructed image of phase n by the analytical FBP/FDK method from the phase binned projection data. The TNLM-based image restoration or enhancement method for 4D-CT/4D-CBCT can be given as ¹³:

$$\begin{array}{l}\left\{{\mathbf{\mu }}^{\ast \{n\}}\right\}=argmin\sum _{n=1}^N\left\{{({\mathbf{\mu }}^{\{n\}}-{\mathbf{g}}^{\{n\}})}^T({\mathbf{\mu }}^{\{n\}}-{\mathbf{g}}^{\{n\}})+\beta [U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})+U({\mathbf{\mu }}^{\{n-1\}},{\mathbf{\mu }}^{\{n\}})]\right\}\\ =argmin\sum _{n=1}^N\left\{{\Vert {\mathbf{\mu }}^{\{n\}}-{\mathbf{g}}^{\{n\}}\Vert }_2^2+\beta U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})\right\}\end{array}$$ (33)

2. TNLM-regularized image reconstruction

Let y^{n} ∈ℝ^I×1 denote the vector of phase binned line integrals of phase n, A^{n} ∈ℝ^I×J represent the projection matrix of phase n that maps the image μ^{n} into a set of projections corresponding to various projection angles, Σ^{n} ∈ℝ^I×I represent the covariance matrix for phase binned line integrals of phase n, then the TNLM-based image reconstruction method for 4D-CT/4D-CBCT can be described as ^{13, 76, 77}:

$$\begin{array}{l}\left\{{\mathbf{\mu }}^{\ast \{n\}}\right\}=argmin\sum _{n=1}^N\left\{{({\mathbf{y}}^{\{n\}}-{\mathbf{A}}^{\{n\}}{\mathbf{\mu }}^{\{n\}})}^T{\mathbf{\sum }}^{-1\{n\}}({\mathbf{y}}^{\{n\}}-{\mathbf{A}}^{\{n\}}{\mathbf{\mu }}^{\{n\}})+\beta [U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})+U({\mathbf{\mu }}^{\{n-1\}},{\mathbf{\mu }}^{\{n\}})]\right\}\\ =argmin\sum _{n=1}^N\left\{{({\mathbf{y}}^{\{n\}}-{\mathbf{A}}^{\{n\}}{\mathbf{\mu }}^{\{n\}})}^T{\mathbf{\sum }}^{-1\{n\}}({\mathbf{y}}^{\{n\}}-{\mathbf{A}}^{\{n\}}{\mathbf{\mu }}^{\{n\}})+\beta U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})\right\}\end{array}$$ (34)

Also, as discussed in Section 3.A.3(1), Eq. (34) may be replaced with the following form when the X-ray flux is relatively high:

$$\begin{array}{l}\left\{{\mathbf{\mu }}^{\ast \{n\}}\right\}=argmin\sum _{n=1}^N\left\{{({\mathbf{y}}^{\{n\}}-{\mathbf{A}}^{\{n\}}{\mathbf{\mu }}^{\{n\}})}^T({\mathbf{y}}^{\{n\}}-{\mathbf{A}}^{\{n\}}{\mathbf{\mu }}^{\{n\}})+\beta [U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})+U({\mathbf{\mu }}^{\{n-1\}},{\mathbf{\mu }}^{\{n\}})]\right\}\\ =argmin\sum _{n=1}^N\left\{{\Vert {\mathbf{y}}^{\{n\}}-{\mathbf{A}}^{\{n\}}{\mathbf{\mu }}^{\{n\}}\Vert }_2^2+\beta U({\mathbf{\mu }}^{\{n\}},{\mathbf{\mu }}^{\{n+1\}})\right\}\end{array}$$ (35)

In these optimization problems, the images at every phase are reconstructed altogether instead of independently.

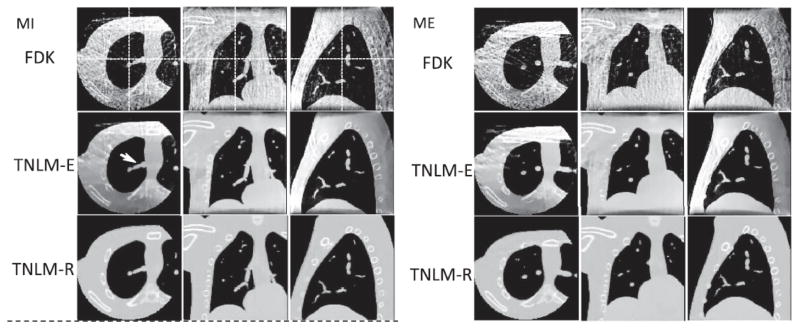
Fig. 8 illustrates the 4D-CBCT images of the NCAT phantom from sparse-view acquisitions (30 projection views spanned evenly in 360⁰ rotation), by the following methods: analytical FDK reconstruction, TNLM-regularized image restoration or enhancement (referred to as TNLM-E) in Eq. (33), and TNLM-regularized image reconstruction (referred to as TNLM-R) in Eq. (35). Both TNLM-E and TNLM-R methods mitigate the view-aliasing artifacts to a large extent, as compared with the FDK method. In the absence of other problems such as data truncation, the TNLM-R method can yield higher image quality than the TNLM-E method ¹³.

Fig. 8.

4D-CBCT images of the NCAT phantom at the maximum inhale (MI) and the maximum exhale (ME) phases generated by three different methods from sparse-view acquisitions. (Figure reprinted from the work of Jia et al ¹³)

Additionally, Kazantsev et al ^{79, 80} argued that structurally similar features may exist in much more distant time frames than simply adjacent ones, although the two neighboring frames have a higher probability to be structurally similar to the central frame. Therefore, they proposed to employ all available temporal data to improve the spatial resolution of each individual time frame. However, this approach would inevitably further increase the computational burden, although the patch selection as in Eq.(10) can be utilized to accelerate the process to some extent.

4. Discussions and Conclusions

This paper reviews various applications of the NLM algorithm in LDCT from low-flux and sparse-view acquisitions. The NLM algorithm can be used as a filter for image/projection filtering, which is a typical non-iterative procedure. The NLM algorithm can also be formulated as a regularization term for regularized image/projection restoration and image reconstruction, routinely performed by optimizing an objective function with an iterative algorithm. Based on the form of objective function, iterative algorithms including gradient descent, conjugate gradient, expectation maximization, iterative coordinate descent, separable paraboloidal surrogates ⁸¹ may be employed to obtain the solution. Moreover, acceleration techniques including ordered subsets ⁸², nonhomogeneous update ⁸³, alternating direction method of multiplier ⁸⁴, first-order method based on Nesterov’s algorithm ⁸⁵ can also be combined. Generally, the computational load of the NLM-regularized strategies is much higher than that of the NLM-based filtering strategies due to iterations. Despite the increased computational time, CT image quality may be remarkably improved. For instance, NLM-regularized image reconstruction takes advantage of projection data (e.g., statistical modeling) and imaging geometry (e.g., projection matrix), and can produce better image quality than NLM-based filtering or restoration strategies, as demonstrated in Fig. 5, Fig. 7, and Fig. 8.

For CT from low-flux acquisitions, the NLM strategies for noise and streak artifacts reduction can operate in both image and projection domains. While the noise and streak artifacts in low-flux CT images cannot be modeled with a general distribution, the noise properties of low-flux projection data are fairly well understood ⁶⁴. Comparing Fig. 7(a) with Fig. 5(b), it is found that the projection denoising performs better than the image denoising in terms of noise and streak artifacts suppression, for this specific patient study. This finding is consistent with the results from a study by Xia et al, who applied a partial diffusion equation based denoising technique for breast CBCT on both projection data and reconstructed images ⁸⁶. However, projection denoising and statistical projection restoration may lose edge sharpness in the ultimate reconstructed image (as shown in Fig. 7), because the edges in the projection domain are usually not as well defined as those in the image domain. Compared Fig. 5(d) with Fig. 7(b), NLM-regularized statistical image reconstruction (operating in image domain) better preserves the edge/detail than the NLM-regularized statistical projection restoration (operating in projection domain). This finding is also consistent with a previous study ⁸⁷ which compared the performances of the image domain and projection domain PWLS implementations using anisotropic diffusion filter-based regularization. Overall, the NLM-regularized statistical image reconstruction in Eq. (21), which optimizes an objective function defined in the image domain and also takes advantage of noise properties of the projection data, seems to yield the best image quality of all NLM strategies.

While the use of previous high quality scan to improve current LDCT image reconstruction has become a research endeavor, one major limitation is that the previous high quality image usually needs be registered to a current low-dose image. The NLM-based strategies do not heavily depend on registration accuracy, hence a rough registration can be sufficient because of the patch-based search mechanism. Because direct filtering of the LDCT image is usually problematic, the introduction of a previous high quality image can significantly improve current low-dose image filtering, as shown in Fig. 2 and Fig. 3. Similarly, a previous high quality image can also be formulated into the NLM-based regularization models, to improve image restoration or reconstruction of the current LDCT. While generic NLM-regularized image restoration or reconstruction may already be able to generate good image quality for LDCT, preHQ-regularized image restoration or reconstruction can potentially further improve image quality or yield as good image from lower dose acquisition. Finally, although preHQ-guided projection data denoising and preHQ-regularized statistical projection restoration can be applied in theory, they may not be practical due to the following reasons: (1) the registration of the projection data is more challenging than the registration of the images; (2) it is more difficult to find sufficient similar patches in the projection data than in the images. Instead, the previous high quality scan-induced NLM strategies in the projection domain can be converted to the image domain strategies (i.e., preHQ-guided image filtering, preHQ-regularized image restoration, and preHQ-regularized statistical image reconstruction) after the FBP reconstruction of previous high quality projection data, so that the edge/detail of the resulting image can be better preserved.

Introducing spatial adaptivity to the NLM algorithm can be beneficial to improve the image quality of LDCT, especially for low-contrast objects and subtle structures, as illustrated in Fig. 5 and Fig. 6. The reason is that uniform smoothing strength can be too weak for some regions but too strong for others within the image, hence the need for spatially-variant adaptive smoothing. Spatial adaptivity can be incorporated into the NLM algorithm in different ways, including designing adaptive filtering parameter h, employing adaptive SW, excluding dissimilar patches within the SW. So far, these adaptive approaches have mainly been explored for generic NLM strategies but rarely for preHQ-induced NLM strategies for two main reasons: (1) it is more difficult to incorporate spatial adaptivity for preHQ-induced NLM strategies because of the introduction of previous high quality image; and (2) it is less important to incorporate spatial adaptivity because the previous high quality image can provide more correspondence to the current LDCT image for structure recovery. However, spatially-variant adaptive smoothing may still be beneficial for preHQ-induced NLM strategies and may be an interesting topic for further investigation. Finally, since anisotropic structure is commonly observed in real-world images, some anisotropic NLM algorithms were also proposed to improve the denoising performance, such as substituting the square patches of fixed size by spatially adaptive shapes ⁸⁸, using image gradient information to estimate the edge orientation ⁸⁹, and incorporating structure tensor into weighing calculation ⁹⁰. Investigation on these strategies for LDCT applications can be another interesting research topic.

While NLM-based strategies have been successfully used in the LDCT scenario, two drawbacks include sophisticated parameter tuning and heavy computational burden. For NLM-based image/projection filtering, four parameters generally need to be tuned: SW size, PW size, standard deviation a of the Gaussian kernel, and filtering parameter h. More parameters may be needed when the adaptive scheme is used. And for NLM-regularized image/projection restoration or image reconstruction, an additional parameter (scalar control parameter β) needs to be selected. Determining the optimal values for these parameters is challenging, and in practice, they are usually set empirically via the extensive trial-and-error process. It was found that SW size, PW size and standard deviation a do not usually have noticeable effects on the reconstructed image when set in a reasonable range; filtering parameter h and control parameter β need to be manually tuned. Also, the superior performance of NLM-based strategies is offset by the cost of increased computational time. One time-consuming procedure is the calculation of patch distance within a large SW. Various schemes have been proposed to speed up this process, including preselecting patches ^{52, 91}, neglecting Gaussian kernel ^{92, 93}, taking advantage of symmetry ¹⁰, and employing GPU for parallel processing ^{10, 94}. For NLM-regularized image reconstruction, employing an iterative algorithm to optimize the objective function is also time-consuming because of multiple re-projection and back-projection operation cycles in the projection and image domains. Many software ^{15, 83–85} and hardware ^95–99 approaches have been investigated to substantially reduce the reconstruction time. With advancements in fast computation through the development of dedicated software and hardware, the computational burden may be not a major challenge in the future, and the NLM-based strategies may move closer for clinical use.

We have only reviewed the applications of the NLM algorithm in a standard LDCT scenario (low-flux or sparse-view acquisition), however, it may also be applied to other low-dose problems such as interior CT and short-scan CT, or to suppress artifacts caused by other imperfections. Moreover, the NLM algorithm may also be used in perfusion CT ^{54, 61, 78, 100}, dual-energy CT ^{101, 102}, and multi-energy CT ¹⁰³ scenarios, although special adjusting strategies are needed to account for changes in pixel intensity due to contrast perfusion or energy differences. We hope this review will motivate more studies in the fields.

Finally, it is worth mentioning that many other filters may potentially be applied to LDCT in similar manners as demonstrated in this review, and the NLM filter is essentially one of them. Because of patch use, NLM-based strategies may yield better image quality than traditional filters-based strategies. Recently, sparse dictionary learning ^{104, 105} has drawn great interest, which also takes advantage of the patches and can be considered as an extension of the NLM algorithm ¹⁰⁶. Successful applications of dictionary learning have been reported in the LDCT scenario for projection denoising ^107–109, image denoising ^110–112 and reconstruction ^113–115. For instance, Chen et al ¹¹² proposed an image-domain artifact suppressed dictionary learning method to suppress the streak artifacts and noise in LDCT image, which designed novel discriminative dictionaries to cancel the streak artifacts in high-frequency bands. Xu et al ¹¹⁴ used the dictionary learning-based sparsification as regularization term in SIR for LDCT, and demonstrated superior performance in noise reduction and structural feature preservation. The other strategies reviewed in this paper may also be explored for dictionary learning in the future.