Optimal reconstruction and quantitative image features for Computer-Aided Diagnosis tools for breast CT

Abstract

Purpose

The purpose of this study is to determine the optimal representative reconstruction and quantitative image feature set for a computer-aided diagnosis (CADx) scheme for dedicated breast computer tomography (bCT).

Method

We used 93 bCT scans that contain 102 breast lesions (62 malignant, 40 benign). Using an iterative image reconstruction (IIR) algorithm, we created 37 reconstructions with different image appearances for each case. In addition, we added a clinical reconstruction for comparison purposes. We used image sharpness, determined by the gradient of gray value in a parenchymal portion of the reconstructed breast, as a surrogate measure of the image qualities/appearances for the 38 reconstructions. After segmentation of the breast lesion, we extracted 23 quantitative image features. Using leave-one-out cross-validation (LOOCV), we conducted the feature selection, classifier training, and testing. For this study, we used the linear discriminant analysis classifier. Then, we selected the representative reconstruction and feature set for the classifier with the best diagnostic performance among all reconstructions and feature sets. Then, we conducted an observer study with six radiologists using a subset of breast lesions (N = 50). Using 1000 bootstrap samples, we compared the diagnostic performance of the trained classifier to those of the radiologists.

Result

The diagnostic performance of the trained classifier increased as the image sharpness of a given reconstruction increased. Among combinations of reconstructions and quantitative image feature sets, we selected one of the sharp reconstructions and three quantitative image feature sets with the first three highest diagnostic performances under LOOCV as the representative reconstruction and feature set for the classifier. The classifier on the representative reconstruction and feature set achieved better diagnostic performance with an area under the ROC curve (AUC) of 0.94 (95% CI = [0.81, 0.98]) than those of the radiologists, where their maximum AUC was 0.78 (95% CI = [0.63, 0.90]). Moreover, the partial AUC, at 90% sensitivity or higher, of the classifier (pAUC = 0.085 with 95% CI = [0.063, 0.094]) was statistically better (p-value < 0.0001) than those of the radiologists (maximum pAUC = 0.009 with 95% CI = [0.003, 0.024]).

Conclusion

We found that image sharpness measure can be a good candidate to estimate the diagnostic performance of a given CADx algorithm. In addition, we found that there exists a reconstruction (i.e., sharp reconstruction) and a feature set that maximizes the diagnostic performance of a CADx algorithm. On this optimal representative reconstruction and feature set, the CADx algorithm outperformed radiologists.

1 Introduction

Investigators are developing dedicated breast Computed Tomography (bCT) systems to improve breast cancer detection and diagnosis. Dedicated bCT allows radiologists to access full 3D volumetric views of breast lesions, which may improve radiologists’ performances when determining the malignancy of given lesions ¹.

To help radiologists achieve better diagnostic performance, researchers are also developing computer aided diagnosis (CADx) schemes to act as a second reader for various imaging modalities, including mammography^2–4, ultrasound⁵ and breast magnetic resonance imaging (MRI)⁶.

Since bCT is a relatively new imaging modality, there are only a few preliminary studies on CADx algorithms for bCT ^7–11. Ray et al. ⁷ trained and tested artificial neural networks (ANN) using morphologic and texture features extracted from lesions in pre- and post-contrasted bCT images. In addition, Kuo et al. ⁹ introduced a 3D spiculation feature that was able to improve the classification performance of a linear discriminant analysis (LDA) classifier by combining it with other traditional quantitative image features. Recently, we introduced novel quantitative image features utilizing the 3D surface information of breast lesions in bCT images ¹¹. These features were total, mean, and Gaussian curvatures summarizing the location variations of the 3D surface curvature of breast lesions. We showed that total curvature holds sufficient information for breast lesion classification such that it can significantly reduce the number of features for a classifier without loss of classification power. All these previous studies showed good performance for classifying malignant and benign breast lesions. However, these studies are limited to one pre-selected reconstruction and trained and tested their models on images reconstructed by one specific algorithm, e.g., Feldkamp-Davis-Kress (FDK) reconstruction¹². It is possible that there are other CT reconstruction algorithms that CADx algorithms work better on than other reconstructions.

In this paper, we investigated various reconstruction algorithms that resulted in various image quality/appearance and evaluated which reconstructions and quantitative image features yielded optimal performance for CADx algorithms in classifying lesions in bCT cases. Using an iterative image reconstruction (IIR) algorithm and changing its variables, we prepared bCT images with different image appearances (or qualities). After that, we segmented the breast lesions in bCT images using an existing algorithm and extracted 23 quantitative image features from the resulting segmentation. Then, we trained and tested a linear discriminant analysis (LDA) classifier for each image appearance to determine the optimal representative reconstruction and quantitative image features for the CADx scheme on bCT images. Then, we compared the performance of the resulting classifier for the selected representative reconstruction to those of radiologists.

2 Methods

2.1 Dataset

This study utilized an image dataset of 137 biopsy proven breast lesions (90 malignant, 47 benign) in 122 non-contrast bCT images of women aged 18 or older at the University of California Davis. Under an institutional review board (IRB) approved protocol, the prototype dedicated bCT system at the University of California at Davis¹ was used to acquire bCT images. Table 1 summarizes the characteristics of the dataset. The image specification was as follows: coronal slice spacing ranged from 200 to 770 μm, and the voxel size in each coronal slice varied from 190 by 190 to 430 by 430 μm, depending on the size of the breast. Figure 1 shows an example of benign and malignant lesions in the dataset.

Table 1.

Characteristics of Breast CT dataset

			All	Selected for train/test the classifier	Selected for the reader study
Subject Age [years]		Mean [min, max]	55.6 [35, 82]	55 [35, 82]	54.6 [37, 82]
Lesion diameter [mm]		Mean [min, max]	13.5 [2.3, 35]	13.4 [2.3, 32.1]	13.3 [4.3, 29.2]
Breast Density		1	16	11	5
		2	51	36	20
		3	51	38	17
		4	19	17	8
Diagnosis*	All lesions	Total	137	102	50
	Malignant	IDC	61	41	18
		IMC	13	10	5
		ILC	8	6	1
		DCIS	7	5	1
		Lymphoma	1	0	0
		Total	90	62	25
	Benign	FA	20	17	11
		FC	7	4	3
		FCC	4	4	1
		PASH	2	2	2
		CAPPS	2	2	2
		Other benign lesions such as sclerosing adenosis and cyst	12	11	6
		Total	47	40	25

^*IDC: Invasive Ductal Carcinoma, IMC: Invasive Mammary Carcinoma, ILC: Invasive lobular Carcinoma, DCIS: Ductal Carcinoma In Situ, FA: Fibroadenoma, FC: Fibrocystic, FCC: Fibrocystic changes, PASH: Pseudoangiomatous stromal hyperplasia, CAPPS: columnar alteration with prominent apical snouts and secretions.

Figure 1.

This figure shows example breast volumes for malignant (top two rows) and benign (bottom two rows) lesion cases with expert’s manual outlines overlaid.

2.2 Image reconstructions and quantification of reconstructed image qualities

Different image reconstructions produced different image appearances and therefore affected the segmentation and classification performance of automated algorithms ¹³. It is possible that there exists a certain image appearance that allows a given CADx algorithm to work better than others. Thus, we utilized an iterative image reconstruction (IIR) algorithm ¹⁴ to create a set of reconstructed images upon which we determined the performance of the CADx algorithm. We also included a clinical reconstruction, i.e., Feldkamp-Davis-Kress (FDK) reconstruction¹², for comparison purposes.

Briefly, the IIR algorithm¹⁴ we used in this study consisted of two sub reconstruction algorithms; one algorithm reconstructs an image holding the gray-scale information, while another algorithm reconstructs the same image holding the edge information. By combining the resulting reconstructions from the two sub-algorithms with different weights, we obtained reconstructed images with different appearances (or qualities).

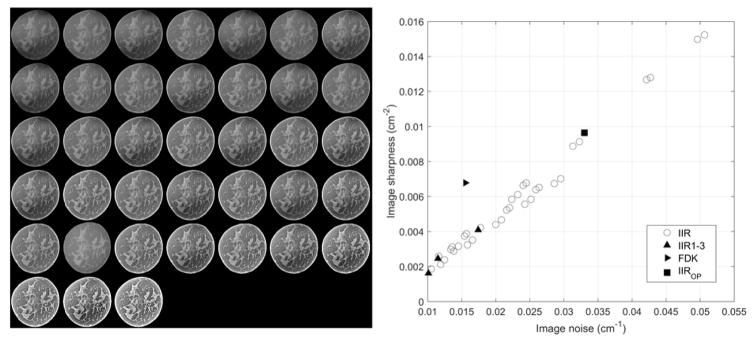
We reconstructed 37 versions of CT images using the above IIR algorithm, and using the FDK reconstruction we had a total of 38 versions of CT images. The left figure of Figure 2 shows an example of the coronal views of a breast for the 38 different reconstructions.

Figure 2.

The left side shows an example of the coronal views of a breast for the 38 different reconstructions used in this study. We ordered the views in terms of their sharpness values (from left to right and from top to bottom, the image sharpness increases). The right side shows the scatter plot of image appearance values (i.e., noise and sharpness) for all 38 reconstructions. IIR1-3 and FDK refer to IIR and FDK reconstruction cases used for the observer study. IIR_OP indicates a candidate reconstruction we found in this study for a CADx algorithm.

To quantify the appearance/quality of each reconstruction, we used the standard deviation of a homogeneous portion (σ_sig) of an example breast in each reconstruction and the gradient of a parenchymal portion (∇_sig) of the same example breast in each reconstruction as an estimate of noise and sharpness of each reconstruction, respectively. Specifically, we manually selected one fatty area in an example breast as the region of interest (ROI) for the image noise statistic and computed the image noise using a cube with a 10 mm edge length. Likewise, using the same size cube and same example breast, we selected one breast fibroglandular area as the ROI to compute the image sharpness statistic. We repeated this process for all 38 reconstructions using the same selected fatty and fibroglandular areas of the same breast to compute image statistics for all 38 reconstructions. The image noise values for all reconstructions ranged from 0.01 to 0.024 (1/cm), while the image sharpness values ranged from 0.002 to 0.015 (1/cm²). The right figure of Figure 2 shows the scatter plot of image noise and image sharpness of each reconstruction considered in this study. We found that there was a strong positive correlation between the image noise and sharpness (rho = 0.98). Thus, we selected the image sharpness as a surrogate measure of image appearance/quality for each reconstruction.

2.3 Segmentation of breast lesions

We utilized a semi-automated segmentation algorithm^{15, 16} to segment breast lesions in all reconstructions. The algorithm needed a seed point (i.e., lesion center) to segment a given lesion. Therefore, a research specialist, with over 15 years of experience in mammography, provided the seed point for the algorithm. Note that we repeated the lesion segmentation process using the above algorithm for all 38 reconstruction cases. Thus, the resulting segmentation outcomes were similar, but different from one reconstruction to another reconstruction.

As poor segmentation can affect the classification performance of a classifier, we evaluated the segmentation outcomes for all lesion cases in all 38 reconstructions and removed any lesions with poor segmentation outcomes. If one lesion in one reconstruction showed poor segmentation quality, we removed that lesion for all 38 reconstructions. We used the DICE coefficient¹⁷ to evaluate the segmentation results by comparing the algorithm’s output to that of the above research specialist. Previous studies reported that segmentations with a DICE coefficient of 0.7 or higher shows good quality¹⁸. Among 137 lesions, we removed a total of 35 lesions (29 bCT images) with poor segmentation outcome (N = 21 lesions with DICE coefficient less than 0.7) or missing data/information (N = 14 lesions, missing seed point or manual segmentation outline data for either IIR or FDK reconstructions). Thus, this study used 102 breast lesions (62 malignant, 40 benign) from 93 bCT images for developing a breast CADx algorithm (Table 1).

2.4 Quantitative image features for breast tumor classification

We extracted a total of 23 quantitative image features from the segmentation results (Table 2). These image features have been used in previous studies for lesion detection and classification ^7–11. The 23 quantitative image features describe various types of information of the segmented lesions that include four histogram, seven shape, five margin, four texture, and three surface curvature descriptors. Histogram descriptors^{7, 8} mainly summarize the gray value variations between the lesion and the background. Shape and margin descriptors^{7, 8} characterize the morphological variations in the whole lesion volume and the margin, respectively. The texture descriptors¹⁰ (3D version of gray-level co-occurrence) quantify lesion texture. In addition, the surface curvature descriptors¹¹ summarize the variations over the given lesion surface. Note that surface curvature descriptors are based on the 3D surface representation (i.e., shallow shell covering the lesion) of a given lesion, while margin descriptors are based on the volumetric representation (i.e., margin with depth) of a given lesion.

Table 2.

List of image features used in this study

Histogram descriptors	Definition*
F1. Average region gray value [HU]	μ (Gray value in V)
F2. Region contrast [HU]	F1 - μ (Gray value outside of V)
F3. Region gray value variation [HU]	σ (Gray value in V)
F4. Margin gray value variation [HU]	σ (Gray value in M)
Shape descriptors
F5. Irregularity	2.2 × V1/3 / M1/2
F6. Compactness	% of volume of V included in SP
F7. Ellipsoid axes min-to-max ratio	Min to max ratio of semi-axes of the ellipsoid fitted to V
F8. Margin distance variation [mm]	σ (distances from the center of V to the margin of V)
F9. Relative margin distance variation	F8 / μ(distances from the center of V to the margin of V)
F10. Average gradient direction	μ (gradient direction of each voxel in M)
F11. Margin volume [mm3]	Σ (voxels in M)
Margin descriptors
F12. Average radial gradient [HU]	μ (radial gradient of each voxel in M)
F13. Radial gradient index (RGI)	F12 / μ (magnitude of image gradient of each voxel in M)
F14. Margin strength 1	μ (magnitude of image gradient of each voxel in M) / F2
F15. Margin strength 2	σ (magnitude of image gradient of each voxel in M) / F2
F16. Radial gradient variation	σ (radial gradient of each voxel in M)
Texture descriptors
F17. GLCM|Energy	3D version of 2D gray-level co-occurrence | Energy
F18. GLCM|Contrast	3D version of 2D gray-level co-occurrence | Contrast
F19. GLCM|Correlation	3D version of 2D gray-level co-occurrence | Correlation
F20. GLCM|Homogeneity	3D version of 2D gray-level co-occurrence | Homogeneity
Surface Curvature descriptors
F21. Total Curvature	μ (|p1| + |p2| over S) / σ (|p1| + |p2| over S)
F22. Mean Curvature	μ ( 0.5 × (p1 + p2) over S) / σ (0.5 × (p1 + p2) over S)
F23. Gaussian Curvature	μ ( p1 × p2 over S ) / σ ( p1 × p2 over S )

^*V refers to the segmented lesion volume. M refers to the margin of the lesion volume. SP refers to the minimum sphere including V. S refers to the surface of V. p₁ and p₂ refer to the first and second principal component of S. μ and σ indicate mean and standard deviation.

2.5 Feature selection, classifier training and testing

We used leave-one-out-cross-validation (LOOCV) to select features, train a classifier, and test the resulting classifier. As there are 38 reconstructions for each bCT exam, we repeated the method described below for all 38 reconstructions.

Among the 23 features, we used a feature selection technique (sequentialfs in MATLAB) to select a few features with the most diagnostic information to classify breast lesions. Note that there may be a few set of features that are correlated to each other by definition, e.g., average radial gradient (F12) and radial gradient index (F13). Sequentialfs function utilizes 10-fold cross validation by default to include only meaningful features to classify breast lesions. Thus, the sequentialfs function can remove any redundant or highly correlated features for the subsequent step, i.e., training an LDA classifier. In addition, the feature selection algorithm stopped selecting features when the sum squared error (SSE) was less than the predefined criteria, which we set as f(x = 0.95, degree of freedom = 1) = 3.84, where f is a Chi-square inverse cumulative distribution function. The number of selected features for training a classifier under each LOOCV training samples typically ranged from two to five. Then, within the same LOOCV training samples, we trained an LDA classifier. We set the biopsy results of each lesion and the corresponding selected image features as dependent variables and independent variables for the LDA classifier, respectively. Then, we evaluated the classification performances of the resulting LDA classifier on a held-out sample. We utilized the area under the receiver operating characteristic curve (AUC) as a figure of merit.

We evaluated the performance of the resulting classifiers on 38 reconstructions in terms of the image quality, i.e., image sharpness of 38 reconstructions. Specifically, we investigated which features were selected for various image qualities and their corresponding classifiers’ AUCs to determine optimal representative reconstruction and quantitative image features for CADx on bCT images.

2.6 Observer study

In our previous study, we investigated radiologists’ diagnostic performances on different breast CT image appearances ¹⁹. We utilized this observer study data to compare the performance of the CADx algorithm on the optimal representative reconstruction to those of the radiologists. Briefly, we recruited a total of six MQSA radiologists (with at least15 years in practice) in specialized in breast imaging for the observer study. We selected four reconstructions (three IIRs and FDK) that spanned a range of smooth to sharp image appearances (Figure 2). We refer to these reconstructions as IIR1, IIR2, IIR3, and FDK. We also sampled 50 lesions (25 malignant, 25 benign) for the observer study to reduce the burden of radiologists reading 408 cases (102 lesions in 4 different reconstructions) to 200 cases (50 lesions in 4 different reconstructions). We divided 200 cases into four study sessions; each session consisted of 50 randomly presented lesions and four selected reconstructions. Radiologists were able to complete up to two sessions during each study visit. However, to reduce the memory effect, we asked radiologists to come back at least one week after their last study visit. We provided entire breast volume per case such that radiologists were able to dynamically move through the slices in sagittal, transverse, and coronal planes. We highlighted and centered target lesions in the viewer center. In addition, radiologists were able to zoom in and out, adjusting contrast level of the displayed breast volume. Each radiologist provided the probability of malignancy with a scale of [0, 100], where 0 indicates absolutely benign and 100 indicates absolutely malignant, for each displayed lesion. We evaluated each radiologist’s diagnostic performance on different image appearances (i.e., smooth to sharp appearance, IIR1 to FDK) using the AUC values.

For the 50 cases, the AUC of the six radiologists ranged from 0.73 to 0.86 for the IIR1 – 3 and FDK reconstructions (Table 3). The purpose of this study was to determine optimal reconstructions and feature sets, and to compare the trained CADx algorithm on the optimal reconstruction and feature set against a pool of radiologists. Thus, we averaged radiologists’ diagnostic performances for each of four selected reconstructions (IIR1-3 and FDK) and treated them as surrogates from a population of radiologists’ diagnostic performances for those selected reconstructions. To reduce individual radiologist’s variations in diagnostic tasks, we used the non-parametric method²⁰ to average radiologists’ ROC curves.

Table 3.

The diagnostic performances (AUC) of radiologists on each reconstruction.

Reconstruction	IIR #1	IIR #2	IIR #3	FDK
Image Sharpness	Low	→		High
Radiologist #1	0.74	0.79	0.73	0.81
Radiologist #2	0.81	0.78	0.79	0.80
Radiologist #3	0.72	0.70	0.74	0.76
Radiologist #4	0.82	0.84	0.81	0.89
Radiologist #5	0.86	0.77	0.85	0.78
Radiologist #6	0.80	0.71	0.75	0.70
Averaged	0.78	0.76	0.77	0.77

2.7 Comparing CADx and radiologists diagnostic performances

It may not be possible to directly compare the performance of the CADx algorithm on the optimal representative reconstruction to that of the radiologists in the current setup, as we sub-sampled the cases (N = 50) for the observer study, instead of using all cases (N = 102), which we used to develop the classifier.

To properly compare the performance of the CADx and that of the radiologists, we used the .632+ bootstrap to train and test the classifier ²¹ and compare its performance to the consolidated performance of the radiologists. Briefly, N lesion cases are sampled with replacement, and then one can observe 0.632N unique cases and 0.368N redundant cases on average from each bootstrap sample. In this setup, we used the first 0.632N unique cases for training the classifier and used the other remaining 0.368N cases for testing it. Among 0.368N test cases, we matched the cases that were used for the observer study, which were 0.184N test cases on average. We compared the performance between the classifier and the radiologists on these unique 0.184N test cases. For each 0.184N test cases, we conducted ROC analysis on the classifier and the radiologists and estimated their AUC values following the method described in the .632+ bootstrap ²¹. We repeated this for 1000 bootstrap samples. Figure 3 shows the diagram illustrating how we divided each bootstrap sample for training and testing the classifier.

Figure 3.

Diagram shows how we divided each bootstrap sample (a total of 1000 samples) to train and test the classifier, and compare the performance of the classifier to that of radiologists.

3 Results

3.1 Optimal reconstruction and quantitative image features for the classifier

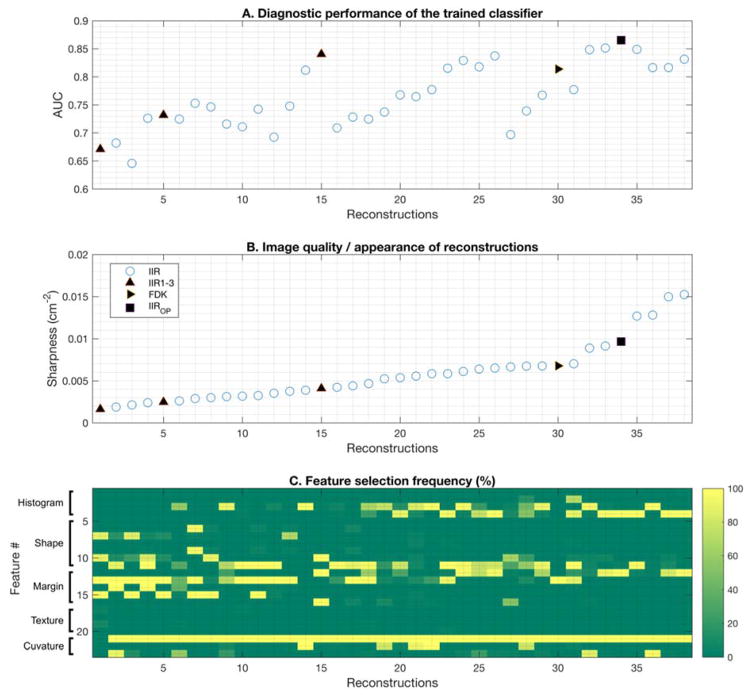
Under the LOOCV, we performed feature selection and classifier training on the training set and tested the resulting classifier on the hold-out data. This process was repeated for all 38 reconstructions. The diagnostic performance of the trained classifiers in terms of AUC ranged from 0.64 to 0.88 (Figure 4.A).

Figure 4.

This figure shows the selected features for the classifier and its diagnostic performances on each reconstruction. A shows the AUC of the classifier on each reconstruction. B shows the sharpness of each reconstruction. C shows the selection frequency of each feature in the classifier for each reconstruction. Feature #1 – #4, #5 – #11, #12 – #16, #17 – #20, and #21 – #23 represent histogram, shape, margin, texture, and curvature features, respectively. As sharpness increased, the diagnostic performance of the classifier improved (A and B). Overall, the total curvature feature (Feature #21) was selected 100% for all reconstructions except the smoothest reconstruction. For smooth reconstruction, the classifier frequently used the shape and margin descriptors. For sharp reconstruction, the classifier frequently used the margin and histogram descriptors. As images got sharper, the type and the number of selected features were reduced and stabilized.

As an image became sharper, the diagnostic performance of the classifier improved, although the improvement became saturated (or plateaued) at very sharp reconstructions, as shown in Figure 4.A and B. Among all reconstructions, reconstruction #34 achieved the highest diagnostic performance (AUC = 0.88), followed by reconstruction #15 (AUC = 0.85) and #30 (AUC = 0.82).

For each reconstruction, different sets of features were selected to train the classifier. The feature selection chose the total curvature feature (F21 in Table 2) for all reconstruction cases except the smoothest reconstruction (i.e., Reconstruction #1, in Figure 4.B). Thus, we concluded that the total curvature feature is the most important feature for the classifier with the best diagnostic information for all reconstructions.

The feature selection frequently selected shape descriptors (F5 – F11) and margin descriptors (F12 – F16) for smooth reconstructions (Reconstruction #1– #19), and histogram (F1 – F4) and margin descriptors for sharp reconstructions (Reconstruction #20 – #38). However, the classifier performed better on sharper reconstructions than on smoother reconstructions. Thus, this trend indicates that more diagnostic information can be obtained as the image gets sharper, and that histogram and margin descriptors contain more relevant information for classification.

In general, the trained classifier performed better when the number of selected features was small (N < 5); the trained classifier for reconstructions #15, #26, and #34 held only 2 – 4 features and achieved high AUC values (0.85 or higher). In addition, we can observe that there was a performance drop (e.g., from Reconstruction #15 to #16, and from Reconstruction #26 to #27) when the classifier held more weak features. In fact, the classifiers with low AUC values (e.g., reconstruction #6, #26, #27) tended to have high variations in selected features during the feature selection step in LOOCV, while the selection step selected consistently a few strong or robust features for the classifiers with high AUC values (e.g., reconstruction #15, #30, #34).

In addition, we observed a few set of features were oscillating across reconstructions, e.g., margin strength 1 (F14) and margin strength 2 (F15) for smooth reconstructions (reconstruction #1 – #10), region gray value variation (F3) and margin gray value variation (F4) for sharper reconstructions (reconstruction #17 – #38). By definition, there is a correlation between these features (Table 2), and they were indeed highly correlated in our dataset (Pearson’s rho > 0.7). However, as we mentioned previously, the feature selection algorithm we used for this study utilizes 10 fold cross-validation to remove highly correlated features. Thus, only a few of those highly correlated features were selected within each reconstruction case (i.e., each column in Figure 4.C). For instance, only margin strength 1 (F14) was frequently selected over margin strength 2 (F15) for reconstructions #1, #3, and #5, while we observed a completely opposite trend for reconstructions #2, #4, and #6.

Reconstruction #34 used margin gray value variation (F4), average radial gradient (F12), and total curvature (F21) features, and achieved an AUC of 0.88. Reconstruction #15 used average gradient direction (F10), average radial gradient (F12), radial gradient variation (F16), and total curvature (F21) features, and achieved an AUC of 0.85. Reconstruction #30 used radial gradient index (F13) and total curvature (F21) features, and achieved an AUC of 0.82. We concluded that these reconstructions and feature sets are possible candidates for the optimal reconstruction and feature set for CADx algorithms. Thus, we re-evaluated the diagnostic performance of the classifier with the above feature sets and reconstructions to select the optimal feature sets and reconstructions for CADx algorithms. Note that we fixed the features of the classifier to be trained on one of the above three feature sets in this subsequent analysis.

Among the candidate feature sets and reconstructions, the feature set of margin gray value variation (F4), average radial gradient (F12), and total curvature (F21) on reconstruction #34 showed the highest AUC values than others (Table 4). Thus, we selected reconstruction #34 and the feature set of margin gray value variation (F4), average radial gradient (F12), and total curvature (F21) as the representative reconstruction and feature set and compared its diagnostic performance to that of radiologists in the following section. We refer to the selected reconstruction #34 as IIR_OP.

Table 4.

Performance of the classifier on selected feature sets and reconstructions

Classifier diagnostic performance (AUC) under LOOCV
Fixed feature sets	Reconstruction #
	#34	#15	#30
Margin gray value variation (F4), Average radial gradient (F12), Total curvature (F21)	0.9	0.85	0.77
Average gradient direction (F10), Average radial gradient (F12), Radial gradient variation (F16), Total curvature (F21)	0.88	0.87	0.8
Radial gradient index (F13), Total curvature (F21)	0.87	0.85	0.82

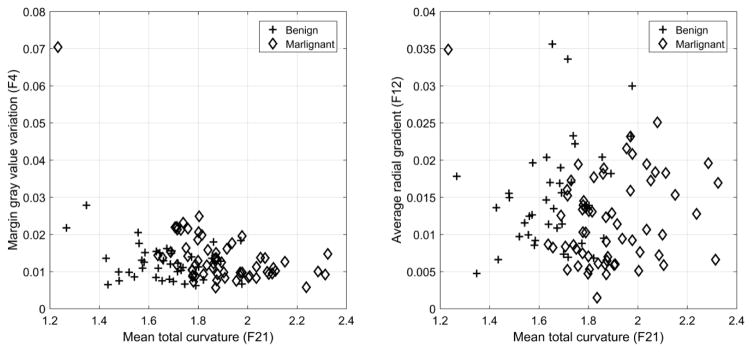
Figure 5 shows the distributions of benign and malignant lesions in the space spanned by the above three features selected for the classifier on the IIR_OP. Malignant lesions tended to have higher margin gray value variation (F4) and total curvature (F21) values and lower average radial gradient (F12) values than benign lesions. Note that there was one malignant lesion with a low total curvature value (left upper corner in Figure 5). Using total curvature (F21) only, this lesion fell into the benign lesion category. However, this lesion had a high value for F4, making it fall into the malignant lesion category.

Figure 5.

This figure shows the scatter plots of the selected features (F4, F12, and F21) for the classifier on the reconstruction #34. Malignant lesions tended to have higher Margin gray value variation (F4) and Total curvature (F21) values and lower Average radial gradient (F12) values than benign lesions.

3.2 Performance comparison between the classifier and radiologists

As previously explained, we used the entire dataset (N = 102) to develop classifiers and used a subset (N = 50) for the observer study. We used the .632+ bootstrap sampling method²¹ with 1000 bootstrap samples to compare the diagnostic performance of the classifiers from the previous section and those of the radiologists.

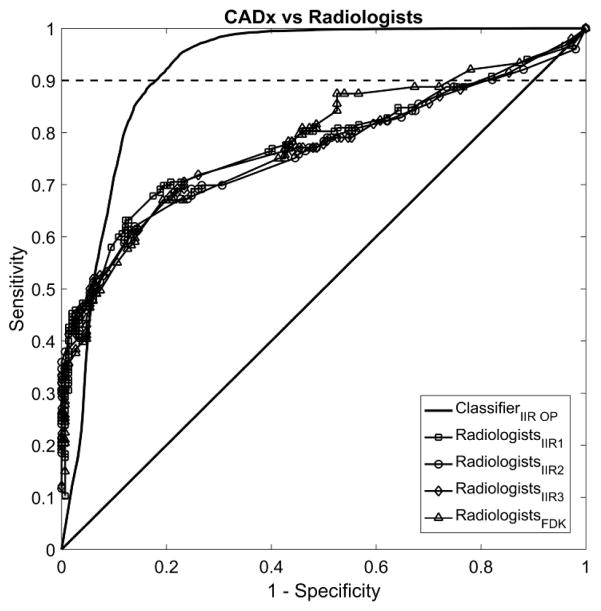
CADx performance on the optimal reconstruction and with the optimal feature set reached an AUC of 0.94 (95% CI: [0.81, 0.98]), while the AUCs for the radiologists ranged from 0.76 to 0.78 (Table 5 and Figure 6). As we repeated the comparisons between CADx and radiologists, we corrected the significance level using the Bonferroni correction; the corrected significance level was 0.05/4 = 0.0125. For all cases, the 95% confidence intervals of the differences in diagnostic performance between the CADx algorithm and radiologists were positive (0.03 – 0.34). However, they were not statistically significant, as their p-values were higher than the corrected significance level 0.0125.

Table 5.

Diagnostic performance comparison in AUC between the classifier and the radiologists

Performance Comparison (AUC)			Difference in AUC
CADx	Radiologists		AUCL – AUCR [95% CI]	p-value
AUCL [95% CI]	Reconstructions	AUCR [95% CI]
0.94 [0.81, 0.98]	IIR1	0.78 [0.63, 0.90]	0.16 [0.03, 0.33]	0.034
	IIR2	0.76 [0.62, 0.88]	0.18 [0.04, 0.34]	0.019
	IIR3	0.77 [0.63, 0.89]	0.17 [0.04, 0.32]	0.016
	FDK	0.77 [0.64, 0.89]	0.17 [0.04, 0.31]	0.019

^*Statistically significant (p-value < 0.0125).

Figure 6.

This figure shows the averaged empirical ROC curves of the CADx and for the six radiologists. The CADx achieved an average AUC of 0.94, which was higher than the radiologists for all 4 reconstructions (IIR1-3 and FDK with AUC of 0.76 – 0.78). The differences did not reach statistical significance after correcting for multiple comparisons. For the partial AUC at 90% sensitivity or higher, i.e., the area between the ROC curve and the dashed line in the figures, CADx showed a statistically better performance than the radiologists on all reconstructions.

In clinical practice, both CADx and radiologists rarely operate at a low sensitivity level for classifying the malignancy of lesions. In this respect, comparing the partial AUC with the sensitivity level above the preselected threshold is more desirable ^22–24. Thus, we computed the partial AUC at 90% sensitivity or higher for both CADx and radiologists. Note that the maximum value for the partial AUC for this scenario is 0.1. The partial AUC at 90% sensitivity or higher for the CADx algorithm was 0.085 (95% CI: [0.063, 0.094]) and it was higher than the radiologists (Table 6 and Figure 6). The difference between the partial AUCs of the radiologists and the CADx was statistically significant (p-values <0.0001).

Table 6.

Diagnostic performance comparison in AUC between the classifier and the radiologists over sensitivity 90 or higher.

Performance Comparison (AUC) over sensitivity 90 or higher			Difference in AUC
CADx	Radiologists		AUCL – AUCR [95% CI]	p-value
AUCL [95% CI]	Reconstructions	AUCR [95% CI]
0.085[0.063, 0.094]	IIR1	0.003 [0, 0.015]	0.061 [0.04, 0.086]	<0.0001*
	IIR2	0.006 [0, 0.026]	0.069 [0.041, 0.089]	<0.0001*
	IIR3	0.009 [0.003, 0.024]	0.085 [0.063, 0.094]	<0.0001*
	FDK	0.004 [0, 0.031]	0.034 [0.013, 0.063]	<0.0001*

^*Statistically significant (p-value < 0.0125).

4 Discussion

In this study, we searched for the best reconstruction algorithm and feature set for a CADx tool for dedicated bCT over a wide range of reconstructions. We found that sharper reconstructions yielded better diagnostic performance for a CADx classifier than smoother reconstructions. This shows that image sharpness is a good indicator to estimate the diagnostic performance of a CADx algorithm for this particular task. In addition, we found that total curvature, which is a surface descriptor of lesions, holds the most diagnostic information compared to the other features. By combining the total curvature feature with a few histogram and margin descriptors, the resulting CADx algorithm achieved an AUC of 0.88 for one of many sharp reconstructions under the LOOCV. Then, we compared the diagnostic performance of the resulting CADx algorithm on the representative reconstruction and feature set to those of radiologists. We found that the CADx algorithm performed better than the radiologists, especially for the case when comparing the partial AUC at 90% sensitivity or higher.

Our data clearly showed that a CADx algorithm should be operated at sharp reconstructions to achieve its best diagnostic performance, while the radiologists performed similarly for smooth to sharp reconstructions. If we set the operating point for the CADx scheme at 90% sensitivity, the resulting specificity of the classifier will be approximately 82%, while radiologists will have a specificity of approximately 30% – 36% at the same sensitivity level (Figure 6). From this, we can expect that radiologists would recommend biopsies for more benign lesions than the CADx scheme on the representative reconstruction and feature set. Unnecessary biopsies can cause adverse effects on patients, such as anxiety and discomfort/pain. As the classifier showed the better specificity, we may expect that the CADx tool may help radiologists to reduce unnecessary biopsies for benign breast disease.

We showed that image sharpness is a good predictor to estimate the diagnostic performance of a given CADx algorithm on a given reconstruction. However, one needs to note that there may be more image quality/appearance descriptors available. As shown Figure 4.A, we can see that there were performance drops of the trained classifier from reconstruction #15 to reconstruction #16, and from reconstruction #26 to reconstruction #27. The image sharpness alone cannot explain these performance drops. Finding other image quality/appearance descriptors that can explain these performance drops would be good follow-up research of this study.

We showed that the optimal feature set for the CADx algorithm included features F4, F12, and F21, which are margin gray value variation, average radial gradient, and total curvature, respectively (Table 2). As the value of the mean total curvature and the margin gray value variation increases, while the value of average radial gradient decreases, the probability of a lesion being malignant increases (Figure 5). The margin gray value variation is defined as the standard deviation of gray level voxel values around the lesion margin (Table 2). In addition, the total curvature is defined as the averaged and normalized absolute sum of two principal curvatures over the segmented three-dimensional lesion surface ¹¹. As the value of total curvature increases, the lesion surface becomes more curved (or bumpy). Moreover, the average radial gradient is defined as the mean value of radial gradient over a segmented lesion margin ²⁵. If the lesion is a perfect sphere, the value of the average radial gradient is maximized. Therefore, as the average radial gradient value decreases, the more the morphological shape of the segmented lesion deviates from the shape of a sphere. Thus, malignant lesions tend to show higher gray value variation in their margin (F4), tend to have a more curved (or bumpy) surface (F21), and tend to be more deviated from the shape of a sphere (F12) than benign lesions. Figure 5 clearly shows this trend as well; malignant lesions tended to have lower F12 values and higher F4 and F21 values.

One may raise the question whether there was possible sampling bias due to the nature of the subsampled bCT cases for the observer study. To check if the selection of 50 cases out of 102 cases biased the diagnostic performance of the classifier and the radiologists, we conducted correlation analysis on the AUC values between each group of radiologists and the classifier on the 0.184N test samples. If the AUC values of the classifier and the radiologists are not correlated, then we can conclude that the selected 50 cases did not introduce meaningful bias to the classifier. Even if they are correlated, then we can conclude that there exists a positive bias on the AUC, but both the radiologists and the classifier gained the same advantage. If they have a strong negative correlation (i.e., large correlation coefficient value), then we can conclude that the comparison in the AUC values between the radiologists and the classifier are unfair, as only the classifier gained the advantage due to the sub-sampling of the 50 cases. We used a Bonferroni correction to correct significant level to account for repeated comparisons. The corrected significance level was 0.05/4 = 0.0125.

For all cases, we found that there was a positive or no correlation in the diagnostic performances (in terms of AUC) between the CADx algorithm and each group of radiologists (Table 7). Thus, we can conclude that there was no meaningful sampling bias that made the comparison in the diagnostic performance between the radiologists and the CADx algorithm to be unfair.

Table 7.

Correlation in AUC between radiologists and CADx among bootstrap samples

Reconstructions	Correlation Coefficient	p-value
IIR #1	0.0725	0.022
IIR #2	0.0695	0.028
IIR #3	0.1167	0.0002*
FDK	0.1462	<0.0001*

^*Statistically significant (p-value < 0.0125).

However, there still exists a chance that the CADx performance on the 50 lesions was optimistically biased, such that the remaining 52 breast lesions may degrade the performance of the CADx algorithm. To prove or refute this, future observer studies with matched samples for both radiologists and the CADx tool will be required. Of course, this future study can be combined with the above follow-up study with larger and independent datasets.

Another possible limitation of our study is that we studied only a subset of all possible image reconstructions. It is possible that some other reconstruction would give either higher performance or select a different optimal feature set, or both. However, the main conclusion that a given CADx algorithm performs better on sharper images would still be valid. A future study with additional reconstructions will be required to confirm this.

In addition, it is possible that we may have introduced a bias on CADx performances when we removed the breast lesion cases with poor computer segmentation outcomes. Note that we utilized one specific computer algorithm to segment breast lesions for the CADx development. As research on developing better computer segmentation algorithms for bCT is ongoing, new and improved computer segmentation algorithms for bCT will be available in future. With the improved algorithms, we may be able to reduce the number of lesions with poor segmentation outcomes, such that we can reduce the possible bias on subsequent CADx diagnostic performances. Searching improved computer segmentation algorithms and conducting follow-up analysis using those algorithms is a potential future study.

An additional limitation of our study is that we treated only cases as a random effect, while we treated the radiologists as a fixed effect in our statistical analysis. The proper way to compare the diagnostic performance of a CADx algorithm and that of radiologists would be to treat both cases and radiologists as random effects; however, there is currently no published method available for such comparison. Once the method is established, we will be able to confirm our finding.

Although we found the optimal reconstruction and feature set for a CADx algorithm for bCT cases, the methodologies described in this manuscript can be extended to other imaging modalities, such as breast MRI or chest CT, where active research is ongoing for developing CADx algorithms. Additional future direction of this research will include exploring the best reconstruction and feature sets for CADx algorithms for those imaging modalities.

In conclusion, this study found that image sharpness measure can be a good candidate to estimate the diagnostic performance of a given CADx algorithm. In addition, we found that there exists a certain reconstruction (i.e., sharp reconstruction) and feature set (margin gray value variation, average radial gradient, and total curvature features in Table 2) that maximizes the diagnostic performance of a CADx algorithm. On this optimal representative reconstruction and feature set, the CADx algorithm performed better than the radiologists.