Monte Carlo study of the chamber-phantom air gap effect in a magnetic field

Abstract

Purpose

The aim of this study was to examine the effect of sub-millimeter air gaps that may exist between an ionization chamber and solid phantoms when measurements are performed in a magnetic field.

Methods

Geant4 Monte Carlo simulations were performed using a model of a PTW 30013 Farmer chamber in a water phantom. Symmetrical and asymmetrical air gaps of various thicknesses were modeled surrounding the chamber, and the dose to the air cavity of the chamber was scored in each case. Magnetic fields were modeled parallel to the long axis of the chamber with strengths of 0, 0.35 T, 1.0 T and 1.5 T. To examine the phenomenon in more detail, the gyroradii of the electrons responsible for the energy deposited in the chamber were scored as they entered the chamber and the total energy deposited was split into three components: energy originating from inside the chamber, in the immediate vacinity of the chamber, or outside the chamber.

Results

Differences in the chamber dose of 1.6% were observed for asymmetric air gaps just 0.2 mm thick. No effect greater than 0.5% was observed for the symmetrical air gaps investigated in this work (1.4 mm thick or less) for this chamber/magnetic field configuration. The mean gyroradius of contributing electrons as they first enter the chamber was 4 mm. The presence of the air gap reduced the energy contributions from electrons released in the immediate vicinity of the chamber, and this loss was not completely compensated for when a magnetic field is present.

Conclusions

The gyroradius of most electrons was too large to be responsible for the air gap effect via the electron return effect; instead, the effect is attributed to the loss of energy contributions from electrons originating inside the air gap volume, which is not completely compensated for by more distant electrons owing to their reduced range in the magnetic field. When the chamber is parallel with the magnetic field, symmetric air gaps have a smaller effect (<0.5%) compared to asymmetric air-gaps (up to 1.6%) in the chamber response.

I. INTRODUCTION

Many groups are currently developing linear accelerators (linacs) with integrated magnetic resonance imaging (MRI).^1–4 The design of these MR-linacs differs significantly from conventional machines and usually involves positioning patients or phantoms inside a cylindrical MRI bore. This bore restricts the space available for the dosimetry equipment that is used for commissioning and routine quality assurance (QA). In particular, full-sized water tank phantoms are too large to be placed inside the bore; moreover, although some degree of water tolerance is to be expected from such devices, smaller phantoms still present a risk of significant water spillage onto the equipment. Consequently, water-equivalent plastic phantoms are an attractive alternative for routine QA because of their compact size, reduced risk of spillage, and ease of use.

However, readings from ionization chambers can be perturbed when placed inside conventional solid water phantoms in a magnetic field.^5–9 This effect manifests as an increase in the orientation dependence of the chamber when rotated about its long axis, with variations for the PTW 30013 Farmer chamber of more than 1% observed by Hackett et al.⁵, for an air gap likely to be on the order of 0.1 mm thick, and up to 3.8% observed by Agnew et al.⁹ for a 0.3 mm asymmetric air gap. We previously reported similar variations.⁸ Agnew et al.⁹ also saw variations as high as 8.5% for the small volume PTW 31006 chamber. Because this effect disappears when the chamber is used in a water phantom⁵, it has been attributed to the presence of small pockets of air trapped between the chamber and the plastic phantom material. Malkov and Rogers¹⁰ used EGSnrc (modified to account for the magnetic field) to simulate the effect of a 0.5 mm and 1 mm uniform air gap surrounding a modeled NE2571 chamber and found that such gaps can change the response by up to 1% depending on the magnetic field strength. Although magnetic fields are known to enhance or suppress the dose at tissue-air interfaces owing to the electron return effect, it is unclear how this could result in such a large effect with the sub-millimeter air gaps found in these phantoms. Without a clear understanding of the mechanism behind this effect, mitigation techniques cannot easily be developed and the utility of plastic phantoms for QA or research purposes is undermined.

Although the effect of air gaps that uniformly surround the chamber in all directions is of interest, such air gaps cannot explain the observed increase in orientation dependence. In that case, the relative position of the internal components of the chamber is the only parameter that could change when the chamber is rotated. If this is causing the effect, then we would expect to observe similar effects when the chamber is used in water phantoms. Hackett et al.⁵ suggested that the effect is actually due to changes in the distribution of the air around the chamber as it is rotated. From this we hypothesize that the orientation dependence is caused by the precession of the ionization chamber about a point inside the insert cavity as it is rotated. This precession shifts the distribution of the air surrounding the chamber. Thus two aspects should be considered in the response of an ionization chamber in a magnetic field in the presence of air gaps: (1) the effect of the presence of an air gap itself and (2) how this effect varies as the chamber precesses.

The aim of this study was to use a Monte Carlo model to quantify the effect of both the presence of air gaps of various thicknesses and also the precession of the chamber inside the insert cavity. We also used the model to better understand the mechanism behind this effect and from our observations suggest potential mitigation strategies.

II. METHODS

II.A. Monte Carlo Model

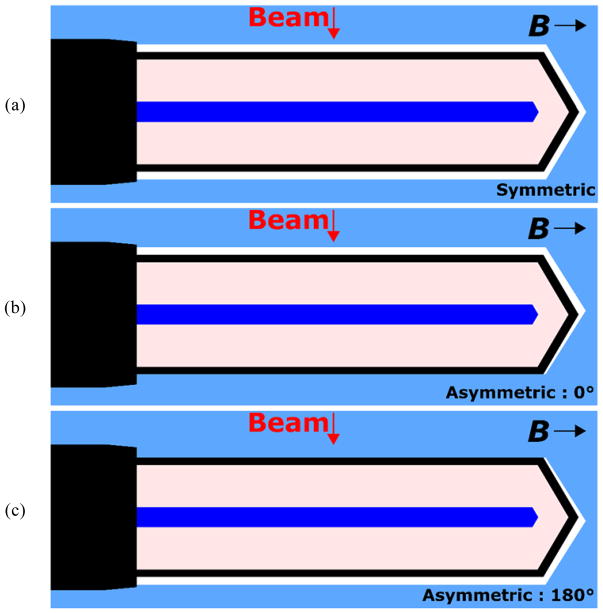
Monte Carlo simulations were performed with the Geant4 Monte Carlo software toolkit (v9.6.p04) using the same physics parameters as we previously showed to pass the Fano cavity test for ionization chamber simulations.⁸ Transport cuts of 10 keV were used for photons and 1 keV for charged particles. A PTW 30013 Farmer chamber was modeled at a depth of 10 cm inside a water phantom (30 × 30 × 30 cm³) with a source-to-surface distance of 133.5 cm. A point source of photons collimated to a 10 × 10 cm² field was used. The field size was defined at a source to surface distance (SSD) of 143.5 cm, corresponding to the Elekta MR-linac isocenter. The energy distribution was sampled in air at isocenter from a full-head Monte Carlo model of the Elekta MR-linac system as in our previous study.⁸ This spectrum had a maximum energy of 7.1 MeV and a mean energy of 2.2 MeV. No variance reduction techniques were used. Two different types of insert cavity, illustrated in Figure 1, were modeled around the chamber; these are the symmetric and asymmetric cavities. Symmetric insert cavities were centered on the chamber central axis and resulted in an air gap of uniform thickness around the chamber wall. Asymmetric insert cavities are the same shape as the symmetric ones but they were displaced with respect to the chamber central axis such that one side was flush with the chamber wall, leaving an air gap with a maximum thickness at the opposite side of the chamber. The orientation of the air gap was varied to simulate the precession of the chamber inside the insert cavity, with 0° representing the case where the maximum thickness of the air gap was on the top of the chamber facing towards the source (Figure 1b) and 180° representing the case where the maximum thickness was on the bottom of the detector facing away from the source (Figure 1c). In each case the stem of the chamber was included in the model and thus an air gap was not modeled on that side of the chamber.

Figure 1.

Illustrations of the modeled symmetric (a) and asymmetric air gaps (b) and (c) between the Farmer chamber and the phantom material. The asymmetric air gap is shown at two orientations: (b) 0° and (c) 180°. This is a side view with the beam direction going from the top of the images to the bottom.

Asymmetric air gaps with maximum thicknesses of 0.05 mm, 0.1 mm and 0.2 mm were modeled in both a 1.5 T magnetic field and without a magnetic field. These air gaps were modeled with orientations between 0° and 315° in 45° intervals. Symmetric air gaps were also modeled with thicknesses from 0.2 mm to 1.4 mm for magnetic fields strengths of 0 T, 0.35 T, 1.0 T, and 1.5 T. All magnetic fields were modeled perpendicular to the beam and parallel to the long axis of the Farmer chamber. This is the most likely ionization chamber configuration to be used with the Elekta MR-linac because the influence of the magnetic field on the chamber response is smaller in this orientation compared to when the chamber is oriented perpendicular to the magnetic field.⁸ Energy deposition was scored inside the air cavity of the Farmer chamber only (i.e. the sensitive volume) and from this the dose for each case was calculated.

To investigate whether the electron return effect could plausibly influence the detector signal across such small distances, the gyroradius (i.e., the radius of curvature) of each electron that traveled from the phantom into the Farmer chamber model and deposited energy to the sensitive volume was recorded as it first entered the wall of the chamber. The gyroradius r_g of each electron was calculated as

$$r_g=\frac{\gamma m_0{v}_{\perp }}{\mid q\mid B}$$ (1)

where γ is the Lorentz factor, m₀ is the rest mass of the electron, v_⊥ is the component of the electron velocity that is perpendicular to the magnetic field, q is the electron charge and B is the magnitude of the magnetic field. The distribution of gyroradii when no air gap is present, weighted by the relative contribution of each electron to the chamber dose, was then plotted to determine the significance of electrons with gyroradii smaller than the thickness of the modeled air gaps. Notably, the calculated gyroradius is the one that the electron would follow if no intervening medium were present. In media, electrons scatter and slow down and therefore do not move in perfectly circular trajectories. In air, however, the electrons follow their circular paths relatively freely owing to the low mass density.

The Monte Carlo geometry was also divided into three regions (Figure 2): the region (A) outside of the Farmer chamber model except for the adjacent region (B) which is defined as the volume of thickness 0.2 mm immediately surrounding the outside of the chamber wall, and (C) the region inside the Farmer chamber model including the chamber wall. For consistency, the adjacent region (B) has a uniform thickness of 0.2 mm around the chamber regardless of the shape and size of the air gap being modeled. The total energy deposited in the sensitive volume of the chamber was divided into three components: the energy deposited by electrons originating from region A, B, or C. The origin point of the electron is the point at which it was first produced either by a photon interaction or by secondary ionizations. To score the origin point and gyroradius, each electron was tagged at production. If the electron crossed from the phantom into the chamber during tracking then this tag was updated with the value of the gyroradius at that point (assuming the electron was originally produced outside of the chamber). Then, if the electron deposited energy in the sensitive volume, the recorded origin point and gyroradius was saved to a file along with the total energy deposition.

Figure 2.

A front view of the Farmer chamber model. The energy deposited in the sensitive volume was split into three components based on whether the energy was deposited by electrons originating from region A, B, or C. The adjacent region (B) is a volume 0.2 mm thick uniformly surrounding the chamber wall in all instances regardless of air gap shape or size.

The dose to the sensitive volume was scored per history and uncertainties were calculated using the history-by-history statistical estimator technique¹¹. For all reported ratios, statistical uncertainties were below 0.3%. Achieving this level of uncertainty required on the order of 8×10⁹ histories and 9×10⁴ CPU hours per condition. This was achieved by running simulations in parallel on a shared institutional cluster and on the Lonestar cluster, one of the distributed computing networks from the Texas Advanced Computing Center (TACC). Typically, ~2400 simulations were run in parallel for each condition. We recognize that Geant4 is currently computationally inefficient to perform such simulations due to the strict transport parameters required⁸ and the lack of variance reduction techniques. Nevertheless, the computing infrastructure that we have available allowed us to perform the simulations. EGSnrc and Penelope can certainly be computationally more efficient while potentially maintaining the same level or better accuracy.

III. RESULTS

III.A. Electron Gyroradii

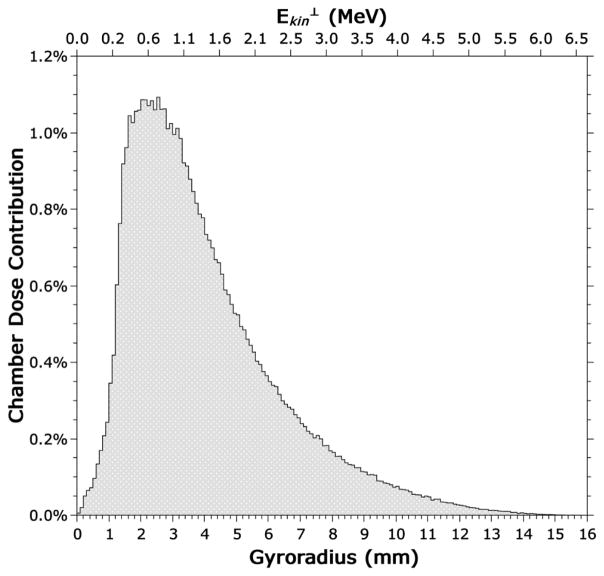
The gyroradii distribution of electrons when they first enter the chamber from the phantom in a 1.5 T magnetic field without an air gap is shown in Figure 3. Only electrons that deposited energy in the sensitive volume are counted. The distribution is broad, with values ranging from ~0 to 1.6 cm with a mean of 0.4 cm and a peak at about 0.24 cm.

Figure 3.

Gyroradii distribution in a 1.5 T magnetic field of electrons as they first enter the chamber from the phantom when no air gap is present. The distribution is weighted by the energy deposited by each electron in the sensitive volume of the ionization chamber. The scale at the top represents the associated electron kinetic energy, assuming that the velocity of each electron was entirely perpendicular to the magnetic field. This is not generally true but it gives an approximation of the electron energies involved.

The air gap effect observed by Hackett et al.⁵ was a reduction in chamber signal associated with sub-millimeter air gap thicknesses, so the energy contributions of most interest are those of electrons with a gyroradius on that scale. The reduction in chamber signal implies the loss of energy reaching the chamber which is why we are studying the electrons as they first enter rather than as they leave. The total energy contribution of electrons with a gyroradius of 1 mm or less is about 1%; however, this drops to 0.2% for electrons with a gyroradius of 0.5 mm or less. The vast majority of contributing electrons are able to cross sub-millimeter air gaps. The gyroradius for a given electron energy increases as the Lorentz force gets weaker, becoming infinite at 0 T. Therefore, for lower magnetic field strengths the contributions from electrons with sub-millimeter gyroradii would be even less.

III.B. Air Gap Effect

The percentage difference to the chamber cavity dose between the case when an air gap is present and the case with no air gap is shown as a function of air gap thickness for symmetrical air gaps in Figure 4 for 0, 0.35, 1.0, and 1.5 T magnetic field strengths. The response of the chamber was within 0.5% of the case with no air gap for each of the air gap thicknesses and magnetic field strengths studied.

Figure 4.

Percentage differences in dose to the sensitive volume with a symmetrical air gap relative to the case with no air gap as a function of the air gap thickness.

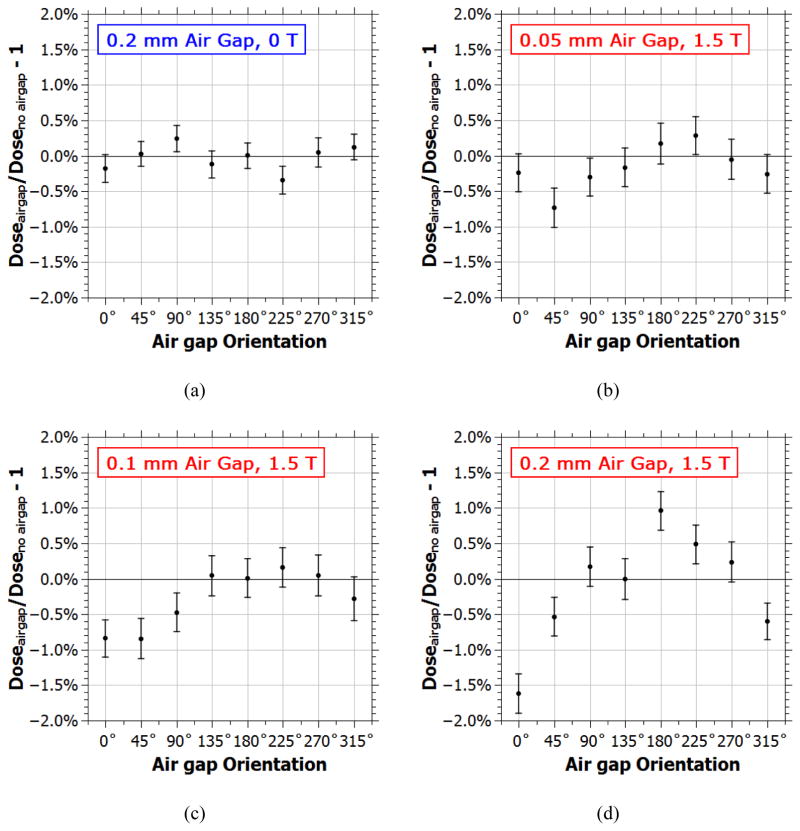
For asymmetric air gaps, the variation of chamber dose with air gap orientation in a 1.5 T magnetic field for air gaps of different maximum thicknesses (0.05 mm, 0.1 mm, and 0.2 mm) relative to the case of no air gap are shown in Figure 5. Also shown are the data for a 0.2 mm thick air gap with no magnetic field. Without the magnetic field, the variations are all within 0.5%. When the magnetic field is present, larger variations exists for each air gap thickness studied. The largest differences are seen at orientations between 0° and 45°. At these orientations the air gap is directly between the chamber and the incoming radiation which, for the electrons, is not exactly aligned with 0° because of the effect of the Lorentz force on the point spread kernel.¹² As the size of the air gap is increased, the differences become larger and also begin to appear around the 180° orientation, where the air gap is downstream of the ion chamber. The largest difference was over 1.5% with the 0.2 mm thick air gap at 0° orientation. However, a total difference of over 2.5% is introduced between orientations 0° and 180°.

Figure 5.

Percentage difference in the dose to the chamber sensitive volume when an asymmetrical air gap surrounds the chamber relative to the case with no air gap as a function of the orientation of the air gap for three different air gap thicknesses: 0.05 mm, 0.1 mm, and 0.2 mm.

III.C. Dose Components

The components of the ionization chamber dose that resulted from electrons originating from regions A, B, or C (as shown in Figure 2) were calculated separately for the case of no air gap, for the case of an asymmetric 0.2 mm air gap oriented at 0° and 180°, and for the case of a symmetric 0.2 mm air gap uniformly surrounding the chamber. These results, with and without a 1.5 T magnetic field, are shown in Table 1. In both cases, 3.2% of the total energy deposited in the chamber cavity came from electrons that originated in the adjacent region. When the air gap is present, depending on its symmetry or orientation, up to 100% of this energy contribution is lost. In the case where no magnetic field is present, this loss is compensated by an increase in the energy contribution from electrons originating from the outside region. However, when the magnetic field is present, this energy contribution is reduced and no longer sufficient to compensate for the loss when an asymmetric air gap is present.

Table 1.

Components of the ionization chamber dose without and with a 1.5 T magnetic field for the following air gap configurations: no air gap, a 0.2 mm thick asymmetric air gap oriented at 0° and 180°, and a 0.2 mm thick symmetric air gap (SYM). Values are normalized to the total value with no air gap. In all cases, “(B) Adjacent” represents a 0.2 mm thick volume uniformly surrounding the chamber wall.

Origin	No Magnetic Field				1.5 T Magnetic Field
	No Gap	0°	180°	SYM	No Gap	0°	180°	SYM
(A) Outside	49.0%	51.7%	49.7%	52.3%	44.6%	46.2%	46.3%	47.5%
(B) Adjacent	3.2%	0.6%	2.6%	0.0%	3.2%	0.8%	2.5%	0.0%
(C) Inside	47.8%	47.5%	47.7%	47.7%	52.3%	51.4%	52.4%	52.6%
Total	100.0%	99.8%	99.9%	99.9%	100.0%	98.4%	101.3%	100.1%

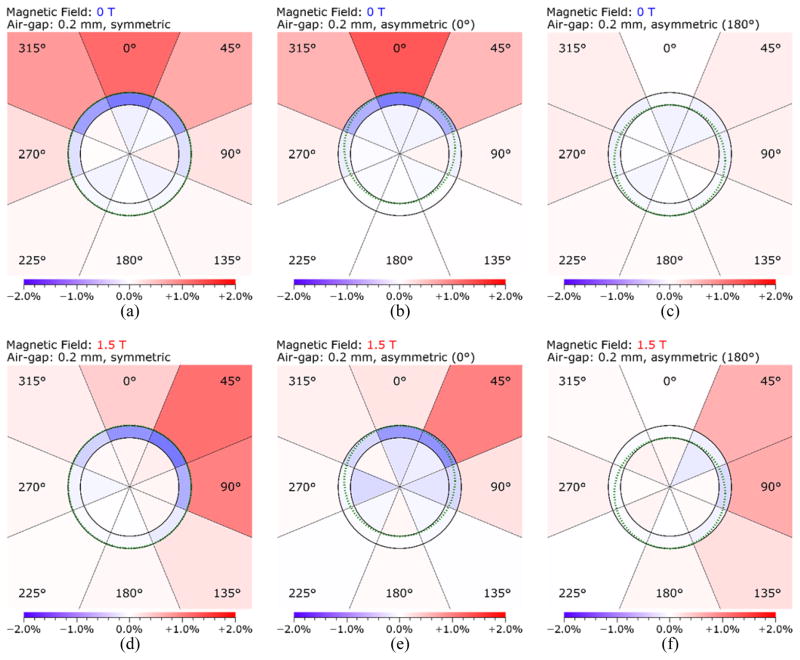
Each region was further subdivided into octants (Figure 6) so that for each scenario the changes in the dose to the chamber cavity as a result of the presence of the air gaps could be traced back to an increase or decrease in electrons coming from different directions around the chamber. Increases in contributions from the outside region when the air gap was upstream of the chamber coincided with the direction from which most of the secondary electrons are coming from, which in the case of the 1.5 T magnetic field (Figure 6d, 6e) was from a modal angle of 39.64° ± 0.15° compared to directly above (0°) when there was no magnetic field (Figure 6a, 6b). Decreases in contributions from the adjacent region also coincided with this direction but also was more pronounced where the air gap was thickest. When the air gap is downstream of the chamber and there is no magnetic field, there is almost no change (<0.2%) in the relative contributions from each direction (Figure 6c). However, when the 1.5 T magnetic field is present there are significant increases (e.g. 0.6% at 45° and 90°) in the contributions from outside lateral electrons (Figure 6f).

Figure 6.

The difference caused by the presence of the air gap to the percentage contribution to the chamber dose by electrons originating from the regions outside, adjacent to, and inside the Farmer chamber (Figure 2). Each region has been further sub-divided into octants to provide better insight into the origin of the differences. The values are relative to the total dose to the chamber when no air gap is present. The dotted green line illustrates the outline of the air gap that was present for each case. The regions are not to scale. The photon beam is directed from the top to the bottom.

IV. DISCUSSION

IV.A. Electron Return Effect

In a 1.5 T magnetic field, the gyroradii of the electrons entering the chamber and contributing to the dose was mostly on the order of 2 to 4 mm (Figure 3), which is 10 times larger than the air gap thicknesses implicated in previous observations.⁵ The total contribution from electrons with gyroradii of the same order as the suspected air gap thicknesses (0.2 mm) was less than 0.2%. Consequently, the air gap effect cannot be attributed to electrons encountering the air gap and looping back as in the case of the electron return effect. It can be noted from Eq. (1) that the gyroradius for a given electron energy increases as the magnetic field strength decreases, and therefore this must also be true for fields weaker than 1.5 T.

IV.B. Air Gap Effect

For asymmetric air gaps, effects greater than 1.5% for gaps just 0.2 mm thick were observed, with the largest differences relative to the case without magnetic field occurring when the air gap was upstream of the chamber. The effect was smaller for thinner air gaps, but still potentially significant (>0.5%) for air gaps as small as 0.05 mm. These results are consistent with the effects measured in previous studies.^5,8,9

No effect greater than 0.5% was seen for symmetrical air gaps with thicknesses of 1.4 mm or less for any of the magnetic field strengths studied. Malkov and Rogers¹⁰ calculated a 0.9% effect for a 0.5 mm symmetrical air gap and a 1.6% effect for a 1.0 mm air gap. Note that Malkov and Rogers¹⁰ performed their simulations with the 1.5 T magnetic field perpendicular to the chamber, the beam was modeled in EGSnrc as a parallel beam using an energy spectrum from a 6 MV Elekta SL25 beam, the chamber used was an NE2571 Farmer chamber and was positioned at the center of a 4.3 cm diameter delrin cylinder representing a measurement in a build-up cap. Also, their values were based on a comparison of the ratios of the chamber response with and without a magnetic field for each air gap, rather than just the ratio of chamber response with and without the air gap. To determine if the orientation of the chamber with respect to the magnetic field was a factor in the difference between these results, we calculated the chamber dose values with the 1.5 T magnetic field perpendicular to the chamber for a 0.5 mm and 1.0 mm symmetrical air gap and for the case with no air gap. The percentage difference between the chamber doses relative to the case with no air gap was 0.5 ± 0.2% for the 0.5 mm air gap and 0.8 ± 0.2% for the 1.0 mm air gap. These results indicate that the chamber dose is more sensitive to symmetrical air gaps when the chamber is oriented perpendicular to the magnetic field. These values are lower than those of Malkov and Rogers¹⁰, the exact cause of which is unknown. However, as noted previously, the simulations also differed in many other respects and the discrepancy may also be attributed to differences in material definitions, transport parameters, cross-sections and the relative robustness of the condensed history algorithm. A more direct comparison would be needed to fully assess the intrinsic differences between these two models.

IV.C. Dose Components

Looking first at the case where no magnetic field is present (Table 1, Figure 6a, Figure 6b and Figure 6c), when no air gap was present the energy deposited in the chamber was roughly split in half between electrons that come from outside the chamber (49.0%) and electrons that come from inside (47.8%). However, a significant point to note is that 3.2% of the energy deposited in the chamber came from electrons that originated in the first 0.2 mm beyond the chamber wall (region (B) in Figure 2). When an air gap was placed upstream of the chamber (0°) most of this energy was lost because the medium in which those electrons were ionized is no longer present. However, this was almost exactly compensated by an increase in energy from electrons coming from the outside region (region (A) in Figure 2). Electrons from just beyond the air gap now skipped over it without losing energy compensating for much of the loss while electrons from further away similarly have their range slightly extended and compensate for the rest (Table 1, Figure 6b). A similar but much smaller effect occurred when the air gap was placed downstream of the chamber (180°). In that case, less energy was lost in the adjacent region because of the air gap being mostly downstream of the chamber, and this smaller loss was compensated by an equally small increase in contributions from lateral electrons (Figure 6c). In the symmetrical air gap case, where the gap is uniform around the chamber, all of the energy from the adjacent region was lost but the compensation from outside also subsequently increased (Table 1, Figure 6a) and it was about equal to the sum of the increases from the 0° and 180° asymmetric cases.

Now looking at the 1.5 T case (Table 1, Figure 6d, Figure 6e and Figure 6f), this time when no air gap was present, the energy deposited from electrons that come from outside of the chamber was only 44.6%. This reduction is expected because of the shortened range of electrons in the magnetic field, which means that the electrons generated furthest from the chamber can no longer reach it, and those that can reach it lose more energy in the process. Meanwhile, the contribution from electrons generated inside the chamber increased as they spent more time spiraling in the chamber’s air cavity. However, the contribution from electrons generated in the first 0.2 mm beyond the chamber wall (region (B) in Figure 2) was the same with or without a magnetic field (3.2%). This is most likely because the electrons are so close to the chamber already that the energy they lose traveling to the chamber does not change appreciably, or is balanced by the extra time they spend there.

When the air gap is placed upstream (0°), most of this energy was lost and the contribution from outside electrons increased. However, because electrons expend more energy traveling to the air gap in the presence of a magnetic field, the further away the electrons are the less they are able to contribute. Consequently, the increase from energy contributions from outside was insufficient (by about 0.8%) to compensate for the loss in the adjacent region. The contribution from electrons generated inside the chamber is also reduced by about 0.9%, possibly because electrons originating from the volume containing the air gap are no longer present to produce further ionizations inside the chamber. This is evidenced by the fact that the losses inside the chamber are clustered near the air gap (Figure 6e). Combined, these losses result in a total reduction in the chamber dose of about 1.7% owing to the presence of the upstream air gap in the magnetic field.

When the air gap was placed downstream (180°), the change in the contribution from electrons generated inside the cavity was insignificant (0.1%), indicating that any electron return effect from electrons escaping the chamber into the air gap is negligible. The loss in energy contributions from the adjacent region was much smaller than in the 0° case. However, unlike when no magnetic field is present, here the increase in contributions from electrons generated outside the chamber was about the same as in the 0° case. This still results mostly from an increase in contributions from lateral electrons, but in this case the presence of the air gap allows more of them to curve towards the chamber. This is evidenced by the fact that the increase now comes mostly from one side of the chamber and from a larger area (Figure 6f) than in the case of no magnetic field (Figure 6c). This gain is larger than the loss from the adjacent region and leads to a net increase in the chamber dose of about 1.2%. This effect was less apparent for smaller air gaps (Figure 5).

When the air gap was uniform around the chamber (symmetric), the energy contributions from the adjacent region drop to zero as in the case of no magnetic field (Table 1) and the increase from the outside region was approximately the sum of the increases from the 0° and 180° asymmetric cases. These two effects essentially balance each other out resulting in no significant net change in the chamber dose. The increase from the outside region was not quite sufficient to balance the loss from the adjacent region but there was also a slight increase in the contributions from inside the chamber (~0.3%). Although this increase was statistically insignificant, it is spread across a wide angle (Figure 6d) and it may indicate that the more consistently wide air gap was allowing more low energy delta rays generated inside the ionization chamber to return to the chamber cavity after leaving.

IV.D. Mitigation Techniques

The air gap effect is mainly attributed to a reduction in ionization produced in the immediate vicinity of the chamber wall as a result of the presence of the air gap, particularly for asymmetric air gaps. Therefore mitigation strategies could involve techniques to eliminate the air gap itself, reducing the potential for asymmetric air gaps, or physically separate the air gap from the immediate vicinity of the chamber wall. Next we discuss potential solutions and their limitations.

Filling the air gap with water would eliminate the air gap entirely and has successfully been used before^5,9. This requires either sealing the phantom insert to prevent leakage or placing the chamber vertically inside the phantom insert. The latter requires the chamber to be positioned perpendicular to the magnetic field for a wide-bore style MR-linac such as the Elekta or ViewRay systems. Orienting the chamber perpendicular to the magnetic field is not recommended because it introduces the largest magnetic field perturbation to the chamber signal and, depending on which direction the beam comes from, can introduce additional chamber stem effects that have large uncertainties.⁸

Our results indicate that the response of the ionization chamber is much less sensitive to the presence of air gaps that are uniform in thickness (symmetrical) relative to asymmetric air gaps. Figure 4 shows that the effect of symmetrical air gaps was less than 0.5% when those gaps were 1.4 mm thick or less in each of the magnetic field strengths examined. Intermediate air gaps (where air exists on both downstream and upstream of the chamber but with different thicknesses) would most likely produce an intermediate effect between the two opposite extremes. Consequently, a phantom could be designed such that an air gap with thickness <1 mm is deliberately introduced into the phantom design or the chamber is permanently attached to the plastic phantom such that the air gaps are consistent. This would also be less effective with the chamber in the perpendicular orientation as symmetric air gaps with thicknesses of 0.5 mm or more can change the response of the chamber by over 0.5% when used in that orientation.

The effect of asymmetric air gaps could also be potentially mitigated by introducing a larger separation between the sensitive volume and any air gaps. Ionizations occurring within the first 0.2 mm beyond the chamber wall were found to contribute 3.2% of the dose to the chamber cavity. However, the contributions from a region of the same thickness but 3 mm away from the chamber wall contributed only 1% of the chamber dose, and from another region 6 mm away the contribution was 0.5%. Therefore, a container that could be filled with water and screwed on to the chamber like a build-up cap could then be placed inside a larger phantom to effectively separate the chamber wall from the air gaps outside.

V. CONCLUSION

The gyroradius of most electrons was too large to be responsible for the air gap effect via the electron return effect; instead, the effect is attributed to the loss of energy contributions from electrons originating inside the air gap volume, which is not completely compensated for by more distant electrons owing to their reduced range in the magnetic field. Air gaps that were completely symmetrical in shape around the chamber were found to have a minimal effect in simulations with the chamber at a depth of 10 cm in a 30 × 30 × 30 cm³ water phantom when the magnetic field was parallel with the long axis of the chamber. However, more realistic asymmetric air gaps introduced effects of up to 1.6%. Mitigation strategies could involve techniques to eliminate the air gap itself, reducing the potential for asymmetric air gaps, or physically separate the air gap from the immediate vicinity of the chamber wall.