MRI-based prostate cancer detection with high-level representation and hierarchical classification

Abstract

Purpose

Extracting the high-level feature representation by using deep neural networks for detection of prostate cancer, and then based on high-level feature representation constructing hierarchical classification to refine the detection results.

Methods

High-level feature representation is first learned by a deep learning network, where multi-parametric MR images are used as the input data. Then, based on the learned high-level features, a hierarchical classification method is developed, where multiple random forest classifiers are iteratively constructed to refine the detection results of prostate cancer.

Results

The experiments were carried on 21 real patient subjects, and the proposed method achieves an averaged section-based evaluation (SBE) of 89.90%, an averaged sensitivity of 91.51%, and an averaged specificity of 88.47%.

Conclusions

The high-level features learned from our proposed method can achieve better performance than the conventional handcrafted features (e.g., LBP and Haar-like features) in detecting prostate cancer regions, also the context features obtained from the proposed hierarchical classification approach are effective in refining cancer detection result.

1. INTRODUCTION

Prostate cancer is one of the major cancers among men in the United States.¹ It is reported that about 28% of cancers in men occur in the prostate, and approximately 16% of men will be diagnosed with prostate cancer in their lifetime.¹ Thus, it is of vital importance to accurately identify prostate cancer as early as possible, which can effectively help reduce the possibility of mortality and improve treatment. Currently, the mainstream clinical method for identification of prostate cancer is random systematic (sextant) biopsies under the guidance of transrectal ultrasound (TRUS) when a patient is diagnosed as a suspicious prostate cancer sufferer with a high prostate-specific antigen (PSA) level or an abnormal screening digital rectal examination (DRE). In practice, a doctor first divides the prostate into several sections according to the number of biopsy points, and then extracts tissue sample from each section by shooting a needle in each section for further detection. Since TRUS-guided biopsy for prostate cancer detection (PCD) has high false-negative results (i.e., it is easy to mis-diagnose a prostate cancer patient as a normal subject), biopsy is usually needed to repeat 5–7 times to increase the detection accuracy. However, as an invasive operation, TRUS-guided biopsy is not suitable for screening a large patient population in prostate cancer detection.² It is reported that Magnetic resonance imaging (MRI) is a powerful, noninvasive imaging tool able to help accurately detect or diagnose many kinds of diseases, such as prostate cancer^3–8 and Alzheimer’s Disease,^9,10 by providing anatomical, functional and metabolic MRI information. In the literature, recent studies have shown that multiparametric MR images, e.g., T2-weighted imaging (T2-weighted), diffusion-weighted imaging (DWI), and apparent diffusion coefficient (ADC) MR images, are very beneficial in targeting biopsies toward suspicious cancer regions and can help select subjects who should undergo anterior biopsy, and can lead to higher detection accuracy.² Unfortunately, MRI-based analysis for PCD not only requires a high level of expertise from radiologists, but also is quite time-consuming due to the large number of 3D images. In addition, there exists significant observer variability from physicians in interpreting the volume and stage of tumor in the prostate MR images.

On the other hand, computer-aided detection (CAD) system for PCD can potentially detect suspicious lesions in prostate MR images automatically, which helps reduce the variability among observers and speed up the reading time. Thus, CAD system for prostate cancer detection becomes an active research topic in the literature. Generally, there are five main stages in a typical CAD system for PCD, i.e., (a) image preprocessing, (b) segmentation, (c) registration, (d) feature extraction, and (e) classification. Specifically, image preprocessing is to normalize/transform raw images to a domain where cancer regions can be easily detected. Segmentation is to segment the prostate region from the whole MR image for subsequent analysis. Registration is to transform different sets of images onto one coordinate system. Feature extraction is to extract distinctive features from targets of interest in the whole prostate region. And classification is to identify whether an unknown region/voxel within prostate region belongs to cancer region or not, based on extracted features. In this study, we focus on both feature extraction and classification stages.

In the last decade, researchers have proposed many CAD systems for prostate cancer detection using different types of features extracted from multiparametric MR images and different classification methods. For example, Chan et al.¹¹ were the first to apply MR images for PCD, where two types of second-order features (i.e., texture features extracted from lesion candidate, and anatomical features described by cylindrical coordinate) and support vector machine (SVM) classifier were employed to identify prostate cancer in the peripheral zone (PZ). Niaf et al.¹² proposed a supervised machine-learning method to separate cancer regions of interest (ROIs) from benign ROIs within the PZ. In their method, the suspicious cancer ROIs are manually annotated by both histopathologist and researcher, and then suspicious ROIs are classified into benign and cancer tissues by using textual information and gradient features extracted from T2-weighted, DWI and dynamic contrast-enhanced (DCE) MR images. Litjens et al.¹³ proposed an automatic CAD system by using intensity, texture, shape anatomy and pharmacokinetic features extracted from MR images. To be specific, they first developed an initial-candidate detection approach to generate a sufficient number of suspicious ROIs for screening, and then used a classification-based method to identify and segment cancer ROIs. Langer et al.¹⁴ developed a multiparametric model suitable for prospectively identifying prostate cancer in the PZ, where fractal and multifractal features were combined together as representation and nonlinear supervised classification algorithms were employed to perform PCD. Kwak et al.¹⁵ proposed a CAD system by using T2-weighted, high-b-value DWI, and texture features based on local binary patterns. In this method, a three-stage feature selection method was employed to provide the most discriminative features.

The main disadvantage of existing PCD methods is that they mainly focus on identifying prostate cancer in the peripheral zone (PZ), instead of the entire prostate region.^11,12,14 Although a few PCD methods^13,16 can detect cancer regions from the whole prostate, they usually need to generate a sufficient number of suspicious ROIs provided by a histopathologist via manually contouring, which is not only labor-intensive and time-consuming, but also subject to manual errors. To address this issue, Qian et al.¹⁷ proposed an automatic PCD method by using random forests and auto-context model. Specifically, they regarded each voxel in prostate regions as a ROI, and directly detected the location of prostate cancer from the whole prostate region by employing the random forests and auto-context model, where random Haar-like features were used for both appearance features and context features. To the best of our knowledge, it is the only work to directly identify cancer regions from the whole prostate without using any manual or automatic method to segment candidate cancer ROIs. Similar to many existing PCD methods, the method proposed by Qian et al.¹⁷ only employed the low-level features or handcrafted features extracted from MR images. In this study, we assume that there exist hidden or latent high-level features in the original features that can help build more robust PCD models. Thus, the problem is now becoming how to extract such high-level features from the datasets at hand.

In recent years, deep learning neural network has been demonstrated to be effective in uncovering high-level nonlinear structure in data and picking out which features are useful for learning.¹⁸ The main promise of deep learning is replacing handcrafted features with multiple levels of representations of data in an unsupervised manner. Here, each representation, corresponding to a level of abstraction, forms a hierarchy of concepts. Recent studies have shown that deep learning provides promising results in computer vision,¹⁹ speech²⁰ and other fields,^18,21 while some studies have shown deep learning-based methods gain much better performance than method using handcraft or low-level features. For example, in,²² Guo et al. learned a latent feature representation of infant MR brain images and obtained at least 5% higher performance than the method using handcraft features including Haar, HoG, and gradients; in,¹⁸ Suk et al. proposed a deep learning-based latent features representation for diagnosis of Alzheimer’s disease and achieved more accurate performance than that based on low-level features.

Inspired by these significant developments, we exploit deep neural networks in this study to extract high-level features for prostate cancer detection. We first propose a novel high-level feature representation for the detection of prostate cancer by using deep learning network. Specifically, we use Stacked Auto-Encode (SAE) model to learn latent high-level feature representation from each type of multiparametric MR images, and then employ such high-level features for subsequent classification or detection. The reason we adopt SAE model here is that it contains an unsupervised pretraining process, and such process allows us to benefit from the target-unrelated samples to discover general latent feature representations. However, in this work, the detection of prostate cancer is a voxel-wise classification task where each voxel is classified independently, so the classification result may be not satisfying due to inconsistent classification in the spatial neighborhood due to classification error. To improve the robustness of the learning system, we further propose a hierarchical classification method to refine the detection results, motivated by the auto-context model.²³ That is, we combine the context features obtained from the estimated cancer probability map in the previous layer with the learned high-level features together to construct a new random forest classifier in the next layer. By using such hierarchical learning structure, we can obtain a refined probability map that can be regarded as the result of cancer detection. To demonstrate the effectiveness of our proposed method, we conduct several groups of experiments on 21 real patient subjects. The experimental results demonstrate that (a) the context features obtained from our proposed hierarchical classification approach are effective in refining the detection result; (b) our proposed method achieves an averaged section-based evaluation (SBE) of 89.90%, an averaged sensitivity of 91.51%, and an averaged specificity of 88.47%. In addition, since combining the high-level features with the original low-level features usually helps build a robust model for disease diagnosis,^18,24 we further try to augment features by a concatenation of the high-level latent features and the original intensity features for constructing hierarchical classifiers. The experimental results show that the original low-level features are still informative for detection of prostate cancer along with the high-level features.

The remainder of this study is organized as follows. We first give a detailed description about our proposed method in Section 2. Then, we elaborate the experimental design, results and analysis in Section 3. In Section 4, we discuss the limitations and disadvantages of our method. Finally, a conclusion is drawn in Section 5.

2. METHOD

Our method consists of two main steps, where the first step is to learn latent high-level feature representation from multiparametric MR images, and the other step is to construct hierarchical classification to alleviate the problem of spatially inconsistent classification. In this section, we will elaborate our proposed method for detection of prostate cancer using multiparametric MRI.

2.A. High-level feature representation learning

Extracting informative features from the target of interest plays a key role in a successful CAD system.^21,25,26 Currently, many kinds of feature representation methods have been developed for computer-aided prostate cancer detection, where typical features for prostate MR images include volume, shape, texture, intensity, and various statistics.^{12,13,17,27,28} For example, Niaf et al.¹² used some image features including gray-level features, gradient features, and texture features, and also some functional features including semi-quantitative and quantitative features. Litjens et al.¹³ used intensity, texture, shape, anatomy, and pharmacokinetic features. Tiwari et al.²⁷ proposed a multimodal wavelet embedding representation to extract features. Liu et al.²⁸ proposed a new feature representation called the location map by applying a nonlinear transformation to the spatial position coordinates of each pixel in MR images. Qian et al.¹⁷ used Haar-like features for constructing appearance features and context features. These methods use only low-level features or handcrafted features for the subsequent prostate cancer detection task. In this work, we focus on mining the latent high-level feature representation conveyed in data. Recent studies have shown that deep learning-based methods provide an effective way to obtain latent high-level features, among which stacked auto-encoder (SAE) is a popular unsupervised deep learning network. In this study, we adopt SAE to learn a latent high-level feature representation for multiparametric MR images. In the following, we will first briefly introduce the SAE model, and then describe our proposed learning method for high-level feature representation via SAE.

In a SAE model, several single auto-encoder (AE) neural networks are stacked in a hierarchical manner.²⁹ Specifically, the output of an AE in a specific layer is treated as the input of the AE in the next layer. For simplicity, we first introduce the construction of a single AE network, and then describe the whole SAE network. In general, an AE neural network is comprised of an encoder and a decoder with a hidden layer. The encoder attempts to seek for a sparse nonlinear mapping W to project the high-dimensional input data x into a low-dimensional hidden layer representation h through a deterministic mapping, i.e., h = s(Wx + b), where s is the sigmoid activation function. The decoder tries to decode the low-dimensional hidden layer representation h to a vector x′, which approximately reconstructs the input vector x by another deterministic mapping W̃, i.e., x′ = s(W̃h + b′) ≈ x. Here, W and W̃ are the weight/mapping matrixes for the encoder and the decoder, respectively; b and b′ are the bias vectors. In practice, we usually set W̃ = W^T (where T denotes transposition), and set both b and b′ to the vector with all elements of one.

In the training stage, an AE network is first trained using the low-level intensity features obtained from the training images. Afterward, the output from the hidden units of this AE is used as the input of the second layer. Similarly, successive AE networks can be trained in a hierarchical manner. After learning the initial weight matrixes of the whole SAE, we need to further fine-tune the entire deep network for finding the optimal weight matrixes (please see²⁹ for details). After training the SAE network, we can obtain a high-level feature representation for a given low-level feature vector. Denote the mapping matrices of the trained L-layer SAE as W₁, W₂, …, W_l,…, W_L, respectively, and the low-level feature vector as x. We can successively obtain a new feature representation in the l-th layer by using the output of the previous layer through x_l = s(W_lx_l−1 + 1⃑)l = 1, 2, …, L, where x₀ = x, and 1⃑ denotes the vector with all elements of one.

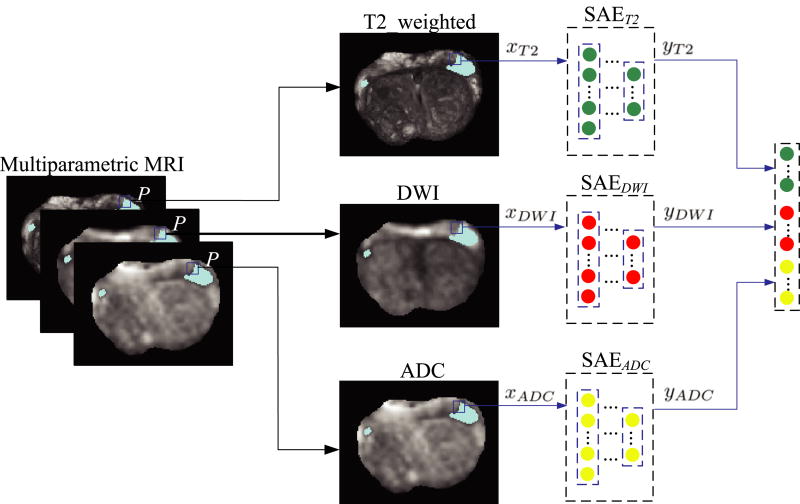
Now, we introduce our proposed high-level feature learning method via SAE, with the detailed process shown in Fig. 1. In our work, we regard the detection of prostate cancer as a voxel-wise classification task where each voxel is treated as a training sample. In this way, our deep learning architecture is learned based on these training samples (i.e., voxels), instead of the entire images. For each type of multiparametric MRI data, we first obtain low-level intensity features of each training sample (or voxel) from its 3D 9 × 9 × 3 patch centered at this voxel, and then treat the intensity low-level features of all training samples as (after reshaping each of them into a column vector) the training data to learn a corresponding SAE model. Note that we use a 3D patch size of 9 × 9 × 3, because we have large slice thickness in the z dimension. In Fig. 1, P is a given point in the multiparametric MRI of the same subject, and x_T2, x_DWI, and x_dADC are the corresponding intensity features in the T2-weightd MRI, DWI and ADC, respectively. Given a certain type of MRI, e.g., x_T2, we can obtain the learned high-level feature vector y_T2 using the SAE_T2 model. Thus, given three types of MRI data, we can learn three high-level feature vectors, i.e., y_T2, y_DWI, and y_dADC. Finally, we concatenate these learned high-level features together i.e., y_SAE = [y_T2; y_DWI; y_dADC], to represent the point P.

Fig. 1.

The illustration of learning the high-level representation from multiparametric MRI. [Colour figure can be viewed at wileyonlinelibrary.com]

2.B. Hierarchical classification

After obtaining the latent high-level feature representation via SAE, we can construct a classifier for the detection of prostate cancer. Many classifiers, such as Support Vector Machine (SVM),³⁰ AdaBoost³¹ and random forests, can be used for detection of prostate cancer. In this work, we resort to the random forest as classifier, which allows us to explore a large number of image features. However, the detection of prostate cancer is a voxel-based classification task where each voxel is classified independently, so there may be inconsistent classification results in the spatial neighborhood due to classification error (as shown in the first column of Fig. 7). Recently, Tu and Bai proposed an effective auto-context model²³ to capture and use context features to refine the classification results in an iterative way. Specifically, given a set of appearance features of training images and their corresponding label maps, the first classifier f₁ can be trained based purely on the appearance features and the corresponding classification results are obtained by using f₁. Afterward, the context features are extracted from the classification results, and then can be combined with the original appearance features to train the second classifier f₂. The algorithm then iterates to approach the ground truth until convergence. In the testing stage, the algorithm follows the same procedure by applying a sequence of trained classifiers to compute classification results.

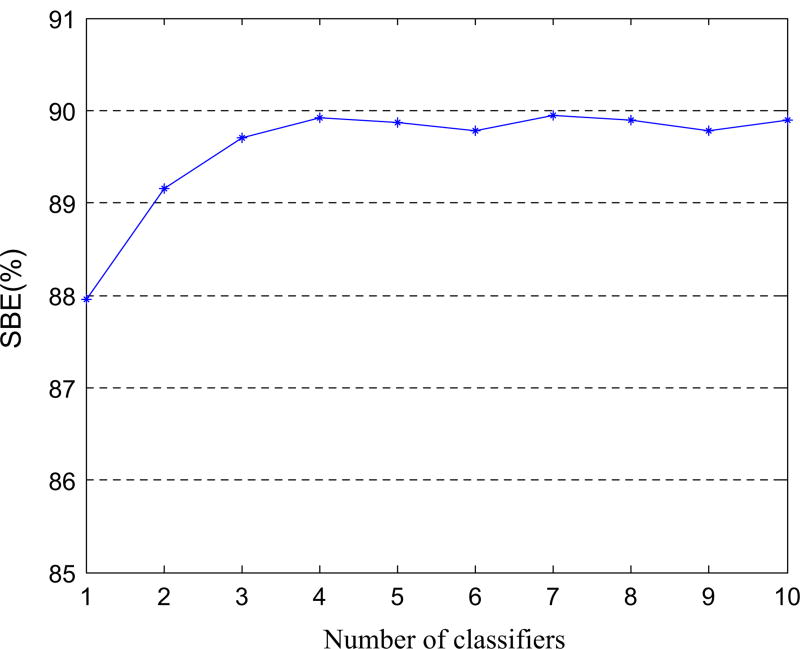
Fig. 7.

The influence of the number of classifiers on the SBE results achieved by the proposed method. [Colour figure can be viewed at wileyonlinelibrary.com]

Inspired by the idea of the auto-context model, we design a hierarchical classification approach by iteratively constructing multiple random forest classifiers to alleviate the problem of spatially inconsistent classification for prostate cancer detection. In the following, we first briefly describe how to train a random forest classifier and how to determine a class label for a given testing sample by using random forests classifier, based on the learned high-level feature representation.

Random forests classifier is an ensemble learning classification method proposed by Breiman et al.³² It consists of multiple decision trees constructed by random perturbing training samples and features subset. Let F_tr = {S₁, S₂, …, S_N} denote the learned high-level feature set of all training voxels for multiparametric MR images, where N is the number of slices, S_i = {S_i,1, S_i,2, …S_i,ni} is the feature set belonging to the i -th slice, and n_i is the number of training voxels of the i -th slice. When constructing a decision tree, we first select a bootstrap set from the entire training samples S_i = {S_i,1, S_i,2, …S_i,ni}(i = 1, …N), and put it at the root node, and then learn a split function³³ to split the root node into left child node and right child node. This splitting process is repeated on each derived subset in a recursive manner until it reaches the constraint conditions. For example, it reaches a specified depth (d), or the criterion that no tree leaf node should contain less than a certain number of training samples. After a decision tree is built, we can obtain the posterior probabilities belong to each class for each leaf node. In the testing stage, each test sample is classified independently by each decision tree. Specifically, starting from the root node of each decision tree, the testing sample is passed down to each node with the corresponding split function on it until reaching a leaf node. When reaching a leaf node, the maximum posterior probability of the leaf node is used to determine the classification result of the testing sample. Since there are multiple decision trees in the whole random forest, there are multiple classification results for the testing sample. Finally, we use the majority voting to combine these classification results to classify the testing sample.

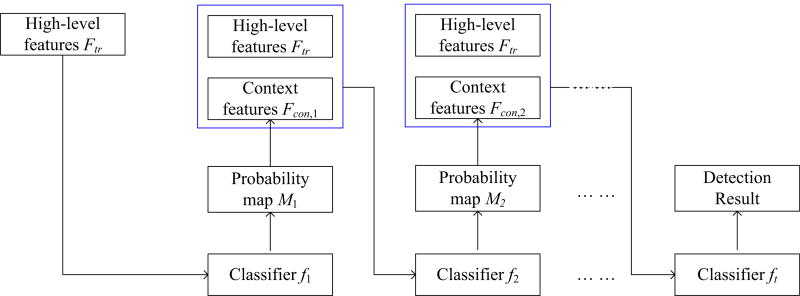
In the following, we will describe our proposed hierarchical classification in detail as shown in Fig. 2. In training stage, we first train a random forest classifier f₁ only using the training set F_tr, through which one can obtain the probability of each training voxel and further obtain the classification probability map set M₁ = {M_1,1, M_1,2, …M_1,N}, where M_1,i(i = 1, …, N) denotes the first probability map of the i-th slice. Letting P_1,map be any pixel in the probability map M_1,i, P be the corresponding voxel in the original MR image, and y_SAE be the appearance feature representation (i.e., learned high-level feature representation) of P, we can extract the context feature y_1,map from the probability map M_1,i by selecting a patch size of 9 × 9 centered at P_1,map (after reshaping each patch into a column vector). It is worth noting that we extract context features from 2D patch instead of 3D patch, since initial context features are extracted from the manual ROIs in the training stage while cancer regions in only 1 to 3 slices were manually delineated for each MRI that consists of 22 to 45 slices. Next, we concatenate the context features y_1,map with the original high-level features y_SAE together for training the second random forest classifier f₂. Such process is repeated t times, where a set of classifiers are constructed in a hierarchical manner.

Fig. 2.

Overview of the proposed hierarchical classification method. [Colour figure can be viewed at wileyonlinelibrary.com]

Similarly, in the testing stage, given a test subject with multiparameter MRI data, we first learn its high-level feature representation, and then obtain the first probability map by classifying the subject using the first trained classifier f₁ using only its high-level representation, and then feed the combination of the context features extracted from the probability map and the learned high-level representation into the next trained classifier for refinement. By repeating these steps, we can get much clearer probability map.

3. EXPERIMENTS

3.A. Dataset and image preprocessing

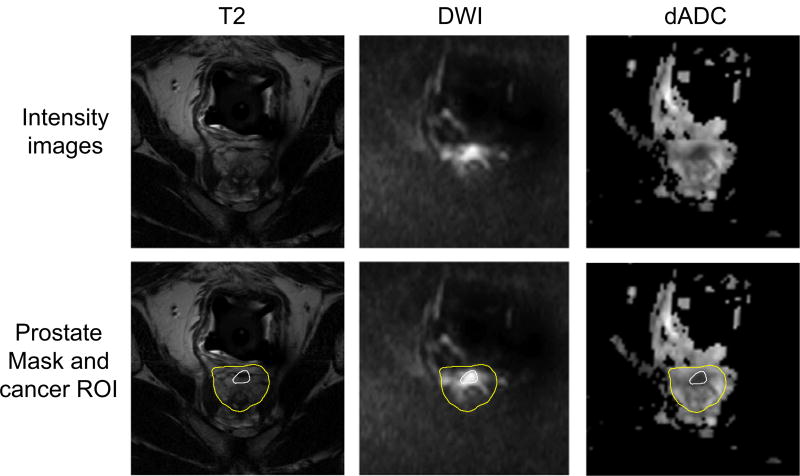
The dataset used in this study consists of multiparametric MR images from 21 prostate cancer patients, including T2-weighted MRI, DWI, and dADC (a type of ADC). Some samples are shown in Fig. 3. All T2-weighted MRI and DWI were acquired (after biopsy) between March 2008 and March 2010 with an endorectal coil (Medrad; Bayer Healthcare, Warrendale, PA, USA) and a phased-array surface coil with a Philips MR scanner (Achieva; Philips Healthcare, Eindhoven, the Netherlands, a 3T imager), and dADC was calculated from DWI by adjusting the b-value. Immediately before MR imaging, 1 mg of glucagon (Glucagon; Lilly, Indianapolis, Ind) was injected intramuscularly to decrease peristalsis of the rectum. The data acquisition parameters are shown in Table I. It is worth noting that dADC was calculated from DWI and dADC shares the same parameters with DWI, so there are no additional parameters for dADC in this table.

Fig. 3.

Sample of T2-weighted MRI, DWI, and dADC. In the second row, inner and outer curves denote prostate cancer regions and prostate regions, respectively. [Colour figure can be viewed at wileyonlinelibrary.com]

Table I.

Acquisition parameters of MR images.

Multiparametric MRI	Sequence type	Repetition time (msec)	Echo time (msec)	Resolution (mm3)	Flip angle (degree)
T2-weighted	Fast spin echo	3166–6581	90–120	0.3125 × 0.3125 × 3	90
DWI	Fast spin echo, echo planar imaging	2948–8616	71–85	1.406 × 1.406 × 3	90

For each subject, 1–3 cancer manual delineations on MR images were done jointly by both a radiologist (with 9 yr of experience in prostate MR imaging) and a pathologist (with 8 yr of experience in genitourinary pathology). These cancer ROIs, totally 37 tumors, including 26 PZ tumors, 11 CG or TZ tumors, were mostly outlined on T2-weighted images, and some were outlined on DWI. In our experiments, all images are resized into 512 × 512 with the resolution 0.3125 × 0.3125 × 3 (mm³) and all DWI and dADC images are aligned to T2-weighted image by using the FLIRT tool.³⁴ Note that, since the contrast of the prostate and other tissues in DWI and dADC is not high enough while the boundary of bladder is obvious, we first align T2-weighted image to DWI along with the bladder masks, and then align DWI to T2-weighted image with the prostate masks. At the same time, histogram matching³⁵ is also performed on each type of MRI across different subjects.

3.B. Experimental settings

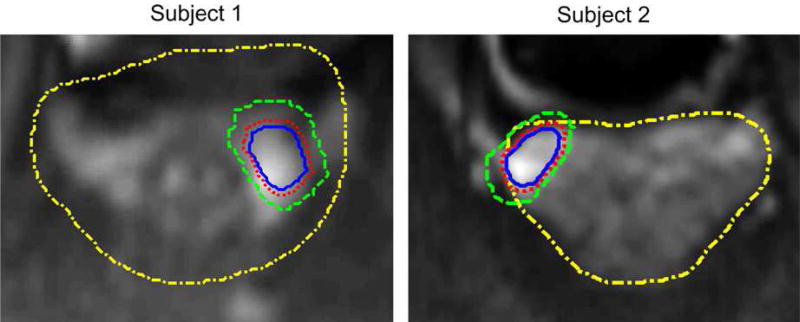
In the experiments, we use a leave-one-subject-out strategy. That is, each time we treat one subject as the testing data, while the remaining 20 subjects are used as the training data. Here, we regard the detection of prostate cancer as a binary classification problem. Specifically, for each training subject, all voxels in cancer-related ROIs are regarded as positive samples and the voxels in noncancer-related ROIs are treated as negative samples. To avoid the sample imbalance problem (i.e., the number of positive samples is far smaller than that of negative samples), in our experiments, we use only voxels around cancer regions as negative samples. Figure 4 shows the acquisition method for both positive samples and negative samples on two subjects. In Fig. 4, we denote the yellow dash-dot curve and the blue solid curve as the prostate region and the prostate cancer region, respectively, while the red dot curve is generated through expanding two pixels from the blue solid curve, and the green dash curve is generated by expanding some pixels from the red dot curve. As shown in Fig. 4, we regard all voxels within the blue solid curve as positive samples, and voxels in the region between the red dot curve and green dash curve as negative samples. It is worth noting that (a) the samples between blue solid curve and red dot curve might be mislabeled samples, so we discard them to avoid the effect of mislabeled samples; (b) how many pixels are expanded from the red dot curve depends on the number of positive samples, since we always wish the number of negative samples is approximate to the number of positive samples; (c) expanding more (than 2) pixels from the cancer annotation is more reasonable, but we only expand 2 pixels because most cancer regions are in PZ region and it is very possible to make some negative samples totally outside of the prostate region when we expand more pixels from the cancer annotation.

Fig. 4.

The acquisition of positive samples and negative samples. [Colour figure can be viewed at wileyonlinelibrary.com]

In addition, we construct a SAE model for each of three MRI modalities using the same setting. Specifically, for each voxel from training set, the 3D patch (with the size of 9 × 9 × 3) centered at this voxel is used as the input to the SAE model. There are four layers in each SAE model, and the number of unit in each layer is 243, 160, 80, and 40, respectively. Note that, we determined the numbers of hidden units by a grid search within a space of [120, 160, 200]−[60, 80, 100]−[30, 40, 50]. In the hierarchical classification scheme, 10 random forest classifiers are constructed for the compromise of computational cost and the classification accuracy. In each of these random forest classifiers, we adopt the same parameters as in,¹⁷ i.e., the number of classification trees is 40 and the tree depth is 50 with a minimum of eight sample numbers for each leaf node. In the training stage, we use all positive samples and partial negative samples (around cancer regions) to train SAE models and hierarchical classifiers; in the testing stage, we treat each voxel in the entire prostate as a testing sample, and classify it by using the trained hierarchical classifiers.

3.C. Evaluation methods

In this work, we employ three measure criteria to evaluate the performance of our proposed method, including section-based evaluation (SBE),³⁶ sensitivity and specificity. In the following, we describe briefly the three measurements.

SBE is defined as a ratio of the number of the sections that automatic method identifies correctly to the number of the total sections that the prostate is divided into. Letting n be the number of the total sections that the prostate is divided into, and A_s and B_s be the detection results of the s-th section by automatic method and expert, respectively, the SBE can then be formulated as follows:

$$\text{SBE}=\frac{{\sum }_{s=1}^{n}L\{A_s,B_s\}}{n}$$ (1)

where L(A_s, B_s) is used to estimate whether A_s and B_s have the same detection results. If yes, L(A_s, B_s) = 1; else L(A_s, B_s) = 0. Note that, A_s and B_s having the same detection results means that both automatic method and expert have detected the suspicious cancer ROIs on the s-th section or not. Obviously, the accuracy of SBE heavily depends on the number of sections of prostate division. The more sections prostate is divided into, the better SBE is able to evaluate the efficacy of a prostate cancer detection system. Usually, in clinical practice, a whole prostate is divided into six or 12 sections (shown in Fig. 5), and then the biopsy is performed in each section. In this situation, each MR image slice can be only divided into two or four parts which may be so large that need more shots for different points in each section to extract cancer tissue. In this study, in the view of the size of each prostate part, we divide the prostate into some sections as shown in Fig. 5(c). That is, the base and mid parts of the prostate are divided into nine sections, while the apex is divided into four sections. Figure 5 shows the division results of a typical prostate slice by using different division sections. From the figure, we can observe that we can more accurately identify cancer sections by dividing the prostate into these fine sections.

Fig. 5.

Conventional prostate division (6-section division and 12-section division) and our section division. [Colour figure can be viewed at wileyonlinelibrary.com]

Sensitivity (SEN) and specificity (SPE) are very popular measure methods used in detection of prostate cancer. In this work, since the detection results of prostate cancer is used for later biopsy, we reformulate the sensitivity and specificity based on the divided prostate sections, instead of voxels. That is, the sensitivity is defined as the ratio of the number of true identified cancerous sections to the sum of the number of true identified cancerous sections and the number of cancerous sections identified as normal sections, and specificity is defined as the ratio of the number of true identified normal sections to the sum of the number of true identified normal sections and the number of normal sections identified as cancerous sections.

3.D. Experimental results and analysis

3.D.1. Evaluation of hierarchical classification

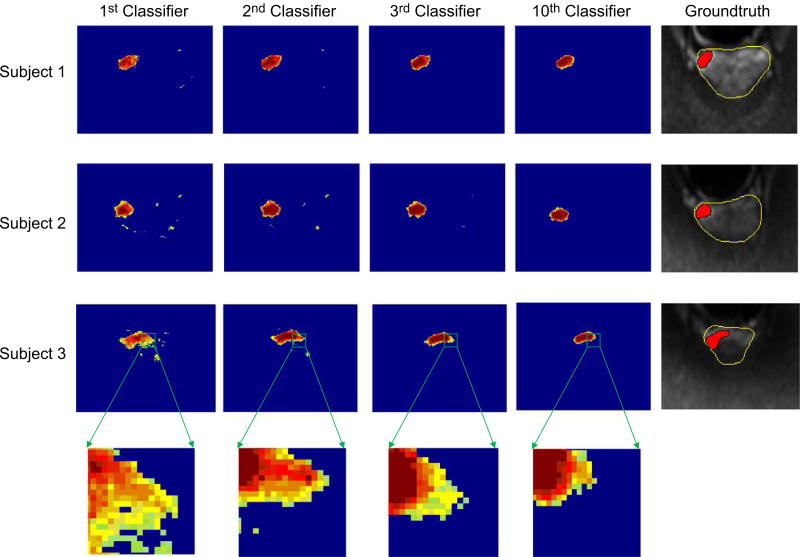
In order to evaluate the effectiveness of our hierarchical classification method, we investigate probability maps obtained from classifiers in different layers. Figure 6 illustrates the ground truth and the probability maps obtained by classifiers on three testing subjects in the 1st layer, the 2nd layer, the 3rd layer, and the 10th layer, respectively. To compare the classification results of each layer classifier clearly, we only show the ground truth on the original MRI. From Fig. 6, we can obtain the following observations. (a) As shown in the first classification results using the 1st layer classifier, there is a problem of spatially inconsistent classification. This can be attributed to the fact that the probability maps are estimated with only the appearance features, i.e., the learned high-level features, and no spatial information about the nearby structures is used. (b) In the subsequent iterations, cancer probability maps become more and more accurate and clearer, by comparing to the ground truth. In other words, by using context features of cancer probability map, our classification results have more uniform high values in the region of the prostate cancer while low values in the background. The underlying reason could be that the context features extracted from the previous probability map do help refine the classification results via the hierarchical classification procedure. (c) The classification result of the 3rd layer classifier is very similar with that of the 10th layer classifier, which indicates that our hierarchical classification can gain satisfying classification result after the second iteration. In addition, Fig. 7 shows the influence of classifier number on the SBE results achieved by the proposed method. It can be seen that the SBE becomes stable after using the 3rd classifier (i.e., two iterations).

Fig. 6.

The probability maps using different classifiers, along with the ground truth (shown on DWI slices). [Colour figure can be viewed at wileyonlinelibrary.com]

3.D.2. Evaluation of prostate cancer detection results

In this sub-section, we use SBE, sensitivity and specificity to evaluate the performance of prostate cancer detection achieved by our proposed methods and those comparison methods. Specifically, we perform prostate cancer detection by comparing the proposed hierarchical classification scheme with the conventional one-layer random forest classifier using five kinds of features (i.e., intensity features, Haar-like features, LBP features, HOG features, and the learned high-level features). The results on 21 subjects are reported in Table II. One could observe two main points from Table II. First, compared with the traditional classification method (i.e., the one-layer random forest), the proposed hierarchical classification method achieves much better results in terms of SBE and specificity, regardless of the use of different features. It demonstrates that the context features obtained from our proposed hierarchical classification approach is effective in refining the detection result. So, we believe that context features can provide complementary information for different types of features. Second, methods using our proposed high-level features consistently outperform those using the conventional features. These results validate the efficacy of our proposed high-level feature extraction method.

Table II.

Results achieved by different methods in prostate cancer detection.

	One-layer random forest			Proposed hierarchical classification (ours)
Method	SBE (%)	SEN (%)	SPE (%)	SBE (%)	SEN (%)	SPE (%)
Intensity features	84.86 ± 6.69	91.37 ± 4.31	82.17 ± 6.36	88.07 ± 5.87	90.68 ± 3.97	87.21 ± 6.24
Haar-like features	84.44 ± 5.81	94.10 ± 3.08	81.27 ± 4.92	87.11 ± 5.53	91.54 ± 3.46	85.09 ± 5.44
LBP features	79.85 ± 4.97	85.41 ± 2.94	78.64 ± 5.14	83.73 ± 5.01	83.68 ± 3.13	83.78 ± 4.92
HOG features	85.31 ± 6.42	92.76 ± 3.32	83.21 ± 5.97	88.14 ± 5.34	91.91 ± 2.96	86.96 ± 5.63
Proposed high-level features	87.95 ± 4.43	92.21 ± 2.42	84.50 ± 3.51	89.90 ± 4.23	91.51 ± 2.53	88.47 ± 3.89

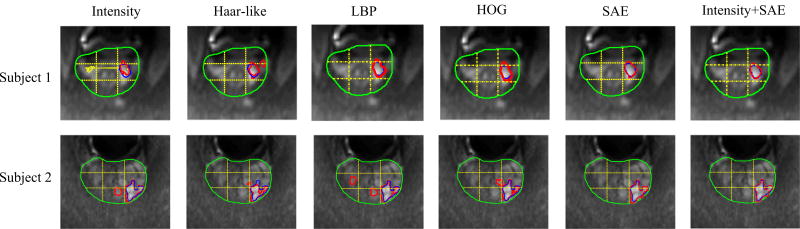
Furthermore, we show the detection results achieved by different methods based on our hierarchical classification methods on two typical subjects in the 1st to the 5th columns of Fig. 8, where the yellow dashed lines represent the division sections for a prostate, the green curves indicate the prostate region, the blue curves indicate manual segmentations (ground truth), and the red curves denote the segmentation results produced by methods using different feature representations including intensity features, Haar-like features, LBP features, HOG features, and our high-level features. From the 1st to the 5th columns of Fig. 8, one can observe that (a) the result of proposed method is better than other four methods, and is very similar to the ground truth, which indicates the efficacy of our proposed method. (b) Our method not only accurately locates PZ cancer (Subject 1), but also can locate TZ cancer (Subject 2) which is more difficult to detect than PZ cancer. (c) For both Subject 1 and Subject 2, all of used methods can accurately locate cancer regions, but some of detected cancer regions by the comparison methods are noisy, which could result in identification of more noncancer regions as suspicious cancer regions for guiding needle placement, while the detected cancer regions by our method are much clearer.

Fig. 8.

Comparison of cancer detection results by using different feature representations, shown on DWI slices of two subjects. [Colour figure can be viewed at wileyonlinelibrary.com]

In addition, we also evaluate the performance for the case of using only using each hidden layer feature representation of SAE to construct a hierarchical classification model. The SAE model, used in our work, consists of four layers, i.e., one input layer (intensity features), two hidden layers, and one output layer (high-level features). The average SBE by using each layer features is 88.07%, 88.96%, 89.54%, and 89.90%, respectively. The average sensitivity is 90.68%, 91.14%, 91.37%, and 91.51%, respectively. And the average specificity is 87.21%, 87.92%, 88.16%, and 88.47%, respectively. From these results, it can be seen that the detection performance is better and better with the use of more layers in SAE.

3.E. Extension by combining high-level features and original intensity features

Recent studies^18,24 show that combining high-level features and hand-crafted features can help build more robust classification models. In the following, we perform experiments by using the concatenation of the low-level original intensity features and learned-based high-level features to construct a hierarchical classification model. The experimental results are shown in Table III. From Table III, we can observe that SBE, SEN, and SPE are improved after combining the low-level features and high-level features, which demonstrates that the original low-level features are still informative for helping detection of prostate cancer, once combined with the latent feature representations. Also, cancer detection results by using the combination of high-level features and intensity features are shown in the last column of Fig. 8, where we can observe that the detection results using combined features are relatively smoother than those using only high-level features, especially for subject 2.

Table III.

Experimental results using the combination of high-level features and intensity features.

Method	SBE (%)	SEN (%)	SPE (%)
High-level features	89.90 ± 4.23	91.51 ± 2.53	88.47 ± 3.89
High-level features + low-level features	91.04 ± 3.94	92.32 ± 1.97	89.38 ± 3.01

4. DISCUSSION

Although our proposed method achieves performance enhancements, there exist some limitations and disadvantages. First, we used a relatively small database (21 patients), therefore the network structures used to discover high-level feature representation in our experiments are not necessarily optimal for other databases. We believe that intensive studies such as learning the optimal network structure from big database are needed for the practical use of deep learning and also extensive validation of our method on a larger scale of dataset will be more convincing. Second, our proposed method needs to learn SAE deep learning networks and train multiple random forest classifiers iteratively, so it is time-consuming in training stage. But, once SAE network and classifier are obtained, it will take less than a minute to get the result for a given patient data in Windows system with Intel core i5 and 16G memory. Third, we independently learned a high-level feature representation for each type of multiple MR images and fused them into a vector by a simple concatenation, thus the complementary information to each other was not used. Actually, each image modality provides different information. For example, T2-weighted MRI can provide the excellent anatomic detail, while DWI can evaluate degree of invasion in quality and quantity. It is interesting to investigate how to efficiently fuse the information of multiparametric MR images. Lastly, we should mention that we did not distinguish cancers in PZ and TZ although there are distinct differences between them in both imaging and biological features. As PIRADS have shown different guidelines for each of these zones, how to use the important prior knowledge to guide cancer identification in PZ and TZ will be a problem worthy of study in our further work.

5. CONCLUSION

In this study, we have proposed a novel multiparametric MR images-based method for automatic detection of prostate cancer by using learned high-level feature representations and hierarchical classification method. Different from conventional prostate cancer detection methods that identify cancer only in the peripheral zone (PZ), or classify suspicious cancer ROIs into benign tissue and cancer tissue, our proposed method directly identifies cancer regions from the entire prostate. Specifically, we first use an unsupervised deep learning technique to learn the intrinsic high-level feature representations from multiparametric MRI. Then, we train a set of random forest classifiers in a hierarchical manner, where both the learned high-level features and the context features obtained from classifiers in different layers are used together to refine the classification probability maps. We evaluate the effectiveness of the proposed method on 21 prostate cancer patients. The experimental results show that the high-level features learned from our method achieve better performance than the conventional handcrafted features, (e.g., LBP and Haar-like features) in detecting prostate cancer regions, and also the context features obtained from our proposed hierarchical classification approach are effective in refining detection result.

APPENDIX

Area under the receiver operating characteristic (ROC) curve (denoted as AUC) is a fair way to compare different approaches. Table A1 lists the average AUC values achieved by different feature representations. From Table A1, two observations can be made: (a) the proposed high-level features method has AUC values that are within 0.01 of the highest performing Haar-like features method for both the traditional one-layer random forest and the proposed hierarchical classification, and (b) the proposed hierarchical classification method achieves better AUC than the traditional one-layer random forest classification regardless of the use of different features, indicating that the proposed hierarchical classification is effective in refining detection results. In addition, with the higher SBE results and also the high AUC results, the proposed method is promising for guiding prostate biopsy, targeting the tumor in focal therapy planning, triage and follow-up of patients with active surveillance, as well as decision making in treatment selection.

Table A1.

The average AUC achieved by different feature representations.

Method	One-layer random forest	Proposed hierarchical classification
Intensity features	0.698	0.743
Haar-like features	0.811	0.826
LBP features	0.742	0.763
HOG features	0.753	0.784
Proposed high-level features	0.805	0.817