Abstract
Motion artifacts are now recognized as a major methodological challenge for studies of functional connectivity. As in-scanner motion is frequently correlated with variables of interest such as age, clinical status, cognitive ability, and symptom severity, in-scanner motion has the potential to introduce systematic bias. In this review, we describe how motion-related artifacts influence measures of functional connectivity, and discuss the relative strengths and weaknesses of commonly used de-noising strategies. Further, we illustrate how motion can bias inference, using a study of brain development as an example. Finally, we highlight directions of ongoing and future research, and provide recommendations for investigators in the field.
Keywords: motion, MRI, functional connectivity, connectomics, artifact
Introduction
Since the advent of medical imaging, it has been recognized that motion artifacts have the potential to degrade image quality. In the context of task-based functional MRI, motion has been known to impact measures of activation for over two decades (Friston et al., 1996). More recently, there has been an acceleration of research regarding covariance in fMRI timeseries—broadly called “functional connectivity” MRI (fc-MRI; Biswal et al., 1995). fc-MRI is a powerful and versatile tool that is capable of delineating functional brain network organization across the lifespan, in both health and disease (Fox and Raichle, 2007; Van Dijk et al., 2010; Craddock et al., 2013). However, despite evidence from task fMRI and other imaging modalities, for the first 20 years of its use investigators largely ignored the implications of in-scanner motion for fc-MRI.
In three reports published near-simultaneously in 2012, independent groups demonstrated that motion artifacts can have a marked impact on fc-MRI (Power et al., 2012a; Satterthwaite et al., 2012; Van Dijk et al., 2012). Indeed, it was quickly recognized that in-scanner motion had the potential to alter inference in studies of lifespan development, individual differences, and clinical groups. This prompted substantial re-evaluation of a broad array of published research, and has spurred a proliferation of techniques to mitigate the impact of motion artifacts on functional connectivity. While the diversity of new techniques has been welcome, it nonetheless has led to significant confusion among investigators, and controversy during peer review.
In this review, we seek to provide an accessible overview of this rapidly evolving sub-field. First, we begin by delineating several basic properties of motion artifacts in fc-MRI. Second, we describe common strategies for minimizing motion artifacts as part of the processing pipeline. In particular, we describe the relative benefits and drawbacks of using global signal regression (GSR), an approach that has generated substantial controversy in the field. Third, we summarize recent data regarding the relative strengths and weaknesses of several approaches as defined by comparison to a set of intuitive benchmarks. Fourth, we use a study of brain development as an example of how motion artifacts may systematically bias inference. We close by examining limitations of current approaches, future directions for additional research, and by providing recommendations for investigators.
Characteristics of Motion Artifacts in fc-MRI
Understanding the characteristics of motion artifacts is a prerequisite for identifying potentially artifactual results and for the development of effective de-noising approaches. Accordingly, here we summarize the spatial and temporal properties of motion artifacts. We begin by providing a brief orientation to the ways in which in-scanner motion is commonly measured in fc-MRI studies.
Measurement of in-scanner motion
In-scanner motion is typically estimated from the functional timeseries itself. During preprocessing each volume of the timeseries is usually rigidly realigned to a reference volume; this produces set of 6 realignment parameters (RPs; 3 translations, 3 rotations) describing how much a given volume within the timeseries must be moved. These realignment parameters can be summarized as the frame displacement (FD), which is computed in relative terms versus the prior volume, thus providing a concise index of volume-to-volume motion (Power et al., 2012a). Motion across an entire scanning sequence for a given subject can be summarized as mean FD.
FD has been calculated in several different ways. Overall, measures tend to be highly correlated, but may scale differently (see Figure 1). For example, FD as calculated by Power et al. (2012a) is approximately twice the magnitude the FD provided by Jenkinson et al. (2002). Work by Yan et al. has shown that the matrix root mean squared formulation derived by Jenkinson et al. aligns best with voxel-specific measures of displacement (Yan et al., 2013a). Below, unless noted otherwise, the FD measures reported and displayed in figures are calculated using FD as implemented in FSL (Jenkinson et al., 2002).
Figure 1. Commonly used of measures of frame displacement (FD) are highly correlated but not identical.
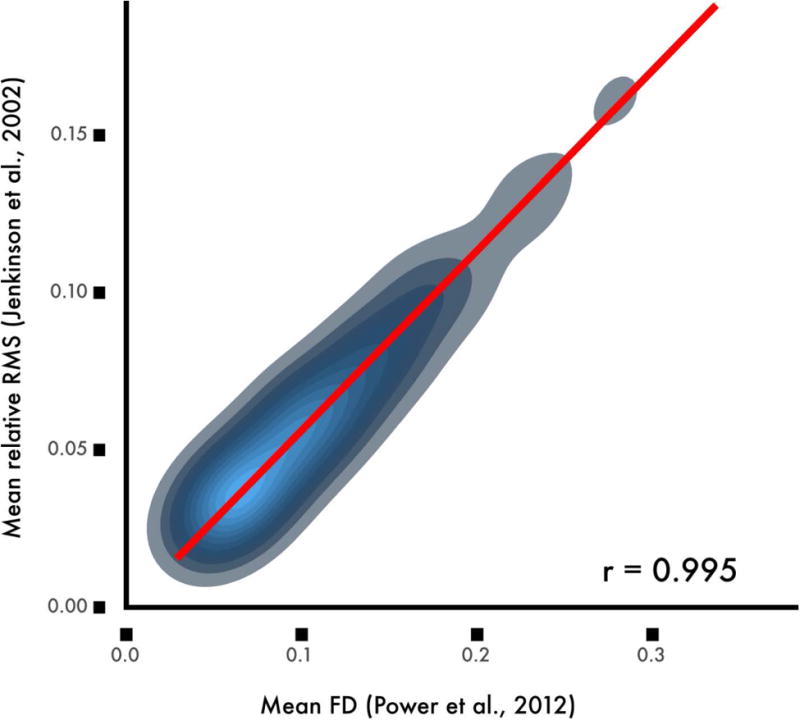
While FD as calculated according to Power et al. (2012a) is correlated at a level of r = 0.99 with the average root mean squared displacement calculated by Jenkinson et al (2002), the scaling varies by an approximately 2:1 ratio. Data from the sample of 393 youth described in Ciric et al., 2017.
Importantly, all such measures are based on volume-based realignment procedures, and thus are limited in temporal resolution, which is equivalent to the repetition time of the image. These methods therefore do not effectively capture within-volume motion. Furthermore, realignment estimates may be inaccurate in images that are substantially corrupted by motion-related artifacts. Perhaps most importantly, FD measures are difficult to compare across studies with different acquisition sequences. With the advent of multiband imaging, repetition times are often only 20% of previous sequences. However, scanning faster does not obviate concerns about motion artifacts, and also makes FD more difficult to compare across studies. For example, a mean FD of 0.2mm denotes much higher motion in a multiband sequence with a repetition time of 600ms compared to a standard sequence with a repetition time of 3000ms. Converting FD into a standardized measure such as millimeters of RMS displacement per minute would alleviate such scaling by the acquisition TR and aid in comparisons of motion across studies (Reuter et al., 2015).
Spatial distribution of motion and motion artifacts
In order to understand the spatial distribution of motion, at least three studies have used voxel-specific measures of FD, which can be computed directly from the image header (Yan et al., 2013a; Satterthwaite et al., 2013; Spisák et al., 2014). As expected by the biomechanical constraints of the neck, motion is minimal near the atlas vertebrae (where the skull attaches to the neck) and increases with the distance from the atlas (Figure 2A; Satterthwaite et al., 2013). Furthermore, the high motion in frontal cortex is most likely due to the preponderance of y-axis rotation, associated with a nodding movement. Nonetheless, the motion as described by voxel-specific measures is quite correlated with global (whole-brain) measures of FD (r=0.89; Figure 2B; Satterthwaite et al., 2013).
Figure 2. Spatial variation of motion artifacts.
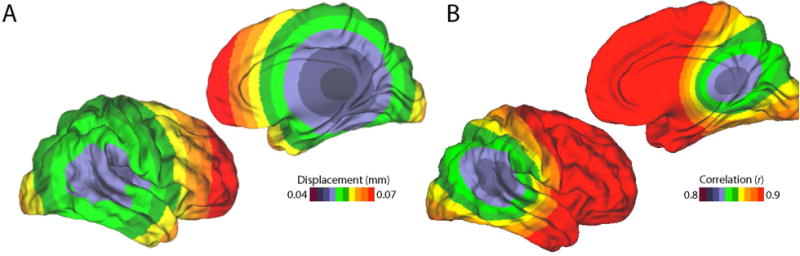
A) Motion is minimal in the center of the brain, and is maximal in frontal cortex. B) Voxel-specific measures of motion are highly correlated with mean FD. Reprinted with permission (Satterthwaite et al., 2013).
Several groups have attempted to leverage spatial heterogeneity of motion in the de-noising process, yet these attempts have not been shown to out-perform other commonly used pipelines (see below). This lack of improvement is most likely due to the fact that motion is highly correlated across voxels, and results in a drop in signal intensity across the entire brain parenchyma (Figure 3A; Satterthwaite et al., 2013). In contrast to signal decrements observed in the brain parenchyma, areas at the edge of the brain demonstrate large increases in signal, most likely due to partial volume effects. Similar partial volume effects occur at tissue class boundaries. Furthermore, Schienost et al. demonstrated that due to these global effects, motion produces increased image smoothness (Scheinost et al., 2014), and accounting for differences in smoothness is a potentially effective post-processing strategy (see below).
Figure 3. Spatial distribution and time course of motion artifacts.
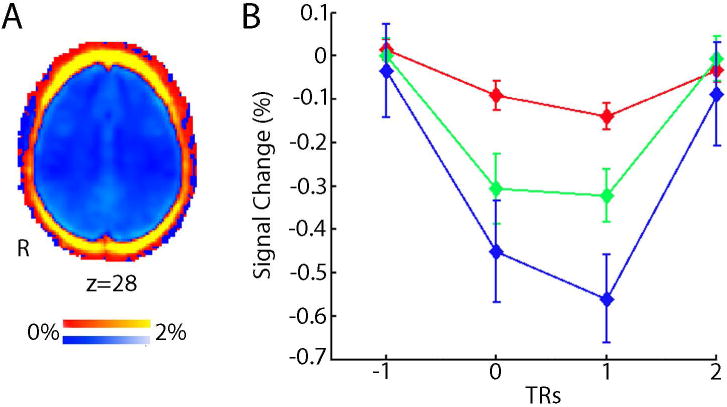
A) Motion reduces BOLD signal (blue, negative % signal change) throughout the brain parenchyma, but increases signal around the rim of brain (red, positive percent signal change). B) Motion produces a large reduction in global BOLD signal that is maximal in the volume following subject movement. The magnitude of signal reduction increases as motion amplitude increases (red, >0.3mm displacements; green, >0.5mm, blue >0.7mm). Results are from a fixed impulse response analysis of the global signal timeseries. Reprinted with permission (Satterthwaite et al., 2013).
Temporal properties of motion artifacts
With the goals of improving de-noising, several studies have examined the temporal characteristics of signal artifacts that result from motion. Our group demonstrated that motion results in a substantial drop in signal immediately following the movement event, which scales with the magnitude of motion (Figure 3B; Satterthwaite et al., 2013). These signal changes are temporally circumscribed, and maximal at the volume being acquired immediately after an observed movement. As described below, censoring techniques target such consistent large-amplitude artifacts for removal.
In addition to such temporally circumscribed artifacts, longer-duration (up to 8-10s) also occur idiosyncratically in individual timeseries (Power et al., 2012a; Power et al., 2013). While at present the origin of these sporadic longer-duration artifacts remains unknown, some speculate that they are due to motion-related changes in CO2 that accompany yawning or deep breathing (Power et al., 2012a; Power et al., 2013). Also, it may be possible that large disruptions in signal induced by motion may only equilibrate over such longer durations. Finally, interactions between the specific direction of motion and the image phase encoding plane may also produce temporally variable results.
These data build upon prior studies that that lend insight into the properties of motion related artifacts based on the MRI physics of image acquisition . Crucially, many of these effects introduce a non-linear relationship between the signal intensity at a particular voxel and head motion. This is important because nonlinearities are difficult to remove using movement of estimates based upon rigid body (affine) models. Examples of non-linear effects include spin excitation history effects, which can persist for some time after movement (Friston et al, 1996). Other important (non-linear) effects include interpolation artefacts during image reconstruction and interactions between the magnetic field and head position, which introduce distortions in EPI time series (Andersson et al., 2001; Grootoonk et al., 2000). As we discuss later, these non-linear effects motivate the use of non-linear motion parameters in confound regression.
Signal frequency of motion artifacts
Convergent data has demonstrated that most functional connectivity signal is driven by low-amplitude fluctuations (Cordes et al., 2001). Accordingly, it is common to use the amplitude of low-frequency fluctuations (ALFF; Yang et al., 2007) or fractional amplitude of low frequency fluctuations (fALFF; Zou et al., 2008) as a voxelwise proxy of connectivity. To retain only frequencies in the low-amplitude range, it is a common but somewhat controversial practice (Carp, 2011), to apply a band-pass filter that retains signals in the 0.01-0.1 Hz range (Weissenbacher et al., 2009). However, based on evidence suggesting that higher-frequency signals also carry connectivity information (Fornito et al., 2011; Niazy et al., 2011), increasingly only a high-pass filter is applied. Understanding which signal frequencies are most impacted by motion artifacts could help investigators decide whether or not to apply temporal filtering, as the temporal filter could be tailored to remove frequency bands that are most contaminated by artifacts.
Relatively little work has focused on spectral properties of motion artifacts. In one earlier study, we found that motion increased the magnitude spectra across all frequencies, but this effect was greater at higher frequencies (Satterthwaite et al., 2013). These results accord well with those from a smaller independent study of adults by Hlinka et al., who found that motion artifacts were more prevalent at high frequencies (Hlinka et al., 2010). Discrepancies in results from both an earlier study from our group (Satterthwaite et al., 2012) and work by Yan et al. (2012) are likely due to the use of standardization procedures (such as z-scoring) of statistical maps in these earlier papers.
Following effective confound regression (with a 36-parameter model and spike regression, see below) we have found that the effect of motion is attenuated in low frequencies but not higher frequencies (Figure 4; Satterthwaite et al., 2013). However, this analysis was limited in that it only considered average effects across 160 nodes covering the brain. In contrast, Kim et al. examined 1000 participants scanned as part of the Genome Superstruct Project, and delineated the impact of motion on voxelwise power-spectrum maps (Kim et al., 2014). When the data was processed without GSR, they found that motion was associated with greater amplitude in both high and low frequency bands, but that artifacts were particularly prominent in frontoparietal and default mode networks. Once GSR was used, they found elevated high-frequency fluctuations with motion, but in fact found reduced signal amplitude in lower frequency bands in select DMN and frontoparietal network regions. Taken together, available data suggests that the impact of motion is consistent at higher frequencies, but varies at lower frequencies on a regional basis in part due to the preprocessing applied.
Figure 4. Motion increases signal magnitude at higher frequencies.
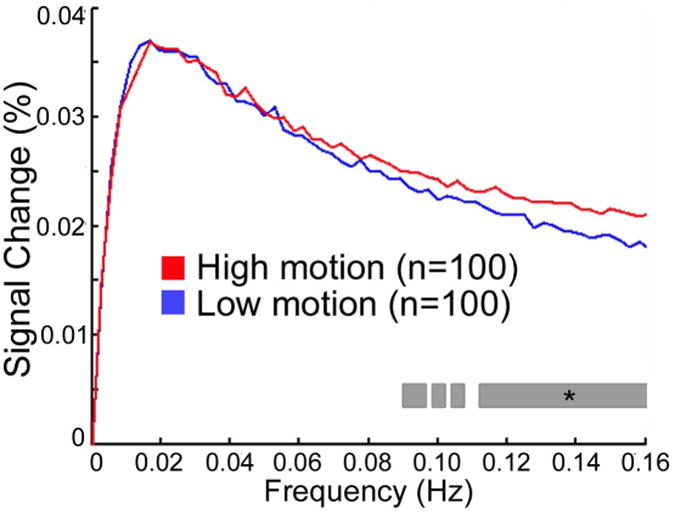
When an effective confound regression model is used (36 parameters + spike regression), demographically-matched high and low motion groups diverge only at frequencies above 0.08 Hz. Starred gray bar indicates a significant difference between magnitude of high and low motion groups at each frequency. Reprinted with permission (Satterthwaite et al., 2013).
Distance-dependence of motion artifacts
One important fact recognized by two of the initial reports on motion artifacts in fc-MRI were that the impact of motion on functional connectivity depended strongly on the Euclidean distance between regions (Power et al., 2012a; Satterthwaite et al., 2012). Specifically, when data were processed using GSR, motion increased the apparent strength of short-range connections, but weakened the apparent strength of long-range connections. This was of particular concern for studies of development in youth, as prior work had reported that long-distance connections strengthened with age (Dosenbach et al., 2010; Fair et al., 2007).
Subsequent work demonstrated that this distance-dependence was strongly modulated by pre-processing strategy, especially the inclusion of GSR. As shown in Figure 5A (Satterthwaite et al., 2013), in data processed without GSR, motion is associated with stronger connectivity of both short and long range connections. While some distance dependence is present, it is relatively minor, with motion producing somewhat less of an increase in connectivity in long-range connections than short-range connections. In contrast, in data processed with GSR (Figure 5B), the effect of motion on connectivity is weaker, but there is marked distance dependence (Satterthwaite et al., 2013). When GSR is used, motion is associated with stronger connectivity for short-range connections, but is conversely associated with weaker connectivity for long-range connections. This demonstrates a critical trade-off in the choice of processing pipeline: while GSR results in reduced impact of motion on connectivity, it tends to exacerbate distance-dependence. While the reason GSR exacerbates distance-dependence is not fully understood, analyses by Power et al. (2012a)a and Satterthwaite et al. (2013a)suggest it relates to the fact that the motion-induced increase in correlation between distant regions is also shared with the global signal and can therefore be removed by GSR. In contrast, regionally-localized motion artifacts will increase local (short-range) connectivity but cannot be readily removed by GSR.
Figure 5. Global signal regression affects distance-dependence of motion artifacts.
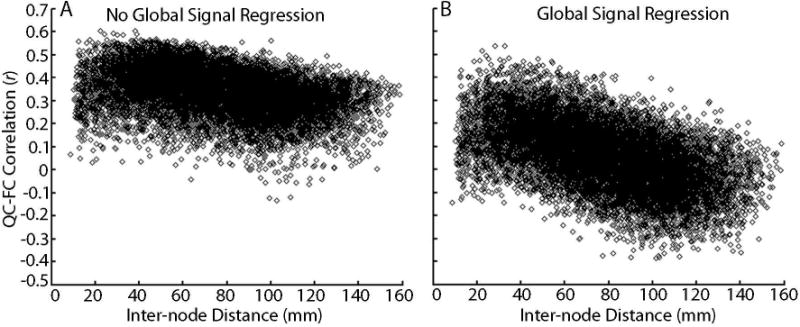
A) Plot of the correlation between mean FD and pairwise connectivity across subjects in a network of 160 ROIs (12,720 unique connections) versus inter-node Euclidean distance, when the global signal is not included in confound regression. Motion tends to increase connectivity between regions; this effect is maximal at short ranges but is present across the range of inter-region distance. B) Plot of the correlation between mean FD and pairwise connectivity in a network of 160 ROIs versus inter-node distance when the global signal is included in confound regression. In this model, motion increases connectivity between adjacent nodes, but diminishes connectivity between more distant nodes. However, when GSR is included in confound regression, on average the effect of motion on connectivity is diminished (i.e., centered around zero). Reprinted with permission from (Satterthwaite et al., 2013).
Processing Approaches to Mitigate Motion Artifacts
Having described certain properties of motion artifacts, we next review common postprocessing strategies to limit their impact on functional connectivity data. In particular, we focus on confound regression approaches, censoring methods, as well as spatial and temporal filtering. It should be noted that this review is not comprehensive: readers should reference original research regarding several novel but less-commonly used techniques, as well as a thorough recent review (Caballero-Gaudes and Reynolds, 2016). We begin with confound regression, which remains the single most common strategy for removing motion artifacts in functional connectivity data. The many confound regression approaches used can be loosely grouped by what signals are regressed from the data: realignment parameters (RPs), tissue-specific signals, the global signal, signals from principal components analysis (PCA), and signals isolated using independent components analysis. For each, the most common implementation is to regress one or more of these confounding signals from the functional timeseries data using linear regression, and then use the residual timeseries for subsequent analyses. Notably, these techniques are not mutually exclusive, and in fact are often applied in combination with each other and with censoring techniques.
Confound regression: realignment parameters
At present, RPs remain the single most common confound regression technique used in fc-MRI de-noising. As noted above, 6RPs are derived from the rigid-body registration of the functional timeseries during realignment, including three translations and three rotations. These 6 RPs are commonly used as nuisance regressors in both task-based and fc-MRI analyses. In order to account for time lags in motion effects, the first temporal derivative of these 6 RPs is often also included (12RP model). Furthermore, over 20 years ago, Friston et al. proposed using a second-order polynomial expansion of the RPs (Friston et al., 1996). In practice, quadratic terms are often calculated for both the original RPs and their temporal derivatives, thus yielding 24 parameters in total (24RP model).
Tissue-specific signals
Beyond RPs, it has been common practice to regress out timeseries from white matter (WM) and cerebrospinal fluid (CSF) voxels, which are impacted both by motion and by physiological signals of no interest such as respiration. Regression of mean gray matter (GM) signal is less common, but due to its near-unity correlation with the global signal (r > 0.97) it should be considered essentially equivalent to GSR. The specific method used in the construction of WM masks is important, as superficial white matter signals are highly correlated with the global signal due to partial-volume effects (r > 0.9); thus investigators who do not erode WM masks may be applying GSR inadvertently (Power et al., 2016). One alternative to using the mean WM signal is ANATICOR (Jo et al., 2010), which was designed to account for spatial heterogeneity in artifacts. The approach uses a local WM regressor for each GM voxel, based on the average signal within an eroded WM mask within a 15mm radius. In theory, this technique allows confound regression to model local disturbances due to scanner artifacts or motion.
Global signal regression
Although currently most common in studies of fc-MRI, global signal regression (GSR) was in fact previously used in PET (Friston et al., 1990) and task fMRI research (Aguirre et al., 1998), and in part led to the use of general linear models for timeseries analyses. GSR was introduced to account for large, non-physiological shifts in the fMRI signal (Fox et al., 2005), and rapidly became a standard part of pre-processing pipelines. It should be noted that GSR is distinct from fMRI preprocessing steps like grand mean scaling (which is typically applied) and volume-based intensity normalization (which is not commonly used). Use of GSR is one of the most contentious debates in neuroimaging, and is the topic of many dedicated articles (Fox et al., 2009; Murphy et al., 2009; Weissenbacher et al., 2009; Gotts et al., 2013; Chai et al., 2012; Saad et al., 2012); a full account is beyond the scope of this review, and the debate is expertly summarized in a recent article by Fox and Murphy (2017). However, accumulating evidence demonstrates that GSR is a simple and highly effective de-noising technique that limits the influence of motion artifacts in studies of functional connectivity. GSR's effectiveness is thought to be largely due to the fact that in-scanner motion causes distributed drops in signal across the brain (see Figure 3A; Satterthwaite et al., 2013). The potential utility of GSR for de-noising is underscored by persuasive recent data from Power et al., who examined over 1000 scans from 8 scanning sites, and demonstrated that artifacts due to head motion, respiration, and scanner artifacts are captured by the global signal across datasets (Power et al., 2016). Furthermore, as described below, recent data from benchmarking studies suggests that adding GSR to de-noising pipelines mitigates the impact of motion artifacts (Burgess et al., 2016; Ciric et al., 2016).
PCA-based confound regression: CompCor
In addition to the use of global or local confound regressors derived from specific tissue classes, many studies have used principal components analysis (PCA) based approaches to identify and remove confounding signals. While PCA could be applied to the complete whole-brain voxelwise timeseries, the two most common PCA approaches attempt to isolate parts of the image that are thought to be more strongly impacted by motion and other noise. Behzadi et al. (2007) introduced two variants of this method as part of the popular CompCor technique (Behzadi et al., 2007): anatomic CompCor (aCompCor) and temporal CompCor (tCompCor). In aCompCor, a PCA is performed on voxelwise CSF signals and eroded WM, whereas in tCompCor high noise regions are identified by their temporal standard deviation. In Behzadi et al. (2007), the number of principle components included was determined using Monte-Carlo simulations (yielding a mean of 4-6 regressors per subject). Building on this work, Muschelli et al. proposed a variant of aCompCor where components explaining the top 50% of signal variance were retained; this approach performed better than using a fixed set of 5 regressors (Muschelli et al., 2014).
Independent component analysis
ICA is a blind source separation technique that seeks to detect mixed signals derived from nearly-independent sources. ICA is among the most commonly used techniques for defining intrinsic connectivity networks at the group level, typically by concatenation of subject timeseries (Beckmann et al., 2005; van de Ven et al., 2004). At the group level, ICA yields spatial maps of functional networks that are present across individuals. However, ICA can also be used for subject-level de-noising, where the timeseries of noise components are regressed from the data (Kochiyama et al., 2005; Tohka et al., 2008; Bhaganagarapu et al., 2013). When ICA is applied to data from individuals, the number, spatial distribution, and temporal characteristics of ICA components vary substantially. Due to the lack of correspondence of components across individuals, several techniques have been developed to identify and remove noise components from single-subject data, which can broadly be grouped as classifiers that require labeled components and automated algorithms.
While many ICA-based de-noising techniques have been described, at present only two have been directly evaluated for the control of motion artifacts in studies of functional connectivity. In a pair of papers, Salimi-Khorshidi et al. and Griffanti et al. introduced and validated ICA-FIX (Salimi-Khorshidi et al., 2014; Griffanti et al., 2014), which is the standard de-noising technique for the Human Connectome Project (Smith et al., 2013). This approach uses a multi-level machine learning classifier to identify noise components with high accuracy. However, this classifier requires labeled training data, ideally from the same scanner and acquisition protocol; use of detailed published procedures for manually identifying noise components aid in this time-consuming process (Griffanti et al., 2016). In contrast, ICA-AROMA identifies noise components using a pre-defined set of features that are extracted automatically from the image (Pruim et al., 2015b; Pruim et al., 2015a).
Temporal censoring
All of the techniques surveyed thus far (RPs, WM signals, GSR, PCA, ICA) are variants of confound regression, and differ mainly in their approaches to identifying noise signals. In addition to regression of nuisance time series, a number of temporal censoring methods are commonly used to reduce the impact of motion artifacts, where motion-corrupted volumes are identified and either excised or interpolated. These approaches include scrubbing (Power et al., 2012b; Power et al., 2012a; Power et al., 2013), spike regression (Satterthwaite et al., 2013), and despiking techniques (Jo et al., 2013; Patel et al., 2014). While these techniques have many similarities, approaches differ in the way motion-corrupted data is identified, what threshold for removal is used, how many volumes are removed, and whether interpolated data is retained in the final timeseries. One potential solution to the problem of thresholding spike regression is the use of a variance-weighting approach that de-weights timepoints along a continuum on the basis of signal quality and the presence of detected artifact (Diedrichsen and Schadmehr, 2005). Although not yet applied to rsfc-MRI data, such an approach could integrate the virtues of a temporal censoring approach but without the need to select an arbitrary threshold for designating the presence of a spike.
Scrubbing and spike regression are highly similar as implemented in most recent approaches: while scrubbing literally excises motion-corrupted timeseries, spike regression removes the influence of that volume in the confound regression step by adding a binary regressor indexing each timepoint where motion occurs. Scrubbing interpolates flagged volumes temporarily before filtering and subsequent removal, ultimately concatenating non-corrupted timeseries (Power et al., 2012b; Power et al., 2012a; Power et al., 2013). In contrast, spike regression interpolates corrupted volumes (Satterthwaite et al., 2013). In both approaches, motion-corrupted data is typically identified using an FD threshold, a signal change threshold, or a combination of the two. Signal change has been most commonly calculated using the DVARS metric introduced by Power et al., which indexes the RMS intensity difference across volumes (Power et al., 2012b). As typically used, FD- and DVARS-based criteria flag entire volumes for removal as part of spike regression or scrubbing. Over time, the threshold for the scrubbing applied has become more stringent (Power et al., 2012b; Power et al., 2012a; Power et al., 2013).
Similarly, there has been substantial variability in the amount of adjacent data removed in spike regression and scrubbing. To eliminate longer-duration artifacts associated with motion, the most commonly implemented version of scrubbing removes one volume before and two after a motion event (Power et al., 2012b; Power et al., 2012a; Power et al., 2013). In contrast, our group typically removes only a single corrupted volume as part of spike regression, allowing retention of more data (Satterthwaite et al., 2013). This is motivated by data from Satterthwaite et al. (2013a), where we found that including spike regressors to cover a larger temporal window did not provide additional de-noising benefit (Figure 6). Furthermore, we found that identifying motion spikes using a dual-criterion FD + DVARS approach did not provide additional benefit beyond a single-criterion (FD-only) approach. However, these results do not fully accord with data from Power et al. (Power et al., 2013), suggesting that optimal censoring parameters may potentially vary by dataset.
Figure 6. Confound regression of motion spikes.
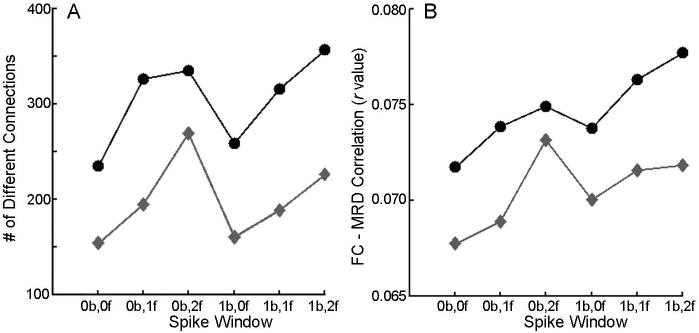
Spike regression was evaluated using a single-criterion identification method (FD, measured as mean relative RMS displacement in FSL; grey diamonds) and a dual-criteria method (FD + DVARS; black circles). These two methods were tested over a range of windows (xb,yf denotes x TRs before spike, y TRs after spike). The single-criterion approach without an expanded temporal window (0b,0f) produced the least number of significantly different connections between high and low motion groups (A) and the lowest mean absolute correlation between FD (mean relative displacement) and functional connectivity (B). Reprinted with permission from (Satterthwaite et al., 2013).
In contrast to scrubbing and spike regression, which remove or adjust all voxels in particular volumes, despiking techniques have been implemented to be spatially adaptive, so that motion-induced signal changes can be selectively removed from voxels affected by artifact. Despiking techniques identify signal spikes in voxel-level timeseries using measures such as the local median absolute deviation (as implemented in AFNI; Cox, 1996). One promising approach uses wavelet decompositions to identify and then remove spikes in the data (Patel et al., 2014). This approach has been shown to be superior to standard despiking methods, but does requires parameter tuning (Patel and Bullmore, 2016). It should be noted that all temporal censoring operations have the potential to alter both the signal dynamics and the autocorrelation structure of the timeseries data.
Temporal and spatial filtering
In contrast to the proliferation of confound regression and censoring approaches, temporal and spatial filtering approaches have received less attention. As noted above, prior work has demonstrated that motion tends to result in increased signal amplitude at higher frequencies (Satterthwaite et al., 2013). However, such effects are clearly dependent on the confound regression strategy used: data processed using pipelines with lower-order confound regression or with pipelines that do not include GSR show less frequency-band selectivity, with motion being associated with higher signal amplitude across a wide range of frequencies (Satterthwaite et al., 2013; Kim et al., 2014). Thus, one strategy for mitigating the impact of motion is to use a low-pass filter that removes higher frequencies that are more susceptible to motion. However, this strategy remains controversial as any connectivity information present at higher frequencies will be lost (Niazy et al., 2011). Indeed, a recent paper by Vergara et al. suggests that multivariate classification performance may be improved when higher frequencies are retained (up to 0.24Hz), although it is unknown if such effects are driven in part by the subtle influences of data quality (Vergara et al., 2016). Furthermore, it is not known how generalizable such frequency-specific effects are across different acquisition protocols that vary in their repetition time: data from both Satterthwaite et al. and Kim et al. used single-band echoplanar imaging, rather than new multiband sequences that provide a great increase in temporal resolution. One pitfall that should be uniformly avoided is performing confound regression on band-pass filtered timeseries with regressors that have not been filtered in the same manner, which can re-introduce artifactual signals in the very frequency bands that were removed by the band-pass filter (Hallquist et al., 2013).
To our knowledge, only one study has examined the impact of spatial filtering on motion artifacts. Scheinost et al. demonstrated that higher motion data has greater smoothness, and that smoothing each dataset to a uniform degree of smoothness can reduce the effect of motion artiacts on functional connectivity (Scheinost et al., 2014). In this approach, higher motion data, which starts out with greater smoothness due to the presence of artifacts, receives less additional smoothing than lower-motion data.
Putting it all together: common combinatorial approaches
The techniques described above do not need to be applied in a mutually exclusive fashion. For example, the pipeline most commonly used in our group uses expansions of the global, white matter, and CSF signals in addition to the realignment parameters (36 parameter model; called “36P” below) and spike regression (Satterthwaite et al., 2013). In contrast, the minimal preprocessing pipeline used by the HCP does not use GSR, but includes 24 realignment parameters and ICA-FIX (Smith et al., 2013). However, recent work by Burgess et al. suggests that a GSR analogue (mean greyordinate timeseries) can improve de-noising when added to ICA-FIX (Burgess et al., 2016). Given the many techniques available and their myriad combinations, the choice of a de-noising strategy has understandably led to confusion among investigators, reviewers, and the field at large. In the next section, we summarize a recent effort from our group to evaluate denoising pipelines according to several intuitive benchmarks.
Comparing Confound Regression Methods
Benchmarks of de-noising success
Before comparing de-noising pipelines, one must first define success. Several different outcome measures have been used in existing de-noising studies. First, the single most intuitive benchmark is the residual relationship with motion, which can be quantified with the correlation between functional connectivity and in-scanner motion after denoising (or “QC-FC” correlation). This correlation is generally taken across subjects. In other words, if subjects who move more show more (or less) functional connectivity, it can be assumed that a portion of functional connectivity can be attributed to movement. Second, prior work has shown that the use of certain de-noising pipelines (especially ones that use GSR) can help mitigate QC-FC correlations but simultaneously result in distance-dependent motion artifacts. Distance dependence is thus a useful secondary benchmark, and can be quantified as the correlation between inter-node Euclidean distance and the effect of motion on connectivity (i.e., the slope of the QC-FC correlation over distance). Third, to ensure that de-noising does not remove a substantial amount of signal along with motion-related noise (Bright and Murphy, 2015), it is useful to evaluate network identifiability. Network identifiability can be summarized as network modularity quality (Q) (Newman, 2006), which quantifies the degree to which structured sub-networks are present; prior studies have also used overlap with a priori templates (Pruim et al., 2015b; Pruim et al., 2015a).
In addition to these three measures, other benchmarks have been proposed and may be of substantial utility. Test-retest reliability is a particularly appealing measure. At present, there is relatively less data on test-retest reliability of different de-noising pipelines (but see: Yan et al., 2013a & 2013b) as large-scale within-subject designs with repeated measurement remain uncommon. Moving forward, this will certainly change as investigators begin to capitalize upon the enormous resources provided by the Consortium of Reliability and Reproducibility (CORR; Zuo et al., 2014), which includes 5,093 scans across 1,629 participants. However, it should be cautioned that test-retest reliability should not be evaluated in isolation: because in-scanner motion itself is relatively consistent within individuals across scanning sessions, there is the potential for residual motion effects to artifactually enhance test-retest reliability. An additional benchmark that may be appealing is discriminability, which summarizes the degree to which a given pipeline enhances sensitivity to group or individual differences. Relatively little prior work has used this outcome measure, which has intuitive appeal (see Vergara et al., 2016 for one example). However, as for test-retest reliability, discriminability should explicitly be evaluated in the context of other benchmarks, as group or individual differences could be inflated by the differential presence of residual noise across individuals or groups, as certain groups (such as children, older adults, and many patient groups) are more likely to move during the scan.
It must be emphasized that the research hypothesis should dictate the choice of benchmark used. For example, in developmental and psychiatric neuroimaging, it is often a primary concern that motion will confound individual or group differences, leading to type I error. For these studies, it is reasonable to prioritize a QC-FC benchmark. In contrast, for studies of network topology that are not focused on individual differences, minimizing distance-dependence may be a reasonable priority. Thus, as previously noted elsewhere, the processing pipeline should be chosen in accordance with the goals, and no single pipeline will be appropriate for all studies.
In this section, we summarize recent work evaluating the performance of 14 commonly used pipelines (Figure 7) in a sample of 393 youth ages 14-22 who underwent neuroimaging as part of the Philadelphia Neurodevelopmental Cohort (PNC) (Satterthwaite et al., 2014; Calkins et al., 2015; Satterthwaite et al., 2015). Note that pipelines that require substantial training (i.e., ICAFIX) or parameter tuning (i.e., wavelet despiking) were not evaluated. For each of these 14 pipelines, we examined the residual relationship with motion, distance dependence, and network identifiability in two different node systems (for full details, see Ciric et al., 2017). As described below, de-noising pipelines have clear trade-offs when multiple benchmarks are evaluated jointly.
Figure 7. Schematic of the 14 de-noising models evaluated.
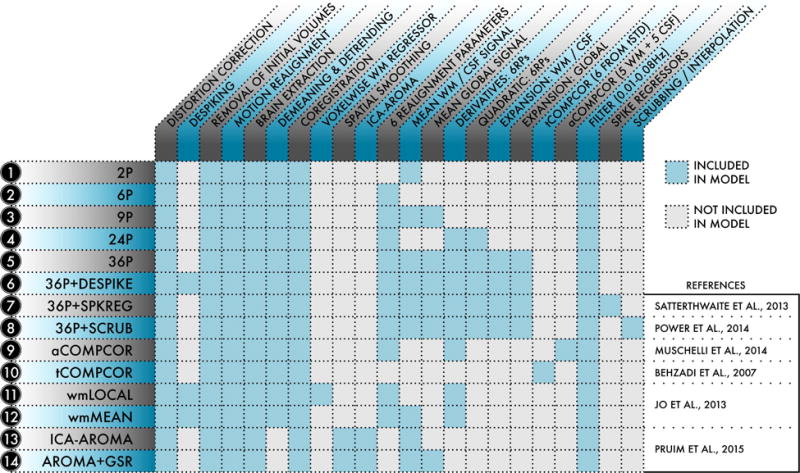
For each of the 14 models indexed at left, the table details which processing procedures and confound regressors were included in the model. De-noising models were selected from the functional connectivity literature and represented a range of commonly-used strategies. Reprinted with permission (Ciric et al., 2017).
De-noising pipelines have differential efficacy in limiting associations between connectivity and motion
A primary benchmark is the residual relationship between motion (estimated prior to preprocessing) and connectivity after preprocessing, which can be quantified as the percentage of edges exhibiting a significant QC-FC relationship. As shown in Figure 8, no pipeline completely abolished the relationship between head movement and connectivity. However, different approaches exhibited widely varying degrees of efficacy, with high convergence among the two node systems evaluated. The top four confound regression strategies all included 36 confound parameters, which is comprised of an expansion of GSR, tissue-specific regressors (WM, CSF), and realignment parameters (36P model). Beyond this 36-parameter model, all censoring techniques provided some additional benefit, reducing the number of edges that were significantly related to motion to less than 7% (and less than 1% in some cases).
Figure 8. Number of edges significantly related to motion after de-noising.
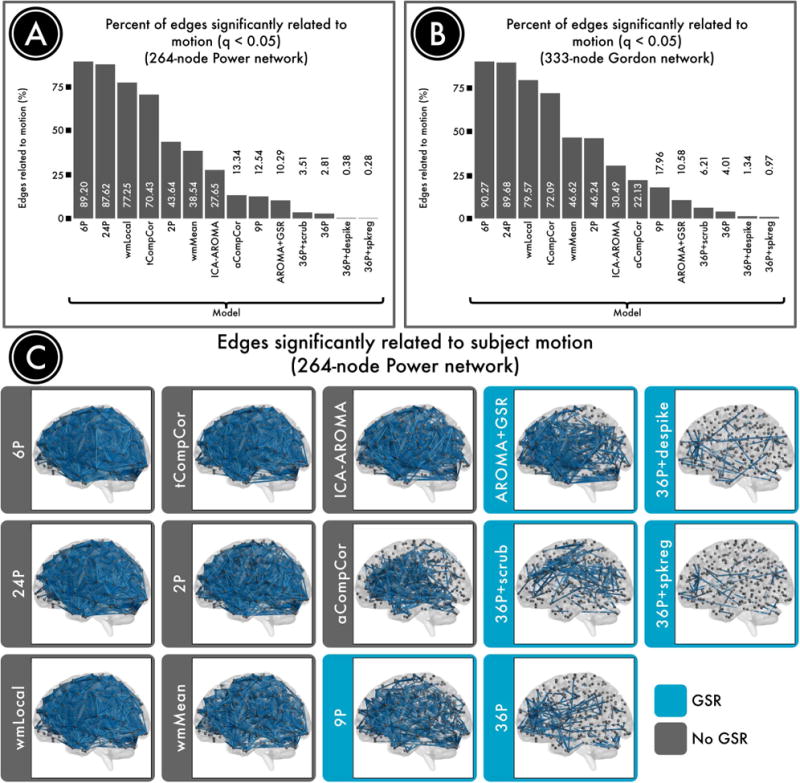
Successful denoising strategies reduced the relationship between connectivity and motion. The number of edges (network connections) for which this relationship persists provides evidence of a pipeline's efficacy. A) The percentage of edges significantly related to motion (FDR Q<0.05) in a 264-node network (Power et al., 2011). Fewer significant edges is indicative of better performance. B) The percentage of edges significantly related to motion (Q<0.05) in a second, 333-node network (Gordon et al., 2014). C) Renderings of significant edges with QC-FC correlations of at least 0.2 for each de-noising strategy, ranked according to efficacy. Strategies that include regression of the mean global signal are framed in blue and consistently ranked as the best performers. Reprinted with permission (Ciric et al., 2017).
In contrast, many commonly-used pipelines performed much less well, as demonstrated by a majority of edges that had a significant relationship with motion even after de-noising. For example, 89% of edges were impacted by motion after employing a simple confound model using 6 RPs; the performance of the commonly-used 24P model comprised of an expansion of the RP parameters was similarly dismal (88% edges). There was no great benefit for use of the local WM regressor included in ANATICOR (77% edges), which in fact performed substantially worse than a model that included the mean WM signal (39% edges). Furthermore, different CompCor approaches using PCA demonstrated markedly divergent performance. Specifically, PCA of WM and CSF in aCompCor clearly outperformed PCA performed within voxels identified by their temporal characteristics (tCompCor; 13% vs. 70% edges). Similar to findings reported by Burgess, who found that addition of a GSR-analogue improved performance of ICA-FIX, we found that adding GSR to ICA-AROMA reduced the residual relationship with motion (28% significant edges without GSR, 13% with GSR). Somewhat to our surprise, the classic 9-parameter de-noising model that includes 6RPs, WM, CSF, and GSR performed relatively well (13%).
Notably, the top-performing pipelines all included GSR. The effectiveness of GSR is most likely due to the nature of motion artifact itself: in-scanner head motion tends to induce widespread reductions in signal intensity across the entire brain parenchyma (see “Spatial distribution of motion artifacts”, above). Recent data from Power et al., 2016 demonstrates that such artifacts are highly reproducible across datasets, and are effectively modeled by GSR. Beyond GSR, a second strategy that clearly minimizes QC-FC relationships is temporal censoring. All three censoring variants we evaluated (including scrubbing, spike regression, and de-spiking) aided in de-noising, above and beyond GSR.
Global signal regression aids de-noising but results in some distance-dependence
While the relationship between motion and connectivity is a reasonable primary benchmark for de-noising pipelines, it should not be considered in isolation. Another benchmark that has received considerable attention is the distance dependence of motion artifacts. Two of the initial studies of motion artifacts demonstrated that in-scanner motion resulted in higher connectivity for short-range connections, and diminished connectivity for long-range connections. However, both of these initial reports included GSR in pre-processing; subsequent work showed that this distance-dependence varied by pre-processing pipeline. Thus, distance dependence is a valuable measure to consider alongside QC-FC relationships. In particular, one prior paper focused on this outcome measure, and suggested using a local WM regressor to minimize distance dependence. While this approach did result in minimal distance-dependence, this was a consequence of lack of efficacy across all distances (i.e., 77% of edges showing a significant relationship with motion).
We found that both GSR and censoring appeared effective in minimizing QCFC relationships, but they exhibited divergent relationships with distance-dependence (Figure 9). While temporal censoring techniques consistently minimized distance-dependence, GSR was associated with increased distance-dependence. In fact, models that include GSR (9-parameter, 36-parameter) had among the greatest distance-dependence. However, is important to underscore that the distance-dependence associated with GSR is not the result of worsening associations with motion in certain connections. Instead, GSR de-noises with differential efficacy, with better performance for long-distance connections than for short-range connections. This is most likely because GSR effectively captures by global artifacts which impact signal in distant brain regions. In contrast, GSR is less effective at removing regionally-specific artifact, which can specifically impact short-range corrections. The resulting distance-dependence that occurs with GSR can be mitigated by the addition of temporal censoring, with scrubbing demonstrating the greatest efficacy compared to spike regression or de-spiking (perhaps due to removing more volumes).
Figure 9. Distance-dependence of motion artifacts after de-noising.
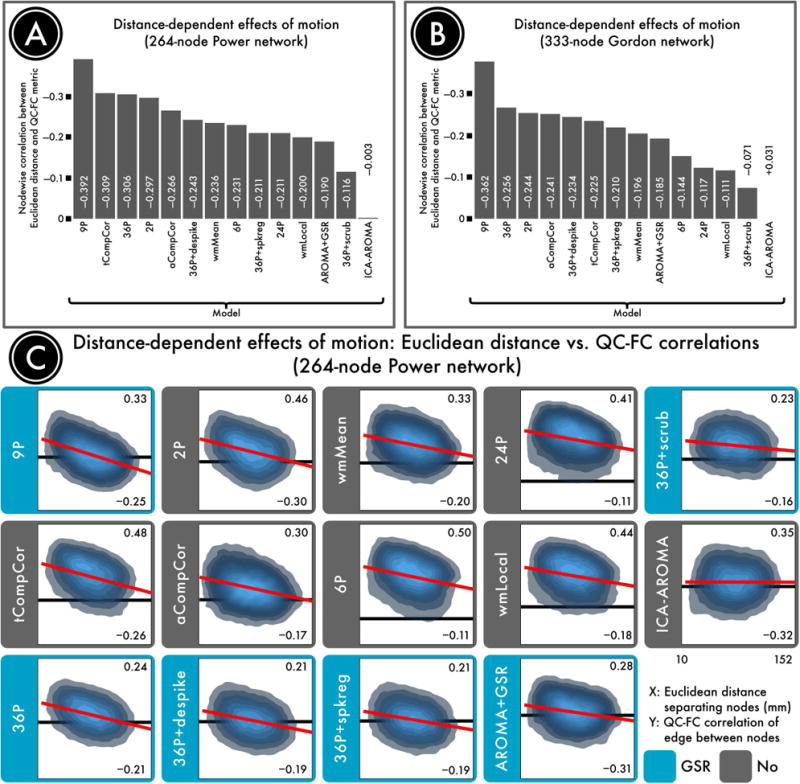
The magnitude of motion artifacts varies with the Euclidean distance separating a pair of nodes, with closer nodes generally exhibiting greater impact of motion on connectivity. A) The residual distance-dependence of motion artifacts in a 264-node network (Power et al., 2011) following confound regression. B) The residual distance-dependence of motion artifacts in a second, 333-node network (Gordon et al., 2014). C) Density plots indicating the relationship between the Euclidean distance separating each pair of nodes (x-axis) and the QC-FC correlation of the edge connecting those nodes (y-axis). The overall trend lines for each de-noising strategy, from which distance-dependence is computed, are indicated in red. For each plot, the ordinate is rescaled to the data; thus, the ordinate does not reflect the width of the distribution of QC-FC correlations. The best performing models either excised high-motion volumes (36-parameter + scrubbing) or used more localized regressors (ICA-AROMA and wmLocal). In general, approaches that made use of GSR without censoring resulted in substantial distance-dependence. This effect was driven by differential efficacy of de-noising, with effective de-noising for long-range connections but not short-range connections. Reprinted with permission (Ciric et al., 2017).
The model that resulted in nearly zero distance-dependence was ICA-AROMA. However, it should be noted that data processed using ICA-AROMA included substantially greater residual relationships with motion than models that included GSR and censoring (i.e., 28% compared to <1%). Furthermore, when GSR was added to ICA-AROMA, there were less edges related to motion but at a cost of an increased distance-dependence, which surpassed that seen with the 36-parameter + scrubbing pipeline.
Effective de-noising enhances network identifiability
In any de-noising process, it is important to evaluate the robustness of residual signal, not just the presence of residual noise. For example, a non-specific de-noising pipeline could potentially minimize the relationship between motion and connectivity, but also remove valuable signal simultaneously. Accordingly, a third benchmark to consider is network identifiability. In Ciric et al. (2017), we operationalized this idea by calculating the modularity quality of the network, which quantifies the presence of structured sub-networks in the data. As displayed in Figure 10, the 4 models that exhibited the strongest residual relationship with motion (6RPs, 24RP, wmLocal, and tCompCor) also were impaired in their ability to reveal functional modules. This suggests that the presence of motion artifacts reduce network identifiability, most likely by blurring signal across functional communities.
Figure 10. Identifiability of network structure after de-noising.
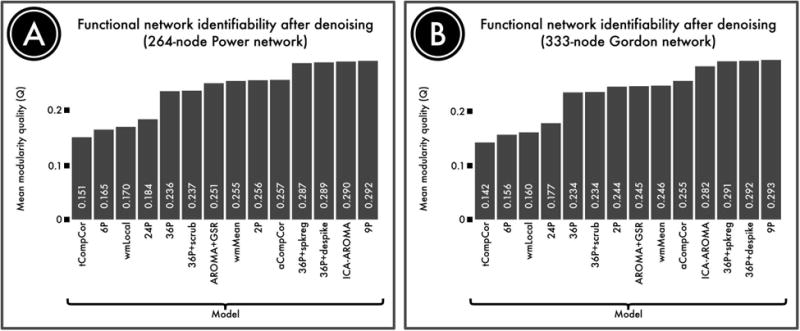
Although de-noising approaches remove motion artifacts from BOLD time series, it is possible that they also remove signal of interest. We quantified the retention of signal of interest using the modularity quality of the de-noised connectome. A) The modularity quality in a 264-node network (Power et al., 2011) following confound regression. B) The modularity quality in a second, 333-node network (Gordon et al., 2014). ICA-, GSR-, and tissue class-based models performed relatively well, while models that allowed substantial noise to be retained (tCompCor, 6P, wmLocal, 24P; see Figure 8) were less able to identify network sub-structure. Reprinted with permission (Ciric et al., 2017).
Similarly, many of the models that yielded the best results in terms of minimizing the residual relationship with motion artifacts (i.e., QC-FC, as above) also performed well in terms of network identifiability. For example, models that combined higher-order confound regression (36P) and temporal censoring tended to have high network identifiability. Among temporal censoring techniques, spike regression and despiking performed better than scrubbing. Together, these results go some distance to allay the concern that these models are overly aggressive and risk removing too much signal along with motion-related noise.
Finally, both the 9P model and ICA-AROMA performed quite well in terms of network identifiability. In fact, the network modularity for the 9P model was numerically higher than both 36P+ despike and 36P + spike regression. However, the difference was quite negligible, and any small marginal benefit in terms of network identifiability should be considered in the context of substantially inferior de-noising efficacy. Overall, these results emphasize and that there is not a clear trade-off between de-noising efficacy and network identifiably. Rather, models that fail to provide effective de-noising tend to have poor network identifiability, and pipelines that successfully mitigate the influence of motion artifacts also allow preserved signal related to subnetwork structure. While speculative, we expect that there is likely to be an “inverted-U” shaped relationship between de-noising aggressiveness and network identifiability. However, the present data suggest current models only sample the “ascending limb” of this curve, and current techniques are not so aggressive that sub-network topology is removed.
Controlling For Motion in Group Level Analyses
When faced with potentially confounding residual effects of motion on connectivity, investigators have frequently included motion as a covariate in group-level analysis. However, by definition, this approach will impede detection of connectivity features that are related to both the subject level variable of interest (e.g., age, disease status) and motion. Thus, inclusion of this as a model covariate is likely to reduce power, and potentially “over-control” for artifacts. This possibility is supported by data showing connectivity differences in individuals who have a propensity for higher motion, even on independent scans where motion was matched to a comparator group (Zeng et al., 2014).
Given this effect, it is preferable to control for motion artifacts during subject-level processing. However, in large datasets with substantial statistical power, there may be a significant residual relationship with motion even when an effective processing pipeline was used. Thus, it is essential to include sensitivity analyses where motion is included as a group-level covariate, and also report associations with both the subject variable of interest (age, clinical group, etc.) and also the imaging measures of interest. It should be noted that a linear FD covariate will not control for nonlinear effects of motion or interactive effects with other subject level variables (e.g., group by motion interactions) unless they are specifically modeled (Power et al., 2013). Indeed, as illustrated by the example in the next section, combining a less-effective preprocessing pipeline and a single linear group-level covariate may not provide adequate protection against the confounding effects of motion. One potential alternative to co-varying for motion is to instead correct for changes in global connectivity (GCOR; Saad et al., 2013); a highly similar approach is to co-vary for the mean of the connectivity matrix in group-level regression (“mean regress”; Yan et al., 2013a; Yan et al., 2013c). However, given the strong relationship between motion and mean connectivity, many of the same caveats described above regarding inclusion of mean FD as a covariate may be relevant for GCOR and mean regress as well.
The Confounding Impact of Motion Artifacts on Inference
Given the clear heterogeneity in the efficacy of commonly-used de-noising pipelines, it is not surprising that preprocessing choices can have a substantial impact on the conclusions of a study. This is particularly problematic when motion is strongly associated with the subject-level variable of interest, such as age, sex, group status, or disease severity. As described below, recent studies have emphasized the degree to which motion can confound such inference.
The potential confounding effects of motion have been investigated most thoroughly in studies of brain development, where motion has a strongly negative association with age (i.e., younger kids move more). Indeed, two of the initial three reports regarding motion artifacts in functional connectivity highlighted the degree to which motion could inflate apparent developmental effects (Power et al., 2012a; Satterthwaite et al., 2012). For example, in Satterthwaite et al. (2014) we evaluated apparent age-related changes in connectivity, comparing a “standard” de-noising pipeline (Fox et al., 2005; the 9-paramter model, which includes 6RPs, WM, CSF, and GSR) and an “improved” pipeline (36-parameter model + spike regression) (Satterthwaite et al., 2013). Furthermore, for each model, we examined age effects with and without the inclusion of mean FD as a group-level model covariate. In this sample, age has a small but highly significant correlation (r = -0.19, p < 0.001) with motion, even after stringent exclusion criteria are applied (i.e., a mean FD of 0.2mm). As shown in Figure 11, this collinearity between age and motion can markedly inflate apparent developmental associations with connectivity. While de-noising with the 9P model and no FD covariate resulted in approximately 15% of edges having a significant (FDR Q<0.05) association with age, use of the 36P + spike regression model and a group level FD covariate reduced this to <5% of edges. Critically, simply adding a group-level FD covariate to the 9P model did not yield equivalent results; the 9P+covariate model had more significant associations with age than a 36P + spike regression model, even without a group-level FD covariate. Furthermore, subsequent work has shown that the 9P model in fact out-performs many other commonly-used pipelines, suggesting that age effects would be much higher if models such as tCompCor, wmLocal (ANATICOR), or 24P were used.
Figure 11. Inadequate de-noising inflates apparent associations with development in youth.
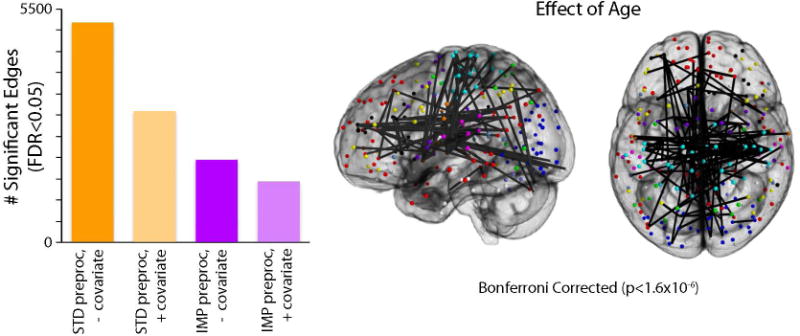
A) Using a sample of 780 youth imaged as part of the PNC, the chart displays the number of statistically significant connections (FDR Q<0.05) within a network 34,716 unique edges (Power et al., 2011). Age effects were evaluated across four different analysis procedures, varying factors of subject-level confound regression and group-level covariation of motion. Standard confound regression included 9 parameters (6 realignment parameters + global, WM, CSF timecourses); improved confound regression included 36 parameters (i.e., standard parameters + their temporal derivatives, quadratic terms, and quadratic of derivative) as well as spike regression. Age effects were investigated at the group level either without a motion covariate or with motion (mean relative displacement) added as a covariate. Sex was included as a covariate in all models. B) Graphical representation of the 42 connections that displayed significant age effects following improved preprocessing and group-level analysis with a motion covariate. Due to the large number of FDR-corrected significant connections, only connections that surpassed a Bonferroni-corrected statistical threshold (corrected p<0.05, uncorrected p<1.4×10−6) are displayed. Reprinted with permission (Satterthwaite et al., 2013).
Other studies have demonstrated that the potential confounding effects of motion are not specific to studies of development. For example, in a recent paper using data from the Human Connectome Project, Siegel et al. demonstrated that observed associations between functional connectivity and various cognitive measures including fluid intelligence were inflated through their shared association with motion (Siegel et al., 2016). Associations between connectivity and IQ were highly significant when using the default HCP pipeline, and markedly reduced when de-noising strategies including GSR and censoring were applied.
Conclusions
While there has been rapid progress in understanding the impact of in-scanner motion on studies of functional connectivity, it should be emphasized that most current studies of motion artifacts and de-noising (and all reviewed here) have primarily considered post-processing strategies to mitigate the influence of artifact in data that has already been acquired. However, improvements in data acquisition have the potential to both reduce the presence of motion artifacts and also aid in de-noising. One promising approach is the use of dual (Bright and Murphy, 2013) or multi-echo acquisitions (Kundu et al., 2015; Kundu et al., 2013). These techniques allow a better separation of signal and noise in the timeseries. Similarly, it should be emphasized that almost all data reviewed here were acquired using standard BOLD sequences that did not utilize multi-band acquisition techniques. While certain studies (such as Burgess et al., 2016) suggest that similar effects are likely to occur with multi-band data, this clearly merits further verification.
Additionally, while existing research suggests that motion impacts all commonly used measures of functional connectivity (Satterthwaite et al., 2012; Yan et al., 2013b), it remains poorly described whether certain outcome measures are more resistant to such artifact. For example, it is not known whether network edges defined using a Pearson's correlation (the most common method) are more or less impacted by motion than alternative approaches such as coherence (Gu et al., 2015) or mutual information (Zhou et al., 2009), or other measures of functional connectivity. Robust techniques that de-weight motion-related timeseries outliers could potentially be quite advantageous, but have not been rigorously investigated. Similarly, it remains unknown how recently-developed network-level representations such as sparse connectivity patterns (Eavani et al., 2014) compare to standard procedures such as ICA.
Additionally, further research is needed to understand how generalizable de-noising results are across acquisition sequences and scanning platforms. While one recent large-scale study regarding the impact of motion artifacts on the global signal suggests that associations are likely to be highly similar across acquisitions and sites (Power et al., 2016), replication of benchmarking results in multiple datasets would help ensure generalizability and increase investigator confidence in choosing a de-noising pipeline. However, preliminary results from a very large-scale study that includes 13 datasets and 64 processing pipelines suggests substantial convergence with several of the results reported here, including the benefit of GSR (Vogelstein and Milham, Personal Communication; see https://github.com/neurodata/discriminability/blob/master/Draft/discriminability.pdf)
These caveats notwithstanding, recent work emphasize the marked performance heterogeneity of commonly-used pipelines. Notably, both GSR and temporal censoring techniques seem to be effective methods for minimizing the residual relationship between functional connectivity and motion artifacts. When GSR is used, investigators should be aware of worsening the distance-dependence of motion artifacts. However, it should be emphasized that this is due to differential de-noising efficacy, and GSR does not induce motion artifacts. In contrast, temporal censoring mitigates such distance-dependence, thus enhancing the benefits of pairing censoring with GSR. Furthermore, available data suggest that the theoretical trade-off between de-noising and signal preservation is not particularly problematic for most commonly-used pipelines. Indeed, motion artifacts tend to obscure network topology, and pipelines that allow artifacts to be retained thus tend to have low network identifiability. Conversely, pipelines that combine GSR and censoring both minimize the relationship between motion and connectivity, and simultaneously allow better detection of functional sub-networks.
In considering available strategies, investigators should be aware of their relative strengths and weaknesses. Clearly, the relative merit of each approach will vary by research question and study design. For example, in studies of network organization, minimizing distance dependence and maximizing network identifiability may be of most interest. In these cases, ICA-AROMA appears to be an excellent choice, as it has high network identifiability and low distance dependence. In contrast, for studies of group or individual differences, minimizing QC-FC relationships is likely to be of paramount importance so as to limit the possibility of Type I error driven by motion artifacts. As illustrated above, this is a particularly relevant concern for studies of brain development, where motion is systematically related to age. For such studies, models that include both GSR and censoring are a good choice.
Lastly, it cannot be over-emphasized that use of a given confound regression pipeline does not alter the need for investigators to investigate and transparently report relevant data regarding associations with motion. Simple and intuitive plots are available for subject-level exploration (Power, 2016); while QC-FC plots are undeniably useful, group level statistics should not be a replacement for careful examination of subject-level data. Furthermore, all papers should clearly report the relationship between motion and both key subject variables as well as functional connectivity measures. Providing this information is a necessary prerequisite for confidence that reported findings are not driven by motion artifacts; group-level sensitivity analyses incorporating motion as a covariate are also helpful. Moving forward, there is no doubt that additional gains will accrue in this rapidly-moving sub-field, but in the meantime such transparency remains critical.
Acknowledgments
Supported by grants from the National Institute of Health: R01MH107703 (TDS), R01MH101111 (DHW), R21MH106799 (DSB & TDS), K01MH102609 (DRR), and R01EB022573 (CD). The content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies.
Footnotes
No authors have any conflicts of interest.
References
- Aguirre GK, Zarahn E, D'Esposito M. The inferential impact of global signal covariates in functional neuroimaging analyses. Neuroimage. 1998;8:302–306. doi: 10.1006/nimg.1998.0367. [DOI] [PubMed] [Google Scholar]
- Andersson JL, Hutton C, Ashburner J, Turner R, Friston K. Modeling geometric deformations in EPI time series. Neuroimage. 2001;13:903–919. doi: 10.1006/nimg.2001.0746. [DOI] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Philos Trans R Soc Lond B Biol Sci. 2005;360:1001–1013. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behzadi Y, Restom K, Liau J, Liu TT. A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. Neuroimage. 2007;37:90–101. doi: 10.1016/j.neuroimage.2007.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhaganagarapu K, Jackson GD, Abbott DF. An automated method for identifying artifact in independent component analysis of resting-state FMRI. Front Hum Neurosci. 2013;7:343. doi: 10.3389/fnhum.2013.00343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Bright MG, Murphy K. Removing motion and physiological artifacts from intrinsic BOLD fluctuations using short echo data. Neuroimage. 2013;64:526–537. doi: 10.1016/j.neuroimage.2012.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bright MG, Murphy K. Is fMRI “noise” really noise? Resting state nuisance regressors remove variance with network structure. Neuroimage. 2015;114:158–169. doi: 10.1016/j.neuroimage.2015.03.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess GC, Kandala S, Nolan D, Laumann TO, Power JD, Adeyemo B, Harms MP, Petersen SE, Barch DM. Evaluation of Denoising Strategies to Address Motion-Correlated Artifacts in Resting-State Functional Magnetic Resonance Imaging Data from the Human Connectome Project. Brain Connect. 2016 doi: 10.1089/brain.2016.0435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caballero-Gaudes C, Reynolds RC. Methods for cleaning the BOLD fMRI signal. Neuroimage. 2016 doi: 10.1016/j.neuroimage.2016.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calkins ME, Merikangas KR, Moore TM, Burstein M, Behr MA, Satterthwaite TD, Ruparel K, Wolf DH, Roalf DR, Mentch FD, Qiu H, Chiavacci R, Connolly JJ, Sleiman PMA, Gur RC, Hakonarson H, Gur RE. The Philadelphia Neurodevelopmental Cohort: constructing a deep phenotyping collaborative. J Child Psychol Psychiatry. 2015 doi: 10.1111/jcpp.12416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carp J. Optimizing the order of operations for movement scrubbing: Comment on Power et al. Neuroimage. 2011 doi: 10.1016/j.neuroimage.2011.12.061. [DOI] [PubMed] [Google Scholar]
- Chai XJ, Castañón AN, Ongür D, Whitfield-Gabrieli S. Anticorrelations in resting state networks without global signal regression. Neuroimage. 2012;59:1420–1428. doi: 10.1016/j.neuroimage.2011.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciric R, Wolf DH, Power JD, Roalf DR, Baum G, Ruparel K, Shinohara RT, Elliott MA, Eickhoff SB, Davatzikos C. Benchmarking confound regression strategies for the control of motion artifact in studies of functional connectivity. arXiv preprint arXiv. 2016 doi: 10.1016/j.neuroimage.2017.03.020. 1608.03616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciric R, Wolf DH, Power JD, Roalf DR, Baum G, Ruparel K, Shinohara RT, Elliott MA, Eickhoff SB, Davatzikos C, Gur RC, Gur RE, Bassett DS, Satterthwaite TD. Benchmarking of participant-level confound regression strategies for the control of motion artifact in studies of functional connectivity. Neuroimage. 2017 doi: 10.1016/j.neuroimage.2017.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes D, Haughton VM, Arfanakis K, Carew JD, Turski PA, Moritz CH, Quigley MA, Meyerand ME. Frequencies contributing to functional connectivity in the cerebral cortex in “resting-state” data. AJNR Am J Neuroradiol. 2001;22:1326–1333. [PMC free article] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Craddock RC, Jbabdi S, Yan CG, Vogelstein JT, Castellanos FX, Di Martino A, Kelly C, Heberlein K, Colcombe S, Milham MP. Imaging human connectomes at the macroscale. Nat Methods. 2013;10:524–539. doi: 10.1038/nmeth.2482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diedrichsen J, Shadmehr R. Detecting and adjusting for artifacts in fMRI time series data. Neuroimage. 2005;27:624–634. doi: 10.1016/j.neuroimage.2005.04.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NUF, Nardos B, Cohen AL, Fair DA, Power JD, Church JA, Nelson SM, Wig GS, Vogel AC, Lessov-Schlaggar CN, Barnes KA, Dubis JW, Feczko E, Coalson RS, Pruett JR, Barch DM, Petersen SE, Schlaggar BL. Prediction of individual brain maturity using fMRI. Science. 2010;329:1358–1361. doi: 10.1126/science.1194144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eavani H, Satterthwaite TD, Filipovych R, Gur RE, Gur RC, Davatzikos C. Identifying sparse connectivity patterns in the brain using resting-state fMRI. Neuroimage. 2014 doi: 10.1016/j.neuroimage.2014.09.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair DA, Dosenbach NUF, Church JA, Cohen AL, Brahmbhatt S, Miezin FM, Barch DM, Raichle ME, Petersen SE, Schlaggar BL. Development of distinct control networks through segregation and integration. Proc Natl Acad Sci U S A. 2007;104:13507–13512. doi: 10.1073/pnas.0705843104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornito A, Zalesky A, Bassett DS, Meunier D, Ellison-Wright I, Yücel M, Wood SJ, Shaw K, O'Connor J, Nertney D, Mowry BJ, Pantelis C, Bullmore ET. Genetic influences on cost-efficient organization of human cortical functional networks. J Neurosci. 2011;31:3261–3270. doi: 10.1523/JNEUROSCI.4858-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S A. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, Raichle ME. The global signal and observed anticorrelated resting state brain networks. J Neurophysiol. 2009;101:3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Liddle PF, Dolan RJ, Lammertsma AA, Frackowiak RS. The relationship between global and local changes in PET scans. J Cereb Blood Flow Metab. 1990;10:458–466. doi: 10.1038/jcbfm.1990.88. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Williams S, Howard R, Frackowiak RS, Turner R. Movement-related effects in fMRI time-series. Magn Reson Med. 1996;35:346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Adeyemo B, Huckins JF, Kelley WM, Petersen SE. Generation and Evaluation of a Cortical Area Parcellation from Resting-State Correlations. Cereb Cortex. 2014 doi: 10.1093/cercor/bhu239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gotts SJ, Saad ZS, Jo HJ, Wallace GL, Cox RW, Martin A. The perils of global signal regression for group comparisons: a case study of Autism Spectrum Disorders. Front Hum Neurosci. 2013;7:356. doi: 10.3389/fnhum.2013.00356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffanti L, Douaud G, Bijsterbosch J, Evangelisti S, Alfaro-Almagro F, Glasser MF, Duff EP, Fitzgibbon S, Westphal R, Carone D, Beckmann CF, Smith SM. Hand classification of fMRI ICA noise components. Neuroimage. 2016 doi: 10.1016/j.neuroimage.2016.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffanti L, Salimi-Khorshidi G, Beckmann CF, Auerbach EJ, Douaud G, Sexton CE, Zsoldos E, Ebmeier KP, Filippini N, Mackay CE, Moeller S, Xu J, Yacoub E, Baselli G, Ugurbil K, Miller KL, Smith SM. ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. Neuroimage. 2014;95:232–247. doi: 10.1016/j.neuroimage.2014.03.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grootoonk S, Hutton C, Ashburner J, Howseman AM, Josephs O, Rees G, Friston KJ, Turner R. Characterization and correction of interpolation effects in the realignment of fMRI time series. Neuroimage. 2000;11:49–57. doi: 10.1006/nimg.1999.0515. [DOI] [PubMed] [Google Scholar]
- Gu S, Satterthwaite TD, Medaglia JD, Yang M, Gur RE, Gur RC, Bassett DS. Emergence of system roles in normative neurodevelopment. Proc Natl Acad Sci U S A. 2015;112:13681–13686. doi: 10.1073/pnas.1502829112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallquist MN, Hwang K, Luna B. The nuisance of nuisance regression: Spectral misspecification in a common approach to resting-state fMRI preprocessing reintroduces noise and obscures functional connectivity. Neuroimage. 2013;82C:208–225. doi: 10.1016/j.neuroimage.2013.05.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hlinka J, Alexakis C, Hardman JG, Siddiqui Q, Auer DP. Is sedation-induced BOLD fMRI low-frequency fluctuation increase mediated by increased motion? MAGMA. 2010;23:367–374. doi: 10.1007/s10334-010-0199-6. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jo HJ, Gotts SJ, Reynolds RC, Bandettini PA, Martin A, Cox RW, Saad ZS. Effective Preprocessing Procedures Virtually Eliminate Distance-Dependent Motion Artifacts in Resting State FMRI. J Appl Math. 2013;2013 doi: 10.1155/2013/935154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo HJ, Saad ZS, Simmons WK, Milbury LA, Cox RW. Mapping sources of correlation in resting state FMRI, with artifact detection and removal. Neuroimage. 2010;52:571–582. doi: 10.1016/j.neuroimage.2010.04.246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Van Dijk KRA, Libby A, Napadow V. Frequency-dependent relationship between resting-state functional magnetic resonance imaging signal power and head motion is localized within distributed association networks. Brain Connect. 2014;4:30–39. doi: 10.1089/brain.2013.0153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochiyama T, Morita T, Okada T, Yonekura Y, Matsumura M, Sadato N. Removing the effects of task-related motion using independent-component analysis. Neuroimage. 2005;25:802–814. doi: 10.1016/j.neuroimage.2004.12.027. [DOI] [PubMed] [Google Scholar]
- Kundu P, Benson BE, Baldwin KL, Rosen D, Luh WM, Bandettini PA, Pine DS, Ernst M. Robust resting state fMRI processing for studies on typical brain development based on multi-echo EPI acquisition. Brain Imaging Behav. 2015;9:56–73. doi: 10.1007/s11682-014-9346-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P, Brenowitz ND, Voon V, Worbe Y, Vértes PE, Inati SJ, Saad ZS, Bandettini PA, Bullmore ET. Integrated strategy for improving functional connectivity mapping using multiecho fMRI. Proc Natl Acad Sci U S A. 2013 doi: 10.1073/pnas.1301725110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muschelli J, Nebel MB, Caffo BS, Barber AD, Pekar JJ, Mostofsky SH. Reduction of motion-related artifacts in resting state fMRI using aCompCor. Neuroimage. 2014;96:22–35. doi: 10.1016/j.neuroimage.2014.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman MEJ. Modularity and community structure in networks. Proc Natl Acad Sci U S A. 2006;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niazy RK, Xie J, Miller K, Beckmann CF, Smith SM. Spectral characteristics of resting state networks. Prog Brain Res. 2011;193:259–276. doi: 10.1016/B978-0-444-53839-0.00017-X. [DOI] [PubMed] [Google Scholar]
- Patel AX, Bullmore ET. A wavelet-based estimator of the degrees of freedom in denoised fMRI time series for probabilistic testing of functional connectivity and brain graphs. Neuroimage. 2016;142:14–26. doi: 10.1016/j.neuroimage.2015.04.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel AX, Kundu P, Rubinov M, Jones PS, Vértes PE, Ersche KD, Suckling J, Bullmore ET. A wavelet method for modeling and despiking motion artifacts from resting-state fMRI time series. Neuroimage. 2014;95:287–304. doi: 10.1016/j.neuroimage.2014.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD. A simple but useful way to assess fMRI scan qualities. Neuroimage. 2016 doi: 10.1016/j.neuroimage.2016.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage. 2012a;59:2142–2154. doi: 10.1016/j.neuroimage.2011.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE. Steps toward optimizing motion artifact removal in functional connectivity MRI; a reply to Carp. Neuroimage. 2012b doi: 10.1016/j.neuroimage.2012.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, Petersen SE. Functional network organization of the human brain. Neuron. 2011;72:665–678. doi: 10.1016/j.neuron.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, Petersen SE. Methods to detect, characterize, and remove motion artifact in resting state fMRI. Neuroimage. 2013;84C:320–341. doi: 10.1016/j.neuroimage.2013.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Plitt M, Laumann TO, Martin A. Sources and implications of whole-brain fMRI signals in humans. Neuroimage. 2016 doi: 10.1016/j.neuroimage.2016.09.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruim RHR, Mennes M, Buitelaar JK, Beckmann CF. Evaluation of ICA-AROMA and alternative strategies for motion artifact removal in resting state fMRI. Neuroimage. 2015a doi: 10.1016/j.neuroimage.2015.02.063. [DOI] [PubMed] [Google Scholar]
- Pruim RHR, Mennes M, van Rooij D, Llera A, Buitelaar JK, Beckmann CF. ICA-AROMA: A robust ICA-based strategy for removing motion artifacts from fMRI data. Neuroimage. 2015b doi: 10.1016/j.neuroimage.2015.02.064. [DOI] [PubMed] [Google Scholar]
- Reuter M, Tisdall MD, Qureshi A, Buckner RL, van der Kouwe AJW, Fischl B. Head motion during MRI acquisition reduces gray matter volume and thickness estimates. Neuroimage. 2015;107:107–115. doi: 10.1016/j.neuroimage.2014.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS, Gotts SJ, Murphy K, Chen G, Jo HJ, Martin A, Cox RW. Trouble at rest: how correlation patterns and group differences become distorted after global signal regression. Brain Connect. 2012;2:25–32. doi: 10.1089/brain.2012.0080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS, Reynolds RC, Jo HJ, Gotts SJ, Chen G, Martin A, Cox RW. Correcting brain-wide correlation differences in resting-state FMRI. Brain Connect. 2013;3:339–352. doi: 10.1089/brain.2013.0156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM. Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. Neuroimage. 2014;90:449–468. doi: 10.1016/j.neuroimage.2013.11.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Connolly JJ, Ruparel K, Calkins ME, Jackson C, Elliott MA, Roalf DR, Ryan Hopsona KP, Behr M, Qiu H, Mentch FD, Chiavacci R, Sleiman PMA, Gur RC, Hakonarson H, Gur RE. The Philadelphia Neurodevelopmental Cohort: A publicly available resource for the study of normal and abnormal brain development in youth. Neuroimage. 2015 doi: 10.1016/j.neuroimage.2015.03.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Gerraty RT, Ruparel K, Loughead J, Calkins ME, Eickhoff SB, Hakonarson H, Gur RC, Gur RE, Wolf DH. An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data. Neuroimage. 2013;64:240–256. doi: 10.1016/j.neuroimage.2012.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Ruparel K, Loughead J, Prabhakaran K, Calkins ME, Hopson R, Jackson C, Keefe J, Riley M, Mentch FD, Sleiman P, Verma R, Davatzikos C, Hakonarson H, Gur RC, Gur RE. Neuroimaging of the Philadelphia neurodevelopmental cohort. Neuroimage. 2014;86:544–553. doi: 10.1016/j.neuroimage.2013.07.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Wolf DH, Loughead J, Ruparel K, Elliott MA, Hakonarson H, Gur RC, Gur RE. Impact of in-scanner head motion on multiple measures of functional connectivity: Relevance for studies of neurodevelopment in youth. Neuroimage. 2012;60:623–632. doi: 10.1016/j.neuroimage.2011.12.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD, Wolf DH, Ruparel K, Erus G, Elliott MA, Eickhoff SB, Gennatas ED, Jackson C, Prabhakaran K, Smith A, Hakonarson H, Verma R, Davatzikos C, Gur RE, Gur RC. Heterogeneous impact of motion on fundamental patterns of developmental changes in functional connectivity during youth. Neuroimage. 2013;83:45–57. doi: 10.1016/j.neuroimage.2013.06.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheinost D, Papademetris X, Constable RT. The impact of image smoothness on intrinsic functional connectivity and head motion confounds. Neuroimage. 2014;95:13–21. doi: 10.1016/j.neuroimage.2014.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegel JS, Mitra A, Laumann TO, Seitzman BA, Raichle M, Corbetta M, Snyder AZ. Data Quality Influences Observed Links Between Functional Connectivity and Behavior. Cereb Cortex. 2016 doi: 10.1093/cercor/bhw253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Beckmann CF, Andersson J, Auerbach EJ, Bijsterbosch J, Douaud G, Duff E, Feinberg DA, Griffanti L, Harms MP, Kelly M, Laumann T, Miller KL, Moeller S, Petersen S, Power J, Salimi-Khorshidi G, Snyder AZ, Vu AT, Woolrich MW, Xu J, Yacoub E, Uğurbil K, Van Essen DC, Glasser MF, WU-Minn HCP, Consortium Resting-state fMRI in the Human Connectome Project. Neuroimage. 2013;80:144–168. doi: 10.1016/j.neuroimage.2013.05.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spisák T, Jakab A, Kis SA, Opposits G, Aranyi C, Berényi E, Emri M. Voxel-wise motion artifacts in population-level whole-brain connectivity analysis of resting-state FMRI. PLoS One. 2014;9:e104947. doi: 10.1371/journal.pone.0104947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tohka J, Foerde K, Aron AR, Tom SM, Toga AW, Poldrack RA. Automatic independent component labeling for artifact removal in fMRI. Neuroimage. 2008;39:1227–1245. doi: 10.1016/j.neuroimage.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Ven VG, Formisano E, Prvulovic D, Roeder CH, Linden DE. Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest. Hum Brain Mapp. 2004;22:165–178. doi: 10.1002/hbm.20022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk KR, Sabuncu MR, Buckner RL. The influence of head motion on intrinsic functional connectivity MRI. Neuroimage. 2012;59:431–438. doi: 10.1016/j.neuroimage.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk KRA, Hedden T, Venkataraman A, Evans KC, Lazar SW, Buckner RL. Intrinsic functional connectivity as a tool for human connectomics: theory, properties, and optimization. J Neurophysiol. 2010;103:297–321. doi: 10.1152/jn.00783.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergara VM, Mayer AR, Damaraju E, Hutchison K, Calhoun VD. The effect of preprocessing pipelines in subject classification and detection of abnormal resting state functional network connectivity using group ICA. Neuroimage. 2016 doi: 10.1016/j.neuroimage.2016.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissenbacher A, Kasess C, Gerstl F, Lanzenberger R, Moser E, Windischberger C. Correlations and anticorrelations in resting-state functional connectivity MRI: a quantitative comparison of preprocessing strategies. Neuroimage. 2009;47:1408–1416. doi: 10.1016/j.neuroimage.2009.05.005. [DOI] [PubMed] [Google Scholar]
- Yan CG, Cheung B, Kelly C, Colcombe S, Craddock RC, Di Martino A, Li Q, Zuo XN, Castellanos FX, Milham MP. A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics. Neuroimage. 2013a;76C:183–201. doi: 10.1016/j.neuroimage.2013.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG, Craddock RC, He Y, Milham MP. Addressing head motion dependencies for small-world topologies in functional connectomics. Front Hum Neurosci. 2013b;7:910. doi: 10.3389/fnhum.2013.00910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG, Craddock RC, Zuo XN, Zang YF, Milham MP. Standardizing the intrinsic brain: towards robust measurement of inter-individual variation in 1000 functional connectomes. Neuroimage. 2013c;80:246–262. doi: 10.1016/j.neuroimage.2013.04.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang H, Long XY, Yang Y, Yan H, Zhu CZ, Zhou XP, Zang YF, Gong QY. Amplitude of low frequency fluctuation within visual areas revealed by resting-state functional MRI. Neuroimage. 2007;36:144–152. doi: 10.1016/j.neuroimage.2007.01.054. [DOI] [PubMed] [Google Scholar]
- Zeng LL, Wang D, Fox MD, Sabuncu M, Hu D, Ge M, Buckner RL, Liu H. Neurobiological basis of head motion in brain imaging. Proc Natl Acad Sci U S A. 2014 doi: 10.1073/pnas.1317424111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou D, Thompson WK, Siegle G. MATLAB toolbox for functional connectivity. Neuroimage. 2009;47:1590–1607. doi: 10.1016/j.neuroimage.2009.05.089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou QH, Zhu CZ, Yang Y, Zuo XN, Long XY, Cao QJ, Wang YF, Zang YF. An improved approach to detection of amplitude of low-frequency fluctuation (ALFF) for resting-state fMRI: fractional ALFF. J Neurosci Methods. 2008;172:137–141. doi: 10.1016/j.jneumeth.2008.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo XN, Anderson JS, Bellec P, Birn RM, Biswal BB, Blautzik J, Breitner JCS, Buckner RL, Calhoun VD, Castellanos FX, Chen A, Chen B, Chen J, Chen X, Colcombe SJ, Courtney W, Craddock RC, Di Martino A, Dong HM, Fu X, Gong Q, Gorgolewski KJ, Han Y, He Y, He Y, Ho E, Holmes A, Hou XH, Huckins J, Jiang T, Jiang Y, Kelley W, Kelly C, King M, LaConte SM, Lainhart JE, Lei X, Li HJ, Li K, Li K, Lin Q, Liu D, Liu J, Liu X, Liu Y, Lu G, Lu J, Luna B, Luo J, Lurie D, Mao Y, Margulies DS, Mayer AR, Meindl T, Meyerand ME, Nan W, Nielsen JA, O'Connor D, Paulsen D, Prabhakaran V, Qi Z, Qiu J, Shao C, Shehzad Z, Tang W, Villringer A, Wang H, Wang K, Wei D, Wei GX, Weng XC, Wu X, Xu T, Yang N, Yang Z, Zang YF, Zhang L, Zhang Q, Zhang Z, Zhang Z, Zhao K, Zhen Z, Zhou Y, Zhu XT, Milham MP. An open science resource for establishing reliability and reproducibility in functional connectomics. Sci Data. 2014;1:140049. doi: 10.1038/sdata.2014.49. [DOI] [PMC free article] [PubMed] [Google Scholar]


