Abstract
Cross-population covariance of brain morphometric quantities provides a measure of inter-areal connectivity, as it is believed to be determined by the coordinated neurodevelopment of connected brain regions. Although useful, structural covariance analysis predominantly employed bulky morphological measures with mixed compartments, whereas studies of the structural covariance of any specific subdivisions like myelin are rare. Characterizing myelination covariance is of interest, as it will reveal connectivity patterns determined by coordinated development of myeloarchitecture between brain regions. Using myelin content MRI maps from the Human Connectome Project, here we showed that the cortical myelination covariance was highly reproducible, and exhibited a brain organization similar to that previously revealed by other connectivity measures. Additionally, the myelination covariance network shared common topological features of human brain networks like small worldness. Furthermore, we found that the correlation between myelination covariance and resting-state functional connectivity (RSFC) was uniform within each resting-state network (RSN), but could considerably vary between RSNs. Interestingly, this myelination covariance-RSFC correlation was appreciably stronger in sensory and motor networks than cognitive and poly-modal association networks, possibly due to their different circuitry structures. This study has established a new brain connectivity measure specifically related to axons, and this measure can be valuable to investigating coordinated myeloarchitecture development.
Keywords: myelination, structural covariance, human, resting-state functional connectivity
Introduction
Cross-population covariance of brain morphometric measures, such as gray matter density or cortical thickness, has been frequently utilized to study brain connectivity (Alexander-Bloch, et al., 2013a; Lerch, et al., 2006; Mechelli, et al., 2005), based on the rationale that synchronized morphological changes measured by structural covariance is determined by coordinated neurodevelopment of connected brain regions (Alexander-Bloch, et al., 2013b). Indeed, the structural covariance analysis has revealed multiple network architectures in both adult (Evans, 2013; Guo, et al., 2015; He, et al., 2007) and developing brains (Alexander-Bloch, et al., 2013b; Zielinski, et al., 2010).
Previous structural covariance analysis predominantly used bulky morphological measures without differentiating separate compartments, whereas our knowledge of the structural covariance of a specific cortical component like myelin content remains rather limited (Accolla, et al., 2014; Carmeli, et al., 2014; Hunt, et al., 2016). Bridging this knowledge gap is of great interest, as characterizing myelination covariance will reveal connectivity patterns determined by coordinated development of myeloarchitecture between brain regions.
In mammals, myelin around axons plays a critical role in the central and peripheral nervous systems, as it is essential for efficient propagation of action potentials (Vanderah, et al., 2016). Myelin density is highly variable across the cortex as revealed by meta-analysis of postmortem histology data (Nieuwenhuys and Broere, 2016). In addition to spatial variability of myelin density within a given subject, variability of myelination across subjects has been reported (Van Essen and Glasser, 2014). Therefore, analysis of cross-subject myelination covariance can provide a new method to measure inter-areal connectivity specifically pertinent to axonal properties. In addition, this connectivity measure allows brain networks to be constructed, and the organizational architecture of such networks can be studied accordingly. Moreover, it is of interest to investigate how cross-subject myelination covariance between brain regions relates to their functional connectivity measured by techniques like resting-state functional magnetic resonance imaging (rsfMRI), as such effort will shed light onto the structure-function relationship in the human brain connectivity.
Recent progress of in vivo MRI has made it possible to non-invasively map the myeloarchitecture of the human brain at high spatial resolutions. Specifically, quantitative T1 images were found to reflect myelin content as measured by histology (Bock, et al., 2009). Quantitative T2* maps were also correlated with the distribution of cortical myelin in the human brain (Cohen-Adad, 2014; Cohen-Adad, et al., 2012). Enhanced myelin contrast was further achieved using the map of T1w/T2w ratio, in which uncorrelated noise in T1w and T2w images can be cancelled (Glasser and Van Essen, 2011). This (T1w/T2w ratio) myelin mapping method has been widely used in neuroimaging studies, which has revealed a critical role of myeloarchitectonics in brain function (Abdollahi, et al., 2014; Grydeland, et al., 2013).
In the present study, we systematically characterized cross-individual myelination covariance of the human cerebral cortex using myelin maps of 881 subjects from the Human Connectome Project (HCP), WU-Minn Consortium. We identified large-scale myelination covariance patterns using independent component analysis (ICA). The whole-brain myelination covariance network was further constructed, and its topological organization was investigated using graph theory. Finally, the relationship between myelination covariance and resting-state functional connectivity (RSFC) was quantitatively evaluated.
Materials and Methods
Dataset
MRI data used in the present study were obtained from the ‘900 Subjects Data Release’ of the Human Connectome Project (HCP, https://www.humanconnectome.org/) (Van Essen, et al., 2013). T1w/T2w ratio myelin maps were generated using HCP preprocessed structural MRI data of 881 healthy subjects (387 males and 494 females; age 22 to 37) (Glasser, et al., 2016; Glasser and Van Essen, 2011). rsfMRI data used were group-averaged grayordinate-wise RSFC matrix, obtained from the HCP ‘Extensively Processed fMRI Data’ of 820 healthy subjects, which is a subgroup of aforementioned 881 subjects (367 males and 453 females; age 22 to 37 (Smith, et al., 2013a; Smith, et al., 2014).
All data were acquired on a 3T Siemens Skyra MRI scanner. T1w structural images were acquired using the 3D magnetization-prepared rapid acquisition gradient echo (3D-MPRAGE) sequence with the following parameters: repetition time (TR) = 2400 ms, echo time (TE) = 2.14 ms, flip angle = 8°, field of view (FOV) = 224 mm × 224 mm, voxel size = 0.7 × 0.7 × 0.7 mm3 (Glasser, et al., 2013). T2w structural images were acquired using the 3D sampling perfection with application-optimized contrast using different flip-angle evolutions (3D-SPACE) sequence with the following parameters: TR = 3200 ms, TE = 565 ms, FOV = 224 mm × 224 mm, voxel size = 0.7 × 0.7 × 0.7 mm3 (Glasser, et al., 2013). rsfMRI images were acquired using a multi-band echo-planar imaging (EPI) sequence with the following parameters: TR = 720 ms, TE = 33.1 ms, flip angle = 52°, FOV = 208 mm × 180 mm, matrix size = 104 × 90, voxel size = 2 × 2 × 2 mm3, slice number = 72, slice thickness = 2 mm, multiband factor = 8 (Feinberg, et al., 2010; Glasser, et al., 2013; Moeller, et al., 2010; Setsompop, et al., 2012). More details of the HCP data acquisition protocols can be found elsewhere (Glasser, et al., 2013). The HCP project was approved by the Institutional Review Board (IRB) of Washington University, and informed consent was obtained from each subject. All reported analyses in the present study were also approved by the IRB of the Pennsylvania State University.
Image preprocessing
HCP structural MRI data preprocessing was carried out using HCP minimal preprocessing pipelines including the PreFreeSurfer, FreeSurfer, and PostFreeSurfer pipelines. Details of these pipelines can be found in (Glasser, et al., 2013) and (Fischl, 2012). Registration of individual brains to the 2 mm-resolution standard space of CIFTI grayordinates was performed by the Multimodal Surface Matching algorithm based on areal features (MSM-All) of cortical folding, myelin and RSFC maps (Glasser, et al., 2016; Robinson, et al., 2014; Smith, et al., 2013b). This method was found to substantially improve the cross-subject registration quality, which consequently rendered remarkably sharper group-average results (Glasser, et al., 2016; Robinson, et al., 2014; Smith, et al., 2013b). Measurement of myelin content was achieved by taking the ratio of T1w over T2w images on a voxel-by-voxel basis (Glasser, et al., 2014; Glasser, et al., 2013; Glasser and Van Essen, 2011).
HCP rsMRI data preprocessing was conducted using fMRIVolume and fMRISurface pipelines (Glasser, et al., 2013), ICA+FIX denoising (Griffanti, et al., 2014; Salimi-Khorshidi, et al., 2014), MELODIC’s Incremental Group Principal Component Analysis (MIGP PCA) (Smith, et al., 2014), and Wishart roll-off correction (Glasser, et al., 2016). The fMRIVolume pipeline performed gradient-nonlinearity-induced geometric distortion correction, head motion correction, cross-modal registration to T1w images, normalization to the MNI space, and grand mean intensity normalization (Glasser, et al., 2013). The fMRISurface pipeline entered fMRIVolume processed data into the standard CIFTI grayordinate space and surface smoothed the data with an FWHM of 2 mm (Glasser, et al., 2013). The MSM-All algorithm was used to register individual brains into the standard space. Artifacts caused by subject motion, cardiac pulsation and the scanner were further cleaned by the ICA+FIX pipeline (Griffanti, et al., 2014; Salimi-Khorshidi, et al., 2014). Demeaned and variance normalized preprocessed time series were concatenated temporally for group analyses, and the MELODIC’s Incremental Group Principal Component Analysis (MIGP PCA) algorithm was applied to the concatenated data for dimensionality reduction (Smith, et al., 2014). Wishart roll-off correction was performed on MIGP PCA series for removing ripple artifact previously found in the group-average results (Glasser, et al., 2016). Group-averaged grayordinate-wise RSFC was computed on these PCA series using Pearson cross correlation. More details about computing this group-averaged dense RSFC can be found in (Glasser, et al., 2016). All image preprocessing procedures mentioned above were carried out by the HCP and these preprocessed data are publicly available in ConnectomeDB (https://db.humanconnectome.org/).
Extraction of myelination covariance patterns using ICA
Large-scale myelination covariance patterns in the cortex were extracted using ICA. Each subject’s myelin map was first normalized (i.e. zero mean and unit variance) (Shafee, et al., 2015). Normalized myelin maps of all 881 subjects were concatenated into a 59412 × 881 matrix. Each element of this matrix contained the value of myelin content (i.e., T1w/T2w ratios) of a grayordinate (59412 cortical grayordinates in total) for a subject (881 subjects in total). A single-session ICA was then performed on this concatenated matrix using FSL’s MELODIC tool (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/MELODIC) (Beckmann, et al., 2005; Guo, et al., 2015). The number of independent components was estimated to be 332 using the method of Laplace approximation to the model evidence (Lap) (Beckmann and Smith, 2004). As a result, the whole-brain myelin content matrix was decomposed into 332 ICA component maps and a mixing matrix (881 subjects by 332 sources). Two out of 332 independent components were identified as artifactual components, based on the criterion that the spatial covariance patterns of these two components were dominated by single subjects (i.e., a single subject had a weight (>15) far greater than any other subjects). Indeed, the spatial maps of these two artifactual components failed to show any meaningful patterns that could be captured by any anatomical or functional brain structures. These two artefactual components were regressed out from the myelin content matrix.
Calculation of the myelination covariance matrix
Myelination covariance between each pair of cortical grayordinates was quantified using the Pearson cross-correlation coefficient of their myelin content across all 881 subjects. This calculation generated a 59412 × 59412 grayordinate-wise myelination covariance matrix.
Reproducibility of myelination covariance
Reproducibility of myelination covariance was assessed by a split-group approach. All 881 subjects were randomly divided into two subgroups: subgroup 1 of 440 subjects (193 males and 247 females) and subgroup 2 of 441 subjects (194 males and 247 females). No family members were assigned to both subgroups in order to ensure subgroup independence. Grayordinate-wise myelination covariance matrix was independently computed for each subgroup. Reproducibility of myelination covariance was evaluated by Pearson correlation of the corresponding grayordinate-wise myelination covariance values between the two subgroups.
Construction of the myelination covariance network
The myelination covariance-based brain network was constructed using brain parcels from a multi-modal parcellation of the human cerebral cortex (360 parcels) as nodes (Glasser, et al., 2016). First, the within-parcel homogeneity of myelination covariance was quantified to assess the suitability of this parcellation scheme for constructing the myelination covariance-based network. For each grayordinate in a given parcel, the Pearson cross-correlation coefficient was computed between the myelin content of this grayordinate and the mean myelin content of all grayordinates within the parcel across subjects. This correlation coefficient was then Fisher Z-transformed and averaged across all grayordinates within the parcel. This averaged Z value was transformed back to r value, which was used to quantify the within-parcel homogeneity.
Edges of the myelination covariance network were defined using significant myelination covariance between parcels. For each subject, the myelin content of each parcel was first quantified by regionally averaging the myelin content of all grayordinates within the parcel. This step obtained a 360 × 881 data matrix. Second, the myelination covariance between each pair of parcels was quantified by the Pearson cross-correlation coefficient between their parcel myelin content across all subjects, which generated a between-parcel myelination covariance matrix (360 × 360). The statistical significance of between-parcel myelination covariance was thresholded at a false discovery rate (FDR) of 0.05 (Genovese, et al., 2002).
Graph analysis of the myelination covariance network
Fundamental global graph properties describing network segregation (average clustering coefficient and modularity), network integration (characteristic path length and global efficiency), network resilience (assortativity) and small-worldness were calculated at each connection density in the range from 0.2 to 0.8 with a step size of 0.01. Specifically, the modularity was calculated based on the Louvain community detection algorithm (Blondel, et al., 2008). For each density, the myelination covariance network was binarized. Average clustering coefficient, characteristic path length and global efficiency were also normalized to a random network at the same density, generated by randomizing the original binarized network, and this process was iterated for 1000 times. Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/) was used to compute all these graph metrics. Detailed definitions of these metrics were reported in (Rubinov and Sporns, 2010).
Evaluation of the relationship between myelination covariance and RSFC
The relationship between myelination covariance and RSFC was grayordinate-by-grayordinate evaluated based on the spatial similarity between whole-brain cortical connectivity profiles measured by myelination covariance and RSFC, respectively. For each cortical grayordinate, its whole-brain cortical connectivity profiles were separately obtained by its cortical myelination covariance and RSFC with all other cortical grayordinates. The spatial similarity between the two profiles was then quantified by their Pearson correlation coefficient. This analysis generated a spatial map of the correlations between myelination covariance and RSFC profiles. To control for the influence of the myelin content variance on the between-profile correlation, group-averaged grayordinate-wise values of myelin content were also regressed out from this between-profile correlation map. These between-profile correlation maps (i.e. without or with the regression of myelin content) were compared against well-established RSNs defined by a RSFC-based parcellation (Gordon, et al., 2016).
Results
Reproducibility of grayordinate-wise myelination covariance
We first show that cross-subject myelination covariance was highly robust. Fig. 1a displays the grayordinate-wise cortical myelination covariance matrix (59412×59412) that contained the myelination covariance value between every pair of cortical grayordinates. Relatively strong myelination covariance was observed between homotopic cortical grayordinates across contralateral hemispheres. To examine the robustness of myelination covariance, we randomly split all subjects into two subgroups. We assigned biologically related subjects to the same subgroup to ensure independence of the two subgroups. Both subgroups displayed almost identical myelination covariance patterns (Fig. 1b), which were also highly consistent with the myelination covariance pattern from all subjects (Fig. 1a). In addition, grayordinate-wise myelination covariance values were highly correlated between the two subgroups with a significant correlation coefficient (r = 0.89, p ≈ 0). The bivariate tiled histogram (Fig. 1c) shows that the vast majority of myelination covariance values from the two subgroups were distributed narrowly along the diagonal, evidenced by a least-square fitting line with a slope close to 1 (0.97) and the intercept close to 0. Taken together, these results indicate that cross-subject grayordinate-wise myelination covariance was highly reliable.
Figure 1.
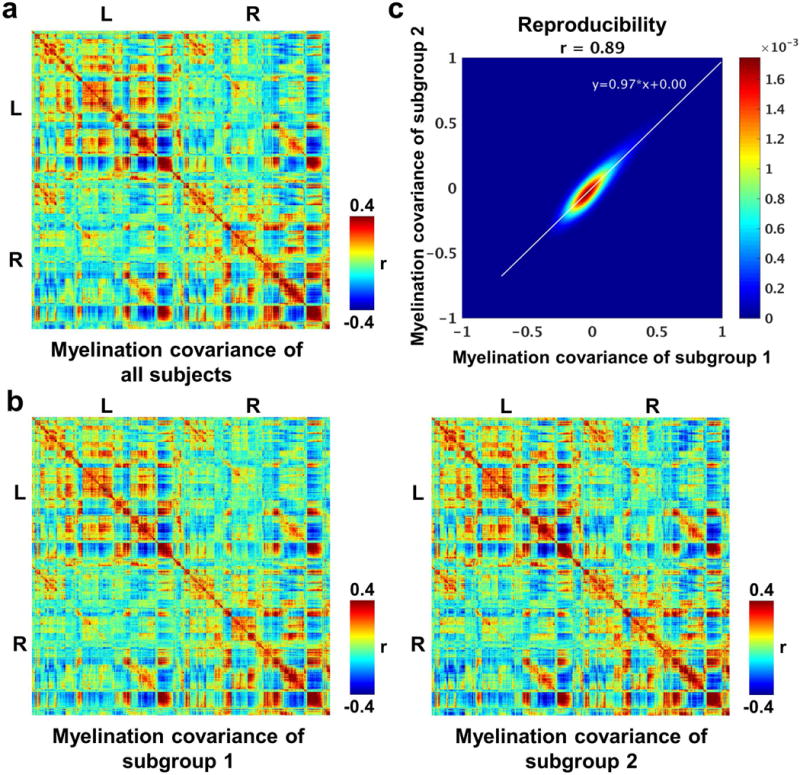
a, Grayordinate-wise myelination covariance matrix of all subjects. b, Grayordinate-wise myelination covariance matrices of subgroups 1 and 2. c, Correlation of grayordinate-wise myelination covariance strength (r values) between two subgroups. No subjects between subgroups have kinship.
Organization of cortical myelination covariance
We next examined inter-subject myelination covariance patterns across the cortex using ICA. Fig. 2a shows the spatial patterns of all (330) myelination covariance ICA components. To avoid potential overlaps between components, each grayordinate was uniquely assigned to the component that it had the largest Z score among all components. 87 of these components were bilateral. The number of ipsilateral components in each hemisphere was approximately the same (118 left components and 115 right components). A number of well-defined brain regions previously reported can be captured by these independent components of myelination covariance (Allen, et al., 2011; Guo, et al., 2015; Smith, et al., 2013a; Smith, et al., 2009; Yeo and Eickhoff, 2016). For instance, Figs. 2b and 2c show components located at the posterior and anterior parts of the primary visual cortex (V1), respectively. Components shown in Figs. 2d and 2e represent ventral and dorsal parts of the primary somatosensory cortex (S1), respectively. Figs. 2f and 2g show the lateral and medial portions of the primary motor cortex (M1), respectively. In addition to sensory and motor components, ICA analysis of myelination covariance revealed functionally well-characterized regions like the posterior cingulate cortex (PCC, Fig. 2h) and orbital frontal complex (OFC, Fig. 2i). Components in Figs. 2j and 2k represent left and right anterior cingulate cortex (ACC), respectively. Taken together, our results suggest that myelination covariance patterns revealed an organization of the human cerebral cortex similar to alternative brain connectivity measures.
Figure 2.
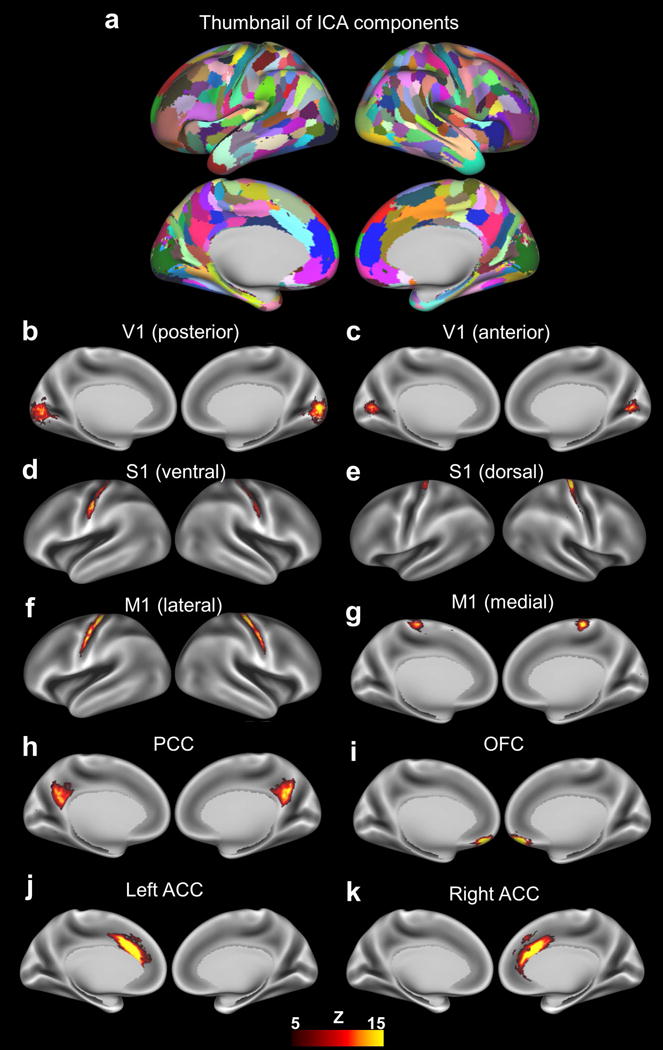
a, Spatial patterns of non-artifactual ICA components with each component displayed in a different color. b–k, Spatial maps of representative ICA components (thresholded at Z>5) of myelination covariance displayed on inflated brain surfaces. V1, primary visual cortex; S1, primary sensory cortex; M1, primary motor cortex; PCC, posterior cingulate cortex; OFC, orbital frontal complex; ACC, anterior cingulate cortex.
Topological features of myelination covariance network
Human brain networks based on various connectivity measures are typically organized in a non-trivial manner and contain common topological features like small worldness (Bullmore and Sporns, 2009; Wang, et al., 2010). Our data demonstrate that the myelination covariance-based network shared this common topological architecture. The myelination covariance network was constructed with nodes defined by parcels in a multi-modal parcellation of the human cerebral cortex (Glasser, et al., 2016), and edges defined by myelination covariance between parcels.
To ensure that this parcellation scheme was appropriate for constructing the myelination covariance network, we first examined the within-parcel homogeneity of myelination covariance (Fig. 3a). Our data show that most parcels had high within-parcel myelination covariance homogeneity (98% parcels’ homogeneity > 0.5). The mean homogeneity (± SD) of all parcels was 0.71 ± 0.09. This result shows that the within-parcel homogeneity was high for small-size parcels in general, but large-size parcels (> 400 grayordinates) also exhibit reasonable homogeneity (> 0.5). These results confirm the validity of adopting this multi-modal parcellation scheme (Glasser, et al., 2016) for constructing the myelination covariance network.
Figure 3.
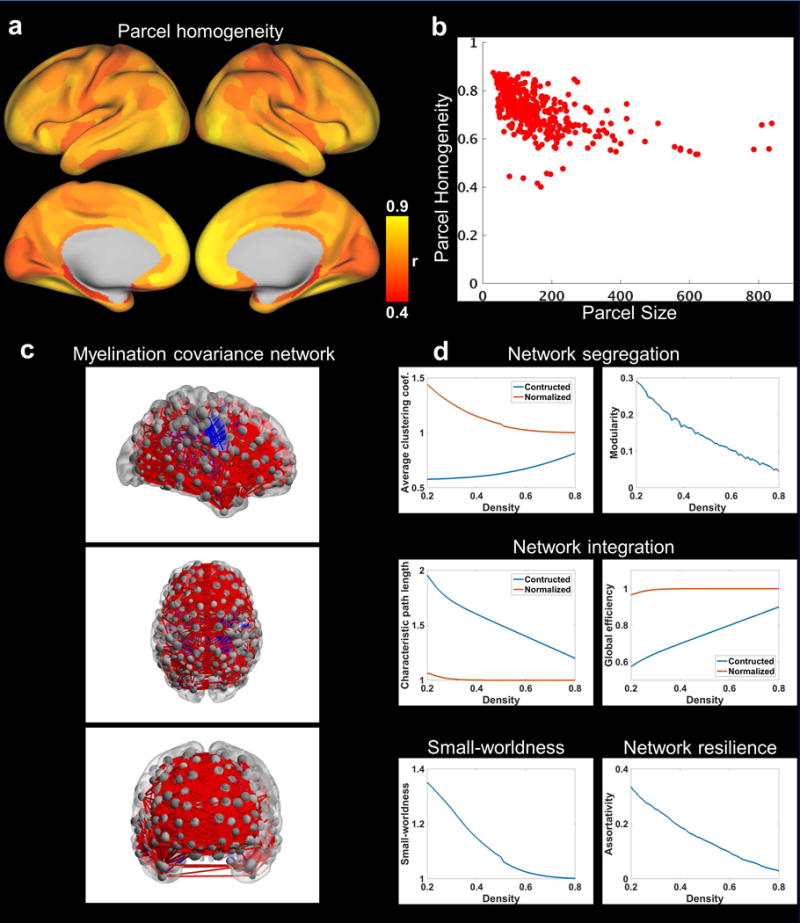
a, Map of parcel homogeneity of myelination covariance. b, Myelination covariance homogeneity value plotted against the corresponding parcel size (in the number of grayordinates). c, Myelination covariance network (thresholded at the connection density of 0.1) displayed in sagittal, axial and coronal views, respectively. Each node represents a brain parcel located at its centroid position with the node size proportional to the number of grayordinates in this parcel. The thickness of edge is proportional to the strength of myelination covariance with red edges representing positive covariance and blue edges representing negative covariance. BrainNet Viewer was used for the display of this network (Xia et al., 2013). d, Global topological metrics of the cortical myelination covariance network as a function of connection density.
Using graph theory analysis, we investigated the intrinsic organization of this myelination covariance network (Fig. 3c). Fig. 3d summarizes fundamental global graph metrics of the myelination covariance network as a function of connection density. Average clustering coefficient and modularity were used to describe network segregation properties. Characteristic path length and global efficiency were used to characterize network integration properties. Small-worldness was adopted to evaluate the balance between network segregation and integration. Assortativity was used to assess network resilience. At relatively low densities (i.e. sparse network, density < 0.5), the clustering property of the myelination covariance network was higher than that of random networks, and the network exhibited a strong modular structure. This network also demonstrated relatively high efficiency reflected by high normalized global efficiency and low normalized characteristic path length. These results indicate that this myelination covariance network has a small-world topology. Additionally, this network displayed positive assortativity, which suggests the presence of a resilient core of interconnected hubs. Taken together, these results indicate that the myelination covariance network contained topological features similar to brain networks generated by other connectivity measures like RSFC (Bullmore and Sporns, 2009; Wang, et al., 2010) and diffusion tractography (Gong, et al., 2012).
The quantitative relationship between myelination covariance and RSFC
We found that the correlation between myelination covariance and RSFC was dependent on specific resting-state networks (RSNs). To quantitatively investigate the relationship between the connectivity measures of myelination covariance and RSFC across the brain, we first computed the profiles of RSFC and myelination covariance of a given cortical grayordinate with all other cortical grayordinates, respectively. The spatial similarity between the brain-wide myelination covariance and RSFC profiles for this grayordinate was then determined using spatial correlation. Fig. 4 shows the map of this grayordinate-wise between-profile correlations. To facilitate the comparison of this between-profile correlation pattern to RSNs, on the same brain surfaces, well-established RSNs were displayed and color coded. These RSNs were defined by a RSFC-based parcellation scheme (Gordon, et al., 2016), in which borders of parcels were also delineated on the same map. The correspondence of myelination covariance and RSFC seemed rather uniform within each RSN, but displayed sharp changes at the borders of different RSNs. For example, myelination covariance-RSFC correlation values were relatively homogeneous within the default-mode, visual and somatomotor networks, but sharply increased from the default-mode network to the visual and somatomotor networks. Importantly, after regressing out the variance of myelin content from the myelination covariance-RSFC correlation map, these aforementioned patterns remained consistent (Fig. S1), which rules out the possibility that such relationship was driven by the variance of myelin content itself. Taken together, these results suggest that the correlation between myelination covariance and RSFC was RSN dependent.
Figure 4.
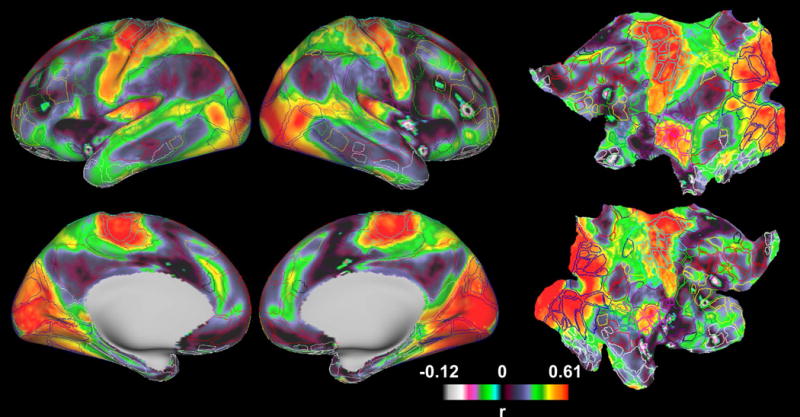
Grayordinate-wise myelination covariance-RSFC correlation map displayed on inflated (columns 1 and 2) and flattened surfaces (column 3). To facilitate the comparison of this correlation map to RSN patterns, on the same brain surfaces, the borders of parcels generated by a RSFC-based parcellation scheme (Gordon, et al., 2016) are delineated and color coded based on the RSN they belong to.
In addition to the spatial specificity at relatively large RSN scales, we asked whether the spatial pattern of myelination covariance-RSFC correlation within a RSN contained more fine-grained functional architecture. To answer this question, the grayordinate-wise between-profile correlation map was compared against retinotopic and somatotopic organizations, obtained from a previously published visual eccentricity map (Glasser, et al., 2016), as well as task-fMRI contrast maps of finger tapping, toe squeezing and tongue moving in the HCP (900 Subjects Data Release). These task-fMRI contrast maps were thresholded at an arbitrary but statistically stringent threshold (Z > 10) to separate hand, foot and tongue areas within somato-motor networks. As shown in Fig. 5a, the pattern of myelination covariance-RSFC correlation within the visual network clearly captured regions corresponding to foveal and peripheral visual areas, as shown in the visual eccentricity map. Similarly, the myelination covariance-RSFC correlation pattern in the somato-motor network could differentiate hand and foot areas revealed by the task-fMRI maps (Fig. 5b, right). Also, the myelination covariance-RSFC correlation pattern largely identified the tongue area (Fig. 5c, right) in the lateral somato-motor network. These results collectively demonstrate that the correlation between whole-brain myelination covariance and RSFC profiles share similar transitions in sensory and motor networks, and reveal fine-grained functional architectures within RSNs.
Figure 5.
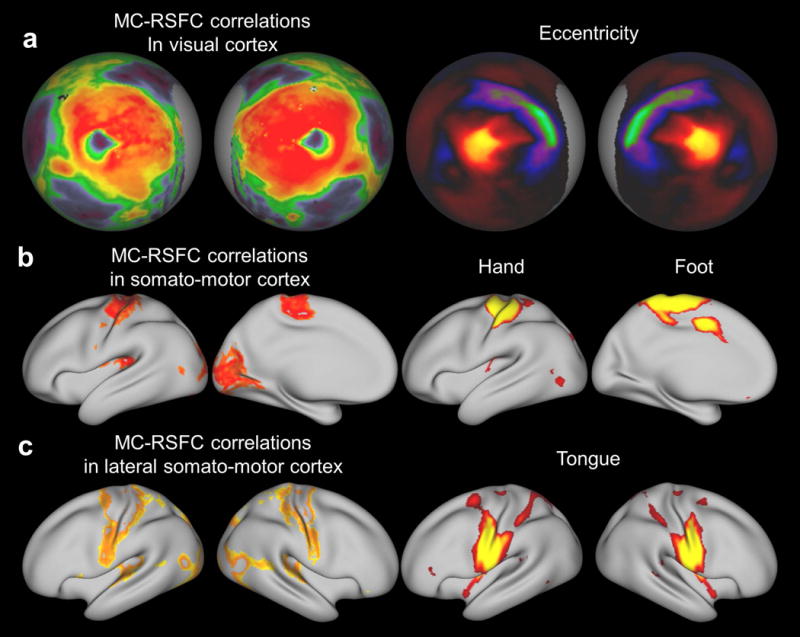
Fine-grained features in the myelination covariance-RSFC correlation map. a, The left two columns are myelination covariance-RSFC correlation in the visual cortex displayed on spherical surfaces. The right two columns are the visual eccentricity contrast map (Glasser, et al., 2016). b, Left two columns are myelination covariance-RSFC correlation in the somato-motor cortex (thresholded at 0.55 < r < 0.65) displayed on inflated surfaces. Right two columns are hand and foot areas obtained by fMRI activation patterns (Z>10) during finger tapping and toe squeezing movement, respectively. c, Left two columns are myelination covariance-RSFC correlation in the lateral somato-motor cortex (thresholded at 0.45 < r < 0.55). Right two columns are the tongue area obtained by the fMRI activation pattern (Z>10) during tongue movement.
Stronger myelination covariance-RSFC correlation in sensory and motor networks than in cognitive and polymodal association networks
We observed that myelination covariance-RSFC correlation was stronger in sensory and motor networks including visual, somato-motor, lateral somato-motor and auditory networks than in cognitive and polymodal association networks including parieto-occipital, attention, salience, default-mode, fronto-parietal, cingulo-opercular and parietal-memory networks. To compare the myelination covariance-RSFC correlation across RSNs, Fisher Z-transformed correlation values within each parcel were averaged. As shown in Fig. 6a, parcels within sensory and motor networks clearly showed higher correlation values than parcels in cognitive and polymodal association networks. Then, we averaged Fisher Z-transformed correlation values for all grayordinates belonging to the same RSN. Fig. 6b shows the mean Z values (± SE) of 12 RSNs. Averaged correlation values were stronger in sensory and motor networks (i.e. visual, somato-motor, lateral somato-motor and auditory networks) than cognitive and polymodal association networks (i.e. parieto-occipital, attention, salience, default-mode, fronto-parietal, cingulo-opercular and parietal-memory networks). One-way analysis of variance (ANOVA) was used to determine whether there was statistical difference among the mean Z values of these 12 RSNs. ANOVA results showed that these 12 means were not all equal (p ≈ 0). Specifically, the mean Z values of visual, somato-motor, lateral somato-motor, auditory, parieto-occipital, fronto-parietal, and default-mode networks were statistically significantly different from each other as well as any other RSNs. For attention-related networks (i.e. dorsal attention, ventral attention and salience networks), their mean Z values were not significantly different among themselves, whereas these three means were significantly different from the other 9 RSNs. The mean Z value of the cingulo-opercular network was not significantly different from that of the parietal memory network, but both of these two networks showed statistically significant difference from the other 10 RSNs. Collectively, these results demonstrate the RSN-specific relationship between myelination covariance and RSFC.
Figure 6.
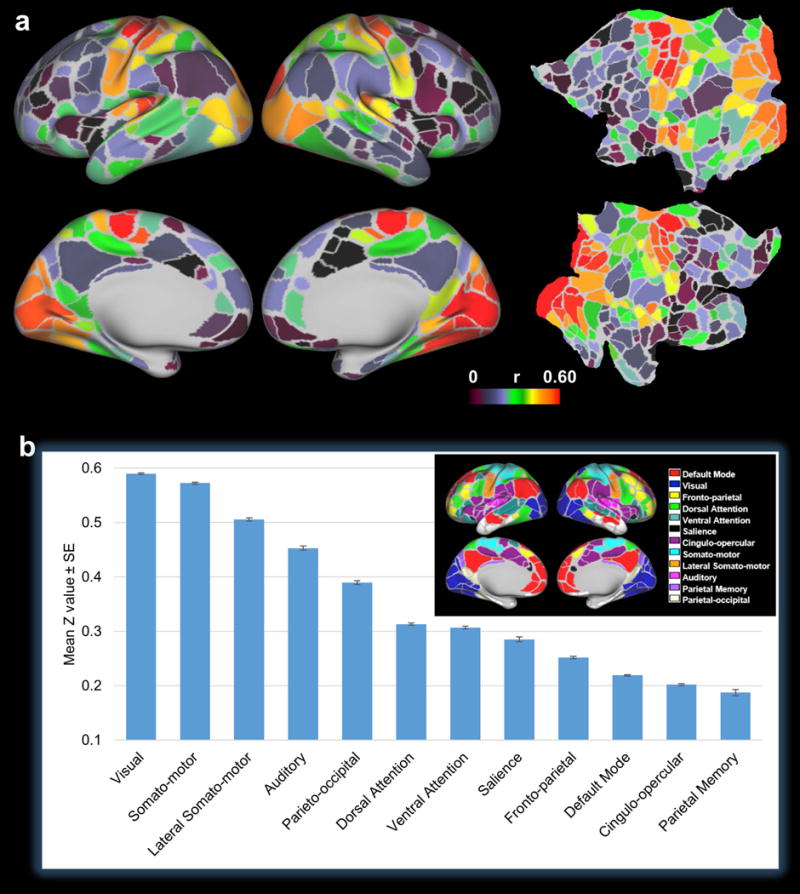
a, Parcel-wise mean correlation map displayed on inflated and flattened surfaces. The myelination covariance-RSFC correlation values of all grayordinates within each parcel (Gordon, et al., 2016) were averaged and the mean correlation values were displayed for all parcels in the map. b, Mean correlation values averaged across all grayordinates within each RSN. The parcellation scheme and network definition are shown in the inset (Gordon, et al., 2016).
Discussion
This work systematically characterized myelination covariance across the entire human cerebral cortex in a large group of subjects (>800) using T1/T2 ratio myelin maps. We first demonstrated that cross-individual myelination covariance was highly robust (Fig. 1). We then showed that large-scale myelination covariance patterns revealed an organization (Fig. 2) comparable to that generated by alternative connectivity measures (Allen, et al., 2011; Guo, et al., 2015; Smith, et al., 2013a; Smith, et al., 2009; Yeo and Eickhoff, 2016). Furthermore, we characterized topological properties of the whole-brain network based on myelination covariance and a well-recognized cortical parcellation scheme (Glasser, et al., 2016)(Fig. 3). Finally, we quantitatively investigated the relationship between myelination covariance and RSFC, and found that their correspondence was dependent on individual RSNs at both large and fine-grained scales (Figs. 4 and 5). Interestingly, myelination covariance-RSFC correlation was higher in sensory and motor networks than in cognitive and polymodal association networks (Fig. 6). Taken together, these results demonstrate a new method to investigate inter-areal connectivity based on cortical myeloarchitectonics—a feature characteristic of axon fibers. This work also provides new insight into our understanding of the structure-function relationship in the human brain connectivity.
Brain organization of myelination covariance
Although the definitive biological mechanisms underlying cross-population covariance of brain morphometric measures are still under active investigation, structural covariance is believed to be attributed to coordinated neurodevelopment of connected brain regions (Alexander-Bloch, et al., 2013a; Alexander-Bloch, et al., 2013b). Direct anatomical connections between brain regions can cause functional co-activation, which in turn lead to coordinated neurodevelopment of brain structures and thus covariant brain morphology (Alexander-Bloch, et al., 2013a). Therefore, cross-population structural covariance can provide a measure of connectivity between regions. Notably, other factors such as genetic and environmental influences, which can control synchronized morphological changes during development, could also affect inter-regional myelination covariance (Alexander-Bloch, et al., 2013a).
Previous studies in this line of research predominantly used bulky morphometric measures with mixed compartments, like gray matter density or cortical thickness (Alexander-Bloch, et al., 2013a; Lerch, et al., 2006; Mechelli, et al., 2005), while such analysis based on a specific subdivision like myelin content is rare. To bridge this knowledge gap, in the present study we systematically analyzed the covariance of myelin content across the cerebral cortex. Our results showed that this axon-related structural covariance can reveal brain connectivity organization consistent with other connectivity measures (Smith, et al., 2009). For example, ICA analysis uncovered myelination covariance in anatomically and functionally well-defined sensory and motor regions like V1, S1 and M1 (Figs. 2b–g), as well as cognition-related regions like ACC, PCC and OFC (Figs. 2h–k). These results uncovered the connectivity patterns between brain regions determined by their coordinated development of myeloarchitecture, and confirm the validity of cross-modality comparison of brain connectivity measures.
Whole-brain network based on myelination covariance
Using myelination covariance as a connectivity measure, we constructed a whole-brain network and evaluated its topological architecture. The node definition was based on a multi-modal parcellation of the human cerebral cortex using structural MRI, task-fMRI, T1w/T2w ratio myelin maps and rsfMRI data in the HCP. This 360-parcel scheme was established using a semi-automatic approach, in which parcel borders were identified based on sharp transitions in cortical myelination, thickness, task fMRI contrasts, RSFC and topography (Glasser, et al., 2016). This approach can detect brain region boundaries not obvious in any single modality, and the consistency across different modalities also increases the confidence of the borders identified in this parcellation scheme (Yeo and Eickhoff, 2016).
We first confirmed that this node definition is appropriate to use for constructing the myelination covariance-based network. Network topological properties are very sensitive to different parcellation schemes (Wang, et al., 2009), and inaccurate parcellation can severely damage the network characterization (Smith, et al., 2011). To avoid this pitfall, a parcellation scheme used to construct a network ought to be homogeneous within individual parcels. Our data show that myelination covariance was highly homogeneous for the vast majority of parcels in this multi-modal parcellation scheme (Fig. 3a–b), suggesting that it is appropriate to construct and evaluate the myelination covariance network using this cortical parcellation scheme.
We found that the resulting myelination covariance network displayed non-random, clustered, modular, and efficient properties at sparse connection densities (Fig. 3d). These topological properties have been repeatedly demonstrated by brain networks generated using various connectivity measures like diffusion tractography and RSFC (Bullmore and Sporns, 2009; Gong, et al., 2012; Wang, et al., 2010). All of these results collectively suggest that myelination covariance-based network is organized in a non-trivial manner and shares the common topological architecture of human brain networks.
RSN-dependent myelination covariance-RSFC relationship
The correspondence between myelination covariance and RSFC across the cortex was quantitatively evaluated by correlating whole-brain myelination covariance and RSFC profiles for each cortical grayordinate. We found that this correspondence was rather uniform within each RSN, but could vary sharply across different RSNs. This nature (i.e. relatively uniform myelination covariance-RSFC correlation in functionally homogeneous units) existed at multiple scales from large-scale networks to fine-grained functional architectures like retinotopic and somatotopic organizations.
Interestingly, stronger myelination covariance-RSFC correlation was observed in sensory and motor networks than in cognitive and polymodal association networks. This result is consistent with a recent study comparing structural covariance of myelination measured by magnetization transfer with RSNs measured by magnetoencephalography, and showed stronger structure-function relationship in the occipital and parietal lobes but weaker relationship in the frontal areas (Hunt, et al., 2016). Our result is also consistent with another report comparing gray matter density covariance and RSFC at the network level, which demonstrated high spatial overlaps between structure covariance and RSFC in the medial and lateral visual cortices as well as the supplementary motor area of the human brain (Segall, et al., 2012).
Differences in the distribution of myelination covariance-RSFC correlation across individual RSNs might be attributed to their different circuitry structures. Notably, sensory and motor networks are usually local networks and characterized by canonical circuit organization, where structurally connected areas tend to be close to each other. On the other hand, cognitive and polymodal association networks are often distributed and possess a non-canonical circuit structure (Buckner and Krienen, 2013). Stronger association between myelination covariance and RSFC in RSNs possessing canonical circuit organization might suggest that short-distance connections similarly affect RSFC and myelination covariance. Conversely, long-distance connections may have more diverse effects on RSFC and myelination covariance in RSNs with the non-canonical circuit structure. These results can help us better understand the structure-function correspondence in different connectivity measurements.
Potential implication in studying axon development
Because myelination covariance might reflect coordinated neurodevelopment of myeloarchitecture between connected brain regions, results of the present study may provide a new avenue to investigating axon fiber development in the human brain. MRI studies have shown that brain regions co-varying in cortical thickness were also correlated in their rate of cortical thickness change during development (Alexander-Bloch, et al., 2013b), suggesting that structural covariance can provide a measure of coordinated neurodevelopment. Importantly, it has been shown that myelination covariant regions were also synchronously myelinated during the development of the neonatal brain (Bozek, et al., 2016). Considering that myelination is specific to axons, myelination covariance analysis might provide great value to the investigation of coordinated axon fiber development between connected brain regions.
Conclusions
The present study has systematically characterized myelination covariance in the human cerebral cortex. We identified reproducible myelination covariance patterns across the human cerebral cortex, and demonstrated the non-trivial topological architecture of the myelination covariance network. Our study also revealed a RSN-dependent relationship between myelination covariance and RSFC. Myelination covariance and RSFC were found to be more strongly correlated in sensory and motor networks, which are dominated by a canonical circuit structure, than in cognitive and polymodal association networks, which possess a noncanonical circuit structure. Taken together, the present study has established a new connectivity measure based on the covariance of the axon-related myeloarchitectonic feature. These results can shed light on the structure-function relationship in brain connectivity organization. They may also be useful for studies of coordinated axon development.
The significance of the present study can be further extended to the research of neurological disorders. Accruing evidence has shown that cortical demyelination is implicated in multiple brain disorders like multiple sclerosis (Hulst and Geurts, 2011), suggesting that cortical myeloarchitecture might be a potential biomarker for these brain diseases. As a result, mapping the myelination covariance pattern of the human cerebral cortex in a healthy group of subjects has provided a critical reference point that can facilitate the identification of abnormal brain myeloarchitecture-related endophenotypes in disease states.
Supplementary Material
Acknowledgments
Data were provided [in part] by the HCP, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University. Some portions of this research were conducted with the high-performance computing resources provided by the Institute for CyberScience at the Pennsylvania State University (https://ics.psu.edu). In addition, we would like to thank HCP-Users mailing list for helpful information, and thank Mr. David Dopfel and Mr. Samuel Cramer for editing the manuscript. The present study was supported by National Institute of Neurological Disorders and Stroke Grant R01NS085200 (PI: Nanyin Zhang, PhD) and National Institute of Mental Health Grant R01MH098003 (PI: Nanyin Zhang, PhD).
Footnotes
Conflict of Interest: none.
References
- Abdollahi RO, Kolster H, Glasser MF, Robinson EC, Coalson TS, Dierker D, Jenkinson M, Van Essen DC, Orban GA. Correspondences between retinotopic areas and myelin maps in human visual cortex. Neuroimage. 2014;99:509–24. doi: 10.1016/j.neuroimage.2014.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Accolla EA, Dukart J, Helms G, Weiskopf N, Kherif F, Lutti A, Chowdhury R, Hetzer S, Haynes JD, Kuhn AA, Draganski B. Brain tissue properties differentiate between motor and limbic basal ganglia circuits. Hum Brain Mapp. 2014;35:5083–92. doi: 10.1002/hbm.22533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander-Bloch A, Giedd JN, Bullmore E. Imaging structural co-variance between human brain regions. Nat Rev Neurosci. 2013a;14:322–36. doi: 10.1038/nrn3465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander-Bloch A, Raznahan A, Bullmore E, Giedd J. The convergence of maturational change and structural covariance in human cortical networks. J Neurosci. 2013b;33:2889–99. doi: 10.1523/JNEUROSCI.3554-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen EA, Erhardt EB, Damaraju E, Gruner W, Segall JM, Silva RF, Havlicek M, Rachakonda S, Fries J, Kalyanam R, Michael AM, Caprihan A, Turner JA, Eichele T, Adelsheim S, Bryan AD, Bustillo J, Clark VP, Feldstein Ewing SW, Filbey F, Ford CC, Hutchison K, Jung RE, Kiehl KA, Kodituwakku P, Komesu YM, Mayer AR, Pearlson GD, Phillips JP, Sadek JR, Stevens M, Teuscher U, Thoma RJ, Calhoun VD. A baseline for the multivariate comparison of resting-state networks. Front Syst Neurosci. 2011;5:2. doi: 10.3389/fnsys.2011.00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM. Investigations into resting-state connectivity using independent component analysis. Philos Trans R Soc Lond B Biol Sci. 2005;360:1001–13. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, Smith SM. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Trans Med Imaging. 2004;23:137–52. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E. Fast unfolding of communities in large networks. J Stat Mech-Theory E 2008 [Google Scholar]
- Bock NA, Kocharyan A, Liu JV, Silva AC. Visualizing the entire cortical myelination pattern in marmosets with magnetic resonance imaging. J Neurosci Methods. 2009;185:15–22. doi: 10.1016/j.jneumeth.2009.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bozek JB, Makropoulos A, Wright R. In-Vivo Cortical Myelination of the Neonatal Brain in the Developing Human Connectome Project. the 22nd Annual Meeting of the Organization for Human Brain Mapping; Geneva, Switzerland. 2016. [Google Scholar]
- Buckner RL, Krienen FM. The evolution of distributed association networks in the human brain. Trends Cogn Sci. 2013;17:648–65. doi: 10.1016/j.tics.2013.09.017. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10:186–98. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Carmeli C, Fornari E, Jalili M, Meuli R, Knyazeva MG. Structural covariance of superficial white matter in mild Alzheimer’s disease compared to normal aging. Brain and behavior. 2014;4:721–37. doi: 10.1002/brb3.252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen-Adad J. What can we learn from T2* maps of the cortex? Neuroimage. 2014;93(Pt 2):189–200. doi: 10.1016/j.neuroimage.2013.01.023. [DOI] [PubMed] [Google Scholar]
- Cohen-Adad J, Polimeni JR, Helmer KG, Benner T, McNab JA, Wald LL, Rosen BR, Mainero C. T(2)* mapping and B(0) orientation-dependence at 7 T reveal cyto- and myeloarchitecture organization of the human cortex. Neuroimage. 2012;60:1006–14. doi: 10.1016/j.neuroimage.2012.01.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans AC. Networks of anatomical covariance. Neuroimage. 2013;80:489–504. doi: 10.1016/j.neuroimage.2013.05.054. [DOI] [PubMed] [Google Scholar]
- Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Gunther M, Glasser MF, Miller KL, Ugurbil K, Yacoub E. Multiplexed echo planar imaging for sub-second whole brain FMRI and fast diffusion imaging. PLoS One. 2010;5:e15710. doi: 10.1371/journal.pone.0015710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B. FreeSurfer. Neuroimage. 2012;62:774–81. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genovese CR, Lazar NA, Nichols T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 2002;15:870–8. doi: 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M, Smith SM, Van Essen DC. A multi-modal parcellation of human cerebral cortex. Nature. 2016;536:171–8. doi: 10.1038/nature18933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Goyal MS, Preuss TM, Raichle ME, Van Essen DC. Trends and properties of human cerebral cortex: correlations with cortical myelin content. Neuroimage. 2014;93(Pt 2):165–75. doi: 10.1016/j.neuroimage.2013.03.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, Consortium, W.U.-M.H. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage. 2013;80:105–24. doi: 10.1016/j.neuroimage.2013.04.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Van Essen DC. Mapping human cortical areas in vivo based on myelin content as revealed by T1- and T2-weighted MRI. J Neurosci. 2011;31:11597–616. doi: 10.1523/JNEUROSCI.2180-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong G, He Y, Chen ZJ, Evans AC. Convergence and divergence of thickness correlations with diffusion connections across the human cerebral cortex. Neuroimage. 2012;59:1239–48. doi: 10.1016/j.neuroimage.2011.08.017. [DOI] [PubMed] [Google Scholar]
- Gordon EM, Laumann TO, Adeyemo B, Huckins JF, Kelley WM, Petersen SE. Generation and Evaluation of a Cortical Area Parcellation from Resting-State Correlations. Cereb Cortex. 2016;26:288–303. doi: 10.1093/cercor/bhu239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffanti L, Salimi-Khorshidi G, Beckmann CF, Auerbach EJ, Douaud G, Sexton CE, Zsoldos E, Ebmeier KP, Filippini N, Mackay CE, Moeller S, Xu J, Yacoub E, Baselli G, Ugurbil K, Miller KL, Smith SM. ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. Neuroimage. 2014;95:232–47. doi: 10.1016/j.neuroimage.2014.03.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grydeland H, Walhovd KB, Tamnes CK, Westlye LT, Fjell AM. Intracortical myelin links with performance variability across the human lifespan: results from T1- and T2-weighted MRI myelin mapping and diffusion tensor imaging. J Neurosci. 2013;33:18618–30. doi: 10.1523/JNEUROSCI.2811-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo X, Wang Y, Guo T, Chen K, Zhang J, Li K, Jin Z, Yao L. Structural covariance networks across healthy young adults and their consistency. J Magn Reson Imaging. 2015;42:261–8. doi: 10.1002/jmri.24780. [DOI] [PubMed] [Google Scholar]
- He Y, Chen ZJ, Evans AC. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb Cortex. 2007;17:2407–19. doi: 10.1093/cercor/bhl149. [DOI] [PubMed] [Google Scholar]
- Hulst HE, Geurts JJ. Gray matter imaging in multiple sclerosis: what have we learned? BMC Neurol. 2011;11:153. doi: 10.1186/1471-2377-11-153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunt BA, Tewarie PK, Mougin OE, Geades N, Jones DK, Singh KD, Morris PG, Gowland PA, Brookes MJ. Relationships between cortical myeloarchitecture and electrophysiological networks. Proc Natl Acad Sci U S A. 2016;113:13510–13515. doi: 10.1073/pnas.1608587113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerch JP, Worsley K, Shaw WP, Greenstein DK, Lenroot RK, Giedd J, Evans AC. Mapping anatomical correlations across cerebral cortex (MACACC) using cortical thickness from MRI. Neuroimage. 2006;31:993–1003. doi: 10.1016/j.neuroimage.2006.01.042. [DOI] [PubMed] [Google Scholar]
- Mechelli A, Friston KJ, Frackowiak RS, Price CJ. Structural covariance in the human cortex. J Neurosci. 2005;25:8303–10. doi: 10.1523/JNEUROSCI.0357-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med. 2010;63:1144–53. doi: 10.1002/mrm.22361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieuwenhuys R, Broere CA. A map of the human neocortex showing the estimated overall myelin content of the individual architectonic areas based on the studies of Adolf Hopf. Brain structure & function. 2016 doi: 10.1007/s00429-016-1228-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson EC, Jbabdi S, Glasser MF, Andersson J, Burgess GC, Harms MP, Smith SM, Van Essen DC, Jenkinson M. MSM: a new flexible framework for Multimodal Surface Matching. Neuroimage. 2014;100:414–26. doi: 10.1016/j.neuroimage.2014.05.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 2010;52:1059–69. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM. Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. Neuroimage. 2014;90:449–68. doi: 10.1016/j.neuroimage.2013.11.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segall JM, Allen EA, Jung RE, Erhardt EB, Arja SK, Kiehl K, Calhoun VD. Correspondence between structure and function in the human brain at rest. Front Neuroinform. 2012;6:10. doi: 10.3389/fninf.2012.00010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med. 2012;67:1210–24. doi: 10.1002/mrm.23097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shafee R, Buckner RL, Fischl B. Gray matter myelination of 1555 human brains using partial volume corrected MRI images. Neuroimage. 2015;105:473–85. doi: 10.1016/j.neuroimage.2014.10.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Beckmann CF, Andersson J, Auerbach EJ, Bijsterbosch J, Douaud G, Duff E, Feinberg DA, Griffanti L, Harms MP, Kelly M, Laumann T, Miller KL, Moeller S, Petersen S, Power J, Salimi-Khorshidi G, Snyder AZ, Vu AT, Woolrich MW, Xu J, Yacoub E, Ugurbil K, Van Essen DC, Glasser MF, Consortium, W.U.-M.H. Resting-state fMRI in the Human Connectome Project. Neuroimage. 2013a;80:144–68. doi: 10.1016/j.neuroimage.2013.05.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF. Correspondence of the brain’s functional architecture during activation and rest. Proc Natl Acad Sci U S A. 2009;106:13040–5. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Hyvarinen A, Varoquaux G, Miller KL, Beckmann CF. Group-PCA for very large fMRI datasets. Neuroimage. 2014;101:738–49. doi: 10.1016/j.neuroimage.2014.07.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW. Network modelling methods for FMRI. Neuroimage. 2011;54:875–91. doi: 10.1016/j.neuroimage.2010.08.063. [DOI] [PubMed] [Google Scholar]
- Smith SM, Vidaurre D, Beckmann CF, Glasser MF, Jenkinson M, Miller KL, Nichols TE, Robinson EC, Salimi-Khorshidi G, Woolrich MW, Barch DM, Ugurbil K, Van Essen DC. Functional connectomics from resting-state fMRI. Trends Cogn Sci. 2013b;17:666–82. doi: 10.1016/j.tics.2013.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Glasser MF. In vivo architectonics: a cortico-centric perspective. Neuroimage. 2014;93(Pt 2):157–64. doi: 10.1016/j.neuroimage.2013.04.095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium, W.U.-M.H. The WU-Minn Human Connectome Project: an overview. Neuroimage. 2013;80:62–79. doi: 10.1016/j.neuroimage.2013.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanderah TW, Gould DJ, Nolte J. Nolte’s The human brain: an introduction to its functional anatomy. Philadelphia, PA: Elsevier; 2016. [Google Scholar]
- Wang J, Wang L, Zang Y, Yang H, Tang H, Gong Q, Chen Z, Zhu C, He Y. Parcellation-dependent small-world brain functional networks: a resting-state fMRI study. Hum Brain Mapp. 2009;30:1511–23. doi: 10.1002/hbm.20623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Zuo X, He Y. Graph-based network analysis of resting-state functional MRI. Front Syst Neurosci. 2010;4:16. doi: 10.3389/fnsys.2010.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BT, Eickhoff SB. Systems neuroscience: A modern map of the human cerebral cortex. Nature. 2016;536:152–4. doi: 10.1038/nature18914. [DOI] [PubMed] [Google Scholar]
- Zielinski BA, Gennatas ED, Zhou J, Seeley WW. Network-level structural covariance in the developing brain. Proc Natl Acad Sci U S A. 2010;107:18191–6. doi: 10.1073/pnas.1003109107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


