Progenitor Cell Self-renewal and Cyclic Neutropenia

Abstract

Cyclic neutropenia (CN) is a rare genetic disorder where patients experience regular cycling of neutrophils and various other hematopoietic lineages. The nadir in the neutrophil count is the main source of problems due to the risk of life-threatening infections. Patients with CN benefit from G-CSF therapy although cycling persists. Mutations in the neutrophil elastase gene (ELA2) have been found in more than half of the patients with CN. However, neither the connection between phenotypic expression of ELA2 and CN nor the mechanism of cycling are known. Recently a multi-compartment model of hematopoiesis that couples stem cell replication with marrow output was proposed. In the following, we couple this model of hematopoiesis with a linear feedback mechanism via G-CSF. We propose that the phenotypic effect of ELA2 mutations leads to a reduction in self-renewal of granulocytic progenitors. The body responds by an overall relative increase of G-CSF and increasing progenitor cell self-renewal leading to cell count cycling. The model is compatible with the available experimental data and makes testable predictions.

INTRODUCTION

Cyclic neutropenia (CN) is a rare hematological disorder characterized by periodic severe neutropenia interspersed by normal or near normal neutrophil counts that repeat every 19 to 21 days (Dale et al., 1988, Haurie et al., 1998). Although the neutrophil nadir is the cause of the symptoms in this disorder, almost all cellular elements in the blood may cycle, being usually out of phase with the neutrophils (Haurie et al., 1998). Mutations in the gene coding for neutrophil elastase 2 (ELA2) have been identified in almost half of the patients with this disorder but the exact mechanisms of how these mutations cause the disease remain unclear (Horwitz et al., 1999, Benson et al., 2003). Therefore it is not surprising that some scepticism about the role of the ELA2 mutation in the etiology of CN persists in the field (Germeshausen et al., 2001). The majority of mutations in the ELA2 gene are base substitutions leading to loss of the splice donor site in exon four. This forces the use of an upstream cryptic splice donor site that results in loss of 30 nucleotides during RNA processing (Horwitz et al., 1999). Patients with CN benefit from pharmacologic doses of granulocyte colony stimulating factor (G-CSF) with rapid recovery of the neutrophil count although cycling of hematopoiesis persists (Hammond et al., 1989, Dale et al., 1993).

Several observations are pertinent to set the stage for modelling the dynamics of this disorder. ELA2 expression is restricted to cells of the granulocyte and monocyte lineage with the highest levels of expression being in promyelocytes and myelocytes. Promonocytes express the gene although at levels significantly lower than granulocyte precursors (Fouret et al., 1989, Campbell et al., 1989). In addition, myeloblasts also express low levels of the enzyme (Fouret et al., 1989). Many mutations in ELA2 identified in patients with CN often result in the aberrant localization of the enzyme in sub-cellular compartments (Benson et al., 2003). G-CSF is the main cytokine that controls the proliferation, survival and differentiation of myeloid precursors (Williams et al., 1990) and accelerates neutrophil maturation (Price et al., 1996). Granulocyte progenitors, isolated from patients with CN are less sensitive to G-CSF compared to normal controls (Hammond et al., 1992). Neutrophils from grey collies with CN express normal numbers of G-CSF receptors that appear to signal normally (Avalos et al., 1994), although similar studies on myeloid progenitor and committed cells in which neutrophil elastase (NE) expression is maximal (Fouret et al., 1989) have not been performed. In vitro, NE antagonizes the action of G-CSF by enzymatic cleavage of the cytokine (El Ouriaghli et al., 2003) but there is no evidence of release of NE in the bone marrow in patients with CN. In vivo studies show that the levels of endogenous colony stimulating factors are highest with the nadir of the neutrophil count (Guerry et al., 1974) and reach a peak concomitant with the monocyte count. Endogenous G-CSF and other cytokines are produced by many cells including endothelial cells, fibroblasts and monocytes (Moore et al., 1974, Barreda et al., 2004). In the grey collie variant of the disease, phlebotomy has no impact on the cycling of reticulocytes or neutrophils. However, erythrocyte hyper-transfusion stops reticulocyte but not neutrophil cycling (Adamson et al., 1974). Neutrophils and their precursors express G-CSF receptors and play an important role in the clearance of the cytokine from the circulation (Ericson et al., 1997). Finally, apart from being the most important cytokine controlling granulocyte production, G-CSF is a growth and survival factor for hematopoietic stem cells (HSC) and granulocyte, erythroid, monocyte and megakaryocyte colony forming units (CFU-GEMM) (Barreda et al., 2004) and may increase peripheral blood lymphocyte counts (Hareng et al., 2002).

Despite such a wealth of knowledge about this disorder, an all encompassing framework to understand its etiology has not been provided. It has been postulated that the defect must reside in the stem cell compartment (Haurie et al., 1998, Colijn et al., 2005). However, this is unlikely, since the 19-21 day cycling is not compatible with the estimated rate of replication of the active stem cell pool (Rufer et al., 1999, Shepherd et al., 2004). Moreover, studies suggest that the effect of the mutated enzyme is restricted to cells that express the gene (i.e. myeloblasts and further cells downstream) (Ancliff et al., 2003). Other investigators have proposed models to explain CN on the basis of a multi-compartment model of hematopoiesis (Schmitz et al., 1990, Schmitz et al., 1995, Schmitz et al., 1996). Hematopoiesis is divided into compartments that harbor stem cells, progenitor cells, more differentiated cells and mature cells that are linked together by cytokine feedback loops. The model specifically considers feedback loops with G-CSF, GM-CSF and erythropoietin (EPO) influencing the dynamics of all compartments downstream of the HSC pool (Wichmann et al., 1983, Schmitz et al., 1990). Schmitz et al proposed that the main defect in CN is narrowing of the variance in transit times of neutrophil precursors. The authors did not provide a biological basis for such a reduction in the variance. However, this model could be used to study the effects of therapy with these cytokines (Schmitz et al., 1995, Schmitz et al., 1996).

Recently, a hierarchical model of hematopoiesis based on steady state fluxes between successive compartments has been proposed. The process is maintained by the replication of hematopoietic stem cells that can feed downstream compartments which metaphorically represent cell lineages at different stages of differentiation (Dingli et al., 2007). The model postulates that cells in a given compartment j divide at a rate r_j that is characteristic of that compartment. During each replication, cells may differentiate (with probability ε) such that the two daughter cells shift to compartment j + 1; with probability 1 − ε the daughter cells retain the properties of their parent cell and remain in compartment j (Figure 1). Under stationary conditions, the size of each compartment is constant and cells lost from one compartment due to differentiation are replaced by cells from the upstream compartment j − 1 (Dingli et al., 2007). Using this model, it is possible to estimate the size of each hematopoietic compartment, the rate of replication of cells and the average time that a given cell type contributes to hematopoiesis (Dingli et al., 2007). We have shown that in this model, the expected number of cell divisions or ‘compartments’ that link the HSC with circulating blood (K = 32, Figure 2) is similar to what has been predicted in other models (Vaziri et al., 1994, Mackey, 2001, Shochat et al., 2002) as well as experimentally inferred from serial telomere shortening (Vaziri et al., 1994). It is important to point out that the notion of ‘compartment’ in this model should not be considered as a quantized image of hematopoiesis where the various ‘compartments’ represent abrupt transitions but rather a continuum between the HSC and the circulating blood with the ‘compartments’ simply being a tool to keep track of the number of cell divisions. Cells may divide and move from one compartment to the next (‘differentiate’), yet morphologically and perhaps functionally may appear to be the same. For example, the CFU-GEMM cells can be accommodated in compartments 5 to 8. This is based on experimental evidence of PIG-A mutations in the neutrophils, monocytes and erythrocytes of healthy adults (Araten et al., 1999). Clearly, these individuals must have at least 1 mutated CFU-GEMM cell and given the ratio of mutated to normal neutrophils, one can estimate the minimum and maximum number of CFU-GEMM cells at risk of mutation. The CFU-GM cells span compartments 9 to 11 while CFU-G span compartments 12 to 16 based on current estimates of the size of the population of cells (Donohue et al., 1958, Cronkite et al., 1964, Finch et al., 1977, Shochat et al., 2002).

Figure 1.

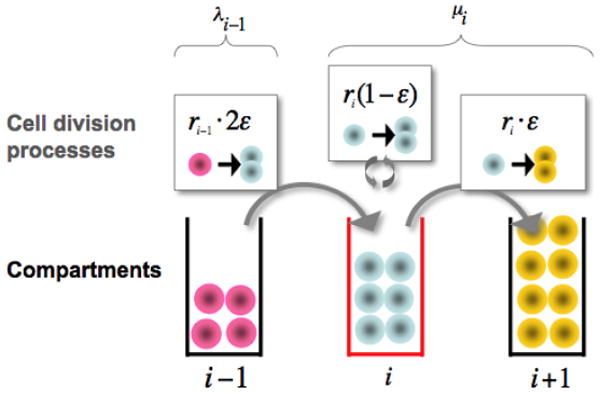
Hematopoietic cell behavior and dynamics across three adjacent compartments in hematopoiesis. Three cell division processes affect the population size in the focal compartment j (lower part of the figure, middle): (i) Differentiation of one cell in compartment j-1 at rate r_j-1 leads to two new cells in compartment j - upper left. (ii) During self renewal at rate r_j, a cell divides and produces an identical daughter cell -upper middle. (iii) Differentiation at rate r_j into the downstream compartment j+1 implies loss of one cell - upper right. The model parameters are fixed assuming that that any compartment maintains a constant population of cells, such that net cell loss μ from one compartment is replaced by cells from the upstream compartment, λ. The parameter ε governing the intensity of self renewal is estimated as ε≈ 0.85.

Figure 2.

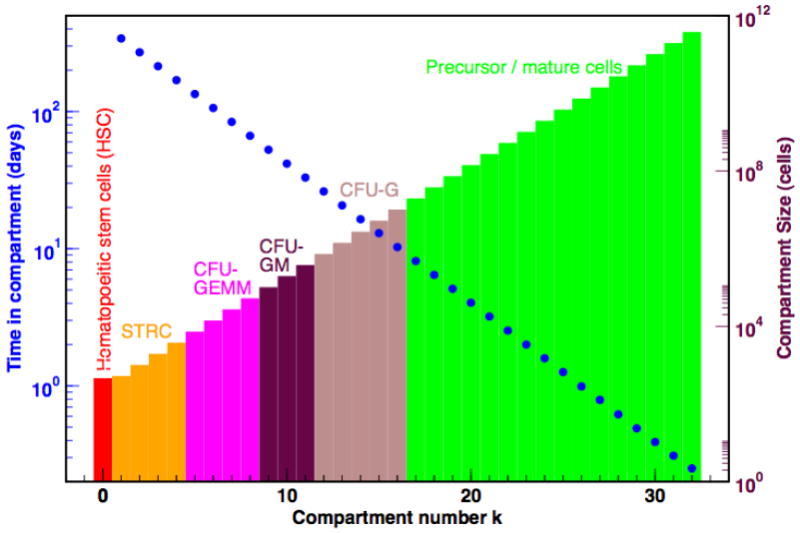
Compartmental architecture and dynamics during normal haematopoiesis. The schema provides a summary of the number of cells at the various stages of differentiation from stem cells to the post-mitotic pool. Cells in adjacent compartments may be morphologically and functionally similar but require a cell division to move from one compartment to the next as they become more differentiated. In the process they replicate faster and remain in subsequent compartments for shorter time intervals (y-axes on the left). The blue dots represent to the average time that a cell will remain in that compartment.

Here, we develop a model of CN based on this framework of hematopoiesis, which i) proposes a mechanism that explains the origin and dynamics of the disease; ii) is compatible with the most salient molecular biological features known to date and, perhaps most importantly, iii) proposes hypotheses that can be tested experimentally.

THE MODEL

Let us focus on the dynamics of a specific compartment j and investigate the time dependence of the number of cells in that compartment, N_j. In keeping with the model of hematopoiesis referred to before (Dingli et al., 2007), we consider two elementary processes: differentiation, ◦ → ••, which occurs with probability ε and self renewal, ◦ → ◦◦, that occurs with probability 1 − ε. The symbol ◦ denotes a cell that stays in compartment j while the symbol • describes a cell that moves to compartment j + 1 (Figure 1). Therefore the behaviour of each cell during any division is stochastic in nature (Gordon et al., 1994, Abkowitz et al., 1996) although the net effect is that cells tend to differentiate rather than self-renew (1 > ε > 0.5), compatible with the view of hematopoiesis as a linear process with net cell flow from HSC to the circulating compartment (Donohue et al., 1958, Cronkite et al., 1964, Finch et al., 1977). Within compartment j, the rate of cell differentiation and transfer into compartment j + 1 is μ_j = r_j (2ε−1) (Dingli et al., 2007). This loss of cells is compensated by the injection of cells from the upstream compartment, taking place at a rate λ_j−1 = r_j−12ε (Figure 1). Consequently, we may readily write down the equation for the time dependence of the number of cells in compartment j:

$$\frac{{\mathit{dN}}_j}{\mathit{dt}}=-{\mu }_j{N}_j+{\lambda }_{j-1}{N}_{j-1}$$ (1)

The stationary solution for Eq. (1) is given by

$$N_j^{\ast }=\frac{1}{2\epsilon }{C}^j{N}_0\mathrm{where}C=\frac{2\epsilon }{R(2\epsilon -1)}>0\mathrm{and}R=\frac{r_{j+1}}{r_j}$$ (2)

Equations (1) and (2) hold for all compartments with 1 ≤ j ≤ K = 31. In the multi-compartment model, N₀ ~ 400 cells and represents the active hematopoietic stem cell pool that remains constant during adult life (Buescher et al., 1985, Dingli et al., 2006, Dingli et al., 2007). We have previously shown that the values of ε and R are robust with respect to changes in the number of active stem cells (N₀) across 4 orders of magnitude and can be considered as characteristics of normal hematopoiesis (Dingli et al., 2007).

The ELA2 gene is expressed during some stages of myeloid differentiation; therefore it has no effect on cell compartments where it is not expressed. However, once it is expressed, the mutated gene alters the sensitivity of the progenitors to G-CSF (Hammond et al., 1992). Indeed, the cells need higher amounts of the cytokine to respond. One of the major effects of G-CSF is to enhance self-renewal of hematopoietic progenitors (Williams et al., 1990). We hypothesize that expression of the mutant ELA2 reduces the self-renewal of cells in some compartment (due to a reduced sensitivity to G-CSF), with the result that the total number of cells will decrease due to efflux to the next compartment. Hence the given compartment will be depleted of cells with the effect slowly transmitted to downstream compartments; hence the neutrophil count will drop.

In order to model cyclic neutropenia, we investigate how small deviations in the number of cells in a given compartment (N_j) alter the flux of cells into and out of that compartment, restricting the analysis to two adjacent compartments. We introduce a linear feedback function such that depletion of cells from compartment j leads to additional influx of cells from compartment j-1. In this way, we obtain a relationship between the compartment j, the probability of self-renewal (ε) and the replication rate of the cells (r) that is defined by

$${\mathrm{\Omega }}_j=4r_1^2{R}^{2j-4}(2\epsilon -1)(2\epsilon R+1)>0.$$ (3)

A detailed explanation of the model is provided in the Appendix. Under defined circumstances, it can be shown that oscillations in the number of cells within a given compartment will occur and persist without damping at a frequency given by

$$\nu =\frac{\sqrt{{\mathrm{\Omega }}_j}}{4\pi }$$ (4)

In other words, Eq. (4) captures the relationship between the frequency of the oscillations and the compartment, j where they start due to a mutation or other insult.

RESULTS

Where does the defect first appear?

In the multi-compartment model of hematopoiesis, stem cells replicate at a rate r₁ =1/365 day^-1 (Rufer et al., 1999, Shepherd et al., 2004) and it was assumed that R and ε are the same for all compartments (Dingli et al., 2007). The free parameters of the model are fixed using data from the expansion during polymorphonuclear leukocyte production, the number of active stem cells and the daily output of the blood system, and the cell division rates of stem cells and granulocyte precursors. This leads to R = 1.26 (cf. Eq. 2) and ε = 0.85 (Donohue et al., 1958, Cronkite et al., 1964, Finch et al., 1977). Given that the period of the cycles in most patients with CN is between 19 and 21 days, using Eqs. 3 and 4, we can estimate the earliest compartment j where the defect has to be active to give the required frequency of oscillations. Our model suggests that j ≈ 21(for both values of the period) which localizes the defect downstream of the CFU-G compartment (cf. Figure 2) (Dingli et al., 2007). For the rare patient with longer cycles (<52 days)(Haurie et al., 1999), the model predicts that j >17 which again places the defect downstream of the CFU-G compartment. In other words, for a period of 19 to 21 days, compartment 20 will be the earliest compartment with a normal ε (ε = 0.85) and we predict that ${\epsilon }_{\ge j}^{\mathit{CN}}>0.85$ in cells of the granulocyte lineage.

Progenitor cell self-renewal and cycling

The above calculations for compartment j assume that R = 1.26 remains constant even in CN. The rationale for this proposition is the observation that therapy with G-CSF mainly shortens the maturation time of cells in the post mitotic compartment rather than to increase the rate at which cells divide upstream in the hematopoietic cascade (Schmitz et al., 1996, Schmitz et al., 1995). Moreover, progenitors from patients with CN are less sensitive to G-CSF (Hammond et al., 1992) and this cytokine is essential for self-renewal of the myeloid progenitors and their progeny cells (Barreda et al., 2004, Marley et al., 2003). Hence, a reduction in sensitivity to G-CSF will reduce the self-renewal of the cells that express ELA2. Consequently, we propose that the variable affected in the disorder is ε. If we accept this conjecture, the model suggests that the defect in CN phenotypically results in ${\epsilon }_{\ge j}^{\mathit{CN}}>0.85$ leading to a decrease in self-renewal of the progenitor cells and ultimately, to a fall in neutrophil production (Figure 3). Consequently, we expect a decrease in cell output due to rapid cell transit of neutrophil precursors during hematopoiesis, a prediction which can be tested. The elevated ε means that neutrophils from patients with CN will have longer telomeres compared to normal controls since their progenitors undergo less divisions compared to normal. Therapy with G-CSF reduces ε and ε^CN and the enhanced progenitor cell renewal results in an increase of neutrophil production, although with a delay since upstream compartments must themselves expand before they can replenish downstream compartments (Figure 3). If this scenario is correct, G-CSF therapy should lead to shortening of neutrophil telomeres. Although G-CSF shortens the period of the oscillations, our model is not in conflict with this fact since the major effect of G-CSF is to shorten the transit time of cells in the post-mitotic pool (Schmitz et al., 1995). In Figure 4, we superimpose serial neutrophil counts observed in a patient with CN with the cycling predicted by the model. The model captures the overall behaviour without delving into the detailed self-regulatory mechanisms of hematopoiesis. Finally note that Eq. (2) can be re-written as $C=\frac{1}{R}{\left(1-\frac{1}{2\epsilon }\right)}^{-1}$; if ${\epsilon }_j^{\mathit{CN}}>0.85$, then the equilibrium value, N_j* is reduced and compatible with the observation that the neutrophil count in patients with CN typically oscillates around a value lower than the average in normal individuals.

Figure 3.

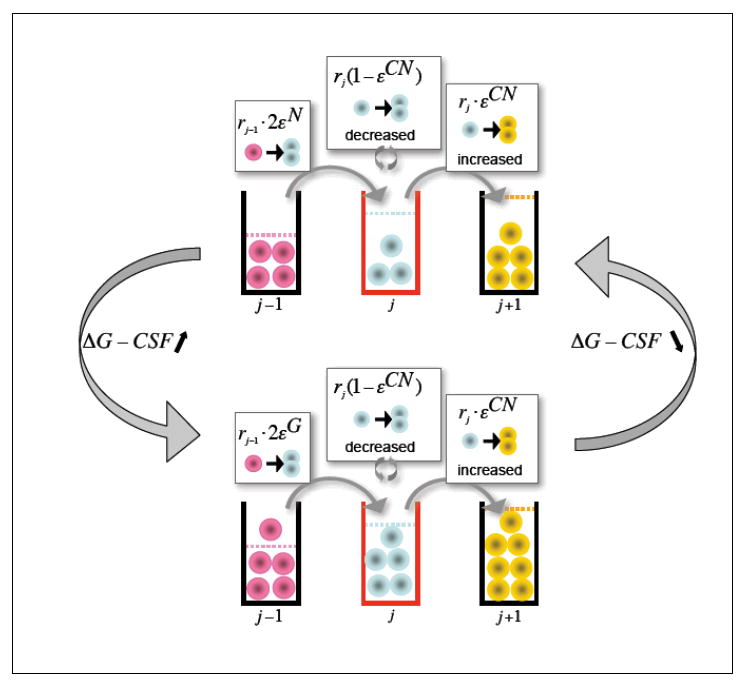
Schematic representation of the mechanism of cyclic neutropenia. Myeloid precursors that express mutated ELA2 have a higher ε (ε^CN>ε, upper panel); their self-renewal capability is therefore reduced and the downstream compartments have less cells due to decreased net output from the compartment where the defect is phenotypically present. The lower neutrophil count increases the G-CSF level. The organism responds to this increase of G-CSF by reducing ε in progenitor cells (ε^G<ε lower panel). The downstream compartments are replenished and neutrophil output increases. This higher neutrophil count will decrease the levels of G-CSF; progenitor cell self-renewal decreases and the cycle repeats itself. Therapy with G-CSF ensures that neutrophil counts do not fall under a critical level.

Figure 4.

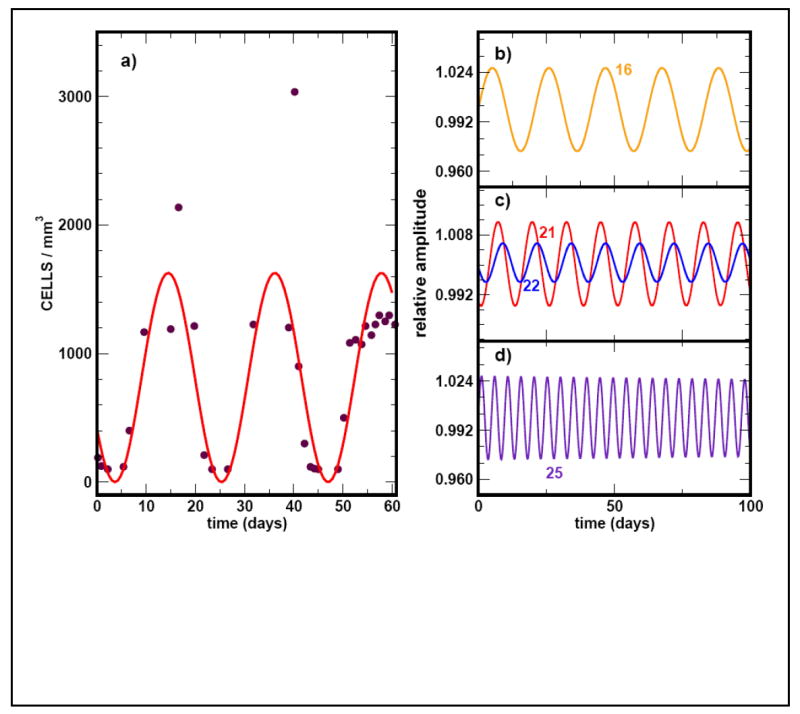
Superposition of neutrophil cycling (solid curve) as predicted by the model with experimental data taken from Hammond et al, 1989 (solid circles). The normal range for neutrophils is 1.9 − 7.0 ×10³/mm³. (A) The simulation is for a mutation that appears in compartment j = 21 with a period T = 21 days. In (B) to (D) we show simulations of the cycling frequency due to hypothetical mutations that occur in upstream (j =16) or downstream compartments (j = 25).

We performed numerical simulations to couple additional compartments downstream of compartment j where the phenotypic effect is first observed in the neutrophil lineage. All the downstream compartments also oscillate at the same frequency but with a delay such that a ‘travelling wave’ appears down the compartments. In other words, the compartments oscillate out of phase. However, the overall frequency of the oscillations is determined by the location of the compartment where the defect initially appears. If the mutation appears in compartment j < 21 or j > 21the frequency of the oscillations will decrease and increase respectively (Figure 4B to D).

DISCUSSION

Despite significant progress in elucidating the molecular biology of CN, the etiology of cycling in this disease has not been adequately explained (Horwitz et al., 2007). Here, we built on a recent multi-compartment model of hematopoiesis (Dingli et al., 2007) to propose a mechanism for explaining the cycling behaviour and a testable hypothesis for this disorder. The underlying premise is feedback regulation between consecutive compartments, a process that is widespread in physiological systems (Layton et al., 1989, von Schulthess et al., 1982, Hirayama et al., 2003). We postulate that the underlying defect in CN leads to a reduction in the self-renewal capability of cells immediately downstream of CFU-G cells i.e. myeloblasts. A reduction in self-renewal that starts in a particular compartment leads to loss of cells from that compartment that ultimately transfers fewer cells to downstream compartments with the associated reduction in granulocyte output. The body responds to the low neutrophil count with a relative increase of G-CSF (and GM-CSF). These cytokines in turn increase the self-renewal capacity of the CFU-GM, CFU-G (Barreda et al., 2004, Marley et al., 2003) and downstream compartments leading to an overall reduction in ε with an associated increase in neutrophil output. However, neutrophils express G-CSF receptors that act as sinks for the cytokine (Ericson et al., 1997). Hence, as the neutrophil count recovers, cytokine concentrations decrease and the process repeats itself, given the incapacity of ε in the original compartment to return to normal values.

It is clear that although hematopoiesis is scattered in multiple sites of red marrow, there must be significant synchronization of cell replication for cycling to be observed. Synchronization of function in the body occurs if cells are coupled together either structurally or functionally via ion channels or chemically. The separation of hematopoiesis in space excludes both structural and electrical cellular coupling leaving chemical coupling as the only alternative. Both G-CSF and GM-CSF could provide such coupling from their known biology. The reader may wonder why oscillations are not seen in healthy adults if these inter-compartment feedback loops are present. The explanation for this is that in normal hematopoiesis, there is no compartment with an abrupt loss of cells as occurs due to mutations in ELA2. It is this loss of cells that amplifies the feedback signal (G-CSF) leading to the oscillations. Under normal physiological conditions, the changes in G-CSF are small enough that the system is essentially always at a steady state. Interestingly, some patients with myelodysplastic syndrome (Abe et al., 2000) or myeloproliferative disorders develop cycling hematopoiesis as an acquired phenomenon, the latter typically after starting therapy with cytoreductive agents such as hydroxyurea (Steensma et al., 2001). These observations can be rationalized by our model since patients with myelodysplasia can have defective differentiation of cells (altered ε) with depletion of specific differentiation compartments in hematopoiesis. Hydroxyurea can reduce neutrophils and their precursors, effectively increasing the half-life of G-CSF with amplification of its circulating concentration and the onset of cycling. It would be of great interest to study the sensitivity of myeloid precursors to G-CSF in such patients.

Our model and the literature

The current model is consistent with the observations that granulocyte committed progenitor cells have a reduced responsiveness to both G-CSF and GM-CSF (Hammond et al., 1992). Both cytokines are known to play important roles on growth, survival and self-renewal of progenitor cells (Barreda et al., 2004, Marley et al., 2003). In the canine variant of the disease (grey collie syndrome), neutrophil progenitors express normal levels of G-CSF receptors (Avalos et al., 1994) and perhaps the same is true for the human disorder. However, both G-CSF and GM-CSF share downstream mediators (Barreda et al., 2004) that could be the target of the abnormal elastase produced in patients with this disease. Indeed, many mutations in ELA2 found in patients with CN lead to abnormal cytoplasmic accumulation of the enzyme (Benson et al., 2003, Kollner et al., 2006) where it may interact with second messengers involved in signalling from activated type 1 cytokine receptors.

Our model predicts that the disorder cannot arise in progenitor cells earlier than CFU-GM and contradicts other suggestions that the disorder is due to a defect at the stem cell level (Haurie et al., 1998, Colijn et al., 2005). The current model fits with the observation that mutations in ELA2 have a local effect in cells where it is expressed (Ancliff et al., 2003). In particular, Eq. (7) allows one to identify the compartment in which the coupling leads to undamped oscillations. Moreover, ELA2 is known to be expressed in cells at the myeloblasts stage (Fouret et al., 1989) which are the closest cells to CFU-GM in the hematopoietic cascade. The model is also compatible with the observation that progenitor cells can also cycle in this disorder (Brandt et al., 1975, Jacobsen et al., 1979). Cycling at the level of the CFU-GM can also explain monocyte oscillations that are observed in this disease. Monocytes are also an important source of G-CSF (Barreda et al., 2004) that can provide the necessary feedback to increase CFU-GM self-renewal with repopulation of the compartments and increased output of neutrophils. However, one may question whether our model could explain cycling in other lineages such as reticulocytes and lymphocytes. Cycling of G-CSF and GM-CSF do not only influence cells at the CFU-GM stage but can increase self-renewal and proliferation of CFU-GEMM (Barreda et al., 2004) that can lead to cells of the erythroid and megakaryocytic lineage with cycling in these cell lineages as well. Finally, G-CSF can also increase lymphocyte counts (Hareng et al., 2002) and cycling of the cytokine could lead to cycling of lymphocytes.

In the grey collie syndrome, neutrophils cycle with a shorter period than typical of the human illness. The rate of HSC replication scales allometrically with the mass of the mammal as R(M) ~ M^−¼ (Dingli et al., 2006). If the human and canine illness are both due to the same genetic problem, and the architecture of hematopoiesis is conserved across mammals (Dingli et al., 2007), allometric scaling allows us to estimate the period (T ) of the canine illness from that of humans. This is simply given by $\frac{T_{\mathit{collie}}}{T_{\mathit{human}}}={\left(\frac{M_{\mathit{collie}}}{M_{\mathit{human}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}$. Given that M_collie ~ 13kg, T_human ~ 20 days, and M_human ~ 70 kg, it follows that T_collie ~ 14 days, as observed in these animals (Haurie et al., 1998).

The proposed model is purposefully kept simple. We consider the dynamic interactions between two adjacent compartments: a normal compartment (j) where the cells do not express ELA2 and an adjacent one (j+1) where cells start to express and be affected by the mutated gene. A linear feedback mechanism between the two compartments is assumed, acting via cytokines such as G-CSF (and others) although their concentrations are not explicitly modeled. Therefore the model, in its present format cannot be used to evaluate the impact of therapies or the potential interaction between cytokines that can act together on various compartments as proposed by other investigators (Schmitz et al., 1996, Schmitz et al., 1995). Moreover, it is possible that more complex behavior, including intermittent peaks (as observed in some patients) may be due to stochastic fluctuations between multiple compartments. These details cannot be captured by our model at its current level of complexity. We also consider that the main effect of G-CSF is to enhance self-renewal of the progenitor cells (Barreda et al., 2004, Marley et al., 2003), leaving the replication rate (r) of the cells constant. Although we cannot exclude an impact of G-CSF on ‘R’, clinical and experimental observations suggest that the rapid release of neutrophils by G-CSF is due to shortening of the transit time of cells in the post-mitotic compartment rather than by accelerating the rate of replication of progenitors (Schmitz et al., 1996, Schmitz et al., 1995), implying that the effect on ε is more important than that on r. Despite its simplicity, our model makes a testable prediction: Neutrophils from patients with CN (before therapy with G-CSF) should have longer telomeres compared to age matched controls. As a corollary, therapy with G-CSF should lead to telomere shortening due to higher self-renewal of progenitors during granulopoiesis.

In summary, our linear response model suggests that one potential mechanism to explain the phenotypic effect of mutations in ELA2 in patients with CN is via a decrease in self-renewal of the late granulocyte-monocyte progenitors and myeloblasts. The effect of G-CSF feedback (in response to the low neutrophil counts) is to increase progenitor cell self-renewal and hence output of neutrophils. Scavenging of G-CSF by the increasing neutrophil count decreases the progenitor pool leading to a reduction of neutrophil output. Pharmacologic (therapeutic) doses of G-CSF increase the self-renewal of CFU-GM and downstream progenitors and increase neutrophil output. Cycling persists due to the scavenging of the cytokine by the neutrophils, the blunted sensitivity of the progenitors to this growth factor, and the persistence of the mutated ELA2 and its effect on ε in the cell compartments where it is expressed.

APPENDIX

Hematopoiesis is a multi-step process whereby cells derived from hematopoietic stem cells progressively expand and differentiate into all the circulating blood cells. Conceptually, each cell replication event is considered to be associated with a decision by the progeny cells to either remain in a given compartment or move to the next where they become more specialized. However, during normal hematopoiesis the number of cells within each compartment remains constant. Let us consider the dynamics of a specific compartment j and investigate the time dependence of the number of cells in that compartment, N_j. In keeping with the multicompartment model of hematopoiesis previously described (Dingli et al., 2007), we consider two elementary processes: differentiation, ◦ → ••, which occurs with probability ε and self renewal, ◦ → ◦◦, that occurs with probability 1 − ε. The symbol ◦ denotes a cell that stays in compartment j while the symbol • describes a cell that moves to compartment j + 1 (Figure 1). The behaviour of each cell during any division is stochastic in nature (Gordon et al., 1994, Abkowitz et al., 1996) although the net effect is such that cells tend to differentiate rather than self-renew (1 > ε > 0.5), compatible with the view of hematopoiesis as a linear process with net cell flow from HSC to the circulating compartment (Donohue et al., 1958, Cronkite et al., 1964, Finch et al., 1977). Within compartment j, the rate of cell differentiation and transfer into compartment j + 1 is μ_j = r_j (2ε −1) (Dingli et al., 2007). This loss of cells is compensated by the injection of cells from the upstream compartment, taking place at a rate λ_j−1 = r_j−12ε (Figure 1). Consequently, we may readily write down the equation for the time dependence of the number of cells in compartment j:

$$\frac{{\mathit{dN}}_j}{\mathit{dt}}=-{\mu }_j{N}_j+{\lambda }_{j-1}{N}_{j-1}$$ (1)

The stationary solution for Eq. (1) is given by

$$N_j^{\ast }=\frac{1}{2\epsilon }{C}^j{N}_0\mathrm{where}C=\frac{2\epsilon }{R(2\epsilon -1)}>0\mathrm{and}R=\frac{r_{j+1}}{r_j}$$ (2)

Equations (1) and (2) hold for all compartments with 1 ≤ j ≤ K = 31. In the multi-compartment model, N₀ ~ 400 cells and represents the active hematopoietic stem cell pool that remains constant during adult life (Buescher et al., 1985, Dingli et al., 2006, Dingli et al., 2007). We have previously shown that the values of ε and r are robust with respect to changes in the number of active stem cells (N₀) across 4 orders of magnitude and can be considered as characteristics of normal hematopoiesis (Dingli et al., 2007).

Let us investigate how the time dependence of N_j is affected by small deviations from its stationary value. The dependence of both coefficients of equation (1) on ε makes it natural to expect that ε may be involved in the response of the hematopoietic system to external perturbations. Let us assume that, due to a mutation in ELA2 there is a small deviation of the size of the cell population N_j in a specific compartment j with respect to its stationary value (N_j*), Eq. (2). To first order we may write for the changes in the rate coefficients

$$\begin{array}{c}{\stackrel{\sim }{\mu }}_{j-1}(N_j)={\mu }_{j-1}+a·n_j\\ {\stackrel{\sim }{\lambda }}_{j-1}(N_j)={\lambda }_{j-1}+a·n_j\end{array}$$ (3)

where n_j = N_j* − N_j, and a > 0 is a parameter that describes the strength of the response (Figure 3). Such response mechanisms can in principle alter either r_j or ε but the effect is such that whenever N_j decreases, there is an increase in the transfer of cells from compartment j − 1 to j. This is based on the well established principle of feedback that occurs in many physiological processes including hematopoiesis (Layton et al., 1989, von Schulthess et al., 1982, Hirayama et al., 2003). In the absence of data suggesting a more complex feedback process, we consider a linear mechanism since it is the simplest. For two consecutive compartments, we may write

$$\frac{d}{\mathit{dt}}\left(\begin{array}{c}{n}_{j-1}\\ n_j\end{array}\right)=\left(\begin{array}{cc}-{\mu }_{j-1}& -\stackrel{\sim }{a}\\ {\lambda }_{j-1}& -{\mu }_j+\stackrel{\sim }{a}\end{array}\right)\left(\begin{array}{c}{n}_{j-1}\\ n_j\end{array}\right)$$ (4)

where ã = aN_j−1*. Depending on the nature of the eigenvalues of the matrix in Eq. (4), several types of behaviour are possible. Here we are interested in exploring the possibility of sustained (undamped) oscillations. These will be present whenever the eigenvalues x_1,2 are purely imaginary. They can be readily computed as

$$x_{1,2}=\frac{\stackrel{\sim }{a}-{\mu }_{j-1}-{\mu }_j\pm \sqrt{-{\mathrm{\Omega }}_j}}{2}$$ (5)

with Ω_j = 4ãλ_j−1 −(μ_j−1 − μ_j+ ã)².

Whenever ã = μ_j−1+μ_j, the real parts of the eigenvalues vanish, with Ω_j reading

$${\mathrm{\Omega }}_j=4r_1^2{R}^{2j-4}(2\epsilon -1)(2\epsilon R+1)>0.$$ (6)

Hence, oscillations will persist without damping at a frequency given by

$$\nu =\frac{\sqrt{{\mathrm{\Omega }}_j}}{4\pi }$$ (7)

In other words, we have established a relationship between the frequency of the oscillations and the compartment location. For the convenience of the readers, a summary description of all the parameters used in the model is provided in Table 1.

Table 1.

Summary of the parameters used to describe the model of hematopoiesis and cyclic neutropenia

Parameter	Description
ε	Self-renewal probability of hematopoietic cells
R	Ratio of cell division rates in adjacent compartments
rj	The rate of replication of cells in compartment j
Nj	The number of cells in compartment j
μj	The rate of net loss of cells from compartment j to j + 1
λj−1	The rate of cell gain from compartment j − 1 to j
a	Factor by which compartment j-1 increases input to compartment j in response to a decrease in Nj
ν	Frequency of the oscillations as a function of the compartment where they arise
Ωj	Summary variable that is a function of r, ε and j