Resilience in mathematics after early brain injury: The roles of parental input and early plasticity

Abstract

Children with early focal brain injury show remarkable plasticity in language development. However, little is known about how early brain injury influences mathematical learning. Here, we examine early number understanding, comparing cardinal number knowledge of typically developing children (TD) and children with pre- and perinatal lesions (BI) between 42 and 50 months of age. We also examine how this knowledge relates to the number words children hear from their primary caregivers early in life. We find that children with BI, are, on average, only slightly behind TD children in both cardinal number knowledge and later mathematical performance, and show only slightly slower learning rates than TD children in cardinal number knowledge during the preschool years. We also find that parents’ “number talk” to their toddlers predicts later mathematical ability for both TD children and children with BI. These findings suggest a relatively optimistic story in which neural plasticity is at play in children’s mathematical development following early brain injury. Further, the effects of early number input suggest that intervening to enrich the number talk that children with BI hear during the preschool years could narrow the math achievement gap.

Introduction

Research on adults with focal brain injury is often used to understand how lesions disrupt normal functioning, and this body of work has played a role in identifying specific regions and networks that are implicated in normal functioning. By contrast, examining brain injury in children is often used to understand the extent and limits of plasticity, allowing us to see the alternative neural systems that can develop following early injury. Moreover, by examining the role of environmental inputs in supporting neural plasticity, it is possible to gain an understanding of the interplay between biological and environmental factors in development.

Previous studies have demonstrated that children with early focal brain injury (BI), unlike adults with similar lesions, show remarkable plasticity for language functions, the domain where most of the literature on this population has focused (Stiles, Reilly, Levine, Trauner & Nass, 2012). After an initial delay in the early stages of language development, children with BI, on average, perform within the normal to low-normal range on measures assessing basic vocabulary and syntactic skills (Bates & Dick, 2002; Feldman, 2005; Stiles, Reilly, Paul, & Moses, 2005; Thal et al., 1991; Rowe, Levine, Fisher, & Goldin-Meadow, 2009; Woods & Teuber, 1978). However, there is large variability within this group, with some children with BI performing below the normal range and others performing within or above this range (e.g., Demir, Fisher, Goldin-Meadow, & Levine, 2014; Sauer, Levine & Goldin-Meadow, 2010). Furthermore, children with BI are more likely to underperform on complex linguistic tasks such as telling well-structured narratives than on simpler linguistic tasks (Demir, Levine, Goldin-Meadow, 2010; Feldman, MacWhinney, & Sacco, 2002; Weckerly, Wulfeck, & Reilly, 2004; Wulfeck, Bates, Krupa-Kwiatkowski, & Saltzman, 2004), suggesting that there may be limits on plasticity after early lesions.

In contrast to these findings in the domain of language, studies of spatial development in children with early BI show deficits that largely mirror the lesion location-symptom correspondences found in brain-injured adults, albeit with more minor deficits (Stiles et al., 2005). Thus, while studies of children with early brain injury suggest a high degree of plasticity for language development, there may be a more rigid pattern of development in the spatial domain.

Although previous research has explored linguistic and spatial development in children with BI, surprisingly little is known about how early brain injury influences numerical development, another central cognitive domain. Because mathematical thinking incorporates both linguistic and spatial processes (Mix et al., 2016; Dehaene, Spelke, Pinel, Stanescu, Tsivkin, 1999), an important question is whether numerical development follows the more plastic pattern of language development or the more rigid pattern of spatial development after early brain injury.

Brain imaging studies with typically developing young babies, children and adults suggest that parietal regions are heavily involved in numerical magnitude processing across development, particularly the intraparietal sulcus [IPS] (Brannon, 2006; Cantlon, Brannon, Carter & Pelphrey, 2006; Hyde, Boas, Blair, & Carey, 2010). Beyond parietal regions, numerical processing also recruits frontal lateral temporal cortex, prefrontal cortex, and hippocampus, but investigators point out that the involvement of these latter regions intersect with domain-general processes, such as working memory (Andres, Pelgrims, Michaux, Olivier, & Pesenti, 2011; Dehaene, Piazza, Pinel, & Cohen, 2003; Menon, 2013; Lee, 2000; Prado et al., 2011; Schmithorst & Brown, 2004). Generally consistent with these imaging findings, lesions that involve the IPS as well as the left angular gyrus have been found to impair numerical processing in adults (Dehaene et al., 2003). Yet there is little known about whether early lesions to these regions differentially affect numerical development, and if so, to what extent.

In addition to brain imaging research identifying the neural correlates of numerical thinking, previous research on children’s early numerical development has highlighted the important role of math input — in particular number talk — in shaping children’s early number knowledge (e.g. Gunderson & Levine, 2011; Levine, Suriyakham, Rowe, Huttenlocher & Gunderson, 2010). Therefore, in the present study we first ask how BI and key characteristics of these lesions (i.e., lesion location, lesion type, presence of seizures) relate to children’s numerical development. We also ask how early parent number talk relates to later numerical understanding in children with early brain injury as compared to the relation of this kind of input to numerical development in their typically developing peers. That is, we ask whether number talk plays a more or less important role in supporting the foundational cardinal number concept of children with BI compared to typically developing children. By probing these relationships, we hope to shed light on the roles of both biological and environmental factors in early mathematical development.

During the preschool years, typically developing children learn the meanings of the number words (i.e. “one”, “two”, “three”, etc.) through a series of protracted steps (Wynn, 1990; 1992). First, children learn to recite a portion of the count list, e.g., numbers “one” through “ten”, but they initially do not understand what these words mean. Next children learn the meanings of the number words one at a time. They first learn what “one” means (“one-knowers”), at which point they can identify instances of one item and respond correctly to requests for one item. Several months later, children respond correctly when asked for one or two items, becoming “two-knowers”. Children then learn the meaning of three (and sometimes four), before finally coming to understand the cardinal principle, that the last number reached when counting the items in a set represents the value of that set. The whole process from first learning the count list to grasping the cardinal principle generally takes one to two years — although there is significant variability (Le Corre & Carey, 2007; Sarnecka & Lee, 2009; Wynn, 1990, 1992).

Part of this variability in learning the number words and mastering the cardinal principle may stem from differences in input children receive in the home. Levine et al. (2010) coded language during naturalistic interactions between parents and their typically developing children when the children were 14 to 30 months of age and found that parent number talk predicted children’s cardinal number knowledge at 46 months, controlling for family SES, other parent talk, and child number talk. In addition to quantity, parents differed in the types of number talk they used with their children, and these differences were also related to children’s subsequent number knowledge. For example, talking about the number of visible objects — either counting sets or labeling the cardinal value of sets — was particularly predictive of children early cardinal number knowledge (Gunderson & Levine, 2011). Consistent with these findings, another study showed that parents’ self-report of their number talk was related to children’s scores on the Test of Early Mathematics Ability — Second Edition (Blevins-Knabe & Musun-Miller, 1996).

Despite the abundance of research supporting the role of number talk in shaping children’s number development, less research has focused on biological differences that may contribute to children’s early number learning. In the current study, we extend our prior work on the role of parent number talk in children’s numerical development to examine the role of number input and biological factors in children’s numerical development. We did this by examining the lesions of children with pre- or perinatal brain injury and by coding the language that occurred during naturalistic interactions between parents and these children. In examining this group of children, we were interested in the joint roles of biological and input factors in children’s numerical development.

We were particularly interested in the plasticity of numerical development when early brain injury affected the intraparietal sulcus (IPS), a brain region that plays a role in representing and comparing approximate numerical magnitudes, dubbed the Approximate Number System (Dehaene, 1997; Feigenson, Dehaene, & Spelke, 2004). In accordance with Weber’s law this system has a ratio signature, such that the discriminability of any two quantities decreases as their ratio approaches 1:1, irrespective of their absolute magnitudes. Individual differences in the acuity of the ANS persist over time, and as early as infancy, the acuity of the ANS has been found to predict children’s math knowledge into school years (Starr, Libertus, & Brannon, 2013a; Starr, Libertus, & Brannon, 2013b; but see De Smedt, Noël, Gilmore & Ansari, 2013 and Lyons & Beilock, 2011 for contrasting views).

Research with adults has shown that damage to the IPS is associated with decreased ability to discriminate numerical magnitudes (Dehaene & Cohen, 1997) and with an increase in the presence of dyscalculia, a mathematical processing disorder (Dehaene, Piazza, Pinel & Cohen, 2003). What is currently not known is whether early damage to parietal regions implicated in this core number system affect mathematical development. Here we ask whether there is marked plasticity for numerical development when lesions occur early in life, as has been reported for language development. We also ask about the role of numerical input — particularly parent talk about number —in supporting plasticity for mathematical development in the face of early lesions as is the case for certain language development.

The current study

In the current study, we assessed the numerical knowledge of children with pre- or perinatal unilateral brain injury (BI) and that of their typically developing peers using a test of cardinal number knowledge and the Test of Mathematical Ability (TEMA-3), a standardized test of tapping the numerical aspects of math. Cardinal number knowledge was assessed using the Point-to-X task (Wynn, 1992), in which children are presented with a single image that has two sets of squares, and are asked to point to the set that represents the number “X.” This task is highly correlated with other measures of children’s cardinal number knowledge (Le Corre, Van de Walle, Brannon & Carey, 2006; Wynn, 1992). Children in our study were given the Point-to-X task at three time points (42, 46 and 50 months) because they show substantial developmental change as well as individual variability during this age range (Le Corre & Carey 2007). Measuring children’s mathematical knowledge at multiple time points also allowed us to assess the rate at which the two groups of children (i.e., BI and TD) learn the cardinal meanings of number words. We also gave children in both groups a standardized test, the Test of Early Mathematical Ability, that assesses a wide range of numerical concepts and skills when they were between 63 and 82 months of age. For both of these measures we asked how performance relates to biological and environmental factors.

Biological factors

Based on findings of adults with brain lesions, as well as the results of fMRI studies of typically developing children, we asked whether children with early focal lesions that involve the parietal lobe show slower development of cardinal number knowledge than typically developing children as well as than children whose lesions do not involve this region.¹ We also asked whether the development of cardinal number knowledge is affected by other lesion characteristics such as lesion laterality (right hemisphere or left hemisphere), lesion type (periventricular [PV] versus cerebral infarction [CI]), and seizure history.

Environmental factors

We also asked how environmental factors, specifically parental talk about numbers, predicts children’s mathematical development in children with early brain injury and typically developing children. We examined instances of parent number talk in naturalistic interactions that were videotaped every four months between child-ages 14 to 30 months. Parents were not told that the study would be investigating talk about numbers, math, or counting, but rather would be about language development more broadly, which in fact was the case. Although the question of how parent number talk relates to later number knowledge has been investigated in the typically developing children included in the current sample (Levine et al., 2010), there is no research addressing the role of parental input for children with early brain injury. We have found that parental language input might play a differentially important role in development for children with early brain injury in certain aspects of language development. For example, certain aspects of parent linguistic input, like decontextualized speech, are more predictive of the language development of children with BI compared to their typically developing peers (Demir, Heller, Goldin-Meadow and Levine, 2015). These findings raise the possibility that parent number talk may be more related to number development in children with BI than for TD children, helping to compensate for the negative effects of early brain injury. Alternatively, parent number talk might be less related to number development for children with BI, perhaps because their lesions limit their ability to profit from this input. Finally, it is possible that input may relate similarly to number development in the two groups.

Understanding the answers to these questions will begin to illuminate the contributions of biological factors and environmental factors (i.e., parental input) to the development of number knowledge and will contribute to our understanding of how children with pre- and perinatal stroke develop knowledge of this critical academic domain. In sum, to better understand how BI affects numerical cognition, the current study 1) compares the number development of typically developing children and children with BI, examining the role of lesion characteristics, 2) investigates the relation between children’s number development and the quantity of number input they receive from their parents, asking whether the role of input differs depending on lesion status.

Methods

Participants

Typically developing [TD] children²

Sixty typically developing (TD) children (N = 29 female) and their primary caregivers (53 mother only, 1 father only, 6 dual parent) participated in the study. Children and their parents were drawn from a sample of 66 children participating in a larger, longitudinal study of the language development of children in the greater Chicago area. Because the study was about language development, all interested families were screened to ensure that the child was being raised in a monolingual, English-speaking home. Parent-child dyads were initially recruited when the child was 14 months old, and families were subsequently visited in their homes every four months. All participants were recruited from the Chicago area via mailings to families in targeted zip codes and via an advertisement in a free parent magazine. Interested families were interviewed and the sample was selected to represent the socioeconomic diversity of the Chicago area. In the current study on math development, dyads were included if the family had at least one visit between child ages 14 to 30 months and if the child completed the outcome task of interest (Point-to-X) at least once between 42 and 50 months. Six of the 66 children were removed from the current sample due to missing Point-to-X data within the 42–50 month age range.

Children with pre- or perinatal unilateral brain lesion

Thirty-one children with pre- or perinatal brain lesions (N = 18 female) and their primary caregivers (23 mother only, 7 dual parent, 1 grandparent) were drawn from a sample of 44 families of children with early brain injury (BI) participating in the same longitudinal language study described above. We recruited children with BI by contacting pediatric neurologists in the greater Chicago area and establishing relationships with parent support groups in the area (Childhood Stroke and Hemiplegia Connections of Illinois, CSHC; Pediatric Stroke Network, PSN; and Children’s Hemiplegia and Stroke Association, CHASA). All interested families were included in the larger longitudinal study if the child had a unilateral, pre- or perinatal brain injury and was being raised in a monolingual, English-speaking home. Dyads were included in the current study if the family had at least one visit between child ages 14 to 30 months and if the child completed the Point-to-X at least once between 42 and 50 months. Because of the challenges of recruiting this special population, not all children in the early BI group entered the study at 14 months. Of the 31 children included in the study, thirteen children entered at 14 months of age, 5 children entered at 18 months, 7 children entered at 22 months, 4 children entered at 26 months, and 2 children entered at 30 months. Thirteen of the original 44 children with BI were not included in the current analyses – 10 were missing all home visits between 14 and 30 months of age because the child was recruited after 30 months of age, and 3 subjects did receive a home visit but were not administered the Point-to-X task at any time between 42 and 50 months of age.

Group comparison

We measured socioeconomic status (SES) in terms of years of education of the primary caregiver and family annual income level. For both measures, data were collected categorically from parents via a questionnaire. Categorical income information was transformed into a continuous scale by using the midpoint of each provided category on the questionnaire (e.g., the category $15,000 – $35,000 was scored as $25,000). Parental education was also collected from this sample, and transformed from a categorical into a continuous scale by using an estimate of the total number of years of schooling (e.g., “high school or GED” was scored as 12 years, “Bachelor’s degree” as 16 years, etc.). See Table 1 for a summary of the group comparisons for income and education.

Table 1.

Income and Parental Education of Participant Families

Category	BI Average	BI Range	TD Average	TD Range	Group Comparison
Income (in USD)	85,167 (SD = 18,557)	<15,000 – 100,000+	63,500 (SD = 30,974)	<15,000 – 100,000+	t(88) = 3.52, p < .001
Education (in years)	15.9 (SD = 1.9)	12–18	15.7 (SD = 2.2)	10–18	t(88) = 0.42, p = .68

Notes. BI = brain injured; TD = typically developing; USD = United States Dollars.

Because parent education and income were correlated (r = .39, p < .001), we combined them into one variable of SES using Principle Components Analysis. The first principle component weighted education and income positively and equally and accounted for 69 percent of the original variance. The mean score of the composite is 0 (SD = 1). Families that score high on the SES composite have high annual income levels and the primary caregiver has a high level of education.³ This single SES factor was used in subsequent analyses.

In addition, the BI group was not as racially diverse as the children in the TD group. Based on parental report, of the 60 included TD children, 36 children were Caucasian, 10 were African-American, 7 were White Hispanic/Latino, and 7 were mixed race/ethnicity. Of the 31 included children with BI, 28 children were Caucasian, 1 was White Hispanic/Latino, and 2 were mixed race/ethnicity.

Coding brain lesion characteristics in children with BI

We obtained lesion information from clinical MRI films or medical reports provided by families for 16 of the children with BI. For the remaining 15 children, MRI studies were conducted as part of the broader longitudinal (5 children were scanned using a 3-tesla GM Scanner at the University of Chicago when they were 5 years of age or older, 7 children were scanned using a 3-tesla Siemens Scanner at Northwestern University when 10 years or older, and 3 at both time points). All scans were evaluated by a pediatric neurologist and a neurologist who coded lesions according to size, location and type. The lesion characteristics we considered in our analysis were lesion size (categorized as small, medium and large), lesion laterality (left, right), lesion type (periventricular [PV] or cerebral infarction [CI]), and involvement of the parietal lobe (+/−). We also considered seizure history.

Cerebral infarcts (CIs) impinged on middle cerebral artery territory and tended to affect the inferior frontal, parietal and/or superior temporal regions. Periventricular lesions (PV) primarily affected subcortical white matter tracts, the thalamus, basal ganglia and/or the medial temporal lobe. All children with PV lesions showed evidence of subcortical injury, enlarged ventricles or reductions in white matter tracts (especially the internal capsule). Lesions were categorized as small, medium, or large in size. Small lesions affected only one lobe or minimally affected subcortical areas. Medium lesions affected more than one lobe or subcortical region. Large lesions affected three or four lobes and often involved the thalamus and subcortical regions – these lesions were typically CIs. We categorized children with small and medium legions into a single group to increase our power and because previous analyses showed that the two groups did not differ from each other on a number of language measures (Brasky, Nikolas, Meanwell, Levine, & Goldin-Meadow, 2005). Children were categorized as not having recurrent seizures (no seizure or a single febrile seizure early in life) or as having recurrent seizures (treated with anticonvulsant medications).

Each child’s lesion characteristics are reported in Table 2. There was no significant association between lesion laterality and type, χ² (1, n = 31) = .79, p > .10, or lesion laterality and size, χ² (2, n = 31) = 1.63, p > .10. However, lesion type and size were significantly related, χ² (1, n = 31) = 10.72, p = .001. Thirteen out of 14 (93%) children with CI had large lesions, whereas only 6 out of 17 children with PV had large lesions (35%). Seizure history was not related to lesion laterality, χ² (2, n = 31) = .39, p > .10, size, χ² (2, n = 31) = .69, p > .10, but it was significantly related to lesion type, χ² (2, n = 31) = 5.13, p = .02. Eleven out of 13 children (83%) with a positive seizure history had CI lesions, whereas only 8 of 18 children (42%) with no seizure history had CI lesions. Given the correlation between lesion type and size and to reduce the number of analyses we ran, our analyses included only lesion type, lesion laterality, whether or not there was involvement of the parietal lobe, and whether or not the child had a history of seizures.

Table 2.

Lesion Characteristics of Children with Pre- or Perinatal Brain Injury

ID	Gender	Side	Type	Size	Areas affected	Seizure history
1	F	LH	CI	Large	F, T, P, O, S	No
2	F	LH	PV	Medium	S	No
3	F	RH	CI	Large	F, T, P, S	Yes
4	M	RH	PV	Small	S	Yes
5	F	RH	PV	Small	T, P, S	No
6	F	RH	CI	Large	F, T, S	Yes
7	F	LH	PV	Small	S	No
8	F	LH	PV	Large	S	No
9	F	RH	CI	Small	F, P	Yes
10	F	LH	CI	Medium	F, P, S	No
11	F	LH	CI	Large	F, T, P, S	No
12	F	RH	PV	Medium	T, S	No
13	M	LH	CI	Large	F, P, S	Yes
14	M	LH	PV	Small	F	Yes
15	F	LH	CI	Large	F, T, P, O, S	No
16	F	LH	CI	Medium	F, T, P	Yes
17	F	LH	PV	Small	S	No
18	M	LH	CI	Small	T, O, S	Yes
19	F	RH	CI	Large	F, T, P, O, S	No
20	M	LH	CI	Large	F, T, P, O, S	Yes
21	F	RH	CI	Large	F, T, P, O, S	Yes
22	F	LH	PV	Small	NA	No
23	M	LH	CI	Medium	F, T, P, S	No
24	M	RH	PV	Small	S	No
25	M	RH	PV	Small	NA	No
26	F	LH	CI	Large	F, T, P, O, S	No
27	M	LH	CI	Medium	NA	Yes
28	M	LH	CI	Large	F, T, P	Yes
29	M	LH	CI	Large	F, P, S	Yes
30	M	LH	CI	Large	NA	No
31	M	LH	PV	Small	S	No

Note. LH = left hemisphere; RH = right hemisphere; CI = cerebrovascular infarct; PV = periventricular; F = frontal; T = temporal; P = parietal; O = occipital; S = subcortical, NA= detailed lesion location information not available.

Procedure

Researchers contacted each family and scheduled home visits at the family’s convenience. At each home visit, the child and their primary caregiver were videotaped for 90 minutes. Parents were asked to interact with their children as they normally would. Typical activities included toy play, book reading and mealtime, but families were not given direction to engage in any particular activities. The current study includes parental talk from all available visits between 14 and 30 months. All caregiver speech that was directed to the target child in the videotaped sessions was transcribed. Transcription reliability was established by having a second person transcribe 20% of each transcriber’s videotapes. Reliability was established when two transcribers agreed on 95% of the utterances.

During the home visit, following the observations of naturalistic interactions, children were also administered various cognitive assessments. At ages 42, 46 and 50 months, children were given a Point-to-X number task. Forty of the 60 TD children and 19 of the 31 BI children included in this study were also given the Test of Early Mathematical Ability — Third Edition [TEMA-3] when they were between 63 and 82 months of age. This test, described in more detail below, served as an additional dependent measure of interest.

Measures

Measures of talk

Parent number word tokens

Number tokens were counted by searching the transcripts for all number words between zero and nine hundred and ninety-nine. Each instance of a number word in this range was coded as a number word token. Thus, if a parent said “four fish,” this would be coded as one number word token.⁴ If a child or parent said “one, two, three,” this would be coded as three number word tokens. Because the word “one” can be used non-numerically, all uses of the word “one” were manually coded by a research assistant as either numerical or non-numerical, and non-numerical uses were excluded from the number tokens count. A second researcher coded a random selection of 20% of the utterances and agreed on 96% of the codes.

Numerical uses of “one” included counting (e.g., “one, two, three”), references to number symbols (e.g., “the number one”), cardinal values (e.g., “there is one airplane”), a reference to time or age (e.g., “one year ago”), and uses of “one” that emphasize numerosity or individuation (e.g., “only one more,” “one at a time,” “just one”). Non-numerical uses of “one” included deictics (e.g., “which one,” “that one”), “one” as a direct object (e.g., “I want the yellow one”), and some idioms (e.g., “one of these days”).

Number word tokens were averaged across each dyad’s available sessions to form the measure of average parent number words per session. Due to scheduling conflicts and late entry into the study for some children with BI, not all families completed all 5 visits. In TD dyads, 53 families completed all 5 visits and 7 families missed 1 visit. In BI dyads, 12 families completed all 5 visits, 4 families missed 1 visit, 7 families missed 2 visits, 4 families missed 3 visits and 2 families missed 4 visits. For families with parent input data at all 5 time points, the amount of parent number talk during each of the 5 time points did not significantly differ, F(2.83, 124.58) = 2.22, p=09. Thus, we used averages of parent number tokens and non-number tokens across all available sessions rather than the total number of tokens.

Parent other word tokens

“Other talk” consisted of the word tokens per session produced by the parent minus their number word tokens. We controlled for other word tokens when we examined the relationship between parent number talk and child outcome measures.

Outcome Measures

Point-to-X task

Children were administered the 16-item Point-to-X task at 42, 46 and 50 months of age. For each item, children were presented with an 8.5 × 11 inch piece of paper that had two vertically arrayed sets of squares, one on each side, separated by a vertical line. For each item, children were asked to “point to the side with X”, where X was a number between 1 and 6. The foil choice and the target differed by no more than three, and by no more than a 2:1 ratio. Children indicated their response by pointing to the set on the left side or the right side of the page. The location of the target set as well as item order was counterbalanced across children. The items administered in this test are listed in Table 3.

Table 3.

Items administered in the Point-to-X Task

Item	Target
1 vs. 2	1
1 vs. 2	2
2 vs. 3	2
2 vs. 3	3
2 vs. 4	2
2 vs. 4	4
3 vs. 4	3
3 vs. 4	4
3 vs. 5	3
3 vs. 5	5
3 vs. 6	3
3 vs. 6	6
4 vs. 5	4
4 vs. 5	5
5 vs. 6	5
5 vs. 6	6

Note. Items were presented in a single random order, and the location of the target number was counterbalanced across children.

Due to scheduling conflicts, time constraints, or lack of child cooperation, some children missed one or more sessions of the Point-to-X task. Of the 60 TD children, 53 children completed the task at all 3 time points, 6 children completed the task at 2 time points, and 1 child completed the task at 1 time point. Of the 31 children with BI, 20 children completed the task at all 3 time points, 8 children completed the task at 2 time points, and 3 children completed the task at 1 time point. Because significantly fewer children with BI completed the Point-to-X task at all 3 time points χ² (2, n = 91) = 7.75, p < .02, we used Hierarchical Linear Modeling (HLM) to analyze the data. An advantage of HLM is its flexibility in dealing with missing data (Raudenbush & Bryk, 2002).

Test of Early Mathematical Ability-Version 3 (TEMA-3)

Children also were administered Form A of the TEMA-3 (Ginsburg & Baroody, 2003) at a testing point between 63 and 82 months of age. The TEMA-3 is a standardized test of early math ability that focuses on the numerical aspects of math. It has been normed for children between the ages of 3 years 0 months and 8 years 11 months. It is composed of 72 items and takes approximately 40 minutes to administer. Forty of the 60 TD children and 19 of the 31 children with BI received the TEMA-3 between 63 and 82 months of age; children who did not receive the TEMA during this time frame either missed visits, had time constraints during visits, or were uncooperative. The average age at administration for all included data points was 70.8 months for TD children and 68.8 months for children with BI. To account for differences in age of administration, raw scores were converted into age-normed, standard scores for all subsequent analyses.

Methodological approach

The two-level model for child-specific growth

As discussed above, we used HLM to examine children’s cardinal number knowledge, i.e. Point-to-X performance between 42 and 50 months, to compare groups (TD, BI) on cardinal number knowledge growth, and to examine relations between parent number talk and children’s cardinal number growth over time.

Our statistical model has two levels: a Level-1 model that accounts for variation in repeated measures within each child; and a Level-2 model that represents variation between children.

At Level-1 (within children), we represent the trajectory of children’s cardinal number knowledge as a linear model. For each child I at time t, we have:

$$Y_{\mathit{ti}}={\pi }_{\mathit{0}i}+{\pi }_{\mathit{1}i}\left(a_{\mathit{ti}}-46\right)+e_{\mathit{ti}}$$

In this equation, a_ti is the age of the child i at time t, π_0i is child i’s status at age 46 months, and π_1i is the child’s linear growth (velocity) at 46 months of age. The residual e_ti is the portion of child i’s cardinal number knowledge at age t not predicted by his or her age.

At Level-2 (between children), we examined whether children’s status (intercept centered at 46 months) and linear growth (velocity) on the Point-to-X task was predicted by group, SES, parent number talk and parent other talk. This provides a between-person model for each variable, in which there is a separate equation for each Level 1 coefficient, π_pi, where p = 0, 1:

$${\pi }_{\mathit{pi}}={\beta }_{p\mathit{0}}+{\beta }_{\mathit{01}}\ast \left(\mathit{SE}{S}_i\right)+{\beta }_{p\mathit{2}}\ast \left(\mathit{Grou}{p}_i\right)+{\beta }_{\mathit{03}}\ast \left(\mathit{Parent}\mathit{number}\mathit{tal}{k}_i\right)+{\beta }_{\mathit{04}}\ast \left(\mathit{Parent}\mathit{other}\mathit{tal}{k}_i\right)+r_{\mathit{pi}}$$

$$p=0,1,2,3,4$$

In this equation, π_pi is the pth growth parameter from the Level 1 model, β_p0, β_p1, β_p2, β_p3, β_p4 are linear regression coefficients, and r_pi is a random effect. We allow random effects to be correlated within children but not between children.

Results

Variation in parent number talk

Across both groups (TD and BI), there was great variability in the amount of number talk as well as other types of talk produced by parents. Parents of TD children ranged from .84 to 135.4 average number tokens per visit, with an overall average of 27.8 number tokens per visit (SD = 26.4). For non-number tokens they ranged from 713.98 to 7751.34, with an average of 3771.1 non-number tokens per visit (SD = 1,592.8). For parents of TD children, the quantity of number tokens was significantly related to the quantity of non-number tokens (r = .34, p < .01). In addition, the quantity of non-number tokens was significantly related to SES (r = .39, p < .001) and the quantity of number tokens was positively but not significantly related to SES (r = .15, p = .25).

Parents of children with BI ranged from 2 to 187.5 average number tokens per visit, with an overall average of 47.1 number tokens per visit (SD = 42.5). For non-number tokens they ranged from 1173.8 to 8,456.8, with an average of 4,393.6 non-number tokens per visit (SD = 1,526.9). In this BI group, despite a positive association, the quantity of non-number tokens was not significantly related to the quantity of number tokens (r = .21, p = .25). Among parents of children with BI, neither number tokens nor non-number tokens were significantly related to SES, (r = .16, p = .24 and r = .10, p = .60, respectively), possibly because the range of SES was relatively narrow in this group, limiting our ability to detect within group effects.

Parents of BI children produced both more non-number and number tokens than parents of TD children. However, the SES of families was higher in the BI group. Controlling for SES, parents of TD and BI children did not differ in non-number talk (F(1, 87) = 1.04, p = .31), but did significantly differ in number talk, in favor of the parents of BI children (F(1, 87) = 6.26, p = .04).

HLM Results

Modeling child Point-to-X performance growth

Our results are presented in two steps. In the first step, we use individual growth modeling (employing HLM; Raudenbush, Bryk, Cheong & Congdon 2000) to model children’s cardinal number knowledge growth between 42 and 50 months (Equation 1 above). In the next model, we incorporate predictor measures taken when the children were between 14 and 30 months (group, SES, parent number input, parent non-number input) in that growth (Equation 2 above). Table 4 presents a taxonomy of models investigating these relations.

Table 4.

Estimates of Fixed Effects, Random Effects, and Goodness of Fit for Cubic Growth Models Using Group, SES, Parent Number Word Input, and Parent Other Word Input to Predict Intercept and Change in Children’s Point-to-X Performance (n = 91)

	Unconditional model	Adding group, SES	Adding SES, number word input, other word input
	Model 1	Model 2	Model 3
Fixed Effects
Intercept	12.19*** (.27)	12.71*** (.30)	12.47*** (.31)
Linear Change	.28*** (.03)	.32*** (.04)	.31*** (.04)
Group		−1.00~ (.58)	−1.43** (.51)
Group × Age		−.13~ (.07)	−0.13~ (.07)
SES		.84*** (.25)	.52* (.23)
SES × Age		−.08** (.03)	−0.08** (.03)
Number word input			.01* (.01)
Number word input × Age			.00005 (.001)
Other word input			.0005** (.0002)
Other word input × Age			.00001 (.00002)
Random effects
Level 2
Intercept	5.78*** (2.40)	4.82*** (2.20)	3.95*** (1.99)
Linear Change	0.01 (.11)	.02 (.12)	.02 (.15)
Goodness of fit −2 log likelihood	1211.46 (4)	1124.60 (4)	1160.67 (4)

Note. SES = socioeconomic status.

^~p < .10.

^*p < .05.

^**p < .01.

^***p < .001

To obtain the best fitting Level 1, or within-person, model for cardinal number knowledge data, we examined empirical plots of all children’s cardinal number knowledge between 42 and 50 months. We fit a linear growth model to the data because it had a lower goodness-of-fit statistic (−2 log likelihood) than a quadratic model and because the plot of the linear model best mirrored the plot of the empirical data. All models were fit using heterogeneous sigma squared, meaning that the variation in children’s number knowledge was allowed to vary over time, and age was centered at 46 months, the midpoint of the Point-to-X data. We looked at fixed effects with robust standard errors. Model 1 in Table 4 is the unconditional linear growth model. This linear model shows that at 46 months, children have an estimated Point-to-X score of approximately 12.19 (max score 16; 76.2% correct), with an estimated increase in score of .28 points per month (or 1 point per 3.6 months) at this age.

Predictors of Point-to-X growth: Group differences

In the next model we evaluate the role of group (TD, BI) in cardinal number knowledge growth, controlling for SES (see Table 4, Model 2 and Figure 1 for histogram of raw data). We find that, when we control for SES, group has a marginal effect on intercept (p = .09), such that children with BI perform marginally worse than TD children on the Point-to-X task at 46 months. Group also has a marginal effect on linear growth (p = .07), such that the Point-to-X scores of children with BI increase at a marginally slower rate than the scores of TD children between 42 and 50 months of age. To better interpret the gap, we calculated the mean difference between TD children and children with BI’s performance on the Point-to-X task in terms of standard deviation differences. At 42 months, children with BI were .18 SD below the TD children (.13 SD controlling for SES), at 46 months children with BI were .15 SD below the TD children (.32 controlling for SES) and at 50 months the difference was .65 SD (.60 controlling for SES) — which is in line with the HLM analysis showing a positive effect of Group on slope.

Figure 1.

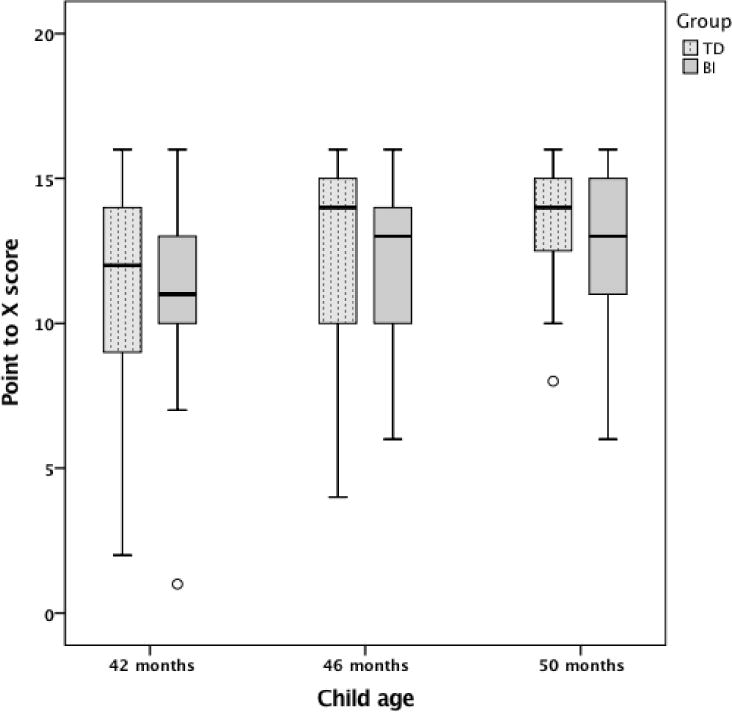
Point-to-X score as a function of group (TD, BI).

Note. The bottom of the box indicates the 25^th percentile and the top of the box represents the 75^th percentile. Whiskers represent 1.5 times the interquartile range. Outliers are cases with values between 1.5 and 3 times the interquartile range. There were no extreme values that fell beyond 3 times the interquartile range.

Predictors of Point-to-X growth: Early parent input (14 – 30 months)

In the final model, Model 3, we add parent number tokens and other word tokens as predictors. We find that, controlling for parent other word tokens, parent number tokens are a significant predictor of intercept (p < .05), but not of linear growth (p = .97). This means that overall, children with parents who say more number words perform better on the Point-to-X task than children with parents who say fewer number words on average at 46 months of age. However, parent number word input does not significantly influence the rate at which children’s scores change on this test between 42 and 50 months of age. When controlling for SES and parent number word input, group is a significant predictor of the Point-to-X intercept at 46 months (p < .01) and is marginally predictive of slope (p = .08). This means that children with BI performed significantly worse than TD children on the Point-to-X task at 46 months of age, with a marginally significant group difference in the rate at which the scores of children in the two groups change over time such that children with BI grow marginally more slowly. The estimated growth in Point-to-X scores as a function of group (TD, BI) and parent number input (high, low) is shown in Figure 2, where we plot hypothetical growth trajectories based on parent number input (1 SD below the mean, 1 SD above the mean) and group (TD, BI), holding other factors (SES, parent other word tokens) constant at their mean.

Figure 2.

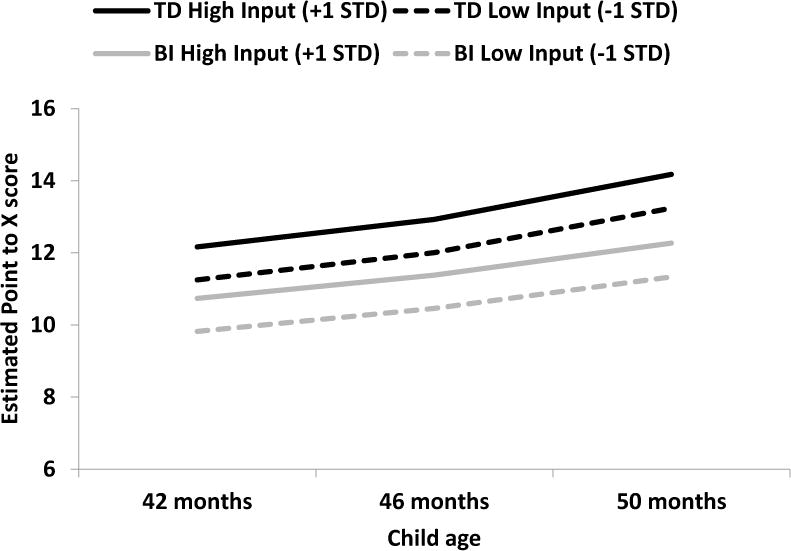
Estimated growth in Point-to-X performance as a function of group (TD, BI) and parent number input (high, low).

Note. High input represents input one standard deviation above the mean and low input represents one standard deviation below the mean.

Predictors of Point-to-X growth: Lesion characteristics

In subsequent models, we included lesion location laterality, lesion type, involvement of the parietal lobe, and seizure history as Level 2 predictors in separate models. Lesion laterality did not influence children’s Point-to-X scores. Intercepts were not significantly different for children with left versus right hemisphere lesions (p > .5), and neither group differed compared to their TD peers (p = .17 in each case). Slopes also were not significantly different for children with left versus right hemisphere lesions (p > .5), and neither group differed from TD children (p = .13 and p = .12, respectively). The presence of a parietal lesion also did not influence the intercept (p = .20) or slope (p = .28) of children’s Point-to-X scores. However, lesion type did influence Point-to-X scores. Children with CI lesions had significantly lower intercepts than TD children (p = .05) and significantly slower growth than TD children (p = .04) whereas children with PV lesions did not significantly differ on intercept (p = .89) or slope (p = .66) from TD children. Further, children with CI lesions had marginally lower intercepts (p = .09) and marginally shallower growth (p=.09) than children with PV lesions. The intercept for the children who experienced seizures differed from TD children (p < .05), and those with seizures had shallower growth than TD children (p < .01). Further, children who experienced seizures had a marginally significantly lower intercept (p = .08) and shallower growth (p = .04) than their peers with BI who did not experience seizures.

Role of the intraparietal sulcus

We examined involvement of the intraparietal sulcus [IPS], a region of the parietal lobe that is known to be involved in numerical processing, to explore whether damage to the IPS was specifically predictive of low performance on the Point-to-X task. We did a qualitative analysis on the 8 children in our BI group with parietal damage for whom we had detailed structural scans. The remaining 8 children with parietal damage had only clinical MRI films or medical reports provided by families. Of the 8 children examined, 6 had damage in the IPS, 2 did not have damage in the IPS. Although the small numbers and heterogeneity in their lesion characteristics do not allow us to draw definitive conclusions, comparisons across two key groups (children with no parietal damage, n = 16 and children with parietal damage involving IPS, n = 6) suggest that the average performance across the three visits was similar across the groups (12.01 and 11.6, respectively). In addition, the range of performance overlapped between children who had IPS damage (range: 7–16) and children who did not have any parietal damage (range: 6–16). In summary, though our sample does not allow us to make definitive conclusions, these data do not suggest that IPS damage is a strong predictor of Point-to-X performance.

Performance on Test of Early Mathematical Ability (TEMA)

In addition to examining performance on the Point-to-X task, we examined children’s performance on the Test of Early Mathematical Ability, Version 3 [TEMA-3]. One potential issue with the Point-to-X assessment is that group differences may have been underestimated, as a number of children, particularly in the TD group reached ceiling performance by the final session at 50 months (13 of the 56 TD children compared to 4 of the 29 children with BI). The intent of including this secondary dependent measure was to address this issue, and to examine our hypotheses using a broader, standardized measure of numerical understanding. Forty of the 60 TD children and 19 of the 30 children with BI were administered this test between the ages of 5 and 7 years. Of note, children who were administered the TEMA-3 versus did not differ in their previous Point-to-X scores from those who were not administered the TEMA (42 months, F(1,68) = .01, p > .10, 46 months, F(1,68) = .51, p > .10, or 50 months, F(1,68) = .53, p > .10 months).

On average, children with BI performed marginally lower on the TEMA than their TD peers (t(57) = 1.7, p = .09; M_BI = 97.2, SD = 17.04, Range = 62 to 122; M_TD = 105, SD= 15.9, Range 67–137). Children with BI were .49 SD behind their TD peers (.59 controlling for SES). The marginal group differences became statistically significant when controlling for parental SES, F(1, 56) = 4.49, p = .04, parental SES, parent number talk, and parent other talk, F(1, 54)= 5.04, p =.03, and parental SES, parent number talk, parent other talk, and age of child at the time of the TEMA test, F(1, 53) = 7.52, p < .01. However, controlling for parental SES and parent other talk, parent number talk at the five sessions between 14 and 30 months did not predict TEMA scores within the BI or TD groups, p >.10.

Children’s TEMA scores were significantly correlated with their Point-to-X scores at ages 42 months, r = .55, p <.01, 46 months, r = .36, p <.01, and 50 months, r = .52, p < .01. It is also important to note that despite group differences, only 4 of the children with BI performed more than 2 standard deviations below the TD mean and only 1 TD child and 2 children with BI performed 2 standard deviations below the mean of the normative sample (100). Performance on TEMA did not differ by laterality, t(17) = .41, p = .11, seizure, t(17)=.88, p =.39, lesion type, t(17) = .42, p =.68, size t(17)=.42, p=.68, or involvement of parietal damage t(17)=.66, p=.51.

Thus, analysis of performance on the TEMA-3 suggests that the group differences reported here are not unique to the Point-to-X task — children with early BI show a modest but not devastating effect of early brain injury on later mathematical understanding. These findings indicate that children with BI are slightly behind in the numerical aspects of math at least through kindergarten. Furthermore, the analyses suggest that children’s performance on the Point-to-X task is meaningfully correlated with a standardized measure of numerical mathematical ability between 63 and 82 months of age.

Discussion

In this study, we compared the mathematical development of children with pre- or perinatal brain injury to that of typically developing children. Specifically, we assessed children’s cardinal number knowledge with the Point-to-X task over three time points between 42 and 50 months, and their number-related mathematical ability using a standardized test, the TEMA-3, between 63 and 82 months of age. To our knowledge, neither numerical understanding nor rate of improvement on numerical understanding has been characterized in children with BI. Additionally, we examined the relation of early parent number talk in children’s level of skill, asking whether this input plays a more (or less) important role in the development of mathematical skills in the group of children with early BI than in typically developing children.

Our analyses revealed that children with early BI scored lower on the Point-to-X task at 46 months, controlling for family SES, parent number talk, and parent other talk. Moreover, we found that children in the BI group learned the cardinal meanings of number words more slowly than their TD peers. These findings suggest that children with early focal lesions may be delayed in getting symbolic number skills off the ground, mirroring findings on language development (Bates & Dick, 2002; Stiles et al., 2012). In addition, compared to TD children, children with BI appear to continue to learn the meaning of number words at a marginally slower rate than their typically developing peers, and perform worse on a standardized test of mathematical ability administered in early elementary school.

Despite these delays, our findings support the claim that early mathematical development, like early language development, is resilient following lesions that impinge on areas of the brain that lead to marked deficits when brain injury occurs later in life. Further, the specific lesion-deficit mappings that are apparent after later lesions are not apparent following early brain injury for either language or number. In this regard, these skills differ from spatial functions, which show similar patterns of deficit, regardless of the timing of lesions. Interestingly, both language and number domains, unlike the spatial domain, involve symbol systems that emerged relatively late in evolutionary time, raising the possibility that more recently developed capacities are more plastic (Stiles et al., 2005).

To further understand the group differences in numerical development between children with early brain injury and TD children, we investigated the role of other factors that are known to be related to children’s early number knowledge: family SES and parental number talk. First, we extended previous research that demonstrated a relation between parent number talk and children’s number knowledge (e.g. Levine et al., 2010) to children with BI. As is the case with parents of TD children, we found marked variability in the frequency of parent number talk when children were between 14 and 30 months of age. We also found that on average, even when controlling for SES and amount of non-number related talk, parents of children with BI used significantly more number words with their children than the parents of TD children in our sample. It is possible that parents of children with BI may have provided more number talk to their children because they were aware of the potential for deficits and were trying to support their children’s mathematical development to compensate for this potential.

We also controlled for both parental number talk and non-number related talk in examining group differences in outcomes. When doing so, we found children’s number knowledge, as measured by the Point-to-X task differed by group, with children with BI performing lower both measured by intercept and rate of growth. These results were mirrored in the TEMA-3, where controlling for parents’ number talk strengthened the observed effect of brain injury on TEMA-3 performance. There are two important implications of this finding. First, the greater proportion of number talk provided to children with BI (or another factor related to number talk) may have reduced the discrepancy in numerical skills between children with BI and TD children. Given the difference in number talk provided to the children in our two samples, initial analyses of both Point-to-X and TEMA-3 likely underestimated the effect of BI on children’s early number development. Second, these findings indicate that parent input related to the number development of children with early BI (as is the case with TD children). Notably, we found that parent number talk was predictive of performance on the Point-to-X task in both groups, with no significant difference in the magnitude of this effect. We did not find that parent number talk was predictive of TEMA-3 performance in either the children with BI or TD children, likely because parent number input was measured less closely in time to the administration of the TEMA-3 task. In addition, school math input may have played a larger role by this time point. An open question is whether later parent mathematical input or practice at home would predict TEMA-3 performance within each group.

Supporting claims about the plasticity of the young brain with respect to symbolic numerical development, we found no effects of the location of children’s BI on their performance on the Point-to-X task or the TEMA-3. In contrast, adults who suffer BI often do show deficits in mathematics performance depending on the location of their injury (Dehaene et al., 2003). Not surprisingly, CI lesions, which tend to be larger and involve more brain area than PV lesions, were associated with poorer performance on the Point-to-X task than PV lesions. It is of note that in the current dataset children with CI lesions were more likely to have a history of recurrent seizures and to be taking anti-convulsant medications, making it difficult to isolate which factor or factors contribute to the lower math scores of these children — lesion type, seizures, and/or the medications children with seizures are taking. Nevertheless, the lesion type/size effects found and the notable lack of lesion location effects mirror prior findings on the language development of this population (Bates & Dick, 2002; Feldman, 2005; Stiles et al., 2005; Thal et al., 1991; Woods & Teuber, 1978). Thus, the young brain appears to be better able to compensate for the kinds of lesions that disrupt mathematical functioning in adults, as demonstrated by the capacity to develop numerical ability in the low normal to normal range even when lesions impinge on brain regions known to be involved in representing and comparing approximate numerical magnitudes. Nonetheless, the plasticity that occurs when lesions are smaller does not seem to extend to larger CI lesions, possibly because large lesions reduce the capacity to form the long range neural connections that are involved higher order cognitive skills (Banich, Levine, Kim, & Huttenlocher, 1990; Booth et al., 2000; Brasky et al., 2005; Levine, Brasky, & Nikolas, 2005; Levine, Kraus, Alexander, Suriyakham & Huttenlocher, 2005; Stam, 2014).

While the group differences reported here were not very pronounced, future work is needed to investigate whether the slower learning observed in children with BI, and the significantly lower scores on a standardized test of numerical ability in early elementary school, have compounding downstream consequences for higher-level math learning. It is possible that children with BI will either catch up to their peers, or fall further behind on even more complex mathematical tasks, as they do on certain complex linguistic tasks such as telling well-structured narratives (Demir et al., 2010; Feldman, MacWhinney, & Sacco, 2002; Weckerly, Wulfeck, & Reilly, 2004; Wulfeck et al., 2004).

Studying children with early brain injury is an important tool in furthering our understanding of the plastic nature of the developing brain, particularly if we examine the development of these children not only with respect to the nature of their lesions but in relation to the environmental supports they receive for developing particular skills. The current investigation takes this approach with respect to early mathematical development, examining the relation of lesion characteristics and early parent number talk to children’s early understanding of cardinal number and their performance on a standardized test assessing numerical aspects of math. Our findings offer an overall positive story of neurological plasticity and development. While children in our sample were delayed in their cardinal number understanding, showed slower learning rates compared to TD children, and had lower scores on the TEMA-3, the differences were not dramatic and there was a strong overall effect of parental number talk, similar to that observed in TD children. These findings suggest that nurture can have powerful remedial effects against the set-backs of nature. Future work is needed to systematically examine the limits and extent of plasticity for mathematical development following early focal brain injury, and the extent to which environmental supports at home and at school can be leveraged to close existing knowledge gaps.