Abstract
This is a letter to the editor clarifying the meaning of the generalizability-theory based coefficients reported in our multisite reliability study of fMRI measures of regional brain activation during an emotion processing task (Gee et al., Human Brain Mapping 2015;36:2558–2579). While the original paper reported generalizability and dependability coefficients based on the design of our traveling subjects study (in which each subject was scanned twice at each of eight sites), those coefficients are of limited applicability outside of the reliability study context. In this letter, we report generalizability and dependability coefficients that represent the reliability one can expect for a multisite study in which a given subject is scanned once on a scanner drawn randomly from the pool of available scanners (i.e., analogous to the more typical multisite study design). We also characterize the implications of a multisite versus single-site study design for statistical power, including a figure that shows sample size requirements to detect activation in two key nodes of the emotion processing circuitry given observed differences in reliability of measurement between single-site and multisite designs.
We take this opportunity to clarify the meaning of the statistics reported in our study examining reliability of fMRI measures of brain activation during an emotion processing task (Gee et al., 2015) and to consider their implications for statistical power in single-site versus multisite designs.
In our report, we used a variance components framework and an application of generalizability theory (Shavelson and Webb, 1991) to probe the robustness of such measures in a multisite context. Given the design of our study, in which eight human subjects were scanned twice on successive days at each of eight sites, the proportion of variance due to person from the variance components analysis (shown in Figure 3 in Gee et al., 2015) represents the reliability one can expect in a typical multisite study where subject measurements are based on single-session fMRI data, each acquired on different scanners depending on the site where the subject was recruited. We wish to make explicit that in applying generalizability theory, we estimated reliability by calculating generalizability and dependability coefficients for a study design corresponding to the design of the full traveling subject study, thus reflecting the reliability in relative and absolute measurement, respectively, that one can expect when every subject is scanned twice on each of eight different scanners. The corresponding generalizability and dependability coefficients (shown in Figure 4 and cited in the Abstract in Gee et al., 2015) ranged from 0.0 to 0.9 for maximum activation across multiple task contrasts and regions of interest, but were generally at or above 0.5, as would be expected when each subject’s measurement is based on the aggregation of sixteen scan sessions. Thus, the coefficients reported apply to the reliability of the measures from the reliability study itself, that is, for task-induced brain activations resulting from analysis of the eight traveling subjects’ fMRI data considered in aggregate across their sixteen scan sessions. Clearly, however, such a design is highly unlikely outside of a reliability study context, and so the reported generalizability and dependability coefficients are of limited applicability, a point that should have been made explicitly in the original paper. As shown in the table, below, when using generalizability theory to model the reliability one can expect when a given subject is assessed on one occasion at a site/scanner drawn randomly from the set of all available sites/scanners, the generalizability and dependability coefficients are more modest (i.e., ranging from 0.0 to 0.38 for maximum activation across the multiple task contrasts and regions of interest) and, in the case of the dependability coefficients, identical to the proportions of the total variance attributable to person from the variance components analyses (as reported in Figure 3 of Gee et al., 2015). Indeed, under these assumptions, these two reliability formulations are mathematically equivalent.
Table.
Generalizability (G-coefficients) and dependability (D-coefficients) estimates of relative and absolute measurement reliability, respectively, for a multisite study design in which each subject is studied on one occasion at a site/scanner drawn randomly from the set of all available sites/scanners, as well as average within-site (test-retest) intraclass correlations (ICCs), for maximum percent signal change in fMRI contrasts and regions of interest and for behavioral measures of emotion processing.
| Contrast of interest | Region of Interest/Measure | G-Coefficient | D-Coefficient | Within-site ICC |
|---|---|---|---|---|
| Emotion processing task1 relative to resting baseline | Left inferior frontal gyrus | 0.27 | 0.27 | 0.40 |
| Right inferior frontal gyrus | 0.15 | 0.15 | 0.25 | |
| Left amygdala | 0.13 | 0.12 | 0.31 | |
| Right amygdala | 0.26 | 0.23 | 0.25 | |
| Left amygdala habituation | 0.04 | 0.04 | 0.23 | |
| Right amygdala habituation | 0.00 | 0.00 | 0.06 | |
| Left anterior cingulate cortex | 0.23 | 0.20 | 0.34 | |
| Right anterior cingulate cortex | 0.14 | 0.12 | 0.27 | |
| Left insula | 0.20 | 0.19 | 0.26 | |
| Right insula | 0.26 | 0.25 | 0.29 | |
| Left fusiform gyrus | 0.20 | 0.18 | 0.28 | |
| Right fusiform gyrus | 0.36 | 0.36 | 0.43 | |
| Emotion processing task1 relative to active control condition2 | Left inferior frontal gyrus | 0.23 | 0.23 | 0.42 |
| Right inferior frontal gyrus | 0.17 | 0.17 | 0.29 | |
| Left amygdala | 0.16 | 0.13 | 0.42 | |
| Right amygdala | 0.25 | 0.23 | 0.37 | |
| Left amygdala habituation | 0.05 | 0.05 | 0.17 | |
| Right amygdala habituation | 0.00 | 0.00 | 0.02 | |
| Left anterior cingulate cortex | 0.25 | 0.23 | 0.40 | |
| Right anterior cingulate cortex | 0.19 | 0.16 | 0.41 | |
| Left insula | 0.07 | 0.06 | 0.08 | |
| Right insula | 0.26 | 0.26 | 0.28 | |
| Left fusiform gyrus | 0.10 | 0.10 | 0.06 | |
| Right fusiform gyrus | 0.38 | 0.37 | 0.54 | |
| Behavioral measures | Accuracy | 0.39 | 0.39 | 0.45 |
| Reaction time | 0.87 | 0.86 | 0.91 |
Emotion labeling for left and right inferior frontal gyrus; emotion matching for all other regions
Emotion matching for left and right inferior frontal gyrus; shape matching for all other regions
Shown explicitly, if , , and correspond to the variance component estimates for the main effects of person, site, and day, respectively; and correspond to the variance component estimates for the two-way interactions between person and site, person and day, and site and day, respectively; and corresponds to the variance component estimate for the residual due to the person × site × day interaction and random error, when the number of sites described by and the number of days described by in the dependability coefficient equation are both set to one, as in the actual NAPLS study where subjects are scanned at one site on one day, (rather than eight and two, respectively, as in the traveling subject study design), the dependability coefficients become equivalent to the proportion of variance due to subject divided by the proportion of variance due to all sources of measurement and error.
Equation 6.17, with expansion of one term as in Equation 6.4, from (Shavelson and Webb, 1991):
Indeed, by varying the values for number of sites ( ) and number of scanning occasions or days ( ), one can use the variance components calculated in the traveling subject study to estimate how the reliability of the fMRI measurements would change if each subject were scanned on a given number of scanners ( ) and/or across a given number of occasions or days ( ). In computing the coefficients reported in the table, the error terms are divided by one, to model the situation in which each subject is scanned once on a single scanner drawn randomly from the pool of available scanners.
The practical implication of less than perfect reliability of measurement is attenuation of effect size and reduction of statistical power (Cohen, 1988). Multisite neuroimaging studies are an increasingly popular option for studying rare conditions, as they provide an efficient means to obtain sample sizes large enough to detect group differences. However, when utilizing multisite studies for this purpose, a key question is how much statistical power is sacrificed by the introduction of variance due to site-related factors when moving from a single-site to a multisite study design, and what sample sizes are necessary to offset the reduction in power due to attenuation of measurement reliability. One way to answer this question is to compare the reliability of the person effect given a multisite design in which individuals are scanned once at a given scanner and data are pooled across sites, to the reliability of the person effect at individual sites, averaged across the sites that would be involved in the multisite design. These latter estimates are shown under the heading “Within-Site ICC” in the table below. With only few exceptions, the reliability of the person effect is appreciably higher in the single-site compared to the multisite design. Cohen (1988) provides a formula for use in power analyses that corrects the effect size for measurement reliability (i.e., , where ES’ is the corrected effect size, ES is the effect size under the assumption of perfect measurement, and r is the estimated reliability of measurement). As shown in the figure below, for nearly all contrasts and regions of interest, such as maximum activation in the right fusiform gyrus and in the right amygdala in the emotion matching versus shape matching contrast, the average within-site intraclass correlation coefficients (i.e., representing single-site reliability estimates for each of the eight NAPLS sites, averaged across sites) are appreciably larger than the corresponding multisite generalizability coefficients, but for a few contrasts and regions of interest, the difference in single-site versus multisite reliability is negligible. As shown in the figure, when accounting for differential reliability in right fusiform gyrus and right amygdala, although higher levels of power are achieved with smaller sample sizes in the single-site compared with multisite context, multisite studies achieve acceptable levels of power (≥0.8) with moderate to large effect sizes (ES ≥0.5) beginning at sample sizes of approximately 85 subjects for the right fusiform gyrus and approximately 125 subjects for right amygdala. These results accord well with the results reported in our original study analyzing single-session scans from 111 healthy subjects, each drawn from one of the eight scanning sites, which observed robust activation in key emotion processing nodes (e.g., amygdala, inferior frontal gyrus, anterior cingulate cortex, fusiform gyrus) whether using image-based-meta-analysis or mixed effects modeling with site as a covariate (Gee et al., 2015), suggesting task-related effect sizes of 0.5 or higher for maximum activation in these regions.
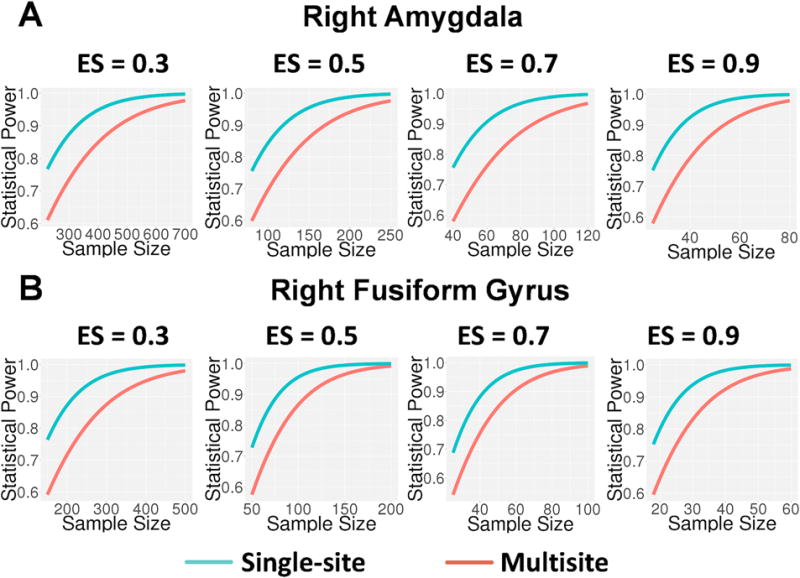
Statistical power as a function of sample size across multiple effect sizes (Cohen’s d for one group test of maximum activation in emotion matching versus shape matching contrast) for right amygdala (A) and right fusiform gyrus (B). The red lines represent power for multisite studies while the blue lines represent power for single-site studies, with nominal effect sizes adjusted downward for observed reliabilities in the multisite and single-site contexts, respectively. Although higher levels of power are achieved with smaller sample sizes in the single-site compared with multisite context, multisite studies achieve acceptable levels of power (≥ 0.8) with at least moderate effect sizes (ES ≥ 0.5) beginning at sample sizes of approximately 125 subjects for right amygdala (A) and beginning at sample sizes of approximately 85 subjects for right fusiform gyrus (B), reflecting the relatively higher cross-site measurement reliability for fusiform gyrus for this task contrast.
Acknowledgments
Funding: Supported by a grant from the National Institute of Mental Health (MH081902) and a gift from the Staglin Music Festival for Mental Health.
References
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd. Lawrence Erlbaum Associates; Hillsdale, NJ: 1988. [Google Scholar]
- Gee DG, McEwen SC, Forsyth JK, Haut KM, Bearden CE, Addington J, Goodyear B, Cadenhead KS, Mirzakhanian H, Cornblatt BA, Olvet D, Mathalon DH, McGlashan TH, Perkins DO, Belger A, Seidman LJ, Thermenos H, Tsuang MT, van Erp TG, Walker EF, Hamann S, Woods SW, Constable T, Cannon TD. Reliability of an fMRI paradigm for emotional processing in a multisite longitudinal study. Hum Brain Mapp. 2015;36:2558–2579. doi: 10.1002/hbm.22791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shavelson RJ, Webb NM. Generalizability theory: A primer. Sage; London: 1991. [Google Scholar]


