Abstract
Purpose
Quantitative assessment of trabecular bone microarchitecture in extremity cone-beam CT (CBCT) would benefit from the high spatial resolution, low electronic noise, and fast scan time provided by complementary metal-oxide semiconductor (CMOS) x-ray detectors. We investigate the performance of CMOS sensors in extremity CBCT, in particular with respect to potential advantages of thin (<0.7 mm) scintillators offering higher spatial resolution.
Methods
A cascaded systems model of a CMOS x-ray detector incorporating the effects of CsI:Tl scintillator thickness was developed. Simulation studies were performed using nominal extremity CBCT acquisition protocols (90 kVp, 0.126 mAs/projection). A range of scintillator thickness (0.35–0.75 mm), pixel size (0.05–0.4 mm), focal spot size (0.05–0.7 mm), magnification (1.1–2.1) and dose (15–40 mGy) was considered. Detectability index was evaluated for both CMOS and a-Si:H flat-panel detector (FPD) configurations for a range of imaging tasks emphasizing spatial frequencies associated with feature size aobj. Experimental validation was performed on a CBCT test-bench in the geometry of a compact orthopedic CBCT system (SAD = 43.1 cm, SDD = 56.0 cm, matching that of the Carestream OnSight 3D system). The test-bench studies involved a 0.3 mm focal spot x-ray source and two CMOS detectors (Dalsa Xineos-3030HR, 0.099 mm pixel pitch) - one with the standard CsI:Tl thickness of 0.7 mm (C700) and one with a custom 0.4 mm thick scintillator (C400). Measurements of modulation transfer function (MTF), detective quantum efficiency (DQE), and CBCT scans of a cadaveric knee (15 mGy) were obtained for each detector.
Results
Optimal detectability for high-frequency tasks (feature size of ~0.06 mm, consistent with the size of trabeculae) was ~4× for the C700 CMOS detector compared to the a-Si:H FPD at nominal system geometry of extremity CBCT. This is due to ~5× lower electronic noise of a CMOS sensor, which enables input quantum-limited imaging at smaller pixel size. Optimal pixel size for high-frequency tasks was <0.1 mm for a CMOS, compared to ~ 0.14mm for an a-Si:H FPD. For this fine pixel pitch, detectability of fine features could be improved by using a thinner scintillator to reduce light spread blur. A 22% increase in detectability of 0.06 mm features was found for the C400 configuration compared to C700. An improvement in the frequency at 50% modulation (f50) of MTF was measured, increasing from 1.8 lp/mm for C700 to 2.5 lp/mm for C400. The C400 configuration also achieved equivalent or better DQE as C700 for frequencies above ~2 mm−1. Images of cadaver specimens confirmed improved visualization of trabeculae with the C400 sensor.
Conclusions
The small pixel size of CMOS detectors yields improved performance in high-resolution extremity CBCT compared to a-Si:H FPDs, particularly when coupled with a custom 0.4 mm thick scintillator. The results indicate that adoption of a CMOS detector in extremity CBCT can benefit applications in quantitative imaging of trabecular microstructure in humans.
1. INTRODUCTION
A variety of dedicated cone-beam CT (CBCT) systems for imaging of musculoskeletal extremities have recently been introduced.1, 2 Owing to the use of a-Si:H flat-panel detectors (FPDs) and compact x-ray sources, extremity CBCT achieves a compact scanner design that offers simplified logistics, lower cost, and lower imaging dose compared to conventional CT. For example, the OnSight 3D system (Carestream Health, Rochester NY) uses a Varex PaxScan2530 FPD (Varex, Salt Lake City UT) with 0.139 mm pixel pitch, 0.7 mm CsI:Tl scintillator, and a 0.5 focal spot (FS, IEC336 standard) stationary anode x-ray source. Scan dose is 5–15 mGy, the field-of-view (FOV) is 20×20×20 cm3, and typical scan time is ~30 s.3 Spatial resolution permits visualization of ~0.25–0.35 mm high-contrast features (frequency at 10% of the modulation transfer function, f10, approximately 1.5–1.8 mm−1), yielding improved visualization of bone detail compared to MDCT.4, 5 A compact gantry with flexible positioning capability permits weight-bearing imaging of lower extremities in addition to non-weight-bearing acquisitions, providing new insight in weight-bearing evaluation of areas such as osteoarthrtis,6–8 patellar malformation,9 and flatfoot deformity.10
The high spatial resolution motivates application of extremity CBCT in quantitative imaging of bone microstructure.11–15 Trabecular and cortical microarchitecture are biomarkers of bone health, with indices of bone microstructure found to improve prediction of fracture risk in osteoporosis (OP)11, 16–24 compared to bone mineral density (BMD). In osteoarthritis (OA), alterations in trabecular microarchitecture of subchondral bone often precede cartilage degeneration,25–27 motivating investigation of structural metrics as an early biomarker of disease. However, trabecular features typically measure 0.05–0.2 mm,28 so ultra-high–resolution pre-clinical micro-CT29 remains the gold standard for bone morphometry. To enable in vivo measurements of microstructure in patients, a dedicated high-resolution peripheral quantitative CT (HR-pQCT) system has been developed30, 31 for use in distal radius and ulna. Applications of HR-pQCT in more attenuating body sites, such as the knee, require long scan times (~20 min) and have limited axial field-of-view (FOV) of ~6 cm.32 Accurate characterization of bone morphometry via multi-detector CT, CBCT, and/or MRI could greatly enhance the clinical utilization of such quantitative biomarkers.
Despite their limited spatial resolution, conventional multi-detector CT and a-Si:H FPD-based CBCT systems have been shown to achieve statistically significant correlation with gold standard micro-CT for a variety of trabecular metrics.21–23 In extremity CBCT, Pearson R-coefficient of 0.9 for Bone Volume (BV/TV), 0.66 for Trabecular Thickness (Tb.Th) and 0.68 for Trabecular Spacing (Tb.Sp) were found in comparison to micro-CT.14 While promising, this result suggests that application of CBCT in quantitative bone imaging would benefit from further improvement in spatial resolution. Complementary metal-oxide semiconductor (CMOS) x-ray detectors offer a compelling alternative to a-Si:H FPDs for such high-resolution applications, owing to their higher readout speed, up to 10× lower electronic noise, and finer pixel pitch (~0.05–0.1 mm).33–36
In the recent years, CMOS detectors emerged as an attractive option for indirect detection x-ray detectors. Early interest in medical applications of CMOS sensors has been primarily focused on breast imaging. In digital breast tomosynthesis (DBT), Choi et al37 and Patel et al38 showed that the low electronic noise of CMOS detectors enables improved angular sampling by lowering the required dose per frame. In breast CBCT, Gazi et al39 and Shen et al36 demonstrated 125% increase in system limiting resolution and 45% enhancement in visibility of microcalcifications, respectively, compared to conventional a-Si:H FPDs. A model by Zhao et al40 found that a commercial CMOS sensor operated in a low capacity, low noise mode can improve contrast-to-noise ratio (CNR) of small microcalcifications (<0.2 mm) at lower mean glandular dose levels compared to an existing commercial DBT system. This analysis was extended to include models of DBT image reconstruction, image display and human observer performance.41 Vedantham et al42 used task-based modelling to investigate the tradeoffs between pixel size and scintillator thickness in breast CBCT and determined that a 0.525 mm thick CsI:Tl scintillator (somewhat thinner than the 0.6–0.7 mm CsI:Tl typically used in FPDs) is optimal for detecting 0.22 mm microcalcifications.
Results of modeling and optimization studies in breast imaging are not directly applicable to extremity CBCT due to differences in x-ray spectrum (~90 kV in extremity CBCT compared to ~30 kV in DBT), object composition, and system geometry. We use a cascaded systems model developed specifically for CMOS-based extremity CBCT to evaluate performance in high-resolution applications using task-based detectability index framework.13, 43 In particular, we investigate the potential benefits of reducing the thickness of the CsI:Tl scintillator below 0.6–0.7 mm as currently used in a-Si:H FPDs and CMOS sensors for CBCT. Thinner CsI:Tl reduces scintillator blur (potentially better matching the blur associated with the finer pixel aperture), but leads to increased noise due to diminished x-ray absorption, especially for the relatively high x-ray energies used in extremity imaging. For high-frequency tasks, however, the benefits of enhanced spatial resolution may outweigh the impact of elevated noise, resulting in improved detectability. Preliminary results15 indicate that the visibility of trabeculae can indeed be improved using a 0.4 mm scintillator compared to the standard 0.7 mm thickness.
The work reported below extends the simulation and experimental studies reported in Ref. 15 to provide a more detailed analysis of CMOS detector performance across a broader scope of system parameters and imaging geometries using a new, continuously tunable spectrum of imaging tasks representative of trabecular bone morphometry. The main contributions of this work include: (a) a model of a CMOS x-ray sensor that incorporates the effects of scintillator thickness; (b) a study of detectability in extremity CBCT as a function of feature size, pixel size, electronic noise, CsI:Tl thickness, focal spot size, dose, and system magnification; and (c) experimental validation in phantom and cadaver studies using two CMOS detectors, one with the current standard CsI:Tl thicknesses of 0.7 mm (denoted C700), and one (C400) custom-made with 0.4 mm thick CsI:Tl. This direct experimental comparison provides new insight into the tradeoffs between resolution, noise, and imaging task that govern the choice of scintillator thickness for high-resolution applications of CMOS sensors. The results motivated implementation of a CMOS detector on a prototype high-resolution extremity CBCT system based on the OnSight 3D gantry.
2. METHODS AND MATERIALS
2.A Task-based evaluation of CMOS detectors in high-resolution extremity CBCT
The performance of CMOS detectors in extremity CBCT imaging was investigated in terms of modulation transfer function (MTF), noise-power spectrum (NPS), detective quantum efficiency (DQE), and detectability index:
| (1) |
The non-prewhitening (NPW) observer model (Equation 1) has been shown to agree reasonably well with human observer performance in CBCT for a wide range of simple imaging tasks.44. The task function, Wtask, is a frequency-domain specification of the feature(s) of interest in detection or discrimination. The NNPS is the normalized NPS, and Tsystem is the MTF of the system. The NPS and MTF were obtained from cascaded systems analysis of CMOS x-ray sensors, as described below. Since the focus of the current study is on the effects of detector design on imaging performance, the modeling was performed in the 2D projection domain and did not include signal and noise propagation in the 3D reconstruction cascade.45, 46 The NPS in the denominator of Eq. (1) is normalized by the mean detector signal squared. As shown by Tward et al45, the resulting NNPS is equivalent to the NPS of log-corrected projection data. The form in Eq. (1) therefore represents a detection task in log-corrected projection data. The detectability index was investigated as a function of scintillator thickness, pixel size, electronic noise, scan dose, focal spot size, and imaging task.
The description of theoretical methods is organized as follows: Section 2.A.1 introduces the basic cascaded systems model and defines fixed system parameters and key variables. Section 2.A.2 describes the modeling of scintillator thickness-dependent system gain, including quantum detection efficiency, generation of optical photons in the scintillator, depth-dependent scintillator escape fraction, and coupling efficiency. Models of thickness-dependent scintillator blur, focal spot blur, and system MTF are discussed in Sec. 2.A.3. Section 2.A.4 concerns the NPS and includes discussion of Swank factor and assumptions regarding Lubberts effect. Section 2.A.5 introduces task functions pertinent to high-resolution extremity imaging, and Sec. 2.A.6 outlines the simulation studies evaluating task-based detectability. The cascaded systems model is consistent with a significant body of previous work modeling a-Si:H FPDs43, 47–50 and more recently CMOS systems40, 51 with details below emphasizing aspects of the model related to scintillator thickness and pixel size.
2.A.1 Cascaded systems model of a CMOS detector with a CsI:Tl scintillator
The analytical detector model consisted of the following 7 stages:43 x-ray absorption in the scintillator (quantum detection efficiency, QDE), generation of light quanta (quantum gain), light spread in the scintillator (including the spread of K-fluorescence photons52), coupling to the photodiode, integration by pixel aperture, sampling, and readout with additive noise. Effects of scatter were not considered in the model. For input-quantum-limited conditions, scatter imparts a scaling of the NPS by a factor of (1 + SPR), where SPR is the scatter-to-primary ratio53. In the majority of studies performed here, various detector configurations are compared at the same system geometry and thus the same SPR. Consequently, it is assumed that the omission of scatter from the model has only minor impact on the metrics of relative detector performance investigated in this study. The parameters of the model are listed in Table 1, with nominal values reflecting two Xineos-3030HR CMOS detectors (Teledyne DALSA) with CsI thicknesses of 0.4 mm and 0.7 mm used in experimental studies (Sec. 2.2 – 2.4).
Table 1.
Glossary of terms and symbols in the cascaded systems model. Model constants include fundamental physical quantities, geometry and typical operating parameters of the extremity CBCT system, and detector parameters that are independent of CsI:Tl thickness. CMOS detector performance was analyzed as a function of quantities denoted as key variables. The derived quantities are functions of the model constants and key variables; their nominal values are given at two detector thicknesses corresponding to the CMOS sensors used in experimental studies, assuming all other parameters are at their nominal value.
| Constants | Notation | Value | Ref. | |
|---|---|---|---|---|
| Beam energy | Emax | 90 kV | 49 | |
| Fluence per exposure pre-object |
|
2.58 ×105 x-rays/mR/mm2 | 54 | |
| Source-detector distance | SDD | 560 mm | 50 | |
| Source-axis distance | SAD | 431 mm | ||
| Total filtration (inh. + added) | 3.4 mm Al+0.2 mm Cu | 55 | ||
| Object | - | 8 cm water + 7.3 cm spongiosa + 0.4 cm cortical bone | ||
| CsI density | ρCsI | 4.51 g/cm3 | - | |
| Packing fraction | fCsI | 0.7 | - | |
| K-edge energy | EK | 35 keV | ||
| K-fluorescence probability | ξ | 0.83 | 56 | |
| K-fluorescence yield | ω | 0.87 | ||
| Work function | W | 55.6 optical photons/keV | ||
| Coupling efficiency |
|
0.59 | - | |
| Fill factor | fpix | 0.85 | - | |
| Electronics noise | σadd | 390 e− | ||
| Conversion gain | k | 139 e−/ADU |
| Key Variables | Notation | Range (nominal value) | Ref. |
|---|---|---|---|
| Dose (mGy) | D | 15–40 (15) | - |
| Focal spot size (mm) | aspot | 0.05–0.7 (0.5) | - |
| CsI:Tl thickness (mm) | tCsI | 0.35–0.75 (0.7) | - |
| Pixel size (mm) | apix | 0.05–0.4 (0.099) | - |
| Magnification | M | 1.1–2.1 (1.3) | - |
| Derived Quantities | Notation | Nominal Values (at apix =0.099 mm) | Ref. | |||
|---|---|---|---|---|---|---|
| @tCsI = 0.4mm @ tCsI = 0.7mm | ||||||
| Focal spot blur | Tspot | Eq. (10) | - | |||
| Quantum detection efficiency |
|
0.47 | 0.66 | |||
| K-fluorescence reabsorption | fK | 0.66 | 0.77 | - | ||
| Escape fraction | ηesc | 0.40 | 0.37 | 57 | ||
| Quantum gain (photons/X-ray) |
|
931.57 | 854.12 | - | ||
| Photodiode aperture (mm) | apd | 0.0913 | - | |||
| Gain (e−/Incident x-ray/pixel) | G | 2.14 | 2.76 | |||
| Scintillator blur | T3 | Eq. (8) | - | - | ||
| Total K-fluor. blur | TKtot | Eq. (9) | - | |||
| Pixel aperture | T5 | - | - | |||
| Sampling function | III6 | - | - | |||
2.A.2. System gain
Using the definitions in Table 1, the system gain G(e−/incident x-ray/pixel) is given by:
| (2) |
where tCsI is scintillator thickness. The mean quantum detection efficiency, ḡ1(tCsI), is calculated by dividing the scintillator into a series of 200 slabs (thickness denoted Δz and integrating over the slab depth (z) measured from the incident surface:48
| (3a) |
| (3b) |
| (3c) |
where is the mass attenuation coefficient of CsI and qdet(E) is the spectrum at the detector (input spectrum q0(E) attenuated by the object). Within each slab, three parallel pathways for the quantum gain g2 are considered: pathway A (gain denoted by ) describes local absorption of an X-ray photon without K-fluorescence; pathway B( ) accounts for locally absorbed energy resulting from K-fluorescent events; and pathway C ( ) involves K-fluorescence x-ray photons produced locally but absorbed at a remote site, with the associated MTF denoted TK:52
| (4a) |
| (4b) |
| (4c) |
The escape fraction ηesc(tCsI,Z) refers to the fraction of optical photons that reach the scintillator exit surface and are subsequently coupled to the photodiode with efficiency . An linear fit to escape fraction estimated by Howansky et al57 for a scintillator with reflective backing was used to compute ηesc:
| (5) |
The quantum gain for each parallel pathway and are combined to form the total gain 52:
| (6) |
The loss of photons in the optical stack between the scintillator exit surface and the photodiode (e.g. due to fiber-optic plate and optical glue) and the conversion efficiency from optical photons to electrons are described together by the optical coupling efficiency . The coupling efficiency was treated as a constant across all detector configurations. The value of was determined empirically to yield a good match between the model and measurements of system gain and noise power spectra (Sec. 2.3). It was found that the estimates of the coupling efficiency were different for the two detectors: for C400 and for C700. This discrepancy is likely due to variations in CsI deposition techniques and in the quality of the interface between the CMOS and scintillator. Such variability represents differences in the manufacturing process rather than true dependence of on scintillator thickness. Therefore, the mean of the two empirical estimates ( ) was used in the detector model to approximate an average coupling efficiency of a CMOS detector of the type used in the experimental studies. The coupling efficiency values found for the two detectors were lower than those reported for a-Si:H FPDs ( ), likely due to light losses in the fiber-optic plate, which is not used in a-Si:H FPDs.
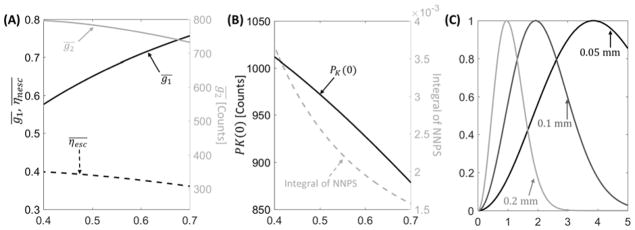
Fig. 1A illustrates the thickness-dependent QDE (black line), escape fraction (dashed black line), and quantum gain (gray line) as functions of CsI:Tl thickness. As anticipated, QDE increases with increasing thickness; however, quantum gain decreases for thicker CsI:Tl because of reduced escape efficiency. Overall, the product is ~21% higher for 0.7 mm CsI:Tl than 0.4 mm CsI:Tl.
Figure 1.
(A) Quantum detection efficiency, escape efficiency (left vertical axis, black lines), and scintillator gain (right vertical axis, gray line) computed as a function of scintillator thickness. (B) Zero-frequency PK and integral of detector NNPS over the Nyquist frequency range (gray line) as a function of CsI thickness. (C) Examples of task functions (Eq. 13, assuming C=1) for three feature sizes: 0.05 mm (solid black line), 0.1 mm (solid dark gray line), and 0.2 mm (solid light gray line). The tasks emphasize distinct frequency bands depending on the underlying feature size.
2.A.3. System MTF, detector blur, and focal spot blur
System MTF is defined as the product of detector and focal spot MTFs: Tsystem(u, v; tCSI, aspot) = Tdet(u, v; tCSI,) · Tsystem(u, v; aspot). The detector MTF, Tdet, is given by:
| (7) |
where T3 denotes scintillator blur, TKtot is the blur associated with the spread of K-fluorescence photons, and T5 is the aperture function T5(u, v) = |sinc(ap,du)sinc(ap,dv)|. Both T3 and TKtot are affected by scintillator thickness tCsI. The scintillator blur is modeled using a two-component form that consists of an exponential term to account for a homogeneous, unstructured layer of CsI:Tl deposited on the surface of the scintillator, and a Lorentzian term describing the blur in the structured, columnar CsI:Tl layer:58
| (8) |
where the terms A and B are independent of CsI:Tl thickness, and H(tCsI) is a polynomial function of scintillator thickness. Each parameter was obtained from an empirical fit to measured presampling MTFs of CMOS detectors with 0.4 mm and 0.7 mm CsI:Tl (Section 2.3).
The total K-fluorescence blur, TKtot, weighs the K-fluorescence blur TK by the gains of the individual pathways of g2:47
| (9) |
where fk(tCsI) is the probability of remote absorption for an K-fluorescence photon, and Tk(tCsI) is the spread associated with that absorption. Both fk(tCsI) and Tk(u,v; tCsI) were computed from analytical models of Chan et al. and Que et al.59, 60
Similar to previous cascaded systems studies of extremity CBCT, a simplified Gaussian model of focal spot blur Tspot was adopted:49, 61
| (10) |
where M = SDD/SAD and the nominal value of parameter aspot was set to 0.5 mm. Note that while the aspot parameter in the simulations has a unit of mm, the x-ray source employed in the experiments is characterized using the focal spot index (IEC 336 standard, denoted FS), representing a range of focal spot size.
2.A.4. Noise-power spectrum in projection images
Using the gain and blur terms defined above, the NPS of a 2D projection image is:
| (11) |
where the functional parameters were omitted for simplicity and is the active pixel area. The comb function III6 = ΣNδ(N/apix) represents aliasing of quantum noise due to pixel sampling. Sadd is the power spectrum of additive noise ( ). Pk is a noise term associated with quantum gain as described by Richard62. In the case of no K-fluorescence, , where εg2A is the Poisson excess associated with local x-ray absorption. Considering K-fluorescence, Pk combines the gain and Poisson excess for the three parallel cascades of (Eq. 4), as well as a cross term in noise between pathways B and C. The Poisson excess in each path is computed from the gain (Eq. 4) and Swank factor specific to each path. The Swank factors were derived from the product of a radiological Swank factor and an optical Swank factor, the same for all pathways, weighted by the gain in each pathway. The CsI thickness-dependent radiological component is associated with polyenergetic absorption and was computed from the result of Zhao et al.58 The optical component is due to light losses in the scintillator. For simplicity, it is assumed to be independent of CsI thickness and equal to 0.95, giving good agreement with the measured NPS on the C400 and C700 CMOS detectors. This value also agrees fairly well with an approximate estimate of the optical Swank factor Iopt given by the following equation from Lubinsky et al 63
| (14) |
This formula yields Iopt = 0.98 for 0.7 mm CsI and Iopt = 0.99 for 0.4 mm CsI. While the above equation is approximate and was derived under certain simplifying assumptions, it further justifies modeling Iopt as largely independent of tCsI and supports the empirical value of 0.95 used in this study.
With the above definitions, the normalized NPS (NNPS) in Eq. 1 is given by:
| (15) |
The noise model accounts for the effects of scintillator thickness on detector gain and MTF. However, the Lubberts effect64, 65 (i.e., noise amplification due to the depth-dependent light spread from individual scintillation events) is assumed to be negligible. This assumption is supported by experimental results for columnar CsI:Tl scintillators66, showing negligible contribution from the Lubberts effect (ratio of the square of detector MTF to NNPS very close to unity) over a broad range of scintillator thickness (~0.2 mm to ~0.6 mm).
The dashed gray line in Fig. 1B shows the integral of NNPS over the Nyquist frequency range as a function of scintillator thickness at an exposure of 0.126 mAs. Despite the increased escape fraction that partly compensates for the reduced QDE of thin scintillators (Fig. 1A) in mean signal, the projection noise substantially increases with decreasing CsI:Tl thickness. The plot of the zero-frequency Pk (black line) in Fig. 1B explains this behavior: the improved of thin scintillators leads to increasing contribution of the associated conversion noise encapsulated by Pk.
2.A.5. Imaging task
We considered task functions representing discrimination of two Gaussian stimuli of different widths, defined in the detector plane as:
| (16) |
where C is a contrast term, M is the system magnification, aobj is the feature size measured in the object plane, and k is a parameter that determines the relative width of the Gaussian stimuli. Here, k was set at 0.8, and aobj was varied to simulate a range of anatomical feature sizes and associated spatial frequency bands (Fig. 1C). In the context of trabecular bone imaging, an increase in detectability of the task in Eq. (13) indicates improved ability to discriminate trabeculae (or trabecular cavities) that differ in size by 20%, and could thus indicate improved assessment of change in trabecular thickness (or trabecular spacing).
Holding other parameters of Eq. (13) fixed, a change in feature size, aobj, implies a change in the area under - i.e., signal power. To account for this scaling, the results below are reported in terms of relative d′2, where the detectability for a given feature size is normalized to a reference value (e.g., the value at nominal system parameters) for the same feature size. Detector performance for various tasks (feature sizes) is then compared in terms of this relative detectability, and the contrast term C cancels out for all cases (can be ignored) and was set to unity.
2.A.6 Simulation studies
Detectability for the task function of Eq. (13) for feature sizes ranging from 0.03 to 0.2 mm28 was studied in relation to five system parameters (Table 1, Key Variables): pixel size (apix), scintillator thickness (tCsI ), focal spot blur (aspot), magnification (M) and bare-beam x-ray exposure.
The x-ray spectrum (q0(E)) was obtained using the Spektr 3.054 implementation of TASMICS67 for a beam energy of 90 kV. Tube inherent filtration was found experimentally by estimating Al thickness that achieved best match of detector entrance dose between Spektr simulations and measurements on the benchtop x-ray source (Sec. 2.2) performed with a Si diode (AccuDose, RadCal Corp., Monrovia, CA) for 70, 80, 90, and 100 kV beams. The added filtration (Table 1) was the same as the filters applied in the experimental setup. Additionally, differences in tube output (mGy/mAs) between the Spektr 3.0 model and the source used in the experiments were accounted for by fitting a constant scale factor.
The nominal SDD was set to 560 mm and nominal magnification was set to 1.3 to emulate the extremity CBCT scanner49 and test bench setup. The x-ray spectrum at the detector, qdet(E), was obtained from the input spectrum, q0(E), attenuated by material approximating a human knee: 8 cm water, 7.6 cm spongiosa and 0.4 cm cortical bone. To investigate the effects of system geometry in hypothetical future system designs, additional geometries with varying magnification were simulated by holding SAD fixed and varying SDD. Tube output was kept the same in all configurations so that the patient dose was constant.
2.B. Experimental setup
Experimental evaluation of CMOS-based extremity CBCT was performed on an imaging test bench (Fig. 2). Two CMOS detectors (Xineos-3030HR, Teledyne DALSA, Eindhoven, NL) were tested, one with CsI:Tl thickness of 0.4 mm (C400) and one with thickness of 0.7 mm (C700). The detectors have a 30 × 30 cm2 FOV, pixel size of 0.099 × 0.099 mm2, 14-bit digitization, and frame rate of up to 30 fps for full resolution readout. The scintillators are deposited on fiber-optic plates made with lead glass. The same set of experiments was performed with both detectors, keeping the geometric configuration and acquisition parameters fixed to provide head-to-head performance comparison for two CsI:Tl thicknesses. The detectors were operated in high-full-well sensitivity mode.
Figure 2.

CBCT test-bench used in experimental studies. The bench was configured with two CMOS sensors, one with CsI:Tl thickness of 0.4 mm (C400) and one with thickness of 0.7 mm (C700).
The test bench employed an IMD RTM 37 rotating anode x-ray source (IMD, Grassobbio, IT) with 3 kW power and nominal focal spot of 0.3 FS (IEC336). The beam energy in all experiments was 90 kV (0.2 mm Cu + 2 mm Al added filtration). The SDD was fixed at ~560 mm and the SAD was ~430 mm, consistent with the geometry of a clinical extremity CBCT developed at our institution.68 The object to be imaged was rotated using a Velmex B4800 rotation stage (Velmex, Bloomfield, NY), and projections were obtained in a step-and-shoot mode of x-ray pulses synchronized with detector readout.
We observed evidence of possible direct x-ray interaction in the crystalline Si (due to the small fraction of x-rays that were not absorbed in the lead glass of the fiber-optic plate) as bright, single-pixel outliers (“speckles”) apparent after gain and offset corrections. The speckles were isolated by applying a Laplacian filter to select pixels that deviated from the mean of the filtered frame by more than 2 standard deviations. Such speckles identified by filtering (typically accounting for <2% of total pixels) were corrected by linear interpolation of nearest neighbors.
2.C. Experimental studies
2.C.1. Measurement of detector MTF, NPS, and scan dose
Measurements of detector MTF and NPS were performed with additional 2.5 mm Cu and 2 mm Al placed in the beam to simulate attenuation by 15 cm of water. Detector MTF was measured using a tungsten edge placed on the detector surface and imaged at ~15° angle to the pixel matrix. The exposure was set to deliver ~90% detector saturation and 100 frames were acquired, gain and offset corrected, and averaged. An oversampled edge-spread function (ESF) was obtained from the projection of the tilted tungsten edge following Samei et al 69. The ESF was oversampled at 20 μm intervals via bilinear interpolation, and the LSF was computed by numerical differentiation of the ESF. The presampling detector MTF was obtained as the absolute value of a Fourier transform of the LSF, divided by a sinc function corresponding to the 20 μm binning.
The parameters of the scintillator blur model T3(u,v; tCsI) in Eq. (8) were estimated by a least-squares fit to the measured MTFs of the two detectors (denoted MTFc400 for the C400 sensor and MTFc700 for the C700 sensor):
| (17) |
where Tktot400 and Tktot700 are the K-fluorescence blur functions for the two CsI thicknesses computed from Eq. (9). The dependence of T3 on CsI:Tl thickness is encapsulated in the function H(tCsI) in Eq. (8), assumed to follow a polynomial of the form . The values of the function H(tCsI) at the CsI:Tl thicknesses of the two detectors, H400 and H700, were obtained through the fit in Eq. (15). The parameters of the polynomial model h1 and h2 were estimated from H400 and H700 by an additional fitting step, resulting in the thickness-dependent . The factors A* and B* were found to be 0.20 (unit-less) and 1.42 mm−1, respectively.
NNPS was computed for detector exposure ranging from 0.019–0.15 mAs/frame (from 3 ms/fame to 24 ms/frame at 6.3 mA). One hundred projections were obtained at each exposure, offset-corrected using a mean of 50 dark images and normalized by the mean of all air projections. Ninety-nine difference images (denoted Δ) were then obtained from pairs of consecutive frames to remove residual structure or low-frequency trends. Effects of detector lag were assumed negligible based on manufacturer specification of 1st frame lag of 0.1%.70 In each difference image, 144 non-overlapping regions of interest (ROIs) of 81×81 pixels were drawn. The NNPS was given by:
| (18) |
where n is the ROI size, N is the total number of ROIs across all difference images, and the factor of 2 accounts for the use of difference images. DQE was computed as:
| (19) |
The x-ray fluence was obtained from Spektr simulation using the source model described in Sec. 2.A.
Dose measurements were performed using three 16 cm diameter CTDI phantoms stacked to cover the longitudinal FOV of the benchtop CBCT. A Farmer chamber (AccuDose, Radcal Corp., Monrovia CA) was placed at the center of the x-ray beam in the central hole of the CTDI phantom. The central CTDI dose per projection was obtained by averaging 110 static exposures of the CTDI phantom for x-ray techniques ranging 0.032–0.16 mAs/exposure (from 5 ms/fame to 25 ms/frame at 6.3 mA).
2.C.2. Cadaver Study
CBCT scans of a cadaver knee were acquired using 420 projections evenly distributed over 220° (equal to 180° + fan angle and thus providing complete sampling). The x-ray technique was varied from 0.038 – 0.15 mAs/frame (from 6 ms/fame to 24 ms/frame at 6.3 mA). Image reconstruction used the Feldkamp algorithm with a Hann-apodized filter and Parker short scan weights71, 72. For high-resolution bone reconstruction, the filter cutoff was 0.9 of the Nyquist frequency (fNyq) and voxel size was 0.025 mm. Soft tissue reconstruction involved 4×4 software projection binning, filter cutoff at 0.8 × fNyq, and 0.3 mm voxel size. Scatter correction was performed assuming that the scatter in each projection view is uniform and equal to a fraction of the mean projection value (empirically set to 0.4) in a 5×5 pixel ROI at the center of the projection.
3. RESULTS
3.A. Detectability index for extremity CBCT
Figure 3 presents the evaluation of task-based detectability with respect to detector pixel size, electronic noise, and scintillator thickness. The nominal extremity CBCT scanner geometry was assumed. Recognizing the multi-dimensional character of this evaluation, a set of two-dimensional optimizations holding other parameters fixed at nominal values was chosen to summarize key findings. The simulated bare-beam x-ray exposure was 0.126 mAs/projection. Based on Farmer chamber measurements (Sec. 2.C.1), the central CTDI scan dose D for this exposure is estimated to be 15 mGy (assuming 420 projections/scan). This value is within the typical dose range for scan protocols in FPD-based extremity CBCT.3
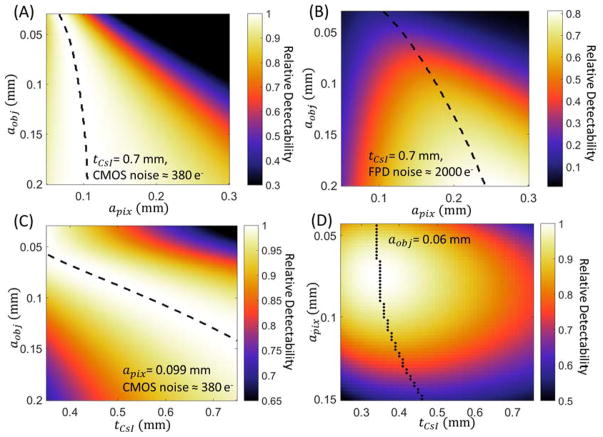
Figure 3.
Task-based evaluation of CMOS detector performance in extremity CBCT. (A) Relative detectability for a range of feature sizes (vertical axis) as a function of pixel size. Scintillator thickness is assumed constant and equal to 0.7 mm. Detectability is normalized to the maximum value for each aobj. Dashed lines indicate maximum d′ for each feature size. (B) Ratio of d′2 achieved with the same scintillator as (A), but at increased electronic noise consistent with an a-Si:H FPD, to maximum d′2 attained for each aobj by the low-noise CMOS detector of (A). (C) Relative detectability of the CMOS detector as a function of scintillator thickness and imaging task, normalized by maximum detectability achieved for each aobj across the range of tCsI. Pixel size is 0.099 mm. (D) Joint optimization of pixel size and scintillator thickness for a “trabecular” imaging task with feature size of 0.06 mm. The graph shows detectability of a CMOS detector (normalized by the maximum).
Figure 3A shows relative detectability for a CMOS detector with tCsI = 0.7 mm as a function of detector pixel size and task. For each task, detectability was normalized by the maximum detectability for that task across all values of apix. The model of focal spot blur was not included in this analysis to elucidate the impact of detector parameters. The optimal pixel size, indicated with a dashed line in Fig. 3A, varies from 0.07–0.11 mm across the investigated range of aobj (0.03–0.2 mm), with smaller feature size favoring smaller apix.
Figure 3B shows the performance of a hypothetical a-Si:H FPD assumed identical to the CMOS detector except for 5× increased electronic noise. At each value of aobj, the detectability values across all values of apix were normalized by the maximum detectability attained by the CMOS detector for the same task. The optimal pixel size for any feature size is larger for the a-Si:H FPD than for CMOS, compensating the increased contribution of electronic noise. For coarse features, this increased apix has only a minor effect on the maximum detectability, which is comparable to that achieved with the CMOS. However, for small feature sizes corresponding to imaging tasks in trabecular bone (0.05–0.1 mm), the maximum detectability of the a-Si:H FPD is only 20%–60% of the maximum d′2 of the CMOS. Due to its lower electronic noise, a CMOS detector is able to better exploit the increased Nyquist frequency and the improved aperture MTF (T5) associated with reduced pixel size, resulting in better performance in high-resolution tasks.
Based on Fig. 3A, the pixel size of the CMOS sensor used in the experimental studies (apix = 0.099 mm) is seen to provide optimal or nearly optimal performance for a broad range of feature sizes. In Fig. 3C, the pixel size was thus fixed at 0.099 mm to investigate the effects of scintillator thickness. The detectability for each aobj was normalized by their maximum value across the investigated range of tCsI. For small feature size, the improvement in spatial resolution provided by a thin scintillator compensates for the increase in quantum noise resulting from reduced QDE (see Sec. 2.A and Fig. 2B), and optimal d′2 is achieved at CsI:Tl thickness of ~0.4 mm for aobj of ~0.07 mm. As the feature size increases, there is less benefit to the improved MTF provided by thin tCsI, and the optimal d′2 shifts toward thicker CsI:Tl to minimize quantum noise (increase QDE). Detectability at aobj of ~0.13 mm is optimized for CsI:Tl thickness of ~0.7 mm, typical for current FPD and CMOS detectors for CBCT applications. This scintillator thickness delivers a balanced performance over a broad range of feature size, achieving d′2 within ~10% of its maximum value (obtained at optimized tCsI) for aobj from 0.08 – 0.2 mm. Using a thin scintillator benefits high-frequency tasks, but results in a relatively steep decline in detectability for coarse features (~20% reduction compared to the value at optimized thickness). This effect, however, can be partly mitigated by additional projection binning and filtering to generate a lower resolution “soft-tissue” image separate from the full resolution “bone” reconstruction.
In Fig. 3D, the detectability for fine feature size (aobj = 0.06 mm) consistent with visualization of trabecular bone is analyzed as a function of tCsI and apix. Recognizing that different diagnostic tasks may be sensitive to features of different size, we chose 0.06 mm (as measured in the object domain in the nominal extremity CBCT geometry) as representative of the lower range of typical human trabeculae in Ref. 28 (0.05 mm – 0.2 mm thick). The values of d′2 are normalized to the maximum over the investigated range of tCsI and apix, achieved at ~0.075 mm detector pixel size and ~0.35 mm CsI:Tl thickness. The dashed line marks the optimal scintillator thickness for each apix. Consistent with Fig. 3A, a pixel size of 0.05–0.1 mm is favored across the entire range of tCsI, providing an optimal tradeoff between noise (increasing for smaller pixels) and aperture size and Nyquist frequency (improving with smaller pixels). There is a sharp drop in detectability at pixel size >0.1 mm, approximately corresponding to the magnified feature size. The relative benefit of using small apix is diminished for thicker tCsI, where scintillator blur dominates the MTF. For the pixel size of current CMOS sensors (0.05–0.1 mm), the detectability for 0.06 mm feature size is maximized using CsI:Tl thicknesses of ~0.4 mm. The optimal thickness is relatively constant for pixels in the 0.05–0.1 mm range (despite the 2-fold change in apix, indicating diminishing benefits of improved scintillator sharpness compared to the increase in quantum noise (reduction in QDE). For the CMOS detector used in the experimental studies (apix = 0.099 mm), a ~20% improvement in d′2 is anticipated at the optimal CsI thickness of ~0.35 mm compared to the commonly employed ~0.7 mm CsI. Beyond apix of ~0.1 mm, the optimal tCsI changes almost linearly with pixel size, indicating that once the system resolution drops below this value, the optimization of d′2 is driven primarily by reduction of projection quantum noise attained using thicker scintillators.
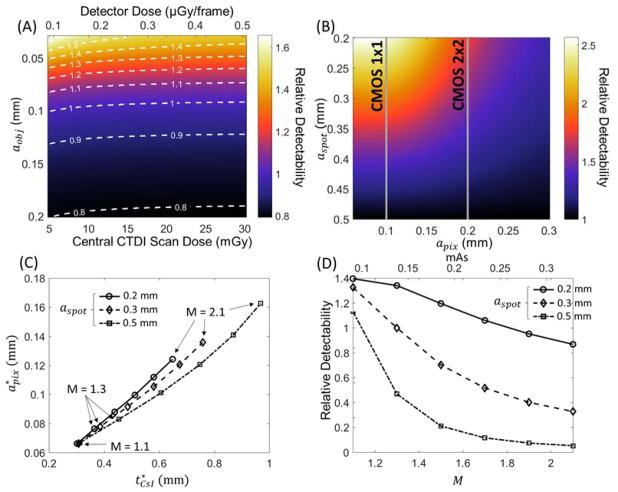
Figure 4 uses the theoretical system model of Sec. 2.A to investigate effects of imaging dose, focal spot size, and system geometry in CMOS-based extremity CBCT. The ratio of d′2 of a CMOS detector with 0.099 mm pixels and tCsI = 0.4 mm (C400) to d′2 of the same detector with tCsI = 0.7 mm (C700) is shown in Figure 4A for the nomimal extremity CBCT system geometry. A dose range typical of extremity imaging is considered (5 – 30 mGy central CTDI scan dose). The d′2 ratio is fairly independent of dose over a broad range. A thin scintillator is preferred for feature size < 0.1 mm, and a slight change in relative detectability of the two detectors occurs at very low dose (likely below practical imaging dose levels) and is due to the effects of electronic noise. At such low dose, the electronic noise terms favor the detector with an even thinner scintillator.
Figure 4.
(A) Ratio of detectability achieved with the C400 detector to that of C700 as a function of imaging task and imaging dose for the nominal extremity CBCT geometry. Top horizontal axis represents detector entrance dose (after attenuation by a simulated knee), and the bottom horizontal axis gives the corresponding measured central CTDI dose in a CBCT scan. (B) Detectability for the trabecular imaging task (aobj=0.06 mm) as a function of focal spot size and pixel size, normalized by the detectability achieved for each aobj using a 0.5 mm focal spot. C700 detector and nominal extremity CBCT geometry are assumed. (C) Pixel size and scintillator thickness yielding optimal detectability for the trabecular imaging task (aobj=0.06 mm) as a function of magnification and focal spot size. (D) Relative detectability values (normalized to detectability at the nominal CBCT geometry and aspot = 0.3 mm) at the optimal detector configurations found in (C).
The current FPD-based extremity CBCT scanner implements a stationary anode x-ray source with a 0.5 FS (IEC336). Clinical protocols use 2×2 detector binning with 0.388 mm pixels to maintain a ~30 sec scan time. In this configuration, there is little benefit from using a smaller focal spot, since detector blur associated with relatively large pixels then dominate the system MTF.49 A CMOS detector provides finer pixels (with similar or faster scan time), motivating reconsideration of the optimal x-ray focal spot size. Fig. 4B shows the detectability for a 0.06 mm feature size as a function of pixel size and focal spot size. To enable comparison with the current system, CsI:Tl thickness of 0.7 mm was assumed (as in the a-Si:H FPD sensor) and d′2 at each apix was normalized by the value at aspot=0.5 mm. For apix = 0.1 mm, the system MTF is dominated by source blur at aspot = 0.5 mm, and a 2× – 2.5× improvement in d′2 can be achieved by adopting an x-ray source with a focal spot of 0.2 – 0.3 mm. The benefits of smaller aspot are less pronounced for pixel size >0.25 mm used in the current extremity CBCT (typically 0.139 mm pixel size).
The selection of the x-ray source for benchtop experimentation and implementation on the CMOS-based prototype balanced the need for small focal spot against design requirements such as x-ray power (≥ 1 kW) and the size of the x-ray unit able to fit inside the CBCT gantry. Based on these considerations, the compact (~40×20×30 cm3) rotating anode IMD RTM 37 tube with 0.3 FS (IEC336) was chosen after survey of commercially available systems.
Figure 4C expands the investigation of CMOS detector configurations to hypothetical system geometries that differ from the current extremity CBCT system in terms of system magnification. Pixel size and scintillator thicknesses yielding optimal d′2 for a 0.06 mm feature size are shown for a range of focal spot sizes (each aspot is one line) and magnifications (each M is a marked as a data point). Since the x-ray exposure was kept constant at 0.126 mAs/projection (as in Fig. 3), the fluence on the detector decreases with M. At M=1.1, the impact of source blur is minimized and the detector fluence is high, and thus the optimization is primarily driven by detector resolution. This results in the same optimal configuration with tCsI of ~0.3 mm and apix of ~0.65 mm for all focal spot sizes. As the magnification increases, the detector input dose decreases, but the resolution requirements for the task diminish because the feature is magnified. The net result is that detector MTF becomes less of a factor at higher magnifications and the optimization shifts towards thicker CsI:Tl and larger pixel sizes to counteract the loss of input quanta. This effect is most noticeable for the focal spot of 0.5 mm (dash-dot line), where source blur dominates at high magnifications and d′2 is primarily driven by reduction in quantum noise with thicker scintillators and larger pixels. For aspot of 0.2 mm (solid line), on the other hand, system MTF is not as strongly affected by focal spot blur. The optimal detector configuration appears to be still partly driven by system resolution, favoring thinner CsI:Tl than for larger focal spots. Configurations with aspot of 0.3 mm (dashed line consistent with the source used in experimental studies) represent a somewhat intermediate case. For magnifications of up to 1.3, the optimal apix and tCsI are similar to those for focal spot of 0.2 mm. At those magnifications, the system MTF is dominated by detector blur for both x-ray focal spots. (Note that the optimal configurations at M=1.3 agree well with the optimum in Fig. 3D, where source blur was not included in the simulation). As M increases above 1.3, source blur becomes more prominent and the optimization switches toward using thicker scintillator and larger pixels to improve the noise component of d′2. In all cases, the diminishing need for high spatial resolution due to magnification of the feature of interest allows for substantial increase in optimal apix and tCsI at high values of M.
Figure 4D shows the detectability as a function of M and tCsI for the optimal detector configurations identified in Fig. 4C. The detectabilities are normalized by the optimal value at the nominal CBCT configuration and aspot of 0.3 mm. Consistent with Fig. 4B, d′2 generally improves with decreasing focal spot size. However, the detectability at optimal detector configuration decreases with increasing M. Despite the diminishing resolution requirements at high magnifications, the increase in optimal apix and tCsI required to compensate for the loss of input quanta associated with long SDDs leads to an unfavorable tradeoff between system MTF and NNPS. The resulting decrease in d′2 is especially pronounced at aspot of 0.5 mm, where system resolution is increasingly dominated by source blur at high values of M. For fixed source output and patient dose, configurations with smaller magnification and thus improved detector input fluence are preferred for the high resolution tasks considered in this work.
3.B. Experimental evaluation
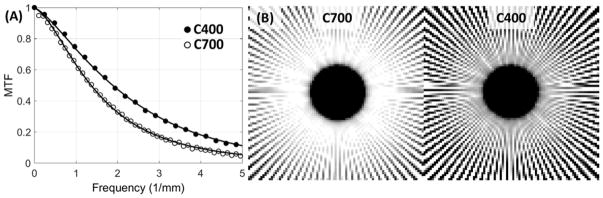
Figure 5A shows MTF measurements for the C400 and C700 configurations. The frequency at 50% modulation (f50) is ~1.4× higher for the detector with thinner scintillator. Solid lines indicate empirical fits to detector MTF used in the cascaded systems model (Eqs. 7, 8 and 17). The parameterization of T3 in Eqs. 8 and 17 appears to adequately capture the thickness-dependent component of scintillator blur, as indicated by good quality of the fit for both configurations. Superior spatial resolution of the C400 is confirmed in Fig. 5B, which show images of a Gammex 91437 (Gammex, WI) radial resolution gauge placed on the surface of each detector (mean of 50 frames acquired at 6.3 mA and 20 ms). Compared to C700 (left panel), C400 (right panel) maintains modulation of the line pattern (i.e., is free from signal aliasing) up to higher spatial frequencies.
Figure 5.
(A) Experimental measurements of detector MTF for CMOS sensors with 0.7 mm CsI:Tl (open circles) and 0.4 mm CsI:Tl (closed circles). Lines represent MTFs computed using the cascaded systems model. (B) Contact images of the GAMMEX 91437 resolution gauge obtained with 0.7 mm CsI:Tl (left) and 0.4 mm CsI:Tl (right).
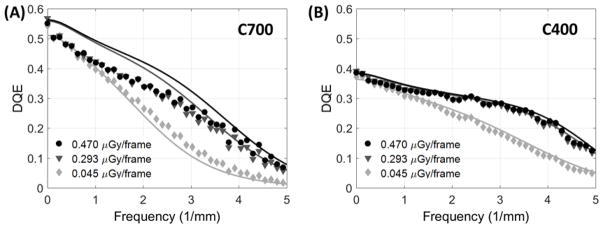
Fig. 6 shows measured DQE for the two detectors (points) along with simulated DQE obtained from the cascaded systems model (lines). DQE is presented for two values of detector entrance dose in the quantum-limited range and at a low entrance dose of ~0.5 mGy/frame, where the impact of electronic noise becomes visible at high frequencies. (All doses were measured behind additional filtration emulating attenuation by 15 cm water; see Sec. 2.C.1). The C700 outperforms C400 for spatial frequencies up to ~3 mm−1, where the DQE of both detectors begins to converge, indicating a regime where the improved MTF of the C400 detector overcomes the elevated noise (reduced QDE) associated with the thinner scintillator. Near the Nyquist frequency, C400 achieves better DQE than C700 for all considered dose levels (0.127 for C400 vs 0.069 for C700 at 0.470 μGy/frame; 0.117 vs 0.057 at 0.293 μGy/frame; 0.049 vs 0.017 at 0.045 μGy/frame). The noise-equivalent dose, the dose at which quantum noise reaches the same magnitude as electronics noise73, is ~0.03 μGy/frame.
Figure 6.
Measured (points) and simulated (lines) DQE for a range of dose levels for the CMOS detector with (A) 0.7 mm thick scintillator and (B) 0.4 mm scintillator.
We observed fair agreement between simulated and measured DQE. Most significant discrepancies were observed at low frequencies for the C700 detector, likely due to inaccuracies in estimation of packing fraction fCsI and K-fluorescence reabsorption blur Tk. Since direct measurements of those parameters for the two sensors were not available, their implementation in the model were based on approximations, namely: the same value of fCsI was used for C400 and C700, chosen empirically to yield fair agreement with measured NNPS(0) for both detectors; however, a better overall fit in DQE could be potentially achieved by adjusting the packing fraction individually for each detector. With respect to Tk, the model uses an analytical formula adapted from the work of Que et al60 The impact of Tk in the total K-fluorescence MTF Tktot (Eq. 9) becomes negligible at ~3 mm−1, reflecting the relatively long range of K-fluorescence photons. This implies that potential inaccuracies in the analytical estimate of Tk (originally derived for amorphous selenium) are most likely to affect low- to mid- frequency DQE. Further refinement of the estimates of fCsI and Tk requires dedicated experimental techniques and more sophisticated scintillator models (e.g., Monte Carlo simulations74, 75) that are beyond the scope of this study. In the present work, the impact of these approximations is limited because we are primarily concerned with tasks emphasizing mid- to high-frequencies (>2 mm−1), where the simulation agrees well with measurements.
3.C. Cadaver Imaging
Reconstructions of a cadaveric knee obtained using the C400 and C700 configurations are shown in Figure 7. The central CTDI dose was 15 mGy in both scans.
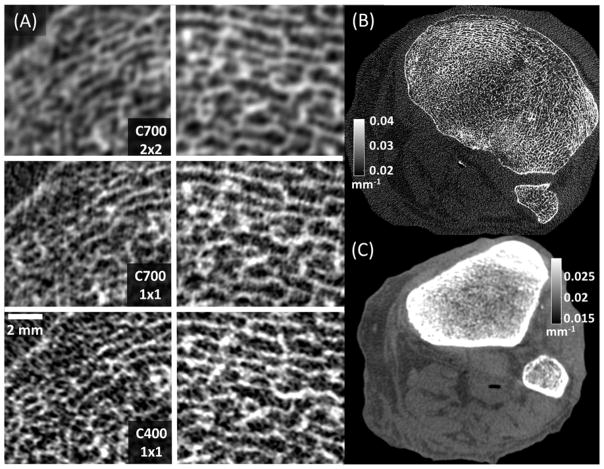
Figure 7.
(A) Magnified views of two trabecular regions in the subchondral bone of a cadaver knee imaged using CMOS detectors with different pixel sizes and scintillator thicknesses. High resolution bone reconstruction was used. (A, top) Reconstructions of 2×2 binned C700 projections, mimicking the pixel size of current a-Si:H FPDs. (A, middle) Reconstructions of C700 projections in 1×1 binning, showing the benefits of reduced pixel size provided by CMOS. (A, bottom) Images acquired with C400 in 1×1 binning, illustrating the visualization of trabecular detail using a thin scintillator. (B) A complete axial slice of C400 reconstruction obtained using high resolution protocol (C) A C400 reconstruction obtained using a soft-tissue protocol with 4×4 pixel binning.
Figure 7A shows details of two trabecular regions in high resolution bone reconstructions of the knee. The images in the top row of Figure 7A were generated using the high-resolution reconstruction protocol, but after digital 2×2 pixel binning of C700 projections to mimic the ~0.2 mm pixels of a-Si:H FPDs operated at full resolution. Comparison with images obtained using C700 and the native pixel size of 0.1 mm in the center row of Fig. 7A reveals the improvement in visualization of trabecular detail enabled by the fine pixel size of CMOS detectors.
Bone protocol reconstruction of projections acquired using the custom CMOS with 0.4 mm CsI:Tl are presented in the bottom row of Figs. 7A (trabecular regions of interest) and 7B (complete axial slice). Adoption of a thin scintillator further enhances the visibility of the trabecular pattern compared to C700. As expected based on the simulation studies, where the increase in d′2 with C400 was ~10–20%, the improvement in visualization of high frequency detail is perceptible, but modest, and accompanied by slightly increased noise. This increased noise might affect visualization of low contrast soft-tissue structures. However, since very high spatial resolution is not essential in soft tissue evaluation, the impact of elevated noise can be mitigated at least in part by binning the projections, using larger voxels and adjusting the reconstruction filter. As shown in Fig. 7C, soft-tissue reconstructions obtained using C400 and the soft-tissue protocol with 4×4 digital binning (Sec. 2.C.2) achieve adequate visualization of soft-tissues.
4. DISCUSSION AND CONCLUSIONS
Analysis of task-based detectability points to the benefits of CMOS detectors in high-resolution applications of extremity CBCT. A CMOS detector was found to achieve ~4× better detectability for 0.06 mm features compared to an otherwise identical detector (apix = 0.1 mm) that exhibited electronic noise comparable to an a-Si:H FPD. This is because the low electronic noise of CMOS detectors allows the system to take advantage of smaller apertures and improved sampling associated with fine detector pixels. Pixel size <0.1 mm was preferred for all tasks considered (aobj = 0.03 to 0.2 mm). In addition to higher spatial resolution, CMOS detectors offer 3–4× faster frame rate than a-Si:H FPDs. Scan times of 20–30 sec are anticipated for CMOS-based extremity CBCT operated at full detector resolution, reducing the risk of patient motion during acquisition.
Since the optimal pixel size for high-frequency tasks is smaller for CMOS detectors compared to a-Si:H FPDs, such applications also benefit from using a scintillator that is thinner than the 0.6–0.7 mm CsI:Tl that is commonly employed. In simulation studies, a ~0.4 mm scintillator was shown to provide 10–20% better detectability for high-frequency tasks compared to a 0.7 mm scintillator for conditions typical of extremity CBCT. DQE measurements of CMOS detectors with 0.4 mm CsI (C400) and 0.7 mm CsI (C700) showed that while C700 showed better DQE at low frequencies, C400 provided improved DQE at frequencies >3 lp/mm. CBCT imaging of a cadaveric knee confirmed a modest but perceptible improvement in delineation of trabecular detail with the custom CMOS detector with 0.4 mm CsI:Tl.
The decrease in DQE and detectability for low-frequency tasks may hamper soft-tissue imaging in a system based on a detector with thin scintillator. However, software binning of projection data obtained with C400 at imaging dose of 15 mGy yielded adequate delineation of soft-tissues (muscles, tendons, and fat). Overall, the prototype CMOS detector with 0.4 mm scintillator provided improved performance in imaging of trabecular bone compared to a conventional screen without major detriment to soft-tissue visualization.
The results discussed above were obtained assuming the geometry of current generation extremity CBCT. This compact configuration was developed specifically to enable weight bearing imaging of a single extremity. The primary constraint resulting from this consideration is that the detector needs to rotate between the legs of the subject, limiting system magnification. It is interesting to consider potential benefits of other system configurations, free of this restriction. To this end, additional study was performed to analyze the impact of altering the magnification by increasing the SDD and keeping the SAD constant. The current value of SAD (~400 mm) cannot be significantly shortened in a realistic system configuration considering spatial constraints (size of the extremity and the collimator box) and the available x-ray source cone angles. When x-ray source output and patient dose are kept constant and SDD (and thus magnification) is increased, the detectability is generally maximized at thicker CsI and larger pixel sizes. This is partly because larger magnifications exhibit somewhat reduced demands on detector resolution, allowing the optimization to be driven by noise reduction. However, the detectability at optimal detector configurations decreases with M, indicating that the overall tradeoff between system MTF and NPS still favors configurations with high enough input fluence to allow using thin scintillators and small pixels to minimize detector blur.
The tradeoffs associated with system magnification would be different in a study where the source output was adjusted to yield constant detector input fluence across all detector configurations. Under such conditions, systems with higher magnification would likely be favored since the optimization would not contend with the loss in input quanta. However, the constraint of fixed source output is a reasonable starting point with respect to fixing the dose to the patient. This is not only due to patient safety considerations, but also because of the limited power available in x-ray tubes with focal spot sizes small enough (≤0.2 mm) not to dominate system resolution at high magnifications.
There are recognized limitations of the CMOS detector model. A slight discrepancy between simulated and measured DQE was attributed primarily to inaccuracy in the model of K-fluorescence blur.60 This discrepancy is unlikely to influence the general conclusions, in particular with respect to medium and high-frequency tasks where there was good agreement between simulation and measurement. Furthermore, the thickness-dependent model of scintillator MTF was parameterized based on measurements on C400 and C700. This parameterization may include effects unrelated to scintillator blur, such as differences in optical coupling between the two sensors. The thickness of the scintillators is also not exactly known and subject to manufacturing tolerances. Nevertheless, we believe that the model properly captures general trends associated with reduced scintillator thickness, as confirmed in experimental studies with the two detectors.
The task model in the current work represents discrimination of two stimuli by an NPW observer. It is recognized that this choice may not exactly represent the performance of a computer algorithm in quantitative analysis of bone quality. Rather, it is intended as a reasonable approximation of the fundamental capability of the system to resolve high resolution details, under an assumption that any improvement in this capability will likely benefit the analysis of trabecular microstructure. Conventionally, such analysis involves thresholding and binarization to extract the bone voxels and measure structural indices,76 which may be more closely related to estimation tasks than detection/discrimination tasks.77 It is anticipated that improved system performance in the discrimination task will translate also to improved performance in the threshold-based quantitative measurements. A potentially more challenging extension of this work might involve predicting the performance of a texture classification algorithm applied to trabecular regions.78–81 The investigation of textural biomarkers of bone quality is still in early stages and there is no consensus yet as to which of the textural features are best suited for diagnostic applications. For some features, such as those based on the grey-level co-occurrence matrix,82 improved conspicuity of fine trabecular detail may improve the sensitivity of classification. However, it is possible that other textural features may be less sensitive to this aspect of system design. Overall, new task functions and observer models specific to the features of interest will need to be developed to enable task-based analysis of textural biomarkers. Such development is beyond the scope of this work.
Finally, the optimization studies were performed in projection domain to focus the analysis on the fundamental aspects of imaging performance. Achieving best possible baseline imaging capability, as reflected in the 2D metrics evaluated in this work, is an essential first step in the development of the new capability for high resolution analysis of bone microstructure. Numerous practical design considerations, more amendable to analysis using models of 3D imaging performance, were not investigated. Such considerations include x-ray scatter, shift-variant x-ray source blur, blur due to gantry motion in continuous pulsed acquisition and reconstruction algorithm.
The current generation extremity CBCT relies on algorithmic scatter correction methods83–85 to achieve adequate soft tissue contrast despite the relatively high SPRs of ~0.5–1.84 Previous work indicated however a modest benefit in contrast-to-noise ratio (CNR) from an anti-scatter grid in extremity CBCT geometry.84 Ongoing work on a prototype CMOS-based system will determine whether the improvement in CNR due to a grid translates to improvement in quantitative metrics of bone microstructure and whether such benefit outweighs potential practical challenges in calibration and grid line artifact correction.
A fairly general, simplified model of x-ray focal spot was used in this work. This model was not intended to simulate any particular x-ray tube, but to provide an adjustable model to investigate “first-order” effects of source blur. This approach assumes that the blur is isotropic and shift-invariant. In practice, neither of those assumptions is perfectly satisfied. Pinhole measurements86 of the focal spot on the RTM37 tube used in this work revealed a complex, non-isotropic shape with full width at half maximum (FWHM) of ~0.2 mm in the cathode-anode direction, close to the stated nominal value. In systems that are not dominated by focal spot blur, such as the proposed CMOS CBCT using ~0.1 mm detector pixels, the shape of the focal spot is unlikely to have substantial impact on system resolution. A potentially more significant effect is the variation in the apparent focal spot size seen in different areas of the detector. For the extremity CBCT geometry, the apparent focal spot width for a 0.3 mm x-ray source is ~0.16 mm at the edge of the 300 mm detector on the cathode side of the source, ~0.1 mm at the center and ~0.025 mm on the anode side. Inside a projection view of ~100 mm diameter object (e.g. human tibia), the apparent focal spot varies from ~0.12 mm on the cathode side to ~0.06 mm on the anode side. In 3D imaging, magnification changes throughout the field of view, resulting in even more complex combination of shift variant source and detector blurs, additionally affected by angular sampling and the imaging orbit (short or full scan). A study evaluating local 3D imaging performance in the presence of shift variant blurs was recently reported.86 An extremities CBCT system with 0.3 mm focal spot size, 0.1 mm detector pixels, and short scan acquisition was simulated using a geometric forward projection model. Fidelity of Feldkamp reconstruction of a trabecular bone phantom was assessed throughout the field of view using Root Mean-Squared Error (RMSE). There was ~7% change in RMSE between the best and worst values. Interestingly, the short scan orbit provided a potential advantage over a full scan in that a region of the field of view was sampled primarily by the cathode side of the source, thereby improving local resolution. Overall, however, the fidelity of the reconstruction was only slightly affected by the shift variant source blur, likely because detector blur dominates in this system geometry.
Another practical consideration not investigated in this study is the effect of continuous gantry rotation. Assuming that the Xineos3030 detector is operating at 30 fps, the total scan time for the 210° trajectory will be ~17 seconds. For 5 ms x-ray pulse length (attainable by the RTM37 tube used here), the distance travelled by an object at the radius of 50 mm from the axis of rotation is 0.055 mm/pulse. After considering system magnification, this distance is less than the pixel size. The resulting motion blur is thus minimal, but detailed investigation of this effect is left to experimental studies on a prototype scanner.
Future work will involve optimization of reconstruction algorithms for trabecular imaging. Of particular interest are novel model-based iterative reconstruction (MBIR) algorithms87 incorporating models of system blur88. Such algorithm are able to account for noise correlations due to blur,88 to incorporate shift-variant source blur86, 89 and potentially to model blur due to gantry rotation. This may improve trabecular imaging by achieving resolution recovery with better resolution-noise properties then using standard deblurring methods.
Based on this study, the custom CMOS detector with 0.4 mm scintillator and the compact rotating anode x-ray source with 0.3 mm focal spot have been translated to the gantry of an extremity CBCT system (OnSight 3D) to develop a prototype high-resolution scanner for clinical studies. Parallel work involves development of motion correction90, 91 and advanced reconstruction algorithms with model-based deburring to further enhance system resolution discussed above.88 Evaluation against gold-standard micro-CT in metrics of bone microstructure using bone core samples is ongoing. A clinical pilot study of test-retest reproducibility in bone morphometry in OA patients is in preparation. It is anticipated that the improved performance in high-frequency imaging tasks provided by the CMOS detector will enable robust measurements of bone microarchitecture in vivo, benefiting image-based assessment of osteoporosis, osteoarthritis, and monitoring of fracture healing.
Acknowledgments
The research was supported by NIH Grant 1R01-EB-018896, 1R21-CA-208821 and 1R21-AR-062293. Qian Cao was supported by the Howard Hughes Medical Institute International Student Research Fellowship. The authors thank Dr. Jennifer Xu and Dr. Grace Jianan Gang (Dept. of Biomedical Engineering, Johns Hopkins University) for useful discussions about cascaded systems modeling. Thanks also to Yves Kessener, Bart Dillen, Greg Combs, and Dr. Inge Peters (Teledyne Dalsa) for their assistance in development of the custom CMOS detector. The cadaver specimen used in this work was acquired from Mr. Ronn Wade (Anatomy Board, University of Maryland) in accordance with state and institutional requirements.
References
- 1.Tuominen EKJ, Kankare J, Koskinen SK, Mattila KT. Weight-bearing CT imaging of the lower extremity. AJR Am J Roentgenol. 2013;200(1):146–8. doi: 10.2214/AJR.12.8481. [DOI] [PubMed] [Google Scholar]
- 2.Segal NA, Frick E, Duryea J, et al. Correlations of medial joint space width on fixed-flexed standing computed tomography and radiographs with cartilage and meniscal morphology on magnetic resonance imaging. Arthritis Care Res. 2016;68(10):1410–1416. doi: 10.1002/acr.22888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Carrino JA, Al Muhit A, Zbijewski W, et al. Dedicated cone-beam CT system for extremity imaging. Radiology. 2014;270(3):816–24. doi: 10.1148/radiol.13130225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Demehri S, Muhit A, Zbijewski W, et al. Assessment of image quality in soft tissue and bone visualization tasks for a dedicated extremity cone-beam CT system. Eur Radiol. 2015;25(6):1742–1751. doi: 10.1007/s00330-014-3546-6. [DOI] [PubMed] [Google Scholar]
- 5.Huang AJ, Chang CY, Thomas BJ, MacMahon PJ, Palmer WE. Using cone-beam CT as a low-dose 3D imaging technique for the extremities: initial experience in 50 subjects. Skeletal Radiol. 2015;44(6):797–809. doi: 10.1007/s00256-015-2105-9. [DOI] [PubMed] [Google Scholar]
- 6.Kothari M, Guermazi A, Von Ingersleben G, et al. Fixed-flexion radiography of the knee provides reproducible joint space width measurements in osteoarthritis. Eur Radiol. 2004;14(9):1568–1573. doi: 10.1007/s00330-004-2312-6. [DOI] [PubMed] [Google Scholar]
- 7.Cao Q, Thawait G, Gang G, et al. Characterization of 3D joint space morphology using an electrostatic model (with application to osteoarthritis) Phys Med Biol. 2015;60:947–960. doi: 10.1088/0031-9155/60/3/947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Segal NA, Nevitt MC, Lynch JA, Niu J, Torner JC, Guermazi A. Diagnostic performance of 3D standing CT imaging for detection of knee osteoarthritis features. Phys Sportsmed. 2015;43(3):213–220. doi: 10.1080/00913847.2015.1074854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Marzo J, Kluczynski M, Notino A, Bisson L. Comparison of a novel weightbearing cone beam computed tomography scanner versus a conventional computed comography scanner for measuring patellar instability. Orthop J Sport Med. 2016;4(12):1–7. doi: 10.1177/2325967116673560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Netto CC, Demehri S, Dein EJ, et al. Flexible adult acquired flatfoot deformity: comparison between weightbearing and nonweightbearing cone-beam CT examinations. AOFAS Annu. Meet; 2016. [Google Scholar]
- 11.Muhit AA, Arora S, Ogawa M, et al. Peripheral quantitative CT (pQCT) using a dedicated extremity cone-beam CT scanner. 2013;8672:867203. doi: 10.1117/12.2006939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Marinetto E, Brehler M, Sisniega A, et al. Quantification of bone microarchitecture in ultra-high resolution extremities cone-beam CT with a CMOS detector and compensation of patient motion. Comput. Assist. Radiol. Surg. 30th Int. Congr. Exhib; 2016. [Google Scholar]
- 13.Cao Q, Brehler M, Sisniega A, et al. High-resolution cone-beam CT of the extremities and cancellous bone architecture with a CMOS detector. AAPM Annu. Meet; 2016; p. 3797. [Google Scholar]
- 14.Brehler M, Marinetto E, Cao Q, et al. Quantitative assessment of trabecular bone microarchitecture using high-resolution extremities cone-beam CT. RSNA Sci. Assem. Annu. Meet; 2016. [Google Scholar]
- 15.Cao Q, Brehler M, Sisniega A, et al. High-resolution extremity cone-beam CT with a CMOS detector: Task-based optimization of scintillator thickness. SPIE Med Imaging. 2017;10132:1–6. doi: 10.1117/12.2255695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Majumdar S, Genant HK, Grampp S, et al. Correlation of trabecular bone structure with age, bone mineral density, and osteoporotic status: in vivo studies in the distal radius using high resolution magnetic resonance imaging. J Bone Miner Res. 1997;12(1):111–118. doi: 10.1359/jbmr.1997.12.1.111. [DOI] [PubMed] [Google Scholar]
- 17.Bredella MA, Misra M, Miller KK, et al. Distal radius in adolescent girls with anorexia nervosa: trabecular structure analysis with high-resolution flat-panel volume CT. Radiology. 2008;249(3):938–946. doi: 10.1148/radiol.2492080173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Issever AS, Link TM, Kentenich M, et al. Assessment of trabecular bone structure using MDCT: Comparison of 64- and 320-slice CT using HR-pQCT as the reference standard. Eur Radiol. 2010;20(2):458–468. doi: 10.1007/s00330-009-1571-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Walsh CJ, Phan CM, Misra M, et al. Women with anorexia nervosa: finite element and trabecular structure analysis by using flat-panel volume CT. Radiology. 2010;257(1):167–174. doi: 10.1148/radiol.10100222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Burghardt AJ, Link TM, Majumdar S. High-resolution computed tomography for clinical imaging of bone microarchitecture. Clin Orthop Relat Res. 2011;469(8):2179–2193. doi: 10.1007/s11999-010-1766-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mulder L, Van Rietbergen B, Noordhoek NJ, Ito K. Determination of vertebral and femoral trabecular morphology and stiffness using a flat-panel C-arm-based CT approach. Bone. 2012;50(1):200–208. doi: 10.1016/j.bone.2011.10.020. [DOI] [PubMed] [Google Scholar]
- 22.Van Dessel J, Huang Y, Depypere M, Rubira-Bullen I, Maes F, Jacobs R. A comparative evaluation of cone beam CT and micro-CT on trabecular bone structures in the human mandible. Dentomaxillofacial Radiol. 2013;42(8) doi: 10.1259/dmfr.20130145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Klintström E, Smedby Ö, Moreno R, Brismar TB. Trabecular bone structure parameters from 3D image processing of clinical multi-slice and cone-beam computed tomography data. Skeletal Radiol. 2014;43(2):197–204. doi: 10.1007/s00256-013-1766-5. [DOI] [PubMed] [Google Scholar]
- 24.Harvey NC, Gluer CC, Binkley N, et al. Trabecular bone score (TBS) as a new complementary approach for osteoporosis evaluation in clinical practice. Bone. 2015;78:216–224. doi: 10.1016/j.bone.2015.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Buckland-Wright C. Subchondral bone changes in hand and knee osteoarthritis detected by radiography. Osteoarthr Cartil. 2004;12(SUPLL):10–19. doi: 10.1016/j.joca.2003.09.007. [DOI] [PubMed] [Google Scholar]
- 26.Weinans H, Siebelt M, Agricola R, Botter SM, Piscaer TM, Waarsing JH. Pathophysiology of peri-articular bone changes in osteoarthritis. Bone. 2012;51(2):190–6. doi: 10.1016/j.bone.2012.02.002. [DOI] [PubMed] [Google Scholar]
- 27.Chappard C, Peyrin F, Bonnassie A, et al. Subchondral bone micro-architectural alterations in osteoarthritis: A synchrotron micro-computed tomography study. Osteoarthr Cartil. 2006;14:215–223. doi: 10.1016/j.joca.2005.09.008. [DOI] [PubMed] [Google Scholar]
- 28.Adams JE. Advances in bone imaging for osteoporosis. Nat Rev Endocrinol. 2012;9(1):28–42. doi: 10.1038/nrendo.2012.217. [DOI] [PubMed] [Google Scholar]
- 29.Jiang Y, Zhao J, Liao EY, Dai RC, Wu XP, Genant HK. Application of micro-ct assessment of 3-d bone microstructure in preclinical and clinical studies. J Bone Miner Metab. 2005;23(SUPPL 1):122–131. doi: 10.1007/BF03026336. [DOI] [PubMed] [Google Scholar]
- 30.Boutroy S, Bouxsein ML, Munoz F, Delmas PD. In vivo assessment of trabecular bone microarchitecture by high-resolution peripheral quantitative computed tomography. J Clin Endocrinol Metab. 2005;90(12):6508–6515. doi: 10.1210/jc.2005-1258. [DOI] [PubMed] [Google Scholar]
- 31.Macneil JA, Boyd SK. Accuracy of high-resolution peripheral quantitative computed tomography for measurement of bone quality. 2007;29:1096–1105. doi: 10.1016/j.medengphy.2006.11.002. [DOI] [PubMed] [Google Scholar]
- 32.Kroker A, Zhu Y, Manske SL, Barber R, Mohtadi N, Boyd SK. Quantitative in vivo assessment of bone microarchitecture in the human knee using HR-pQCT. Bone. 2016;97:43–48. doi: 10.1016/j.bone.2016.12.015. [DOI] [PubMed] [Google Scholar]
- 33.Zentai G, Fellow I. Comparison of CMOS and a-Si flat panel imagers for x-ray imaging. IEEE Int Conf Imaging Syst Tech. 2011:194–200. [Google Scholar]
- 34.Konstantinidis AC, Szafraniec MB, Speller RD, Olivo A. The Dexela 2923 CMOS X-ray detector: A flat panel detector based on CMOS active pixel sensors for medical imaging applications. Nucl Instruments Methods Phys Res Sect A Accel Spectrometers, Detect Assoc Equip. 2012;689:12–21. [Google Scholar]
- 35.Esposito M, Anaxagoras T, Fant A, et al. DynAMITe: a wafer scale sensor for biomedical applications. J Instrum. 2011;6(12):C12064–C12064. [Google Scholar]
- 36.Shen Y, Zhong Y, Lai CJ, Wang T, Shaw CC. Cone beam breast CT with a high pitch (75 μm), thick (500 μm) scintillator CMOS flat panel detector: Visibility of simulated microcalcifications. Med Phys. 2013;40(10):101915. doi: 10.1118/1.4820440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Choi JG, Park HS, Kim Y, Choi YW, Ham TH, Kim HJ. Characterization of prototype full-field breast tomosynthesis by using a CMOS array coupled with a columnar CsI(Tl) scintillator. J Korean Phys Soc. 2012;60(3):521–526. [Google Scholar]
- 38.Patel T, Klanian K, Gong Z, Williams MB. Detective quantum efficiency of a CsI-CMOS x-ray detector for breast tomosynthesis operating in high dynamic range and high sensitivity modes. Int Work Digit Mammogr. 2012:80–87. doi: 10.1007/978-3-642-31271-7_11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gazi PM, Yang K, Burkett GW, Aminololama-Shakeri S, Anthony Seibert J, Boone JM. Evolution of spatial resolution in breast CT at UC Davis. Med Phys. 2015;42(4):1973. doi: 10.1118/1.4915079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhao C, Kanicki J, Konstantinidis AC, Patel T. Large area CMOS active pixel sensor x-ray imager for digital breast tomosynthesis: Analysis, modeling, and characterization. Med Phys. 2015;42(11):6294–6308. doi: 10.1118/1.4932368. [DOI] [PubMed] [Google Scholar]
- 41.Zhao C, Kanicki J. Task-based modeling of an 5k ultra-high-resolution medical imaging system for digital breast tomosynthesis. IEEE Trans Med Imaging. 2017;(99):1–1. doi: 10.1109/TMI.2017.2695982. [DOI] [PubMed] [Google Scholar]
- 42.Vedantham S, Shrestha S, Shi L, Vijayaraghavan G, Karellas A. Task-specific optimization of scintillator thickness for CMOS-detector based cone-beam breast CT. AAPM Annu. Meet; American Association of Physicists in Medicine; 2016. p. 3346. [Google Scholar]
- 43.Siewerdsen JH, Antonuk LE, El-Mohri Y, et al. Empirical and theoretical investigation of the noise performance of indirect detection, active matrix flat-panel imagers (AMFPIs) for diagnostic radiology. Med Phys. 1997;24(1):71. doi: 10.1118/1.597919. [DOI] [PubMed] [Google Scholar]
- 44.Gang GJ, Lee J, Stayman JW, et al. Analysis of Fourier-domain task-based detectability index in tomosynthesis and cone-beam CT in relation to human observer performance. Med Phys. 2011;38(4):1754–1768. doi: 10.1118/1.3560428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tward DJ, Siewerdsen JH. Cascaded systems analysis of the 3D noise transfer characteristics of flat-panel cone-beam CT. Med Phys. 2008;35(12):5510. doi: 10.1118/1.3002414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Tward DJ, Siewerdsen JH. Noise aliasing and the 3D NEQ of flat-panel cone-beam CT: effect of 2D/3D apertures and sampling. Med Phys. 2009;36(8):3830–3843. doi: 10.1118/1.3166933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cunningham IA, Yao J, Subotic V. Cascaded models and the DQE of flat-panel imagers: noise aliasing, secondary quantum noise and reabsorption. Med Imaging Phys Med Imaging Proc SPIE. 2002;4682:61–72. [Google Scholar]
- 48.Vedantham S, Karellas A, Suryanarayanan S. Solid-state fluoroscopic imager for high-resolution angiography: Parallel-cascaded linear systems analysis. Med Phys. 2004;31(5):1258–1268. doi: 10.1118/1.1689014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zbijewski W, De Jean P, Prakash P, et al. A dedicated cone-beam CT system for musculoskeletal extremities imaging: design, optimization, and initial performance characterization. Med Phys. 2011;38(8):4700. doi: 10.1118/1.3611039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Prakash P, Zbijewski W, Gang GJ, et al. Task-based modeling and optimization of a cone-beam CT scanner for musculoskeletal imaging. Med Phys. 2011;38(10):5612–29. doi: 10.1118/1.3633937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zhao C, Konstantinidis AC, Zheng Y, Anaxagoras T. 50 μm pixel pitch wafer-scale CMOS active pixel sensor x-ray detector for digital breast tomosynthesis. Phys Med Biol. 2015;60:8977. doi: 10.1088/0031-9155/60/23/8977. [DOI] [PubMed] [Google Scholar]
- 52.Yao J, Cunningham IA. Parallel cascades: new ways to describe noise transfer in medical imaging systems. Med Phys. 2001;28(10):2020–2038. doi: 10.1118/1.1405842. [DOI] [PubMed] [Google Scholar]
- 53.Siewerdsen JH, Jaffray DA. Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography) Med Phys. 2000;27(8):1903–1914. doi: 10.1118/1.1286590. [DOI] [PubMed] [Google Scholar]
- 54.Punnoose J, Xu J, Sisniega A, Zbijewski W, Siewerdsen JH. Technical Note: spektr 3.0—A computational tool for x-ray spectrum modeling and analysis. Med Phys Med Phys Med Phys Med Phys Med Phys. 2016;43(3057):4711–41906. doi: 10.1118/1.4955438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Berger M, Hubbell JH, Seltzer SM, et al. XCOM: photon cross sections database. NIST Stand regerence database. 1998;8(1):3587–3597. [Google Scholar]
- 56.Metz CE, Vyborny CJ. Wiener spectral effects of spatial correlation between the sites of characteristic x-ray emission and reabsorption in radiographic screen-film systems. Phys Med Biol. 1983;28(5):547–564. doi: 10.1088/0031-9155/28/5/008. [DOI] [PubMed] [Google Scholar]
- 57.Howansky A, Peng B, Lubinsky AR, Zhao W. Deriving depth-dependent light escape efficiency and optical Swank factor from measured pulse height spectra of scintillators. Med Phys. 2017;(November):1–14. doi: 10.1002/mp.12083. [DOI] [PMC free article] [PubMed]
- 58.Zhao W, Ristic G, Rowlands J. X-ray imaging performance of structured cesium iodide scintillators. Med Phys. 2004;31:2594–2605. doi: 10.1118/1.1782676. [DOI] [PubMed] [Google Scholar]
- 59.Chan HP, Doi K. Energy and angular dependence of x-ray absorption and its effect on radiographic response in screen--film systems. Phys Med Biol. 1983;28(5):565–79. doi: 10.1088/0031-9155/28/5/009. [DOI] [PubMed] [Google Scholar]
- 60.Que W, Rowlands J. X-ray imaging using amorphous selenium: Inherent spatial resolution. Med Phys. 1995;22(4):365. doi: 10.1118/1.597471. [DOI] [PubMed] [Google Scholar]
- 61.Barrett H, Swindell W. Radiological Imaging: The Theory of Image Formation, Detection, and Processing. Academic; New York: 1981. [Google Scholar]
- 62.Richard S. Optimization of imaging performance and conspicuity in dual-energy x-ray radiography. University of Toronto; 2008. [Google Scholar]
- 63.Lubinsky AR, Zhao W, Ristic G, Rowlands JA. Screen optics effects on detective quantum efficiency in digital radiography: zero-frequency effects. Med Phys. 2006;33(5):1499–1509. doi: 10.1118/1.2188082. [DOI] [PubMed] [Google Scholar]
- 64.Lubberts G. Random noise produced by x-Ray fluorescent screens. J Opt Soc Am. 1968;58(11):1475. [Google Scholar]
- 65.Badano A, Gagne RM, Gallas BD, Jennings RJ, Boswell JS, Myers KJ. Lubberts effect in columnar phosphors. Med Phys. 2004;31(11):3122–3131. doi: 10.1118/1.1796151. [DOI] [PubMed] [Google Scholar]
- 66.Howansky A, Lubinsky A, Ghose S, Suzuki K, Zhao W. Direct measurement of Lubberts effect in CsI: Tl scintillators using single x-ray photon imaging. Proc SPIE. 2017:9. [Google Scholar]
- 67.Hernandez AM, Boone JM. Tungsten anode spectral model using interpolating cubic splines: unfiltered x-ray spectra from 20 kV to 640 kV. Med Phys. 2014;41(4):42101. doi: 10.1118/1.4866216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zbijewski W, De Jean P, Prakash P, et al. Design and optimization of a dedicated cone-beam CT system for musculoskeletal extremities imaging. Med Phys. 2011;38(8):4700. doi: 10.1118/1.3611039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Samei E, Flynn MJ, Reimann DA. A method for measuring the presampled MTF of digital radiographic systems using an edge test device. Med Phys. 1998;25(1):102–113. doi: 10.1118/1.598165. [DOI] [PubMed] [Google Scholar]
- 70.Teledyne DALSA. Xineos-3030HR Specifications. 2015:8–11. [Google Scholar]
- 71.Parker DL. Optimal short scan convolution reconstruction for fanbeam CT. Med Phys. 1982;9(2):254–257. doi: 10.1118/1.595078. [DOI] [PubMed] [Google Scholar]
- 72.Silver MD. A method for including redundant data in computed tomography. Med Phys. 2000;27(4):773–774. doi: 10.1118/1.598939. [DOI] [PubMed] [Google Scholar]
- 73.Maes WH, Peters IM, Smit C, Kessener Y, Bosiers J. Low-dose performance of wafer-scale CMOS-based X-ray detectors. SPIE Med Imaging. 2015;9412(1):94120C. [Google Scholar]
- 74.Badano A, Sempau J. MANTIS: combined x-ray, electron and optical Monte Carlo simulations of indirect radiation imaging systems. Phys Med Biol. 2006;51:1545–1561. doi: 10.1088/0031-9155/51/6/013. [DOI] [PubMed] [Google Scholar]
- 75.Freed M, Miller S, Tang K, Badano A. Experimental validation of Monte Carlo (MANTIS) simulated x-ray response of columnar CsI scintillator screens. Med Phys. 2009;36(11):4944–4956. doi: 10.1118/1.3233683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Bouxsein ML, Boyd SK, Christiansen BA, Guldberg RE, Jepsen KJ, Muller R. Guidelines for assessment of bone microstructure in rodents using micro-computed tomography. J Bone Miner Res. 2010;25(7):1468–1486. doi: 10.1002/jbmr.141. [DOI] [PubMed] [Google Scholar]
- 77.Kupinski MA, Clarkson E, Gross K, Hoppin JW. Optimizing imaging hardware for estimation tasks. Proc SPIE - Int Soc Opt Eng. 2003;5034:309–313. doi: 10.1117/12.480330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Valentinitsch A, Patsch JM, Burghardt AJ, et al. Computational identification and quantification of trabecular microarchitecture classes by 3-D texture analysis-based clustering. Bone. 2013;54(1):133–140. doi: 10.1016/j.bone.2012.12.047. [DOI] [PubMed] [Google Scholar]
- 79.Valentinitsch A, Fischer L, Patsch JM, et al. Trabecular bone class mapping across resolutions: translating methods from HR-pQCT to clinical CT. SPIE Med Imaging. 2015:94131D. [Google Scholar]
- 80.Paniagua B, Ruellas AC, Benavides E, Marron S, Wolford L, Cevidanes L. Validation of CBCT for the computation of textural biomarkers. SPIE Med Imaging. 2015;9417:1–15. doi: 10.1117/12.2081859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.MacKay JW, Murray PJ, Low SBL, et al. Quantitative analysis of tibial subchondral bone: Texture analysis outperforms conventional trabecular microarchitecture analysis. J Magn Reson Imaging. 2016;43(5):1159–1170. doi: 10.1002/jmri.25088. [DOI] [PubMed] [Google Scholar]
- 82.Haralick RM. Statistical and structural approaches to texture. Proc IEEE. 1979;67(5):786–804. [Google Scholar]
- 83.Zbijewski W, Sisniega A, Vaquero JJ, et al. Dose and scatter characteristics of a novel cone beam CT system for musculoskeletal extremities. Proc SPIE. 2012;8313(February):831317–831318. [Google Scholar]
- 84.Sisniega A, Zbijewski W, Badal A, et al. Monte Carlo study of the effects of system geometry and antiscatter grids on cone-beam CT scatter distributions. Med Phys. 2013;40(5):51915. doi: 10.1118/1.4801895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Sisniega A, Zbijewski W, Xu J, et al. High-fidelity artifact correction for cone-beam CT imaging of the brain. Phys Med Biol. 2015;60(4):1415. doi: 10.1088/0031-9155/60/4/1415. [DOI] [PubMed] [Google Scholar]
- 86.Tilley S, II, Zbijewski W, Stayman JW. High-Fidelity Modeling of Shift-Variant Focal-Spot Blur for High-Resolution CT. Proc Int Meet Fully Three-Dimensional Image Reconstr Radiol Nucl Med. 2017:752–759. [Google Scholar]
- 87.Hsieh J, Nett B, Yu Z, Sauer K, Thibault JB, Bouman C. Recent advances in CT image reconstruction. Curr Radiol Rep. 2013;1:39–51. [Google Scholar]
- 88.Tilley S, II, Siewerdsen JH, Stayman JW. Model-based iterative reconstruction for flat-panel cone-beam CT with focal spot blur, detector blur, and correlated noise. Phys Med Biol. 2016;61:296–319. doi: 10.1088/0031-9155/61/1/296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Tilley S, Zbijewski W, Siewerdsen JH, Stayman JW. Modeling shift-variant X-ray focal spot blur for high-resolution flat-panel cone-beam CT. 4th Int. Conf. Image Form. X-Ray Comput. Tomogr; 2016; pp. 463–466. [PMC free article] [PubMed] [Google Scholar]
- 90.Sisniega A, Stayman JW, Cao Q, Yorkston J, Siewerdsen JH, Zbijewski W. Image-based motion compensation for high-resolution extremities cone-beam CT. Proc SPIE. 2016;9783:97830K. doi: 10.1117/12.2217243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Sisniega A, Stayman J, Yorkston J, Siewerdsen J, Zbijewski W. Motion compensation in extremity cone-beam CT using a penalized image sharpness criterion. Phys Med Biol. 2017;62:3712–3734. doi: 10.1088/1361-6560/aa6869. [DOI] [PMC free article] [PubMed] [Google Scholar]