Efficient estimation of personalized biventricular mechanical function employing gradient-based optimization

Abstract

Individually personalized computational models of heart mechanics can be used to estimate important physiological and clinically-relevant quantities that are difficult, if not impossible, to directly measure in the beating heart. Here, we present a novel and efficient framework for creating patient-specific biventricular models using a gradient-based data assimilation method for evaluating regional myocardial contractility and estimating myofiber stress. These simulations can be performed on a regular laptop in less than 2 h and produce excellent fit between measured and simulated volume and strain data through the entire cardiac cycle. By applying the framework using data obtained from 3 healthy human biventricles, we extracted clinically important quantities as well as explored the role of fiber angles on heart function. Our results show that steep fiber angles at the endocardium and epicardium are required to produce simulated motion compatible with measured strain and volume data. We also find that the contraction and subsequent systolic stresses in the right ventricle are significantly lower than that in the left ventricle. Variability of the estimated quantities with respect to both patient data and modeling choices are also found to be low. Because of its high efficiency, this framework may be applicable to modeling of patient specific cardiac mechanics for diagnostic purposes.

1 | INTRODUCTION

Cardiac computational modeling has emerged as both a powerful method to provide basic insight into cardiac function/dysfunction and as a support tool to improve current clinical practice. Its development is in part driven by significant advancements in medical imaging techniques,^1–3 which now provide a wealth of information about cardiac structure and kinematics. Merging this information with biophysical descriptions of cardiac behavior allows for the creation of powerful patient specific models of the heart.^4–6 Such models can be used to predict the outcome of different treatment strategies⁷ or to extract useful indicators of mechanical function, such as myocardial contractility^8,9 and myofiber stress,^10,11 potential biomarkers that are currently difficult, if not impossible, to measure directly using imaging techniques. ¹²

Of particular importance is ventricular myofiber stress,¹³ which is hypothesized to be a key driver of pathological remodeling processes in cardiac diseases.¹⁴ Correspondingly, quantifying stress and determining how cardiac interventions may reduce abnormal stress is considered a useful avenue in developing treatments for heart failure.¹⁵ However, while measurements of heart motion are possible using an array of imaging techniques, no direct measurements of the load experienced by myocytes are currently possible in vivo and estimates are used instead. One widely used method is the law of Laplace, a simplified model that takes into account pressure, wall thickness, and curvature, and can be used to evaluate stress in idealized geometries. However, despite its wide use, it has been shown that this law severely under-estimates myofiber stress in largely irregular patient-specific ventricular geometries.¹⁶ Furthermore, regional stresses also cannot be accurately estimated using this idealized law.

To overcome these limitations, patient specific simulation using finite element modeling is widely accepted as a viable way to accurately estimate myofiber stresses in the complex geometry of the heart and has been used in designing heart failure treatments to reduce myocardial stress.^15,17,18 However, one of the many challenges faced by researchers developing patient specific models is to efficiently and accurately incorporate individual data into the them, which often requires determining model parameters that best reproduce the observations, ie, data assimilation.^19,20 Typically, one defines a cost function representing the mismatch between simulated and observed data and searches for model parameters that minimize this cost function. Several techniques have been employed to solve this minimization problem. Global methods, using parameter sweeps^21–23 or genetic algorithms,^24,25 are attractive because they can cover the entire parameter space, and are therefore more likely to retrieve the global mimumum of the cost function. However, such methods require an extensive number of functional evaluations, which in the case of heart mechanics can be computationally expensive. Local optimization methods, on the other hand, typically start at some given initial guess, and iteratively search the local neighborhood for better candidates in the minimization of the cost function. These methods are typically faster than global methods but have the drawback that the solution may depend on the initial guess. One example of a local method is the reduced order unscented Kalman filtering approach, ²⁶ which has been applied to personalize cardiac electromechanical models from cine MRI. ²⁷

Another class of local optimization methods are the gradient-based methods, which successively reduce the cost functional by searching along the gradient descent direction. While these methods may substantially improve the convergence towards the minimum, estimating the gradient in these methods, however, introduces significant additional computational costs. Specifically, estimating the gradient by standard finite differences typically requires as many functional evaluations as the number of control parameters (N + 1 evaluations for N parameters). Gradient-based methods are therefore impractical if the number of control parameters is large. Nevertheless, gradient-based approaches have been applied to personalize cardiac mechanics models in several studies.^20,28–30 For example, in the study of Wang et al,³⁰ a sequential quadratic programming optimization technique was utilized to estimate passive material parameters, while in the study of Göktepe et al,³¹ a Levenberg-Marquardt method was used to estimate material parameters from shear data. In the study of Delingette et al,²⁹ the minimization was performed using a quasi-Newton Broyden-Fletcher-Goldfarb-Shanno Bounded (BFGS-B) method, where the gradient was computed using the adjoint method. In this study, however, the adjoint equation was derived analytically, which may be challenging in more complex problems of cardiac mechanics. More recently, a new approach based on automated derivation of functional gradients via solving the corresponding adjoint system have emerged.³² Overcoming the issue that gradient-based methods face in dealing with a large number of parameters, this approach enables one to compute the functional gradient at a computational expense that does not depend on the number of control parameters. ²⁸

Here, we apply such a gradient-based data assimilation framework in order to fuse clinical imaging data from a cohort of healthy subjects to a biventricular mechanics model accurately and efficiently. By relating physical processes to the kinematics observed in medical images, we extracted clinically important quantities from these subject-fitted models and evaluated the sensitivity of these quantities to modeling choices such as fiber architecture and model for active contraction.

The paper is organized as follows. In section 2, we present the pipeline for data assimilation that includes an outline of the underlying ventricular mechanics model and solution methods. Section 3 presents the results of applying the framework to imaging data acquired from 3 healthy subjects, including a comparison of model prediction with the observed data, analysis of mechanical parameters extracted from the model, and a sensitivity analysis of model parameters to the input data. Finally, in sections 4 and 5, we discuss the performance of the framework and draw conclusions about its applicability in clinical settings.

2 | METHODS

2.1 | Data acquisition and preprocessing

Cine magnetic resonance (MR) images of 3 healthy subjects, referred here as CASE1, CASE2, and CASE3, were acquired at the National Heart Centre of Singapore and written informed consent was obtained from all participants. Three-dimensional biventricular geometries of each subject were manually segmented from the MR images at multiple cardiac time points using the medical image analysis software MeVisLab (http://www.mevislab.de).

Cavity volumes of the left ventricle (LV) and right ventricle (RV) were computed from the segmented geometries at different time points in a cardiac cycle in each subject. Using a method described in the study of Xi et al,¹¹ these volumes were paired with normal left and right ventricular pressure wave forms from previous studies³³ to construct pressure- volume loops of the LV and RV. Based on a previous empirical study,³⁴ LV pressure for each subject was also scaled so that the end-systolic pressure is 90% of the measured cuff pressure.

The observed regional circumferential and longitudinal Green-Lagrange strains in the LV free wall (LVFW), septum, and RV free wall (RVFW) were estimated from the MR images in each subject using a hyperelastic warping technique.^35,36 The output of this preprocessing step is used to calculate the estimated regional strain-time data. Briefly, a biventricular finite element model reconstructed from the end-systolic (template) image was registered to all other cine (target) images acquired in the cardiac cycle by minimizing the squared difference between the target and template image intensities. This ill-posed correlation problem is regularized by also minimizing a prescribed (Neo-Hookean) strain energy function over the mesh. We note that other regularization approaches have also been proposed, such as regularization based on incompressibility³⁷ or on equilibrium.^38,39 Hyperelastic warping offers a good balance between regularization and strain estimation.³⁵ The implementation of the image correlation procedure is based on FEniCS,⁴⁰ and is freely available^*.

Three-dimensional biventricular meshes of the 3 normal subjects were created using Gmsh⁴¹ with the number of elements ranging from 4000 to 8000 tetrahedral elements. The chosen reference geometries were reconstructed from MR images in late diastole, and all meshes were uniformly refined in order to perform a convergence analysis.

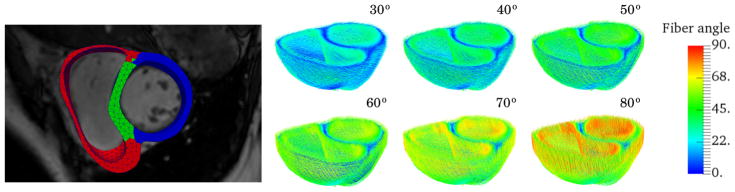
Rule-based fibers were assigned using the Laplace Dirichlet Rule-Based (LDRB) algorithm.⁴² Although previous histological studies⁴³ suggest that myofiber helix angle varies transmurally from +60° at the endocardium to −60° at the epicardium, variability in fiber angle, nevertheless, exists between individuals. Therefore, we seek to also test how different fiber angle gradient alters the parameter estimation and the extracted outputs. More specifically, an angle +α/−α is prescribed on the endo- and epicardium for α ranging from 30° to 80° at increments of 10°. If not otherwise specified, an angle of +60° and −60° on the endo- and epicardium, respectively, is prescribed. In Figure 1, we show this range of fiber fields for one of the subjects.

FIGURE 1.

Left: finite element mesh of a biventricular geometry reconstructed from MR images separated into 3 material regions, namely, left ventricle free wall (blue), septum (green), and right ventricle free wall (right). Right: myocardial fiber orientation are assigned using the LDRB algorithm⁴² with an angle +α and −α prescribed on the endocardium and epicardium, respectively. Here showing the fiber architecture for α ranging from 30° to 80° with increments of 10°, where the absolute value of the fiber angle is used as color map

2.2 | Mechanical modeling

We consider a configuration of a biventricular continuum body ℬ, which is a function κ: ℬ → ℝ³, and denote the reference and current configurations by Ω₀ = κ₀(ℬ) and Ω = κ(ℬ), respectively. Letting X and x be the coordinates of a given material point in the reference and current configuration, respectively, we have the corresponding displacement field U=x–X, and the deformation gradient

$$\mathbf{F}=\frac{\partial \mathbf{U}}{\partial \mathbf{X}}+\mathbf{I}.$$ (1)

Mechanics of the heart wall was described using an active strain formulation⁴⁴ that assumes a multiplicative decomposition of the deformation gradient,

$$\mathbf{F}={\mathbf{F}}_e{\mathbf{F}}_a.$$ (2)

Here, F_a is associated with an inelastic deformation resulting from the actively contracting muscle fibers, whereas ${\mathbf{F}}_e=\mathbf{F}{\mathbf{F}}_a^{-1}$ is associated with the elastic deformation that preserves compatibility in the tissue and passively carrying the mechanical load. We choose F_a to have the specific form

$${\mathbf{F}}_a=(1-\gamma ){\mathbf{f}}_0\otimes {\mathbf{f}}_0+\frac{1}{\sqrt{1-\gamma }}(\mathbf{I}-{\mathbf{f}}_0\otimes {\mathbf{f}}_0),$$ (3)

in which the parameter γ is associated with the relative active shortening along the muscle fibers. The same form of the active deformation gradient has previously been applied in other studies.^28,45

We consider the transversely Holzapfel and Ogden hyperelastic material⁴⁶ model that has the strain energy density function

$$\mathrm{\Psi }(\mathbf{F})=\frac{a}{2b}\left(e^{b(I_1-3)}-1\right)+\frac{a_f}{2b_f}\left(e^{b_f{(I_{4{\mathbf{f}}_0}-1)}_{+}^2}-1\right),$$ (4)

where the invariants are given by

$$I_1=\text{tr}\mathbf{C},I_{4{\mathbf{f}}_0}={\mathbf{f}}_0·(\mathbf{C}{\mathbf{f}}_0).$$ (5)

Here C=F^TF is the right Cauchy Green tensor, and f₀ denotes the unit fiber vector field in the reference configuration. Within the active strain formulation, the strain energy depends only on elastic deformations, and so the modified strain energy function Ψ = Ψ̃ (F_e) was used instead.

For comparison, we also test the more frequently used active stress formulation.⁴⁷ In this formulation, the total Cauchy stress tensor is additively decomposed into a passive and an active component, ie,

$$\sigma ={\sigma }_p+{\sigma }_a,$$ (6)

where the passive stress tensor is given by

$${\sigma }_p=\frac{1}{J}\frac{\partial \mathrm{\Psi }}{\partial \mathbf{F}}{\mathbf{F}}^T,$$ (7)

and the active stress tensor is given by

$${\mathit{\sigma }}_a=T_a[\mathbf{f}\otimes \mathbf{f}+\eta (\mathbf{I}-\mathbf{f}\otimes \mathbf{f})].$$ (8)

Here, T_a is the magnitude of the active stress and η controls the amount of transverse active stresses. Although active stresses, in principle, develop along the fiber direction, studies have shown⁴⁸ that active stresses in the transverse direction are nonnegligible due to imperfect alignment of the muscle fibers. We therefore set η=0.2,⁴⁹ and note that transverse active stresses are naturally embedded in the active strain formulation by requiring det F_a=1.

Myocardium was assumed to be incompressible. The incompressibility was enforced in the model using a 2-field variational approach, in which the term −p(J–1) was added to the total strain energy with p denoting a Lagrange multiplier that represents the hydrostatic pressure. The deviatoric and volumetric mechanical responses were also uncoupled by multiplicatively decomposing the deformation gradient,⁵⁰

$$\mathbf{F}={\mathbf{F}}_{\text{iso}}{\mathbf{F}}_{\text{vol}}$$ (9)

and letting the strain energy be a function of only isochoric deformations, ie, Ψ = Ψ̄ (F_iso).

Ventricular base was fixed in the longitudinal direction, and the biventricular geometry was anchored by constraining the epicardial surface using a Robin-type boundary condition with a linear spring¹¹ of stiffness k=0.5 kPa/cm². Measured cavity pressure in the LV (p_lv) and RV (p_rv) were applied as a Neumann condition at the endocardial surfaces. The Euler-Lagrange equations in the Lagrangian form reads: find (U, p)∈V×Q such that for all (δU, δp)∈V×Q and ${(\mathbf{U}·\mathbf{N})\mid }_{\partial {\mathrm{\Omega }}_0^{\text{base}}}=0$,

$$\delta \mathrm{\Pi }(\mathbf{U},p)=\underset{{\mathrm{\Omega }}_0}{\int }[\mathbf{P}:\nabla \delta \mathbf{U}-\delta p(J-1)-pJ{\mathbf{F}}^{-T}:\nabla \delta \mathbf{U}]\mathrm{d}V+\delta {\mathrm{\Pi }}_{\text{ext}}=0,$$ (10)

with

$$\delta {\mathrm{\Pi }}_{\text{ext}}=\underset{\partial {\mathrm{\Omega }}_0^{\text{endo}\text{LV}}}{\int }{p}_{\text{lv}}J{\mathbf{F}}^{-T}\mathbf{N}·\delta \mathbf{U}\mathrm{d}S+\underset{\partial {\mathrm{\Omega }}_0^{\text{endo}\text{RV}}}{\int }{p}_{\text{rv}}J{\mathbf{F}}^{-T}\mathbf{N}·\delta \mathbf{U}\mathrm{d}S+\underset{\partial {\mathrm{\Omega }}_0^{\text{epi}}}{\int }k\mathbf{U}·\delta \mathbf{U}\mathrm{d}S.$$ (11)

Here V=H¹(Ω₀), completed with homogeneous Dirichlet boundary data, Q=L²(Ω₀), N is the outward pointing unit normal and P is the first Piola-Kirchhoff stress tensor.

For an incompressible, hyperelastic, continuum body, the total Cauchy stress tensor is given by

$$\mathit{\sigma }=\frac{1}{J}\frac{\partial \mathrm{\Psi }(\mathbf{F})}{\partial \mathbf{F}}{\mathbf{F}}^T-p\mathbf{I}.$$ (12)

With the decoupling of the isochoric and volumetric deformation according to (9), the first term in (12) represents the deviatoric stresses and p is the hydrostatic pressure. Myofiber stress was computed by first a push forward of the fiber field to the current configuration, f=Ff₀, and then an inner product with the stress tensor σ_f=f·σf. The average fiber stress in a given region Ω_j was computed by integrating the fiber stress over that region and dividing by the volume, ie, ${\overline{{\mathit{\sigma }}_{\mathbf{f}}}}^{{\mathrm{\Omega }}_j}={\mid {\mathrm{\Omega }}_j\mid }^{-1}\underset{{\mathrm{\Omega }}_j}{\int }{\mathit{\sigma }}_{\mathbf{f}}\mathrm{d}V$

2.3 | PDE-constrained optimization

The ventricular mechanics model outlined in section 2.2 contains model parameters that may vary from individual to individual. Calibration of these model (or control) parameters was achieved by solving a PDE-constrained optimization problem, where we minimized a cost functional representing the mismatch between the simulated and observed data, subject to the constraint of satisfying (10) to (11). The minimization problem can be formally stated as

$$\begin{array}{ll}\underset{m}{\text{minimize}}\hfill & \mathcal{J}((\mathbf{U},p),m)\hfill \\ \text{subject}\text{to}\hfill & \delta \mathrm{\Pi }(\mathbf{U},p)=0.\hfill \end{array}$$ (13)

Here, 𝒥 is the objective functional that we want to minimize, which depends on the state variable (U, p) and the control parameter(s) m. The state variables may also depend on the control parameters (U, p)=(U(m), p(m)). To ease notation, this dependency is not explicitly stated here.

Minimization of the cost functional 𝒥, should bring the simulated results closer to the clinical observations. Therefore, 𝒥 should reflect a distance between the simulated results and the observed data. Given a measurement point i, let (Uⁱ, pⁱ) be the simulated state variables at that point, and let mⁱ represents any generic model parameter that we want to estimate. The cost functional is then given by

$$\mathcal{J}(({\mathbf{U}}^i,p^i),m^i)=\alpha {\mathcal{J}}_{\text{volume}}(({\mathbf{U}}^i,p^i),m^i)+\beta {\mathcal{J}}_{\text{strain}}(({\mathbf{U}}^i,p^i),m^i)+\lambda {\mathcal{J}}_{\text{reg}}(m^i).$$ (14)

The first 2 terms represent the mismatch between simulated and observed strains and volumes, whereas 𝒥_reg is a regularization term that penalizes nonsmooth values of the control parameter mⁱ for numerical stability. The weights α, β, and λ control what terms is favored in the optimization.

The cavity volume was given by

$$\stackrel{\sim }{V}.=-\frac{1}{3}\underset{\partial {\mathrm{\Omega }}_o^{\text{endo}}}{\int }(\mathbf{X}+\mathbf{U})J{\mathbf{F}}^{-T}\mathbf{N}\mathrm{d}S.$$ (15)

This equation holds as long as the base remains flat and is located at the x=0 plane. We let 𝒥_volume be the sum of the squared relative volume error in each chamber

$${\mathcal{J}}_{\text{volume}}(({\mathbf{U}}^i,p^i),m^i)={\left(\frac{V_{\text{LV}}^i-{\stackrel{\sim }{V}}_{\text{LV}}^i}{V_{\text{LV}}^i}\right)}^2+{\left(\frac{V_{\text{RV}}^i-{\stackrel{\sim }{V}}_{\text{RV}}^i}{V_{\text{RV}}^i}\right)}^2.$$ (16)

Here, (Ṽ_LV, Ṽ_RV) and (V_LV, V_RV) are the simulated and measured cavity volumes, respectively.

Volumetric averaged strains were computed in each material region (ie, LVFW, RVFW, and septum) using end-diastole (ED) as reference. Letting F_ED be the deformation gradient tensor associated with ED, the Green-Lagrange strain tensor with ED as reference was given by $\stackrel{\sim }{\mathbf{E}}=\frac{1}{2}({\mathbf{F}}^T{\mathbf{F}}_{\text{ED}}^{-T}\mathbf{F}{\mathbf{F}}_{\text{ED}}^{-1}-\mathbf{I})$. Averaged normal strain along the circumferential direction e_circ in material region Ω_j was defined by

$${\stackrel{\sim }{\epsilon }}_j=\frac{1}{\mid {\mathrm{\Omega }}_j\mid }\underset{{\mathrm{\Omega }}_j}{\int }{\mathbf{e}}_{\text{circ}}·\stackrel{\sim }{\mathbf{E}}{\mathbf{e}}_{\text{circ}}\mathrm{d}V.$$ (17)

Correspondingly, the strain mismatch functional was given by the total squared error between the simulated circumferential strain ${\stackrel{\sim }{\epsilon }}_j^i$ and the measured circumferential strain ${\epsilon }_j^i$ over all material regions

$${\mathcal{J}}_{\text{strain}}(({\mathbf{U}}^i,p^i),m^i)=\sum _{j=1}^N{\left({\epsilon }_j^i-{\stackrel{\sim }{\epsilon }}_j^i\right)}^2.$$ (18)

Finally, the regularization term was defined as the total squared distance from the mean value, that is, if mⁱ=(m₁,···, m_N), then

$${\mathcal{J}}_{\text{reg}}(m^i)=\sum _{j=1}^N{(m_j^i-{\overline{m}}^i)}^2,{\overline{m}}^i=\frac{1}{N}\sum _{j=1}^N{m}_j^i.$$ (19)

As noted above, the purpose of this term is to avoid numerical instabilities by penalizing large variations in the control parameters.

The functional gradient

$$\frac{\mathrm{d}\mathcal{J}}{\mathrm{d}m}=\frac{\partial \mathcal{J}}{\partial m}+\frac{\mathrm{d}\mathcal{J}}{\mathrm{d}\mathbf{w}}\frac{\partial \mathbf{w}}{\partial m},\mathbf{w}=(\mathbf{U},p)$$ (20)

points in the direction of steepest descent and is required in gradient-based optimization methods. While the terms $\frac{\partial \mathcal{J}}{\partial m}$ and $\frac{\mathrm{d}\mathcal{J}}{\mathrm{d}\mathbf{w}}$ are typically straightforward to compute, the term $\frac{\partial \mathbf{w}}{\partial m}$ cannot be computed easily, since the state variable w can only be determined by solving the force-balance Equation 10. Specifically, estimating this term with N control parameters using a finite difference approach will require one to solve the (typically computational expensive) force-balance equation N + 1 times, becoming impractical when N is large. Instead, it is possible to transform the system of equations into its adjoint system, where the gradient is given by

$$\frac{\mathrm{d}\mathcal{J}}{\mathrm{d}m}=\frac{\partial \mathcal{J}}{\partial m}-z^{\ast }\frac{\partial (\delta \mathrm{\Pi })}{\partial m},$$ (21)

with (·)^*. referring to the adjoint (or Hermitian transpose) and z is the solution of

$${\left(\frac{\partial (\delta \mathrm{\Pi })}{\partial \mathbf{w}}\right)}^{\ast }z={\left(\frac{\partial \mathcal{J}}{\partial \mathbf{w}}\right)}^{\ast }.$$ (22)

We can therefore solve the adjoint Equation 22 first, and then compute the functional gradient by plugging the solution z into (21). Hence, computing the functional gradient using the adjoint approach requires only 1 additional solve of a linearized system that is independent of the number of control parameters.

2.4 | Parameter estimation

The pipeline for fitting the model to patient data was divided into 2 sequential phases: a passive phase where we estimated the material parameters that define the passive behavior of the myocardium, and an active phase where we estimated the amount of active contraction. In both cases, the control parameters were spatially resolved. During the passive phase, the control parameter was allowed to vary spatially on the LV (LVFW + septum) and RV segments, while in the active phase the LV was separated into LV free wall and septal segments, which provided additional degrees of freedom to allow for nonhomogeneous LV contraction.

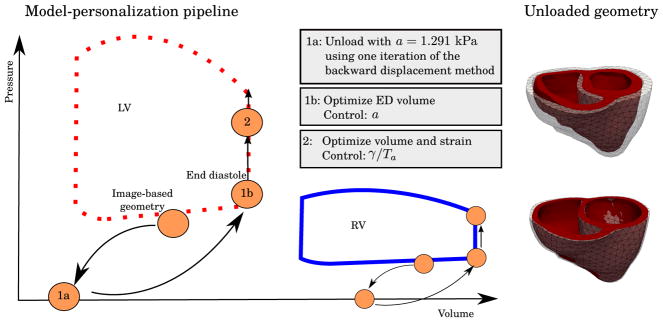
Geometries used in the simulation were reconstructed from medical images. These geometries are, in principle, not load free. Hence, we need to estimate the unloaded (zero pressure) geometries, which will revert back to the original reconstructed geometries when loaded with the measured pressure. Several methods exists for estimating the unloaded geometry.^51,52 Among the most simplest ones is the backward displacement method^53,54 that can also be used to incorporate residual stresses into the finite element models by simulating tissue growth.⁵⁵ Nevertheless, this inverse problem (of finding the unloaded geometry) has been shown to produce nonunique solutions, especially when buckling is present,⁵² although relaxation techniques can be used to improve convergence and stability.⁵⁶ For the case of a biventricular geometry, buckling may occur due to the thin RVFW and a high RV pressure. For this reason, we choose a simpler approach to estimate the unloaded configuration. As shown in the left of Figure 2, we start by applying 1 iteration of the backward displacement method with initial values prescribed for the material parameters followed by the material parameter estimation as outlined below. This will result in a deflated geometry as shown in the right of Figure 2. A sensitivity analysis (A) was conducted to assess how the choice of the initial material parameter values affects our results.

FIGURE 2.

To the left, we see the model-personalization pipeline. The image-based geometry corresponds to some image frame taken at mid-diastole. An estimate of the unloaded geometry was found by applying 1 iteration of the backward displacement method using a=1.291 kPa according to Asner et al,²¹ followed by an estimation of a by minimizing the fit of the end-diastolic volumes (EDV). During systole, both cavity volumes and circumferential strain were used in the optimization to determine the amount of active contraction in terms of the active control, which are, respectively, γ and T_a in the active strain and active stress formulation. To the right, we show a comparison of the unloaded geometry for CASE 3. The upper figure shows the resulting unloaded, zero pressure geometry in red and the the original image-based geometry in transparent, while the bottom figure shows the unloaded geometry, inflated to the target pressure in the image-based geometry, and the original image-based geometry in transparent for comparison

Four material parameters, ie, a, a_f, b, and b_f (4) have to be estimated in the passive phase. Due to the sparsity of passive data used for the optimization, if we let all these parameters vary freely, we may end up in a situation where multiple parameter sets will equally minimize the cost functional, and the optimal control will depend heavily on the initial guess of the optimization. We therefore restricted our control parameter to be only the linear isotropic parameter with an initial guess a=1.291 kPa and have the remaining parameters fixed according to Asner et al²¹ (Table 2, case 2). The weights were set α=1.0, β=0.0, and λ=10⁻⁶ in (14) so that only ED volumes were used for fitting. Since fitting the left and right ventricular, end-diastolic volumes might require different material properties of the left and right ventricular wall, the parameter a was spatially resolved with 1 parameter associated with the LV (LVFW + septum) and 1 parameter associated with the RVFW.

TABLE 2.

Average LV and RV fiber stress and end-diastole and end-systole

Patient ID	LV (ED)	RV (ED)	LV (ES)	RV (ES)
CASE1	5.76	4.87	48.3	19.2
CASE2	4.04	3.57	54.4	22.7
CASE3	9.94	8.34	40.3	18.2
Average ± std	6.58 ± 2.48	5.59 ± 2.01	47.65 ± 5.74	20.03 ± 1.91

Abbreviations: ED, end-diastole; ES, end-systole; LV, left ventricle; RV, right ventricle.

In the active phase, the optimized passive material parameters were fixed and the relative active fiber shortening γ in (3) was chosen as control parameter. For this phase, the weights in (14) were set to α=0.1, β=1.0, and λ=10⁻⁴, so that both strain and volume are considered in the optimization. This choice of weighting was made ad hoc, reflecting the relative size of the different terms in the cost functional. It should also be noted that the volume functional in (16) is a relative error while the strain functional in (18) represents a total error. The cost function parameter values were taken from Balaban et al,²⁸ where they were chosen based on an L-curve type analysis.

For each time point, we estimated γ locally in the LVFW, RVFW, and septum. The initial guesses for the optimization were set to 0 in the first iteration. In subsequent iterations, the initial guesses were set to the optimized values found in the previous iteration. Note that in the case when active stress formulation was used instead, the parameter T_a in 8 was used as the control parameter and estimated in a similar fashion. A schematic illustration of the full optimization pipeline is provided to the left in Figure 2.

The control parameter in the active phase represents an index of contractility,⁹ meaning that the higher the value of the control parameter, the more forcefully the myocardium is trying to contract against the external loads. To separate between the LV and RV contractility, we extracted the average value of this control parameter in these 2 segments. Another index of contractility is the end systolic elastance, ⁵⁷ which we have also estimated in the LV and RV by perturbing the loading conditions at the end-systolic state and estimate the slope of the resulting pressure-volume relationship. ⁹

2.5 | Implementation details

The force-balance equations of this incompressible nonlinear elasticity problem were solved using the finite element method with Lagrange elements. More specifically, the displacement and hydrostatic pressure fields were interpolated using piecewise quadratic and linear Lagrange basis functions, respectively. These mixed elements, known as the Taylor-Hood finite elements,⁵⁸ are known to satisfy the discrete inf-sup condition⁵⁹ and leads to a stable discretization. The solver was implemented in FEniCS,⁶⁰ which is an open-source platform for solving PDEs using the finite element method. Nonlinear systems of equations were solved using Newton’s method, and a distributed memory parallel LU solver⁶¹ was used to solve the linear systems.

To solve the optimization problem (13), we applied a sequential quadratic programming algorithm.⁶² This gradient-based optimization algorithm requires the functional gradient (20). This gradient was computed by solving an automatically derived adjoint equation using dolfin-adjoint.³² The full source code is publicly available^†.

3 | RESULTS

In this section, we present the results from the model personalization process. Results of the data matching are presented in Section 3.1, together with a validation of the model and analysis of the solver performance. To validate the model, we compare the simulated and measured longitudinal strain that was not used in the optimization. In Section 3.2, we present the results of the extracted mechanical features such as indices of contractility and fiber stress. We also investigated the efficiency of the algorithm and the effect of mesh refinement and found that the chosen refinement level was sufficient to yield convergent solutions.

3.1 | Data assimilation, validation, and solver performance

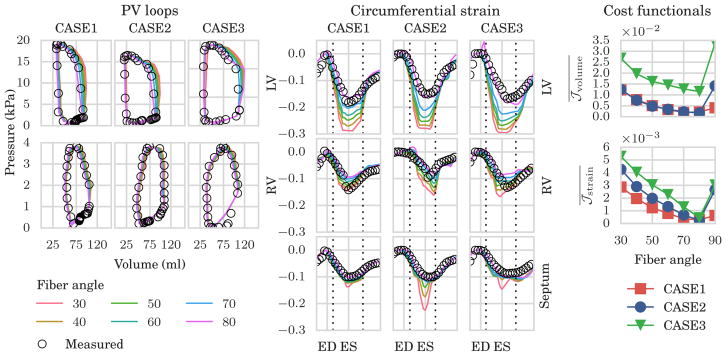
The simulated and measured pressure-volume (PV) loops of the RV and LV, as well as circumferential strain in the LV, septum and RV are shown in Figure 3. We found that the fit of the data was highly dependent on the choice of fiber angles, which affects both volume change and circumferential shortening. Plotting the average value of the volume cost functional (as defined in (16)) for each choice of fiber angles (see the upper right panel in Figure 3) revealed that the optimal value of α lies in the range 70° to 80° for all 3 cases.

FIGURE 3.

Results of the gradient-based minimization of model-data mismatch for different choice of fiber angles. Left: simulated (color lines) and measured (black circles) pressure volume (PV) loops in the left ventricle (LV, top row) and right ventricle (RV, bottom row). Center: simulated (color lines) and measured (black circles) circumferential strain in the left ventricle (top row), right ventricle (middle row), and septum (bottom row). Right: average values of cost functional for the volume (top row) and strain (bottom row), for each choice of fiber angle

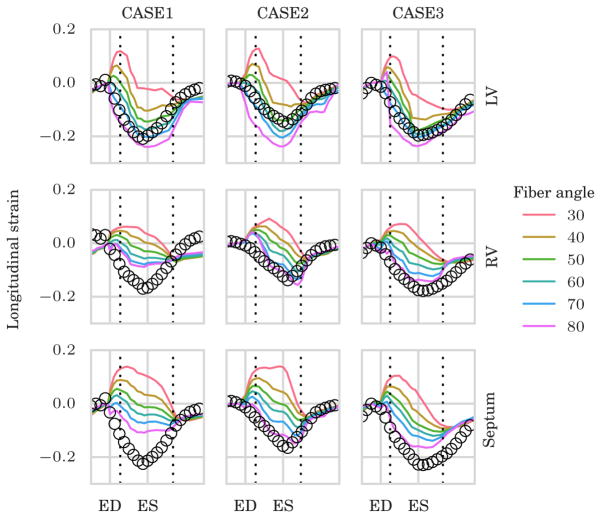
Although available, we chose not to use longitudinal strain data in the optimization. Therefore, the comparison of model-predicted longitudinal strain with the measurements serves as a validation of the model-personalization process. The simulated and measured LV longitudinal strain curves are shown in Figure 4. We note that the fit in all regions was again highly sensitive to the choice of fiber angle. Choosing α=70° produced the best fit for the LV longitudinal strain for CASE1 and CASE3, while an angle 60° gave the best fit for CASE2. The septal and RV longitudinal strain was best fitted with α=80°.

FIGURE 4.

Validation of the model-personalization process using simulated and measured longitudinal strain that was not used in the optimization. Upper, middle, and lower panel show the longitudinal strain curves for different choice of fiber angles in the left ventricle (LV), right ventricle (RV), and septum, respectively. ED, end-diastole; ES, end-systole

We further evaluated the solver performance in the optimization process. In this work, all computations were performed on a computing cluster using 1 node with 8 cores. In Table 1, we present timings for evaluation of the forward model (ie, evaluation of the cost functional) and timings for evaluation of the gradient, as well as the average number of such evaluations and the standard deviations. These timings are shown for optimizations using the original and refined meshes with a fiber angle of 60°.

TABLE 1.

Timings for evaluation (eval) of the forward model and the gradient, running on 1 computing node with 8 cores for the different subjects with different mesh resolutions

Patient ID	Elements	Forward eval time, s	Forward eval	Gradient eval time, s	Gradient eval	Total run time, h
CASE1	7362	32 ± 19.8	9 ± 1.6	9 ± 0.1	8 ± 1.5	1.97
	58 896	668 ± 529.8	9 ± 1.7	81 ± 1.3	7 ± 1.6	36.1
CASE2	4755	19 ± 9.6	9 ± 2.1	8 ± 0.1	8 ± 2.0	1.88
	38 040	387 ± 325.8	9 ± 2.5	47 ± 0.4	8 ± 2.2	32.6
CASE3	4377	17 ± 5.3	10 ± 2.1	8 ± 0.9	8 ± 2.1	1.35
	35 016	259 ± 146.3	9 ± 2.4	42 ± 0.7	8 ± 2.2	15.6

The average number of forward and gradient evaluations for each measurement points are also shown along with the standard deviations.

3.2 | Mechanical analysis

3.2.1 | Cardiac contraction

The estimated active strain parameter γ in (3), which served as the control parameter during the optimization in the active phase, is plotted for various fiber angles to the left in Figure 5. This parameter varies regionally in the LVFW, septum, and RVFW, but is shown here as an average in the LV containing LVFW + septum (top) and RV containing only RVFW (bottom). As shown in the figure, time variation and magnitude of γ were similar in the 3 cases and insensitive to the prescribed fiber angles.

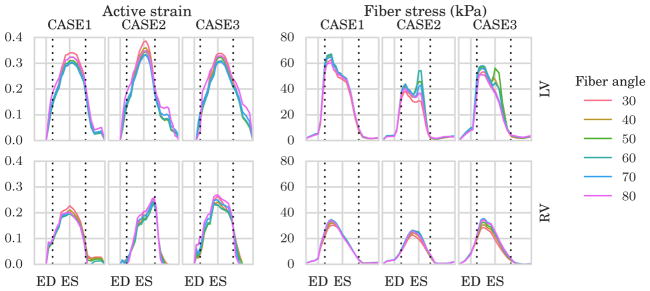
FIGURE 5.

To the left, average traces of the active strain parameter γ in (3) in the left ventricle (LV, top) and right ventricle (RV, bottom) for different choice of fiber angle. To the right, average traces of Cauchy fiber stress in the LV (top) and RV (bottom) for different choice of fiber angle. The fiber angles were defined symmetrically across the wall with a negative angle on the epicardium and a positive angle on the endocardium ranging from 30° to 80° with increments of 10°. On the x–axis, we plot the normalized time with respect to end-diastole (ED) and end-systole (ES). Horizontal dotted lines indicate timings of opening of the aortic and mitral valve

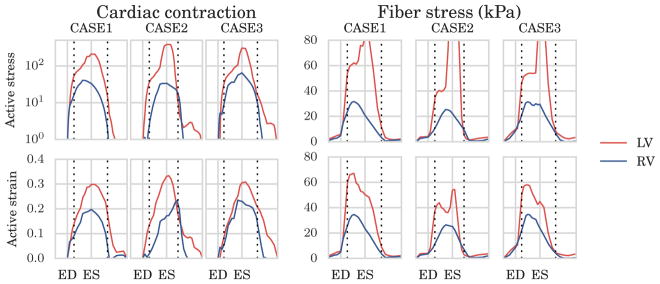
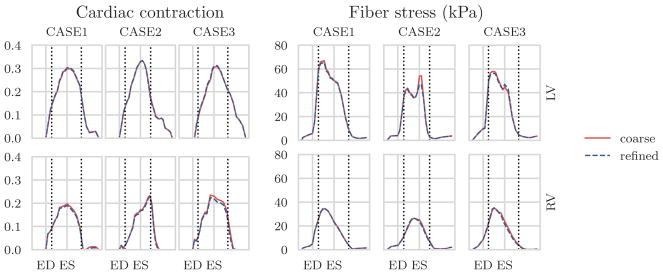
Time traces of the active strain parameter γ found in the LV and RV are plotted together for the 60°-fiber angle case in the left of Figure 6 in order to better compare their differences. A similar plot of the active stress parameter T_a in logarithmic scale is also shown in the same figure. As shown in the figure, the time-variations of T_a and γ, which are indices of cardiac contractility, were largely similar between the LV and RV with peak values located approximately at end-systole. Peak values found in the RV were, however, lower than those found in the LV. These findings were consistent across all the 3 cases. A similar plot in Figure 7 shows that the active strain γ is insensitive to the mesh resolutions listed in Table 1.

FIGURE 6.

Comparison of fiber stress and cardiac contraction using the active strain and active stress approach using 60° fiber angle. To the left, average traces of the active stress (top) parameter T_a in (8), and the active strain (bottom) parameter in 3. The active stress parameter, with unit kPa, is plotted on a logarithmic scale for easier comparison with the active strain parameter. To the right, estimated Cauchy fiber stress using the active stress (top) and active strain formulation (bottom). On the x–axis, we plot the normalized time with respect to end-diastole (ED) and end-systole (ES). Horizontal dotted lines indicate timings of opening and closing of the aortic valve. LV, left ventricle; RV, right ventricle

FIGURE 7.

Results obtained using different mesh resolutions as listed in Table 1. To the left and right, respectively, the active strain and fiber stress traces, in the left ventricle (LV, top) and right ventricle (RV, bottom) estimated using the coarse and refined geometry. ED, end-diastole; ES, end-systole

3.2.2 | Fiber stress

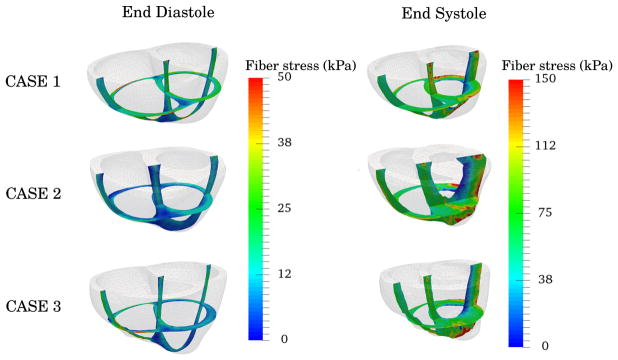
Time traces of the average Cauchy fiber stress are shown on the right of Figure 5 for different fiber angle variations. Only very small variations in the average fiber stress were found with respect to the choice of fiber angle in the optimization process. Snap shots of the fiber stress distribution at ED and ES are plotted in Figure 8 for the 60°-fiber angle case. Regional variation of fiber stress was largely consistent between the 3 cases with pockets of high and low stresses found, respectively, at the apex-epicardial and endocardial regions at ES.

FIGURE 8.

Snap shots of the end-diastolic and end-systolic configuration and the estimated fiber stresses shown as colormap. ED, end-diastole; ES, end-systole

In Figure 6, we compare the average fiber stress time variation found using the 2 different active contraction formulations, either active strain or active stress. As shown in the figure, fiber stress in the RV computed using active stress and active strain formulations behaved similarly with time. Similar regional variation was also found where both formulations predicted higher fiber stress in the LV than in the RV. Peak fiber stress predicted in the LV, however, was different in the 2 formulations with higher stress occurring at isovolumic relaxation in the active stress formulation.

The specific average value of the end-diastolic and end-systolic fiber stress for the case of a 60°-fiber angle are displayed in Table 2, showing small variability between patients, despite differences in individual PV loops.

3.2.3 | Ventricular elastance

Table 3 shows the estimates of ES elastance in the LV and RV that were computed using the active strain formulation. The table shows the average ± 1 standard deviation of the ES elastance over various fiber angles. Elastance was consistently found to be approximately 10 times larger in the LV than in the RV and was largely insensitive to the prescribed fiber angle as indicated by the small standard deviation.

TABLE 3.

LV and RV end-systolic elastances estimated by perturbation of model at the end-systolic state.

Patient ID	LV, kPa/mL	RV, kPa/mL
CASE1	1.96 ± 0.06	0.23 ± 0.02
CASE2	1.94 ± 0.14	0.18 ± 0.01
CASE3	1.52 ± 0.07	0.21 ± 0.01

Average values and standard deviation with respect to varying fiber angle are shown.

4 | DISCUSSION

In this study, we have presented a novel and highly-efficient method for noninvasive personalization of an image-based biventricular mechanics model based on regional measurements of circumferential strain, as well as global measurements of volumes and pressures in the LV and RV. A gradient based optimization method was used to minimize the model-data mismatch by solving a PDE-constrained optimization problem for each measurement point in order to calibrate model parameters. Passive material parameters and an unloaded (zero-pressure) geometry were estimated using the biventricular geometry that was reconstructed from MR images acquired at late diastole. Time variation of an active contraction parameter was estimated throughout the cardiac cycle starting from ED.

This framework was applied using measurements from 3 normal subjects to extract estimates of regional fiber stress as well as indices of myocardial contractility. Sensitivity analysis of the model outputs with respect to the choice of fiber angle distribution, mesh resolution, and active formulation were also conducted. The described framework is effective and efficient in capturing cardiac mechanical behavior throughout the cardiac cycle and gave low patient-to-patient variability in the extracted mechanical features. As such, it has potential clinical utility in the quantification of contractile function and myocardial stress in vivo and the potential differentiation of pathological states.

4.1 | Data compatibility and multiobjective optimization

The objective functional in problem (13) consists of a weighted sum of different objective functionals. Such problems are referred to as multiobjective optimization problems.⁶³ While it is possible to perfectly match the strain or volume data individually with the chosen control parameters (data not shown), there is expected to be a trade-off when fitting both the volume and strain data in a combined objective functional. In such cases, a single, unique optimum does not always exist, but rather a family of so-called Pareto optimal solutions can be found.⁶³ The particular solution found will depend on the chosen weights of each objective.

In a previous study,²⁸ the weights in the total functional given in (14) were determined by performing an exhaustive search, by testing several combinations of weights of the strain and volume functionals, and by choosing the corner point of strain versus volume error curve. However, the weights will depend on the data source, and in our case, choosing the weights proposed in other studies²⁸ resulted in an excellent fit of the volume, while a relatively poor fit of the strain, and hence, a higher weight was chosen for the strain. Nevertheless, neither was captured exactly, and which data source is more important for model utility remains to be determined. In addition, other general methods for solving multiobjective optimization problems ⁶³ may be superior to the weighted sum method used here and will be considered in future studies.

4.2 | Effect of mesh resolution

As shown in Table 1, the total run time is substantially larger for a refined mesh (35 000–60 000 elements) compared with a coarser mesh (4000–8000 elements). Since computing time is an important factor that may limit the application of computational models in the clinic, we have investigated the accuracy of our predictions from the coarse meshes. Our results show that the accuracy of the extracted features related to cardiac contraction and fiber stress are not very sensitive to mesh resolution beyond the coarsest levels of approximately 4000 elements. As seen in Figure 7, the fiber stress and active strain traces obtained on the coarse and fine meshes are very similar, indicating that the coarsest meshes give sufficient accuracy for the extracted mechanical features.

4.3 | Fiber angle sensitivity

In this work, we applied a rule-based algorithm⁴² to assign myocardial fiber orientations to the biventricular geometries and investigated the sensitivity of the data matching and the extracted mechanical features to the choice of fiber field. Different fiber fields, in which the fiber angle varies linearly across the myocardium wall from α at the endocardium to −α at the epicardium were tested, for the range 30°≤α≤80°. Our results show that α has to be in the upper part of the range, ie, 70° to 80°, in order to fit the PV loop and circumferential strain measurements simultaneously. The validation study (Section 3.1), where we compared our model results with the longitudinal strain, confirms this finding.

This highlights a major challenge in building accurate mechanics models of the myocardium. The choice of fiber field is very important, as it controls the amount of longitudinal and radial shortening during contraction. Unless the correct fiber field is used, strain measurements cannot be reproduced simultaneously in the model with the measured pressure volume relationships. Accurate measurements of the underlying ventricular microstructure are lacking, however, and therefore, rule-based methods⁴² are often the only alternative to prescribe muscle fiber field in subject-specific modeling of cardiac mechanics. Our fundamental knowledge of the myocardial architecture is based largely on early histological studies,⁴³ which found that the muscle fiber orientation varies linearly across the myocardial wall with an angle α=60° at the endocardium α=−60° at the epicardium. This fiber field is often prescribed in ventricular models without questioning. On the other hand, diffusion tensor MRI (DT-MRI) is now becoming an important tool to measure fiber orientations and could potentially do so in vivo.⁶⁴

More recent histological studies⁶⁵ on the canine left ventricle have shown that the muscle fibers are more longitudinally oriented at the subendocardium and subepicardium than those obtained using DT-MRI, and such fiber orientation can better reproduce the longitudinal motions observed in the experiments.⁶⁶ Our results support this finding.

A few hypotheses on the basis of cardiac muscle fiber orientation in the ventricles have been put forward. For example, it has been hypothesized that myocardial fiber orientations adapts to achieve a minimal fiber-cross fiber shear strain during the cardiac cycle.⁶⁷ While our results showed that the active strain parameter γ varied a little with respect to the different fiber angle α prescribed in the model, they also show that the peak active strain γ is lowest when α lies between 60° and 70° in all 3 cases. This finding suggests that the tight range of α found here is optimal in the sense that the active shortening necessary to produce the same stroke volume is at its minimum.

4.4 | Fiber stress

As there is no direct way to measure myocardial fiber stresses, we have compared our results with other patient specific modeling studies. The range of reported values for humans are broad and are mostly confined to the LV. For example,¹⁰ reported fiber stress computed at ED (2.21±0.58 kPa) and ES (16.64±4.73 kPa) in normal humans, whereas Scardulla et al⁶⁸ conducted a stress analysis on healthy bi-ventricles and found that wall stress at ES was 65.7±12.3 kPa in the LV and 23.6±14.2 kPa in the RV.

Our estimated average fiber stresses (Table 2) are well within the range of values reported in these studies. Fiber stress distributions at ED and ES (Figure 8) are also consistent in the 3 subjects investigated here. Furthermore, our results also show small variations in fiber stress with respect to the choice of fiber field. Fiber stresses obtained from active strain and stress formulations are also comparable during late diastole and early systole. A large difference in the fiber stress between these 2 formulations, however, can be found at late systole and during the isovolumic relaxation when the ventricles are in their most compressed state. In particular, the active stress formulation produces elevated stresses during this time interval. The same phenomenon was observed in a sensitivity analysis (A) on the initial passive material parameter a used to find the unloaded geometry. We found that the elevated stresses are always accompanied by very high hydrostatic pressure p, suggesting that the enforcement of incompressibility, which does not hold in vivo because of blood perfusion in the myocardial wall, is causing this artifact. Future studies are needed to examine the effect of compressibility to our results.

4.5 | Contractility

Higher value of the active strain parameter γ or the active stress parameter T_a indicates that the myocardium is contracting more forcefully, and our results also suggest that the LV generates a higher contractile force per myocardial volume than the does RV. One of the underlying mechanisms that modulate the contractile forces is calcium dynamics, ^44,47 and while T_a and γ cannot be directly compared with the calcium concentration because of the difference in units, their time traces have similar shapes when compared with the calcium transient. This finding is independent of the prescribed fiber field and the initially assigned passive material parameter a, as shown in. Further investigation of these estimates is needed, but we hypothesize that these measurements may provide useful biomarkers. Due to the observed consistent results in normal patients, even for wide-ranging PV loops, these estimates of contractility could therefore potentially serve as important diagnostic estimates in cases where disease alters myocardial contractility.

4.6 | Elastance

End-systolic elastance is widely recognized as an important determinant of systolic function.⁵⁷ However, its use in clinical practice is limited due to the need for invasive measurements of pressure and volume in response to varying loading conditions.

In the present work, we have simulated a change in loading condition by perturbing only the ES pressure (keeping all other quantities fixed) and computing the ES elastance from the slope of the resulting pressure-volume relationship. This approach has previously been applied to obtain LV ES elastance,⁹ but has not been applied to find RV ES elastance in biventricular geometries.

The resulting LV ES elastances range from approximately 1.0 to 2.0 kPa/mL. These values are higher than previous measurements in healthy human hearts, which range from 0.26 to 0.4 kPa/mL. ⁶⁹

There are few reported values of normal human RV elastance. However, ⁷⁰ reported values of the maximal RV elastance in the range of 0.32 to 1.23 mmHg/mL/m² in normal humans. Using a body surface area of 2 m²(typical in humans), this range translates to 0.08 to 0.32 kPa/mL. Our estimated value of approximately 0.2 kPa/mL is well within this range. It should be noted here that our estimated values of ES elastance do not take into account any physiological responses of the tissue, such as a change in active tension in response to an increased load. As such, these values represent only a local estimate of the elastance, since all other quantities were held fixed during the perturbation of the pressure. Because of these limitations, our elastance estimate will make most sense in the active strain formulation as a force-length dependence is implicitly included in this formulation. No such relation is, however, included in the simple active stress model here. Correspondingly, the active stress does not change as the load is perturbed, which may lead to an underestimation of the elastance.

4.7 | Limitations and future directions

In this work, we clearly see a variability of model-data fit with respect to choice of the fiber angle, suggesting that the fiber field can be calibrated to better fit the data. Here, we have only prescribed a linear transmural fiber angle variation that has opposite signs at the endo- and epicardium in both LV and RV. Dissection studies, however, generally found that the fibers are more circumferentially oriented at the subepicardium and more longitudinally orientated at the subendocardium in the RV.⁷¹ This suggests that one should also consider nonsymmetric fiber fields across the wall as well as different fiber field in the LV and RV. We seek to investigate these issues in future studies, possibly together with in vivo measures of fiber angles.

As noted above, the constants that balance the terms of the cost functional (14) were adjusted based on a previous study²⁸ of a single LV, where an L-curve type analysis was performed to estimate an optimal set of weights. Since the present study also considers the RV and the current cost functional form differs from the LV case, it is likely that these differences may affect the optimal choice of weight parameters. Hence, although the chosen parameter values gave good results for our applications here, there may exist even better choices.

While we were able to obtain stress measures across a small cohort of healthy subjects that were both internally consistent as well as in broad agreement with other published studies, the effect of our modelling assumptions remains to be determined. Here we used an incompressible model of the myocardium, even though it is well known that the myocardium is compressible due to perfusion of blood. Future studies should investigate the role of compressibility and, in particular, how fiber stress is altered when the material is allowed to compress. We clearly see stress effects related to the hydrostatic term in our model, and this will be investigated more closely in future studies.

Residual stresses are hypothesized to be important in stress estimation in soft biological tissue,⁷² and can be incorporated into the finite element model.^55,73 Because it has been shown in a previous study that residual stresses have little effects on ventricular function,⁷⁴ they were not considered in the present study. Nevertheless, the effect of including residual stresses in the estimation of fiber stress and contractility remains to be investigated in future studies.

The late diastolic pressure-volume curve is fitted by estimating 1 material parameter, while fixing the remaining parameters to previously reported values.²¹ This is a limitation in our study, and future studies will be geared towards reducing the need for fixing these model parameters by incorporating more clinical data or by revising the constitutive model. In particular, the incorporation of diastolic strains may be useful in more clearly defining material properties.

The simple estimation of unloaded configuration using only 1 iteration of the backward displacement method can be used with different initial material parameters and still recapitulate the end-diastolic volumes with different optimized material parameters. Several studies have jointly estimated the unloaded left ventricular geometry and material parameters, ^9,21,75 but estimation of the unloaded configuration with biventricular geometries is not a well-posed problem, since buckling of the RVFW might occur. More work on formulating well-posed algorithms for determining the unloaded configuration should be considered in future studies.

Finally, in this study, we only considered 3 normal subjects, and in the future, we would like to apply this framework to more individuals and use it to study larger cohorts as well as patients with cardiac pathology.

5 | CONCLUSION

Patient-specific simulations can now be assembled via adjoint-based data assimilation techniques, using no more than a few hours on a regular laptop. From these simulations, we are able to extract information about myocardial contractility and fiber stress that shows low variability in the modeling choices that we make. Validation of these models should be the main objective in the years to come in order to translate cardiac computational modeling into clinical utility.

APPENDIX A

SENSITIVITY TO UNLOADED CONFIGURATION

The choice of initial material parameter a in the unloading algorithm will influence the estimated unloaded configuration. A softer material will result in a lower unloaded volume; hence, the optimized material parameter will be softer to compensate for the greater volume increase from the reference to the end diastolic state. In the results presented in this study, the value a=1.291 kPa was chosen based on a parameter set used in other studies.²¹

To analyze the sensitivity of the results to the choice of material parameters used to unload the geometry, we unloaded the geometries using 4 different material parameters, ie, a = 0.5, 1.0, 2.0 and 4.0 kPa, and evaluated the corresponding model outputs. The resulting optimized material parameters, unloaded cavity volumes, and value of the mismatch functional during the passive phase are shown in Table A1.

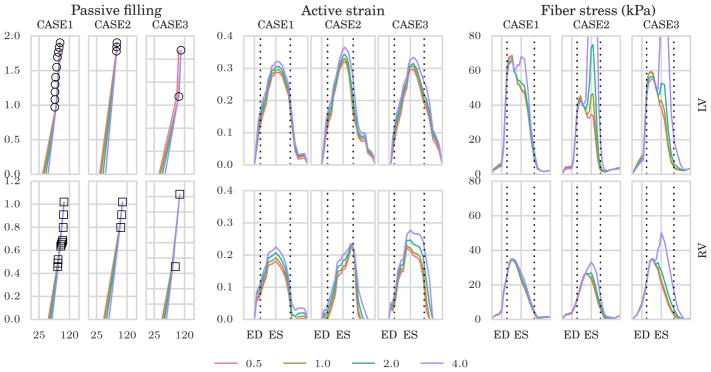
For a more visual presentation, the LV and RV filling curves are presented to the left in Figure A1 for the different choices of unloaded configuration. From these results, it is clear that even though the different choices results in very different unloaded geometries and passive material parameters, the mismatches between simulated and measured volumes are very small in all cases, except for a=0.5, which hit the lower bound (of 0.05 kPa) set in the optimization.

TABLE A1.

Optimized material parameters in kPa for different choice of unloaded configuration

Patient ID	Initial a	aLV	aRV	𝒥data (passive)	$V_0^{\text{LV}}$	$V_0^{\text{RV}}$
CASE1	0.5	0.05	0.321	0.000551	36.2	53.8
CASE1	1	0.165	0.699	7.13e-08	40.4	56.6
CASE1	2	0.64	1.49	1.81e-07	45.9	60.5
CASE1	4	1.92	2.91	2.46e-07	52.8	65.4
CASE2	0.5	0.05	0.29	0.000447	34.5	46.9
CASE2	1	0.168	0.736	8.06e-08	38.9	50.7
CASE2	2	0.642	1.79	3.27e-07	44.9	56.1
CASE2	4	2.03	4.01	9.79e-07	52.8	63.3
CASE3	0.5	0.05	1.03	0.00417	40.3	49.4
CASE3	1	0.0895	1.9	8.24e-07	44.8	52.8
CASE3	2	0.48	3.71	2.61e-06	50.8	57.5
CASE3	4	1.86	7.03	6.69e-06	59	63.5

Fiber stress and active strain are fairly consistent despite different unloaded geometries and material parameters (Figure A1). However, elevated fiber stresses can be seen during late systole for higher initial values of a. Furthermore, the magnitude of the active strain is increased in response to stiffening of the material.

FIGURE A1.

To the left, we show the passive-filling curves with volume in mL on the x–axis and pressure in kPa on the y–axis with different unloaded volume resulting from different material parameters used to estimate the unloaded geometries. Middle and right panels show average time traces of estimated active strain and Cauchy fiber stress, respectively, for different choices of unloaded configuration. Top row shows the results in the left ventricle (LV) while bottom row shows the results in the right ventricle (RV). Here, the values a=0.5, 1.0, 2.0 and 4.0 kPa are used to unload the ventricles. ED, end-diastole; ES, end-systole