The Health Effects of Medicare for the Near-Elderly Uninsured

Abstract

Objective

To determine whether Medicare enrollment at age 65 has an effect on the health trajectory of the near-elderly uninsured.

Data Sources

Eight biennial waves (1992 to 2006) of the Health and Retirement Study, a nationally representative panel survey of non-institutionalized 51–61 year olds and their spouses.

Study Design

We use a quasi-experimental approach to compare the health effects of insurance for the near-elderly uninsured with previously insured contemporaneous controls. The primary outcome measure is overall self-reported health status combined with mortality (i.e. excellent to very good, good, fair to poor, dead).

Results

The change in the trajectory of overall health status for the previously uninsured that can be attributed to Medicare is small and not statistically significant. For every 100 persons in the previously uninsured group, joining Medicare is associated with 0.6 fewer in excellent or very good health (95% CI: −4.8, 3.3), 0.3 more in good health (95% CI: −3.8, 4.1), 2.5 fewer in fair or poor health (95% CI: −7.4, 2.3), and 2.8 more dead (−4.0, 10.0) by age 73. The health trajectory patterns from physician objective health measures are similarly small and not statistically significant.

Conclusions

Medicare coverage at age 65 for the previously uninsured is not linked to improvements in overall health status.

Introduction

While 25% of Americans in the 55 to 64 age group experience gaps in health insurance coverage (Baker et al., 2005), starting at age 65 virtually all Americans have affordable, comprehensive health insurance coverage through the Medicare program. By reducing the out-of-pocket costs for medical care including that which would be otherwise unaffordable, Medicare for the previously uninsured increases medical service use for the previously uninsured (McWilliams et al., 2007a). Whether this increase in medical care for the previously uninsured ultimately results in health status gains remains an open question (McWillaims et al, 2007b; Card, Dobkin, and Maestas, 2004; and Ross and Mirowsky (2000).

A negative association between lacking health insurance and health has been well established in hundreds of studies reviewed by Brown et al. (1998), Hadley (2003), and the Institute of Medicine (2002). While many of these studies have been cross-sectional in design, this association has also been shown in longitudinal studies (Baker et al., 2001, Franks et al., 1993; Sorlie et al., 1994). While the RAND Health Insurance Experiment (HIE), the only randomized experiment of the effect of health insurance, also examined this issue it is of limited use for our purposes because (1) it did not include a study group with no health insurance; and (2) it excluded the Medicare-eligible population and thus excluded the elderly population.

In this paper, we use a quasi-experimental approach to establish the effects of Medicare insurance coverage on the health trajectories of the previously uninsured. Experimental designs are critical to the study of health and insurance because the observed association between health insurance and health may reflect the effects of health on health insurance (reverse causation/selection) or the effects of some other unobserved third factor on both health insurance and health (residual confounding) (Levy and Meltzer, 2004). This is because individuals under age 65 who acquire or drop health insurance typically do so for a reason related to a recent or projected change in health status: for example, they may enroll in a health plan because of a predicted health expense, they may lose their job and its health insurance coverage as a result of a health event, or they may qualify for public coverage as a result of poverty or disability. By contrast, because government policy restricts entry into Medicare until age 65 for most Americans, those who take up Medicare insurance (at age 65, but not those before age 65) do so for reasons other than changes in health status (of eligible aged beneficiaries, 99% enroll in Medicare Part A and 94% enroll in Medicare Part B). Thus aging into insurance at 65 creates the natural experiment to assess the effect of health insurance on the health of the previously uninsured.

The previously uninsured may be particularly vulnerable to any contraction in Medicare coverage because Medicare arrives at an age when affordable coverage is difficult to find for those lacking health insurance, especially if they have existing health conditions. As a result, several policy proposals have emerged to address being uninsured in the 55 to 64 age group including providing them with early access to the Medicare program. Understanding whether there is a health benefit to the near-elderly uninsured from the Medicare program is an important aspect of policy debates regarding expanding and limiting Medicare coverage.

Methods

Data

The data were obtained from the original age-eligible cohort of the Health and Retirement Study (HRS). The HRS began in 1992 as a national longitudinal study of the noninstitutionalized population born between 1931 and 1941 (i.e., persons age 51 to 61 at the time of the baseline survey) and their spouses. Respondents and their spouses have been reinterviewed every two years since. We use all biannual waves from 1992 to 2006.

Our study sample includes primary respondents and spouses from birth cohorts 1932–1937 (N = 7,501). These birth cohorts have the potential to be observed at least twice upon reaching the age of 65. Using the same participants for the pre- and post-eligibility periods removes the possibility of a birth cohort effect; we excluded the 1938–1941 birth cohorts for this reason. We start following all subjects when they are 59/60 (61/62 in the case of the 1931 cohort), to remove the possibility of left-censoring bias that would result from a differential death rate by insurance status and age cohort.

We also excluded persons who dropped out or died before age 59/60 (n = 759), those with missing insurance status (n = 76), the few persons who reported never receiving Medicare after age 65 (n = 98), those with no follow-up after age 59/60 (n = 358), and those on Medicare or Medicaid at age 59/60 (n = 740). We used sensitivity analysis to test the influence of this last exclusion. Our final study sample consists of 5,479 persons observed over an average of 6.5 waves. With the occasional survey non-response among the study sample addressed through listwise deletion, there were 29,426 observations for analysis.

The HRS sample weights account for attrition (in addition to the complex sample design) through a post-stratification of the HRS to the Current Population Survey (CPS) by age, sex, race, ethnicity, and marital status groups. This stratification explains differential non-response over time by those major demographic groups. Because differential attrition by insurance status remained (i.e. persons who were uninsured are more likely to be lost to follow-up than persons who were insured), we used the CPS to apply an additional adjustment to the HRS weights to hit insurance status totals within the 16 cells determined by age, race, labor force status, and education (Polsky et al, 2005). The adjusted weights are used in all analyses.

Insurance Status

In each wave, HRS respondents provided detailed information about their current insurance coverage. The uninsured are defined as those who indicated that they had no form of private or public insurance. Those uninsured at age 59/60 represent the uninsured group (n=738) and those insured at age 59/60 represent the insured group (n=4,741). Everyone is insured through Medicare once they cross the age 65 threshold, but the analytical labels for our comparison groups are held fixed according to their insurance status at age 59/60. Our primary analysis is based on the initial insurance status (i.e. insurance status at age 59/60). In a sensitivity analysis, we compare the group continuously insured and the group continuously uninsured between age 59/60 and age 65/66.

Outcome measures

The primary outcome measure is self-reported health status combined with mortality. The former is measured by the question, “Would you say that your health is excellent, very good, good, fair, or poor?” Self-reported health status has been used as a measure of health for many previous studies that related insurance coverage to health outcomes (Fihn and Wicher, 1988; Hafner-Eaton, 1993; Lurie et al., 1984; Short and Lair, 1994) and has been shown to have predictive validity for both future health care utilization and subsequent mortality (Manning et al., 1987; DeSalvo, 2006). Due to the small sample sizes on the extremes of this scale, we combine the excellent and very good health into a single category, and the fair and poor categories into another category. Because self-reported health status is a subjective assessment, we also analyzed secondary outcomes which were based on measures using more objective criteria to assess aspects of health. These outcomes are mobility (can walk one block and one flight of stairs, can walk one block or one flight of stairs, neither), agility (no difficulties, difficulty with only one among sitting for 2 hours; getting up from a chair; stooping, kneeling, or crouching; lifting 10 lb; pushing or pulling large objects; or extending one’s arms above shoulder level, difficulty with more than one), pain (no trouble, mild, moderate or severe) and depressive symptoms measured by from an adapted 8 question version of the Center for Epidemiologic Studies Depression (CES-D) (categorized as none (0), sub-threshold, scale (1–2), or active (>=3)). Mortality is reported by surviving family members or other contacts, and non-reported mortality is obtained through a link of the HRS files with the National Death Index. A category denoting whether the respondent died is added to all health measures.

Control variables

The core control variables include sex, age, education, ethnicity, race, and census region. Baseline marital status, income, and wealth and time-varying covariates of retirement status, receipt of Social Security payments, and marital status are included as explanatory variables in sensitivity analyses only because these variables are potentially endogenous. Wealth and income measures are converted to 2004 real U.S. dollars adjusted by the Consumer Price Index. Retirement status is based on self-reported categories of not retired, fully retired, partially retired, or not applicable. Coverage that supplements Medicare includes self-purchased, employer-provided retiree health benefits and Medicaid.

Empirical Model

We use a difference in difference estimator that takes into account several issues. First, initial insurance status is not randomly assigned, which could bias our findings; certain factors, such as low socioeconomic status, can cause poor health and lower rates of health insurance coverage. This problem is minimized by looking at health status before and after 65 for the same individuals. Second, the possibility that there may be a differential rate of change in health between the insured and uninsured groups is controlled for by our model which estimates health state transition rates before and after age 65. Third, it is possible that other changes confounded with health status may also occur near age 65, including retirement and Social Security payments. We consider the change in trajectory of the insured as a proxy for these and other contemporaneous changes. We also directly consider how sensitive our comparisons are to the time-dependent (but potentially endogenous) characteristics such as retirement status, employment status, and Social Security payments.

We estimate health state transitions between health state at age t (H_t) and the health state at age t+2 (H_t+2), one survey wave later. The transitions from H_t to H_t+2 are estimated by using the following multinomial logit model:

$$\begin{array}{l}ln\left[\frac{{\text{p}}_{\text{ij}}}{{\text{p}}_{\text{iE}}}\right]={\beta }_{\text{ij}0}+{\beta }_{\text{ij}1}{\text{H}}_{\text{t}}+{\beta }_{\text{ij}2}{\text{U}}_{\text{t}}+{\beta }_{\text{ij}3}{\text{M}}_{\text{t}}+{\beta }_{\text{ij}4}{{\text{H}}_{\text{t}}}^{\ast }{\text{U}}_{\text{t}}+{\beta }_{\text{ij}5}{{\text{H}}_{\text{t}}}^{\ast }{\text{M}}_{\text{t}}+{\beta }_{\text{ij}6}{{\text{M}}_{\text{t}}}^{\ast }{\text{U}}_{\text{t}}\\ +{\beta }_{\text{ij}7}{{\text{H}}_{\text{t}}}^{\ast }{{\text{U}}_{\text{t}}}^{\ast }{\text{M}}_{\text{t}}+{\beta }_{\text{ij}8}{\text{Age}}_{\text{t}}+{\beta }_{\text{ijn}}{\text{X}}_{\text{n}}\end{array}$$

where p_ij is the probability of being in health state category j for participant i at age t+2 given his or her health and other characteristics X: p_ij = pr(H_t+2 = j|H_t = i; age_t; X); H is a set of indicators for health state; U is an indicator for being uninsured at age 59–60; M is an indicator for being Medicare eligible. While we considered an ordered logit specification for this model because our measure of health status is ordered, we abandoned this approach for two reasons: (1) its poor performance on the Brant test for the proportional assumption in the ordered logit; and (2) the multinomial logit generally passed the modified Hosmer-Lemeshow test (Hosmer and Lemeshow 1989), while the ordered logit universally failed this test. The use of the multinomial may lead to some loss of efficiency, but does not have the same risk of inconsistency as the ordered logit. We estimated standard errors and significance in the multinomial logit using robust standard errors correcting for clustering at the person level.

Because our interest is in understanding the health trajectory of an aging insured and uninsured subject in terms of discrete health states, we use the model parameter estimates from the multinomial to simulate the implied health trajectories of the estimated health state transitions from ages 61/62 to 73/74 to predict what they would have done with and without Medicare at age 65. Our estimate of the impact of insurance status is the difference between what would have happened with Medicare at 65 versus what did happen. To control for trend and aging effects, these are differenced again between the previously insured and uninsured.

Our simulation begins with the sample when they are 59/60. We then use the estimated multinomial coefficients from the health transition model to predict their probability of being in each of the four health states at 61/62. Each subject’s realized health state at 61/62 is then determined from a random draw from a uniform distribution on the unit interval. We then repeat this process using the predicted health states at 61/62 as their baseline health state for the prediction of the probability of being in each of the four health states at 63/64. This process is repeated until each subject is aged to 73/74. Those subjects who enter the dead state are treated as dead for all remaining ages in the simulation and are dropped from the repeated predictions for subsequent ages. In addition to simulating the health of subjects as they age onto Medicare, we simulate the health of subjects as they age from 65 to 73 assuming they did not receive Medicare. This out-of-sample simulation is performed by not “turning on M” for ages beyond 65 (See Appendix, Section A for further details on simulation).

When the simulation is complete, the average proportion of subjects in each health state at each age for each insurance group is estimated as well as for the counterfactual post period of U and I. We then estimate the change in health state over a 6-year period for each insurance group (i.e. U_pre, I_pre, U_post, I_post) by subtracting the health state probability at age 73 from the health state probability at age 65. Therefore, U_pre and I_pre represent the counterfactual of the health change between 65 and 73 had pre-65 insurance status been maintained rather than transitioning onto Medicare while U_post and I_post represent the health change between 65 and 73 under Medicare. We then define ΔU and ΔI by the within insurance group difference between the change in health state from 65 to 73 under Medicare compared to the counterfactual had the previous insurance status been maintained [(U_post − U_pre) and (I_post − I_pre)]. Finally, ΔU − ΔI gives the change in health status caused by Medicare enrollment at age 65 for the uninsured, controlling for any contemporaneous changes in health over time. Confidence intervals for the simulated results are estimated through a nonparametric bootstrap that accounts for the autocorrelation in the data (Bertrand, Duflo, and Mullainathan, 2004).

We estimate the base model for several important subgroups (continuous insurance groups, by gender, for low income and low wealth, and for those with and without supplemental insurance) as well as conduct several robustness checks. We explore whether the results are robust to additional control variables such as time-dependent labor force participation and Social Security payments, to alternative age specifications, to alternative health status categorizations, to weighting, and to the timing of Medicare eligibility.

Results

Table 1 shows the baseline characteristics of the study sample by insurance status. The insured and uninsured groups in the HRS at age 59/60 are representative of these groups in the United States. The uninsured are more likely to be in fair or poor health, to be African American or Hispanic, and to have lower education and lower income, and are less likely to work. Table 2 shows the estimated odds ratios (and their individual p-values) of the multinomial regression of health status, with the excellent/very good group being treated as the reference category. The tests of significance for key groups of variables are displayed at the bottom of the table. Here we see that the health of the uninsured is different from that of the insured both before the Medicare-eligible age and afterwards. The health status differences before and after Medicare within insurance group are significant at the p=.05 level. The difference in the rates of change pre- vs. post-Medicare between the uninsured and insured is marginally statistically significant (p=0.093).

Table 1.

Baseline characteristics

	Insured N=4741	Uninsured N=738
Health Status
Excellent/Very good	54.4%	38.4%
Good	29.4%	30.5%
Fair/Poor	16.3%	31.1%
Male	48.9%	45.2%
Race
White	87.3%	64.4%
Black	7.6%	14.6%
Hispanic	3.5%	16.7%
Other	1.7%	4.3%
Education
High school drop-out	16.9%	48.1%
High school graduate	41.2%	30.7%
Some college	20.8%	12.7%
College graduate	21.2%	8.5%
Marital status
Married	79.6%	65.6%
Single	2.7%	3.2%
Divorced/Separated	10.7%	16.8%
Widowed	7.0%	14.5%
Region
Midwest	26.5%	15.8%
Northeast	21.6%	15.4%
South	32.3%	47.0%
West	19.6%	21.8%
Total Assets
Negative	1.8%	8.0%
0–35,000	9.9%	33.1%
35,001–100,000	15.4%	18.9%
100,001–230,000	25.8%	17.1%
230,001 and above	47.1%	22.9%
Total Income
0–20,000	11.6%	48.3%
20,001–40,000	21.5%	25.7%
40,001–75,000	34.0%	15.2%
75,001 and above	32.9%	10.8%
Social Security Recipient	4.5%	8.4%
Retirement Status
Not Retired	64.1%	60.0%
Fully Retired	17.8%	13.9%
Partly Retired	10.0%	9.6%
Not Applicable	8.1%	16.6%

^*P-values for all group tests are significant at .001 level

Table 2.

Multinomial Logit Regression of Health Status in t+2

	Good vs. Exc/VG		Fair/Poor vs. Exc/VG		Dead vs. Exc/VG
	Odds Ratio	p-value	Odds Ratio	p-value	Odds Ratio	p-value
Health Status
Good	7.40	<.001	10.49	<.001	4.56	<.001
Fair/Poor	11.38	<.001	131.67	<.001	66.40	<.001
Uninsured	1.35	0.005	1.90	<.001	1.35	0.440
Post (Medicare)	0.87	0.047	0.84	0.162	0.59	0.026
Uninsured*Health Status
Good	0.70	0.041	0.67	0.062	1.18	0.746
Fair/Poor	0.58	0.027	0.42	0.003	0.74	0.522
Post (Medicare)*Health Status
Good	0.86	0.060	0.98	0.868	1.58	0.085
Fair/Poor	0.94	0.698	1.04	0.839	1.49	0.124
Uninsured*Post (Medicare)	0.70	0.026	1.03	0.903	2.83	0.032
Uninsured*Post (Medicare)*Health Status
Good	1.55	0.087	0.89	0.711	0.44	0.208
Fair/Poor	1.24	0.546	0.72	0.413	0.24	0.022
Age	1.05	<.001	1.07	<.001	1.14	<.001
Age*Age	1.00	0.003	1.00	0.561	0.99	0.026
Male	1.08	0.041	1.16	0.002	1.84	<.001
Race/Ethnicity
Black	1.34	<.001	1.59	<.001	1.46	<.001
Hispanic	1.31	0.002	1.59	<.001	0.82	0.244
Other Race	1.28	0.127	1.07	0.667	0.79	0.399
Education
High School Graduate	0.77	<.001	0.54	<.001	0.66	<.001
Some College	0.76	<.001	0.47	<.001	0.65	0.001
College Graduate	0.60	<.001	0.31	<.001	0.51	<.001
Region
Northeast	0.96	0.479	0.94	0.388	1.01	0.951
South	0.98	0.656	1.16	0.013	1.13	0.210
West	0.83	0.001	1.05	0.552	1.03	0.820
P-value of the χ2 Tests on the set of coefficients representing the following Null Hypotheses:
Hypothesis:					P-value
Upre = Ipre					0.001
Upost = Ipost					0.000
Upre = Upost					0.021
Ipre = Ipost					0.024
(Upost − Upre) = (Ipost − Ipre)					0.093

Reference group: Exc/VG, insured, Pre, female, white, High school drop-out, and midwest

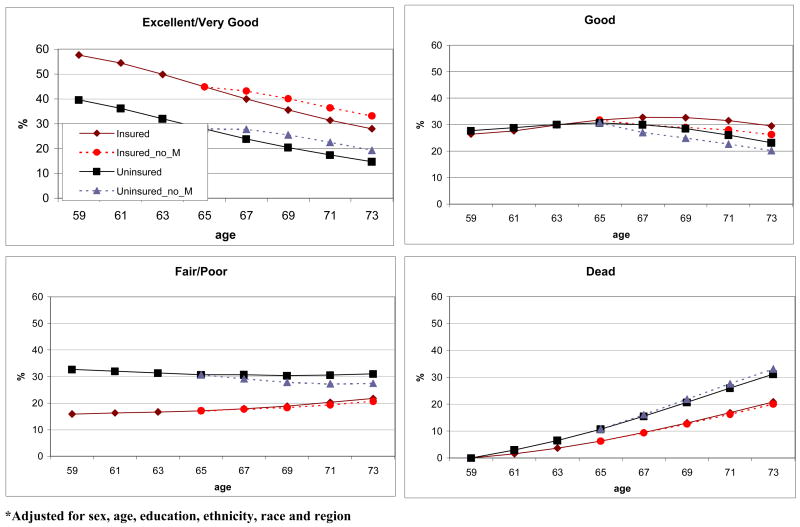
To better understand the direction of these health changes, we simulated the health trajectories depicted in Figure 1. In the northwest quadrant, we see the trajectory for the excellent/very good health status. The darker lines represent the uninsured group trajectory and the lighter lines represent the insured group trajectory. The uninsured trajectory is below the insured trajectory representing their inferior health. Both lines decline with age representing deteriorating health with age. The kink at age 65 represents the change in the rate of health decline post Medicare enrollment. The dashed line represents the counterfactual i.e. the pre-65 trajectory, based on the pre-65 transition probabilities, extended into the post-65 ages. The divergence between the two lines for each insurance group represents the effect of Medicare on that insurance group. Here we see the increase in the likelihood of excellent/very good health with Medicare for both the uninsured and insured groups. The divergence is greater for the uninsured group. The other panels illustrate the trajectories for the other health status categories. It is notable that by age 73 the fair/poor trajectories for the insured and uninsured groups converge.

Figure 1.

Health Status Trajectories by Insurance Group from Simulation*

As a check on the fit of our simulation we graphically plotted the raw trajectories with the trajectories from our fitted data. The lines were virtually identical providing strong evidence as to the remarkable fit of our model (See Appendix Figure A1).

Table 3 displays the simulated incremental effects between health trajectories based on the coefficient estimates from Table 2. In column [E] we see that for every 100 persons in the uninsured group, from age 65 to 73 joining Medicare at age 65 is associated with 4.6 more uninsured people reporting excellent or very good health, 3.0 fewer reporting good health, 3.6 fewer reporting fair or poor health, and 2.0 more as dead. Similar patterns are observed for the insured group from age 65 to 73, where joining Medicare at 65 is associated with 5.2 more insured people reporting excellent or very good health, 3.3 fewer reporting good health, 1.1 fewer reporting fair or poor health, and 0.8 fewer dead (column [F]). The magnitude of the values for the insured and uninsured groups are similar, but because of the larger sample size in the insured group the increase in excellent or very good and the decrease in good are statistically significant for the insured group and not statistically significant for the uninsured group. We note that the estimated confidence intervals account for the uncertainty generated by both sampling variation and some remaining simulation variation. If the remaining simulation variation was removed, we estimate that the confidence intervals would be at most 10–12 percent narrower which would put the uninsured results into the range of significance.

Table 3.

Predicted Probabilities of Health Status Changes Simulated between Age 65 and 73

	U post	U pre	I post	I pre	ΔU	ΔI	ΔU − ΔI
					[A] − [B]	[C] − [D]	[E] − [F]
	[A]	[B]	[C]	[D]	[E]	[F]	[G]
N	1729	2151	11588	13958
Excellent/VG	−8.6	−13.2	−11.7	−16.9	4.6 (0.2, 8.4)	5.2 (1.9, 8.5)	−0.6 (−4.8, 3.4)
Good	−10.5	−7.5	−5.5	−2.3	−3.0 (−7.6, 1.3)	−3.3 (−6.4, −0.1)	0.3 (−3.8, 4.1)
Fair/Poor	−3.2	0.4	3.6	4.6	−3.6 (−9.3, 2.3)	−1.1 (−4.2, 2.1)	−2.5 (−7.4, 2.3)
Dead	22.3	20.4	13.7	14.5	2.0 (−5.3, 9.5)	−0.8 (−5, 2.5)	2.8 (−4, 10)

Adjusted for sex, age, education, ethnicity, race, and region

The comparisons between the insured and uninsured groups in column [G] show the uninsured with 0.6 fewer in excellent or very good health, 2.5 fewer in fair or poor health and 2.8 more dead. These differences are not statistically significant and are small in magnitude. Given the variability in the difference-in-difference estimates as reflected by the 95% confidence intervals, we would have 80% power to detect differences of about 6 points between the uninsured and insured groups at the p<0.05 level. This is considerable power given that this represents a narrowing of less than 50% in the baseline health disparity between the insured at uninsured based on in terms of the 13 point differential probability of being in excellent or very good health.

A number of sensitivity analyses were conducted to show the robustness of this result. The details are presented in the Appendix (See Appendix, Section B and Tables A1 and A2). Similar pattern of results were found when the analysis was limited to comparing those continuously uninsured in the pre period with those continuously insured, but the death rate for the continuously uninsured is higher than the entire group of uninsured. When the uninsured are compared to those insured through Medicaid only, there is a strong relative improvement for the uninsured primarily because Medicare enrollment does little to change the health trajectory of those insured through Medicaid. This is a useful comparison because the uninsured are economically and demographically more similar to the Medicaid cohort than the privately insured cohort. There were no differences between women and men and low-income and low-wealth sub-groups look remarkably similar to the overall result. The main results were not sensitive to changes in retirement status, employment status, marital status, or Social Security eligibility, which suggests that the difference within the insured and uninsured groups are unlikely be attributed to these often contemporaneous changes at age 65. A series of other sensitivity analyses suggest that the results are insensitive to various alternative specifications.

Table 4 displays the simulation for models of all of the secondary outcomes. In each case, with the notable exception of depression, there is no relative improvement in health for the previously uninsured relative to the previously insured. For depression, however, there is a 7.4 percentage point decline in active depression for the uninsured group compared to 2.3 for the insured group; a statistically significant difference of 5.1 percentage points that can be attributed to Medicare for the previously uninsured. On the whole, these secondary outcomes suggest that lack of an effect for the health status trajectory comparison between insurance groups is robust to other, more objective, measures of physical health.

Table 4.

Predicted Probabilities of Health Outcome Changes Simulated between Age 65 and 73

	U post	U pre	I post	I pre	ΔU	ΔI	ΔU − ΔI
					[A] − [B]	[C] − [D]	[E] − [F]
	[A]	[B]	[C]	[D]	[E]	[F]	[G]
N	1729	2151	11588	13958
Change of Health Status
Better	−3.9	−4.0	−3.4	−3.1	0.1 (−2.6, 1.2)	−0.3 (−2.4, 0.5)	0.4 (−1.8, 1.8)
Same	−19.2	−18.0	−14.7	−13.9	−1.2 (−7.8, 4.8)	−0.8 (−4.5, 1.9)	−0.4 (−6.4, 5.5)
Worse	−2.3	−1.3	3.3	2.4	−1.0 (−4.3, 4.6)	0.9 (−1.3, 4)	−1.9 (−5.2, 2.9)
Dead	25.4	23.3	14.8	14.5	2.1 (−5.4, 8.5)	0.2 (−2.9, 3.5)	1.9 (−6.1, 7.9)
Mobility
No difficulties	−22.4	−20.4	−19.5	−18.4	−2.0 (−8.7, 2.5)	−1.1 (−4.7, 2.6)	−0.9 (−7.6, 2.7)
1 difficulty	−0.9	−2.9	−0.9	−0.8	2.0 (−1.4, 5.7)	−0.1 (−3.4, 2.1)	2.1 (−0.6, 5.9)
>1 difficulty	0.8	2.9	6.6	4.8	−2.1 (−5.7, 4.1)	1.8 (−1.5, 5.1)	−3.9 (−7.2, 2)
Dead	22.4	20.4	13.8	14.4	2.1 (−3.9, 9.3)	−0.6 (−3.3, 2.8)	2.7 (−3.8, 9.3)
Agility
No difficulties	−16.9	−15.7	−17.9	−16.4	−1.3 (−6.1, 3)	−1.5 (−5, 2.1)	0.3 (−4.4, 3.9)
1 difficulty	−2.1	−2.2	−0.2	−0.1	0.1 (−3.6, 3)	−0.1 (−3.2, 1.5)	0.1 (−2.3, 3.6)
>1 difficulty	−5.4	−4.6	3.8	1.9	−0.8 (−5.9, 5.4)	1.9 (−1.3, 5.4)	−2.7 (−7.5, 2.9)
Dead	24.5	22.5	14.3	14.7	2.0 (−5.1, 8.3)	−0.3 (−3.3, 2.7)	2.3 (−4.4, 8.2)
Pain
No troubles with pain	−18.4	−17.4	−16.2	−13.5	−1.0 (−8.8, 5.9)	−2.7 (−5.6, 1.7)	1.7 (−5, 7.2)
Mild pain	−1.8	−1.2	0.7	−0.5	−0.6 (−2, 1.7)	1.2 (−0.5, 2.1)	−1.8 (−2.8, 0.6)
Moderate/Severe pain	−2.3	−2.4	1.6	−0.3	0.1 (−4.1, 4)	1.9 (−1.4, 4.4)	−1.9 (−5, 2.5)
Dead	22.6	21.0	13.9	14.4	1.5 (−5.8, 8.1)	−0.4 (−3.4, 2.9)	2.0 (−4.3, 8.2)
Depression
None	−4.3	−11.4	−6.0	−11.6	7.1 (0.2, 10.3)	5.6 (1.7, 8.3)	1.5 (−4.3, 4.7)
Sub-threshold	−10.3	−9.2	−7.5	−5.3	−1.1 (−3.8, 4.7)	−2.2 (−4.6, 1)	1.1 (−1.2, 6.1)
Active	−9.7	−2.2	−1.0	1.3	−7.4 (−12.1, −2.8)	−2.3 (−4.8, 0.2)	−5.1 (−9.3, −1.3)
Dead	24.2	22.8	14.5	15.6	1.4 (−5.6, 8.2)	−1.1 (−4.3, 2.5)	2.5 (−4.5, 9.2)

Adjusted for sex, age, education, ethnicity, race, and region

Conclusion

Because some of the near elderly have few affordable alternatives for health insurance, those near elderly without health insurance are an important group to consider for policy interventions. The lack of financial protection from unexpected health care expenses which are more likely to occur with advancing age can have devastating direct financial consequences (Himmelstein, et al., 2005) and the difficulties in accessing adequate health care without health insurance (Hadley, 2003) may indirectly result in a more rapid deterioration of health. By using Medicare as a quasi-experiment, we have explored whether the indirect health consequences of lacking health insurance could be arrested by providing health insurance to the uninsured. For both subjective and objective health status measures, we did not detect a relative slowing of health decline for the previously uninsured between ages 65 and 73 when compared to the previously insured.

Our evidence that Medicare does not improve the physical health status of the uninsured relative to the insured is consistent with the lack of detectible health effects from the more generous coverage groups in the Rand Health Insurance Experiment (Manning et al, 1987). The RAND Health Insurance Experiment, the only randomized trial to look at the question of whether generosity of benefit design in plans (with a catastrophic cap on out-of-pocket expenditures) affects health, found that while people receiving free care used more services, they did not have better health outcomes among a broad array of health measures than those with less generous coverage. The RAND study did not randomize people to no insurance. Results from studies that compare longitudinal changes in the health of insured and uninsured adults without experimental assignment of insurance status are mixed. Ross and Mirowsky (2000) find no difference in health declines by insurance status and Baker et al., (2001) and Dor, Sudano, and Baker (2006) find more rapid declines among the near-elderly uninsured.

Results from studies of the impact of health status on the uninsured that take advantage of the experimental opportunity of Medicare eligibility at age 65 are generally inconsistent with our finding of no effect. Card, Dobkin, and Maestas (2004) track changes in cross sectional self-reported health status over time for groups with different probabilities of being uninsured prior to age 65. Their results are mildly suggestive of a positive link between self-reported health status and insurance coverage. McWilliams et al, (2007b) used the same data and a similar strategy as this paper, but found the acquisition of Medicare coverage to be associated with improved trends in health for the previously uninsured. These two papers ignore deaths in their analysis; they implicitly or explicitly treat subjects who died as a missing-at-random survey non-response. As we show in detail in our appendix, when deaths are erroneously treated as a missing-at-random survey non-response, the health effects for the uninsured are much greater than the insured, but when deaths are modeled as the health outcome of death, there is no significant detectable health effect for the uninsured relative to the insured. Ignoring deaths leads to a biased inference regarding the effect of Medicare on health status.

Hadley and Waidmann (2006), using an instrumental variables analysis approach with pre-65 HRS data only, find that extending insurance coverage to the near-elderly uninsured would result in large increases in the proportion of people at age 65 in excellent and very good health. Yet, as pointed out in a commentary by Kronick (2006), the magnitude of the health changes found in Hadley and Waidmann (much larger than those found here) seem implausible. Part of this may be due to issues with the appropriateness of their instruments, but part may be due to their use of an inappropriate instrumental variables estimator for nonlinear estimators for endogenous categorical health status and dependent variables (Newey, 1987; Terza, 2006). Another possible explanation for the differences between Hadley and Waidmann’s results and ours is their use of an ordered logit. As indicated earlier, our data reject that specification of the model.

We find no insurance coverage effect on mortality for the previously uninsured which is consistent with Finkelstein and McKnight (2008). They found that the establishment of Medicare in 1965 had no discernible impact on the mortality of the elderly in the 10 years following Medicare’s enactment. However, Card, Dobkin, and Maestas (2007), who track mortality following hospitalizations, find a strong effect from higher rates of insurance as a result of joining Medicare.

We did find that Medicare at 65 is associated with slower health declines in terms of an increase in the probability of being in excellent or very good health, a corresponding decrease in the probability of being in good health, and no detectible differences in mortality or the fair or poor health group. While this suggests that Medicare may have a health effect for the relatively healthy 65 year olds, independent of insurance status, it may also reflect unmeasured factors. For example it could be attributed to the security of guaranteed health insurance coverage through Medicare until the end of life that is not available when insurance is tied to employment. For example, recovery from cancer can be inhibited when one must maintain employment to maintain coverage (Bradley et al., 2005). But this hypothesis would require further testing. We explored alternative mechanisms, such as the sharp increase in retirement and Social Security payments at 65, but our findings suggest that health results are insensitive to these mechanisms.

An important limitation of our quasi-experimental design is that the “intervention” of insurance through Medicare may not be of uniform intensity for both the previously insured and uninsured. Gaps in Medicare coverage such as prescription drug coverage through 2006 and 20% coinsurance for outpatient and physician services are typically filled through a variety of forms of Medicare supplemental coverage. We found that only 49% of the previously uninsured had supplemental coverage through retiree health insurance, privately purchased supplemental coverage or Medicaid, compared to 74% for the previously insured group. Because the previously uninsured generally have low incomes, these gaps may still provide sufficient disincentive for using the types of health services that may improve health such as preventive services and prescription drug use for the control of chronic diseases. A second important limitation is that even with an increase in the use of preventive services (McWilliams et al., 2003), the positive health effects may take years before they can be detected in population averages.

When considering the value of health insurance, however, health is only one important aspect. Health insurance is designed to provide financial security to families by protecting them from potentially devastating financial consequences that can result from unexpected health care expenses (see the review by Cutler and Zeckhauser, 2000). The more direct financial justification for health insurance should not be forgotten as we seek to better understand its indirect health consequences.