Abstract
Purpose:
A remote imaging system tracking Cherenkov emission was analyzed to verify that the linear accelerator (linac) beam shape could be quantitatively measured at the irradiation surface for Quality Audit (QA).
Methods:
The Cherenkov camera recorded 2D dose images delivered on a solid acrylonitrile butadiene styrene (ABS) plastic phantom surface for a range of square beam sizes, and 6 MV photons. Imaging was done at source to surface distance (SSD) of 100cm and compared to GaF film images and linac light fields of the same beam sizes, ranging over 5×5cm2 up to 20×20cm2. Line profiles of each field were compared in both X and Y jaw directions. Each measurement was repeated on 2 different Clinac2100 machines. An inter-reader comparison of the beam width interpretation was completed using procedures commonly employed for beam to light field coincidence verification. Cherenkov measurements are also done for beams of complex treatment plan and isocenter QA.
Results:
The Cherenkov image widths matched with the measured GaF images and light field images, with accuracy in the range of +/−1mm standard deviation. The differences between the measurements were minor and within tolerance of geometrical requirement of standard linac QA procedures conducted by human set up verification, which had a similar error range. The measurement made by the remote imaging system allowed for beam shape extraction of radiation fields at the SSD location of the beam.
Conclusions:
The proposed Cherenkov image acquisition system provides a valid way to remotely confirm radiation field sizes and provides similar information to that obtained from the linac light field or GaF film estimates of the beam size. The major benefit of this approach is that with a fixed installation of the camera, testing could be done completely under software control with automated image analysis, potentially simplifying conventional QA procedures with appropriate calibration of boundary definitions, and the natural extension to capturing dynamic treatment beamlets at SSD could have future value, such as verification of beam plans with complex beam shapes, like IMRT or “star-shot” QA for the isocenter.
Keywords: Cerenkov, QA, dosimetry, radiotherapy, linear accelerator, light field
1. INTRODUCTION
Verification of the accuracy of the linac radiation beam, as shaped by jaws and MLCs, is a critical quality assurance component in clinical radiotherapy. The radiation beam is not visually seen, but the projected light field from the linac head is used as a surrogate to visualize the projection of the beam on the table, phantom, or patient. The guidelines to verify that the size of beam agrees with prescription are very tight, and so the radiation field shape measurement is generally performed using radiographic film or external portal imaging devices (EPID) with appropriate markers such as BBs to mark the field line edges. The medical physicist compares the film or EPID readout with that of light field.1–4 Both the film and EPID measurement can achieve submillimeter precision. However, due to penumbra effects, the boundaries of the radiation are not always as clear as might be desired,5 and thus there remains some subjectivity in the determination of the beam boundaries from either film, EPID or light field. This is compounded when beams are very small or large, or when complex shapes are used. Physicists’ time and equipment required are the limiting factors associated with workload in linac QA.6 The calibration procedures are required to interpret dose reading from the film and EPID measurement, which also increase the work load of the physicists to do the 2D dose measurements using film and EPID.7,8 There is an opportunity to do beam shape verification completely electronically if a secondary measurement of shape could be acquired at the SSD of the patient, and in this study Cherenkov imaging was evaluated for this application.
Ionization chambers and diodes are widely used in linac QA to measure point dose because of their accuracy and fast readout.7,9,10 Many recent studies and products have been developed using 2D or 3D arrays of ionization chambers or diodes to extract dose distributions in phantoms to verify the treatment plans in external beam radiation therapy (EBRT). Such applications have also been used to extract lateral dose profiles to do light field congruence test in linac QA, or even in more complex QA such as multi-leaf collimator (MLC) shape verification, or even IMRT plan verifications.11–14 However, due to the large size of individual ionization chambers or diodes, these tools do not permit high resolution dose measurement.9,15 The common resolution of the ionization chamber is 5 mm,13 which is much larger than the resolution of radiographic film, which can approaches 0.1 mm.6 In addition to the problem of lower resolution, the observed error can reach up to 10% for ionization chambers measurements due to their large size.12 In addition, ionization chamber and diodes cannot measure the light field at the same time of dose measurement, requiring the physicists to do light field measurements manually, which should agree with the beam size to a tolerance of 2mm or 1%.1–3 These latter measures are often taken by physicists using graph paper or other methods of physical alignment.
Cherenkov emission was recently adapted as a tool to analyze dose distribution on the surface of phantoms and patients’ skin16,17. Experiments have shown that the Cherenkov signal intensity is linearly correlated with dose delivered to the surface of a plastic phantom.18 Based on this relationship of linearity, human studies have been done to evaluate the surface dose distribution on skin in breast treatment19 and total body electron treatment,20 as a verification of the treatment plan. This clinical work is still ongoing to determine the potential value, but imaging of the 3D dose distributions in a water tank, appears to agree very well with dose distributions simulated by the treatment planning system (TPS) and verified by film.21–23 Recent work has also extended this to verify beam shapes of complex radiation treatment plans, such as IMRT, and confirm the match lines between adjacent beams.24 These Cherenkov signals can be directly read using camera systems with a time-gated intensified camera.24,25 These cameras can have high pixel density, and so it is feasible to acquire high resolution dose delivery shapes of the beams incident upon solid phantoms, or even patients, from Cherenkov imaging.16,26 The Cherenkov camera can also acquire linac light field images/videos, which makes it possible to compare light field shapes to dose delivery shapes. Since both Cherenkov and light field information are saved as digital images/videos, image processing techniques could make the analysis of light field and radiation field coincidence seamlessly automated, and more objective than the physicist visually verifying light field projection images on grid paper as compared to the film images.
2. METHODS
2. a. Measurement and Experiment Setup
Measurements were conducted in two treatment rooms with two different medical linear accelerators (Varian 2100CD, Varian Medical Systems, Palo Alto, CA). Beams of 6MV photons were used to irradiate the phantom and film. The dose rate of the beam was 600 Monitor Units/minute (MU/min) delivered at an SSD of 100cm. For each measurement imaging Cherenkov emission, a total of 200 MUs were delivered and to maximize the signal on each film, a total of 1000 MUs were used. During the measurement, the gantry and the collimator of each linac were fixed at 180° angle in Varian coordinate. Square beam shapes were using the XY jaws, setting the beam sizes of 5×5, 10×10, 15×15 and 20×20 cm2.
Two different camera systems were used to assess performance, having been produced by DoseOptics LLC as early prototypes of time-gated intensified CMOS cameras (C-Dose™, DoseOptics, LLC, Lebanon, NH). Both image acquisition systems were coupled with fixed focal length lens (50mm f/1.8, Nikon Inc., Belmont, CA), and calibration of each included flat field response correction using a custom LED panel for continuous bright non-saturating signal (Thorlabs, Newton, NJ) and dark field correction with the lens cap on the camera to simulate the camera sensor closed to light.
A square beige Acrylonitrile Butadiene Styrene (ABS) plastic slab (40cm×40cm×1cm), served as the phantom for imaging both light field and Cherenkov emissions, as well as placement of the film. This was placed in the horizontal plane with SSD=100cm and centered on the beam axis. The edges of the slab were oriented in parallel with the axes created from the alignment laser, in both X and Y directions. The focal plane of each image acquisition system pointed at the isocenter of the linac, and each were positioned 3 meters above the ground, on the right side of the treatment couch from the patient’s perspective, to make sure the ABS slab was in the field of view of the image acquisition system. During the measurement, the room lights in each treatment room were turned off to minimize the background noise.
2. b. Position calibration for Cherenkov imaging
Before the measurements of Cherenkov emission were done, a transformation matrix was calculated to correct for the skewed perspective angle of the camera, relative to the plane of the imaged phantom. A checkerboard pattern was placed on the surface of ABS slab and used to construct this projective transformation matrix. The pattern was composed of 6×8 squares with consecutive black and white grids and the side of each grid had a length of 2.3 cm square. Images of the pattern were post-processed using OpenCV checkerboard function, based on the Harris corner detector algorithm,27 extracting pixel locations of the corners in the image as discrete points to map to.
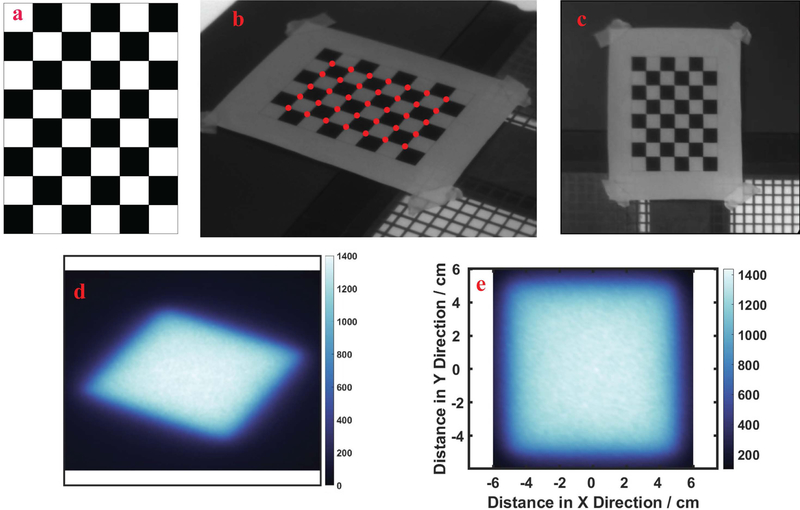
The point locations i are defined as pi = [xi, yi, 1]T, in which xi and yi are the X and Y components and the 1 as the third augmented term. The corresponding physical location of i was defined as qi = [Xi, Yi, 1]T The pixel and physical locations of all corners can be summarized as matrices p = [p1, p2, …, pn] and Q = [q1, q2, …, qn], where n is total number of corners in the pattern. Then the relationship between the physical locations and image pixel locations can be expressed as Q = AP, in which A is 3×3 perspective projection matrix. It is feasible to calculate matrix A from the matrices P and Q with enough measurements of the corner locations. This was implemented in the image processing toolbox of MATLAB (v 9.2.0 R2017a, The Mathworks, Natick, MA), and allowed the optical intensity of Cherenkov signal and light field shown in the skewed camera perspective to be mapped into the physical locations on the plane of the slab, as illustrated in Figure 2.
FIG. 2:
In (a) the square patterned board used for calibration is illustrated, with (b) a calibration image taken from camera showing the corners detected (red dots) using the OpenCV library, and remapped (c) to be projected as the undistorted board image. In (d) a Cherenkov image of a 10×10 cm2 beam is shown, and (e) the remapped Cherenkov image is shown as a square.
2. c. Cherenkov and light field imaging
During beam delivery, images were acquired at a frame rate of 23 frame per second for approximately 460 video frames, in 20 seconds. At the end of each measurement, background frames were extracted for an additional 20 seconds, to allow for background subtraction. The raw video frames were first post-processed with three image processing procedures: frame averaging, flat-field/dark-field correction28 and background subtraction. The flat dark field video frames are taken with a lens cap attached to the camera system, while the flat field frames are taken with a flat field correction panel attached to the lens. The light intensity is distributed uniformly in the flat field correction panel. In the frame averaging stage, a single image labeled as Il, Ic, Ib, Id and If, is created by taking a moving window temporal average of 100 frames in the middle of each piece of video, for each of light field, Cherenkov, background, dark-field and flat-field. Then the images of light field, Cherenkov and background were processed with pixel-wise flat-field/dark-field correction, using equations listed in I, II, and III, below, where the front factor is simply to normalize the intensity to the maximum of the flat field measurement, and the latter factor removes the effect of dark field pixel variation.
| (I) |
| (II) |
| (III) |
where i, j are the pixel indices in the X and Y directions of one image, and I(i, j) is the corresponding pixel reading and max(I) is the maximum pixel reading of one whole image. , , and are the Cherenkov, light field and background images processed by correction. In the last step of image processing, the background image is subtracted from the Cherenkov and light field images using equation IV and V, to remove the background noise. The background image is taken when there is no radiation field, to include the background light signals.
| (IV) |
| (V) |
The resulting 2D distributions of Cherenkov and light field were reconstructed through equation VI to VIII, with the perspective projection matrix A, derived from the spatial transformation calibration. The line profiles could then be extracted in both X and Y directions for Cherenkov and light field.
| (VI) |
| (VII) |
| (VIII) |
The value of x and y define the physical location, as shown in Figure 2(e), and D(x, y) is the corresponding Cherenkov or light field distribution at that location, as shown in Figure 2(d). The profile of the squared beam width is measured in the X and Y directions of jaws.
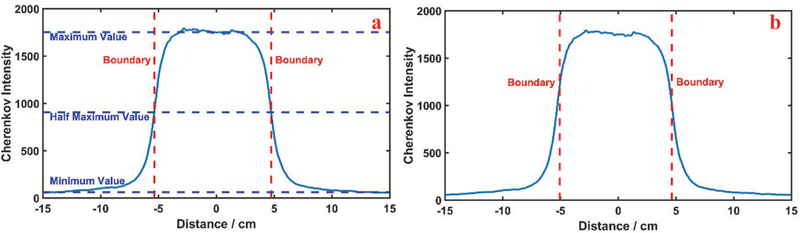
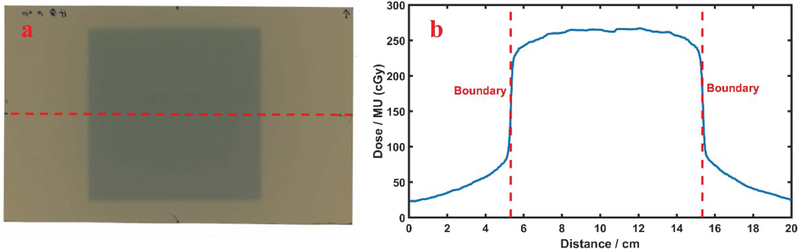
The boundaries from each image are not perfectly clear in light field, the Cherenkov emission image, or the film, due to the noise of the camera’s image sensor and beam penumbra. Thus, two standards were examined to determine the boundaries of Cherenkov signal or light field images: 1) the full width at half maximum (FWHM) and 2) maximum slope profile estimate. The standard of FWHM is estimated with average values of the maximum and minimum signal intensity, along the profile line, but the definition of the width necessarily depends upon the definition of the maximum and minimum values, as illustrated in Figure 3(a). Thus, when peak and background intensities are noisy, the pixel readings need to be averaged to estimate the peak value of the curve. Also, when the light imaged is diffused by the test object, it may be that the lateral diffusion alters the apparent penumbra of the imaged beam. The second standard definition for boundary edges is the location of slope maxima, as defined by the extrema points of the first derivative of the profile line. These locations are illustrated in Figure 3(b), and for a typical profile plot are noticeably a few millimeters narrower than the FWHM definition. Both were tested here.
FIG. 3:
The sequence of image analysis is shown in (a) with a line profile from the Cherenkov image showing the standard of Full Width Half Maximum Illustration (c): Boundaries extracted using the standard of maximum derivatives.
2.d. Beam measurement by film analysis
The film measurement served as the gold standard for measurement to evaluate the performance of light field and Cherenkov measurements. In this paper, the GaF films (Ashland Advanced Materials, Bridgewater, NJ) were used to measure the 2D dose distribution of the surface at the phantom surface. The films were then digitized by a film scanner (Epson, Long Beach, CA), and the intensity of the red channel was used to calculate dose, due to its higher sensitivity to dose change than the green or blue channels.6
In order to calibrate the film intensity to dose units, multiple 2”×2” squared patches were used and placed in solid water at dmax = 1.6cm for a 6MV photon beam, with full backscatter, and absorbed doses between 0 and 500cGy, were delivered. A third-order polynomial equation was used to fit the correlation curve of dose to film reading.6
In the 2D dose measurement, solid water slabs of 60cm thickness were placed on the treatment couch to provide backscattering, and one piece of film was taped on the top surface at SSD = 100cm, with the central axes aligned to the linac isocenter. About 300 to 400 cGy was delivered in the central region. Each piece of film was read directly after the measurement and converted into a dose distribution according to the calibration equation. The boundary standards used in Cherenkov and light field analysis were also applied to dose distributions, to extract the widths of beams in X and Y directions. The width of dose profile was defined as beam width, as shown in the bar graphs.
**2.e. Inter-observer analysis of the field size estimation
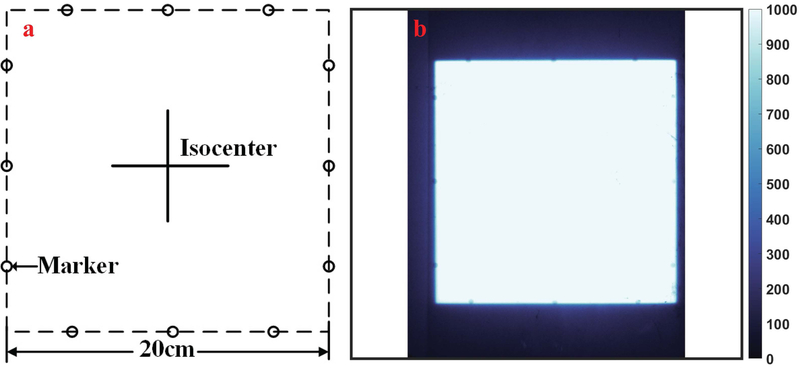
An inter-observer analysis was conducted to measure how accurate any single visual estimate of the field edge could be achieved by spatial coincidence testing between the film and the observed light field, as is commonly done in quality assessment procedures. In this analysis, each of two medical physicists participated to measure the size of the light field for ten repeated measurements of a beam, with side lengths varying randomly from 19.5cm to 20.5cm at 0.1 increments. The sequence of beam sizes was generated randomly by computer, and the display panel of the linac was obscured to ensure the physicists did not know the beam size planned. During the measurement, they used grid paper and a ruler to measure the beam size and recorded the results of each beam side distance. These distances were then compared to the known input sizes.
A standard light field to beam edge coincidence test was performed with a piece of grid paper with radio-opaque markers on the edges for a 20cm×20cm square, and a piece of phosphor film. Before the light field congruence test, the phosphor film was placed underneath the grid paper and the grid paper was aligned with the light field of a 20cm×20cm square beam, so that the edges of light field bisected the ball bearing markers, as illustrated in Figure 5(a). As in the film measurement, the couch was set to SSD = 100cm, and the grid paper was placed at the isocenter. In the congruence test, the phosphor film was irradiated with 2MU using a 6MV photon beam and a dose rate at 600MU/Min. After the film was exposed and scanned into the computer, the physicists checked the location of the markers projected on the phosphor film, as shown in Figure 5(b). The locations of the beads are used to determine success in the beam edge position localization. In this sensitivity analysis, there were eleven squared beams used, with the size of the beam ranging from 19.5cm to 20.5cm, with 0.1cm increment. Images for analysis were then chosen at random for measurement.
FIG. 5:
A common method used in light field quality assessment is illustrated with (a) a pattern used for a 20×20cm2 square beam. In (b) one example processed phosphor film is shown after exposure, with the location of the circular bead markers visible on each of the 4 edges.
3. RESULTS
3.a. Image Transformation Verification
The matrix used for image transformation are verified using checkerboard patterns and black squared patterns. The checkerboard patterns consist of 22×16 black or white cells. The size of each cell is 1×1cm. In the verification test, the images of the checkerboard patterns are acquired by the Cherenkov image acquisition system. The pixel locations of the grid corners (21×15) are extracted and their physical locations are translated using the transformation matrix derived before. The physical locations derived for the cell corners are compared with their real locations measured by hand. The errors of the derived physically locations are within 1mm on average, with less than 1mm standard deviations.
The sizes of the black squared patterns range from 5cm×5cm to 20cm×20cm, to simulate the beam shape of radiation and light fields. The widths of the black squared patterns are measured by the same methods as that for the radiation and light fields. The measurement made by the Cherenkov image acquisition system has the error within 1mm for all sizes of the squared pattern. In both measurement of checkerboard and black squared patterns, the lens correction has also been tested and its impact is minor for the measurement error using the image transformation matrix.
3.b: Square beam width estimation
The results of measurements are summarized numerically in Table 1, listing the width from light field, Cherenkov emission analysis, and film measurement. These values show the better width estimation of maximum slope on each edge, which matched the true beam sizes better than FWHM. Mean distance error were about 1mm to 2mm for the max slope method for light field and Cherenkov emission analysis, respectively. This was averaged over all beam size ranges from 5cm×5cm to 20cm×20cm, and the width was classified into X and Y jaw directions. When comparing to the GaF film measurements, the light field measurement is generally within QA guidance tolerance (the greater value of 2mm or 1%) using either definition. However, some measures of Cherenkov width with FWHM estimation were not within tolerance using the standard FWHM definition, suggesting that the optical scattering of the edge was likely widening the estimated edge more than would be desired. As such, the width measurement performed better using the definition of the edges by their extrema difference, as defined as the maximum slope of each of the lines. There was not a significant difference observed between directions of measurement nor between the two different rooms.
Table 1:
Summary of results of beam width measurements as measured from two independent linac tests
| Location | Direction | Nominal Beam Size/cm | Film Width/cm | Light Field Width/cm | Cherenkov Width/cm | Light Field Error/mm | Cherenkov Error/mm |
|---|---|---|---|---|---|---|---|
| linac 1 | X | 5 | 5.0 | 4.8 | 5.3 | 2 | 3 |
| 10 | 10.0 | 9.7 | 9.9 | 3 | 1 | ||
| 15 | 15.0 | 14.9 | 15.1 | 1 | 1 | ||
| 20 | 20.0 | 19.9 | 19.9 | 1 | 1 | ||
| Y | 5 | 5.1 | 4.9 | 5.0 | 2 | 1 | |
| 10 | 10.0 | 9.8 | 10.4 | 2 | 4 | ||
| 15 | 15.0 | 15.0 | 15.0 | 0 | 0 | ||
| 20 | 20.0 | 19.8 | 20.0 | 2 | 0 | ||
| Mean Error | 1.6mm | 1.4mm | |||||
| linac 2 | X | 5 | 4.9 | 4.9 | 5.1 | 0 | 2 |
| 10 | 9.9 | 9.9 | 9.7 | 0 | 2 | ||
| 15 | 14.9 | 14.9 | 15.1 | 0 | 2 | ||
| 20 | 19.9 | 19.9 | 20.0 | 0 | 1 | ||
| Y | 5 | 4.9 | 4.9 | 5.1 | 0 | 2 | |
| 10 | 9.9 | 9.9 | 10.2 | 0 | 3 | ||
| 15 | 14.9 | 15.0 | 15.1 | 1 | 2 | ||
| 20 | 19.9 | 20.0 | 20.0 | 1 | 1 | ||
| Mean of Error | 0.3mm | 1.9mm | |||||
3.c. Sensitivity Test of Light Field measurement
In the light field width matching, the inter-observer study used light field alignment using grid paper, and then x-ray exposure to bead markers of a fixed 20×20 beam, and exposure to phosphor film, to check if the radiation field on the film matched with the light field as seen at the SSD location. As shown in Fig. 5b, the markers on the edge of the squared pattern leave shaded areas on the phosphor film underneath the paper. However, due to the penumbra effect of radiation fields, the dose distribution changes gradually near the boundaries. In the observer test with 11 repeated test patterns, with human estimation of the light field, the inter-observed error of two physicists had a total range of 0 to 2.0mm, with a 1.0mm average inter-observer error. These error estimates from light field are within the tolerance given by the guidelines of linac QA.3
3.d: Measurement of Cherenkov field of complex treatment plan
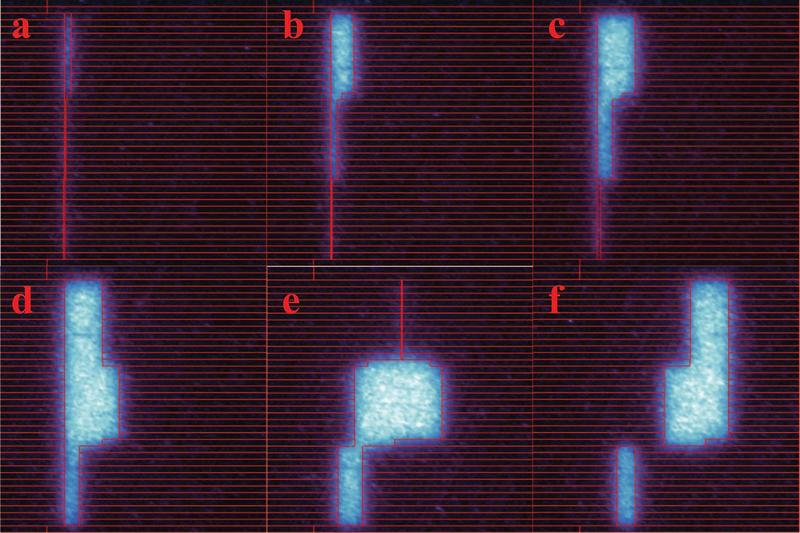
Measurement was done to analyze the beam shapes of complex treatment plan. In this experiment, the Cherenkov field of an IMRT QA plan with both moving and complex shapes were acquired using the Cherenkov imaging system. The shapes of the fields were transformed into the isoplane, and compared with the contours of MLC configurations, extracted from the dynalog files of the treatment. The shapes of Cherenkov fields after transformation matches the patterns of MLC projected on the isoplane.
3.e: Isocenter measurement by rotating collimators
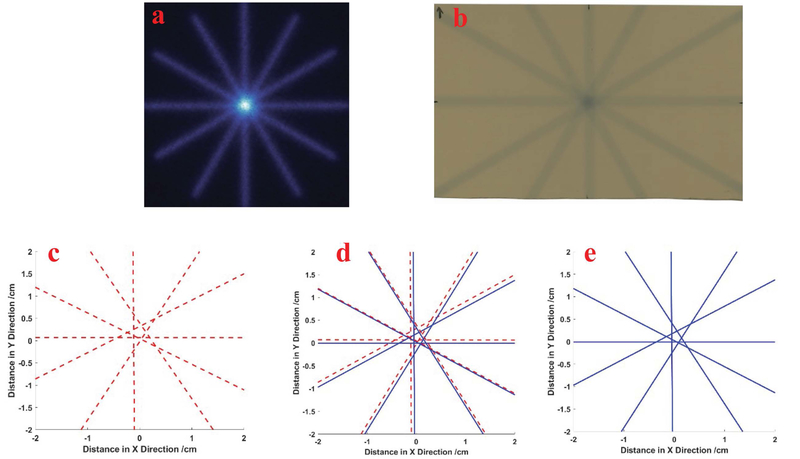
The isocenter measurement, commonly fulfilled by the “star-shot” analysis, can also be fulfilled by the Cherenkov image analysis. In this experiment, the 30cm×0.5cm squared beams radiated the plastic phantom on the isoplane, with collimator angles of 30°, 90°, 150°, 180°, 240° and 300°, to form a star pattern in the isocenter. The 2D dose distribution is also measured by film for the beams with these collimator angles. For each collimator angle, 400 MUs are delivered from the linac machine to get high contrast of film reading.
The central axes are extracted using the methods in “star-shot” QA analysis for both Cherenkov and film measurements29,30. The locations of the central axes and star shapes formed by the axes are similar for Cherenkov and film profiles. For Cherenkov profile, the radius of the star is about 2.1mm, while it is 1.9mm for the film profile. Cherenkov measurement achieves similar performance as film measurement in the “star-shot” QA of isocenter for varied collimator angle. Similar procedures of Cherenkov image analysis can be done for varied bench angles in the “star-shot” analysis. Thus, Cherenkov image analysis is a potential tool for linac QA of isocenter.
4. DISCUSSION
The results here demonstrate that there is good spatial agreement between the measurements of light field, Cherenkov emission and film using the two boundary standards of half maximum and extrema difference. Based upon physical principles, ideally, we expect there to be a perfect match between the film measurement of the beam and the Cherenkov images, because both signals are produced by the beam dose and it is known that both are monotonically related to dose.18 As such, the idea of using Cherenkov imaging as a replacement for film makes intuitive sense, and the primary value is in the ease of use of electronic imaging (Cherenkov) versus physical imaging using film. Other than the submillimeter error in the process of the image transformation, the likely areas for spatial disagreement between them would be in areas of penumbra or scattering, attributed to the scattering of Cherenkov light signal inside the plastic phantom. From this aspect though, the non-linearity of film is well known, and the inherent value of the linearity of Cherenkov emission with dose should be superior.18 There are known variations in sensitivity to beam energy and beam type of electrons or photons in both, but each of these factors can be calibrated for, if necessary. However, the value of this study has largely been in the simple confirmation of the ability to spatially map the linac beam as observed through imaging with film, Cherenkov imaging and the light field.
The observer study of using the light field to estimate the beam size and comparison of testing for a fixed 20cmx20cm x-ray beam helps illustrate that fact that most alignment is done with a +/−1mm tolerance on average with a 0–2mm range of error. It is well known that there is this level of subjectivity when physicists are involved in deciding the boundary of the radiation field manually. So as a result, there is a preference to complete light field to beam congruence validation electronically wherever possible. The value of Cherenkov imaging is that the images are acquired at the location of the surface, at SSD = 100cm, similar to film. Also, the value of all electronic capture and electronic image processing evaluation removes human errors from the post-processing evaluation of this data, which can be especially accurate and potentially time saving for routine quality assessments. In principle, imaging can be fully automated, other than placement of the board upon which the irradiation is completed.
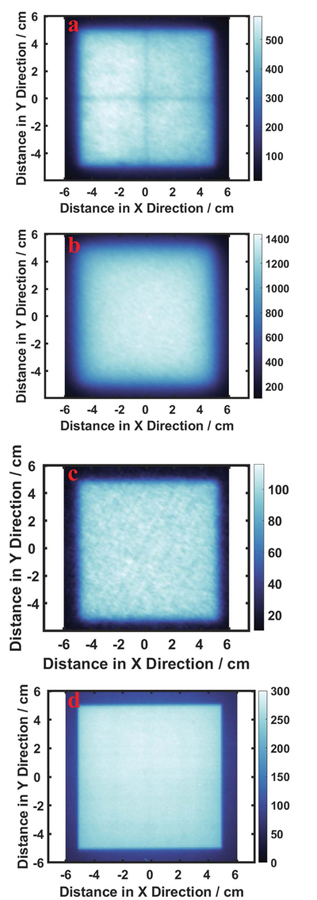
One issue to consider is the observed value of the linac light field and Cherenkov emission relative to the film. They are very similar, as shown in FIG. 9, and the size of light field and Cherenkov emission are accurate representations of the beam shape derived from the GaF film. However, the boundaries of optical images (a) and (b) on an ABS phantom, and (c) on a solid water phantom are more blurred than those of the radiation field as reported by the film (d). Part of the blurring effect likely comes from the scattering of the beige plastic board, which has also been observed in many other plastic materials. Some plastic material, such as solid water phantom (d), can have sharper penumbra than the ABS phantom, due to the optical properties of different plastic materials. A physicist can determine the edge of the light field by visual inspection, while the light field derived from the camera system has more blurred boundaries and care must be taken to estimate the edges accurately. Therefore, modifications of the board could potentially reduce the penumbra size of both light field and Cherenkov emission. In the future, a less translucent plastic sheet could be used in the measurement to improve the light signal while minimizing the optical scatter diffusion at the edges. The ABS sheet was chosen as a general-purpose board for testing, due to its higher Cherenkov response, and it is still likely that superior materials, such as a solid water phantom with brighter colors, may be available to maximize light field edge imaging. GaF film was used as a gold standard comparator here because it is maximally sensitive to higher energy photons, as compared to phosphor film which is also sensitive to lower energy photons. Thus, the penumbra effect of radiation field in the phosphor film in Figure 5(b) is more obvious than that seen in the radiation field measured by GaF film, as in Figure 9(d). To reduce this effect, the phosphor film is always used with film cassette to filter out lower energy photons.
FIG. 9:
Comparison between the 2D profiles of light field, Cherenkov, and dose of 10×10cm2, 6MV, photon beam. (a): 2D profile of light field, (b): 2D profile of Cherenkov emission in an ABS board, (c): 2D profile of Cherenkov emission on a solid water phantom, (d): 2D profile of dose from GaF film measurement.
Using appropriate definition of the boundaries for the Cherenkov emission and light field, such as the extrema of derivative, shown here, the sizes of the light field and Cherenkov emission spatially matched that of the light field, albeit with edges which were more diffuse than observed with the film, but they were substantially similar to the observed edges of the light field. Sizes estimates derived from FWHM showed less accuracy with some variation up to 3 to 5mm, for the measurement of light field and Cherenkov emission image, relative to the film. However, measurement of both light field and Cherenkov emission image achieved much less error when using the maximum slope estimates of edges.
The beam shape analysis protocol using Cherenkov image acquisition system can be extended to other QA procedures using beam shapes, such as MLC verification and isocenter QA, as shown by the star shot analysis. The results section shows the match between Cherenkov and radiation fields for complex shapes, although in this preliminary work the match to the MLCs was just shown for qualitative reference. Future work on using Cherenkov imaging for IGRT is possible, although this needs to be examined in future studies. The QA process using a Cherenkov image acquisition system has potential advantage in terms of time and workload as compared with film and/or manual measurement of the light field. Even though the Cherenkov camera needs to be installed in the treatment room, once it is installed, the system, the acquisition and processing can be fully automated.
5. CONCLUSION
We have demonstrated the use of electronic imaging of Cherenkov emission to test the ability of using Cherenkov imaging to verify radiation field beam sizes from medical linear accelerators. This system can take images/video frames of Cherenkov emission and light field of square beams but has potential for arbitrary shaped beams and more complex tests such as star shots. The measurements of Cherenkov emission show good congruence with film measurement and light field, with some caution needed in the appropriate standard of a boundary definition. Without calibration of the image acquisition system, the discrepancy between light field or film and the Cherenkov image is about 1–2mm or 1% on average, which is within the tolerance given by the QA routinely used for medical linear accelerators.3 Therefore, it is feasible to use this image acquisition tool to run QA procedures with appropriate refinement of the software tool used.
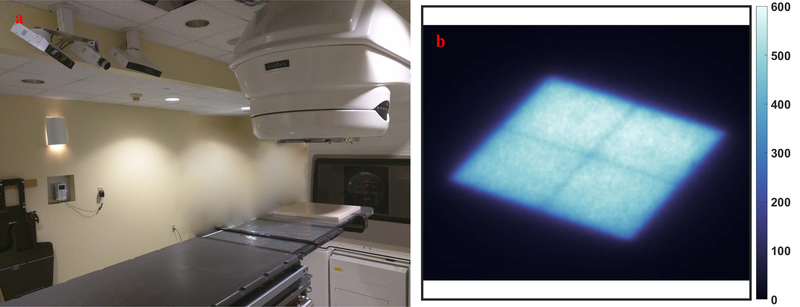
FIG. 1:
The treatment room is shown with the ABS test plate placed at isocenter on the couch and camera mounted to the ceiling, shown in (a). A typical image of the linac light field on the board is shown from a 10×10 cm beam in (b), as captured by the Cherenkov camera in image sensor reading.
FIG. 4:
Beam width measurement using GaF films (a): Film scan for 10cmx10cm beam and 5cmx5cm beam, with line profile region in 10cmx10cm beam (b): Dose profile along the line, with red lines representing the boundaries extracted through maximum derivative method.
FIG. 6:
Paper image patterns to verify the errors of image transformation: (a): Checkerboard patterns with 1cm×1cm cells, (b): 15cm×15cm black square pattern to simulate radiation and light field with the same size.
FIG. 7:
Cherenkov images of IMRT QA plan on the isoplane, compared with MLC shapes projection, with leaves marked by red rectangles.
FIG. 8:
Star shot analysis using measurement of Cherenkov and film, (a): the Cherenkov field measurement; and (b): the film measurement of 30cm×0.5cm radiation beams for different collimator angles, the center axis of beams extracted in the Cherenkov profile (c) and film profile (e), with the comparison shown in (d).
6. ACKNOWLEDGEMENTS
This work has been financially supported by NIH grants R01EB023909, R44CA199836 and R44CA199681.
Footnotes
7. DISCLOSURE OF CONFLICTS OF INTEREST
Authors Brian Pogue, Michael Jermyn, Venkataramanan Krishnaswamy and William Ware all disclose that they are employed and financially involved with the company DoseOptics LLC, whose camera and software were used in acquisition of data in this manuscript. Author Petr Bruza has sponsored research financially supported by DoseOptics LLC, through his employment at Dartmouth College to disclose. Authors Tianshun Miao, Frank Rafie, David Gladstone and Benjamin Williams have no financial interests to disclose related to this work.
REFERENCES
- 1.Nath R, Biggs PJ, Bova FJ, et al. , “AAPM code of practice for radiotherapy accelerators: Report of AAPM Radiation Therapy Task Group No. 45,” Med. Phys 21, 1093–1121 (1994). [DOI] [PubMed] [Google Scholar]
- 2.Kutcher GJ, Coia L, Gillin M, et al. , “Comprehensive QA for radiation oncology: Report of AAPM Radiation Therapy Committee Task Group 40,” Med. Phys 21, 581–618 (1994). [DOI] [PubMed] [Google Scholar]
- 3.Klein EE, Hanley J, Bayouth J, et al. , “Task Group 142 report: Quality assurance of medical accelerators,” Med. Phys 36, 4197–4212 (2009). [DOI] [PubMed] [Google Scholar]
- 4.American Association of Physicists in Medicine. Basic quality control in diagnostic radiology. American Association of Physicists in Medicine; 1978. [Google Scholar]
- 5.García-Garduño OA, Celis MÁ, Lárraga-Gutiérrez JM, et al. , “Radiation transmission, leakage and beam penumbra measurements of a micro-multileaf collimator using GafChromic EBT film,” J. Appl. Clin. Med. Phys 9, 90–98 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Xu LB. “Commissioning of a GafChromic EBT Film Dosimetry Protocol at Ionizing Radiation Standards Group of National Research Council,” M.S. thesis, McGill University, Montreal, 2009, pp.70–72. [Google Scholar]
- 7.Bouchard H, Seuntjens J, “Ionization chamber-based reference dosimetry of intensity modulated radiation beams,” Med. Phys 31, 2454–2465 (2004). [DOI] [PubMed] [Google Scholar]
- 8.Sun B, Yaddanapudi S, Goddu SM, Mutic S, “A self-sufficient method for calibration of Varian electronic portal imaging device,” Journal of Physics: Conference Series 573, 012041 (2015). [Google Scholar]
- 9.Létourneau D, Gulam M, Yan D, Oldham M, Wong JW, “Evaluation of a 2D diode array for IMRT quality assurance,” Radiother. Oncol 70, 199–206 (2004). [DOI] [PubMed] [Google Scholar]
- 10.Nilsson B, Rudén B-I, Sorcini B, “Characteristics of silicon diodes as patient dosemeters in external radiation therapy,” Radiother. Oncol 11, 279–288 (1988). [DOI] [PubMed] [Google Scholar]
- 11.Dobler B, Streck N, Klein E, et al. , “Hybrid plan verification for intensity-modulated radiation therapy (IMRT) using the 2D ionization chamber array I’mRT MatriXX—a feasibility study,” Phys. Med. Biol 55, N39–N55 (2010). [DOI] [PubMed] [Google Scholar]
- 12.Leybovich LB, Sethi A, Dogan N, “Comparison of ionization chambers of various volumes for IMRT absolute dose verification,” Med. Phys 30, 119–123 (2003). [DOI] [PubMed] [Google Scholar]
- 13.Poppe B, Blechschmidt A, Djouguela A, et al. , “Two-dimensional ionization chamber arrays for IMRT plan verification,” Med. Phys 33, 1005–1015 (2006). [DOI] [PubMed] [Google Scholar]
- 14.Sotiri S, “Ionization chamber array for patient specific VMAT, Tomotherapy and IMRT QA,” Journal of Physics: Conference Series 250, 012029 (2010). [Google Scholar]
- 15.Van Esch A, Basta K, Evrard M, et al. , “The Octavius1500 2D ion chamber array and its associated phantoms: Dosimetric characterization of a new prototype,” Med. Phys 41, 091708 (2014). [DOI] [PubMed] [Google Scholar]
- 16.Snyder C, Pogue BW, Jermyn M, et al. “Algorithm development for intrafraction radiotherapy beam edge verification from Cherenkov imaging,” SPIE, 10, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pogue BW, Zhang R, Glaser A, et al. , “Cherenkov imaging in the potential roles of radiotherapy QA and delivery,” Journal of Physics: Conference Series 847, 012046 (2017). [Google Scholar]
- 18.Zhang R, Gladstone DJ, Jarvis LA, et al. , “Real-time in vivo Cherenkoscopy imaging during external beam radiation therapy,” J. Biomed. Opt 18, 110504 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jarvis LA, Gladstone DJ, Pogue BW, et al. , “Cherenkoscopy for Treatment Verification: Correlation of Radiation Dose to Cherenkov Emission Intenisty in Whole Breast Radiation Therapy,” Int. J. Radiat. Oncol. Biol. Phys 99, E673 (2017). [Google Scholar]
- 20.Andreozzi JM, Zhang R, Gladstone DJ, et al. , “Cherenkov imaging method for rapid optimization of clinical treatment geometry in total skin electron beam therapy,” Med. Phys 43, 993–1002 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Glaser AK, Andreozzi JM, Zhang R, Pogue BW, Gladstone DJ, “Optical cone beam tomography of Cherenkov-mediated signals for fast 3D dosimetry of x-ray photon beams in water,” Med. Phys 42, 4127–4136 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Glaser AK, Voigt WHA, Davis SC, et al. , “Three-dimensional Cerenkov tomography of energy deposition from ionizing radiation beams,” Opt. Lett 38, 634–636 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Andreozzi JM, Mooney KE, Brůža P, et al. , “Remote Cherenkov imaging-based quality assurance of a magnetic resonance image-guided radiotherapy system,” Med. Phys 45, 2647–2659 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Black PJ, Velten C, Wang YF, Na YH, Wuu CS, “An Investigation of Clinical Treatment Field Delivery Verification Using Cherenkov Imaging: IMRT Positioning Shifts and Field Matching,” Med. Phys [DOI] [PubMed] [Google Scholar]
- 25.Andreozzi JM, Zhang R, Glaser AK, et al. , “Camera selection for real-time in vivo radiation treatment verification systems using Cherenkov imaging,” Med. Phys 42, 994–1004 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang R, Colleen JF, Adam KG, David JG, Brian WP, “Superficial dosimetry imaging of Čerenkov emission in electron beam radiotherapy of phantoms,” Phys. Med. Biol 58, 5477 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Harris C, Stephens M. “A combined corner and edge detector,” Alvey Vision Conference, 50, pp.147–151, 1988 [Google Scholar]
- 28.Seibert JA, Boone JM, Lindfors KK. “Flat-field correction technique for digital detectors,” Medical Imaging 1998: Physics of Medical Imaging, SPIE, 348–354, 1998 [Google Scholar]
- 29.González A, Castro I, Martínez JA, “A procedure to determine the radiation isocenter size in a linear accelerator,” Med. Phys 31, 1489–1493 (2004). [DOI] [PubMed] [Google Scholar]
- 30.Depuydt T, Penne R, Verellen D, et al. , “Computer-aided analysis of star shot films for high-accuracy radiation therapy treatment units,” Phys. Med. Biol 57, 2997 (2012). [DOI] [PubMed] [Google Scholar]