Skip to main content
PMC home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2011 Mar 21.
Published in final edited form as: J Acoust Soc Am. 2010 Feb;127(2):990–1001. doi: 10.1121/1.3283014

Median-plane sound localization as a function of the number of spectral channels using a channel vocoder

Matthew J Goupell 1,a), Piotr Majdak 1, Bernhard Laback 1
PMCID: PMC3061453  EMSID: UKMS33722  PMID: 20136221

Abstract

Using a vocoder, median-plane sound localization performance was measured in eight normal-hearing listeners as a function of the number of spectral channels. The channels were contiguous and logarithmically spaced in the range from 0.3 to 16 kHz. Acutely testing vocoded stimuli showed significantly worse localization compared to noises and 100 pulse/s click trains, both of which were tested after feedback training. However, localization for the vocoded stimuli was better than chance. A second experiment was performed using two different 12-channel spacings for the vocoded stimuli, now including feedback training. One spacing was from experiment 1. The second spacing (called the speech-localization spacing) assigned more channels to the frequency range associated with speech. There was no significant difference in localization between the two spacings. However, even with training, localizing 12-channel vocoded stimuli remained worse than localizing virtual wideband noises by 4.8° in local root-mean-square error and 5.2% in quadrant error rate. Speech understanding for the speech-localization spacing was not significantly different from that for a typical spacing used by cochlear-implant users. These experiments suggest that current cochlear implants have a sufficient number of spectral channels for some vertical-plane sound localization capabilities, albeit worse than normal-hearing listeners, without loss of speech understanding.

I. INTRODUCTION

Vertical-plane sound localization (i.e., the perception of elevation and the discrimination of front from back sound sources) depends primarily on directionally-dependent filtering introduced by reflections from the pinnae, head, and torso (e.g., Middlebrooks, 1999a; Algazi et al., 2001). For free-field sources, these vertical-plane cues, together with the binaural cues (interaural time and level differences) for horizontal-plane localization, are typically represented by acoustical transfer functions called head-related transfer functions (HRTFs) (Shaw, 1974; Møller et al., 1995). Due to the size of the pinnae, the relevant peaks and notches resulting from diffraction effects used in vertical-plane localization occur for frequencies between about 4 and 16 kHz (Blauert, 1969; Hebrank and Wright, 1974; Morimoto and Aokata, 1984; Middlebrooks, 1992; Blauert, 1997; Langendijk and Bronkhorst, 2002).

Despite the substantial amount of previous work on understanding the role of HRTFs in vertical-plane sound localization, it is still unclear as to the type, scale, size, and position of spectral features most important to this task. What is clear is that HRTFs are subject dependent (Wightman and Kistler, 1989; Wenzel et al., 1993; Middlebrooks, 1999a). One method to investigate the role of spectral features has been to test localization abilities with spectrally-distorted HRTFs. These spectral distortions have been performed in a fairly uncontrolled way by occluding pinnae with some substance (Gardner and Gardner, 1973; Musicant and Butler, 1984; Oldfield and Parker, 1984; Hofman et al., 1998). In more controlled experiments, signal processing methods have been used to distort spectral localization cues. For example, HRTF spectral distortions have been done by truncating HRTF impulse responses (Zahorik et al., 1995; Senova et al., 2002).

Several studies have shown that relatively broad high-frequency spectral features (on the order of octaves) are the relevant vertical-plane sound localization cues (Asano et al., 1990; Kistler and Wightman, 1992; Kulkarni and Colburn, 1998; Langendijk and Bronkhorst, 2002; Macpherson and Middlebrooks, 2003; Kulkarni and Colburn, 2004; Qian and Eddins, 2008). For example, Kulkarni and Colburn (1998) systematically removed fine-scale HRTF spectral components and showed that substantial spectral smoothing of the HRTF spectrum could be performed before listeners’ elevation errors and number of front-back confusions increased. Langendijk and Bronkhorst (2002) performed another type of spectral distortion by flattening 1/2-, 1-, and 2-octave bands in the sound spectrum. They found that there was no effect on sound localization when one 1/2-octave band was flattened in the sound spectrum. However, for the broader bands, a large effect was found. For the flattening of a 2-octave band, sound localization was impossible.

The experiments reported in this paper evaluated the potential of cochlear-implant (CI) users to perform median-plane sound localization via another method of spectral alteration. We tested median-plane sound localization in normal-hearing (NH) listeners using a CI simulation and investigated the number of channels necessary to present adequate spectral localization information. The advantages of using CI simulations with NH listeners were that the population of NH listeners was much more readily available for the long testing times needed for sound localization experiments, and the interindividual variability is typically much less for NH listeners. The latter reason is due to many factors that affect CI users’ performance, including the placement of the electrode array and the number of surviving spiral ganglion cells. CI simulations with NH listeners often provide an upper bound on CI user’s performance in psychophysical tasks (e.g., Dorman and Loizou, 1997; Fu et al., 1998; Friesen et al., 2001; Carlyon and Deeks, 2002; van Wieringen et al., 2003; Carlyon et al., 2008; Goupell et al., 2008b).

Sound localization in the horizontal plane in CI users has been the topic of many recent papers. In particular, with the ever increasing number of bilaterally-implanted CI users, there has been much work on interaural time and/or level difference sensitivity (Lawson et al., 1998; Long et al., 2003; Laback et al., 2004; Majdak et al., 2006; Laback et al., 2007; van Hoesel, 2007; Grantham et al., 2008; Laback and Majdak, 2008; van Hoesel, 2008) and sound localization in the horizontal plane (van Hoesel and Tyler, 2003; Nopp et al., 2004; Seeber et al., 2004; van Hoesel, 2004; Schoen et al., 2005; Seeber and Fastl, 2008; van Hoesel et al., 2008). However, much less attention has been paid to localization in the vertical planes in CI users. Results from a recent study by Majdak et al. (2008) showed that CI listeners using current clinical speech processors with behind-the-ear microphones had a substantial deterioration of vertical-plane localization performance compared to NH listeners.

The speech processors of multi-channel CIs typically separate acoustic signals into several spectral channels. This information is used to stimulate different tonotopic places with electrical pulse trains. The amount of transmitted spectral information is determined by the number of spectral channels used to analyze the signal, the amount of tonotopic overlap that occurs when the electrical pulse trains excite the auditory nerve, and the sensitivity in the excited region. Present day CIs typically have 12–24 electrodes. The bandpass signals typically subdivide the spectrum logarithmically between frequencies on the order of 0.1 and 10 kHz. For example, a MED-EL Combi 40+ implant has 12 electrodes that typically subdivide an incoming acoustic sound spectrum between 0.3 and 8.5 kHz. This means that there are nine electrodes presenting acoustic information below 4 kHz and three electrodes above 4 kHz. Since median-plane sound localization relies on frequencies above 4 kHz, using only three electrodes for this frequency region places CI listeners at a noticeable disadvantage for this task compared to NH listeners. Additionally, a large portion of the relevant sound spectrum (between 8.5 and 16 kHz) is omitted in this example, which may further hinder median-plane localization for CI listeners. Lastly, the typical placement of the microphone behind the ear and above the pinna causes a lack of directional filtering from the pinna, arguably the most important anatomical vertical-plane directional filter. It is obvious that substantial changes to CI speech processing strategies and systems are needed if they are to incorporate vertical-plane localization cues. However, these changes must respect the primary use of a CI, which is to provide speech understanding to profoundly hearing-impaired and deaf individuals. Therefore, new processing strategies should carefully balance the competing needs for speech understanding and sound localization.

Although spectral distortions can cause decreased localization performance, it has been shown that NH listeners can adapt to some localization-cue modifications after long-term, real-world experience (Hofman and Van Opstal, 1998). This is promising for CI users who, if post-lingually deafened, will have to relearn their auditory spatial map. Additionally, as mentioned above, studies show that vertical-plane localization relies upon fairly broadly tuned features in the HRTF spectrum. This is a necessity for CI users who, for this generation of CIs, can be presented only a few channels of spectral localization information.

The goal of this study was to determine the number of spectral channels necessary to perform median-plane sound localization. If this number is sufficiently low, then it may be possible for CI users to perform the task. The experiments tested median-plane localization in NH listeners using a CI simulation. The first experiment consisted of extensive procedural training and localization training to wideband (WB) virtual stimuli. This was followed by the localization of vocoded stimuli, where the number of logarithmically-spaced frequency channels was varied from 3 to 24, which were acutely tested. The second experiment consisted of long-term localization training and testing for the vocoded stimuli, which focused on two 12-channel spacings, one from experiment 1 and one with a custom configuration of channels designed to balance speech and vertical-plane localization cues. An additional experiment investigated a potential deterioration in speech understanding using a clinical spacing and the spacing introduced in experiment 2.

II. EXPERIMENT 1: ACUTE VOCODER MEASUREMENTS

A. Listeners and equipment

Eight listeners participated in the experiment. All eight listeners had audiometrically normal hearing and were between 21 and 46 years old.

The virtual acoustic stimuli were presented via headphones (Sennheiser HD580) in a semi-anechoic room. A digital audio interface (RME ADI-8) was used to present stimuli with a 48-kHz sampling rate and 24-bit resolution.

A visual environment was presented via head-mounted display (HMD; Trivisio 3-Scope). It provided two screens with a field of view of 32° ×24° (horizontal×vertical dimensions). The HMD did not enclose the entire field of view. The visual environment was presented binocularly, the same picture used for both eyes. Listeners could adjust the inter-pupillary distance and the eye relief so that they viewed a single focused image. The position and orientation of the listener’s head were measured by an electromagnetic tracker (Ascension Flock of Birds) in real-time. One tracking sensor was mounted on the top of the listener’s head. The second tracking sensor was mounted on the end of a pointer, which was held by the listener. The tracking device was capable of measuring six degrees of freedom (three translations, three rotations) at a rate of 100 measurements per second for each sensor. The tracker accuracy was 1.7 mm for translations and 0.5° for rotations.

B. HRTF measurements

The HRTFs were measured for each listener individually. Twenty-two loudspeakers (custom-made boxes with VIFA 10 BGS as drivers) were mounted on a metal arc (1.2-m radius) at fixed elevations from −30° to +80° relative to the listener’s eye level. The loudspeakers were driven by amplifiers adapted from Edirol MA-5D active loudspeaker systems. The loudspeakers and the arc were covered with acoustic damping material to reduce the reflections from the construction. The listeners were seated in the center of the arc and had microphones (Sennheiser KE-4-211-2) placed in his/her ear canals, which were connected via pre-amplifiers (RDL FP-MP1) to the digital audio interface. Each HRTF was measured with a 1728.8-ms exponential frequency sweep from 0.05 to 20 kHz. The multiple exponential sweep method (MESM) was used to measure HRTFs in an inter-leaved and overlapped fashion for one azimuth and all elevations (Majdak et al., 2007). After measuring HRTFs for 0° azimuth, the listener was rotated by 2.5° and the measurement of HRTFs for the next azimuth began. In total, 1550 HRTFs were measured for one listener, where the positions were distributed with a constant spherical angle on the sphere. During the procedure, the head position and orientation were monitored with the head tracker. The entire HRTF measurement procedure lasted approximately 20 min. The HRTFs were calculated from the recordings according to the MESM system identification procedure (Majdak et al., 2007).

The equipment transfer functions were derived from a reference measurement performed by placing the in-ear microphones in the center of the arc and using the system identification procedure as before. The transfer function of the equipment was individually measured for each loudspeaker and removed from the HRTF measurements by filtering each HRTF with the appropriate inverse equipment transfer function.

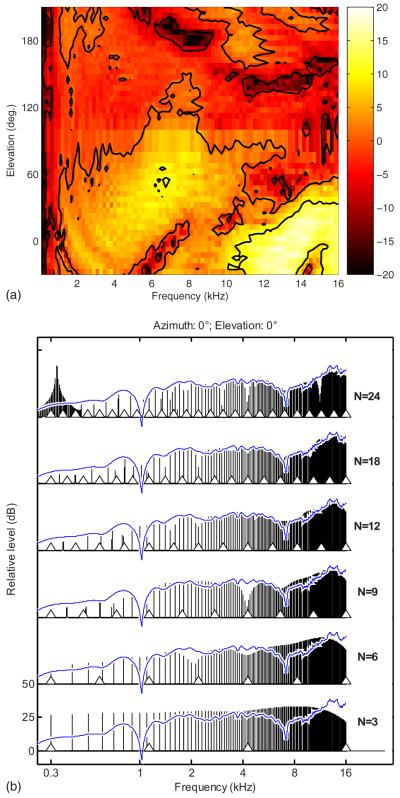
Directional transfer functions (DTFs) were calculated according to the procedure of Middlebrooks (1999b). The magnitude of the common transfer function (CTF) was calculated by averaging the log-amplitude spectra of all the HRTFs. The phase of the CTF was the minimum phase of the CTF amplitude spectrum. The DTFs were the result of filtering the HRTFs with the inverse complex CTF. Since the headphone transfer function is the same for all positions, removing the CTF removes the headphone transfer function, which is known to be important for proper virtual stimulus externalization (Pralong and Carlile, 1996). No further headphone transfer function compensation was used. Finally, all the DTFs were temporally windowed with a Tukey window to a 5.33-ms duration. A typical set of DTFs for the median plane is shown in Fig. 1(a). More details about the HRTF measurement procedure can be found in Majdak et al. (2010).

FIG. 1.

FIG. 1

Open in a new tab

(Color online) A set of DTFs in the median plane for a typical listener. Panel (a) shows the measured DTF. Panel (b) shows the amplitude spectra of the same DTF for 0° azimuth and 0° elevation (solid thin line) and processed by the GET vocoder (vertical lines) for different numbers of channels (N). Channel corner frequencies are marked by the triangles.

C. Stimuli

Three types of free-field stimuli were used as acoustic targets: WB Gaussian noises, WB click trains, and vocoded pulse trains. They were uniformly distributed along the median plane of a virtual sphere with the listener in the center of this sphere. Positions from −30° to +210° in elevation, relative to the eye level of the listener, were tested. These positions varied within the lateral range of ±10° of the median plane. Therefore, 290 of the 1550 measured DTFs were used.

The level of the stimuli was 50 dB with respect to the hearing threshold. The hearing threshold was estimated in an experimenter-controlled manual up-down procedure using a target positioned at an azimuth and elevation of 0°. In the experiment, the level for each presentation was randomly roved within the range of ±5 dB to reduce the possibility of localizing targets based on level.

1. Wideband signals

The WB Gaussian white noises (to be called WB noises) and 100 pulse/s WB click trains (to be called WB clicks) had 500-ms duration, which included temporal shaping by a Tukey window with a 10-ms rise-fall time. The stimuli were filtered with the listener-specific DTFs.

2. Vocoded signals

A Gaussian-enveloped tone (GET) vocoder (Lu et al., 2007) was used to simulate CI sound processing. A more conventional vocoder was not used for the following reasons. A sine vocoder has a sparse spectral representation, meaning that there is a single sine tone at the center frequency of the channel and possible sidebands, which may hinder the peak and notch detection necessary for vertical-plane sound localization. A GET vocoder has spectrally full channels with harmonics spaced at the pulse rate of the stimuli. We think that spectrally full channels better reproduce the electrical stimulation of a CI. A noise vocoder generates a non-deterministic signal, where random fluctuations make the characteristic spectral peaks and notches between 4 and 16 kHz difficult to visually identify. On the other hand, a GET vocoder generates a deterministic signal. Thus we needed only one token, and there was no problem in visually identifying the spectral peaks and notches. Lastly, we think that presenting pulsatile stimulation, albeit relatively lowrate acoustic pulses, better represents the electrical pulse trains delivered by a CI.

Detection of GETs has been previously studied in NH listeners (Gabor, 1947; van den Brink and Houtgast, 1990; van Schijndel et al., 1999). Our targets were multi-channel GET trains with incorporated spatial information. The total processing scheme can be seen in Fig. 2. A single WB click was filtered with a DTF corresponding to the particular position of the target. The resulting directional impulse response was filtered into N=3, 6, 9, 12, 18, or 24 contiguous channels by a filter bank. The filters were eighth-order Butterworth bandpass filters. The lowest corner frequency was 0.3 kHz. The highest corner frequency was 16 kHz. The other corner frequencies were logarithmically spaced according to the value of N. Each channel, n, had a center frequency, fn, defined as the geometric mean of the channel’s corner frequencies. After filtering the DTF, each channel had energy, En.

FIG. 2.

FIG. 2

Open in a new tab

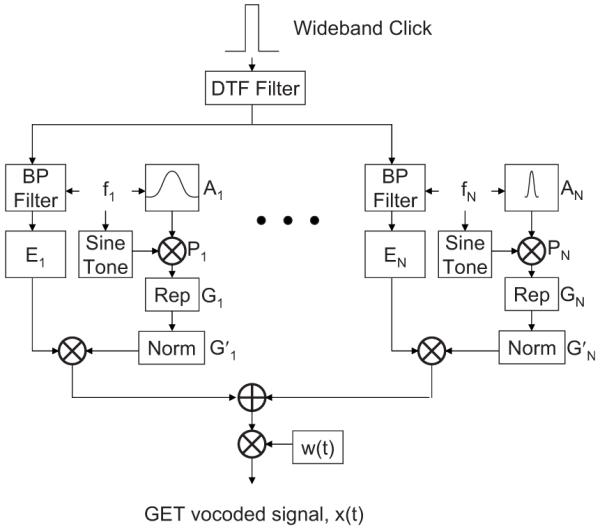
Processing scheme for the GET vocoder. DTF information is bandpass filtered (BP filter) into N channels, where the energy (En) is measured. Gaussian envelopes modulate a sine tone, are replicated, and delayed (Rep) to make a GET train. The GET trains are energy normalized, weighted by the energy En from a channel of the DTF, and summed. After temporal windowing, the result is the GET-vocoded signal.

For a single channel, n, a Gaussian pulse, An(t), is given by

graphic file with name ukmss-33722-ig0006.jpg

where αn is the shape factor. The value of αn was chosen so that the equivalent rectangular bandwidth, Bn=αnfn, equaled the bandwidth of the corresponding bandpass filter for that channel. A GET, Pn(t), is created by modulating a sinusoidal carrier with frequency fn by the Gaussian pulse:

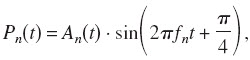
graphic file with name ukmss-33722-ig0007.jpg

where the phase shift of π/4 was used to keep Pn(t)’s energy independent of fn (van Schijndel et al., 1999). The single-channel GET train, Gn(t), is the sum of 50 delayed GETs:

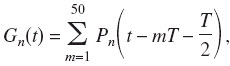
graphic file with name ukmss-33722-ig0008.jpg

where T is the delay between each GET. The delay was 10 ms, which corresponds to a rate of 100 pulses/s. The T/2 phase shift was used to have Gn(t) not begin at a maximum.

Note that for low fn, especially when N is relatively large, Gn(t) would have overlapping GETs. Hence, the modulation depth is not 100%. In such cases, if the Gaussian pulses modulate the carrier before being summed into a GET train, a spurious higher-order modulation of the signal would be introduced from the interfering phases of adjacent pulses. We determined that a modulation depth of 99% occurred if the equivalent rectangular duration of An(t) was longer than 3.75 ms. To avoid overlapping pulses and unwanted modulations, if An(t) is longer than 3.75 ms, then Gn(t) is the sum of 50 Gaussian pulses, which then modulate the carrier:

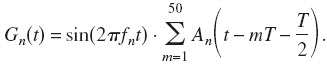
graphic file with name ukmss-33722-ig0009.jpg

Note that by using this method, in the worst case of 0% modulation depth, the GET vocoder reduces to a sine vocoder.1

The amount of energy in Gn(t) depends on fn. Therefore, Gn(t) was normalized with respect to its total energy, called 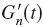Inline graphic. Finally, the multi-channel GET train x(t) is the sum over the normalized GET trains 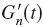Inline graphic weighted by the energy En from the spatial information (i.e., the energy from each channel of the DTF):

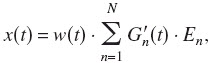
graphic file with name ukmss-33722-ig0011.jpg

where w(t) is a Tukey window with a 10-ms rise-fall time. Figure 1(b) shows amplitude spectra of the same DTF as in Fig. 1(a) for 0° azimuth and 0° elevation (horizontal line) and processed by the GET vocoder (vertical lines) for different N values.2

D. Procedure

The listeners were immersed in a virtual sphere with a 5-m diameter. To facilitate the listeners’ orientation, horizontal grid lines were placed every 5° and vertical grid lines every 11.25°. The reference position (azimuth and elevation of 0°), horizontal plane, and medial plane were marked with small spheres. Rotational movements were rendered in the virtual environment but not translational movements. The listeners could see the visualization of the hand pointer and its projection upon the sphere whenever they were in the listeners’ field of vision. The projection of the pointer direction on the sphere’s surface, calculated from the position and orientation of listeners’ head and the pointer, was recorded as the indicated target position.

Prior to the acoustical tests, listeners performed a procedural training. In order to familiarize the listeners with the equipment and virtual environment, the listeners were trained to quickly and accurately respond to visual targets presented on the sphere. After the training, the listeners were able to respond to visual targets with an error smaller than 2°.

Acoustical sound localization training was provided, which was similar to that provided to listeners in Zahorik et al. (2006). In the acoustic training, at the beginning of each trial, the listeners aligned their head to the reference position. By pressing a button, the acoustic target was presented. During the presentation, the listeners were instructed not to move. After the acoustic presentation, the listeners were asked to point to the perceived position with the pointer and respond by pressing a button. This response was collected for further analysis. Next, a visualization of the acoustic target appeared on the surface of the sphere. The listeners were instructed to find the visualization, to point and respond to the visualization, and return to the reference position. After pressing the button, the same acoustic target with visualization was presented to the listeners and they had to point and respond to the acoustic target again. In total, for each acoustic target, listeners heard the stimulus twice, responded once to the initial perceived position, and responded twice to the actual position. The training was performed in blocks of 50 targets. Each block lasted for approximately 20–30 min. More details on the procedure and training are given in Majdak et al. (2010).

Listeners were first trained to WB noises within ±10° around the median plane (290 possible positions). For six listeners, the training consisted of 500–600 trials. For the other two listeners, the training consisted of 300 trials because they had extensive localization training over the entire sphere from previous studies. After training to WB noises, listeners were trained to WB clicks for 100 trials.

Seven conditions were tested in this experiment, the vocoded stimuli with N=3, 6, 9, 12, 18, and 24 channels and the WB clicks. As in the training, stimuli were randomly chosen from ±10° around the median plane. Due to the large number of positions, the same number of responses was not required from each position. Each condition consisted of three blocks of 100 trials and no feedback on the target position was given. The blocks were presented in random order for each listener.

E. Results

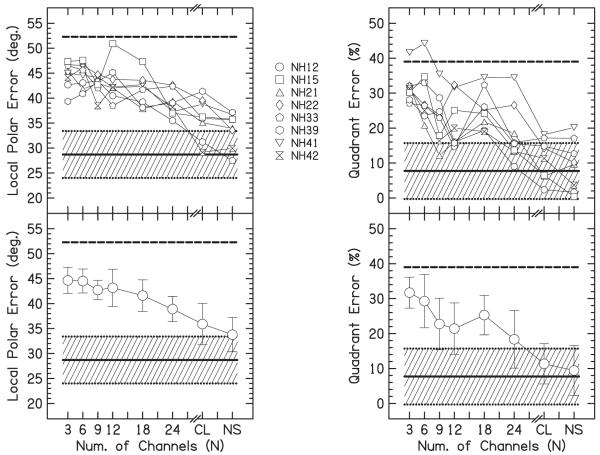
The metrics used to evaluate localization ability were the local polar error and the percentage of trials with quadrant errors. Localization errors were calculated by subtracting the target polar angles from the response polar angles. The polar error was the root-mean-square of the localization error. A quadrant error was defined as having an absolute polar error of greater than 90°. In tests with a large number of quadrant errors, the polar error is highly correlated to the quadrant error rate, showing the dominant role of the quadrant error rate in the metric. Therefore, the local polar error was used, which was the polar error after removing all the quadrant errors.3 Assuming uniformly distributed random responses (i.e., guessing) within the range from −45° to 225°, the local polar error converges at 52° and the percentage of quadrant errors converges at 39%.4

Figure 3 shows the individual (top panels) and average (bottom panels) localization results. Data from the WB noise localization training were included with the experimental conditions. The local polar error and quadrant error rate for the WB clicks were similar to those for the WB noises. In general, the local polar error and quadrant error rate increased from the WB conditions to the vocoded conditions. For the local polar error, performance becomes worse for a decreasing number of channels, which appears to plateau around 18 channels. For the quadrant error rate, there seems to be a relatively flat plateau between 9 and 24 channels and increases for fewer channels. All of the conditions showed average local polar errors and average quadrant error rates much better than chance. Only one listener (NH41) showed chance performance for any vocoded condition.

FIG. 3.

FIG. 3

Open in a new tab

Results of experiment 1. The upper panels show the individual data. The lower panels show the listener average and ±1 standard deviation. The left column shows the local polar error in degrees as a function of the number of channels. The right column shows the percentage of quadrant errors. Results for the WB clicks (CL) and WB noises (NS) are also included. The dashed lines show chance performance. The shaded area shows the average (solid line) and ±1 standard deviation (dotted lines) of the results from Middlebrooks (1999b) for virtual WB noise stimuli.

For the WB noises, individual listener quadrant error rates were mostly within the measured range reported by Middlebrooks (1999b) for virtual WB noise stimuli. The local polar error shows some listeners near the lower limit of the Middlebrooks range. However, the average local polar error is near the upper limit of the Middlebrooks range. This discrepancy may be due to the fact that Middlebrooks tested targets distributed in the whole lateral range, not just near the median plane. The average quadrant error rate and standard deviation correspond well to the Middlebrooks range.

A repeated-measures analysis of variance (RM ANOVA) was performed on the factor N, including the WB noises and WB clicks as additional factor levels for the local polar error and quadrant error rate. There was a significant effect of N for both metrics (p<0.0001 for both).

Tukey HSD post-hoc tests were performed for the local polar error and quadrant error rate. For the local polar error, there was no significant difference between the WB noises and WB clicks (p=0.75). There were significant differences between the WB conditions and the vocoded conditions (p<0.007 for all), with the exception of the difference between N=24 and the WB clicks (p=0.33). The differences between N=24 and N=18, 9, and 6 were not significant (p>0.1 for all), but the differences between N=24 and N=12, 6, and 3 were significant (p<0.05 for all). There were no significant differences between any pair of N=18, 12, 9, 6, and 3 at the 0.05 level.

For the quadrant error rate, there was no difference between the WB noises and WB clicks (p=0.99). There were significant differences between the WB conditions and the vocoded conditions (p<0.011 for all). The difference between N=24 and N=18 was not significant (p=0.090), but the differences between N=24 and N=12, 9, 6, and 3 were significant (p<0.003 for all). The differences between N=18 and N=12, 9, 6, and 3 were not significant (p>0.098 for all). The difference between N=12 and N=9 was not significant (p=1), but the differences between N=12 and N=6 and 3 were significant (p<0.038 for both). The difference between N=9 and N=6 was not significant (p=0.14), but the difference between N=9 and N=3 was significant (p=0.011). The difference between N=6 and N=3 was not significant (p=0.97).

F. Discussion

The localization of WB noises corresponded well to that measured by Middlebrooks (1999b), who tested well-practiced listeners with virtual acoustic WB noises in both the horizontal and vertical dimensions. As expected, the localization of our virtual sources is worse than that of the real sources measured in Middlebrooks (1999b). In our experiment, there was no significant difference between the WB noises and clicks, even though there was markedly less training for the clicks. Several studies have found that there are level, duration, and rate effects in vertical-plane localization (e.g., Vliegen and Van Opstal, 2004). However, few studies on vertical-plane localization have directly compared long-duration WB noises and click trains. Hartmann and Rakerd (1993) tested 880-ms WB noises and 10.4 pulses/s click trains in a speaker identification task. For levels comparable to the levels used in our experiment, localization performance of click trains appeared slightly worse than that of WB noises. Macpherson and Middlebrooks (2000) showed that the localization of click stimuli was qualitatively similar to 3-ms noise bursts. Hofman and Van Opstal (1998) tested 500-ms WB noises and 500-ms burst trains (3-ms noise bursts) at various rates, including 100 pulses/s. They found that the localization performance in the vertical direction for burst trains at 100 pulses/s was comparable to that for WB noises. Lower rates caused worse performance for burst trains compared to the WB noises. However, all three of these studies did not include a statistical comparison of the localization of clicks and noises. Also, the localization training for these three studies was not extensive; some testing could be considered acute for some listeners. Hence, our result that there is no significant difference in the localization of WB noise and clicks is not inconsistent with these studies.

There was a marked increase in the local polar error and quadrant error rate when the GET vocoder was used, even for 24 channels. On one hand, performance was expected to be worse because the spectral cues were intentionally degraded and listeners received no training for the vocoded conditions, unlike the WB conditions. On the other hand, this is slightly surprising because it has been shown that the broadband spectral cues are sufficient for vertical-plane localization. For example, Kulkarni and Colburn (1998) showed that HRTF amplitude spectra smoothed to as few as 32 Fourier coefficients could be used before sound localization significantly deteriorated.5 This corresponds to approximately five peaks and five notches in the sound spectrum in the frequency range from 4 and 16 kHz. Our 24-channel vocoded signal has approximately nine channels in the same frequency range, thus having nine potential critical points in the sound spectrum. However, it may be that the spectral contrast between channels in the vocoder is less than that of a HRTF with a smoothed sound spectrum. The GET vocoder had channels that were contiguous with respect to their corner frequencies, and the slopes of the channels were approximately 12 dB/oct; thus the channels have spectral profile information that overlaps. An extrapolation of this result to CI users, who typically have extensive channel interactions, which are analogous to overlapping channels, is that vertical-plane sound localization may be limited by the spectral resolution and contrast, even for 24 electrodes.

A recent study by Qian and Eddins (2008) explored the effect of varying the spectral modulation content of WB noises on virtual localization performance. In that study it was found that removing spectral modulation from 0.1 to 0.4 cycles/octave or from 0.35 to 0.65 cycles/octave resulted in significantly poorer localization (unsigned elevation difference between target and response angle) for low elevations (−30° to −20°) for three of six listeners. The vocoder used in the present experiment removed spectral modulation content, especially for a small number of channels. For example, for a stimulus at −30° elevation, the modulation spectrum was at least 10 dB down between 0.3 and 0.4 cycles/octave for N=3 compared to a WB noise. We analyzed a portion of our data as a function of angle by splitting the data into low elevation target (−30° to 0°) and high elevation target (0° to 30°) groups. Using a RM ANOVA (factors N and elevation), for the local polar error, there was a significant effect of N (p<0.0001), no significant effect of elevation (p=0.26), and no significant interaction between N and elevation (p=0.083). For the quadrant error, there was a significant main effect of N (p<0.0001), no significant effect of elevation (p=0.97), and no significant interaction between N and elevation (p=0.84). The RM ANOVA was repeated with just WB noises and N=3, the comparison that should show the largest contrast in spectral modulation content. The results did not change for the quadrant error rate, but did change for the local polar error because the interaction between N and elevation became significant (p=0.028). Therefore, this significant interaction may show modest support that removing spectral modulation information around 0.3–0.4 cycles/octave affects localization performance at low elevations. Note that there are several differences between this study and Qian and Eddins (2008), the most important being that we used individualized HRTFs while they used non-individualized HRTFs (although they did customize the HRTFs to each listener). As expected when using individualized vs non-individualized HRTFs, the overall performance of their listeners was much poorer than ours. For example, their average front-back confusion rate was 31±8% compared to our 9.4±7.2% average quadrant error rate for WB noises. Hence, it appears that the quality of the HRTFs used may affect the interpretation of the importance of spectral modulation cues in vertical plane sound localization.

Although localization performance was worse for the vocoder conditions, it was always better than chance. Said another way, CI listeners with their poorer frequency selectivity will be hindered in localizing sounds compared to NH listeners, but it seems possible to present salient vertical-plane localization cues to CI users. In the experiment, performance was roughly constant from 3 to 18 channels in local polar error and from 9 to 18 channels in quadrant error rate. Listeners also retained some sense of front-back directionality even for three channels. Median-plane sound localization with three channels may seem surprising at first. However, examining a typical set of DTFs [see Fig. 1(a)], the back positions can be approximated as a low-pass filtering of the front positions. Hence, one might predict some median-plane localization abilities with as few as two channels, a low-frequency channel to be used as a reference and a high-frequency channel for the front-back information. A similar view to median-plane localization was taken by Iida et al. (2007).

III. EXPERIMENT 2: VOCODER TRAINING

The results of experiment 1 showed that there is little difference in localization ability for NH listeners acutely tested using a CI simulation from 9 to 18 channels. This experiment will address two issues from experiment 1: long-term training with GET-vocoded stimuli and maintaining adequate resolution for the low-frequency channels associated with speech understanding. Majdak et al. (2010) showed that training on the order of several hundred trials is essential for saturation in the localization performance of virtual sound sources. It was hypothesized that listeners would need training for saturation in localization performance for GET-vocoded virtual sound sources, and that the results of experiment 1 underestimate the localization performance. It was also hypothesized that given the results of speech understanding tests from Goupell et al. (2008b), it would be possible to balance the competing demands of speech understanding and vertical-plane sound localization without significant loss of performance in either.

A. Stimuli

Stimuli were GET vocoded like those in experiment 1. The number of channels was fixed at N=12, which corresponds to the number of electrodes in the MED-EL Combi 40+, Pulsar, and Sonata implants. This condition showed localization performance better than chance in experiment 1, and little decrease in localization performance compared to N=24, the maximum number of electrodes available for any current CI.

Two spacings were used in this experiment. The first, called the “Log” spacing, corresponded to the spacing used for N=12 of experiment 1. The second, called the “speech-localization (SL)” spacing, represented an attempt to preserve speech information with a minimal sacrifice of spatial information. It is justified as follows.

Goupell et al. (2008b) low-pass filtered speech signals at cutoff frequencies of 8500, 4868, 2788, 1597, or 915 Hz for CI and NH listeners using a CI simulation while keeping the lower-frequency boundary fixed at 300 Hz. They found that there is almost no improvement in speech understanding performance beyond eight spectral channels (cutoff frequency of 2788 Hz). Keeping this in mind, the corner frequencies for the SL spacing were chosen such that the first eight low-frequency channels were logarithmically spaced from 0.3 to 2.8 kHz. This allowed for adequate resolution of the speech signal over the first two formants of speech. We refer to these eight channels as “speech” channels. The four higher-frequency channels were nearly logarithmically spaced from 2.8 to 16 kHz.6 This was to include more of the high-frequency vertical-plane localization information that is typically omitted in CI processing of acoustic waveforms. We refer to these four channels as “spatial” channels. Visual inspection of the individualized HRTFs showed that this choice of corner frequencies yields reasonable contrast for the spatial channels so that vertical-plane sound localization might still be possible. Therefore, we chose the SL spacing in an attempt to allow for both good speech understanding and vertical-plane localization ability. As in experiment 1, the center frequency of each channel of the GET vocoder corresponded to the geometric mean of the corner frequencies. The information for each channel is given in Table I.

TABLE I.

Stimulus information for the spacings used in experiment 2

Mapping Channel flower
(Hz)		 fupper
(Hz)		 fc
(Hz)		 BW
(Hz)
Log 1 300 418 354 118
2 418 582 493 164
3 582 811 687 229
4 811 1 129 957 318
5 1 129 1 573 1 333 444
6 1 573 2 191 1 856 618
7 2 191 3 052 2 586 861
8 3 052 4 251 3 602 1199
9 4 251 5 921 5 017 1670
10 5 921 8 247 6 988 2326
11 8 247 11 487 9 733 3240
12 11 487 16 000 13 557 4513
SL 1 300 396 345 96
2 396 524 456 128
3 524 692 602 168
4 692 915 796 223
5 915 1 209 1 052 294
6 1 209 1 597 1 390 388
7 1 597 2 110 1 836 513
8 2 110 2 788 2 425 678
9 2 788 4 200 3 422 1412
10 4 200 6 400 5 185 2200
11 6 400 10 000 8 000 3600
12 10 000 16 000 12 649 6000
Open in a new tab

B. Procedure

The eight listeners of experiment 1 were split into two groups of four listeners each. The groups were chosen with respect to the rank-ordered quadrant error rate from experiment 1 for the condition N=12, which attempted to balance the average quadrant error rate for the groups. One group had listeners ranked 1, 4, 5, and 8 (average quadrant error rate was 22.0%). The other group had listeners ranked 2, 3, 6, and 7 (average quadrant error rate was 20.8%).

Both groups were provided acoustic training to Log-spaced or SL-spaced vocoded signals before testing. The training was similar to that in experiment 1. As before, listeners were trained until performance saturated. This was between 300 and 700 items depending on the listener. After the training, listeners were tested without feedback for 300 items. After data were taken for one type of spacing, the listeners were trained and tested on the other type of spacing in a similar fashion. Therefore, the results of experiment 2 show data from all eight listeners for each condition.

C. Results

The results of the experiment are shown in Fig. 4. Note that the WB noise and WB click data were taken from experiment 1. Qualitatively, the results show that the local polar error and quadrant error rate were smallest for the WB noise, followed by the WB clicks, followed by the Log spacing, followed by the SL spacing. The errors for the SL spacing were slightly larger than the errors for the Log spacing. Results for all conditions were much better than chance performance. Comparing the results of the training on the Log spacing to the same condition with acute testing (experiment 1, condition N=12), on average, the local polar error decreased by 4.6° and the quadrant error rate decreased by 6.8%.

FIG. 4.

FIG. 4

Open in a new tab

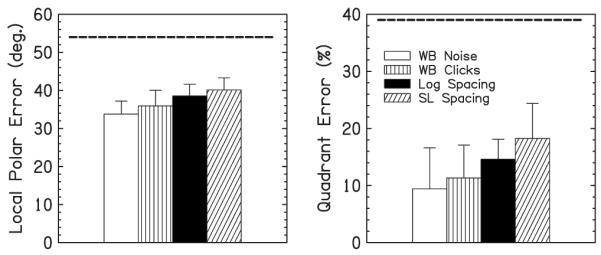
Results of experiment 2 averaged over listeners. Error bars show one standard deviation of the mean. The dashed lines show chance performance. Listeners were trained to all conditions before testing. Data from the WB noise and WB click conditions are repeated from experiment 1.

A RM ANOVA was performed over the factor condition for the local polar error and the quadrant error rate. There was a significant effect of condition for the local polar error and quadrant error rate (p<0.0001 and p=0.006, respectively). Table II shows p-values for post-hoc tests for both metrics. The WB conditions were significantly different from the vocoded conditions for the local polar error. The WB conditions were significantly different from the SL spacing for the quadrant error rate. The differences were not significant between WB conditions for both metrics. The differences were not significant between the Log and SL spacings for both metrics.

TABLE II.

Experiment 2: p-values for differences between conditions. Significant p-values (at the 0.05 level) are in bold

Local polar error WB clicks Log SL
WB noise 0.14 0.0003 <0.0001
WB clicks ··· 0.047 0.001
Log ··· ··· 0.37
Quadrant error WB clicks Log SL
WB noise 0.84 0.15 0.005
WB clicks ··· 0.51 0.034
Log ··· ··· 0.42
Open in a new tab

D. Discussion

This experiment aimed to test two hypotheses. The first hypothesis was that listeners could improve their localization performance of GET-vocoded stimuli with training when compared to experiment 1. Listeners’ performance did improve significantly, but performance for the GET-vocoded stimuli remained slightly worse than that for the WB noise. Although there is a small but significant difference in localization performance between the Log spacing and the WB noise, listeners still performed much better than chance.

The second hypothesis was that listeners could localize using the SL spacing, which attempts to compromise between adequate spectral resolution of low frequencies (required for speech understanding) and the necessity of spectral information from 4 to 16 kHz (required for verticalplane localization), without a marked decrease in localization performance. Listeners localized well below chance performance with the SL-spacing stimuli. This performance was significantly worse than that for the WB noise, but there was no significant difference from the Log-spacing stimuli.

IV. EXPERIMENT 3: SPEECH TEST

The previous experiment showed that NH listeners using a CI simulation could localize in the median plane relatively well using only 12 channels, 8 channels assigned to speech frequencies and 4 channels assigned to spectral localization frequencies. To ensure that the SL spacing does not degrade speech understanding, we performed a speech test using this spacing and a spacing similar to the clinical mapping used in current CI processing strategies.

A. Methods

Three sessions of feedback training and subsequent testing of speech understanding were performed using the Oldenburg Sentence Test. The procedure was similar to that in experiment 2 of Goupell et al. (2008b). The feedback training session consisted of listening to sentences with visual feedback on the computer screen. Eighty sentences were presented at four different signal-to-noise ratios (SNRs): +10, 5, and 0 dB, or in quiet. The testing session consisted of 40 sentences presented in a random order either at a 0-dB SNR or in quiet, 20 sentences for each SNR. Because of ceiling effects, it was not necessary to include the 10- and 5-dB conditions. At beginning of each session, ten sentences were presented in quiet to eliminate any short-term adaptation effects. The percentage of correct words was calculated from the third of the three sessions.

The training and testing were performed for two spacings, the SL spacing and a spacing similar to the processing of the Combi40/40+ and Pulsar CIs, called the “clinical map.” The clinical map was the baseline condition in Goupell et al. (2008b). It had a lower-frequency boundary of 300 Hz, an upper-frequency boundary of 8500 Hz, and had 12 contiguous logarithmically-spaced frequency channels. A noise vocoder was used to simulate CI processing and the corner frequencies of the synthesis channels corresponded to that of the analysis channels. More details of the vocoder and procedure can be found in Goupell et al. (2008b).

The listeners were the same as the previous experiments, except that NH42 did not participate because of her limited availability. NH42 was replaced by NH10, the first author of the paper, who had audiometrically normal hearing and was 29 years old.

B. Results and discussion

Figure 5 shows the results of the experiment. There was very little difference between the two spacings, as expected. In a RM ANOVA (factors: SNR and spacing), the difference was significant between SNRs (p<0.0001), but not between spacings (p=0.58). The interaction was also not significant (p=0.58). Therefore, the small change to the SL spacing did not decrease speech scores from the reference map for NH listeners. This was expected given the results of Goupell et al. (2008b), who tested speech understanding with a similar condition (called the extended-frequency range mapping or “M14N12”) that had an upper-frequency boundary of 16 kHz. The difference between the SL spacing and the extended-frequency range mapping is that the SL spacing mapped frequencies to the appropriate tonotopic places, while the extended range mapping compressed the frequency information from 0.3 to 16 kHz to tonotopic places from 0.3 to 8.5 kHz. NH listeners did not show a decrease for the extended-frequency range mapping compared to the clinical map. CI listeners did show a significant decrease between these conditions. Thus, if CI listeners were tested with the SL spacing, it remains possible that they will have decreased speech understanding. Therefore, it is imperative that CI speech understanding is tested in future experiments for any novel spacing that includes a larger than typical frequency range.

FIG. 5.

FIG. 5

Open in a new tab

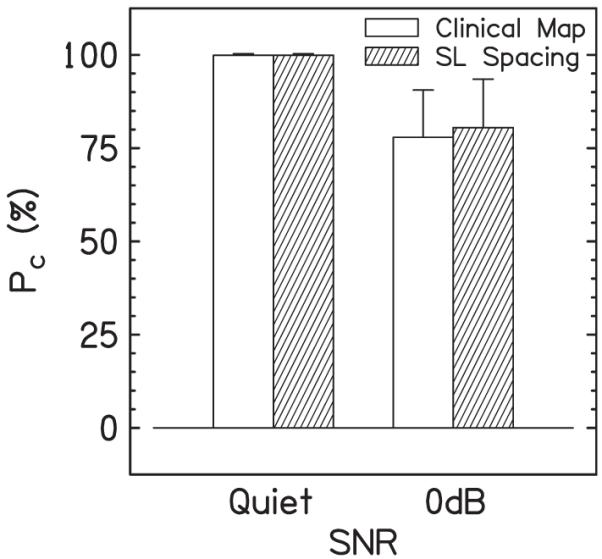
Results of experiment 3 averaged over listeners, the percentage of correct words (Pc) for two spacings, and two SNRs in a speech understanding test. Error bars show one standard deviation of the mean.

V. GENERAL DISCUSSION

Experiments 1 and 2 tested NH listeners’ ability to localize WB and GET-vocoded sound sources in the median plane. The experiments showed that while localization performance was worse for the spectrally degraded vocoded stimuli, localization performance was better than chance. This result validates results from previous studies, which maintain that the gross spectral structure is needed for vertical-plane sound localization (e.g., Kulkarni and Colburn, 1998; Langendijk and Bronkhorst, 2002; Qian and Eddins, 2008). In fact, our reasonably good localization performance was maintained for 9 or 12 channels logarithmically spaced from 0.3 to 16 kHz. Such a result is promising for the incorporation of spectral localization information in CI processing strategies.

Experiment 2 included a special 12-channel spacing, called the SL spacing, in the localization tests. The idea behind this spacing was a compromise between the competing demands of including adequate speech and median-plane localization information. Assuming that frequencies up to 2.4 kHz are essential for adequate vocoded-speech understanding (Goupell et al., 2008b), the Log spacing provided seven speech channels and the SL spacing provided eight speech channels, thus a difference of approximately one channel assigned to spatial information. Experiment 2 showed that localization with the SL spacing was not different from localization with the Log spacing, which means that it is a viable option for future vertical-plane localization testing in CI listeners. Experiment 3 confirmed that speech understanding was not hindered by using the SL spacing.

Of course, localization of real sounds is better than virtual sounds. The local polar error is 22.7±5.1° for real sounds compared to 28.7±4.7° for virtual sounds, and the quadrant error rate is 4.6±5.9% for real sounds compared to 7.7±8.0% for virtual sounds (Middlebrooks, 1999b). For the 12-channel vocoder with the SL spacing of channels, there was an average degradation of 6.3° in local polar error and 8.8% in quadrant error rate for the virtual vocoded stimuli compared to the virtual WB noises. There was an average degradation of 17.4° in local polar error and 13.6% in quadrant error rate compared to the real WB sounds of Middlebrooks (1999b). Assuming no other deficits from using a CI than channelization, CI users will have less ability to distinguish elevation (increase in local polar error in the range from 6.3° to 17.4°) and will confuse front and back more often (increase in quadrant error rate in the range from 8.8% to 13.6%) than NH listeners.

All of the tests were performed with NH listeners using a CI simulation. Testing with CI listeners will also need to be done to determine the usefulness of the SL spacing for vertical-plane localization and speech understanding. Currently, CI listeners using behind-the-ear microphones and a clinical processing scheme (the highest frequency used was 8.5 kHz) cannot localize in the vertical planes (Majdak et al., 2008). This study shows that the incorporation of high frequencies and spectral HRTF information, possibly by an in-the-ear microphone or other types of directional microphone, may provide salient cues for CI listeners, but perception of these cues is understandably worse than for NH listeners. Vertical-plane localization in CI users is expected to be even worse than that measured here for the NH listeners using a CI simulation for a myriad of reasons. One reason is that electrode arrays do not necessarily stimulate tonotopic places with matching frequency information. Ketten et al. (1998) reported the most apical electrode of some CIs, which often receive frequency information around 300 Hz, at a cochlear place tuned to greater than 1.4 kHz. Such a frequency-to-place mismatch is detrimental to speech understanding (e.g., Fu and Shannon, 1999). It could also be detrimental for vertical-plane sound localization, assuming that the CI user previously had hearing and developed an auditory map of space. The problem of tonotopic mismatch could be compounded by dead regions in the cochlea (Shannon et al., 2001); important spectral features may be lost for some elevations, which would probably greatly hinder vertical-plane localization. Another reason is that the fidelity of current CI processing schemes cannot completely reconstruct a CI listener’s individualized HRTF. It is well known that verticalplane localization is worse with non-individualized than individualized HRTFs (e.g., Wenzel et al., 1993). Despite all of these hurdles to overcome, it is possible that the plasticity of the auditory system would be able to cope with these potential problems. CI users may be able to learn a new auditory map of space, which was shown to be possible in NH listeners by Hofman et al. (1998).

Vertical-plane sound localization will also be affected by the poor spectral resolution in CI listeners. CIs typically produce relatively large excitation patterns in the cochlea (Nelson et al., 2008). This large spread of excitation translates to a much poorer spectral resolution for CI listeners compared to NH listeners, which has been measured with a ripple-noise reversal test (Henry and Turner, 2003; Henry et al., 2005). Related to this is the small number of perceptual channels available in CI users. Although we have assumed that 12 electrodes will translate to 12 perceptual channels for sound localization, many speech studies have shown that there are only about eight distinct perceptual channels in CI users (Dorman and Loizou, 1997; Fu and Shannon, 1999; Friesen et al., 2001; Başkent and Shannon, 2005). Nevertheless, we have shown that median-plane sound localization remains quite good for as little as nine channels, nearly the same performance as 18 channels. Additionally, vertical-plane sound localization remains possible even with as few as three or six channels, although approaching chance performance. Even if the inclusion of spectral localization cues to CI processing simply gives the ability to distinguish front from back sources, this may well be worth it.

Lastly, Goupell et al. (2008a) showed that CI listeners depended mostly on intensity cues rather than spectral shape cues in several types of profile analysis tasks, tasks that are necessary to detect spectral vertical-plane sound localization cues. Detecting spectral shape cues may be the major challenge to cope with in addressing vertical-plane sound localization in CI users.

ACKNOWLEDGMENTS

We would like to thank our listeners for participating in this study and Michael Mihocic for running the experiments. We would also like to thank the Associate Editor John Middlebrooks, Fred Wightman, and an anonymous reviewer for comments about a previous version of this work. Portions of this study were presented at the Conference on Implantable Auditory Prostheses in Lake Tahoe in 2009. This study was funded by the Austrian Science Fund (FWF Project No. P18401-B15).

Footnotes

1

The advantage of the first method of generating GET trains (generating a single Gaussian envelope, modulating the carrier with a fixed phase, and summing several GETs into a GET train) over the second method (generating the envelope for the entire train and modulating the carrier to obtain a GET train) is that the peak amplitude in all single GETs is constant for the first method but not necessarily constant for the second. Although the second method removes some higher-order modulations due to overlapping GETs, it cannot control the peak amplitude in each GET.

2

The first channel for N=24, the smallest analysis bandwidth used in this experiment, had an unstable filter configuration. This perceptually translated into a strong pitch around 300 Hz. The entire stimulus was not perceptually distinct from the N=18 condition. Because of low frequency of this anomaly, we assumed that it would not affect median-plane sound localization.

3

Middlebrooks (1999b) removed all targets that were outside a ±30° lateral region. We removed all responses that were outside a ±30° lateral region. For experiment 1, 8.2% of the data were removed because of this.

4

Although the range of the experimental stimuli was from −30° to 210°, listeners were not restricted to this range in their responses. Hence, we used a slightly larger range in the calculation of chance performance to simulate this.

5

Note that the smoothing performed in Kulkarni and Colburn (1998) was linear-frequency based, not log-frequency based. Although the high-frequency spectral localization features appear to have approximately linear-frequency scaling, since the auditory system has approximately log-frequency scaling, there was effectively less smoothing at higher frequencies than low frequencies.

6

Impulse responses between n=9 and 10 canceled with logarithmic spacing, so we chose slightly different corner frequencies to avoid this.

PACS number(s): 43.66.Qp, 43.66.Ts, 43.66.Ba [JCM]

References

  1. Algazi VR, Avendano C, Duda RO. Elevation localization and head-related transfer function analysis at low frequencies. J. Acoust. Soc. Am. 2001;109:1110–1122. doi: 10.1121/1.1349185. [DOI] [PubMed] [Google Scholar]
  2. Asano F, Suzuki Y, Sone T. Role of spectral cues in median plane localization. J. Acoust. Soc. Am. 1990;88:159–168. doi: 10.1121/1.399963. [DOI] [PubMed] [Google Scholar]
  3. Başkent D, Shannon RV. Interactions between cochlear implant electrode insertion depth and frequency-place mapping. J. Acoust. Soc. Am. 2005;117:1405–1416. doi: 10.1121/1.1856273. [DOI] [PubMed] [Google Scholar]
  4. Blauert J. Sound localization in the median plane. Acustica. 1969;22:205–213. [Google Scholar]
  5. Blauert J. Spatial Hearing. MIT; Cambridge, MA: 1997. [Google Scholar]
  6. Carlyon RP, Deeks JM. Limitations on rate discrimination. J. Acoust. Soc. Am. 2002;112:1009–1025. doi: 10.1121/1.1496766. [DOI] [PubMed] [Google Scholar]
  7. Carlyon RP, Long CJ, Deeks JM. Pulse-rate discrimination by cochlear-implant and normal-hearing listeners with and without binaural cues. J. Acoust. Soc. Am. 2008;123:2276–2286. doi: 10.1121/1.2874796. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Dorman MF, Loizou PC. Speech intelligibility as a function of the number of channels of stimulation for normal-hearing listeners and patients with cochlear implants. Am. J. Otol. 1997;18:S113–114. [PubMed] [Google Scholar]
  9. Friesen LM, Shannon RV, Başkent D, Wang X. Speech recognition in noise as a function of the number of spectral channels: Comparison of acoustic hearing and cochlear implants. J. Acoust. Soc. Am. 2001;110:1150–1163. doi: 10.1121/1.1381538. [DOI] [PubMed] [Google Scholar]
  10. Fu QJ, Shannon RV. Recognition of spectrally degraded and frequency-shifted vowels in acoustic and electric hearing. J. Acoust. Soc. Am. 1999;105:1889–1900. doi: 10.1121/1.426725. [DOI] [PubMed] [Google Scholar]
  11. Fu QJ, Shannon RV, Wang X. Effects of noise and spectral resolution on vowel and consonant recognition: Acoustic and electric hearing. J. Acoust. Soc. Am. 1998;104:3586–3596. doi: 10.1121/1.423941. [DOI] [PubMed] [Google Scholar]
  12. Gabor D. Acoustical quanta and the theory of hearing. Nature (London) 1947;84:591–594. doi: 10.1038/159591a0. [DOI] [PubMed] [Google Scholar]
  13. Gardner MB, Gardner RS. Problem of localization in the median plane: Effect of pinnae cavity occlusion. J. Acoust. Soc. Am. 1973;53:400–408. doi: 10.1121/1.1913336. [DOI] [PubMed] [Google Scholar]
  14. Goupell MJ, Laback B, Majdak P, Baumgartner WD. Current-level discrimination and spectral profile analysis in multi-channel electrical stimulation. J. Acoust. Soc. Am. 2008a;124:3142–3157. doi: 10.1121/1.2981638. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Goupell MJ, Laback B, Majdak P, Baumgartner WD. Effects of upper-frequency boundary and spectral warping on speech intelligibility in electrical stimulation. J. Acoust. Soc. Am. 2008b;123:2295–2309. doi: 10.1121/1.2831738. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Grantham DW, Ashmead DH, Ricketts TA, Haynes DS, Labadie RF. Interaural time and level difference thresholds for acoustically presented signals in post-lingually deafened adults fitted with bilateral cochlear implants using CIS+ processing. Ear Hear. 2008;29:33–44. doi: 10.1097/AUD.0b013e31815d636f. [DOI] [PubMed] [Google Scholar]
  17. Hartmann WM, Rakerd B. Auditory spectral discrimination and the localization of clicks in the sagittal plane. J. Acoust. Soc. Am. 1993;94:2083–2092. doi: 10.1121/1.407481. [DOI] [PubMed] [Google Scholar]
  18. Hebrank J, Wright D. Spectral cues used in the localization of sound sources on the median plane. J. Acoust. Soc. Am. 1974;56:1829–1834. doi: 10.1121/1.1903520. [DOI] [PubMed] [Google Scholar]
  19. Henry BA, Turner CW. The resolution of complex spectral patterns by cochlear implant and normal-hearing listeners. J. Acoust. Soc. Am. 2003;113:2861–2873. doi: 10.1121/1.1561900. [DOI] [PubMed] [Google Scholar]
  20. Henry BA, Turner CW, Behrens A. Spectral peak resolution and speech recognition in quiet: Normal hearing, hearing impaired, and cochlear implant listeners. J. Acoust. Soc. Am. 2005;118:1111–1121. doi: 10.1121/1.1944567. [DOI] [PubMed] [Google Scholar]
  21. Hofman PM, Van Opstal AJ. Spectro-temporal factors in two-dimensional human sound localization. J. Acoust. Soc. Am. 1998;103:2634–2648. doi: 10.1121/1.422784. [DOI] [PubMed] [Google Scholar]
  22. Hofman PM, Van Riswick JGA, Van Opstal AJ. Relearning sound localization with new ears. Nat. Neurosci. 1998;1:417–421. doi: 10.1038/1633. [DOI] [PubMed] [Google Scholar]
  23. Iida K, Itoh M, Atsue I, Morimoto M. Median plane localization using a parametric model of the head-related transfer function based on spectral cues. Appl. Acoust. 2007;68:835–850. [Google Scholar]
  24. Ketten DR, Skinner MW, Wang G, Vannier MW, Gates GA, Neely JG. In vivo measures of cochlear length and insertion depth of Nucleus cochlear implant electrode arrays. Ann. Otol. Rhinol. Laryngol. Suppl. 1998;175:1–16. [PubMed] [Google Scholar]
  25. Kistler DJ, Wightman FL. A model of head-related transfer functions based on principal components analysis and minimum-phase reconstruction. J. Acoust. Soc. Am. 1992;91:1637–1647. doi: 10.1121/1.402444. [DOI] [PubMed] [Google Scholar]
  26. Kulkarni A, Colburn HS. Role of spectral detail in sound-source localization. Nature (London) 1998;396:747–749. doi: 10.1038/25526. [DOI] [PubMed] [Google Scholar]
  27. Kulkarni A, Colburn HS. Infinite-impulse-response models of the head-related transfer function. J. Acoust. Soc. Am. 2004;115:1714–1728. doi: 10.1121/1.1650332. [DOI] [PubMed] [Google Scholar]
  28. Laback B, Majdak P. Binaural jitter improves interaural time-difference sensitivity of cochlear implantees at high pulse rates. Proc. Natl. Acad. Sci. U.S.A. 2008;105:814–817. doi: 10.1073/pnas.0709199105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Laback B, Majdak P, Baumgartner WD. Lateralization discrimination of interaural time delays in four-pulse sequences in electric and acoustic hearing. J. Acoust. Soc. Am. 2007;121:2182–2191. doi: 10.1121/1.2642280. [DOI] [PubMed] [Google Scholar]
  30. Laback B, Pok SM, Baumgartner WD, Deutsch WA, Schmid K. Sensitivity to interaural level and envelope time differences of two bilateral cochlear implant listeners using clinical sound processors. Ear Hear. 2004;25:488–500. doi: 10.1097/01.aud.0000145124.85517.e8. [DOI] [PubMed] [Google Scholar]
  31. Langendijk EHA, Bronkhorst AW. Contribution of spectral cues to human sound localization. J. Acoust. Soc. Am. 2002;112:1583–1596. doi: 10.1121/1.1501901. [DOI] [PubMed] [Google Scholar]
  32. Lawson DT, Wilson BS, Zerbi M, van den Honert C, Finley CC, Farmer JC, Jr., McElveen JT, Jr., Roush PA. Bilateral cochlear implants controlled by a single speech processor. Am. J. Otol. 1998;19:758–761. [PubMed] [Google Scholar]
  33. Long CJ, Eddington DK, Colburn HS, Rabinowitz WM. Binaural sensitivity as a function of interaural electrode position with a bilateral cochlear implant user. J. Acoust. Soc. Am. 2003;114:1565–1574. doi: 10.1121/1.1603765. [DOI] [PubMed] [Google Scholar]
  34. Lu T, Carroll J, Zeng FG. On acoustic simulations of cochlear implants; Conference on Implantable Auditory Prostheses; Lake Tahoe, CA. 2007. [Google Scholar]
  35. Macpherson EA, Middlebrooks JC. Localization of brief sounds: Effects of level and background noise. J. Acoust. Soc. Am. 2000;108:1834–1849. doi: 10.1121/1.1310196. [DOI] [PubMed] [Google Scholar]
  36. Macpherson EA, Middlebrooks JC. Vertical-plane sound localization probed with ripple-spectrum noise. J. Acoust. Soc. Am. 2003;114:430–445. doi: 10.1121/1.1582174. [DOI] [PubMed] [Google Scholar]
  37. Majdak P, Balazs P, Laback B. Multiple exponential sweep method for fast measurement of head-related transfer functions. J. Audio Eng. Soc. 2007;55:623–637. [Google Scholar]
  38. Majdak P, Goupell MJ, Laback B. 3-D localization of virtual sound sources: Effects of visual environment, pointing method, and training. Attention, Perception, and Psychophysics. 2010;72:454–469. doi: 10.3758/APP.72.2.454. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Majdak P, Laback B, Goupell MJ. 3-D localization of virtual sound sources in normal-hearing and cochlear-implant listeners (A) J. Acoust. Soc. Am. 2008;123:3562. doi: 10.1097/AUD.0b013e3181f4dfe9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Majdak P, Laback B, Baumgartner WD. Effects of interaural time differences in fine structure and envelope on lateral discrimination in electric hearing. J. Acoust. Soc. Am. 2006;120:2190–2201. doi: 10.1121/1.2258390. [DOI] [PubMed] [Google Scholar]
  41. Middlebrooks JC. Narrow-band sound localization related to external ear acoustics. J. Acoust. Soc. Am. 1992;92:2607–2624. doi: 10.1121/1.404400. [DOI] [PubMed] [Google Scholar]
  42. Middlebrooks JC. Individual differences in external-ear transfer functions reduced by scaling in frequency. J. Acoust. Soc. Am. 1999a;106:1480–1492. doi: 10.1121/1.427176. [DOI] [PubMed] [Google Scholar]
  43. Middlebrooks JC. Virtual localization improved by scaling non-individualized external-ear transfer functions in frequency. J. Acoust. Soc. Am. 1999b;106:1493–1510. doi: 10.1121/1.427147. [DOI] [PubMed] [Google Scholar]
  44. Møller H, Sørensen MF, Hammershøi D, Jensen CB. Head-related transfer functions of human subjects. J. Audio Eng. Soc. 1995;43:300–321. [Google Scholar]
  45. Morimoto M, Aokata H. Localization cues of sound sources in the upper hemisphere. J. Acoust. Soc. Jpn. (E) 1984;5:165–173. [Google Scholar]
  46. Musicant AD, Butler RA. The influence of pinnae-based spectral cues on sound localization. J. Acoust. Soc. Am. 1984;75:1195–1200. doi: 10.1121/1.390770. [DOI] [PubMed] [Google Scholar]
  47. Nelson DA, Donaldson GS, Kreft H. Forward-masked spatial tuning curves in cochlear implant users. J. Acoust. Soc. Am. 2008;123:1522–1543. doi: 10.1121/1.2836786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Nopp P, Schleich P, D’Haese P. Sound localization in bilateral users of MED-EL COMBI 40/40+ cochlear implants. Ear Hear. 2004;25:205–214. doi: 10.1097/01.aud.0000130793.20444.50. [DOI] [PubMed] [Google Scholar]
  49. Oldfield SR, Parker SP. Acuity of sound localisation: A topography of auditory space. II. Pinna cues absent. Perception. 1984;13:601–617. doi: 10.1068/p130601. [DOI] [PubMed] [Google Scholar]
  50. Pralong D, Carlile S. The role of individualized headphone calibration for the generation of high fidelity virtual auditory space. J. Acoust. Soc. Am. 1996;100:3785–3793. doi: 10.1121/1.417337. [DOI] [PubMed] [Google Scholar]
  51. Qian J, Eddins DA. The role of spectral modulation cues in virtual sound localization. J. Acoust. Soc. Am. 2008;123:302–314. doi: 10.1121/1.2804698. [DOI] [PubMed] [Google Scholar]
  52. Schoen F, Mueller J, Helms J, Nopp P. Sound localization and sensitivity to interaural cues in bilateral users of the Med-El Combi 40/40+cochlear implant system. Otol. Neurotol. 2005;26:429–437. doi: 10.1097/01.mao.0000169772.16045.86. [DOI] [PubMed] [Google Scholar]
  53. Seeber BU, Baumann U, Fastl H. Localization ability with bimodal hearing aids and bilateral cochlear implants. J. Acoust. Soc. Am. 2004;116:1698–1709. doi: 10.1121/1.1776192. [DOI] [PubMed] [Google Scholar]
  54. Seeber BU, Fastl H. Localization cues with bilateral cochlear implants. J. Acoust. Soc. Am. 2008;123:1030–1042. doi: 10.1121/1.2821965. [DOI] [PubMed] [Google Scholar]
  55. Senova MA, McAnally KI, Marin RL. Localization of virtual sound as a function of head-related impulse response duration. J. Audio Eng. Soc. 2002;50:57–66. [Google Scholar]
  56. Shannon RV, Galvin JJ, III, Baskent D. Holes in hearing. J. Assoc. Res. Otolaryngol. 2001;3:185–199. doi: 10.1007/s101620020021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Shaw EA. Transformation of sound pressure level from the free field to the eardrum in the horizontal plane. J. Acoust. Soc. Am. 1974;56:1848–1861. doi: 10.1121/1.1903522. [DOI] [PubMed] [Google Scholar]
  58. van den Brink WAC, Houtgast T. Spectro-temporal integration in signal detection. J. Acoust. Soc. Am. 1990;88:1703–1711. doi: 10.1121/1.400245. [DOI] [PubMed] [Google Scholar]
  59. van Hoesel RJM. Exploring the benefits of bilateral cochlear implants. Audiol. Neuro-Otol. 2004;9:234–246. doi: 10.1159/000078393. [DOI] [PubMed] [Google Scholar]
  60. van Hoesel RJM. Sensitivity to binaural timing in bilateral cochlear implant users. J. Acoust. Soc. Am. 2007;121:2192–2206. doi: 10.1121/1.2537300. [DOI] [PubMed] [Google Scholar]
  61. van Hoesel RJM. Observer weighting of level and timing cues in bilateral cochlear implant users. J. Acoust. Soc. Am. 2008;124:3861–3872. doi: 10.1121/1.2998974. [DOI] [PubMed] [Google Scholar]
  62. van Hoesel RJM, Bohm M, Pesch J, Vandali A, Battmer RD, Lenarz T. Binaural speech unmasking and localization in noise with bilateral cochlear implants using envelope and fine-timing based strategies. J. Acoust. Soc. Am. 2008;123:2249–2263. doi: 10.1121/1.2875229. [DOI] [PubMed] [Google Scholar]
  63. van Hoesel RJM, Tyler RS. Speech perception, localization, and lateralization with bilateral cochlear implants. J. Acoust. Soc. Am. 2003;113:1617–1630. doi: 10.1121/1.1539520. [DOI] [PubMed] [Google Scholar]
  64. van Schijndel NH, Houtgast T, Festen JM. Intensity discrimination of Gaussian-windowed tones: Indications for the shape of the auditory frequency-time window. J. Acoust. Soc. Am. 1999;105:3425–3435. doi: 10.1121/1.424683. [DOI] [PubMed] [Google Scholar]
  65. van Wieringen A, Carlyon RP, Long CJ, Wouters J. Pitch of amplitude-modulated irregular-rate stimuli in acoustic and electric hearing. J. Acoust. Soc. Am. 2003;114:1516–1528. doi: 10.1121/1.1577551. [DOI] [PubMed] [Google Scholar]
  66. Vliegen J, Van Opstal AJ. The influence of duration and level on human sound localization. J. Acoust. Soc. Am. 2004;115:1705–1713. doi: 10.1121/1.1687423. [DOI] [PubMed] [Google Scholar]
  67. Wenzel EM, Arruda M, Kistler DJ, Wightman FL. Localization using nonindividualized head-related transfer functions. J. Acoust. Soc. Am. 1993;94:111–123. doi: 10.1121/1.407089. [DOI] [PubMed] [Google Scholar]
  68. Wightman FL, Kistler DJ. Headphone simulation of freefield listening. II: Psychophysical validation. J. Acoust. Soc. Am. 1989;85:868–878. doi: 10.1121/1.397558. [DOI] [PubMed] [Google Scholar]
  69. Zahorik P, Bangayan P, Sundareswaran V, Wang K, Tam C. Perceptual recalibration in human sound localization: Learning to remediate front-back reversals. J. Acoust. Soc. Am. 2006;120:343–359. doi: 10.1121/1.2208429. [DOI] [PubMed] [Google Scholar]
  70. Zahorik P, Wightman FL, Kistler DJ. On the discriminability of virtual and real sound sources; Proceedings of the ASSP (IEEE) Workshop on Applications of Signal Processing on Audio and Acoustics; IEEE, New York. 1995. [Google Scholar]

RESOURCES