Abstract
We examined how changes in intensity and interaural time difference (ITD) influenced the coding of low frequency sounds in the inferior colliculus (IC) of male gerbils at both the single neuron and population levels. We found that changes in intensity along the positive slope of the rate-level function (RLF) evoked changes in spectrotemporal filtering that influenced in the overall timing of spike events, but preserved their precision across trials such that the decoding of single neuron responses was not affected. In contrast, changes in ITD did not trigger changes in spectrotemporal filtering, but had strong effects on the precision of spike events and, consequently, on decoder performance. However, changes in ITD had opposing effects in the two brain hemispheres, and, thus, canceled out at the population level. These results were similar with and without the addition of background noise. We also found that the effects of changes in intensity along the negative slope of the rate-level function (RLF) were different from the effects of changes in intensity along the positive slope in that they evoked changes in both spectrotemporal filtering and in the precision of spike events across trials, as well as in decoder performance. These results demonstrate that, at least at moderate intensities, the auditory system employs different strategies at the single neuron and population levels simultaneously to ensure that the coding of sounds is robust to changes in other stimulus features.
Keywords: auditory, coding, decoding, spectrotemporal filtering, ITD, midbrain
Introduction
In the early auditory pathway, spike patterns generally reflect the fine structure of the sound waveform (for neurons with low preferred frequencies) and/or its amplitude envelope (for neurons with high preferred frequencies). The overall spike rate of auditory neurons, adaptive adjustments in dynamic range notwithstanding (Dean et al., 2005; Wen et al., 2009), typically increases with increasing mean intensity, though it may saturate or decrease at high intensities. In addition to modulating spike rate, changes in intensity can also have an indirect effect on the timing of spike patterns by evoking changes in the way in which sounds are filtered. For example, temporal filtering for high frequency sounds is adapted to changes in intensity such that the system is always optimized for the current operating regime: for soft sounds, temporal filtering is lowpass so that resources are focused on low modulation frequencies where the signal to noise ratio (SNR) in natural sounds is typically highest, while for loud sounds, temporal filtering is bandpass, so that the redundancy in natural sounds at low modulation frequencies can be reduced (Rees and Moller, 1987; Nagel and Doupe, 2006; Lesica and Grothe, 2008a). Such changes in spectral and/or temporal filtering can help to ensure that the flow of information in the periphery is robust to changes in intensity and may provide a substrate for invariant responses in the cortex (Billimoria et al., 2008; Sadagopan and Wang, 2008).
Space is not represented topographically within the brain areas of the early auditory pathway, but is instead encoded directly in neuronal responses such that the spike rate evoked by a given sound is dependent not only on its intensity, but also on its spatial location. In the inferior colliculus (IC), for binaural neurons with low preferred frequencies, spike rate varies with the interaural time difference (ITD), typically as a monotonic function within the range of ITDs corresponding to realizable azimuthal angles (McAlpine et al., 2001; Groh et al., 2003; Hancock and Delgutte, 2004; Lesica et al., 2010). It is unknown whether, as described above for intensity, ITD-dependent changes in spike rate are accompanied by changes in spectral and/or temporal filtering that help to maintain the flow of information. Furthermore, while changes in intensity and ITD may have similar effects on the spike rate of a given neuron, they are certain to have different effects on spike rates across the entire population. A change in intensity will cause, on average, the same change in spike rate in both hemispheres of the brain, while a change in ITD will have opposing effects on the two hemispheres, which, in terms of ITD sensitivity, are mirror images of each other. In this study, we compared the effects of changes in intensity and ITD on the coding of low frequency sounds at both the single cell and population levels and examined how these effects were influenced by the addition of background noise.
Methods
Physiological recordings
Surgical procedures have been described in detail previously (Lesica et al., 2010). All experiments were approved according to the German Tierschutzgesetz (AZ 211-2531-40/01 and AZ 211-2531-68/03). Briefly, adult male gerbils were anesthetized with an initial injection of ketamine (20%) and xylazine (2%) and continuously infused for the duration of the experiment. Animals were secured in a stereotaxic device in a sound-attenuated chamber and a craniotomy was made over the inferior colliculus. A multi-electrode microdrive (Thomas Recording) was used to advance 7 independently moveable microelectrodes into the central nucleus of the inferior colliculus. Recordings were made in the low frequency lamina of the rostrolateral quadrant of the IC, where inputs from the MSO are clustered (Cant and Benson, 2006) and cells are likely to be ITD sensitive. Recordings were analyzed using a free offline program MClust (A. D. Redish) to isolate action potentials from single units. Only those units with an ‘isolation distance’ > 10 were included in this study (Schmitzer-Torbert et al., 2005).
Sounds were delivered to speakers (ER2, Etymotic Research) coupled to tubes which were inserted into the ear canals along with microphones (ER10B, Etymotic Research). Speakers were calibrated to have a flat frequency response (±5 dB SPL from 0.1 to 10 kHz) after coupling to the ears at the beginning of each experiment. At each recording site, a sequence of sounds with various frequencies, intensities, and ITDs were presented to characterize basic response properties. First, 100 ms pure tones of various intensities and frequencies were presented, separated by 150 ms periods of silence, to determine the frequency response area (FRA, see supplementary figure 1a). Tones were presented binaurally with zero ITD and had a rise/fall time of 5 ms. Next, 8 repeated presentations of a 250 ms token of ‘frozen’ Gaussian noise at ITDs ranging from −2 ms to 2 ms were presented, separated by 500 ms periods of silence, to compute noise delay functions (NDFs, see supplementary figure 1b). The noise was filtered to contain only frequencies between 200 and 4000 Hz and had a rise/fall time of 5 ms. The intensity of the noise was 50 dB SPL. Finally, the sounds used for the main decoding analysis were presented: 20 repeated presentations of 8 different 250 ms noise tokens (filtered as above) at 5 different ITDs (−135, −67.5, 0, 67.5, and 135 μs) and 3 different intensities (43, 63, and 83 dB SPL), separated by 500 ms periods of silence. The same tokens were then presented a second time with added broadband background noise (different on every trial) with a signal to noise ratio of 0 dB.
Decoding spike trains
We decoded spike trains (i.e. used the spike trains to infer the sound that evoked them) using the metric introduced by Victor and colleagues (Victor and Purpura, 1996), which measures the distance between two spike trains as the overall cost of the set of operations required to transform one spike train into the other, with possible operations including the insertion of a spike, the deletion of a spike, and the time-shift of a spike (software available at http://neuroanalysis.org/toolkit). By changing the cost of time-shifting a spike relative to deleting the spike at one time and inserting it at another, the metric can be used to evaluate the distance between spike trains at different timescales. The details of the implementation of the metric can be found in Victor and Purpura (1996). We also decoded spike trains using the metric of Van Rossum (2001), but, as decoder performance was similar with both metrics, only results from decoding with the Victor and Purpura metric are shown in the Results.
Decoding using this metric was performed as follows: 1) A single spike train was removed from the full set of all spike trains. 2) The distance between the removed spike train and each of the remaining spike trains in the set was computed. 3) The removed spike train was assigned to the sound for which its average distance to the remaining spike trains evoked by that sound was smallest. This process was repeated for all spike trains in the set to obtain an overall percent correct. For population spike trains, the distances for individual neurons were summed before decoding.
The sound tokens used for the decoding analysis were 250 ms in duration, but, in all cases, responses to the first 50 ms were discarded because many neurons responded strongly to the onset of all of the different tokens and, thus, decoding token identity based on this portion of the response was not possible. For testing the significance of tuning to intensity, ITD, and token identity in single neurons as described below, responses to the remaining 200 ms of sound were used. For testing the effects of changes in ITD and intensity on decoding of token identity in single neurons, the duration that yielded decoder performance of approximately 50% percent correct for the base condition was determined individually for each neuron, and the same duration was used for the ΔITD and ΔSPL conditions. For testing effects of changes in ITD and intensity on decoding of token identity in populations, responses from 50 to 65 ms after sound onset were used for the analysis without background noise and responses from 50 to 200 ms were used for the analysis with background noise.
Evaluating tuning significance
The significance of each neuron’s tuning to sound intensity, ITD, and token identity was determined by comparing decoder performance on the actual responses to performance after randomly reassigning the stimulus value associated with each response. Decoding was performed on 100 different sets of randomized responses and the significance threshold was defined as 2 standard deviations above the mean percent correct for the randomized sets. For evaluating the significance of ITD and intensity tuning, responses to all tokens for each intensity and ITD were combined and decoding was based only on spike rate. In order to be included in the full analysis comparing the effects of changes in ITD and intensity on the decoding of token identity, a neuron had to be significantly tuned to changes in ITD at all intensities and significantly tuned to changes in intensity at all ITDs. For evaluating the significance of tuning to token identity, decoding was performed at a range of timescales as described above. In order to be included in the full analysis, a neuron had to be significantly tuned to token identity at all ITDs and intensities for at least one timescale.
Signal to noise ratio
Signal to noise ratio (SNR) of responses (in 1 ms bins) was calculated as described by Borst and Theunissen (1999). First, the signal spectrum was obtained by computing the power spectrum of the response after averaging across all trials. Next, to obtain the noise power, the response from each trial was subtracted from the average response and the power spectrum of this difference was computed. These difference spectra were averaged over all trials to yield the overall noise spectrum. The SNR at each frequency was defined as the ratio of the power of the signal and noise spectra at that frequency and the total SNR was defined as the ratio of the sum of the power of the signal and noise spectra over all frequencies (i.e. the ratio of the variances of the signal and noise).
Results
To investigate the influence of intensity and ITD on the ability of auditory neurons to encode low frequency sounds, we made extracellular single-unit recordings from the central nucleus of the IC in anesthetized gerbils using a multi-electrode array. Recordings were made in the low frequency lamina of the rostrolateral quadrant of the IC, where inputs from the medial superior olive (MSO) are clustered (Cant and Benson, 2006) and cells are likely to be ITD sensitive. Because these cells are sensitive only to low frequencies, ITD is the only available cue for azimuthal angle (Maki and Furukawa, 2005). Of our original population of 55 neurons, we analyzed only the 33 that were significantly tuned to changes in intensity, ITD, and sound token identity (see Methods for definition of significant tuning). All of these neurons had significant sustained responses to broadband binaural sounds (spike rates between 50 ms and 100 ms after sound onset were greater than spontaneous spike rates; Wilcoxon rank-sum tests, p < 0.05). The distributions of preferred frequencies and ITDs for the population are shown in supplementary figure 1.
Changes in intensity and ITD influence the precision and timing of spike events
To determine the effects of changes in intensity and ITD on the ability of single neurons to encode low frequency sounds, we analyzed responses to 20 repeated trials of 8 different sound tokens (Gaussian noise band-pass filtered between 200 and 4000 Hz) at 3 different intensities (43, 63, and 83 dB SPL) and 5 different ITDs (evenly spaced between ±135 μs, spanning the physiological range for gerbils (Maki and Furukawa, 2005); positive ITDs indicate that the sound reached the ear contralateral to the recording site first), for a total of 25 different intensity/ITD combinations. The different tokens reliably evoked different spike patterns, as illustrated in the responses of a typical neuron to sounds presented at 63 dB SPL with 0 μs ITD shown in figure 1a. In order to study the effects of changes in intensity and ITD beyond those that result from changes in overall spike rate, we analyzed only responses from those neurons for which we found a decrease in intensity and a negative change in ITD that caused approximately the same decrease in spike rate relative to an arbitrary base condition (the relationship between the three conditions is illustrated in the schematic diagram in figure 1b; the base condition could be any intensity/ITD combination and was chosen independently for each cell). Because our sampling of the space of possible intensity/ITD combinations was relatively sparse, only 19 neurons satisfied this criterion (the reductions in spike rate for the intensity change (ΔSPL) condition and ITD change (ΔITD) conditions relative to the base condition for these neurons were not significantly different; paired Wilcoxon test, p = 0.08; median reduction was 29% for ΔSPL and 30% for ΔITD). The requirement that a decrease in intensity cause a decrease in spike rate ensured that the analysis was restricted to the range of intensities corresponding to the positive slope of the rate-level function (RLF; the function relating sound intensity to overall spike rate, see inset), even for neurons with non-monotonic RLFs (analysis of responses from the negative slope of the RLF are presented below).
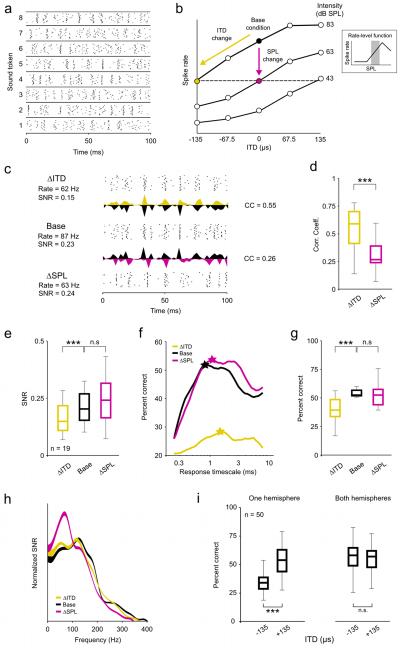
Figure 1. Changes in ITD and intensity have different effects on the coding of low frequency sounds.
a) A raster plot showing the spike trains recorded from a typical neuron in response to 20 repeated presentations of 8 different sound tokens presented at 63 dB SPL with 0 μs ITD. b) A schematic diagram depicting the relationship between the three stimulus conditions: the base condition, the ITD change (ΔITD; a decrease in ITD) condition, and the intensity change (ΔSPL; a decrease in intensity) condition. Only those cells for which the ΔSPL condition could be defined by a change in intensity along the positive slope of the RLF were analyzed. c) Raster plots and PSTHs showing the responses of a typical neuron to the same sound token for the three conditions. The mean overall spike rates and response signal to noise ratios (SNRs) are shown for each condition, and the correlation coefficients (CCs) between the PSTHs for the base condition and each of the two change conditions are shown. Different PSTHs extend upward and downward from the same axis for ease of visual comparison. d) Box plots showing the distribution of CCs between the PSTHs for the base condition and each of the two change conditions for a sample of 19 neurons. In each plot, the central mark indicates the median, the edges of the box indicate the 25th and 75th percentiles, and the whiskers extend to the most extreme values. The results of paired Wilcoxon tests comparing the medians of the distributions are indicated. e) Box plots showing the distribution of response SNRs for each of the three stimulus conditions, presented as in d. f) Decoder performance as a function of response timescale for a typical neuron under the three stimulus conditions. The stars indicate the timescale corresponding to the best performance. g) Box plots showing the distribution of decoder performance at the optimal timescale for each of the three stimulus conditions, presented as in d. Chance level performance was 12.5%. h) The SNR as a function of response frequency under the three stimulus conditions, averaged across all cells in the sample and normalized such that the area under each curve is the same. The thickness of the lines indicates the standard error of the mean. i) Box plots showing the distribution of decoder performance for 50 randomly chosen populations of 10 cells with either all cells from the same hemisphere or half of the cells from each hemisphere, presented as in d. Only the distributions for responses to sounds at 83 dB SPL are shown, but the distributions for other intensities were similar. All neurons were in fact recorded in the same hemisphere, but responses to sounds at −135 μs ITD and +135 μs ITD were switched for half of the neurons to simulate responses from both hemispheres.
The responses of a typical neuron to one sound token for the base, ΔSPL, and ΔITD conditions are shown in figure 1c. The changes in intensity and ITD had similar effects on the spike rate, but they had different effects on the timing of spikes within the response: relative to the base condition, the change in intensity caused a change in the overall timing of events, but had little impact on precision of spike timing across trials, while the change in ITD caused a decrease in precision of spike timing across trials but left the overall timing of spike events largely unchanged. To quantify the effects of changes in intensity and ITD on the overall timing of events, we measured the correlation coefficient (CC) between the PSTHs (in 1 ms time bins) for each of the change conditions and the base condition. As shown in figure 1d, across our sample of neurons, the CC between responses for the ΔITD and base conditions were significantly larger than those between responses for the ΔSPL and base conditions (paired Wilcoxon test, p < 0.001). To quantify the effects of changes in intensity and ITD on precision, we measured the signal to noise ratio (SNR) of the responses (see Methods). SNR, a measure commonly used to describe the precision of spike trains in early sensory systems, compares the power in the part of the response that is repeatable from trial to trial (the PSTH) with that which is variable from trial to trial (the deviation from the PSTH on each trial). As shown in figure 1e, across our sample of neurons, the change in ITD caused a significant decrease in SNR relative to the base condition, while the change in intensity had no significant effect (paired Wilcoxon tests, p < 0.001 for ΔITD and p = 0.18 for ΔSPL). These results suggest that changes in intensity and ITD have different effects on the timing of spikes: a change in intensity causes a change in the overall timing of spike events, while a change in ITD causes a change in the precision of spike timing across trials.
Changes in ITD, but not intensity, influence decoder performance
To determine the impact of the observed effects of changes in intensity and ITD on coding, we used a decoder to infer which sound token evoked each response for each stimulus condition. The performance of the decoder for a given condition reflects how well information about token identity is encoded in the spike trains for that condition; if the spike trains evoked by a given token are similar to each other, but different from the spike trains evoked by the other tokens, then the decoder will correctly assign the spike trains to the tokens that evoked them (note that this approach is different from training the decoder for one condition and testing its performance for a different condition to examine the degree of invariance in how the information is encoded (Billimoria et al., 2008)). Because the tokens were exactly the same for each condition, the difference in the performance of the decoder for the three stimulus conditions provides a direct measure of the effects of changes in intensity and ITD on coding.
The decoder was based on a metric that computes the distance between two spike trains at a specified timescale (Victor and Purpura, 1996). To decode a given spike train, the decoder measured its distance to all of the other spike trains evoked by each sound token and chose the token for which the mean distance was smallest (see Methods). This decoder is not designed to mimic the function of a neuron in any particular downstream auditory area, but simply to serve as tool for assessing how well information about token identity is encoded in IC responses.
The performance of the decoder at different timescales for a typical neuron for the base, ΔSPL, and ΔITD conditions is shown in figure 1f. For this neuron, the decoder performance was unaffected by the change in intensity, but was severely degraded by the change in ITD. As shown in figure 1g, across our sample of neurons, the change in ITD caused a significant decrease in decoder performance (at the timescale for which performance was maximal for each neuron) relative to the base condition, while the change in intensity had no significant effect (paired Wilcoxon tests, p < 0.001 for ΔITD and p = 0.27 for ΔSPL). Thus, the change in the precision of spike timing across trials caused by a change in ITD had a strong effect on the ability of IC neurons to encode low frequency sounds, while the change in the overall timing of spike events caused by a change in intensity did not (at least for the restricted range of intensities corresponding to the positive slope of the RLF; see results for intensities corresponding to the negative slope of the RLF below).
Changes in intensity, but not ITD, evoke a change in spectrotemporal filtering
Previous studies have demonstrated that changes in intensity evoke a shift in spectral and/or temporal filtering properties that may help to preserve the flow of auditory information in the face of changes in the SNR of incoming sounds (Lesica and Grothe, 2008a; Nagel and Doupe, 2006; Rees and Moller, 1987). For example, as intensity is decreased, temporal filtering shifts toward low frequencies where the SNR in natural sounds is likely to be the largest (Lesica and Grothe, 2008a; Singh and Theunissen, 2003). To investigate whether such shifts could account for the differences in the effects of changes in intensity and ITD on the coding of low frequency sounds illustrated above, we measured the SNR as a function of response frequency for the neurons in our sample. Because the sound tokens were identical for all three stimulus conditions and were uncorrelated (i.e. had equal power at all frequencies), the SNR at each response frequency is a direct reflection of the net effect of the spectrotemporal filtering properties of the system (note that we use the term spectrotemporal filtering because the neurons in our sample have low preferred frequencies and response power at a given frequency can reflect filtering of both envelope and fine structure). The mean SNR as a function of response frequency for the base, ΔSPL, and ΔITD conditions for our sample of neurons are shown in figure 1h (line thickness indicates standard error), normalized such that the area under each curve is the same to compensate for the overall differences in SNR described above. As expected, the change in intensity caused a clear shift toward low response frequencies relative to the base condition. In contrast, the SNR as a function of response frequency for the base and ΔITD conditions were nearly identical, indicating that the change in ITD did not evoke a shift in spectrotemporal filtering properties. Thus, the system appears to shift its spectrotemporal filtering properties to preserve the ability of single neurons to encode low frequency sounds in response to changes in intensity, but not in response to changes in ITD.
Coding is robust to changes in ITD at the population level
The results described above demonstrate that changes in intensity and ITD have different effects on the coding of low frequency sounds in the responses of single neurons. However, these changes also have different effects on the overall spike rates of the entire population. For example, an increase in intensity will cause, on average, an increase in spike rate for the whole population (except, perhaps, at very high intensities). In contrast, because most binaural neurons with low preferred frequencies (including all in this study, see supplementary figure 1) respond most strongly to sounds located on the side contralateral to the brain hemisphere that they are in (corresponding to positive ITDs in this study), a change in the ITD of a sound will cause, on average, an increase in spike rate for neurons in one hemisphere and a decrease in spike rate for neurons in the other hemisphere. To determine how changes in intensity and ITD influenced the coding of sound content at the population level, we decoded the responses of many different random subpopulations of neurons using the same metric as described above. As shown in figure 1i, when all of the cells in the population were taken from a single hemisphere, the change in ITD from +135 μs to −135 μs (corresponding to a change in location from the contralateral side to the ipsilateral side) caused a decrease in decoder performance similar to that observed in single cells (Wilcoxon test, p < 0.001, n = 50 different random subpopulations of 10 neurons). However, when half of the population was drawn from each hemisphere, the performance of the decoder was independent of ITD (Wilcoxon test, p = 0.96). These results suggest that opposing effects of a change in ITD in the two hemispheres offset each other; a change in ITD that degrades the coding of low frequency sounds in one hemisphere enhances it in the other, such that there is no net change across the entire population.
The effects of intensity and ITD on coding are similar with and without background noise
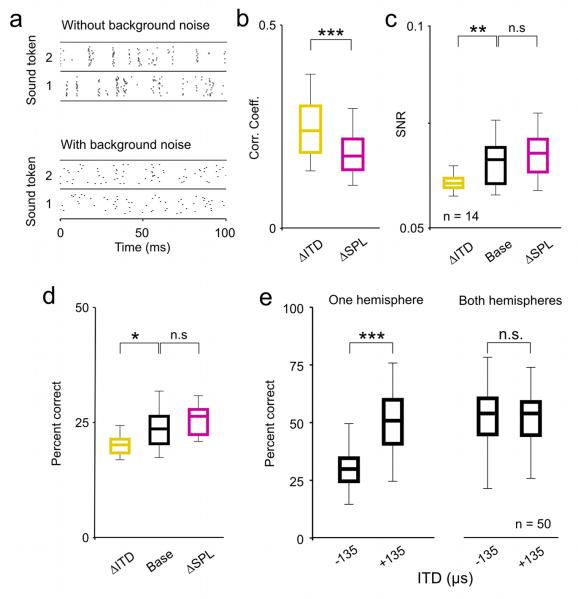
Changes in listening conditions such as the addition of background noise have been shown to have strong effects on the processing of sound content in the IC (Kvale and Schreiner, 2004; Lesica and Grothe, 2008a; Rees and Palmer, 1988). To determine whether the observed effects of changes in intensity and ITD on coding described above were also evident in the presence of background noise, we recorded responses of the same neurons to the same sound tokens in the presence of broadband background noise (SNR = 0 dB). The responses of a typical neuron to one sound with and without background noise presented at 63 dB SPL with 0 μs ITD are shown in figure 2a. Again, in order to study the effects of changes in intensity and ITD beyond those that result from changes in overall spike rate, we analyzed only those neurons for which we found a decrease in intensity and a negative change in ITD that caused approximately the same decrease in spike rate relative to an arbitrary base condition (n = 14). For this subset of neurons, the reductions in spike rate for the ΔSPL and ΔITD conditions relative to the base condition were not significantly different (paired Wilcoxon test, p = 0.54; median reduction was 31% for ΔSPL and 32% for ΔITD). The effects of changes in intensity and ITD on the timing of spike events with background noise were similar to those without: the CCs between responses for the ΔITD and base conditions were significantly larger than those between responses for the ΔSPL and base conditions (figure 2b; paired Wilcoxon test, p < 0.001) and the change in ITD caused a significant decrease in SNR relative to the base condition, while the change in intensity had no significant effect (figure 2c; paired Wilcoxon tests, p = 0.002 for ΔITD and p = 0.24 for ΔSPL). The effects of changes in intensity and ITD on coding with background noise were also similar to those without: a change in ITD resulted in a significant decrease in decoder performance for single neurons relative to the base condition, while the change in intensity had no significant effect (figure 2d; paired Wilcoxon tests, p = 0.02 for ΔITD and p = 0.61 for ΔSPL) and the effects of a change in ITD were canceled out at the population level when the population contained neurons from both hemispheres (figure 2e; Wilcoxon tests, p < 0.001 for one hemisphere, p = 0.58 for both hemispheres, n = 50 different random subpopulations of 10 cells). The similarity of the results in figures 1 and 2 suggest that, at least at a qualitative level, the effects of changes in ITD and intensity on the coding of low frequency sounds are independent of background noise level.
Figure 2. The effects of ITD and intensity on the coding of low frequency sounds are similar with and without background noise.
a) A raster plot showing the spike trains recorded from a typical neuron in response to 20 repeated presentations of one sound token presented at 63 dB SPL with 0 μs ITD with and without background noise at a signal to noise ratio of 0 dB. b-e) Distributions of response CCs, SNRs, and decoder performance for a sample of 14 single neurons, and decoder performance for randomly chosen populations with either all cells from the same hemisphere or half of the cells from each hemisphere, presented as in figure 1.
Changes in intensity along the positive and negative slope of the RLF have different effects on coding
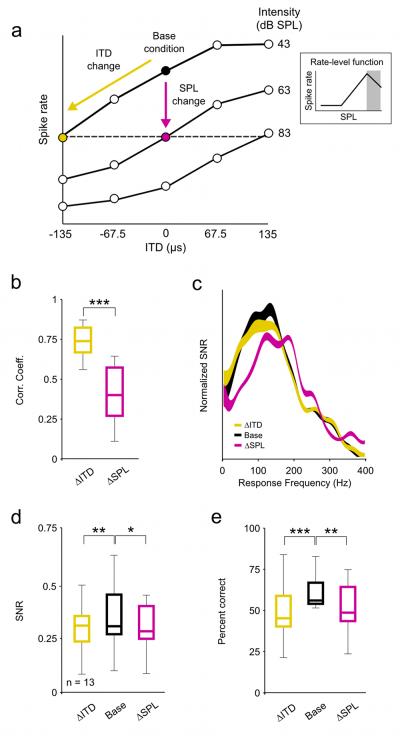
Many neurons in the auditory system have RLFs that are non-monotonic, i.e. spike rate increases with increasing intensity for soft sounds, but decreases with increasing intensity for loud sounds. To determine whether the observed effects of changes in intensity on coding differ depending on whether the changes are along the positive or negative slope of the RLF, we performed the same set of analyses on responses of those neurons (n = 13) for which we found an increase in intensity and a negative change in ITD that caused approximately the same decrease in spike rate relative to an arbitrary base condition (see schematic diagram in figure 3a). For this subset of neurons, the reductions in spike rate for the ΔSPL and ΔITD conditions relative to the base condition were not significantly different (paired Wilcoxon test, p = 0.12; median reduction was 20% for ΔSPL and 21% for ΔITD). As with changes in intensity along the positive slope of the RLF (figure 1d), changes in intensity along the negative slope of the RLF had a much stronger effect than changes in ITD on the overall timing of spike events: the CCs between responses for the ΔITD and base conditions were significantly larger than those between responses for the ΔSPL and base conditions (figure 3b; paired Wilcoxon test, p < 0.001). This result was consistent with the shift in spectrotemporal filtering reflected in the frequency content of responses for the ΔSPL condition (figure 3c; because the change in intensity is positive, the shift for the ΔSPL condition is toward higher frequencies). However, unlike changes in intensity along the positive slope of the RLF which had no effect on SNR (figure 1e), changes in intensity along the negative slope of the RLF caused a decrease in SNR similar to that caused by a change in ITD (figure 3d; paired Wilcoxon tests, p = 0.006 for ΔITD and p = 0.05 for ΔSPL). As a result, the effects of changes in intensity along the negative slope of the RLF on coding were similar to those caused by a change in ITD: both changes resulted in a significant decrease in decoder performance for single neurons relative to the base condition (figure 3e; paired Wilcoxon tests, p < 0.001 for ΔITD and p = 0.01 for ΔSPL). Thus, the ability of single neurons to encode low frequency sounds appears to be robust to changes in intensity along the positive slope of the RLF, but not to changes in intensity along the negative slope of the RLF.
Figure 3. The effects of intensity on the coding of low frequency sounds differ for changes in intensity along the positive and negative slopes of the RLF.
a) A schematic diagram depicting the relationship between the three stimulus conditions. Only those cells for which the ΔSPL (an increase in intensity) condition could be defined by a change in intensity along the negative slope of the RLF were analyzed. b-e) Distributions of response CCs, mean SNR as a function of response frequency, and distributions of SNRs and decoder performance for a sample of 13 single neurons, presented as in figure 1.
Discussion
We have demonstrated that even when changes in intensity and ITD have similar effects on the spike rate of a single neuron, they can have different effects on the neuron’s ability to encode low frequency sounds. We found that a change in intensity along the positive slope of the RLF evoked a change in spectrotemporal filtering properties that changed the overall timing of spike events, but preserved the precision of spike timing across trials such that decoding of sound token identity from the responses of single neurons was not affected. In contrast, a change in ITD did not evoke a change in spectrotemporal filtering properties and, thus, had little impact on the overall timing of spike events, but had strong effects on the precision of spike timing across trials, and, consequently, on decoding. However, because the two brain hemispheres are mirror images of each other in terms of ITD sensitivity, changes in ITD had no net effect on coding across the entire population. These effects were robust to the addition of background noise at both the single neuron and population level. We also found that the effects of changes in intensity along the negative slope of the RLF were different than those of changes along the positive slope. Changes in intensity along the negative slope of the RLF caused changes in both the overall timing of spike events and the precision of spike timing across trials, and had effects on decoding that were similar to those caused by a change in ITD.
Our results show that, at least at moderate intensities, the auditory system can simultaneously employ fundamentally different strategies to maintain the flow of information in the face of changes in intensity and ITD. Because a change in intensity will have a similar effect on all neurons in the population, mechanisms that adjust the response properties of single neurons are necessary to preserve the flow of information at the population level. On the other hand, because a change in ITD will enhance coding in single neurons in one hemisphere and degrade it in the other, its effects will balance out at the population level and no mechanisms that adjust the response properties of single neurons are necessary. The location and nature of the integration of the information about ITD from the two hemispheres remains a source of speculation (Porter and Groh, 2006). It seems clear that this integration does not take place in primary auditory cortex (Eggermont and Mossop, 1998; King and Campbell, 2005; Stecker et al., 2005), but there is evidence suggesting that it may take place in higher cortical areas (Stecker et al., 2003; Miller and Recanzone, 2009).
The intensity-dependent changes in spectrotemporal filtering properties observed here, as well as the associated changes in the overall timing of response events, are similar to those that have been observed throughout the auditory system (Moller, 1977; Nagel and Doupe, 2006; Lesica and Grothe, 2008b). These effects are due, at least in part, to the nonlinear properties of the basilar membrane, but central mechanisms such as inhibition within the IC may also play a role (Caspary et al., 2002). The origin of the ITD-dependent changes in the precision of spike timing across trials is less clear. Since a change in ITD does not actually affect the responses in the auditory nerves, but only the timing between them, the ITD-dependent changes that we observe must arise centrally after binaural convergence. One possible source of the observed effects is the coincidence detection mechanism in the MSO (which, presumably, provides the primary inputs to the IC cells studied here), the reliability of which has long been known to vary with overall spike rate (Goldberg and Brown, 1969).
Our results describe the effects of intensity and ITD on the coding of low frequency sounds. It remains to be seen whether or not similar effects are evident for high frequency sounds. The mechanisms that optimize response properties in single neurons in response to changes in intensity operate across a wide range of frequencies (Lesica and Grothe, 2008a; Nagel and Doupe, 2006; Rees and Moller, 1987), so the effects of changes in intensity on coding are likely to be similar for low and high frequency sounds. For high frequency sounds, there are two important spatial cues: interaural level differences (ILDs) and spectral notches. Like ITDs, ILDs are computed centrally after binaural integration and have opposing effects on different subsets of the population, so no mechanism to compensate for changes in ILD at the single neuron level may be necessary (note the critical distinction between the changes in spectrotemporal filtering properties at issue here and mechanisms that adjust dynamic response range, which appear to operate in response to changes in both ITDs and ILDs (Dahmen et al., 2010; McAlpine et al., 2000; Spitzer and Semple, 1991)). Spectral notches, which are imposed by the pinnae, only affect a small subset of cells for a sound at any given location, so, again, no mechanism to adjust coding strategy may be necessary. However, because spectral notches are already present in the ear, it may be possible for the system to use some of the same machinery that compensates for changes in intensity with little additional overhead.
Supplementary Material
Acknowledgements
We thank Benedikt Grothe for the use of experimental equipment and Michael Pecka for helpful comments on the manuscript. This work was supported by the ERASMUS Program (Horvath) and the German Research Foundation and the Wellcome Trust (Lesica).
References
- Billimoria CP, Kraus BJ, Narayan R, Maddox RK, Sen K. Invariance and sensitivity to intensity in neural discrimination of natural sounds. J. Neurosci. 2008;28:6304–6308. doi: 10.1523/JNEUROSCI.0961-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cant NB, Benson CG. Organization of the inferior colliculus of the gerbil (Meriones unguiculatus): differences in distribution of projections from the cochlear nuclei and the superior olivary complex. J Comp Neurol. 2006;495:511–28. doi: 10.1002/cne.20888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caspary DM, Palombi PS, Hughes LF. GABAergic inputs shape responses to amplitude modulated stimuli in the inferior colliculus. Hear. Res. 2002;168:163–173. doi: 10.1016/s0378-5955(02)00363-5. [DOI] [PubMed] [Google Scholar]
- Dahmen JC, Keating P, Nodal FR, Schulz AL, King AJ. Adaptation to Stimulus Statistics in the Perception and Neural Representation of Auditory Space. Neuron. 2010;66:937–948. doi: 10.1016/j.neuron.2010.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat. Neurosci. 2005;8:1684–1689. doi: 10.1038/nn1541. [DOI] [PubMed] [Google Scholar]
- Eggermont JJ, Mossop JE. Azimuth coding in primary auditory cortex of the cat. I. Spike synchrony versus spike count representations. J. Neurophysiol. 1998;80:2133–2150. doi: 10.1152/jn.1998.80.4.2133. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Brown PB. Response of binaural neurons of dog superior olivary complex to dichotic tonal stimuli: some physiological mechanisms of sound localization. J. Neurophysiol. 1969;32:613–636. doi: 10.1152/jn.1969.32.4.613. [DOI] [PubMed] [Google Scholar]
- Groh JM, Kelly KA, Underhill AM. A Monotonic Code for Sound Azimuth in Primate Inferior Colliculus. J. Cog. Neurosci. 2003;15:1217–1231. doi: 10.1162/089892903322598166. [DOI] [PubMed] [Google Scholar]
- Hancock KE, Delgutte B. A physiologically based model of interaural time difference discrimination. J. Neurosci. 2004;24:7110–7117. doi: 10.1523/JNEUROSCI.0762-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King AJ, Campbell RA. Cortical Processing of Sound-Source Location. Acta Acustica. 2005;91:399–408. [Google Scholar]
- Kvale MN, Schreiner CE. Short-term adaptation of auditory receptive fields to dynamic stimuli. J. Neurophysiol. 2004;91:604–612. doi: 10.1152/jn.00484.2003. [DOI] [PubMed] [Google Scholar]
- Lesica NA, Grothe B. Efficient temporal processing of naturalistic sounds. PLoS ONE. 2008a;3:e1655. doi: 10.1371/journal.pone.0001655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesica NA, Grothe B. Dynamic spectrotemporal feature selectivity in the auditory midbrain. J. Neurosci. 2008b;28:5412–5421. doi: 10.1523/JNEUROSCI.0073-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesica NA, Lingner A, Grothe B. Population Coding of Interaural Time Differences in Gerbils and Barn Owls. J. Neurosci. 2010;30:11696–11702. doi: 10.1523/JNEUROSCI.0846-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maki K, Furukawa S. Acoustical cues for sound localization by the Mongolian gerbil, Meriones unguiculatus. J. Acoust. Soc. Am. 2005;118:872–886. doi: 10.1121/1.1944647. [DOI] [PubMed] [Google Scholar]
- McAlpine D, Jiang D, Palmer AR. A neural code for low-frequency sound localization in mammals. Nat. Neurosci. 2001;4:396–401. doi: 10.1038/86049. [DOI] [PubMed] [Google Scholar]
- McAlpine D, Jiang D, Shackleton TM, Palmer AR. Responses of Neurons in the Inferior Colliculus to Dynamic Interaural Phase Cues: Evidence for a Mechanism of Binaural Adaptation. J Neurophysiol. 2000;83:1356–1365. doi: 10.1152/jn.2000.83.3.1356. [DOI] [PubMed] [Google Scholar]
- Miller LM, Recanzone GH. Populations of auditory cortical neurons can accurately encode acoustic space across stimulus intensity. Proc. Natl. Acad. Sci. U.S.A. 2009;106:5931–5935. doi: 10.1073/pnas.0901023106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moller AR. Frequency selectivity of single auditory-nerve fibers in response to broadband noise stimuli. J. Acoust. Soc. Am. 1977;62:135–142. doi: 10.1121/1.381495. [DOI] [PubMed] [Google Scholar]
- Nagel KI, Doupe AJ. Temporal processing and adaptation in the songbird auditory forebrain. Neuron. 2006;51:845–859. doi: 10.1016/j.neuron.2006.08.030. [DOI] [PubMed] [Google Scholar]
- Porter KK, Groh JM. The “other” transformation required for visual-auditory integration: representational format. Prog. Brain Res. 2006;155:313–323. doi: 10.1016/S0079-6123(06)55018-6. [DOI] [PubMed] [Google Scholar]
- Rees A, Moller AR. Stimulus properties influencing the responses of inferior colliculus neurons to amplitude-modulated sounds. Hear. Res. 1987;27:129–143. doi: 10.1016/0378-5955(87)90014-1. [DOI] [PubMed] [Google Scholar]
- Rees A, Palmer AR. Rate-intensity functions and their modification by broadband noise for neurons in the guinea pig inferior colliculus. J. Acoust. Soc. Am. 1988;83:1488–1498. doi: 10.1121/1.395904. [DOI] [PubMed] [Google Scholar]
- van Rossum MC. A novel spike distance. Neural Comput. 2001;13:751–63. doi: 10.1162/089976601300014321. [DOI] [PubMed] [Google Scholar]
- Sadagopan S, Wang X. Level invariant representation of sounds by populations of neurons in primary auditory cortex. J. Neurosci. 2008;28:3415–3426. doi: 10.1523/JNEUROSCI.2743-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitzer-Torbert N, Jackson J, Henze D, Harris K, Redish AD. Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience. 2005;131:1–11. doi: 10.1016/j.neuroscience.2004.09.066. [DOI] [PubMed] [Google Scholar]
- Singh NC, Theunissen FE. Modulation spectra of natural sounds and ethological theories of auditory processing. J. Acoust. Soc. Am. 2003;114:3394–3411. doi: 10.1121/1.1624067. [DOI] [PubMed] [Google Scholar]
- Spitzer MW, Semple MN. Interaural phase coding in auditory midbrain: influence of dynamic stimulus features. Science. 1991;254:721–724. doi: 10.1126/science.1948053. [DOI] [PubMed] [Google Scholar]
- Stecker GC, Harrington IA, Middlebrooks JC. Location coding by opponent neural populations in the auditory cortex. PLoS Biol. 2005;3:e78. doi: 10.1371/journal.pbio.0030078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stecker GC, Mickey BJ, Macpherson EA, Middlebrooks JC. Spatial Sensitivity in Field PAF of Cat Auditory Cortex. J Neurophysiol. 2003;89:2889–2903. doi: 10.1152/jn.00980.2002. [DOI] [PubMed] [Google Scholar]
- Victor JD, Purpura KP. Nature and precision of temporal coding in visual cortex: a metric-space analysis. J Neurophysiol. 1996;76:1310–26. doi: 10.1152/jn.1996.76.2.1310. [DOI] [PubMed] [Google Scholar]
- Wen B, Wang GI, Dean I, Delgutte B. Dynamic range adaptation to sound level statistics in the auditory nerve. J. Neurosci. 2009;29:13797–13808. doi: 10.1523/JNEUROSCI.5610-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.