Learning optimal adaptation strategies in unpredictable motor tasks

Abstract

Picking up an empty milk carton that we believe to be full is a familiar example of adaptive control, because the adaptation process of estimating the carton's weight must proceed simultaneously to the control process of moving the carton to a desired location. Here we show that the motor system initially generates highly variable behavior in such unpredictable tasks but eventually converges to stereotyped patterns of adaptive responses predicted by a simple optimality principle. These results suggest that adaptation can become specifically tuned to identify task-specific parameters in an optimal manner.

Introduction

Flexible motor control is an essential feature of biological organisms that pursue their goals in the face of uncertainty and incomplete knowledge about their environment. It is therefore not surprising that the phenomenon of adaptive behavior pervades the entire animal kingdom from simple habituation to complex reinforcement learning (Reznikova, 2007). Conceptually, learning is naturally understood as an optimization process that leads to efficient motor control. Thus, once learning has taken place and stable motor responses have formed, complex motor behaviors can often be understood by simple optimality principles that trade off attributes such as task success and energy expenditure (Todorov, 2004). In particular, optimal feedback control models have been successful in explaining a wide variety of motor behaviors on multiple levels of analysis (Todorov and Jordan, 2002; Scott, 2004; Diedrichsen, 2007; Guigon et al., 2007; Liu and Todorov, 2007). Optimal control models typically start out with the dynamics of the environment (e.g. dynamics of the arm or a tool) and a performance criterion in the form of a cost function (Stengel, 1994). The optimal control is then defined as a feedback rule that maps the past observations to a future action. This feedback rule minimizes the cost and is usually compared to the control actions chosen by a human or animal controller in an experiment (Loeb et al., 1990; Todorov and Jordan, 2002).

Importantly, optimal feedback control requires knowledge of the environmental dynamics in the form of an internal model. Consider, for example, that we wish to move a milk carton with known weight to a new location. An internal model would predict the future state of the controlled system x_t+1 (e.g. future carton and hand position, velocity, etc.) from the current state x_t and the current action or control u_t (e.g. a neural control command to the muscles). Mathematically, the internal model can then be compactly represented as a mapping F with x_t+1 = F(x_t, u_t). Experimentally, such internal models have been shown to play a crucial role in human motor control (Shadmehr and Mussa-Ivaldi, 1994; Wolpert et al., 1995; Wagner and Smith, 2008). However, the question arises whether adaptive behavior in an environment where the dynamics are not completely known can be understood by the same principles. Mathematically, we can formalize an adaptive control problem as a mapping x_t+1 = F(x_t, u_t, a) with unknown system parameters a that have to be estimated simultaneously with the control process (Sastry and Bodson, 1989; Åström and Wittenmark, 1995). For example, in the case of a milk carton with an unknown weight, the motor system must adapt its estimate of the carton's weight (the parameter a in this case), while simultaneously exerting the necessary control to bring the carton to a desired location. This raises a fundamental question as to whether such estimation and control is a generic process operating whenever the motor system faces unpredictable situations or whether the adaptation process itself undergoes a learning phase so as to become tuned to specific environments and tasks in an optimal manner. Here we design a visuomotor learning experiment to test the hypothesis that with experience of an uncertain environment the motor system learns to perform a task-specific, stereotypical adaptation and control within individual movements in a task-optimal fashion. In the following we will refer to changes in the control policy that occur within individual movements as ‘adaptation’ in order to distinguish it from ‘learning’ processes that improve these adaptive responses across trials.

Materials and Methods

Data Acquisition

Nineteen healthy naive subjects participated in this study and gave informed consent after approval of the experimental procedures by the Ethics Committee of the Albert-Ludwigs-University, Freiburg. Subjects controlled a cursor (radius 1cm) on a 17″ TFT computer screen with their arm suspended by means of a long pendulum (4m) that was attached to the ceiling. Subjects grabbed on to a handle at the bottom of the pendulum and moved it in the horizontal plane. Movements were recorded by an ultrasonic tracker system (CMS20, Zebris Medical GmbH, Germany, 300Hz sampling, 0.085mm accuracy). The screen displayed eight circular targets (radius 1.6cm) arranged concentrically around a starting position (center-target distance 8cm). Subjects were asked to move the cursor swiftly into the designated target and each trial lasted two seconds (therefore in early trials subjects often did not reach the target within the time window).

Experimental Procedure

Two groups of subjects underwent two experimental blocks (2000 trials each) in which participants performed reaching movements in an uncertain environment. In both blocks the majority of trials were standard trials. However, on 20% of randomly selected trials a visuomotor perturbation was introduced. Each perturbation trial was always followed by at least one standard trial so that random perturbation trials were interspersed individually amongst the standard trials. In the first group (rotation group, 10 subjects) the perturbation was always a random visuomotor rotation with a rotation angle drawn from a uniform distribution over {±30°, ±50°, ±70°, ±90°}. Thus, the majority of trials had a normal hand-cursor relation and in visuomotor rotation trials the rotation angle could not be predicted prior to movement, requiring subjects to adapt online within a single trial in order to achieve the task. In the second group (target jump group, 9 subjects) the first block of 2000 trials were target jump transformations where the target jumped unpredictably to a rotated position (rotation angles drawn randomly again from a uniform distribution over {±30°, ±50°, ±70°, ±90°}). In target jump trials the jump occurred when then hand had moved 2cm away from the origin. In the second block of 2000 trials the target jump group also experienced random rotations just like the first group. Thus, all subjects performed 4,000 trials in total. We analyzed the first 2000 trials to assess how performance changed as subjects learned to adapt to the task requirements. Performance was assessed as the minimum distance to the target within the 2 second trial period, the magnitude of the second velocity peak and movement variability. To calculate movement variability each two-dimensional positional trajectory was temporally aligned to the speed threshold of 10cm/s and then the variance of the x and y positions were calculated for each time point across the trajectories and subjects (time 0s corresponds to 200ms before the speed threshold). The total variance was taken as the sum of the variance in x position and y position and the square-root of the variance (standard deviation) was plotted. The last 2000 trials of the first group were used for fitting subjects' stationary patterns of adaptation to an optimal adaptive control model.

Adaptive Optimal Control Model

To model adaptation and control we used a linear model of the hand/cursor system and a quadratic cost function to quantify performance (Kording and Wolpert, 2004). Full details of the simulations are provided in the Supplementary Methods. As we include the effects of signal-dependent noise on the motor commands (Harris and Wolpert, 1998) the resulting optimal control model belongs to a class of modified linear quadratic-Gaussian systems (Todorov and Jordan, 2002). The equations we used are:

$$\begin{array}{cc}\hfill & \text{State update}{\mathbf{x}}_{t+1}=F\left[\varphi \right]{\mathbf{x}}_t+G{\mathbf{u}}_t+\text{signal-dependent noise}\hfill \\ \hfill & \text{observation}{\mathbf{y}}_t=H{\mathbf{x}}_t+\text{additive noise}\hfill \end{array}$$

The state x_t represents the state of the hand/cursor system (a point mass model) and the observation y_t represents the delayed sensory feedback to the controller. The state update equation depends on the current state (first term), the current motor command (second term) and signal dependent noise (details in Supplementary Methods). The observation equation relates the sensory feedback to the current state x_t and the additive observation noise. The important novelty here is that the forward model of the system dynamics F depends in a nonlinear way on the rotation parameter φ between the hand and cursor position. This parameter is unknown to subjects before each trial and must be estimated online during each movement.

The hand was modeled as a planar point-mass (m = 1kg) with position and velocity vectors given by ${\mathbf{p}}_t^H$ and v_t respectively. The cursor position is given by a rotation of the hand position ${\mathbf{p}}_t^C=D_{\varphi }{\mathbf{p}}_t^H$, where D_φ is the rotation matrix for a rotation of angle φ. The two-dimensional control signal u_t is transformed sequentially through two muscle-like low-pass filters both with time-constants of 40 ms to produce a force vector f_t on the hand (with g_t representing the output of the first filter)—see (Todorov, 2005) and Supplementary Material for details. Thus, the 10-dimensional state vector can be expressed as where p^TARGET corresponds to the target position in cursor space. Sensory feedback y_t is given as a noisy observation of the cursor position, hand velocity and force vector with a feedback delay of 150ms. In our results section we also compute the angular momentum as the cross product ${\mathbf{p}}_t^H\times {\mathbf{v}}_t$ multiplied by the point-mass m = 1kg.

The cost function J can be expressed as follows

$$\text{Cost}J=\frac{1}{2}E\left[\underset{t=0}{\overset{\infty }{\Sigma }}\left\{{\mathbf{x}}_t^{T}Q{\mathbf{x}}_t+{\mathbf{u}}_t^{T}R{\mathbf{u}}_t\right\}\right]$$

The matrix Q is designed to punish positional error between cursor and target and high velocities and is parameterized accordingly with two scalar parameters w_p and w_v. The matrix R punishes excessive control signals and was taken as the identity matrix scaled by a parameter r. Since the absolute value of the cost J does not matter for determining the optimal control, i.e. only the ratio between Q and R is important, we set w_p = 1. We chose a cost function without a fixed movement time (i.e. an infinite horizon cost function) so the amount of time required for adaptation to reach the target might vary. Such a cost function allows computing the state-dependent optimal policy at each point in time considering the most recent estimate of φ. Since the trial duration was relatively long (2s) this cost function allowed reasonable fits to the data.

The optimal policy of the above control problem is the feedback rule that minimizes the cost function J. Since the parameter φ is unknown, this adaptive optimal control problem can only be solved approximately by decomposing it into an estimation problem and a control problem (certainty-equivalence principle). The estimation problem consists of simultaneously estimating the unobserved state x_t and the unknown parameter φ from the observations y_t. This can be achieved by introducing an augmented state x̃_t = [x_t; φ_t] and using a nonlinear filtering method (e.g. Unscented Kalman filter) for the estimation ${\widehat{\tilde{\mathbf{x}}}}_t=[{\widehat{\mathbf{x}}}_t;{\widehat{\varphi }}_t]$ in this augmented state space—see Supplementary material for details. In order to allow the controller to adapt its estimate of φ we model the parameter as a random walk with covariance Ω_v which determines the rate of adaptation within a trial. The optimal control command at every time point can then be computed as a feedback control law u_t = −L[φ̂_t]x̂_t, where L[φ̂_t] is the optimal feedback gain for a given parameter estimate φ̂_t. To allow for the uncertainty of the parameter estimate to affect the control process (non certainty –equivalence effects) we introduce two additional cautiousness parameters λ_p and λ_v. Based on the models uncertainty in the rotation parameter φ, these reduce the gains of the position and velocity components of the feedback thereby slowing down the controller in the face of high uncertainty (equivalent to making the energy component of the cost more important). Importantly, the cautiousness parameters do not introduce a new optimality criterion; rather it provides a heuristic to find an approximation to the optimal solution and is often used in adaptive control theory when faced with an analytically intractable optimal control problem (see Supplementary Material). Accordingly, the costs achieved by a cautious adaptive controller can be lower than by a non-cautious adaptive controller—see Supplementary Material for details.

Parameter Fit

Some of the parameters of the model were taken from the literature as indicated above. There were six free scalar parameters that were fit to the data and these are (i) the cost parameters w_v and r, (ii) the cautiousness parameters λ_p and λ_v, (iii) the adaptation rate Ω_v and (iv) the signal-dependent noise level. We adjusted these parameters to fit the mean trajectory of the 90°-rotation trials (by collapsing the + and −90° trials into one angle). These parameter settings were then used to extrapolate behavior to both the standard trials and all other rotation trials. The reason we chose 90° is that the perturbation has the strongest effect here and therefore the fit would have the best signal-to-noise ratio to allow us to get the most precise estimates of the parameters. Thus, the issue of over-fitting is avoided as the model predictions are evaluated for non-fitted conditions. The fit was to the 2^nd 2000 trials when subjects of the rotation group exhibited stationary responses to the visuomotor rotations. Details of the parameter fits can be found in the Supplementary Material.

Results

To test the hypothesis that the motor system can learn to adapt optimally to specific classes of environments we exposed a first group of participants to a reaching task in which on 20% of the trials a random visuomotor rotation was introduced. Since these random rotations could not be predicted (and were zero-mean across all rotations), participants had to adapt to the perturbations online during the movement. This online adaptation is different from online error correction (Diedrichsen et al., 2005), since the rules of the control process—i.e. the ‘control policy’ that maps sensory inputs to motor outputs—has to be modified. Importantly, the modification of the control law is a learning process, whereas online error correction, e.g. to compensate for a target jump, can take place under the same policy without learning a new controller. To enforce online adaptation the vast majority of trials had a standard hand/cursor relationship and only occasional trials were perturbed. Thus, movements typically started out in a straight line to the cursor target because subjects assumed by default a standard mapping between hand and cursor — see Figure 1A. However, after a time delay of 100-200ms into the movement subjects noticed the mismatch between hand and cursor position in random rotation trials and started to modify their movements. This adaptive part of the movement can be seen from the change of direction in the trajectory and the appearance of a second peak in the speed profile (Fig. 1B).

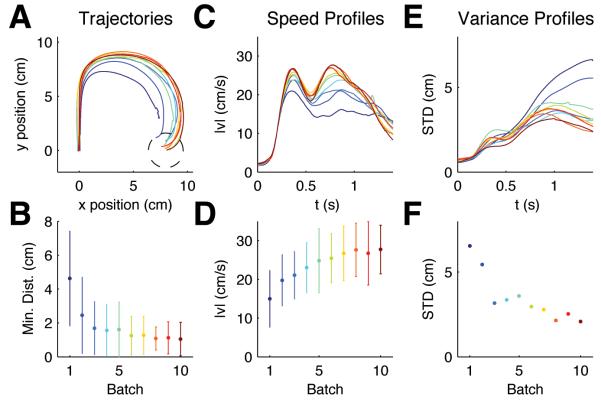
Figure 1.

Evolution of within-trial adaptive behavior for random rotation trials. (A) Mean hand trajectories for ±90° rotation trials in the first 10 batches averaged over trials and subjects (each batch consisted of 200 trials, approximately 5% of which were ±90° rotation trials). The −90° rotation trials have been mirrored about the y axis to allow averaging. Dark blue colors indicate early batches, green colors intermediate batches, red colors indicate later batches. (B) The minimum distance to the target averaged for the same trials as A (error bars indicate standard deviation over all trajectories and all subjects). This shows that subjects' performance improves over batches. (C) Mean speed profiles for ±90° rotations of the same batches. In early batches, movements are comparatively slow and online adaptation is reflected in a second peak of the speed profile which is initially noisy and unstructured. (D) The magnitude of the second peak increases over batches (same format as B). (E) Standard deviation profiles for ±90° rotation trajectories computed for each trial batch. (F) Standard deviation of the last 500ms of movement. Over consecutive batches the variability is reduced in the second part of the movement.

To assess our hypothesis of task-optimal adaptation we first investigated whether subjects showed any kind of improvement in adapting to the unpredictable perturbations during the movements. Indeed, we found that the adaptation patterns in random rotation trials were very different in early trials compared to the same rotations performed later in the experiment (Fig. 1D-F). In the beginning, large movement errors occurred more frequently, i.e. subjects often did not manage to reach the target precisely within the prescribed 2s time window (Fig. 1D). The difference in the minimum distance to the target within this allowable time window between the first and last batch of 200 trials was significant (p<0.01, Wilcoxon ranksum test). In early trials the second peak of the speed profile was barely visible as movements were relatively unstructured and cautious, but in later trials a clear second speed peak emerged (Fig. 1B). Early trials also showed high variability in the second part of the movement, whereas in later trials adaptive movements were less variable and therefore more reproducible between subjects (Fig. 1F) – the variability in the last 500ms of the movement in the first batch was significantly larger than in the last batch (p<0.01, F-test). The color code in Figure 1A-C indicates that the second part of the movement converged to a stereotyped adaptive response. To test for the possibility that subjects simply became non-specifically better at feedback control, a second group of participants performed a target jump task for the first 2000 trials. In direct correspondence to the random rotation task 20% of the trials were random target jump trials. Since a target jump does not require learning a new policy but simply an update of the target position in the current control law, we would expect to see no major learning processes in this task. This is indeed what we found. In Fig. 2 we show the same features that we evaluated in the random rotation trials to assess over-trial evolution of sensorimotor response patterns (Fig. 2A-E).

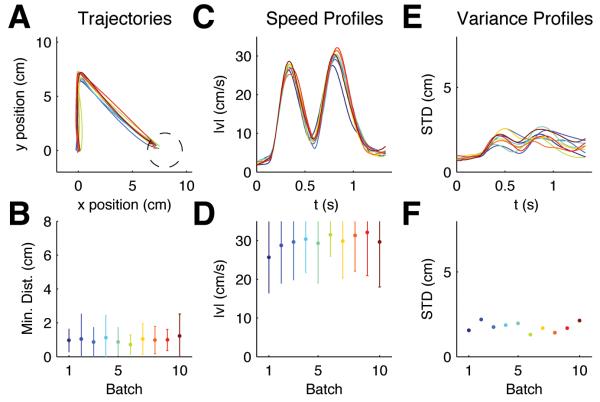
Figure 2.

Evolution of motor responses to random target jumps. (A) Mean trajectories for ±90° target jumps over batches of 200 trials, approximately 5% of which were ±90° target jump trials. Dark blue colors indicate early batches, red colors indicate later batches. (B) The lower panel shows that subjects' performance did not significantly improve over trials. Error bars indicate standard deviation over all trials and subjects. (C) Mean speed profiles for ±90° target jumps of the same trial batches. A second velocity peak is present right from the start. (D) The lower panel shows the evolution of the magnitude of the second speed peak. (E) Standard deviation for ±90° target jumps computed over the same trial batches. Over consecutive batches the variance remains constant. (F) Standard deviation over the last 500ms of movement.

To test whether the change in behavior over trials might represent an improvement—in the sense of minimizing a cost function—we computed the costs of the experimentally observed trajectories for 90° rotations. We used the inverse system equations to reverse-engineer the state space vector x_t and the control command u_t from the experimental trajectories. We then used a quadratic cost function that successfully captured standard movements and computed the costs of all the trajectories of the experiment. We found that the cost of the trajectories with regard to the quadratic cost function decreased over trials (Fig. 3A). This shows that the observed change in adaptation can be understood as a cost-optimization process. In contrast to the first group, the second group showed no trend that would indicate learning – there is no significant difference between the minimum distance to the target between the first and the last batch (p>0.01, Wilcoxon ranksum test). The reverse-engineered cost function for the 90° target jumps was flat over trial batches (Fig. 3B).

Figure 3.

Left Panel: Rotation Group. Relative cost of subjects' movements in response to ±90° visuomotor rotations. Over trial batches (200 trials) the cost of the adaptive strategy decreases. Right Panel: Target Jump Group. Relative cost of subjects' movements in response to ±90° target jumps. There is no improvement over trials. In both cases the costs have been computed by calculating the control command and the state space vectors from the experimental trajectories by assuming a quadratic cost function. The cost has been normalized to the average cost of the last three trial batches.

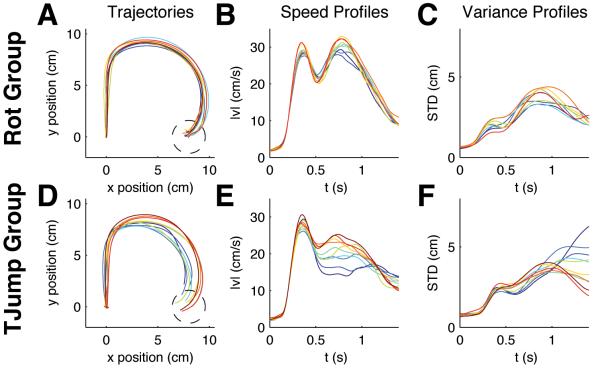
After the first block of target jump trials, the second group experienced a second block of random rotation trials identical to the second block the first group experienced. If the first group learned a feedback control policy specifically for rotations in the first block of trials then both groups should perform very differently in the second block of trials where both groups experienced random rotation trials. Again this hypothesis was confirmed by our results. The first group that was acquainted with rotations showed a stationary response to unexpected rotations (Fig. 4A-C). Performance error, speed profiles and standard deviation showed no changes over trials (Fig. 5A-C). Thus, there was no significant difference between the minimum distance to the target between the first and the last trial batches (p>0.01, Wilcoxon ranksum test). In contrast the second group initially performed not better than naïve subjects; i.e. their performance was the same as the performance of the rotation group in the beginning of the first block (Fig. 4D-E). Then, over the first few trial batches this group substantially improved (Fig. 5D-E) and the difference in minimum target distance between the first batch and the last are highly significant (p<0.01, Wilcoxon ranksum test). Therefore, the experience of unpredictable target jumps did not allow for learning an adaptive control policy that is optimized for unpredictable visuomotor rotations.

Figure 4.

Evolution of within-trial adaptation and control for ±90° random rotations in the second block of 2000 trials. (A) Movement trajectories averaged over batches of 200 trials for the group that had experienced unexpected rotation trials already in the previous 2000 trials. Dark blue colors indicate early batches, red colors indicate later batches. This group shows no improvement. (B) Speed profiles of the same trial batches. (C) Standard deviation in the same trials. There is no trend over consecutive batches. (D) Average movement trajectories averaged over batches of 200 trials for the group that had experienced unexpected target jump trials in the previous 2000 trials. This group shows learning. (E) Speed profiles of the target jump group. (F) Standard deviation in the same trials. The movement characteristics change over consecutive batches.

Figure 5.

Evolution of within-trial adaptive control for random rotations in the second block of 2000 trials. (A) Minimum distance to target in ±90° rotation trials averaged over batches of 200 trials for the group that had experienced unexpected rotation trials already in the previous 2000 trials. This group shows no improvement. Error bars show standard deviation over all trials and subjects. (B) Mean magnitude of the second velocity peak over batches of 200 trials for the rotation group. (C) Standard deviation in the last 500ms of movement for ±90° rotations computed over the same trial batches for the rotation group. There is no trend over consecutive batches. (D) Minimum distance to target in ±90° rotation trials averaged over batches of 200 trials for the group that had experienced unexpected target jump trials in the previous 2000 trials. This group shows a clear improvement. (E) Mean magnitude of the second velocity peak over batches of 200 trials for the target jump group. (F) Standard deviation in the last 500ms of movement for ±90° rotations computed over the same trial batches for the target jump group. The standard deviation clearly decreases over consecutive batches.

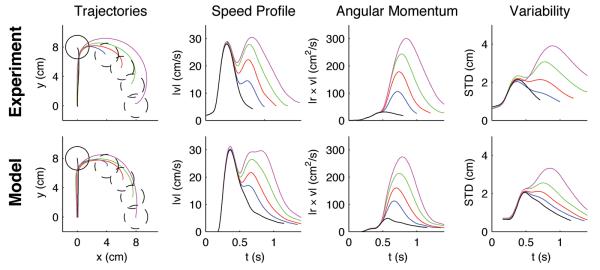
Finally, we investigated whether the stationary adaptation patterns observed in later trials of the first group could be explained by an adaptive optimal feedback controller that takes the task-specific parameters of a visuomotor rotation explicitly into account. Importantly, a non-adaptive controller that ignores the rotation becomes quickly unstable (Fig. S4). The adaptive optimal controller has to estimate simultaneously the arm and cursor states as well as the hidden ‘visuomotor rotation’-parameter online (see Methods). This results in the online estimation of the forward model for the visuomotor transformation. The estimated forward model, in turn, together with the estimated cursor and hand state can be used to compute the optimal control command at every point in time. At the beginning of each trial the forward model estimate of the adaptive controller is initialized to match a standard hand-cursor mapping without a visuomotor rotation (representing the prior, the average of all rotations). Due to feedback delays, any mismatch between actual and expected cursor position can only be detected by the adaptive controller some time into the movement. The observed mismatch can then be used both for the adaptation of the state and parameter estimates and for improved control (supplementary figure S3). To test this model quantitatively, we adjusted the parameters of the model to fit the mean trajectory and variance of the 90°-rotation trials and used this parameter set to predict behavior on both the standard and other rotation trials. In the absence of the ‘cautiousness’ parameters which slow down control in the presence of uncertainty about the rotation parameter, the predictions gave hand speeds that were higher than those in our experimental data (Supplementary Figure S5). In the presence of the ‘cautiousness’ parameters not only was the cost of the controller lower, but we also found that the adaptive optimal control model predicted the main characteristics of the paths, speed and angular momentum as well as the trial-to-trial variability of movements with high reliability (Fig. 6)—the predictions yielded r² > 0.83 for all kinematic variables. Both model and experimental trajectories first move straight towards the target and then show adaptive movement corrections after the feedback delay time elapsed. Both model and experiment show a characteristic second peak in the velocity profile, and the model predicts this peak correctly for all rotation angles. Also the trial-by-trial variability is correctly predicted for the different rotations.

Figure 6.

Predictions of the adaptive optimal control model compared to movement data. Averaged experimental hand trajectories (left column), speed profiles (second column), angular momentum (third column) and trajectory variability (right column) for standard trials (black) and rotation trials (±30° (blue), ±50° (red), ±70° (green), ±90° (magenta)). The second peak in the speed profile and the magnitude of the angular momentum (assuming m=1kg) reflect the corrective movement of the subjects. Higher rotation angles are associated with higher variability in the movement trajectories in the second part of the movement. The variability was computed over trials and subjects. The trajectories for all eight targets have been rotated to the same standard target and averaged, since model predictions were isotropic. The model consistently reproduces the characteristic features of the experimental curves.

Discussion

Our results provide evidence that the motor system converges to task-specific stereotypical adaptive responses in unpredictable motor tasks that require simultaneous adaptation and control. Moreover, we show that such adaptive responses can be explained by adaptive optimal feedback control strategies. Thus, our results provide evidence that the motor system is not only capable of learning non-adaptive optimal control policies (Todorov and Jordan, 2002; Diedrichsen, 2007) but also of learning optimal simultaneous adaptation and control. This shows that the learning process of finding an optimal adaptive strategy can be understood as an optimization process with regard to similar cost criteria as proposed in non-adaptive control tasks (Kording and Wolpert, 2004).

Previous studies have shown that optimal feedback control successfully predicts behavior of subjects that have uncertainty about their environment (e.g. a force-field) that changes randomly from trial-to-trial (Izawa et al., 2008). However, in these experiments subjects did not have the opportunity to adapt efficiently to the perturbation within single-trials. Rather the perturbation was modeled as noise or uncertainty with regard to the internal model. In our experiments subjects also have uncertainty over the internal model, but they have enough time to resolve this uncertainty within the trial and adapt their control policy accordingly. Another recent study (Chen-Harris et al., 2008) has shown that optimal feedback control can be successfully combined with models of motor learning (Donchin et al., 2003; Smith et al., 2006) to understand learning of internal models over the course of many trials. Here we show that learning and control can be understood by optimal control principles within individual trials.

Optimal within-trial adaptation of the control policy during a movement presupposes knowledge of a rotation-specific internal model x_t+1 = F(x_t, u_t, a), where a denotes the system parameters the motor system is uncertain about (i.e. a rotation-specific parameter). This raises the question of how the nervous system could learn that a is the relevant parameter and that F depends on a in a specific way. In adaptive control theory this is known as the structural learning problem (Sastry and Bodson, 1989; Åström and Wittenmark, 1995) as opposed to the parametric learning problem of estimating a given knowledge of F(*, a). In our experiments subjects in the rotation group have a chance to learn the structure of the adaptive control problem (i.e. visuomotor rotations with a varying rotation angle) in the first 2000 trials of the experiment in which they experience random rotations. As previously shown (Braun et al., 2009), such random exposure is apt to induce structural learning and can lead to differential adaptive behavior. Here we explicitly investigate the evolution of structural learning for the online adaptation to visuomotor rotations (Fig. 1) and, based on an optimal adaptive feedback control scheme, show that this learning can be indeed understood as an improvement (Fig. 3) leading to optimal adaptive control strategies. It should be noted, however, that learning the rotation structure does not necessarily imply that the brain is learning to adapt literally a single neural parameter, but that exploration for online adaptation should be constrained by structural knowledge leading to more stereotype adaptive behavior. In the latter 2000 trials, when subjects know how to adapt efficiently to rotations, their behavior can be described by a parametric adaptive optimal feedback controller that exploits knowledge of the specific rotation structure.

In the literature there has been an ongoing debate whether corrective movements and multiple velocity peaks indicate discretely initiated sub-movements (Lee et al., 1997; Fishbach et al., 2007) or whether multimodal velocity profiles are the natural outcome of a continuous control process interacting with the environment (Kawato, 1992; Bhushan and Shadmehr, 1999). Our model predictions are consistent with the second view. Although corrective movements in our experiments are certainly induced by unexpected perturbations, the appearance of corrections and multimodal velocity profiles can be explained by a continuous process of adaptive optimal control.

As already described, online adaptation should not to be confused with online error correction (Diedrichsen et al., 2005). Online correction is, for example, required in the case of an unpredicted target jump. Under this condition the same controller can be used, i.e. the mapping from sensory input to motor output is unaltered. However, unexpectedly changing the hand-cursor relation (e.g. by a visuomotor rotation) requires the computation of adaptive control policies. This becomes intuitively apparent in the degenerate case of 180° rotations, as any correction of a naïve controller leads to the opposite of its intended effect. However, it should be noted that the distinction between adaptation and error correction can be blurry in many cases. Strictly speaking, an adaptive control problem is a nonlinear control problem with a hyper-state containing state variables and (unknown) parameters. This means in principle no extra theory of adaptive control is required. In practice, however, there is a well-established theory of adaptive control (Sastry and Bodson, 1989; Åström and Wittenmark, 1995) that is built on the (somewhat artificial) distinction between state variables and (unknown) parameters. The two quantities are typically distinct in their properties. In general, the state, for example the position and velocity of the hand, changes rapidly and continuously within a movement. In contrast, other key quantities change discretely, like the identity of a manipulated object, or on a slower time-scale, like the mass of the limb. We refer to such discrete or slowly changing quantities as the ‘parameters’ of the movement. Therefore, state variables change on a much faster time scale than system parameters and the latter need to be estimated to allow for control of the state variables. This is exactly the case in our experiments where the parameters (rotation angle) change slowly and discretely from trial-to-trial, but the state variables (hand position, velocity, etc.) change continuously over time (within a trial). Thus, estimating uncertain parameters can subserve continuous control in an adaptive fashion. In summary, our results suggest that the motor system can learn optimal adaptive control strategies to cope with specific uncertain environments.