Fluorescence Correlation Spectroscopy Close to a Fluctuating Membrane

Abstract

Compartmentalization of the cytoplasm by membranes should have a strong influence on the diffusion of macromolecules inside a cell, and we have studied how this could be reflected in fluorescence correlation spectroscopy (FCS) experiments. We derived the autocorrelation function measured by FCS for fluorescent particles diffusing close to a soft membrane, and show it to be the sum of two contributions: short timescale correlations come from the diffusion of the particles (differing from free diffusion because of the presence of an obstacle), whereas long timescale correlations arise from fluctuations of the membrane itself (which create intensity fluctuations by modulating the number of detected particles). In the case of thermal fluctuations this second type of correlation depends on the elasticity of the membrane. To illustrate this calculation, we report the results of FCS experiments carried out close to a vesicle membrane. The measured autocorrelation functions display very distinctly the two expected contributions, and allow both to recover the diffusion coefficient of the fluorophore and to characterize the membrane fluctuations in term of a bending rigidity. Our results show that FCS measurements inside cells can lead to erroneous values of the diffusion coefficient if the influence of membranes is not recognized.

INTRODUCTION

Fluorescence correlation spectroscopy (FCS) is a method allowing the study of the dynamics of phenomena involving fluctuations in the fluorescence signal collected from a confocal detection volume. The principle is to compute the autocorrelation function of this signal: each process leading to a variation in fluorescence at a particular timescale will be reflected in the autocorrelation function at the same timescale. FCS was originally introduced to observe chemical reactions in solution (Magde et al., 1972), but many other processes can be studied. The simplest is the free diffusion of fluorescent particles (Aragón and Pecora, 1976; Rigler et al., 1993), where FCS allows retrieving both their diffusion coefficient and their concentration. Rotational diffusion (Ehrenberg and Rigler, 1974; Kask et al., 1987), residence of the fluorophore in a triplet state (Widengren et al., 1995), directed motion (Köhler et al., 2000), and photobleaching (Widengren and Rigler, 1997), among other phenomenon, can also be observed (see e.g., Thompson, 1991, or Webb, 2001 for reviews).

The dimensions of the confocal detection volume can typically be smaller than giving submicron spatial resolution in the two lateral directions, and corresponding to a volume of <1 fl, to be compared with the typical length (≃ 10 μm), and volume (≃ 1 pl) of a cell. The photomultipliers or avalanche photodiodes used for FCS experiments can detect single fluorophores with CW excitation intensities of the order of 10 μW/μm², levels supposed to be nondamaging for most biological systems. Used in its single-molecule range of application (i.e., with an average of less than one molecule in the detection volume), FCS allows working with concentrations as low as 1 nM. The time resolution of the correlators used to calculate the autocorrelation function in real time can be as low as 10 ns. For all these reasons, there is a very strong interest in applying FCS to biological systems (Berland et al., 1995; Brock et al., 1998; Politz et al., 1998; Schwille et al., 1999; Wachsmuth et al., 2000; Gennerich and Schild, 2000; Cluzel et al., 2000; Dittrich et al., 2001; Nomura et al., 2001).

However, when examining the specific issue of the diffusion of macromolecules inside cells, one invariably observes long time correlations in the autocorrelation function, and faces the difficulty to identify the cause. Anomalous diffusion, on one hand, or slowing down of one part of the fluorophore population, on the other, perhaps by nonspecific binding or compartmentalization, have been proposed as interpretations (Wachsmuth et al., 2000). The cellular medium being crowded by large-scale objects such as lipid membranes (for example the cellular membrane, the endoplasmic reticulum, and the nuclear membrane), mitochondria, or cytoskeleton, it is somewhat obvious that these will influence macromolecular diffusion nearby (see e.g., Zimmerman and Minton, 1993), and hence that their effect should be taken into account when analyzing FCS measurements inside cells. Nevertheless, this complex problem has received limited attention so far. Calculations have been made for diffusion between two rigid membranes in the case of regular FCS experiments (Gennerich and Schild, 2000), and for diffusion and binding close to a single rigid membrane in the case of a nonstandard geometry (FCS used with total internal reflection) (Starr and Thompson, 2001), showing that the restriction of diffusion in one dimension has a strong effect on the residence time measured by FCS, and hence on the extracted diffusion coefficient if this effect is not accounted for. We consider in this paper the case of diffusion close to a single soft membrane (able to undergo fluctuations such as thermal fluctuations) studied by standard FCS. This case will be relevant to most FCS experiments in biological systems, inasmuch as they are usually bounded by soft lipidic membranes, but most particularly to studies of phenomena occurring close to the cellular or nuclear membranes.

MATERIALS AND METHODS

Fluorescence correlation spectroscopy

Set-up

The home-built FCS set-up used for the experiments is a classical one, as described for example in Thompson (1991), based on a modified upright microscope equipped with differential interference contrast imaging. Fluorescence is excited by a CW HeNe laser (1674P, JDS Uniphase, San Jose, CA, USA), whose 543.5-nm wavelength is selected by an excitation filter (HQ545/30, Chroma Technology, Brattleboro, VT, USA). The beam passes through a beam expander, which allows spatially filtering it by placing a 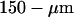pinhole at the focus (to keep only the fundamental Gaussian mode of the laser), and to increase its 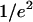waist to a value of 2.8 mm before entering the 6-mm back aperture of a 100× oil objective (Achrostigmat 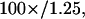Zeiss, Göttingen, Germany), resulting in a theoretical halfwidth of the focal volume of 300 nm (Rigler et al., 1993). The output power of the laser is attenuated by a system of two polarizers to obtain a radiant exposure of order 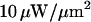at the focus. The exact intensity is monitored by an amplified silicon detector (PDA55, Thorlabs, Newton, NJ, USA) measuring the excitation intensity transmitted by the dichroic mirror, which amounts to 10.4% of the actual intensity arriving on the sample. The emitted fluorescence is filtered by an emission filter (HQ610/75, Chroma Technology), focused through a 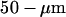diameter pinhole (hence theoretically giving a confocal detection volume with a 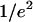radius of 250 nm, and a half-height of 825 nm (Rigler et al., 1993)), and then detected by a photon counting head (H7421, Hamamatsu Photonics, Shimokanzo, Japan). The output signal is fed into a correlator (Flex99R-12D, Correlator.com, Bridgewater, NJ, USA). The measurement durations for curves (presented in the section FCS measurements near a vesicle membrane) were either 30 s or 60 s. The vertical position of the objective and horizontal position of the sample in one direction can be adjusted by means of home-built piezoelectric-driven objective and sample holder. Monitoring of the objective height and of the sample position is achieved using a multifunctional input/output board (PCI-1200, National Instruments, Austin, TX, USA) and a program written for LabView (Labview 5.1, National Instruments). Analyses of the measured autocorrelation functions were performed with a program using the NonlinearRegress function of Mathematica (Mathematica 4.0, Wolfram Research, Champaign, IL, USA).

Autocorrelation function

The normalized autocorrelation function of a signal I(t) fluctuating around its mean value 〈I(t)〉 is (adopting the convention that the deviation of any quantity X from its mean value 〈X〉 will be noted δX):

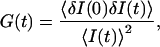(1)

where all averages are taken over time and stationarity of the system has been assumed.

In the simple case of one single fluorophore freely diffusing in solution (with a diffusion constant D), an analytical expression of this autocorrelation function can be derived by assuming the intensity profile of the detection volume to be Gaussian (Aragón and Pecora, 1976). This assumption is justified when the laser beam is spatially filtered and underfills the back aperture of the objective. The detectable emission intensity is then written:

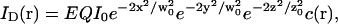(2)

where w₀ and z₀ are the radius of the 1/e² contour in, respectively, the radial and axial directions (cf. Fig. 1); Q is the quantum efficiency of the fluorophore and c(r) its concentration; E is the collection efficiency of the optical system; and I₀ the maximum laser intensity in the focal plane.

FIGURE 1.

Geometry of the considered system. Fluorescent molecules are represented by spheres. Dark gray spheres correspond to molecules in the detection volume, whose fluorescence will be detected by the optical system. The membrane separates space into a region (x<〈W〉) containing fluorophores with an average concentration 〈c〉, and a region (x>〈W〉) containing no fluorophores.

In the case where the average concentration of the fluorophore is constant over space, and considering a total background intensity I_B(t), one has:

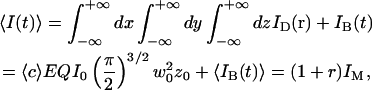(3)

writing 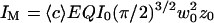and introducing the ratio .

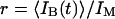Assuming that the background intensity is not correlated in time and that the system is stationary (which ensures that ):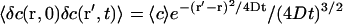

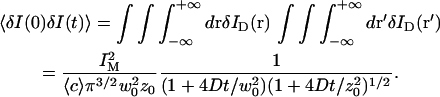(4)

The autocorrelation function is then given by the classical expression (Aragón and Pecora, 1976):

(5)

where 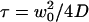would be the average residence time of a fluorophore in an infinite cylinder of radius 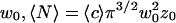is the average number of fluorophores in the effective volume 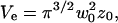and 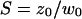is the aspect ratio of the detection volume. At long time this leads to the scaling 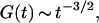the probability for a random walking particle in three dimensions to return to the origin.

In practice, one also has to take into account the fact that a fraction T of the fluorophores is in a nonfluorescent triplet state with an average half-life time τ_T, which adds a supplementary contribution to the autocorrelation function (Palmer and Thompson, 1987; Widengren et al., 1995). Finally, the autocorrelation function obtained from the simple free diffusion of a single fluorophore in an infinite solution is correctly described by:

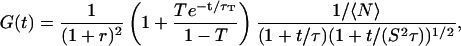(6)

If the diffusion is obstructed by the presence of obstacles in the solution, it was proposed that this could in some cases be accounted for by considering a mean-square displacement of the particles 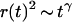(Bunde and Havlin, 1995; Saxton, 1994) where the exponent 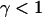characterizes the anomalous diffusion. If the diffusion coefficient 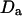of the particles undergoing anomalous diffusion is defined by 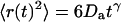(which can be seen alternatively as having a time-dependent diffusion coefficient 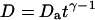), the autocorrelation function (easily obtained by replacing Dt by 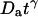in Eq. 6) reads:

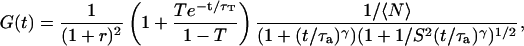(7)

where the quantity τ_a is again the average residence time of a particle in an infinite cylinder of radius w₀, only this time it is given by 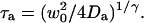The anomalous-diffusion coefficient D_a is in units of m²/s^γ.

Calibration

The set-up was calibrated each time experiments were carried out by fitting the autocorrelation function obtained from the free diffusion of Rhodamine 610 (Exciton Chemical, Dayton, OH, USA) in water with Eq. 6, and assuming D = 280 μm²/s (Rigler et al., 1993). Values obtained for the experiments presented here were τ = 47 μs and S = 8, giving for the half-waists of the detection volume w₀ = 230 nm and z₀ = 1.8 μm. The effective volume is then V_e = 0.53 fl.

Vesicle preparation

DOPC (1,2-Di[cis-9-octadecenoyl]-sn-glycero-3-phosphocholine, also known as diC18:1c9, purchased from Avanti Polar Lipids, Alabaster, AL) vesicles were prepared either by gentle hydration (Needham and Evans, 1988) or by electroswelling (Angelova et al., 1992) (the latter method yields a higher proportion of unilamellar vesicles). For gentle hydration, ∼50 μl of DOPC dissolved in chloroform (4 mg/ml) was dried on a roughened Teflon plate, after which 5 ml of a 0.1 M Pipes buffer (pH = 7.4) supplemented with 0.2 M glucose was added, and vesicles were grown overnight at 37°C. For electroswelling, the same quantity of the DOPC solution was dried on an Indium Tin Oxide glass plate, and closed by another Indium Tin Oxide plate separated by neoprene spacers. The 1 ml enclosed volume was then filled with 0.1 M sucrose solution. An alternating electric potential was applied, 1 V peak-to-peak amplitude, 10 Hz for 2 h, followed by 1 Hz for 1 h. After 2-h annealing, the vesicle-containing solution was harvested gently. Before experiments, a stock of vesicles was mixed with an equal volume of a 10% hypertonic glucose solution (instead of sucrose), and with a concentration of fluorescent material (either streptavidin labeled with Cy3 dye, purchased from Amersham, [Buckinghampshire England] or tetramethyl rhodamine-labeled 10-kDa dextran, purchased from Molecular Probes, Eugene, OR) at double the desired final concentration. This ensured that the vesicles, filled with a less dense medium, would float upward and fix themselves on the upper coverslip of the sample, making their observation in our upright microscope easier, and allowing to carry out all the FCS experiments within 20 μm of the upper coverslip. Also this way a compartmentalization was created between the inside of the vesicles, void of fluorophore, and the outside of the vesicles, containing fluorophores.

DERIVATION OF THE AUTOCORRELATION FUNCTION IN PRESENCE OF A FLUCTUATING MEMBRANE

General expression in presence of a vertical fluctuating membrane

We first consider a planar membrane separating space into a region void of fluorophore and a region with an average fluorophore concentration 〈c〉 constant over space, and call W(t) the position of this membrane relative to the center of the detection volume (see Fig. 1). We will assume the membrane to be vertical and perpendicular to the x axis (as shown in Fig. 1) in all the following derivations, and indicate how the results are changed if the membrane is horizontal (perpendicular to the optical axis). We will suppose that the membrane position is varying with time around an average position 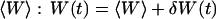(hence excluding from the calculation drifts in the position of the membrane). We will also assume that the membrane movements are slow enough compared to free diffusion of the fluorophores that we can decouple these two motions (adiabatic approximation). Finally we will neglect all interactions of the membrane with the strong electric field in the vicinity of the laser focus (Bar-Ziv et al., 1995), which should be justified for the very low laser intensities used in FCS experiments.

Average intensity as a function of the distance to the wall

As a fraction of the space enclosed by the detection volume may be devoid of fluorophores, the expression for the average intensity in the detector is different from the one derived in the classical case (Eq. 3), and now depends on the membrane position:

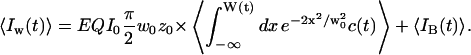(8)

Because a negligible coupling between the fluctuations in fluorophore concentration and the fluctuations in position of the membrane has been assumed, one can separate the averaging on c and δW, obtaining:

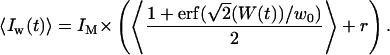(9)

The intrinsic width of the membrane (head-to-head distance between the polar heads of lipid molecules) is of the order of 5 nm for phospholipids (Rawicz et al., 2000), which is negligible compared to w₀. Although the roughness of the membrane contributes to the statistical width of the interface, we will consider the case where the amplitude of the membrane fluctuations remains small compared to w₀, which will be the case for membranes with sufficiently high bending rigidity. This hypothesis can be easily verified during experiments by checking that the amplitude of the intensity fluctuations are small compared to the difference in intensity between the inside and the outside of the vesicle. In this case the intensity profile is a simple error function:

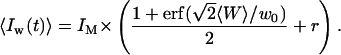(10)

Autocorrelation function

We have now:

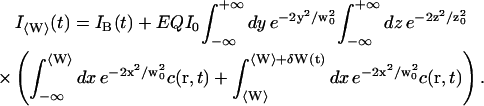(11)

Using again the fact that the statistical fluctuations of the interface should be small (δW ≪ w₀), and keeping only first order terms in δW and δc, we get:

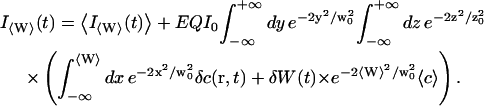(12)

Then, considering that the fluctuations of the wall and the movements of the fluorophores are not coupled, and that the background intensity is noncorrelated in time, we obtain:

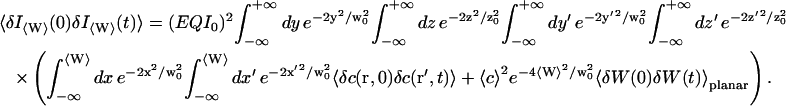(13)

The first term corresponds to the diffusion of the fluorophores in solution, modified by the presence of a flat vertical obstacle. It is exactly equal to the autocorrelation function that would be obtained if the obstacle were a fixed, rigid wall (δW(t) = 0). The second term reflects the influence of the position fluctuations of the obstacle, and has to be added in the case of a soft fluctuating membrane. By its motion, the membrane modulates the number of fluorophores that can be observed in the detection volume, causing fluctuations in the total detected intensity. The related correlations are not due to individual particle motions, as in the case of the first term, but to variations in the number of detected particles (where the diffusional fluctuations have already been averaged). The characteristic times of these correlations will then depend only on the characteristic times of the membrane fluctuations. The subscript of has been added to remind that this function has to be calculated for a membrane that is flat (no curvature and no roughness) at the scale of the detection volume. The total autocorrelation function then reads:

(14)

where the part corresponding to the modified diffusion of the fluorophore is (for the geometry depicted in Fig. 1):

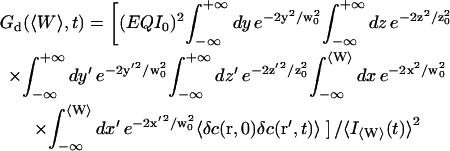(15)

and the part corresponding to the membrane fluctuations is:

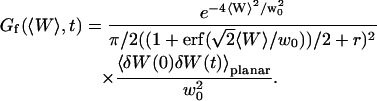(16)

Diffusion term

Derivation of the diffusion term under reflecting boundary conditions

In this section, we calculate 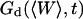from Eq. 15 assuming that the particles are reflected by the membrane. This is equivalent to assuming that the fluorophores do not interact at all with the membrane: they do not (even transiently) bind to it, nor do they diffuse across it. We can consider (Aragón and Pecora, 1976):

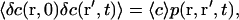(17)

where 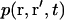is the probability to find a fluorophore in 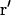at t if it was in r at t = 0.

In the presence of a membrane perpendicular to the x axis (placed in x = W), and assuming reflecting boundary conditions at the membrane surface, (our calculation can be readily adapted to absorbing boundary conditions if particles are adsorbed by the membrane, or semireflective boundary conditions if only part of the particles are reflected by the membrane by modifying Eq. 18 in consequence) this probability is given by:

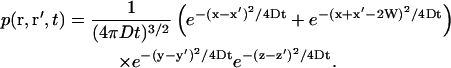(18)

By integration, and neglecting the time-dependent fluctuations in W (adiabatic approximation) in this term, we get:

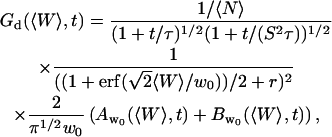(19)

with:

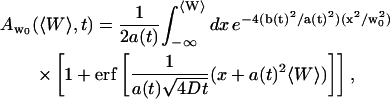(20)

and:

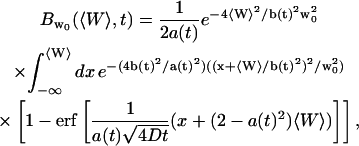(21)

using the notations:

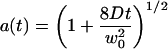(22)

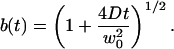(23)

In the particular cases when (wall infinitely remote) and 〈W〉 = 0 (wall in the center of the detection volume), it is straightforward to verify that Eq. 5 is retrieved: the autocorrelation function measured is the same as in the case of free diffusion.

Because 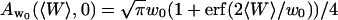and , the value of the autocorrelation function at t = 0 is given by:

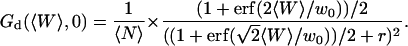(24)

In the case where the membrane is perpendicular to the optical axis (and at an average distance 〈Z〉 from the center of the detection volume), it is easy to show that Eq. 19 has to be replaced with:

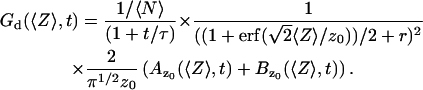(25)

Influence of a stationary membrane on G_d

Taken alone (without the fluctuation part G_f), Eq. 19 gives the exact expression for the autocorrelation function measured by FCS in presence of a fixed, rigid, and reflecting wall placed at x = 〈W〉. Autocorrelation functions calculated from this expression for different representative values of 〈W〉 are shown in Fig. 2 a. They illustrate the two different effects due to the presence of the wall: a change in the geometry of the detection volume, and a change in the diffusion pattern of the molecules.

FIGURE 2.

(a) Autocorrelation functions calculated for different values of 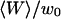, normalized by their values at t=0, as a function of t/τ, where 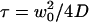is the free-diffusion residence time. The curves have been calculated for a typical value of the detection volume aspect ratio S = 6.4. For illustration, the characteristic residence time 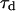, defined by 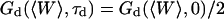, is indicated for one of the curves. (b) Value of the characteristic residence time 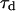as a function of (continuous thick line), compared with the values of the residence time estimated by fitting the autocorrelation functions calculated from Eq. 19 by a free-diffusion autocorrelation function (Eq. 6, continuous thin line) or by an anomalous-diffusion autocorrelation function (Eq. 7, dashed thin line). All curves have been normalized by the free-diffusion residence time 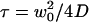. (c) Anomalous exponent γ obtained by fitting the autocorrelation functions calculated from Eq. 19 using an anomalous-diffusion model (Eq. 7). Note that for b and c, the x axis has been inverted, so that the plot is read from left to right as the detection volume approaches the membrane.

As the detection volume approaches and touches the wall, part of this volume becomes inaccessible to the fluorescent particles. Hence the average number of fluorophores in the detection volume decreases, leading to an increase in the relative fluorescence fluctuations, and hence to an increase in the value of G_d(〈W〉,0) (Eq. 24). This is balanced by the existence of a nonzero noise level (r ≠ 0), which prevents the divergence of G_d(〈W〉,0) as 〈W〉 goes to −∞. (Effects of the membrane on the amplitude of G_d will be discussed in more details in the section on Relative amplitudes of the fluctuation and diffusion terms, and a plot of G_d as a function of 〈W〉/w₀ can be found in Fig. 5 a). The reduction of the effective detection volume has consequences not only on the amplitude of the autocorrelation function, but also on the characteristic time over which it decays, which is closely related to the average residence time of a fluorescent particle in the detection volume. Because the size of the detection volume decreases, the time particles spend diffusing through the detection volume decreases as well.

FIGURE 5.

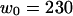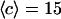(a) Amplitude of the two separate contributions (gray line: diffusion term, Eq. 24; black line: membrane fluctuations term, Eq. 33) and of the complete autocorrelation function (dashed line). The curves have been calculated for nm, , nM, 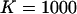k_BT, and 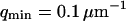. (b) Relative amplitude of the membrane fluctuation term 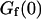to the diffusion term 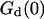, calculated for the same set of parameters as in a. Note that the x axis has been inverted as in Figs. 2 and 3.

The other factor, the change in the diffusion pattern of the molecules because of the presence of an obstacle, also influences the residence time of particles in the detection volume. If a particle is reflected by a close by membrane, it can immediately reenter the detection volume. This hence leads to an increase of the residence time of particles in the detection volume, and consequently to an increase of the characteristic decay time of G_d.

The characteristic decay time τ_d of the function G_d can be defined by 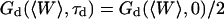(this definition is illustrated in Fig. 2 a for one of the autocorrelation functions). In the cases of either free or anomalous diffusion, and for an infinite aspect ratio S of the detection volume, we have, respectively, τ_d = τ or τ_d = τ_a, i.e., τ_d is rigorously equal to the average residence time of a particle in the detection volume (a cylinder in those cases). For finite aspect ratios of the detection volume, τ_d is still a very good approximation for the average residence time of the particles in the detection volume. τ_d is plotted in Fig. 2 b as a function of 〈W〉/w₀, and the two contradictory effects mentioned above can be observed: the decrease in the detection volume causes a decrease in the residence time at small and negative 〈W〉/w₀ (note the +1 slope around 〈W〉 ≃ 0, due to the 〈W〉/w₀ dependence of the cross-sectional area of the detection volume, and hence of the residence time), whereas the reflection of particles on the obstacle causes an increase of the residence time at larger 〈W〉/w₀. This leads to the existence of a maximum around 〈W〉/w₀ = 0.6, at which τ_d/τ = 1.43.

The shape of the autocorrelation function is also modified due to the change in geometry and in diffusion pattern. This can be appreciated by inspection of the curves shown in Fig. 2 a. For example, for 〈W〉/w₀ = 0.6, the fact that molecules might be reflected by the wall and reenter the detection volume is apparent in the tail acquired at longer times by the autocorrelation function when compared to the free-diffusion autocorrelation function.

Consequences for the analysis of FCS measurements

One may try to analyze the autocorrelation functions calculated from Eq. 19 (such as those shown in Fig. 2 a) assuming either free or anomalous diffusion of the fluorophores (i.e., assuming either Eq. 6 or Eq. 7 holds true). The average residence times estimated this way (τ in the case of free diffusion and τ_a in the case of anomalous diffusion) are plotted in Fig. 2 b together with τ_d. In the case of an anomalous-diffusion model, the actual shape of G_d will be partly accounted for by a change in the anomalous coefficient γ, which allows adjustment of the slope of the autocorrelation function. A plot of γ as a function of 〈W〉/w₀ is shown in Fig. 2 c.

It can be seen from Fig. 2 b that the residence times estimated with these simple models are quite comparable to the actual characteristic time τ_d. It would be incorrect, however, to equate them with, respectively, the residence time for free diffusion 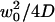or the residence time for anomalous diffusion . This would lead to an error in the diffusion constant D that can be as large as 43%, as can be seen in Fig. 3, where diffusion coefficients estimated by using these two models and assuming they are valid (i.e., writing in the first case 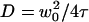and in the second case 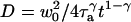) are compared to the actual diffusion coefficient.

FIGURE 3.

Diffusion coefficients (normalized by the actual diffusion coefficient) calculated from the residence times obtained by fitting the autocorrelation functions calculated with Eq. 19 using a hindered-diffusion model (thick black line), a free-diffusion model (thin black line), or an anomalous-diffusion model. In this last case, the quantity plotted is 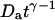, for t = 1 s (dashed black line), and for 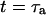(dashed gray line).

Figs. 2 and 3 point out that the presence of a simple boundary approaching the detection volume modifies the autocorrelation function in a way that may be misinterpreted as evidence for anomalous diffusion, or more simply that may lead to the extraction of an erroneous diffusion constant.

Fluctuation term

Derivation of the fluctuation term 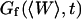in the case of thermal fluctuations

In this section, we calculate 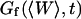from Eq. 16 assuming the membrane fluctuations are caused by thermal agitation. This allows us to express G_f in terms of the elastic properties of the membrane.

We have in this case to take into account the fact that the membrane fluctuates at all scales, and that it can no longer be seen as a planar object. Mathematically speaking, it means that the transversal displacement of the membrane W(t) is now also a function of r_M, r_M being a point on the membrane. To calculate the correlation function 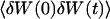, it is convenient to decompose 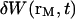into a Fourier sum:

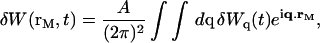(26)

where A is the area of the membrane. The integral runs over all modes that can be excited on the membrane, from the mode of smallest wave vector (q_min ∼ 1/R in the case of a vesicle of radius R) to the mode of largest wave vector (q_max ≃ π/a where a is a typical molecular length).

Henceforth:

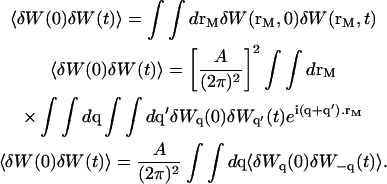(27)

In the case of the thermal undulations of a membrane, it has been shown that (Brochard and Lennon, 1975; Zilman and Granek, 1996):

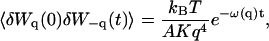(28)

where K is the rigidity of the layer, η the viscosity of the solvent, and

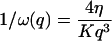(29)

is the characteristic time associated with the damping of a mode of wave vector q.

We obtain:

(30)

We now have to remember that the correlation function that appears in Eq. 16 is 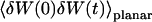, because we were in the case where the membrane was flat at the scale of the detection volume. In the case of a fluctuating membrane, the use of this equation is strictly justified only if the dominating wavelength of the undulations is larger than z₀. In the case of thermal undulations, the dominating wavelength at time t is of order 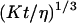(cf. Eq. 29), which means we must have 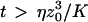. To overcome this difficulty, we introduce the wave vector 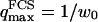, which marks the limit between undulations whose wavelengths are larger than the detection volume and undulations whose wavelengths are smaller. In the first case, 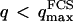, we can consider that the membrane inside the detection volume is moving as whole, and that our derivation of Eq. 16 is correct. In the second case, 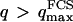, on the other hand, the membrane will exhibit undulations inside the detection volume, and the net change in effective detection volume will be zero at all times: the FCS experiment is not sensitive to these undulations, and they shouldn't be considered in our calculation. So finally 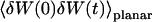can be written as an integral running only over wave vectors from 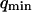to :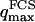

(31)

Inserting Eq. 31 into Eq. 16 then leads to:

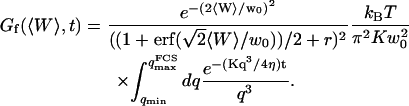(32)

The indefinite integral associated with Eq. 32 may be expressed in terms of gamma functions, hence simplifying its numerical computation:

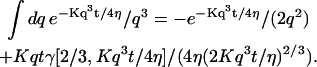Equation 32 equation can be readily adapted to the case where the membrane is perpendicular to the optical axis (and at a distance 〈Z〉 on average from the center of the detection volume) by replacing 〈W〉 by 〈Z〉 and w₀ by z₀.

The characteristic time of the fastest mode is given by 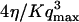, which corresponds, for a membrane of rigidity as low as 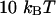in aqueous solution (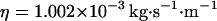), to ∼1 ms. This is one order of magnitude slower than the residence time of a typical fluorophore in the detection volume (∼0.1 ms), and hence justifies the separation into diffusion and fluctuation regimes.

The amplitude of this part of the autocorrelation function is given by:

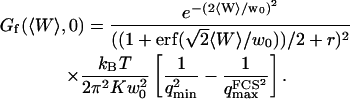(33)

Dependence of G_f on the bending rigidity of the membrane

It can be seen directly from Eq. 32 that the shape of the function G_f does not depend on 〈W〉, only its amplitude depends on the membrane position. Furthermore, in the case when 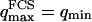, using Eq. 33 and making the change in variable 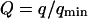, G_f can be rewritten as:

(34)

It then appears that 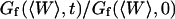has a universal shape if time is normalized by the characteristic time of the smallest wave vector mode 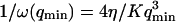. This universal shape is shown in Fig. 4. In this case, the characteristic decay time of the autocorrelation function 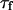, defined as 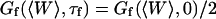, is obtained for τ_f ≃ 0.175/ω(q_min). The influence of the cutoff of the highest wavevector modes is visible only when we no longer have q_max ≫ q_min: as can be seen in Fig. 4 (thin line), the shape of G_f is then modified. But in general (q_max ≫ q_min) we have:

(35)

FIGURE 4.

Part of the autocorrelation function due to the fluctuations of the membrane, calculated for 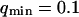μm⁻¹ (thick line) and for 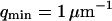(thin line). In both cases, 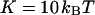and 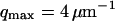. The time has been normalized by 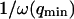and the amplitude of the curve by the value of 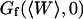(Eq. 33). The characteristic decay time 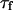of the autocorrelation function calculated for 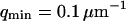is indicated.

The characteristic decay time of G_f is then inversely proportional to the bending rigidity K of the membrane, and to the third power of the smallest wave vector that can be excited on the membrane, 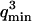. Measurements of 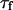will therefore give a good estimation of K only if 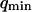is known with very good precision. This characteristic decay time is very roughly of the order of 1 s for membranes with rigidity in the range 20–500 k_BT, and for 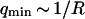corresponding to a membrane typical size of the order 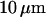. This is typically the range of rigidity expected for most biological membranes, inasmuch as the very flexible plasma membrane of red blood cells has been shown to be of order 50 k_BT (Evans, 1983; Hochmuth and Waugh, 1987) (just slightly higher than the rigidity of a simple lipid bilayer), whereas on the other end of the spectrum the rigidity of the supported double bilayer delimitating the nucleus is expected to be as high as 1000 k_BT (Helfer et al., 2000). This shows that the thermal fluctuations of biological membranes should lead to long time correlations, causing the appearance of tails in the autocorrelation functions measured by FCS.

The amplitude 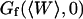of is inversely proportional to K and to 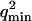(cf. Eq. 33, in the case when 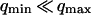). Estimations of K based on the measurements of 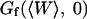will hence be more precise than those based on the measurements of 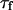. For each autocorrelation function measured, those two estimations are independent.

Relative amplitudes of the fluctuation and diffusion terms

The amplitude 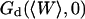and 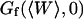depends strongly on 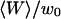. This dependence, as well as that of the amplitude of the total correlation function G(0), is shown in Fig. 5 a. As the detection volume approaches the membrane, the relative contribution of the fluctuation term over that of the diffusion term (see Fig. 5 b) increases dramatically (meanwhile, the signal-to-noise ratio is decreasing). A tail corresponding to the fluctuation term will be visible in the autocorrelation function whenever 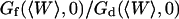stops being negligible, i.e., roughly when 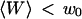(Fig. 5 b) or, if one considers a membrane perpendicular to the optical axis (at an average distance 〈Z〉 from the center of the detection volume), when 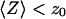. Because is typically ≃ 1−5 μm in an FCS experiment, which is only slightly less than the characteristic dimension of most cells, it will be difficult avoiding having the plasma membrane at a distance 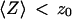when carrying out an in vivo FCS experiments, meaning it will be difficult avoiding getting tails in the autocorrelation function (provided the plasma membrane indeed separates a fluorescent environment from a nonfluorescent environment, which will be the case if the cell contains fluorophores and the outside medium does not).

Three other factors play a part in the relative amplitude of the two terms: the bending rigidity of the membrane (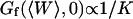), the average concentration of the fluorophore (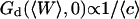), and the wavevector of the longest mode that can be excited on the membrane (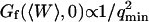). The more rigid the membrane, the less important its fluctuations will be. On the other hand, the higher the fluorophore concentration, the smaller the diffusion term will be. The membrane fluctuation term will then become very apparent at large 〈c〉. This is illustrated in Fig. 6. Note that even for biological membranes, whose rigidity is expected to be very high in some cases, in the range 50 k_BT–1000 k_BT (Helfer et al., 2000), and for small fluorophore concentrations (as low as 10 nM), the fluctuation term should be detectable.

FIGURE 6.

(a) Variation of the relative amplitude of the two terms 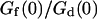with the bending rigidity of the membrane K (all other parameters as in Fig. 5), for two particular distances of the detection volume to the membrane: (gray line) and (black line). The dashed line indicates the value of K used for the curves of Fig. 5. (b) Variation of 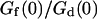with the fluorophore concentration (other parameters values as in Fig. 5), again for 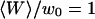(gray line) and 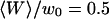(black line). The dashed line indicates the value of 〈c〉 used for the curves of Fig. 5.

MEASUREMENTS NEAR A VESICLE MEMBRANE

DOPC vesicles were prepared with both low (≃ 10 nM) and high (≃ 500 nM) concentrations of fluorophores outside the vesicles, to ascertain the influence of this parameter on the existence and amplitude of the fluctuation term. Two different types of fluorescent species were used (a fluorescent streptavidin and a fluorescent 10-kDa dextran, see section “Materials and Methods”) to detect an eventual influence of fluorophore interaction with the membrane (transient binding or membrane penetration for example). Dextrans should be particularly inert. Experiments were performed at 25°C. At this temperature the unsaturated lipid used is in the fluid 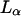phase (Koynova and Caffrey, 1998). FCS measurements were carried out in the equatorial plane of several different giant vesicles (one of them is shown in Fig. 7 a), with radii varying between 5 μm and 15 μm. During the experiment, the sample was moved step by step so that the focus of the laser would come progressively closer to the membrane and eventually cross it. At each point the intensity was measured for a given period of time, and the autocorrelation function of the signal computed. Typical autocorrelation curves (streptavidin, low concentration), obtained for different distances of the detection volume to the membrane, are shown in Fig. 8.

FIGURE 7.

(a) DIC photograph of one of the vesicles used for the presented experiments. The radius of the vesicle is 14.4 μm, giving 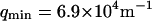if 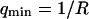. (b) Measured average intensity profile coming from the fluorescence of the Cy3-streptavidin present outside the vesicle, as a function of the distance of the detection volume from the membrane (circles). The line is only a guide to the eye. The maximum signal intensity is I_M = 12.5 kHz, and the relative amount of noise is r = 0.1. Note that the scales of figures a and b are different and that the x axis in b runs from positive to negative values.

FIGURE 8.

Typical measured autocorrelation functions, for a 6.8-nM concentration of Cy3-streptavidin outside a vesicle, and for different position of the membrane relative to the detection volume: membrane infinitely remote (black dots), 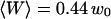(empty circles), 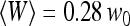(empty triangles), and 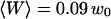(empty squares). These positions have been calculated from the measured average intensity using Eq. 10. As explained in the text, continuous black lines are fits obtained using Eq. 36.

To test the mechanical and optical stability of our set-up, we also performed FCS measurements close to a fixed rigid wall, constituted by the side of a glass coverslip. None of the effects that we observed in the vicinity of the vesicle membranes and that we attribute to membrane fluctuations could be observed in this case (see section “Amplitude of the fluctuation term”), ruling out mechanical or optical instability as the cause of these effects.

Intensity profile across the membrane

Fig. 7 b shows a typical intensity profile measured as a function of position, with steps of 35 μm, and a counting time of 30 s. It shows that a signal is obtained outside the vesicle, whereas only a background noise is observed inside the vesicle, demonstrating the nonpermeability of the lipid bilayer to the fluorescent species, in this case a 66-kDa Cy3-streptavidin. A similar observation was made with the 10-kDa dextran also used in our experiments, even at the highest used concentration, although we observed that free dyes such as rhodamine tend to penetrate the membranes and slowly fill the vesicles. The amplitude of the intensity fluctuations was always small compared to the average intensity outside the vesicles (data not shown), showing that the roughness of the membrane was small enough to justify the use of Eq. 10. As the precision on the sample position was not good enough to fit the intensity profile of Fig. 7 b with this equation, we simply used it to deduce from the measured average intensity the normalized distance 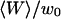of the detection volume to the wall. Values for the parameters 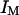and r are needed for this. They were derived by identifying the average intensity outside the vesicle and far from the membrane with 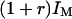, and the average intensity inside the vesicle and far from the membrane with 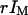. The relative level of background intensity r evaluated this way was found to vary from r = 0.04 for a fluorophore concentration around 500 nM (I_M ≃ 700 kHz) to r = 0.1 for a fluorophore concentration around 5 nM (I_M ≃ 10 kHz, see Fig. 7 b).

Free diffusion of the fluorescent species

FCS measurements were performed outside and far from any vesicle (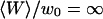) to characterize the free diffusion of the fluorescent species in the buffer supplemented with sucrose and glucose. All the autocorrelation curves measured far from the membrane were very satisfactorily described assuming a free-diffusion model, and using the corresponding Eq. 6 (see for example the curve represented by black diamonds in Fig. 8). Fitting these curves with this equation, we find the average residence time of the Cy3-streptavidin in the detection volume to be τ = 0.300 ± 0.005 ms, implying a diffusion coefficient of the fluorophore in the sucrose/glucose buffer D = 44 ± 1 μm²/s. For the measurements presented here (Figs. 7–11), we also find 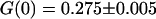, corresponding to an average number of fluorophores in the detection volume and to a concentration 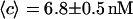(assuming 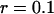as suggested by the intensity curve shown in Fig. 7 b). Each Cy3-streptavidin molecule yields an average intensity of 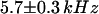. For the parameters related to the triplet state of this fluorophore, the fits gave: 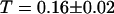and . For the 10-kDa dextran, we find τ = 0.150 ± 0.005 ms, corresponding to D = 88 ± 2 μm²/s. Results for two different concentrations of this fluorophore are presented (Figs. 9 and 10): a low concentration measured to be 23 ± 1 nM and a high concentration measured to be 490 ± 2 nM. In both cases the average intensity per molecule is 3.7 ± 0.1 kHz. The triplet state is characterized by T = 0.16 ± 0.02 and 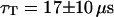at low intensity 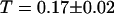and and 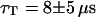at high intensity.

FIGURE 11.

Autocorrelation function (on a log-log scale) measured for a 6.8-nM concentration of Cy3-streptavidin outside a vesicle at 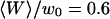(gray open symbols), and best fit obtained using the complete model derived in this paper (thick black line). The diffusion part 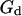(thin black line) and fluctuation part 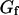(thin gray line) of the fit are also shown. The diffusion coefficient retrieved from the fit is 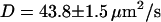, whereas the bending rigidity is 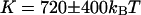(assuming ).

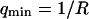FIGURE 9.

Amplitude of the fluorophore diffusion contribution of the autocorrelation function, as a function of 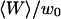, for a 6.8-nM concentration of streptavidin (filled circles), and 23.8-nM (open squares) and 490-nM (open triangles) concentrations of dextran. The best fits using Eq. 24 are indicated (bold continuous line, continuous line, and dotted line, respectively).

FIGURE 10.

Amplitude of the membrane fluctuations contribution in the autocorrelation function as a function of 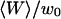, for a 6.8-nM concentration of streptavidin (filled circles), and 23.8-nM (open squares) and 490-nM (open triangles) concentrations of dextran. The radii of the vesicles were, respectively, 14.4 μm, 9.1 μm, and 7.3 μm. The best fits using Eq. 33 are indicated (bold continuous line, continuous line, and dotted line). The small filled lozenge symbols along the horizontal axis correspond to the measured amplitude of the fluctuation term in the case of a fixed, rigid wall.

Measured autocorrelation functions and amplitude of the different contributions

Autocorrelation functions

Fig. 8 shows typical autocorrelation functions, measured at low concentration of Cy3-streptavidin, far away from the membrane (filled symbols) and close to the membrane (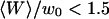, empty symbols). Far from the membrane, the only characteristic time observed is the one coming from the free diffusion of the streptavidin molecules through the detection volume (τ = 0.3 ms). Close to the membrane, two characteristic times can be observed, one at short timescales (τ_d (〈W〉) ≃ 0.5 ms) corresponding to the modified diffusion of the fluorophore close to the membrane, and one at long timescales (τ_f ≃ 5 s) attributed to thermal fluctuations of the membrane. Because of the three orders of magnitude difference in their respective characteristic times, these two contributions can be clearly distinguished. In this case (low concentration of the fluorophore) the contribution of the diffusion term is dominant, although the fluctuation term is very clearly visible. To evaluate the respective amplitudes of both contributions, and check that they obey Eqs. 24 and 33, the autocorrelation functions were first fit from 0.002 ms to 200 ms (i.e., for t = τ_f, where it can be considered that G(t) = G_d(t)+G_f(0)) with a modified form of Eq. 10, fixing to the value found in the case of free diffusion (so that the change in shape of the diffusion contribution could not be compensated for by a mistaken 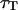), and adding a constant baseline corresponding to :

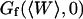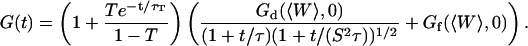(36)

This simple fit allows to retrieve values for 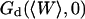and 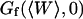. Several of these fits are shown in Fig. 8.

Amplitude of the diffusion term

The amplitude of the diffusion contribution as a function of position is shown in Fig. 9 for the three different systems studied (Cy3-streptavidin at low concentration and 10-kDa dextran both at low and high concentration). The three curves obey Eq. 24, as can be seen in the figure. Values for the relative noise contribution r can be obtained from this fit, independently from the value obtained from the intensity profile, and found to be systematically slightly higher in the first case (ranging from r = 0.16 ± 0.03 at low fluorophore concentration to r = 0.060 ± 0.004 at high fluorophore concentration) than in the second case (see section “Intensity profile across the membrane”). This might be due to the fact that noise gets higher close to the membrane, perhaps due to some adsorption of fluorophores to the lipid bilayer or scattering of light at the membrane. As expected, the amplitude of this term is extremely sensitive to the concentration of the fluorophore, being inversely proportional to the average number of particles present in the detection volume.

Amplitude of the fluctuation term

The amplitude of the membrane fluctuation contribution as a function of position is shown in Fig. 10, for the same three systems than in Fig. 9, and for the case of the immobile glass wall. The striking feature here is that the amplitude of this term does not depend on concentration: in fact, for the two measurements done with the 10-kDa dextran at very different concentrations, the amplitude is exactly the same. This demonstrates that the origin of this term cannot be attributed to any phenomenon involving particle correlation, which would always give rise to correlations having an amplitude proportional to the inverse of the particle concentration (as for particle diffusion). In the important case of transient binding of the fluorophore to the membrane, which can lead to intensity correlations as well, the eventual corresponding term in the autocorrelation function would have a very small amplitude at high concentration (see for example the exact derivation that can be found in (Starr and Thompson, 2001)), exactly as in the case of the fluctuation term (cf. Fig. 9). On the contrary, we have here a concentration-independent term, which is in agreement with our attribution of the signal to membrane fluctuations restricting access of the fluorophores to the detection volume in a time-correlated manner. The effect vanishes completely in the case of an immobile wall. Our measurements also suggest that the amplitude of this term is linked to the size of the vesicle, as expected from Eq. 33 that links 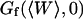to the vesicle diameter 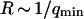: the two measurements made with the smaller vesicles (R = 7.3 ± 0.2 μm and R = 9.1 ± 0.2 μm, cf. Fig. 10) exhibit smaller amplitudes for this term than the one made with a larger vesicle (R = 14.4 ± 0.3 μm). This is in agreement with our model, as a larger vesicle is expected to undergo more fluctuations (as modes with larger wavelengths are allowed to propagate on the surface, i.e., as 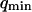is smaller), which will cause the fluctuation term to have a larger amplitude. The curves of Fig. 10 can be satisfactorily fit by Eq. 33, as can be seen in the figure. The fits allow attributing values for the relative noise ratio r (independently from the other two measurements presented in sections “Intensity profile across the membrane” and “Amplitude of the diffusion term”) and to the quantity 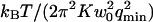. If we further assume that 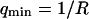, we respectively retrieve for the three different vesicles studied: 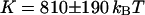(vesicle obtained by gentle hydration, 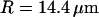), , and (vesicles obtained by electroswelling, R = 9.1 and 7.3 μm). The difference in elasticity between the vesicles obtained by gentle hydration and those obtained by electroswelling is probably due to the fact that in the first case the vesicles tested were multilamellar whereas in the second case unilamellar vesicles were selected (by minimal optical contrast using differential interference contrast optics). It might also be due to the difference in osmotic pressure between the inside and outside of the vesicles achieved for this second set of experiments: a lower osmotic pressure inside the vesicle will cause an increase of the surface area over volume ratio of the vesicle, resulting in an enhancement of the fluctuations (not taken into account in our calculations) and an increase in the value of 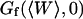, which we might mistake for a smaller bending rigidity. Other measurements on similar systems have typically yielded lower values: 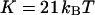for unilamellar DOPC vesicles (micropipette aspiration) (Rawicz et al., 2000), and ∼100 k_BT for a stack of lipidic dipalmitoylphosphatidylcholine membranes (using electric-field induced bending deformation of cylindrical tubes) (Mishima et al., 2001). Discrepancy with our measurements may come from the model-dependent estimation of 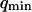. If we assume instead that 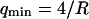, we extract an experimental value 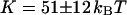for the vesicle obtained by gentle hydration 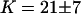and and 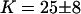for the vesicles obtained by electroswelling, in good agreement this time with other experiments. Because of the ambiguity on 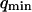, which cannot be lifted, it is difficult to extract exact absolute bending rigidities of the membranes from the measurement of 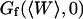, but their relative propensity to fluctuate can be readily observed: on Fig. 10, the difference between the soft lipid bilayer membranes (filled circles, open squares, and open triangles) and the rigid wall (filled lozenges), for example, is striking.

Fit of one autocorrelation function and derived values of K and D

Fig. 11 shows an example of an autocorrelation function (measured for Cy-3 streptavidin at low concentration, for a vesicle radius 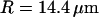, and for 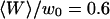) fit by the complete diffusion model derived in this paper. For this fit, Eqs. 19 and 32 were inserted into Eq. 14, and the multiplicative term 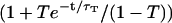, accounting for the residence of the fluorophores in their triplet state, was added. To avoid too many free parameters, the value of 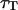was fixed to 11 μs (value measured far from the vesicle), and 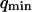was fixed to 0.69 μm⁻¹ (expected value supposing 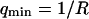), whereas 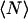, T, r, D, and K were allowed to vary. From the fit we retrieve , and 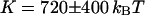. The diffusion coefficient of the molecules close to the membrane is measured to be equal to the diffusion coefficient infinitely far from the membrane, and the value measured for the bending rigidity is consistent with the one derived from the amplitude of the fluctuation term (see previous section and Fig. 10). The precision obtained on K is not very good, as instabilities in the vesicle position prevented measurement of the autocorrelation functions over a time much larger than the characteristic time of the fluctuations themselves. Also, once again, K depends on our estimation of 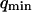. If we assume 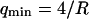, then we retrieve a much smaller value of the bending rigidity: 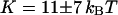. It can clearly be seen in Fig. 11 that the fluctuation term 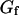, calculated assuming that thermal fluctuations of the membrane were responsible for the observed long-term correlations, indeed describes very correctly the part of the autocorrelation function obtained at large times.

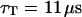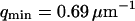The measured value of the diffusion coefficient is to be compared with those obtained using either a free-diffusion model or an anomalous-diffusion model to fit the diffusion part of the autocorrelation function (i.e., substituting either Eq. 6 or Eq. 7 for G_f in Eq. 14, and keeping Eq. 32 to describe the part due to the membrane fluctuations). In these cases also, we fixed and . Using the free-diffusion model, we find 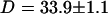, and . 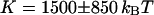Using the anomalous-diffusion model, we get 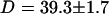, , 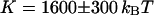and 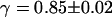. In both cases, the diffusion coefficient obtained is significantly lower than the value measured from free diffusion far away from the vesicle membrane. This is the expected result: an increase of the residence time due to the modification of the particle diffusion by the membrane, mistaken for a decrease of the diffusion coefficient, as discussed in section “Derivation of the diffusion term under reflecting boundary conditions”. In the case of the anomalous-diffusion model, we observe also that the change in slope of the autocorrelation function, as compared to a free-diffusion autocorrelation function, is mistaken for anomalous diffusion. The obtained anomalous exponent 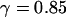is even lower than the one predicted for 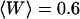(cf. Fig. 2 c), probably because fitting the fluctuation term at the same time as the diffusion term allowed for larger admissible range for γ.

When the center of the detection volume passes through the time-averaged membrane position (), we observe residence times and autocorrelation functions shapes that cannot be explained by our model, suggesting either interactions of the fluorophores used with the membrane, or, more likely, noise levels too high to obtain meaningful curves in this region.

CONCLUSIONS

We have shown that when FCS measurements are carried out close to a membrane, the usual expression for the autocorrelation function has to be modified, and in the case of a fluctuating membrane separating two media with different concentrations of fluorophores, a new term should be added. For a soft membrane undergoing thermal fluctuations, the latter term depends only on the bending rigidity and surface area of the membrane, and has a characteristic decay time much larger than the one corresponding to the diffusion of the fluorophores.

To illustrate our calculation, we performed FCS measurements in the proximity of phospholipid bilayer vesicles. We observed both the modification of the diffusion term according to our calculation (except very close to the membrane, where binding or adsorption of the fluorophore on the membrane, which we have neglected, might play a role), and the appearance of a long decay-time membrane fluctuation term in the autocorrelation function. As expected, the amplitude of the first term was observed to depend inversely on the concentration of fluorophores, whereas the amplitude of the second term was independent of that quantity. We were able to extract from these measurements both the correct diffusion coefficient of the fluorophore and an estimation of the bending rigidity of the membrane.

The modification of the diffusion term, due to the presence of a vertical obstacle in one direction of space, becomes dramatic as soon as 〈W〉/w₀ ≃ 1.5, that is before the detection volume even touches the obstacle. Far from the membrane it is caused primarily by the reflection of the fluorophores on the obstacle leading to enhanced correlations, and close to the membrane by the reduction of the effective detection volume. Consequently, the shape of the correlation function is modified, and the average residence time is no longer linked to the diffusion coefficient by the simple relation: D = w₀²/4τ, as is the case for free diffusion. Erroneous interpretations of the nature of the observed diffusion may easily be assigned, if this effect is not acknowledged. The issue is particularly acute for studies inside living cells, where membrane barriers abound. It could be useful to investigate whether other types of analysis of the fluorescence fluctuations (Qian and Elson, 1990; Chen et al., 1999; Kask et al., 1999) might prove more reliable for in vivo studies.

The fact that the membrane fluctuations themselves have an influence on the autocorrelation function, causing correlations to appear at characteristic times of order roughly 1 s for typical biological membranes, could account for many of the long time tails observed in autocorrelation functions when taking measurements in cells. In fact, our calculation shows that any soft membrane delimiting regions with different concentrations of fluorophore will lead to long time correlations in the autocorrelation function measured by FCS. Because the amplitude and characteristic time of the term coming from the membrane fluctuations depend on its elasticity, FCS provides a way to estimate this parameter. Absolute measurements are difficult though, because they depend on the model used to describe the membrane fluctuations, and are altered by the absence (even in the case of a spherical membrane) of an exact relationship between the membrane surface area and wave vector of the larger mode propagating on the membrane. Nevertheless, this method might prove to be an interesting way for evaluating the out-of-plane elasticity of biological membranes, inasmuch as it is sensitive to high bending rigidities (∼100 k_BT–1000 k_BT), and contrary to traditional methods (such as light or x-ray scattering) it can be used in situ on biological membranes, even those, as the nuclear membrane or endoplasmic reticulum for example, that are buried inside the cell. It is also noninvasive, which might be an advantage compared to methods relying on deformation of the membrane or insertion of a bead as a tracer (Dimova et al., 2000; Helfer et al., 2000). Finally, it allows spatial resolution in the plane perpendicular to the optical axis. This last feature could be useful in the case of membranes exhibiting domain segregation, or in the case of cell membranes, whose elastic properties depend on the local cytoskeleton arrangement and membrane protein composition and concentration (Discher et al., 1994).

APPENDIX: RELATIONSHIP BETWEEN G_f(t) AND THE t^2/3 DEPENDENCE OF A MEMBRANE TRANSVERSE MSD

The transverse mean-square displacement (MSD) of a membrane has been shown (Zilman and Granek, 1996; Granek, 1997) to behave as t^2/3 for 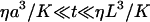, where L is the characteristic size of the membrane, and a a typical molecular length. This means that a particle attached to the membrane undergoes anomalous diffusion in the direction perpendicular to the membrane, with an anomalous exponent γ = 2/3. We discuss in this appendix how this is related to our experiment.

The quantity measured by FCS in the case when fluorescent particles are present on only one side of the membrane is related to the mean autocorrelation function of the membrane position in the transverse direction, 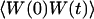, which is in turn related to the transverse MSD of the membrane 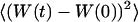by:

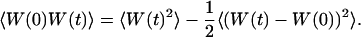(37)

An approximate expression for the MSD can be found (Granek, 1997) provided that we are in the time range 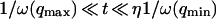( 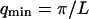and are the same quantities that have been defined in section “Derivation of the fluctuation term”), which ensures that we are far from both cutoffs in term of excitable wavelengths on the membrane, and that the limits of the integration that has to be performed over all modes (which is exactly the same as in Eq. 32) can be set to zero and infinity, respectively. However in our case 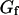is proportional to 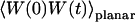, which is the autocorrelation function if only the modes for which 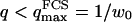(and to which the FCS experiment is sensitive) contribute. In this case, the same approximate form is found for the corresponding MSD:

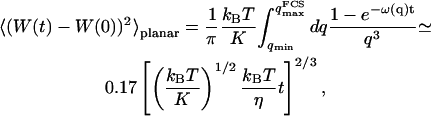(38)

but the approximation is valid only for .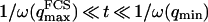

It can also be shown (Granek, 1997) that the MSD reaches a saturation value at long times (as the autocorrelation function of 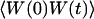goes to zero), which is:

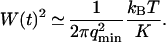(39)

It follows from the previous equations, and from the fact that 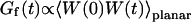, that within the correct time range:

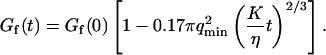(40)

In our case, this expression will be valid only if 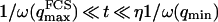, where 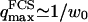is the cutoff imposed by our experiment, much before we reach the molecular cutoff.

The t^2/3 dependence of the transverse MSD of membranes has been indirectly observed in the stretched exponential decay of the dynamic structure factor measured by light-scattering experiments (Nallet et al., 1989; Sigaud et al., 1993). To check if it could directly be seen with FCS, we plotted the quantity 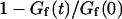(as calculated from Eqs. 32 and 33) on a log-log scale (Fig. 12). It can be seen that the curve as indeed a slope 2/3 over the range of time 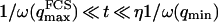. This time range can be increased, to observe this power law, by increasing 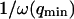(using larger vesicles), inasmuch as 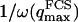is fixed by the optical resolution w₀. For high concentrations of fluorophores (and hence disappearance of the diffusion term in the autocorrelation function), and for a large 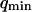, it should hence be possible to observe by FCS the t^2/3 time dependence of the membrane transverse MSD.

FIGURE 12.

Log-log plot of the quantity 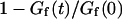as calculated exactly with our model from Eqs. 32 and 33 (thick continuous line), and approximated expression using the t^2/3 dependence of the transversal MSD of a membrane in the time range 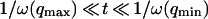(thin continuous line). The dashed lines indicate the respective positions of 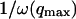and .