Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2005 Apr;14(4):1039–1048. doi: 10.1110/ps.041124705

Ca2+-induced structural changes in phosphorylase kinase detected by small-angle X-ray scattering

Timothy S Priddy 1,2, Brian A Macdonald 3, William T Heller 4, Owen W Nadeau 2, Jill Trewhella 3,5, Gerald M Carlson 2
PMCID: PMC2253434  PMID: 15741333

Abstract

Phosphorylase kinase (PhK), a 1.3-MDa (αβγδ)4 hexadecameric complex, is a Ca2+-dependent regulatory enzyme in the cascade activation of glycogenolysis. PhK comprises two arched (αβγδ)2 octameric lobes that are oriented back-to-back with overall D2 symmetry and joined by connecting bridges. From chemical cross-linking and electron microscopy, it is known that the binding of Ca2+ by PhK perturbs the structure of all its subunits and promotes redistribution of density throughout both its lobes and bridges; however, little is known concerning the interrelationship of these effects. To measure structural changes induced by Ca2+ in the PhK complex in solution, small-angle X-ray scattering was performed on nonactivated and Ca2+-activated PhK. Although the overall dimensions of the complex were not affected by Ca2+, the cation did promote a shift in the distribution of the scattering density within the hydrated volume occupied by the PhK molecule, indicating a Ca2+-induced conformational change. Computer-generated models, based on elements of the known structure of PhK from electron microscopy, were constructed to aid in the interpretation of the scattering data. Models containing two ellipsoids and four cylinders to represent, respectively, the lobes and bridges of the PhK complex provided theoretical scattering profiles that accurately fit the experimental data. Structural differences between the models representing the nonactivated and Ca2+-activated conformers of PhK are consistent with Ca2+-induced conformational changes in both the lobes and the interlobal bridges.

Keywords: phosphorylase kinase, small-angle X-ray scattering, modeling, solution structure, Ca2+

In the cascade activation of glycogenolysis leading to energy production in skeletal muscle, phosphorylase kinase (PhK), a 1.3-MDa (αβγδ)4 hexadecameric complex, phosphorylates and activates glycogen phosphorylase. The activity of PhK, catalyzed by its γ subunit, is tightly controlled by neural (Ca2+), metabolic (ADP), and hormonal (phosphorylation and Ca2+) stimuli, which it integrates through allosteric sites on its three regulatory (α, β, and δ) subunits (for reviews, see Heilmeyer 1991 and Brushia and Walsh 1999). The catalytic activity of γ in the PhK complex is absolutely dependent on Ca2+ (Meyer et al. 1964; Brostrom et al. 1971), which provides a mechanism for coupling energy production with muscle contraction. Although the δ subunit, a nondissociable endogenous calmodulin molecule (Cohen et al. 1978), confers Ca2+-dependence on PhK activity (Brostrom et al. 1971; Cohen 1980; Burger et al. 1982), it is unclear exactly how the binding of Ca2+ by this subunit relays structural information to the remainder of the enzyme complex. Ca2+-dependent differential cross-linking among the δ, γ, and α subunits in the PhK complex supports the existence of a Ca2+-sensitive communication network connecting these subunits (Nadeau et al. 1997b), with the C-terminal regulatory tail of γ mediating the interactions within an αγδ network (Rice et al. 2002). This regulatory region of the γ subunit interacts with both the α (Nadeau et al. 1999; Rice et al. 2002) and δ subunits (Dasgupta et al. 1989; Harris et al. 1990; James et al. 1991). That Ca2+-binding by δ also affects the conformation of β is consistent with differential proteolysis (Trempe and Carlson 1987) and cross-linking (Nadeau et al. 1997b, 1999) studies, and with the close proximity of the δ subunit to the interlobal bridges (Traxler et al. 2001), which are thought to comprise the β subunits (Trempe and Carlson 1987). Together, these studies suggested that a global conformational change in the PhK complex is induced by Ca2+.

The first direct evidence for such a widespread Ca2+-induced conformational change came from comparing three-dimensional (3D) reconstructions of electron microscopy (EM) images of negatively stained nonactivated and Ca2+-activated conformers of PhK (Nadeau et al. 2002). As revealed by EM (Norcum et al. 1994; Nadeau et al. 2002), the nonactivated PhK complex is composed of two arched octameric (αβγδ)2 lobes arranged back-to-back, with over-all D2 symmetry arising from head-to-head packing of αβγδ protomers (Wilkinson et al. 1994). The two large lobes were observed to be oriented ~68° with respect to each other and connected by two small bridges (Nadeau et al. 2002). A similar overall architecture was observed for the Ca2+-activated conformer; however, a significant redistribution of density was observed in both the lobes and bridges in the presence of the cation, concomitant with a change in the orientation of the bridges with respect to each other. The dihedral angle between the lobes for the Ca2+-activated conformer (51°) also changed; however, this measurement varied the most in reconstructions from three different enzyme preparations for both the nonactivated and Ca2+-activated conformers. The dihedral angles of all the structures derived from negatively stained molecules of the kinase also differed by more than 20° from the value of ~90° obtained in the first 3D reconstruction of nonactivated PhK from unstained molecules in ice (Nadeau et al. 2005). Taken together, these results suggest that the orientation of the large lobes, and by default the small connecting bridges, are subject to distortions imposed by surface contact interactions with the carbon viewing surface, negative staining, and/or drying.

To avoid potential deformations induced in the holoenzyme by negative staining or surface contact interactions, evident through comparing the nsEM and cryoEM structures of nonactivated PhK (Nadeau et al. 2005), small-angle X-ray scattering data were collected for nonactivated and Ca2+-activated conformers of PhK in solution. Small-angle scattering data can provide accurate measurements of the shapes of monodispersed macromolecules in solution (for reviews, see Trewhella 1997; Wall et al. 2000; and Svergun and Koch 2002). We report here the first successful solution scattering experiments of the Ca2+-activated conformer of PhK and a structural comparison with its nonactivated counterpart, analyzed under identical conditions. Analysis of the data revealed Ca2+-induced perturbations in the scattering profile of the holoenzyme that are reflected in models constructed using two ellipsoids and four cylinders to approximate the lobe and bridge structures observed in the 3D cryoEM reconstruction of nonactivated PhK (Nadeau et al. 2005). The dimensions and orientations of these shapes were varied and tested against the scattering data. The structural differences observed between models giving scattering profiles that fit the scattering data from nonactivated and Ca2+-activated PhK generally correspond to those previously observed in EM structures of negatively stained PhK complexes, indicating a global conformational change induced in the holoenzyme by activating Ca2+ ions (Nadeau et al. 2002).

Results

Small-angle X-ray scattering from PhK

Scattering data were collected from solutions of nonactivated PhK in 5% sucrose in the absence or presence of saturating Ca2+ ions. For convenience, the two corresponding conformers will be referred to as nonactivated and Ca2+-activated. Scattering intensity profiles for both nonactivated and Ca2+-activated PhK, each extending to 0.125 Å−1 in q, are shown in Figure 1A ▶. Guinier plots (Guinier 1939) for both data sets are linear and extend to low q values (Fig. 1B ▶), as expected for monodisperse particles free of nonspecific aggregation. There is a very slight downturn in the data for the Ca2+-activated sample involving the two lowest measurable data points (Fig. 1B ▶), which is likely due to inter-particle interference effects arising with the change in total charge on the particle (Glatter 1982).

Figure 1.

Figure 1.

Open in a new tab

Small-angle X-ray scattering data from nonactivated and Ca2+-activated PhK. (A) Intensity profiles of nonactivated (□) and Ca2+-activated (×) PhK and the theoretical scattering profile of each model, respectively (solid curves); symbols are conserved throughout Figure 1. Model scattering intensity profiles were calculated from P(r) curves corresponding to a q range of 0.0054–0.0989 Å−1. The scattering profile of the Ca2+-activated conformer was arbitrarily shifted along the ordinate for clarity. (B) Guinier plot of the low-q region of the intensity profiles including the fit to the data (solid lines) in the linear Guinier region corresponding to a q range of 0.01–0.015 Å−1. (C) Guinier plot of intensity profiles corresponding to the ranges used to calculate rod-like features of the holoenzyme reported as apparent Rc1, from 0.0149 to 0.029 Å−1 in q, and apparent Rc2, from 0.0406 to 0.055 Å−1 in q (both linear fits are represented by solid lines).

By taking the inverse Fourier transform of the scattering data, one obtains P(r), the probable distribution of distances between scattering centers within the scattering particle (defined by equation 2, Materials and Methods). P(r) approaches zero at the maximum linear dimension, dmax, of the scattering particle, while the zeroth and second moments of P(r) yield values for the forward scattering, I0, and radius of gyration, Rg, respectively. The indirect Fourier transform method (Moore 1980) used to calculate P(r) from scattering data includes a correction for instrument geometry (Heidorn and Trewhella 1988). Conversely, in the reverse process to calculate the theoretical scattering of models, a “smearing” correction was performed to account for instrument geometry, thus allowing comparison of the model and experimental scattering profiles and evaluation of the fit. A comparison of the I0 values of each PhK conformer against those of a lysozyme standard (Krigbaum and Kügler 1970) yields the ratios expected on the basis of each protein’s molecular weight, thus confirming that the samples were aggregate-free (Materials and Methods). The Rg and dmax values determined from P(r) are the same, within experimental error, for the nonactivated and Ca2+-activated forms, indicating that the dimensions of the overall envelope do not change upon Ca2+-activation. The Rg value of ~93 Å is in good agreement with that previously determined by Henderson et al. (1992) using small-angle neutron scattering for the nonactivated kinase (94 Å).

The Guinier plots in Figure 1, B and C ▶, are shown in the form used for globular particles to estimate the radius of gyration (Rg) (Fig. 1B ▶), and also in the form used to determine the radius of gyration of cross-section values (Rc) (Fig. 1C ▶) when there are asymmetric or rod-like features in a particle (Sosnick et al. 1991). The data in Figure 1 ▶ are the measured scattering data and are not corrected for the slit geometry of the scattering instrument. As a result, the Rg and Rc values determined are “apparent” Rc values only and may not be interpreted directly in terms of structural features, but are simply used to provide a quantitative measure of the differences in the shapes of the scattering profiles, particularly in the mid- to high-q experimental range. Although there are mathematical algorithms that “desmear” data to remove the effects of instrument geometry, instrument errors cannot be propagated accurately; therefore, for evaluating differences in the scattering profiles, it is preferable to look at the uncorrected data. It is evident from Figure 1 ▶ and from the apparent Rc values in Table 1 that there are significant differences in the shapes of the scattering profiles for the nonactivated and Ca2+-activated forms of PhK in the q range 0.0149–0.07 Å−1. Differences in scattering within this q range reflect Ca2+-induced changes in internal structures within the PhK holoenzyme having dimensions ranging from ~40 to 200 Å, which are consistent with some structural elements in the PhK complex observed by EM.

Table 1.

Comparison of experimental and best-fit model parameters for the nonactivated and Ca2+-activated conformers of PhK

Units Nonactivated PhK Ca2+-activated PhK
Guinier analysis (scattering data)
    Apparent Rg (Å) 90 ± 3 91 ± 3
    q range (Å−1) 0.01–0.015 0.01–0.015
    X2 0.42 0.42
    Apparent Rc1 (Å) 43.4 ± 0.6 45.5 ± 0.9
    q range (Å−1) 0.0149–0.03 0.0149–0.029
    X2 0.98 0.89
    Apparent Rc2 (Å) 24.8 ± 0.8 22.7 ± 1.1
    q range (Å−1) 0.0434–0.068 0.0434–0.068a
    X2 0.068 1.0
P(r) analysis (scattering data)
    Rg (Å) 93.1 ± 1.3 92.8 ± 1.5
    dmax (Å) 270 ± 10 270 ± 10
    X2 1.65 1.07
Model parameters
    Rg (Å) 90.9 91.1
    dmax (Å) 265 265
    Dihedral angle between lobes 84° 86°
    Bridge angle 73° 58°
    Bridge separation (butterfly view) (Å) 30 12
    Bridge separation (cube view) (Å) 55 60
    F values for best models 1.8 1.4
Open in a new tab

a While the values are quoted for the same Q-range as the nonactivated sample, the linear region for the Ca2+-activated sample extends from q values of 0.0406 through 0.079 Å−1.

To evaluate the distances that are changing in PhK upon activation by Ca2+, it is useful to look at the difference P(r) function. Figure 2, A–C ▶, shows the P(r) functions calculated for the nonactivated and Ca2+-activated forms (Fig. 2A,B ▶, respectively) and their difference (Fig. 2C ▶). A 4 Å shift was observed between the most common distance separating pairs of scattering centers [where r is equal to the P(r) maximum] for nonactivated (123 Å) and Ca2+-activated PhK (119 Å). Additionally, the presence of a shoulder, located at ~50 Å, is more prominent in the P(r) profile for Ca2+-activated PhK (Fig. 2B ▶). The difference P(r) (Fig. 2C ▶) shows significant differences in vector lengths ~20 Å and ~100 Å, with each of these appearing to be a reflection of the observed shift in the maximum and emergence of the shoulder feature upon activation by Ca2+.

Figure 2.

Figure 2.

Open in a new tab

Probable vector length distribution functions, P(r) curves, for nonactivated and Ca2+-activated PhK. (A) P(r) curve of nonactivated PhK (|) overlaid by the calculated P(r) curve of the nonactivated model (□). (B) P(r) curve of Ca2+-activated PhK (|) overlaid by the calculated P(r) curve of the Ca2+-activated model (○). (C) Difference length pair distribution function: Effect of Ca2+-activation (Consler et al. 1988). Difference P(r) plot relative to nonactivated PhK.

A previous comparison of EM structures for both PhK conformers also indicated that Ca2+ promotes a redistribution of density throughout the lobe and bridge regions of the kinase without altering its maximum dimensions (Nadeau et al. 2002). Because of the complexity of the PhK structure, we used modeling to aid in the interpretation of the changes in the scattering data and to determine if insights could be gained regarding the specific structural features that are altered by Ca2+.

Modeling

Models were constructed using basic shapes (two ellipsoids and four cylinders) to approximate the bridged bilobal envelope of the cryoEM reconstruction of PhK, and the dimensions and positions of these component shapes were allowed to vary as they were tested against the scattering data as described in Materials and Methods. Because the results from solution scattering represent a time and ensemble average of unoriented macromolecular structures, a single fit to the experimental data yielding a unique and correct model is not guaranteed, especially in the case of complex-shaped structures. Recognizing this limitation, a two-tiered approach was devised to evaluate the 640,000 candidate models generated for each conformer and to select those that “best fit” all of the experimental data. The first criterion was the quality of the statistical fit to the experimental scattering data as evaluated by a least-squares fit parameter F (defined in Materials and Methods) and the Rg and dmax values. Only seven of the nonactivated and 11 of the Ca2+-activated conformers of PhK were noted to have F values ≤2. Among these models, for both conformers, were several that bore no resemblance to any physical structure of PhK observed to date using any technique (lobes not bridged or else lying flush against each other with bridges at tips). These nonphysical models were eliminated. The best-fit models presented, besides reflecting known structural elements of PhK observed in EM and the dimensions calculated by SAXS, are consistent with the occurrence in solution of a global Ca2+-dependent conformational change, which has been previously observed in nsEM reconstructions of PhK (Nadeau et al. 2002).

The “best-fit” models described above are displayed in Figure 3 ▶ in the various perspectives corresponding to the characteristic orientations of PhK observed in EM, namely, chalice, cross, butterfly, and cube (columns 1–4, respectively). The model for the nonactivated conformer shown in the four characteristic orientations is arrayed in row A, the model for the Ca2+-activated conformer in row B, and the overlay of the two models in row C. The rotations necessary to interconvert the various views of the models are listed in Table 2, as are the dimensions of the lobes (ellipsoids) and bridges (cylinders). As a pair, these conformers represent the first successful modeling of the effects of Ca2+ on the overall structure of PhK in solution. The models, both of which were derived independently from the scattering data, bear a close resemblance to the 3D reconstructions from 2D images of unstained PhK (−Ca2+) in cryoEM (Nadeau et al. 2005) and, to a lesser extent, of negatively stained PhK reconstructions (±Ca2+) (Nadeau et al. 2002).

Figure 3.

Figure 3.

Open in a new tab

Models of nonactivated and Ca2+-activated PhK. (Row A) Nonactivated models of PhK represented by white spheres for the lobes (ellipsoids) and red spheres for the bridges (cylinders). (Row B) Ca2+-activated models of PhK represented by blue-green spheres for the lobes and red spheres for the bridges. (Row C) Nonactivated and Ca2+-activated models overlaid for contrast. The colors used for the lobes in rows A and B were transferred to the entire model in row C. (Column 1) Chalice view. (Column 2) Cross view. (Column 3) Butterfly view. (Column 4) Cube view.

Table 2.

Model rotations and output parameters

Nonactivated Ca2+-activated
Chalice Initial orientation Initial orientation
Cross Rotate x 90° Rotate x 90°
Butterfly Rotate y 90°, x −42° Rotate y 90°, x −43°
Cube Rotate x 90°, z 90° Rotate x 90°, z 90°
Nonactivated dimensions Ca2+-activated dimensions
The upper portion of the table presents the rotations necessary to convert the models in Figure 3 ▶ from the initial chalice orientation to the cross, butterfly, and cube orientations. The lower portion of the table reports the dimensions of the ellipsoids and cylinders from the output files for the models of each conformer.
Lobes (ellipsoids)
    Long axis diameter (a) 245 Å 220 Å
    Cross section diameter (b) 77 Å 84 Å
    Cross section diameter (c) 98 Å 97 Å
    Interlobe separation 74 Å 78 Å
Bridges (cylinders)
    Cross-sectional radius 22.5 Å 24.4 Å
    Calculated Rc 15.9 Å 17.3 Å
Open in a new tab

In Figure 1 ▶, the replicate-average experimental scattering profile of each conformer is overlaid by the scattering profile of its respective theoretical model I(q) to illustrate the fit of the model to the data over the q range 0.0054–0.0989 Å−1. The calculated P(r) functions for each model are similarly displayed in Figure 2, A and B ▶. Although the dmax values derived from the P(r) functions are slightly smaller for the two models than for that value derived from the experimental data (Table 1), the shape of each curve has features that essentially mirror those for the data-derived functions, including Ca2+-induced effects in the 10–125 Å range. It is not unexpected to observe slight differences between the absolute measurements of particles in solution compared to those of their models (Pilz 1982), based in part on the oversimplification of complex shapes in the former by an assemblage of simple geometrical shapes in the latter. In addition, we have not attempted to model hydration layer effects that produce a small difference in scattering density between the bulk solvent and hydration shell (Lehmann and Zaccai 1984; Svergun et al. 1998). Despite the simplifications inherent in our models, the quality of their fit to the experimental data is good, particularly for the data ranging from 0.0054 Å−1 to ~0.0875 Å−1 (Fig. 1A ▶), where the scattering profile is dominated by the overall dimensions of the models and their primary elements. For q values >0.0875 Å−1, which correspond to higher-resolution structural features, we expect to see deviations between the experimental and model scattering profiles, because the models have uniform density shapes that do not precisely represent the detailed shape of the molecular boundary nor electron density fluctuations within the PhK complex.

Discussion

Previous studies comparing intersubunit cross-linking of nonactivated and Ca2+-activated PhK in solution by a variety of chemical cross-linkers showed significant differences in subunit cross-linking patterns (Nadeau et al. 1997a,b, 1999; Ayers et al. 1998), suggesting that the Ca2+-induced conformational changes might be sufficiently great to be detected through biophysical approaches. In fact, such changes were observed by comparing the EM reconstructions of the two conformers (Nadeau et al. 2002); by necessity, however, surface-adsorbed rather than solvated molecules were used in that study. To avoid artifactual structural deformations that might be caused by surface adsorption, we sought to determine whether the Ca2+-induced structural rearrangements occurring within the PhK complex could be detected in solution using SAXS; and if so, whether models selected on the basis of scattering data using simple shapes to approximate structures derived from EM would show structural rearrangements. The results herein represent the first report of such structural differences being accurately measured in PhK using SAXS. Previous scattering studies by Henderson et al. (1992) using both small-angle X-ray and neutron scattering reported a dmax of 280 Å and an Rg of 94 Å for the nonactivated conformer, which are similar to the values reported herein (Table 1); attempts by those workers to collect data for the Ca2+-activated conformer were unsuccessful because of aggregation. Our ability to acquire scattering data of acceptable quality for both conformers of PhK during the long data collection period of 9–10 h was the result of the utilization of size-exclusion HPLC (SE-HPLC) to remove PhK aggregates prior to analyses (Traxler et al. 2001) and the inclusion of sucrose throughout (Henderson et al. 1992).

Some of the calculated parameters from our scattering data for the two conformers of PhK are virtually identical, namely, Rg and dmax. Because Rg and dmax are conserved in both conformers, they provide constraints on the Ca2+-induced structural changes that do occur. These constraints are that any intramolecular rearrangements taking place within the PhK complex must be balanced by compensatory rearrangements to maintain the Rg and that the complex neither extends, compacts, nor dissociates upon activation (otherwise the dmax and the Rg would be significantly altered). Such compensatory rearrangements were also observed in EM reconstructions of the nonactivated and Ca2+-activated conformers, both of which had nearly identical overall dimensions, but exhibited differential distributions of density throughout their lobe and bridge regions (Nadeau et al. 2002). Similar Ca2+-induced structural changes are observed in the scattering model for each conformer (Fig. 3 ▶, row C), reflecting changes in both P(r) (Fig. 2C ▶) and apparent Rc values (Table 1).

Considering the lobes, the most striking distinction between them in the two models is the Ca2+-induced redistribution of scattering density contained within the pair of ellipsoidal envelopes representing them, i.e., their alteration in shape. The dimensions of the ellipsoids are listed in Table 2. Especially noteworthy are the decrease in lobe length and increase in lobe width caused by Ca2+, which is evident in Figure 3 ▶, column 2. The density contained within the ellipsoid representing each lobe shifts from a relatively long, narrow arrangement, defined by three distinct radial axes in the nonactivated conformer, to a shape approaching that of a regular prolate ellipsoid in the Ca2+-activated form. These changes are consistent with shape changes observed in the P(r) functions for each conformer and are similar to those observed for 3D EM reconstructions of negatively stained conformers, where distal structural features were assimilated into the bulk density of the lobes in the presence of Ca2+ (Nadeau et al. 2002). In contrast to the visible shape changes, the position of the lobes with respect to each other remains relatively unchanged in the two conformers (Fig. 3 ▶, row B), as indicated by a difference of only 2° in the dihedral angle between the lobes (Table 1). For nonactivated PhK, similar values were measured for the dihedral angles of the solution scattering model (84°) and the cryoEM 3D reconstruction (~90°), derived, respectively, from hydrated molecules of the kinase in solution and in ice (Nadeau et al. 2005). Both of these values differed markedly, however, from that of the angle determined for the EM structure obtained from surface-adsorbed negatively stained molecules (68°) (Nadeau et al. 2002), further indicating possible distortions imposed on the lobes by surface contact interactions in the negative staining procedure.

The reconstructions of negatively stained PhK clearly indicate that two visible bridges must predominate in the majority of the EM images of the complex; however, an earlier 3D model of PhK, also based on negatively stained protein, proposed that the complex contained four, rather than two, interlobal bridges (Norcum et al. 1994). Moreover, the recent reconstruction of images of frozen hydrated nonactivated PhK from cryoelectron microscopy also indicates the existence of four interlobal bridges (Nadeau et al. 2005). Consequently, we modeled our scattering data with four cylindrical bridges connecting the two ellipsoidal lobes. The assumption of four bridges resulted in models for both conformers that closely fit the scattering data over the q range 0.0054–0.0989 Å−1 (Fig. 1A ▶), as indicated by the fit parameter F in Table 1 (see Materials and Methods). In our scattering models, the four bridges in the nonactivated conformer change positions in the Ca2+-activated conformer to nearly abut one another as opposing pairs. This approach of the bridges is readily observed in the cross and butterfly views. Equivalent rotamers of the former view of both models is shown in Figure 4 ▶, column 1; column 2 of this figure shows a magnified cutout of only the bridge portions from the butterfly view of the two conformers. That Ca2+ could cause such changes in the positioning of the bridges is consistent with the location of PhK’s four intrinsic calmodulin subunits, δ, being identified to occur on the interior lobe faces, proximal to the bridges (Traxler et al. 2001).

Figure 4.

Figure 4.

Open in a new tab

Ca2+-induced structural changes in the bridges of nonactivated and Ca2+-activated PhK. (Row A) Model structures of nonactivated PhK. (Row B) Model structures of Ca2+-activated PhK. (Column 1) Models in the cross orientation with semitransparent lobes to reveal the positions of the red interlobal bridges. (Column 2) Expanded cutout of only the bridge regions of the models in the butterfly orientation.

Materials and methods

Materials

Nonactivated PhK was isolated from white fast-twitch skeletal muscle of New Zealand White rabbits (King and Carlson 1981) and stored at −80°C in 50 mM HEPES buffer, 0.2 mM EDTA, and 10% (w/v) sucrose at pH 6.8. The aqueous mobile phase for the SE-HPLC purification step, implemented to remove aggregates of PhK immediately prior to SAXS analyses, contained 50 mM HEPES, 200 mM NaCl, 0.2 mM EGTA, and 5% (w/v) sucrose at pH 6.8. SE-HPLC analyses of the originally eluted, hexadecameric native peak containing sucrose remained unchanged for up to 72 h (data not shown). After this time, a small but significant amount of aggregation occurred; consequently, fresh samples were prepared before each run. Sucrose also effectively inhibited aggregation in the presence of Ca2+, even during the long data acquisition intervals (9–10 h), and allowed the use of relatively high concentrations of PhK (2.5–3 mg/mL), which Henderson et al. (1992) were unable to achieve. Lysozyme was purchased from Sigma and was used without further purification as a calibration standard for the SAXS measurements (Krigbaum and Kügler 1970).

Sample preparation for analyses

Freshly thawed 200-μL aliquots of PhK were centrifuged to remove any insoluble components, and the supernatant was removed using a Hamilton Gastight syringe and injected onto a Varian HPLC system equipped with a Phenomenex BioSep SEC S4000 gel filtration column equilibrated with the mobile phase described above. Fractionation of the native, hexadecameric PhK from its aggregated counterparts was achieved at a flow rate of 0.4 mL/min at ambient temperature (Traxler et al. 2001). The concentration of the native protein was determined by UV absorbance at 280 nm (Cohen 1973), following which it was concentrated to 2.5–3.0 mg/mL PhK in Centricon 10 (Amicon) centrifugal concentrators (MW cutoff of 10,000) at 4°C.

For scattering experiments on nonactivated PhK, the protein samples were added directly to microcapillary sample cells. For Ca2+-activated PhK, the appropriate volume of 25 mM CaCl2 (dissolved in HPLC mobile phase) was added to a final concentration of 0.8 mM Ca2+, or four times the concentration of chelator. The samples were loaded into the sample cells using a bench-top centrifuge.

Data collection

Scattering data were collected with the line source instrument at Los Alamos National Laboratory (Heidorn and Trewhella 1988) with the sample maintained at a constant temperature of 18°C. Data were collected for ~12 h with intermittent manual saves of the data every 2.5–3 h to monitor possible sample aggregation. The files used for our analyses consisted of data collected for 9–10 h. The calculations, figures, and models in this report were based on data that were the average of replicate runs from two different enzyme preparations, each analyzed ±Ca2+. Data reduction followed published procedures to correct for detector sensitivity and background signal (Heidorn and Trewhella 1988). Samples were characterized for artifacts due to aggregation or interparticle interference by comparing the forward scatter, I0, against a lysozyme standard (Krigbaum and Kügler 1970). A five-point concentration series of lysozyme data was collected and extrapolated to infinite dilution. The extrapolated I0 of the lysozyme standard is related to the I0 of the protein sample through the following equation: I0(lys)/M(lys) = I0(PhK)/M(PhK)C(PhK), where (lys) is lysozyme, M is the molecular weight, and C is the concentration in milligrams per milliliter.

Small-angle scattering data analyses

The small-angle scattering intensity profile of monodisperse, identical particles in solution can be written as

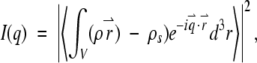graphic file with name M1.gif (1)

where ρ(r⇀) is the scattering length density of the particle and ρs is the average scattering length density of the solvent. The momentum transfer, q⇀ has the magnitude 4π (sin Θ)/λ, where 2Θ is the scattering angle and λ is the wavelength. The integration over the particle volume is rotationally averaged. The experiment measures the time and ensemble averaged information for all particles in solution. Small-angle scattering data were analyzed according to Guinier (1939) to give an estimate of the radius of gyration, Rg. Additionally, a fit to the low q region of Ln(q*I(q)) versus q2 was used to evaluate differences in the shapes of the scattering profiles. The probable distribution of vector lengths between scattering centers within the scattering object, P(r), provides more information about the shape. The relationship between I(q) and P(r) is given by the Fourier transform in equation 2.

graphic file with name M2.gif (2)

The indirect Fourier transform algorithm developed by Moore (1980) was used to determine P(r) from the measured intensity profile. An expansion in sin(qr)/qr is used to describe the intensity profiles. The boundary conditions P(r)/r at r = 0 and dmax are applied to P(r). The algorithm includes corrections for the slit smearing of the instrument (Heidorn and Trewhella 1988).

Modeling

Structural models of PhK (640,000 for each conformer) were produced from the X-ray scattering data using software developed at Oak Ridge National Laboratory. The final models shown in Figure 3 ▶ were selected on the basis of their fit to the data (determined by the fit parameter F, equation 3, below), agreement with dimensions calculated from the scattering data, and having the basic structural features observed in 3D structures of PhK derived from EM (Nadeau et al. 2002, 2005). The models were composed of two ellipsoids connected by four cylinders. The semiaxes of the two identical ellipsoids were chosen randomly from the ranges (75–125 Å), (35–65 Å), and (35–65 Å) for the x, y, and z semiaxes, respectively. The ellipsoids were rotated about the z-axis in opposite directions by a randomly chosen angle between 0° and 45°. Then, the two ellipsoids were translated in opposite directions along the z-axis by a randomly chosen distance ranging from the z semiaxis to 100 Å. To place the first cylinder, random coordinates in the xy plane were chosen from the range (0–a) and (0–b), where a and b are the x and y semiaxes of the ellipsoids. This cylinder was then rotated about the z-axis to the final position (xc, yc) by the same angle as the ellipsoid translated in the positive z-direction. The remaining three cylinders’ axes were placed in the xy plane at the remaining permutations of (±xc, ±yc). The radii of the identical cylinders were randomly chosen from the range (10–25 Å). The cylinders extended along the z-direction from the distance that the upper ellipsoid was translated to that of the lower ellipsoid. This arrangement ensures that the two ellipsoids, which have been rotated about the z-axis in opposite directions, are related to the group of cylinders in an identical manner.

The scattered intensity of each model was calculated according to a Monte Carlo method used previously (Heidorn and Trewhella 1988; Olah and Trewhella 1994). The model data are then smeared to account for the scattering instrument geometry. The quality of the fit of the model to the measured intensity profile was characterized using F, defined by equation 3. It is related to the reduced X2 parameter resulting from the P(r) fitting, but does not take into account the number of degrees of freedom used for the fit.

graphic file with name M3.gif (3)

Npts is the number of points in the data set; I(q) and Im(q) are the experimental and model intensities, respectively; and σ(q) is the experimental uncertainty of I(q).

Acknowledgments

We thank Dr. Donald K. Blumenthal of the University of Utah for helpful discussions throughout this project. This work was supported by NIH Grant DK32953 to G.M.C. and was performed in part under the auspices of the Department of Energy under contract DE-AC05-00OR22725 with Oak Ridge National Laboratory, managed and operated by UT-Battelle, LLC.; and contract W-7405-ENG-36 with Los Alamos National Laboratory, managed and operated by the University of California. W.T.H. and J.T. were supported by the DOE Office of Science/BER program in support of the Oak Ridge Center for Structural Molecular Biology.

Abbreviations

  • cryoEM, cryoelectron microscopy

  • dmax, maximum linear dimension

  • EM, electron microscopy

  • nsEM, negatively stained electron microscopy

  • PhK, phosphorylase kinase

  • Rc, radius of gyration of cross section

  • Rg, radius of gyration

  • SAXS, small-angle X-ray scattering

  • SE-HPLC, size exclusion–high performance liquid chromatography

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.041124705.

References

  1. Ayers, N., Nadeau, A., Read, O.W., Ray, P., M.W., and Carlson, G.M. 1998. Effector-sensitive cross-linking of phosphorylase b kinase by the novel cross-linker 4-phenyl-1,2,4-triazoline-3,5-dione. Biochem. J. 331 137–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Brostrom, C.O., Hunkeler, F.L., and Krebs, E.G. 1971. The regulation of skeletal muscle phosphorylase kinase by Ca2+. J. Biol. Chem. 246 1961–1967. [PubMed] [Google Scholar]
  3. Brushia, R.J. and Walsh, D.A. 1999. Phosphorylase kinase: The complexity of its regulation is reflected in the complexity of its structure. Front. Biosci. 4 D618–D641. [DOI] [PubMed] [Google Scholar]
  4. Burger, D., Cox, J.A., Fischer, E.H., and Stein, E.A. 1982. The activation of rabbit skeletal muscle phosphorylase kinase requires the binding of 3 Ca2+ per δ subunit. Biochem. Biophys. Res. Commun. 105 632–638. [DOI] [PubMed] [Google Scholar]
  5. Cohen, P. 1973. The subunit structure of rabbit-skeletal-muscle phosphorylase kinase, and the molecular basis of its activation reactions. Eur. J. Biochem. 34 1–14. [DOI] [PubMed] [Google Scholar]
  6. ———. 1980. The role of calcium ions, calmodulin and troponin in the regulation of phosphorylase kinase from rabbit skeletal muscle. Eur. J. Biochem. 111 563–574. [DOI] [PubMed] [Google Scholar]
  7. Cohen, P., Burchell, A., Foulkes, J.G., Cohen, P.T.W., Vanaman, T.C., and Nairn, A.C. 1978. Identification of the Ca2+-dependent modulator protein as the fourth subunit of rabbit skeletal muscle phosphorylase kinase. FEBS Lett. 92 287–293. [DOI] [PubMed] [Google Scholar]
  8. Consler, T.G., Uberbacher, E.C., Bunick, G.J., Liebman, M.N., and Lee, J.C. 1988. Domain interaction in rabbit muscle pyruvate kinase II. Small angle neutron scattering and computer simulation. J. Biol. Chem. 263 2794–2801. [PubMed] [Google Scholar]
  9. Dasgupta, M., Honeycutt, T., and Blumenthal, D.K. 1989. The γ-subunit of skeletal muscle phosphorylase kinase contains two noncontiguous domains that act in concert to bind calmodulin. J. Biol. Chem. 264 17156–17163. [PubMed] [Google Scholar]
  10. Glatter, O. 1982. Data treatment. In Small angle X-ray scattering (eds. O. Glatter and O. Kratky), pp. 119–165. Academic Press, New York.
  11. Guinier, A. 1939. La diffraction des rayons X aux tres petit angles: Application à létude de phénomènes ultramicroscopique. Ann. Phys. (Paris) 12 161–237. [Google Scholar]
  12. Harris, W.R., Malencik, D.A., Johnson, C.M., Carr, S.A., Roberts, G.D., Byles, C.A., Anderson, S.R., Heilmeyer Jr., L.M.G., Fischer, E.H., and Crabb, J.W. 1990. Purification and characterization of catalytic fragments of phosphorylase kinase γ subunit missing a calmodulin-binding domain. J. Biol. Chem. 265 11740–11745. [PubMed] [Google Scholar]
  13. Heidorn, D.B. and Trewhella, J. 1988. Comparison of the crystal and solution structures of calmodulin and troponin c. Biochemistry 27 909–915. [DOI] [PubMed] [Google Scholar]
  14. Heilmeyer Jr., L.M.G. 1991. Molecular basis of signal integration in phosphorylase kinase. Biochim. Biophys. Acta 1094 168–174. [DOI] [PubMed] [Google Scholar]
  15. Henderson, S.J., Newsholme, P., Heidorn, D.B., Mitchell, R., Seeger, P.A., Walsh, D.A., and Trewhella, J. 1992. Solution structure of phosphorylase kinase studied using small-angle X-ray and neutron scattering. Biochemistry 31 437–442. [DOI] [PubMed] [Google Scholar]
  16. James, P., Cohen, P., and Carafoli, E. 1991. Identification and primary structure of calmodulin binding domains in the phosphorylase kinase holoenzyme. J. Biol. Chem. 266 7087–7091. [PubMed] [Google Scholar]
  17. King, M.M. and Carlson, G.M. 1981. Synergistic activation by Ca2+ and Mg2+ as the primary cause for hysteresis in the phosphorylase kinase reactions. J. Biol. Chem. 256 11058–11064. [PubMed] [Google Scholar]
  18. Krigbaum, W.R. and Kügler, F.R. 1970. Molecular conformation of egg-white lysozyme and bovine α-lactalbumin in solution. Biochemistry 9 1216–1223. [DOI] [PubMed] [Google Scholar]
  19. Lehmann, M.S. and Zaccai, G. 1984. Neutron small-angle scattering studies of ribonuclease in mixed aqueous solutions and determination of the preferentially bound water. Biochemistry 23 1939–1942. [DOI] [PubMed] [Google Scholar]
  20. Meyer, W.L., Fischer, E.H., and Krebs, E.G. 1964. Activation of skeletal muscle phosphorylase b kinase by Ca2+. Biochemistry 3 1033–1039. [DOI] [PubMed] [Google Scholar]
  21. Moore, P.B. 1980. Small-angle scattering. Information content and error analysis. J. Appl. Cryst. 13 168–175. [Google Scholar]
  22. Nadeau, O.W., Sacks, D.B., and Carlson, G.M. 1997a. Differential affinity cross-linking of phosphorylase kinase conformers by the geometric isomers of phenylenedimaleimide. J. Biol. Chem. 272 26196–26201. [DOI] [PubMed] [Google Scholar]
  23. ———. 1997b. The structural effects of endogenous and exogenous Ca2+/calmodulin on phosphorylase kinase. J. Biol. Chem. 272 26202–26209. [DOI] [PubMed] [Google Scholar]
  24. Nadeau, O.W., Traxler, K.W., Fee, L.R., Baldwin, B.A., and Carlson, G.M. 1999. Activators of phosphorylase kinase alter the cross-linking of its catalytic subunit to the C-terminal one sixth of its regulatory α subunit. Biochemistry 38 2551–2559. [DOI] [PubMed] [Google Scholar]
  25. Nadeau, O.W., Carlson, G.M., and Gogol, E.P. 2002. A Ca2+-dependent global conformational change in the 3D structure of phosphorylase kinase obtained from electron microscopy. Structure 10 23–32. [DOI] [PubMed] [Google Scholar]
  26. Nadeau, O.W., Gogol, E.P., and Carlson, G.M. 2005. Cryoelectron microscopy reveals new features in the three-dimensional structure of phosphorylase kinase. Protein Sci. (this issue). [DOI] [PMC free article] [PubMed]
  27. Norcum, M.T., Wilkinson, D.A., Carlson, M.C., Hainfeld, J.F., and Carlson, G.M. 1994. Structure of phosphorylase kinase: A three-dimensional model derived from stained and unstained electron micrographs. J. Mol. Biol. 241 94–102. [DOI] [PubMed] [Google Scholar]
  28. Olah, G.A. and Trewhella, J. 1994. A model structure of the muscle protein complex 4Ca2+ • troponin C • troponin I derived from small-angle scattering data: Implications for regulation. Biochemistry 33 12800–12806. [DOI] [PubMed] [Google Scholar]
  29. Pilz, I. 1982. Proteins. In Small angle X-ray scattering (eds. O. Glatter and O. Kratky), pp. 239–293. Academic Press, New York.
  30. Rice, N.A., Nadeau, O.W., Yang, Q., and Carlson, G.M. 2002. The calmodulin-binding domain of the catalytic γ subunit of phosphorylase kinase interacts with its inhibitory α subunit. J. Biol. Chem. 277 14681–14687. [DOI] [PubMed] [Google Scholar]
  31. Sosnick, T., Charles, S., Stubbs, G., Yau, P., Bradbury, E.M., Timmins, P., and Trewhella, J. 1991. Orienting rigid and flexible biological assemblies in ferrofluids for small-angle neutron scattering studies. Biophys. J. 60 1178–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Svergun, D.I. and Koch, M.H.J. 2002. Advances in structure analysis using small-angle scattering in solution. Curr. Opin. Struct. Biol. 12 654–660. [DOI] [PubMed] [Google Scholar]
  33. Svergun, D.I., Richard, S., Koch, M.H.J., Sayers, Z., Kuprin, S., and Zaccai, G. 1998. Protein hydration in solution: Experimental observation by X-ray and neutron scattering. Proc. Natl. Acad. Sci. 95 2267–2272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Traxler, K.W., Norcum, M.T., Hainfeld, J.F., and Carlson, G.M. 2001. Direct visualization of the calmodulin subunit of phosphorylase kinase via electron microscopy following subunit exchange. J. Struct. Biol. 135 231–238. [DOI] [PubMed] [Google Scholar]
  35. Trempe, M.R. and Carlson, G.M. 1987. Phosphorylase kinase conformers: Detection by proteases. J. Biol. Chem. 262 4333–4340. [PubMed] [Google Scholar]
  36. Trewhella, J. 1997. Insights into biomolecular function from small-angle scattering. Curr. Opin. Struct. Biol. 7 702–708. [DOI] [PubMed] [Google Scholar]
  37. Wall, M.E., Gallagher, S.C., and Trewhella, J. 2000. Large scale shape changes in proteins and macromolecular complexes. Annu. Rev. Phys. Chem. 51 355–380. [DOI] [PubMed] [Google Scholar]
  38. Wilkinson, D.A., Marion, T.N., Tillman, D.M., Norcum, M.T., Hainfeld, J.F., Seyer, J.M., and Carlson, G.M. 1994. An epitope proximal to the carboxyl terminus of the α-subunit is located near the lobe tips of the phosphorylase kinase hexadecamer. J. Mol. Biol. 235 974–982. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES