Evaluating putative mechanisms of the mitotic spindle checkpoint

Abstract

The mitotic spindle checkpoint halts the cell cycle until all chromosomes are attached to the mitotic spindles. Evidence suggests that the checkpoint prevents cell-cycle progression by inhibiting the activity of the APC-Cdc20 complex, but the precise mechanism underlying this inhibition is not yet known. Here, we use mathematical modeling to compare several mechanisms that could account for this inhibition. We describe the interplay between the capacities to strongly inhibit cell-cycle progression before spindle attachment on one hand and to rapidly resume cell-cycle progression once the last kinetochore is attached on the other hand. We find that inhibition that is restricted to the kinetochore region is not sufficient for supporting both requirements when realistic diffusion constants are considered. A mechanism that amplifies the checkpoint signal through autocatalyzed inhibition is also insufficient. In contrast, amplifying the signal through the release of a diffusible inhibitory complex can support reliable checkpoint function. Our results suggest that the design of the spindle checkpoint network is limited by physical constraints imposed by realistic diffusion constants and the relevant spatial and temporal dimensions where computation is performed.

The eukaryotic cell cycle is driven by a self-sustained oscillator that propagates through the periodic activation of cyclin-dependent kinases. Checkpoints are surveillance pathways that monitor key events of the cell cycle. When sensing a delay in execution, the checkpoint halts the normal cell-cycle progression, thus ensuring that key events will occur only upon the successful completion of earlier ones (1). For example, a mitotic cell should not segregate its chromosomes until it has completely replicated its genome, because attempting to do so would lead to aneuploidy, which can result in lethality, birth defects, and cancer (2-5).

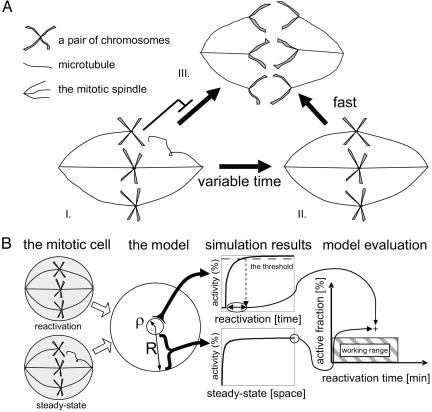
The spindle checkpoint is an evolutionarily conserved mechanism that ensures correct segregation of chromosomes at mitosis and meiosis (6-9). The checkpoint restrains cells from entering anaphase until all replicated chromatids are properly attached to the bipolar spindle (Fig. 1A). The checkpoint signal is generated at the kinetochore, a large multiprotein subunit that is located on the centromere of each chromosome and mediates the attachment of chromosomes to the mitotic spindle (7, 10). Importantly, even a single unattached kinetochore is sufficient to withhold cell-cycle progression (11).

Fig. 1.

Modeling framework. (A) A scheme of the mitotic spindle checkpoint. As long as even a single chromosome is unattached to the mitotic spindles, the anaphase does not commence, and the chromosomes do not separate (I). Once all chromosomes are properly attached, the cohesin connecting the chromosome is signaled for rapid degradation (II), and the anaphase starts (III). (B) To evaluate different models, we examined their compatibility with the physical parameters shown in Table 1. We focus on two properties of the checkpoint. First, we measure the extent of cell-cycle inhibition at steady state, before all chromosomes are attached. Second, we measure the time for reactivation once all kinetochores are properly attached. The mitotic cell is modeled as a sphere (radius R) with the last unattached kinetochore as a centrally located subsphere (radius ρ). At steady state, the extent of c-inhibition is measured by its fraction furthest away from the kinetochore. The reactivation time is defined as the time it takes for the level of uninhibited c proteins in the kinetochore vicinity to reach a certain threshold (taken here as 90%). A particular model with a given set of parameters defines a point in the “evaluation graph.” The working range corresponds to low enough inhibition (<5%) and rapid enough reactivation (<3 min).

The spindle checkpoint halts cell-cycle progression by preventing the degradation of the cohesin protein Scc1 (12), which holds the two chromatids attached and prevents their segregation to the two opposite poles. Cohesin is degraded by means of the separase protease (Esp1), which is held inactive by the securin protein (Pds1) (13). The onset of anaphase is marked by activation of the APC-Cdc20 complex (14), which degrades securin, thus triggering cohesion degradation and chromosomal separation.

The precise mechanism by which the spindle checkpoint inhibits the APC-Cdc20 activity is not yet clear. Several key proteins for checkpoint function were identified (15, 16) and were shown to be dynamically localized to unattached kinetochores (17). Unattached kinetochores stimulate the formation of at least one protein complex, the Mitotic Checkpoint Complex (MCC), which is composed of the checkpoint proteins Mad2, Mad3/BubR1, Bub3, and Cdc20 (18-20). It was suggested that the MCC prevents the formation of an active APC-Cdc20 complex either by competitively binding or by phosphorylation (21-23). Whether this inhibition is exclusive to the site of the kinetochore is not yet known. It also was argued that some amplification mechanisms are required to ensure an effective inhibition of cell-cycle progression by a single unattached kinetochore (7, 8). Such amplification could be achieved, for example, if inhibited Cdc20 was to facilitate the inhibition of additional Cdc20 molecules away from the kinetochore site (24). Nevertheless, the implication of those different propositions to kinetochore function was not yet examined rigorously.

In this work, we compare different possible checkpoint mechanisms with respect to two central requirements: (i) the capacity of a single kinetochore to maintain a tight inhibition of the APC-Cdc20 complex throughout the nucleus, and (ii) the rapid removal of this inhibition once the final kinetochore is attached. We find that, at least for budding yeast, restricting the inhibition to the kinetochore does not support reliable checkpoint function when realistic diffusion parameters are considered. Similarly, a model where the checkpoint signal is amplified by allowing inhibited Cdc20 to autocatalyze the inhibition of additional Cdc20 molecules away from the kinetochore fails to explain the checkpoint behavior. In contrast, good checkpoint function is obtained in a model where the kinetochore catalyzes the formation of a freely diffusible complex, which can inhibit Cdc20 away from the kinetochore.

Methods

Model Geometry. The mitotic cell was modeled as a sphere with radius R, with the last unattached kinetochore as a centrally located subsphere with radius ρ (Fig. 1B).

Model Assumptions. We assume all boundary conditions to be reflective and the numbers of all interacting particles to be conserved. Furthermore, because of the choice of geometry the equations are assumed to be spherically symmetric.

Numerical Calculations. Each model of the mitotic spindle checkpoint was characterized by a set of reaction-diffusion equations (see Fig. 2 D-F). We used the matlab (Mathworks, Natick, MA) function “PDEPE” to solve these equations numerically. Reactions depending on the kinetochore were restricted to a small internal sphere (Fig. 1B). Attachment of the last kinetochore was modeled by resetting the rates of all kinetochore-dependent reactions to zero. PDEPE solves parabolic equations on a semidynamic space-time grid. Several grid sizes were tested to ensure that the obtained solutions were independent of the grid sizes. A typical run on a grid of size 100 × 300 (space × time) with a personal computer (Pentium 4, 2.60 GHz) took ≈3.5 s. The direct-inhibition model in steady state also was solved analytically (for a complete derivation, see Supporting Text, which is published as supporting information on the PNAS web site).

Fig. 2.

Three possible models of the mitotic spindle checkpoint. (A) The direct inhibition model. Here the c proteins are only inhibited at the kinetochore itself. (B) The self-propagated inhibition model. The c proteins are inhibited at the kinetochore itself but also can catalyze the inhibition of additional c molecules everywhere in the nucleus at some rate κ.(C) The emitted inhibition model. Here the kinetochore catalyzes the formation of an inhibitory complex e^*, which diffuses and inhibits the c molecules everywhere at some rate γ. The activated complexes also can decay spontaneously at some rate λ, and the total amount of e complexes is denoted as E_tot. Note that the inhibited complex c^* actually consists of both c and e. A scheme of each model is shown in A-C, and the corresponding equations are shown in D-F. G-L display an example of the steady-state activation level before the attachment and the temporal increase in activation once the kinetochore is attached for a typical set of parameters: D_f = D_i = 1 μm²·s^-1, kinetochore size ρ = 0.01 μm, α = 0.02 s^-1, κ = 0.38 μM^-1·s^-1, γ = 2.5 μM^-1·s^-1, E_tot = 10C_tot, and λ = 0.1 s^-1. Note that all concentration units are defined by the amount of c molecules, which is taken here as 1,000. Changing this number will somewhat change the levels of γ and κ, but it will have no effect on our qualitative results.

Results

General Framework. To rigorously compare different mechanisms that may underlie the spindle checkpoint, we considered a simplified geometry, where a single kinetochore is approximated as a small sphere with radius ρ located at the center of a larger sphere of radius R (the nucleus; see Fig. 1B). We only considered one chromosome, representing the last chromosome that remained unattached. Indeed, because of the stochastic process governing the attachment of the chromosomes to the mitotic spindle, ≈25% of the attachment time is indeed devoted for capturing this last chromosome (see Supporting Text and Fig. 4, which is published as supporting information on the PNAS web site). We assume that cell-cycle progression is triggered by a protein c, which diffuses throughout the nucleus with some diffusion constant D. The checkpoint prevents mitotic progression by inhibiting this protein through a mechanism that is specified by each particular model.

Two parameters are used to quantify checkpoint function. First, we considered the capacity of the checkpoint to inhibit the c protein. This capacity was quantified by the steady-state fraction of uninhibited c, measured at the point furthest away from the kinetochore (close to the boundary, Fig. 1B). We denote this fraction A_c. The smaller the A_c, the more efficient is the checkpoint in inhibiting mitotic progression. Second, we considered the rate by which c inhibition is removed once the last kinetochore is attached. This rate was quantified by the time it takes to increase the level of active c back to 90% of its maximum, measured at the kinetochore vicinity (Fig. 1B). We denote this time by T_b. The shorter T_b, the more efficient is the checkpoint in removing the inhibition, thus triggering cell-cycle progression once all kinetochores are attached. We note that it appears to be equally detrimental for the cell if inhibition is too weak or if it its removal is overly prolonged (25, 26).

Several physical parameters need to be considered when evaluating checkpoint function (see Table 1). First, good inhibition of the c protein should be maintained throughout the nucleus, or at least in the region where chromosomes are present. We estimate this typical radius as 1 μm, the size of the budding yeast nucleus (27). In comparison, the size of the kinetochore that is the source of signaling is estimated to be of the order of 10 nm = 0.01 μm (7). A second important parameter is the rate of protein diffusion, which defines the time it takes for the signal to spread throughout the nucleus. Measurements of protein diffusion constants within cells have consistently found diffusion constants of the order of 0.3-3 μm²·s^-1 (28-30), approximately an order of magnitude less than the diffusion of molecules of similar molecular weight in water.

Table 1. The physical parameters controlling the spindle checkpoint function.

Physical constants (S. cerevisiae)	Denotation	Value	Ref.
Size of the nuclear radius	R	≈1 μm	27
Size of the kinetochore radius	ρ	≈0.01 μm	7
Intracellular diffusion	D	≈1 μm2·s−1	28-30
Time between final attachment and beginning of the anaphase	Tb	<3 min	5,31

Any model describing the checkpoint mechanism should comply with these parameters.

The parameters that quantify checkpoint function T_b and A_c also are constrained. A normal metaphase for budding yeast takes ≈15 min (31) and consists of two phases: a checkpoint-dependent phase before the chromosomes attach and a checkpoint-independent phase where a cascade of reactions triggered by APC activation culminates in cohesin degradation and chromosomal separation. In the budding yeast, this second phase lasts for ≈5 min (5). Due to these facts, we estimate T_b to be no longer than 3 min.

Finally, although the precise level of APC-Cdc20 inhibition that is required to prohibit premature chromosomal segregation was not yet measured, we assume that to maintain good inhibition, at least 95% of the local c molecules should be inhibited, corresponding to an A_c < 0.05. Together, those limits define the “working range” required for efficient checkpoint performance (Fig. 1B). We note that assuming different threshold level of A_c does not change our qualitative results but merely shifts the boundary of this working range.

Direct Inhibition Model. We used mathematical modeling to examine the compatibility of different checkpoint mechanisms with the physical constraints described above. Three models were formulated that correspond to alternative propositions of how the kinetochore inhibitory signal is controlled (Fig. 2 A-C). The “direct inhibition model” (Fig. 2 A and D) corresponds to the simplest situation, where inhibition is restricted to the kinetochore itself. In this model, the c molecules diffuse freely in the nucleus, with a diffusion coefficient D_f. Once a c molecule hits the kinetochore region, it becomes immediately inhibited (c^*). This inhibited molecule diffuses with a diffusion coefficient D_i and loses its inhibition at some constant rate α. Note that in this model, α is the only parameter that is not restricted by the physical constraints mentioned above.

The steady-state concentration profile of an uninhibited c molecule in the presence of an unattached kinetochore and its temporal increase once the kinetochore is attached to the spindle are shown in Fig. 2 G and J. For this typical set of parameters, the time of activation is rapid enough (T_b ≈ 1.5 min), but inhibition is quite poor (A_c ≈ 0.4, corresponding to 40% of the c molecules in their uninhibited state). Analyzing different parameters revealed an interplay between the capacity to inhibit c and the time to return back to steady state: improving inhibition comes at the expense of activation time and vice versa (Fig. 3A). Moreover, for realistic diffusion parameters (≈0.3-3 μm²·s^-1), the checkpoint performance is always outside working range (Fig. 3A). That is, for any set of realistic parameters, either the inhibition is not sufficiently tight, or the resumption of the cell-cycle progression is too slow.

Fig. 3.

Evaluation graphs for the three models described in Fig. 2. The steady-state level of active c is plotted as a function of the reactivation time. Points were generated for increasing α, as indicated. The two dashed curved correspond to different diffusion constants of the free c (A and B) and the diffusion constant of the emitted inactive complex (C), as indicated. (A) The direct inhibition model. Here, α varies between ≈0.006 and ≈0.07 s^-1.(B) Self-propagating inhibition model with κ = 0.05 μM^-1·s^-1 and α between ≈0.014 and ≈0.09 s^-1. Increasing κ provides better inhibition but leads to infinite reactivation times. (C) The emitted inhibition model. Here, λ = 0.1 s^-1, γ = 2 μM^-1·s^-1, E_tot = 10C_tot and α between ≈0.007 and ≈0.14 s^-1.

To better understand this interplay, we solved analytically and numerically for the level of inhibition (A_c) and the reactivation time (T_b) as a function of the model parameters (see Supporting Text and Fig. 5, which is published as supporting information on the PNAS web site). We found that A_c and T_b are given by the following expressions:

[1]

and

[2]

where ρ = 0.01 μm denotes the size of the kinetochore. For diffusion coefficients D = 1 μm²·s^-1, the smallest α that fulfills the reactivation constraint T_b < 180 s is ≈0.01 s^-1. However, for this value, inhibition is quite poor, with A_c ≈ 0.25. The only way of improving the inhibition without affecting the reactivation time is either by increasing the size of the kinetochore or by assuming faster diffusion, above the values that have been measured inside cells. Taken together, it appears that a system that relies solely on inhibition at the kinetochore itself cannot support good inhibition while maintaining rapid reactivation time.

“Self-Propagating Inhibition” Model. Next, we analyzed the possibility of amplifying the kinetochore signal through a positive feedback. To capture this possibility, we included an additional interaction in the model, whereby an inhibited molecule c^* can bind at some rate κ to an uninhibited c molecule and catalyze its inhibition (24). We assume that this reaction can occur everywhere in the nucleus (Fig. 2 B and E). Note that in the limit of κ → 0, the model is reduced back to the direct inhibition model considered above (see Fig. 6, which is published as supporting information on the PNAS web site).

The steady-state concentration profile of c in the presence of an unattached kinetochore and its temporal increase once the kinetochore is attached to the mitotic spindle are shown in Fig. 2 H and K. We considered here the same set of parameters used in the first model (Fig. 2 G and J), with κ = 0.4 μM^-1·s^-1. We observed that although inhibition is sufficiently tight, the system remains inhibited also upon the binding of the last kinetochore. Examining a more complete set of parameters, we observed here the same interplay between A_c and T_b as seen in the first model: improving inhibition comes at the expense of either increasing activation time (altering α) or reducing the number of activated molecules in the unattached state (altering κ). Also here, none of the parameters can support the working regime (Fig. 3B and Fig. 7, which is published as supporting information on the PNAS web site).

To better understand the behavior of this model, we examined in more details the effect of introducing the self-catalytic constant κ. Because in the limit of small κ the model is reduced back to the direct inhibition model, we considered first the limit of large κ. In this limit, the spatial c distribution is approximately uniform, and the inhibition level is given by:

[3]

Increasing κ thus can provide good inhibition. However, in this limit, once inhibition was initiated, the solution becomes self-sustained. As a result, inhibition is maintained also after the kinetochore is attached and no reactivation is possible. In fact, the maximum reactivation level is inversely proportional to κ (see Figs. 8 and 9, which are published as supporting information on the PNAS web site).

Improvement on the first model is thus in principle possible only in intermediate κ. However, exhaustive search revealed that at intermediate κ levels, neither requirement is fulfilled, even if we significantly reduce the activation threshold (see Fig. 10, which is published as supporting information on the PNAS web site).

“Emitted Inhibition” Model. An alternative means for extending the direct inhibition model is by assuming that inhibition does not occur solely on the kinetochore but that the kinetochore catalyzes the formation (or activation) of an inhibitory complex “e” that then can diffuse away from it and inhibit the c molecule everywhere (32). There are at least two ways of achieving this inhibition, either through competitive binding or phosphorylation (23). For simplicity, we consider here the former, although the latter gives equivalent results (see Supporting Text and Fig. 11, which is published as supporting information on the PNAS web site). We assume that the bound complex can exist in two possible states, an active (or assembled) state (e^*), where it can inhibit the c molecules, and an inactive (or disassembled) state (e), where it does not function as an inhibitor (Fig. 2 C and f). Although activation occurs only on the kinetochore, inactivation occurs either spontaneously or by interaction with c. This extended model includes additional parameters that define the complex diffusion and stability, (D_e, D^*_e, and λ, respectively) the number of inhibitory particles, (E_tot), and the rate of inhibition, (γ).

A typical steady-state concentration profile of c in the presence of unattached kinetochore and its temporal increase once the kinetochore is attached are shown in Fig. 2 I and L. Again, we consider the same set of parameters used to evaluate the previous two models (Fig. 2 G, H, J, and K). In contrast to the previous two models, here we observe both good inhibition and rapid reactivation times, which are well within the checkpoint working range. Indeed, although the interplay between the inhibition level and reactivation time still persists, this extended model can support proper checkpoint function for a wide range of parameters (Fig. 3C).

To further understand the behavior of this model, we performed an exhaustive numerical analysis characterizing the dependence of the extent of inhibition, A_c and the reactivation time T_c on the model parameters (see Supporting Text and Fig. 12, which is published as supporting information on the PNAS web site). We found that, in most of the working range, inhibition is given by

[4]

Here ρ denotes the size of the kinetochore, where the formation of the active complexes is catalyzed. The reactivation time is given by T_c = 2.63 α^-1 (see Fig. 13, which is published as supporting information on the PNAS web site). Note that this time is somewhat longer than in the direct inhibition model. The lag reflects the time it takes to degrade the e^* (see Supporting Text). Thus, either by allowing the emitted proteins to be more reactive (increasing γ) or by raising their numbers, the present model can support tight inhibition without compensating the reactivation time. We note that although the reaction rate (γ) cannot exceed the diffusion controlled limit, this boundary is well within the checkpoint working range (see Supporting Text).

Discussion

The mitotic spindle checkpoint is a complex machine, consisting of a large number of known components and perhaps of additional components that have not yet been identified. To precisely describe its function, the detailed characteristics of each component and the interactions between them have to be elucidated. However, regardless of those details, the checkpoint mechanism needs to comply with two basic physical constraints. The first constraint is imposed by the typical spatial dimension of the nucleus, estimated to be of the order of a micrometer, where strict inhibition of APC-Cdc20 activity is maintained. The second is imposed by the need to rapidly release the inhibition once the last kinetochore is attached. Based on typical cell-cycle times, we estimated this time to be no longer then a few minutes.

In this work, we examined the impact of those physical constraints on the possible checkpoint mechanisms. We did not simulate the full complexity of the network underlying the checkpoint but, rather, compared classes of mechanisms. Each class may be realized by a range of molecular machineries, but its essence can be summarized by a simple model, composed of just a few components.

Three models, with increasing levels of complexity, were considered. In all three models, inhibition is generated at the kinetochore. However, whereas in the first model inhibition is confined only to this region (direct inhibition), the other two models allow for its amplification elsewhere in the nucleus. The self-propagating inhibition assumes that inhibited molecules are autocatalyzed by inhibited molecules, whereas the emitted inhibition model assumes that the kinetochore catalyzes the formation of an inhibitory complex that can diffuse and act throughout the nucleus. By using rigorous mathematical formulations, we derived analytically and numerically the extent of inhibition at steady state, before the kinetochore is attached to the mitotic spindle and the time of release from inhibition once the kinetochore is becoming attached.

All models demonstrated an interplay between the extent inhibition and the time for release from inhibition. Parameters that optimize inhibition generate long reactivation time and vice versa. The constraint on optimized inhibition stems from the spatial dimension of the nucleus. In fact, the larger the nucleus, the harder it is to achieve strong inhibition. This fact may account for the observation in early Xenopus embryos that the spindle checkpoint does not become active until cells are below a certain critical volume (33).

Considering realistic parameters for diffusion inside the nucleus (D ≈ 0.3-3 μm²·s^-1) and kinetochore size (10 nm), we find that only the emitted inhibition model can simultaneously support both tight inhibition and rapid reactivation.

Our result that direct inhibition at the kinetochore cannot support reliable checkpoint function conforms to the common intuition that a single kinetochore cannot by itself inhibit APC-Cdc20 activity. Importantly, our analysis highlights the reason for this insufficiency: It is in fact possible for a single kinetochore to generate tight inhibition; however, the difficulty arises in simultaneously supporting rapid reactivation. Indeed, if an individual molecule transits a kinetochore only infrequently, it must reactivate slowly so that most molecules will revisit the kinetochore before reactivating. In fact, if diffusion inside the nucleus would have been the same as in water (>10 μm²·s^-1; ref. 34) or if the cell-cycle times were significantly longer, direct inhibition could support reliable checkpoint function.

We further find that amplifying the inhibition signal through a positive feedback is not sufficient for ensuring effective checkpoint function. The problem with such positive feedback is that it renders the fully inhibited state self-sustained. In principle, release from such self-sustained state can be catalyzed by a specific molecule, such as p31^comet, that is capable of activating Cdc20 (35, 36). However, to prevent premature reactivation, such a molecule should only be functional upon the attachment of the last kinetochore. It is not immediately apparent what mechanism could ensure such a restriction. Moreover, in yeast, no such molecule has yet been identified (36).

The effects of physical constraints on cellular mechanisms were studied extensively in the context of individual interactions. It is well known that reactions cannot proceed at a rate that is higher than the upper bound set by the diffusion-controlled limit (37). In contrast, most studies of biological networks ignore the impact of the spatial cellular dimension but assume that proteins are uniformly distributed. Our analysis here suggests that the need to comply with the typical spatial and temporal dimension, although maintaining realistic diffusion constants, may impact the design of the Mitotic Spindle Checkpoint. It is likely that the design of additional information-processing networks within cells are also limited by such physical constrains, and it will be interesting to explore what general designs are favored by such constraints.