Crystalline molecular machines: Encoding supramolecular dynamics into molecular structure

Abstract

Crystalline molecular machines represent an exciting new branch of crystal engineering and materials science with important implications to nanotechnology. Crystalline molecular machines are crystals built with molecules that are structurally programmed to respond collectively to mechanic, electric, magnetic, or photonic stimuli to fulfill specific functions. One of the main challenges in their construction derives from the picometric precision required for their mechanic operation within the close-packed, self-assembled environment of crystalline solids. In this article, we outline some of the general guidelines for their design and apply them for the construction of molecular crystals with units intended to emulate macroscopic gyroscopes and compasses. Recent advances in the preparation, crystallization, and dynamic characterization of these interesting systems offer a foothold to the possibilities and help highlight some avenues for future experimentation.

The design and construction of artificial mechanomolecular machines is one of the most interesting scientific challenges of our times (1, 2), and a deeper understanding of structure–property relations in several biological motors (3, 4) have led to considerable insights in the past few years. However, the formulation, design, and materialization of truly serviceable artificial molecular machines remains a major challenge. Whereas initial efforts have been centered on isolated molecules randomly tumbling in solution, most biomolecular systems and macroscopic machines are complex, multiple-component, densely packed assemblies, supported on membranes or within the bulk of larger structures.

In this Perspective, I will describe our group's recent efforts on a quest to control the structure and dynamics of closed-packed molecular assemblies. Our thesis is based on the premise that information contained at the molecular level in the form of topology, size, shape, nonbonding interactions, electronic structure, etc. will dictate the aggregation, dynamics, actuation possibilities, and mechanical functions. One of our initial goals is to uncover the relation between supramolecular structure and intermolecular dynamics by taking advantage of dynamic stereochemistry, self-assembly, and crystal engineering. To document this relation with as high precision and certainty as possible, we have chosen the crystalline solid state as a promising model. Structural characterizations can be carried out by single-crystal x-ray diffraction measurements, and dynamic properties can be determined over a wide range of time scales by techniques that include variable-temperature solid-state NMR, dielectric spectroscopy, and inelastic neutron scattering, among several others.

From Molecular Structure Information to Self-Assembly and Dynamics

A machine is defined as “an assemblage of parts that transmits forces, motion, or energy from one to another in a predetermined manner” (5). Not explicit in the dictionary's definition are the precisely built structures of every component, the highly correlated dynamics of many moving parts, and the need for switches, actuators, and an energy source to make it function. With an intuition that arises from handling molecular models, organic chemists have recognized that forces, motion, and energy can be transferred within molecules, or from one molecule to another, in a manner that depends on the structure of the assembly, the medium, and temperature (6). With an emphasis on information contained in the form of structure and energy, machines may be formulated in terms of the changes in degrees of freedom that occur when a collection of rigid parts is assembled (Fig. 1) (7).

Fig. 1.

The blueprints contain all of the structural information necessary to build and assemble the components of a mechanical wristwatch. Each component must have the precise structural information to fit within the assembly so as to surrender its own degrees of freedom to the degrees of freedom of the collective.

Machine Blueprints

The construction of complex machines begins with carefully designed blueprints such as those used by a watchmaker to fabricate and assemble the components of a wristwatch (Fig. 1). Wheels, ratchets, pivots, shafts, screws, cocks, barrels, etc. must be designed with micrometric precision to fit their role within the functional assembly. While the N-rigid components have a total of 3N degrees of freedom, the end product is a single unit with 3 rotational and 3 translational whole-body degrees of freedom and as few as only 1 internal degree of freedom that defines the function of the assembly. The larger the number of rigid components and the higher the density, the greater the precision required. In the case of biomolecular machines, a similar analysis starts with different types of atoms as the primary and only rigid components. Through covalent bonds, atoms come together to form (l)-α-amino acids and polypeptide chains. With structural information in the form of torsion potentials, hydrogen bonds, salt bridges, π-stacking, and hydrophobic interactions, polypeptide chains fold into precise three-dimensional structures. In subsequent hierarchical levels, proteins aggregate with each other and/or associate with membranes in sequentially more complex structures such as those observed in the bacterial flagellum, ATP-synthase, the skeletal muscle, and many others (3, 4, 8).

Naturally, there are many distinctions between macroscopic and biomolecular machines (3, 4). The internal motion and functions of macroscopic machines may be described by Newtonian dynamics and deterministic models. In contrast, biomolecular machines operating in aqueous media are subject to drag forces and random collisions with solvent molecules (thermal forces), which lead to wide distributions of trajectories that are describable by Brownian dynamics (9, 10). Whereas macroscopic machine parts may be welded together into rigid bodies carrying no internal degrees of freedom, every additional atom or group atoms in molecular machines adds to the 3N - 6 internal degrees of freedom of the system. In addition, whereas inertia is exceedingly important in macroscopic objects, biomolecular systems in aqueous media are strongly overdamped and dissipate their momenta very rapidly.

Interpolating from the high rigidity and packing density of complex macroscopic machines to the high fluidity and relatively low density of biomolecular systems, the construction of crystalline molecular machines is an intriguing mid-point. One may envision molecules and molecular components acting as gears, shafts, pivots, etc., so that they communicate their state of motion through steric contacts, electrostatic interactions, or magnetic forces. Alternatively, the function of crystalline molecular machines may rely on the collective response of reorienting dipoles to the presence of external fields, including electronic excitation by photonic stimuli (11). Dipolar arrays involving two-dimensional grids and theoretical models describing the behavior of one-dimensional dipole chains recently have been considered by the groups of Michl (12) and Ratner (13).

Structural Control of Rigidity and Motility: Amphidynamic Crystals

Experience indicates that most crystalline solids are too dense and viscous to permit any significant molecular motion. Molecular crystals tend to have high packing densities and restricted molecular dynamics (14). In going from gases and liquids to crystals, the kinetic energy of the system changes from translation, rotation, and conformational motions of individual molecules, to the collective displacements of their center of mass about their equilibrium position, known as lattice vibrations or phonons (15). Therefore, to understand and exploit the dynamics of molecules in crystals, one must learn how lattice vibrations may couple with desirable conformational modes.

A starting point in a search for a relation between molecular structure, phase order, and molecular dynamics in condensed media is given by analysis of Fig. 2. Measures of phase order and molecular motility are represented on the vertical axis and horizontal axis, respectively. Conventional molecular crystals of molecules with arbitrary shapes occupy the top left. They have the highest degree of order and the lowest molecular motility. Liquids represent the region of the map where molecules experience the greatest amounts of molecular freedom and the lowest amount of order. The smallest amount of order and motion on the bottom left is occupied by molecules in the amorphous or glassy state. Along the top left to bottom right diagonal, with decreasing amounts of order and greater amounts of motion we find plastic crystals and liquid crystals. Plastic crystals are made up of molecules with globular or cylindrical shapes that undergo rapid whole-body rotations while retaining their positional order in a homogeneous periodic arrangement (16, 17). Finally, liquid crystals have preferred molecular orientations but experience rapid rotational and translational motion. The formation of liquid crystals is also influenced by structural factors. Liquid-crystal-forming structures, or mesogens, tend to have rigid elongated (calamitic liquid crystals), bent-shaped (“banana” liquid crystals), or circular (discotic liquid crystals) rigid cores with long floppy chains (18).

Fig. 2.

Phase order–molecular motion diagram illustrating possible forms of condensed-phase matter. Crystalline molecular machines would require a combination of rigidity and mobility to warrant a high level of order and desirable dynamic processes.

It may be extrapolated from Fig. 2 that phases with high mobility and order will also require very specific structural attributes. Rigid frameworks holding dynamic components are a natural choice. Notably, the combination of opposites within a given structure tends to result in properties that are not observed in any of the components, as is the case with amphiphiles (hydrophilicity/hydrophobicity) and amphoteres (acidic/basic), among others. With the suffix “amphi” meaning “both sides,” we refer to the structures in the upper right portion of Fig. 2 as “amphidynamic” crystals. We believe that the phase order and molecular motility envisioned in amphidynamic systems will be among the most indispensable attributes of artificial molecular machines.

Volume-Conserving Motions

Complex dynamics in high-density machines such as automobile engines, typewriters, mechanical clocks, etc. rely on volume-conserving periodic processes. Although most of these are rotary, small-amplitude linear displacements can also be tolerated by taking advantage of free space or by correlating the motion of adjacent components. In fact, volume-conserving molecular motions have been well documented in crystalline solids. It is well known that methyl, tert-butyl, phenyl, and other highsymmetry substituents may have fast rotational dynamics in the solid state (19–21). Because of their relatively small size and high rotational symmetry, methyl groups experience “jumps” or dynamic “exchange” between sites related by a local threefold symmetry axis. Notably, the rates of methyl rotation in crystals can be almost as high those observed in the gas phase. Slightly larger in size, tert-butyl groups experience a three-site dynamic exchange between the three methyl groups and a similar process for each hydrogen atom within the three methyl groups. The dynamics of phenyl groups have also been investigated in terms of a twofold flipping process, as expected by their local symmetry (22).

Molecular Gyroscopes and Compasses

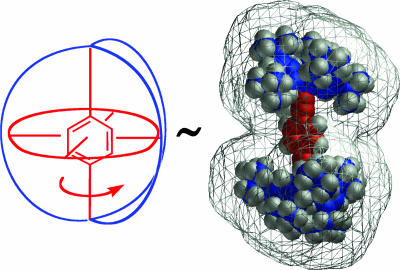
Molecular gyroscopes and compasses provide one of the most promising structural designs for the realization of amphidynamic materials (Fig. 3). Both rely on a rigid frame and one internal degree of freedom related to motion of a central rotary element. Although the two structures may be considered topologically equivalent (homeomorphic), their functions differ by their state motion and the presence of a permanent dipole that can interact with external fields. A simple gyroscope is a device consisting of a spinning mass, or rotator, with a spinning axis that projects through the center of the mass, which is mounted within a rigid frame, or stator [Michl et al. (23) have suggested that the term “rotors” be reserved to describe entire molecular assemblies, “rotators” to define the rotary units, and “stators” to depict the frames that contain the axle of rotation and the rotator]. Macroscopic gyroscopes are used as navigational devices to sense changes in orientation regardless of their frame of reference by a function that relies on the conservation of angular momentum. Gyroscopes mounted on gimbals have additional degrees of freedom and form the basis of inertial navigation systems (INS) used in airplanes and satellites. Macroscopic compasses have a similar topology, but their function depends on the response of their magnetic dipole to Earth's magnetic field.

Fig. 3.

Macroscopic gyroscopes and compasses retain their dynamic capabilities both as isolated units and as aggregates. A proposed molecular structure that may emulate their function consists of a rigid frame, or stator (in blue), and a rotator linked by a barrierless axle (in red).

Although the realization of molecular analogs of macroscopic gyroscopes presents serious challenges and limitations, the unique attributes of the molecular system may lead to many other interesting applications. Some of the challenges and limitations at the molecular level include the construction of frictionless rotators, the need for flat (or barrierless) potential energy surfaces, mechanisms to introduce a controlled impulse or a constant force to power the rotator, and, most importantly, the fact that momentum and energy are internally redistributed within a few picoseconds in dissipative molecular systems, making it very challenging to induce unidirectional rotation (9). Molecular analogs of macroscopic compasses face similar challenges. However, given that their function relies on the orientation-dependent energy of their internal dipoles with respect to external fields, closer analogies between the macroscopic and molecular worlds may be expected. Molecular compasses may be envisioned with electric or magnetic dipoles so that their bulk properties may be affected by external electric, magnetic, and electromagnetic fields. Interesting photonic, dielectric, and phonon phenomena are expected from molecular compasses arrays (13). These include addressable ferroelectric and antiferroelectric phases, polar rotary phonons that propagate at velocities slower than the typical speed of sound, and Nambu–Goldstone dipole-wave quanta, which have been suggested as potential carriers of ordering information in quantum models of the brain (24).

Crystalline Molecular Rotors

The first step to realize a macroscopic object at the molecular level is to select the atomic and molecular components that may emulate the desired structure and its function. In this case, the rotator may be any symmetric group with its center of mass aligned along a single bond that supplies both the rotary axis and the point of attachment to the static framework. The stator should provide an encapsulating frame to shield the rotor from steric contacts with adjacent molecules in the crystal. A simple molecular design, illustrated in Figs. 3 and 4, involves the use of acetylene groups as the axle for rotation and linkage, a para-phenylene as a rotator, and two triply bridged triphenylmethyl (11) or triptycyl groups (25) as the stator. The triply bridged macrocyclic structure in Fig. 3 encodes the desired elements to emulate some of the functions of a macroscopic gyroscope at the molecular level. Semiempirical quantum mechanical calculations (9, 18) and experimental observations with other triple-bonded structures (26) suggest that rotation of the central phenylene rotator should be virtually barrier-free. Because the intrinsic barriers for rotation about single bonds formed between sp–spⁿ carbons are ≈0.1 kcal/mol (9, 18, 19, 20), any hindrance observed in the solid state may be assigned to steric contacts with the stator or with neighbors in the close-packed crystal lattice.

Fig. 4.

Molecular gyroscopes with open topologies based on triptycyl (compounds 1 and 5) and triphenylmethyl (2–4) frames and phenylene rotators. Rates of “gyroscopic” rotation at the corresponding temperatures are shown below (arrows are not intended to suggest unidirectional rotation).

Synthesis and Solid-State Characterization

Our synthetic studies started a few years ago with the preparation of molecular gyroscopes with a phenylene rotator, and either triptycyl (1) (11, 24) or tri- phenylmethyl (2) groups as stators (Fig. 4). Both structures provide a rigid frame that can be refined to fine-tune material solubility, crystal packing, and the barrier for rotation. Highly convergent strategies based on Pd(0)-catalyzed alkyne-arylhalide coupling reactions make it possible to prepare a wide range of analogs. Several structures related to 1 with 4,4′-biphenylene, 9,10-anthracenylene, and 2,7-pyrenylene rotators have been described (25), and a series of isotopologues of 2 for spectral assignments and dynamic measurements in the solid state were efficiently prepared by similar methods (11). Substituents on the triptycyl and triphenylmethyl stators may be incorporated to modulate the amount of steric shielding and to attach bridges that close the topology of the frame; an elegant bridging strategy based on alkene metatheses reactions was recently developed by Gladysz et al. (27). Notably, rigid rod-like structures like those in Fig. 4 are expected to facilitate a parallel molecular alignment (28) as required for many potential photonic and dielectric applications (29).

Compounds 1 and 2 have open topologies and were prepared primarily as synthetic models, not necessarily expecting that they would exhibit efficient rotation of the central phenylene in the solid state. Diffraction-quality single crystals of 1 were obtained from meta-xylene, which was incorporated in the lattice in a 1:1 ratio. As expected from its rigidity and aspect ratio, molecules of 1 crystallize with their long axes parallel to each other, their triptycyl units strongly interdigitated by edge-to-face and face-to-face contacts with their closest neighbors, and meta-xylene molecules wedged as spacers (Fig. 5A) (25). Samples of 2 crystallized from benzene and from CH₂Cl₂ (11). Crystals grown from benzene formed a cage structure, or solvent clathrate, with two benzene molecules per cavity. Fig. 5B illustrates the structure of the cage, which is formed by four molecules acting as pillars. A parallel-displaced benzene dimer (shown in light blue) occupies the cavity's interior. Crystals from CH₂Cl₂ were solvent-free and slightly more dense than those from benzene. The structure of the solvent-free crystal (Fig. 5C) is related to that of the benzene clathrate by displacement of two molecules along their molecular axis so that their trityl groups fill-in the space left by the benzene dimer. Analysis of the two packing structures confirmed that all molecules in the crystal have their long axes aligned in the same direction. Infinite linear chains with an axis that coincides with the long molecular axis are formed by complementary edge-to-face aromatic interactions between adjacent molecules in the crystal. This robust interaction, known as a sixfold trityl embrace (30), can be used as a supramolecular synthon to guide the crystallization of these compounds (31).

Fig. 5.

Space-filling models illustrating the packing relation between solvent molecules (light blue), the central rotator (red), and the frame provided by the triptycyl or trityl groups. (A) Three views of 1 illustrating the interdigitation experienced by neighboring molecules and meta-xylene. (B) Partial structure of the benzene-clathrate of 2 with a molecule in the front plane removed to illustrate the parallel-displaced benzene dimer. (C) Packing structure of the solvent-free structure of 2 showing the proximity between trityl groups and central rotators.

Rotational Dynamics in Crystals

The closely packed structure and high rigidity observed in crystals of compound 1 illustrate the steric barriers encountered by potential rotators in the solid state. In contrast, despite its open topology and the presence of benzene molecules in the lattice, the packing density of molecular gyroscope 2 in the region of the phenylene rotator is slightly lower and suggests that rotary motion in the solid state could occur within a measurable range. To investigate this and set a benchmark for comparison of other structures we explored the use of solid state NMR, including line shape analysis methods such as variable temperature (VT) cross polarization and magic angle spinning (CPMAS) ¹³C NMR and broadband ²H NMR (25). These methods have complementary dynamic ranges and are relatively simple. The former relies on sufficient chemical-shift differences between carbons atoms at exchanging positions (32), and the latter relies on spectral changes caused by dynamic averaging of the orientation-dependent interaction between the ²H nuclear quadrupole moment and the electric field gradient at the nuclear position. With chemical-shift differences of ≈0.5–5 ppm at 75 MHz, one may expect ¹³C NMR to provide information in the range of ≈100–2,000 s^-1 and activation energies in the range of ≈10–20 kcal/mol. In contrast, ²H NMR provides rate information in the range of ≈10³ s^-1 to 10⁸ s^-1 and makes it possible to differentiate process involving continuous rotation, exchange between positions related by angular displacements of 180°, 120°, and 60°, and more complex motions (33). It should be pointed out that site exchange rates determined by NMR methods provide no information on the sense of rotation, which under thermal equilibrium is expected to be equally likely in either direction.

Although the rate ranges analyzed are different, activation energies for phenylene rotations obtained in the solid state by VT ¹³C and ²H NMR measurements with samples of 2 were internally consistent. An energy barrier of 12–14 kcal/mol for a motion involving angular displacements of 180° for the central phenylene was unprecedented for a crystalline solid and validated our original hypothesis (11, 34, 35). As indicated in Fig. 4, rates of rotation in the megahertz (10⁶ s^-1) range may be observed at a relatively low temperature of ≈65°C. The rotary dynamics of the benzene molecules in the solvent clathrate of 2 was also investigated by ²H NMR with crystals grown from C₆D₆ (34). In agreement with previous studies (36, 37) and as expected for a volume-conserving process, benzene molecules were found to undergo in-plane whole-body rotations described by 60° jumps with rate constants exceeding 10⁸ s^-1, even at 200 K.

Controlling the Barrier for Phenylene Rotation by Adjusting the Structure of the Frame

The theoretical limit for phenylene rotation estimated from its moment of inertia along the 1,4 axis falls in the terahertz regime (≈10¹² s^-1) (38). Setting our sights on barrierless rotors and using molecular mechanics as a guideline, we determined that substituents at both meta positions of each phenyl group on the trityl framework should diminish interdigitation of adjacent molecules and reduce the hindrance for rotation of the central phenylene. The hexamethoxy derivative 3 (T.-A. V. Khuong, J. Nunez, and M.A.G.-G., unpublished results) and the dodeca-tert-butyl derivative 4 (39) were prepared to determine this effect (Fig. 4). The structure of 3 is of particular stereochemical interest because of its numerous stereogenic elements (40). The axial chirality of the propeller shaped trityl groups, the planar chirality of the meta-substituted benzenes, and the relative orientation of the methoxy groups result in several isomers and crystal forms that are currently under investigation (T.-A. V. Khuong, J. Nunez, and M.A.G.-G., unpublished results). From the various crystal forms, we have analyzed the dynamic properties of crystals grown from benzene, which, unlike crystals of 2, incorporate only one solvent molecule per cavity. As expected from its lower density, phenylene rotation in 3 is faster than that in 2. An energy barrier of 11.7 kcal/mol was determined by VT ¹³C CPMAS NMR, and a barrier of 11.5 was determined by ²H NMR line-shape analysis.

In a significant step toward the construction of crystalline-free rotors, samples of the highly shielded compound 4 (Fig. 6) obtained from CH₂Cl₂ were shown to give room-temperature ²H NMR spectra corresponding to the fast exchange limit, with exchange frequencies faster than 100 MHz (39). As illustrated with a space-filling model in Fig. 6, the 12 tert-butyl groups in the structure effectively shield the rotator by forming a local cavity that prevents the interdigitation of adjacent molecules in the lattice. Unfortunately, crystals of 4 turned out to be very fragile and to lose their integrity upon cooling so that we were not able to estimate the rotational barrier. Clearly, in addition to providing suitable shielding, an ideal stator should also guide the formation of a robust crystal lattice. After a close analysis of the packing interactions in the crystal structure of compound 1, we determined that alkyl substitution at the peripheral positions of the triptycyl frames would be a promising alternative (Fig. 7).

Fig. 6.

Suggested analogy between a gyroscope schematic and a filling model from the x-ray structure of the dodeca-tert-butyl compound 4 with a 3-Å solvent-accessible surface illustrating the steric shielding provided by the tert-butyl groups. Rotation of the central phenylene (in red) at 300 K occurs at a frequency higher than 100 MHz (39).

Fig. 7.

The synthesis of molecular gyroscope 5 can be accomplished by a highly convergent method from simple chemicals (41). Crystals grown from bromobenzene, removed from the center of a cage formed by four molecular gyroscopes, result in gyroscopic rotation with a barrier of only 4.3 kcal/mol.

The introduction of 12 methyl substituents on the periphery of the triptycyl groups of structure 1 led to the least hindered molecular gyroscope prepared so far in our group. Compound 5 was obtained both in its natural abundance and phenylene deuterated forms by a highly convergent synthesis that begins with butadiene, para-quinone, and maleic anhydride (Fig. 7) (41). Analysis of single crystals obtained from bromobenzene by ²H NMR at ambient temperature revealed a remarkably narrow spectrum with a line shape that approaches the continuous rotary motion of a free rotor (C. E. Godinez and M.A.G.-G., unpublished results). In fact, the sample had to be cooled down to -90°C for the rotator to enter the intermediate regime of the ²H NMR experiment (k ≈ 10⁷ s^-1). A remarkably low activation barrier of only 4.3 kcal/mol was determined from measurements carried between -80 and -130 K. Notably, this value is only 1.3 kcal/mol higher than the gas phase barrier of 3.0 kcal/mol for the rotation of the two methyl groups in ethane. The favorable packing arrangement and relatively low packing density of compound 5 clearly suggest the feasibility of engineering a crystalline-free rotor. We believe that this feat could be accomplished with structures having closed topologies such as that shown in Fig. 3, and by using rotators with more cylindrical shapes and symmetries of high rotational order (42).

Perspective

The results on the synthesis, crystal packing, and internal rotation of molecular gyroscopes presented in this Perspective are very encouraging. Yet, in and of themselves, crystalline molecular gyroscopes cannot be labeled as molecular machines. While they are a strong lead-in to structures that may ultimately facilitate the transmission of forces, momentum, and energy, a molecular machine must respond to intended stimuli to fulfill specific functions. Amphidynamic crystals made up of structures with rotary dipolar elements will be a step closer (Fig. 8). We expect their dipolar arrays to lead into materials with promising electrooptic and dielectric functions. Our initial efforts on the preparation and evaluation of structures with polar rotators have centered on analogs of 2 with phenylene groups possessing fluoro (2F), cyano (2CN), nitro (2NO₂), amino (2NH₂), ortho-diamino-[2(NH₂)₂], and para-nitroanilino (2NH₂NO₂) substituents. These structures have dipole moments ranging from 0.74 to 7.30 Debye (43). Recognizing the steric similarity between fluorine and hydrogen atoms and having confirmed that they form isomorphous crystals (43), we recently investigated the rotary dynamics of the monofluoro derivative 2F by ²H NMR. Satisfyingly, the energy barrier for phenylene rotation in 2F (≈13 kcal/mol) is very similar to that of the parent compound 2 (≈14 kcal/mol). In addition, the dynamic coupling of dipolar motion with external AC fields currently under investigation by dielectric spectroscopy reveals very similar activation parameters (R. D. Horansky, L. I. Clarke, J. C. Price, T.- A. V. Khuong, P. D. Jarowski, and M.A.G.-G., unpublished results). We believe that rapid progress in the last 3 years portends an extremely bright future for molecular machines and materials based on dynamically functional crystals.

Fig. 8.

Suggested analogy between a macroscopic compass and the space-filling models of compound 2 and the monofluoro derivative 2F. The isosteric structures form isomorphous crystals, which have very similar rotary dynamics in the solid state.