Rapid hydrolysis of ATP by mitochondrial F₁-ATPase correlates with the filling of the second of three catalytic sites

Abstract

Strong positive catalytic cooperativity is a central feature of the binding change mechanism for F₁-ATPases. However, a detail of the mechanism that remains controversial is whether the kinetic enhancement derived from using substrate-binding energy at one catalytic site to promote product release from another site occurs upon the filling of the second or third of three catalytic sites on F₁. To address this question, we compare the ATP concentration dependence of the rate of ATP hydrolysis by F₁ from beef heart mitochondria to the ATP concentration dependence of the level of occupancy of catalytic sites during steady-state catalysis as measured by a centrifuge filtration assay. A single K_m(ATP) is observed at 77 ± 6 μM. Analysis of the nucleotide-binding data shows that half-maximal occupancy of a second catalytic site occurs at 78 ± 18 μM ATP. We conclude that ATP binding to a second catalytic site is sufficient to support rapid rates of catalysis.

During oxidative and photo-phosphorylation, F_oF₁-ATP synthases couple the movement of protons down an electrochemical gradient to the synthesis of ATP. The F_o sector is composed of membrane-spanning subunits that conduct protons across the membrane, whereas the F₁ sector is an extrinsic complex that contains the catalytic sites for ATP synthesis. F₁ can be removed from the membrane in a soluble form that functions as an ATPase. A high-resolution structure of beef heart mitochondrial F₁ (MF₁) shows a hexamer of alternating α- and β-subunits, surrounding a single γ-subunit (1). The three catalytic sites of F₁ are located on the three β-subunits at α/β-subunit interfaces.

A model for energy coupling by F_oF₁-ATP synthase that has gained widespread support is called the binding change mechanism (2). According to this proposal, the major energy-requiring step is not the synthesis of ATP at catalytic sites, but rather the highly cooperative binding of substrates to, and release of product from, these sites (3, 4). Furthermore, it is proposed that these affinity changes are coupled to proton transport by the rotation of a complex of subunits that extends through F_oF₁ (5). Rotation of the γ-subunit in the center of F₁ (6–8) deforms the surrounding catalytic subunits to give the required binding changes, whereas rotation of subunits in F_o (9–14) is required for completion of the proton pathway.

With the presence of three catalytic sites on F₁, the simultaneous occupancy of one, two, or three sites during turnover is denoted as uni-site, bi-site, or tri-site catalysis, respectively (15). Also, the term multi-site catalysis is used to refer to turnover at more than one site, without specifying whether two or three sites become occupied.

Measurements of uni-site catalysis by MF₁ have shown this mode of catalysis to be very slow due to a severe rate limitation in the product-release step (16). It is thought that, as ATP binds at a single site, the protein collapses around the ligand to form a very high-affinity site, where ATP hydrolysis is rapid and reversible, but product release is very slow. However, if additional ATP binds at an adjacent site or sites, product release from the previously loaded site becomes very rapid. The promotion of product release that accompanies substrate binding is mediated by the rotation of the γ-subunit. Energy derived from the tight binding of ATP at one site drives γ rotation, which, in turn, drives an energy-requiring conformational change at an adjacent site where stabilizing interactions between the protein and bound ADP and P_i are disrupted and product is released. The kinetic advantage of multi-site catalysis has been quantitated. The V_max for multi-site catalysis by MF₁ is 100,000-fold that of the uni-site rate (17).

A detail of the binding change mechanism for F₁ that has remained controversial is whether this strong positive catalytic cooperativity depends upon binding ATP at a second (bi-site activation) or third (tri-site activation) site. A number of laboratories have shown that, in the transition from uni-site to multi-site catalysis, the rate of product release increases as a function of the rate of ATP binding, consistent with ATP-promoted product release being rate limiting. The fact that this phenomenon is observed at nanomolar ATP concentrations led to the suggestion that ATP binding at a second site provides the major kinetic enhancement seen in multi-site catalysis (15). Additional studies of ATP synthesis and hydrolysis have provided support for this concept (18–20). However, other studies, where the occupancy of catalytic sites on Escherichia coli F₁ (EcF₁) was monitored by the fluorescence of a substituted tryptophan residue, led to the proposal that all three sites must be occupied to achieve multi-site rates (21).

In an attempt to resolve this controversy, we have measured catalytic-site occupancy during ATP hydrolysis by MF₁. In previous studies (17, 22, 23), where occupancy was measured by using a Sephadex column-centrifugation procedure (24), a maximum of ≈1 mol of ANP (ADP and/or ATP) bound per mol MF₁ was reported over a wide range of ATP concentrations. The inability of this technique to detect higher levels of occupancy is attributed to the fact that, as the enzyme passes through the column, medium ATP is removed and intermediates of multi-site catalysis decay rapidly, converting the enzyme to a uni-site mode of catalysis. Because the rate of product release during uni-site catalysis is slow compared with the time of passage through the column, the enzyme emerges in the effluent with one site occupied. To avoid this limitation, we have measured catalytic-site occupancy of MF₁ using a modification of a pressure-filtration method (18) that does not involve separation of the enzyme from medium ATP, and thus has the potential for detecting possible short lived bi-site and/or tri-site intermediates. The results show that, as the ATP concentration is increased from that which supports very low multi-site rates to a level that supports rates approaching 50% of the maximal velocity, catalytic-site occupancy increases from 1.0 to ≈1.5 mol/mol MF₁. These results demonstrate that bi-site activation is primarily responsible for multisite catalytic rates.

Experimental Procedures

Materials. ATP, potassium phosphoenolpyruvate (PEP), potassium pyrophosphate (PP_i), NADH, Tris, Sephadex G-50-80 and G-50-150, BSA, lyophilized pyruvate kinase, and lactate dehydrogenase were obtained from Sigma. Mops was from Fluka, and Bio-Safe II scintillation mixture was from Research Products International. Microcon centrifugal filter devices, YM-50, having a molecular weight limit of 50 × 10³, were from Millipore. [2,5′,8-³H]ATP (37 Ci/mmol) (1 Ci = 37 GBq) was from Amersham Pharmacia.

Enzyme Preparation. MF₁ was prepared from beef heart mitochondria (25). The enzyme was >95% pure as judged by polyacrylamide gel electrophoresis in the presence of SDS, and the specific activity for ATP hydrolysis was 120 and 58 units/mg when assayed at 30°C and 22°C, respectively. Nucleotide-depleted MF₁ (ndMF₁) was obtained by the procedure of Garrett and Penefsky (26) by using a column of Sephadex G-50-150 (1.5 × 70 cm) at a flow rate of 0.1 ml/min. Fractions with A₂₈₀/A₂₆₀ ratios >1.85 were pooled and used. The nucleotide content of the ndMF₁ preparation used in these studies was 0.46 mol/mol MF₁. Enzyme was stored at a concentration of 50–60 μM in a buffer containing 100 mM Tris/SO₄, pH 8.0, 4 mM EDTA, and 50% glycerol.

Except where noted, to minimize nucleotide binding at noncatalytic sites, ndMF₁ was preincubated with PP_i at room temperature (22°C) for 1 h. In this treatment, enzyme was diluted ≈5-fold with buffer to give final concentrations of 20 mM Mops/Tris, pH 8.0, 1.0 mM EDTA, 0.25 M sucrose, 3 mM PP_i, and 3 mM Mg(CH₃COO)₂. PP_i-treated ndMF₁ was used within 5 h of preparation.

Nucleotide-Binding Assays. The binding of [³H]ANP to PP_i-treated ndMF₁ during [³H]ATP hydrolysis was measured at 22°C by using a Microcon YM-50 centrifugal filter device to separate unbound [³H]ANP from MF₁. Reaction mixtures in a final volume of 480 μl contained 0.85 μM PP_i-treated ndMF₁, 20 mM Mops/Tris, pH 8.0, 0.2 mM EDTA, 2.2 mM Mg(CH₃COO)₂, 10 mM CH₃COOK, 20 mM KHCO₃, 10 mM PEP, 1 mg/ml pyruvate kinase, 50 nM [³H]ATP (≈7 × 10⁵ cpm), carrier ATP, and 0.5 mM MgPP_i. In experiments conducted with 1.7 μMPP_i-treated ndMF₁, components of the ATP-regenerating system were increased to 25 mM PEP and 4mg/ml pyruvate kinase. These increases ensured that even at the highest ATP concentration tested, a steady-state hydrolysis rate was maintained during the time required to complete the binding measurements. In fact, the upper limit in ATP concentration that could be tested was determined by this requirement. Controls lacking MF₁ received an equivalent volume of the enzyme storage buffer. Reaction was started by addition of PP_i-treated ndMF₁. After 5 s of mixing, a 400-μl aliquot was transferred to the sample reservoir of a centrifugal filter device. The device was placed in a fixed-angle rotor of a Sorvall/Heraeus Pico Biofuge and centrifuged at a speed setting of 13 × 10³ rpm. The centrifugation time included 13 s for acceleration, 7 s at full speed, and 11 s to stop the rotor. The receiving vial containing 23–28 μl of filtrate was discarded and replaced with a new vial. The centrifugation step was then repeated a second time. †The second filtrate (23–28 μl) was obtained within 80–85 s after initiating the reaction. Three 5-μl aliquots of this filtrate were transferred to separate scintillation vials, each containing 80 μl of water. After addition of 4 ml of Bio-Safe II scintillation mixture, vials were counted to a precision that varied from 2% at the lowest ATP concentrations tested to 0.7% at the highest ATP concentrations. Controls lacking MF₁ showed no detectable level of [³H]ATP binding to pyruvate kinase or the filter device.

The concentration of free [³H]ATP, and the stoichiometry of [³H]ANP bound to MF₁ were calculated for each sample after averaging the counting results and correcting for the fraction of radioactive impurities in the carrier-free [³H]ATP stock that was unable to bind to MF₁ (0.1007 ± 0.0011; b in the equations presented below). To determine the amount of such contaminants, 50 nM carrier-free stock [³H]ATP, with or without 200 nM carrier ATP, was incubated with a large molar excess of PP_i-treated ndMF₁ (0.4–1.7 μM) and subjected to centrifugal filtration as described above. Radioactivity in the filtrates was plotted versus the reciprocal of the enzyme concentration and extrapolated to infinite enzyme concentration by using a linear regression analysis. The average of the values obtained with 50 and 250 nM [³H]ATP was used.

The stoichiometry of total [³H]ANP bound to MF₁, N_t, was calculated according to the equation:

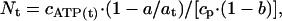[1]

where a_t is the radioactivity in 5 μl of reaction medium before centrifugation, calculated by using the radioactivity of added [³H]ATP determined at a counting precision of better than 0.2% by using at least four samples (standard deviation 0.24–0.27%), a is the average radioactivity in 5 μl of the second filtrate (the standard deviation for triplicate measurements of 79 samples in four independent experiments varied from 0.06% to 2.75% with an average value of 0.80 ± 0.5%), b is the fraction of impurities in [³H]ATP determined as described above, c_ATP(t) is the concentration of ATP including that added with [³H]ATP, and c_p is the concentration of MF₁. The concentration of free ATP, c_ATP(f) was calculated according to the equation:

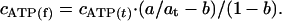[2]

To determine the stoichiometry of [³H]ANP bound specifically at catalytic sites, the total [³H]ANP bound must be corrected for ligand bound at noncatalytic sites. For this purpose, 80-s incubations were repeated under the conditions described above, followed by addition of a large excess of unlabeled ATP (2 mM) to promote dissociation of labeled nucleotide from catalytic sites. After 30 s, 100-μl aliquots were applied to 2-ml Sephadex G-50-80 centrifuge columns equilibrated with buffer containing BSA (27) to remove unbound ligand. Effluents were collected directly in scintillation vials containing 20 μl of 5% SDS. Samples were counted after addition of 4 ml of Bio-Safe II mixture. As expected, the amount of [³H]ANP retained at noncatalytic sites was low due to the pretreatment of ndMF₁ with PP_i (28, 29).

Controls lacking both preincubation with PP_i and the presence of PP_i in the reaction buffer were also conducted by the procedures described above. Although the absence of PP_i did not affect the stoichiometry of [³H]ANP bound at catalytic sites on ndMF₁, it did result in a significant increase in binding at noncatalytic sites. This increase resulted in the need for a much larger correction in calculating catalytic site-bound nucleotide, thereby limiting the upper range of substrate concentrations that could be tested. For example, this correction amounted to <0.1 mol/mol at substoichiometric ATP and 0.5, 1.4, and 1.9 mol/mol at 5, 20, and 50 μM ATP, respectively.

Other Assays. ATP hydrolysis by PP_i-treated ndMF₁ was measured spectrophotometrically (30) at 22°C. The assay contained 1 ml of 20 mM Mops/Tris, pH 8.0, 0.2 mM EDTA, 2.2 mM Mg(CH₃COO)₂, 10 mM CH₃COOK, 20 mM KHCO₃, 0.5 mM MgPP_i, 10 mM PEP, 0.3 mM NADH, 0.15 mg/ml pyruvate kinase, 0.15 mg/ml lactate dehydrogenase, and 2.5–1000 μM MgATP. Reaction was initiated by adding PP_i-treated ndMF₁ (final concentration 1–20 nM, depending on the ATP concentration), and data acquisition (2 points per s) was initiated within 3 s. ATP hydrolysis rates were calculated by using linear regression analysis of data points collected during the first 85 s of assay, although rates remained constant for at least 5 min.

Protein was determined by a modified Lowry procedure (31). BSA was used as a protein standard, and the values for MF₁ were divided by 1.18 to convert to dry weight (26). A value of 371 kDa was used as the molecular mass of MF₁ (32).

Results

To accurately determine the stoichiometry of [³H]ANP bound at catalytic sites during hydrolysis of [³H]ATP, it was important to avoid dilution of the specific activity of the radioisotope due to release of endogenous ANP (≈3 mol/mol) from native MF₁. For this reason, we prepared ndMF₁ as described under Experimental Procedures. Furthermore, to decrease [³H]ANP binding at noncatalytic sites, we preincubated ndMF₁ with PP_i and included 0.5 mM MgPP_i in binding and activity assays. Although PP_i significantly diminishes nucleotide binding at noncatalytic sites (28, 29), it does not affect the kinetic properties of MF₁ (33). By using this form of the enzyme, calculating the amount of [³H]ANP bound at catalytic sites from the total amount bound, as measured by a centrifuge-filtration assay, required only a small correction for [³H]ANP bound at noncatalytic sites (Fig. 2, filled symbols). An additional benefit of the presence of PP_i was that it significantly decreases the onset of MgADP-induced inhibition during ATP hydrolysis by MF₁ (28, 33, 34). Such inhibition is due to formation of an inactive, slowly reversible MgADP·enzyme complex (35) in which the inhibitory ligand is bound at a catalytic site (36). To further reduce the possibility of MgADP inhibition, we included an activating anion, bicarbonate (37, 38), in our nucleotide binding and ATP hydrolysis assays. It is important to note that a steady-state hydrolysis rate was maintained during the time required to complete all binding measurements.

Fig. 2.

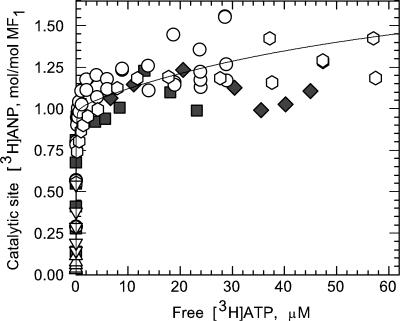
Analysis of the binding data. The results for [³H]ANP binding to PP_i-treated ndMF₁ catalytic sites (Fig. 1, open symbols) and noncatalytic sites (filled symbols) are presented in a semilogarithmic plot. The solid line represents a best fit of the data (open symbols) to an equation N = N_m·(2[ATP]² + [ATP]·K_s,2)/([ATP]² + [ATP]·K_s,2 + K_s,1·K_s,2) that describes the sequential occupancy of two catalytic sites on MF₁, where N is the measured stoichiometry of nucleotide bound at catalytic sites, K_s,1 and K_s,2 are ATP concentrations required for half-maximal occupancy of the first and second sites, respectively, and N_m is the stoichiometry of ANP that binds to each site at saturation. The best-fit values obtained by a nonlinear regression analysis for K_s,1, K_s,2, and N_m are ≤15 nM, 78 ± 18 μM, and 1.00 ± 0.02 mol/mol of MF₁, respectively. It should be noted that, as expected from the large difference between K_s,1 and K_s,2, the same values were obtained for a fit that does not require sequential binding.

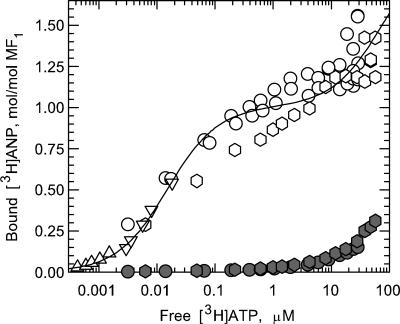
Fig. 1 shows the ATP concentration dependence of [³H]ANP binding at catalytic sites on PP_i-treated ndMF₁ (open symbols) during [³H]ATP hydrolysis by using centrifugal filtration to measure total nucleotide binding, and column centrifugation, after a cold chase, to measure nucleotide bound at noncatalytic sites. The results demonstrate that low MgATP concentrations suffice to saturate one catalytic site on MF₁, consistent with earlier studies using the column-centrifugation method (15, 17, 22, 23). More importantly, the results show that a second catalytic site is not saturated in the presence of low micromolar concentrations of MgATP. Analysis of the data (Fig. 2, open symbols) yields substrate concentrations required for half-maximal saturation of the first (K_s,1) and second (K_s,2) catalytic sites on MF₁ of ≤15 nM and 78 ± 18 μM, respectively.

Fig. 1.

Dependence of MF₁ catalytic-site occupancy on substrate concentration. Total and noncatalytic site binding of [³H]ANP to MF₁ were measured as described under Experimental Procedures. The stoichiometry of nucleotide bound at catalytic sites was obtained by subtracting the amount bound at noncatalytic sites from the total bound, and the results were plotted on the y axis. PP_i-treated ndMF₁ at 0.85 μM (circles) or 1.7 μM (hexagons) was incubated with varying [³H]ATP concentrations, or [³H]ATP at 50 nM (triangles) or 250 nM (inverted triangles) was incubated with varying MF₁ concentrations. Measurements were repeated omitting PP_i and using 0.85 μM (filled squares) or 1.7 μM (filled diamonds) ndMF₁.

To test for a possible competitive effect of PP_i on nucleotide binding at catalytic sites, we repeated the measurements, omitting pretreatment of ndMF₁ with PP_i and excluding PP_i from the assay buffers. As shown in Fig. 1 (filled squares and diamonds), omitting PP_i does not result in an increase in nucleotide binding at catalytic sites. However, as noted under Experimental Procedures, corrections for binding at noncatalytic sites were much larger.

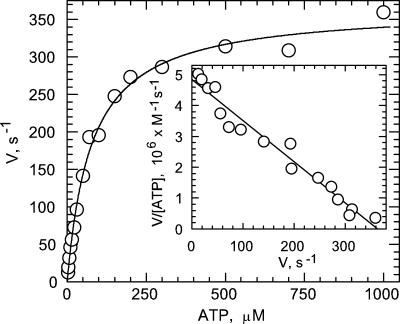
Fig. 3 shows the substrate concentration dependence of the ATP hydrolysis activity of PP_i-treated ndMF₁ under conditions similar to those used for the binding experiments. The results do not exhibit significant deviation from Michaelis–Menten kinetics as evidenced by a good fit of the experimental points to the theoretical line, and by the lack of significant deviations from linearity in Eadie–Hofstee (Fig. 3, Inset) and Lineweaver–Burk (data not shown) plots. Such a result is as expected under conditions that prevent MgADP-induced inhibition from occurring during assay (39). The K_m value for MgATP obtained from Fig. 2 is 77 ± 6 μM in agreement with the K_s,2 value obtained for filling a second catalytic site (Fig. 2). The results show that, during steady-state, multi-site catalysis, MgATP binding to a second catalytic site is sufficient to support rapid multi-site rates.

Fig. 3.

Dependence of MF₁ rates of catalysis on substrate concentration. The rate of ATP hydrolysis by PP_i-treated ndMF₁ was measured as described under Experimental Procedures. Solid line, best fit of the data to the Michaelis–Menten equation (K_m = 77 ± 6 μM; V_max = 367 ± 8 s^–1). (Inset) An Eadie–Hofstee analysis of the same data.

Discussion

The most important conclusion drawn from the current study is that bi-site activation is responsible for the major catalytic rate enhancement that results from subunit cooperativity during multi-site catalysis by MF₁. Early kinetic studies of uni-site catalysis by MF₁ showed that, when a single catalytic site is loaded, the rate-limiting step is the slow release of product from a high-affinity site (16). However, when substrate is allowed to bind at multiple sites, release of product is accelerated by up to 100,000-fold (17). It was suggested that the major rate enhancement occurred upon binding substrate at a second site, and that the loading of the third site provided little or no additional enhancement. This model was supported by several observations. First, beginning at ≈1 nM ATP, over four-orders of magnitude below the K_m, the rate of catalysis by MF₁ increases linearly with increase in ATP concentration (15, 17). This result has recently been confirmed in single-molecule measurements with a subcomplex of Bacillus PS3 F₁ where the frequency of γ rotation steps is seen to increase linearly with increase in ATP >1 nM concentration (40). It seems likely that these rate accelerations are due to binding substrate at a second site rather than binding at both a second and third site. In the latter case, if the K_s for the second site were >1 nM, a lag in the response to increased ATP concentration would have been expected in contrast to the linear response observed. Alternatively, if the K_s for the second site were <1 nM, the occupancy of a second high-affinity site should have been readily detected by a centrifuge column-binding assay. In contrast to this prediction, when MF₁, which is undergoing steady-state, multi-site catalysis over a wide range of ATP concentrations, is passed through a centrifuge column, a single catalytic-site bound nucleotide is retained (17, 22). However, the possibility existed that removal of medium ATP during the few seconds it takes for enzyme to pass through a centrifuge column might have destabilized a doubly loaded, low-activity form. Data presented in Figs. 1 and 2 show that this is not the case. In a centrifuge-filtration assay, where MF₁ remains in contact with medium ATP, catalytic-site occupancy increases from 1.0 to 1.5 mol/mol as multi-site rates are increased from very low levels to a rate approaching 50% of V_max.

These results are not consistent with models that propose that all three sites must be occupied for rapid catalysis because they predict 2.0–2.5 sites occupied over this range of multi-site rates. The most frequently cited support for such models comes from measuring changes in the fluorescence of a tryptophan substituted at each catalytic site of EcF₁ (21). In fact, on the basis of such measurements, it has been claimed that bi-site catalysis makes little or no contribution to the rate of multi-site catalysis (41).

Although EcF₁ has proven a very useful system to study because of the ease of genetic manipulations, in our experience, it is much less tractable in kinetic studies for the following reasons: (i) EcF₁ is much more sensitive to MgADP inhibition than MF₁ (42), (ii) EcF₁ is strongly inhibited by its ε-subunit (43), whereas its homolog in MF₁ is noninhibitory, (iii) it is more difficult to control for nucleotide binding at noncatalytic sites on EcF₁, and (iv) activating anions such as selenite are problematic with EcF₁ because they not only decrease MgADP inhibition at low concentrations, but also depress catalytic activity at high concentrations. Specific problems that may have been encountered in attempting to use Trp fluorescence to correlate catalytic-site occupancy with catalytic rates have been summarized elsewhere (2, 40, 44).

Perhaps the strongest evidence for tri-site activation comes from single-molecule measurements, which show that the binding of Cy3-ATP is followed by the binding of two additional ATP, detected by the accompanying rotational events, before product Cy3-ADP is released (45). However, the authors point out that Cy3-ADP may be retained at the catalytic site more tightly than ADP, thereby requiring the binding of a second ATP to promote its release (see discussion below).

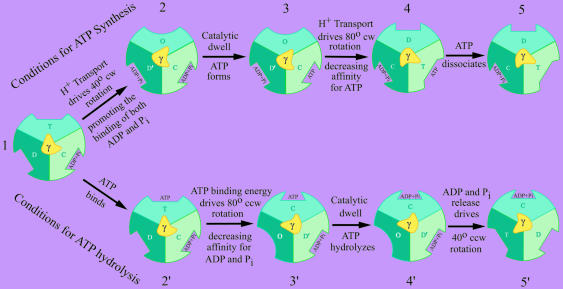
The advantages of a bi-site model have recently been reviewed (44). Having a transitory intermediate with two empty sites allows one of the sites to have a preference for ADP binding (Fig. 4, conformations D and D′) and the other for ATP binding (conformation T) (46). As shown in Fig. 4, which site on F₁ loads first and which direction the γ-subunit rotates will depend on the relative concentrations of ATP and ADP/P_i as well as on the magnitude of the electrochemical gradient. Under conditions favoring ATP synthesis (Fig. 4, upper pathway), catalysis progresses sequentially through intermediate forms 1 to 5. These transitions include the energy-driven binding of ADP and P_i (1 → 2), the formation of ATP at the high-affinity, catalytically competent C site (2 → 3), and the energy-driven release of ATP from the high-affinity site (3 → 5). In the energy-driven steps, protons moving down an electrochemical gradient drive subunit rotation in F_o, which in turn drives a 40° (1 → 2) and an 80° (3 → 4) clockwise rotation of γ in F₁ (47, 48). The 40° rotation drives a conformational change (D → D′) that promotes the binding of substrates, and the 80° rotation drives a conformational change (C → T) that promotes the release of product. In the latter step, binding energy derived from an increase in affinity for ADP and P_i bound at an adjacent site (D′ → C) may assist in driving γ rotation (49, 50).

Fig. 4.

A model for the mechanism of ATP synthesis and hydrolysis by F_oF₁-ATP synthases. Each schematic cross section of F₁, as viewed from the membrane surface, depicts three stationary catalytic sites (different shades of blue/green) surrounding the asymmetric rotor shaft of the γ-subunit (yellow). The orientation of γ determines the properties of the catalytic sites, where the conformational states are defined as follows: C, a high-affinity catalytic site at which ATP forms reversibly and spontaneously [designated in earlier versions of this scheme (54) as T for tight]; D, a conformation of the catalytic site that binds ADP preferentially; D′, a conformation that readily binds both ADP and P_i; T, a conformation that binds ATP preferentially; and O, a low-affinity transitional conformation between the D and T states. In the upper pathway, ATP synthesis at the site positioned at 4 o'clock occurs by sequential passage through intermediate stages 1 to 5. The clockwise (cw) rotational steps (1 → 2 and 3 → 4) are driven by proton transport through F_o. In the lower pathway, ATP hydrolysis at the site positioned at 12 o'clock occurs by sequential passage through intermediate stages 1 to 5′. In this case, the counterclockwise (ccw) rotational steps are driven by ATP binding energy derived from the T → C transition (2′ → 3′) and by the D′ → D conformational change (4′ → 5′). Only one third of the catalytic cycle is shown for either synthesis or hydrolysis. In the complete cycle, γ rotates 360°. Form 1 is identical to forms 5 and 5′ except that γ has rotated +120° and –120°, respectively, with the associated binding changes.

Under conditions favoring ATP hydrolysis (Fig. 4, lower pathway) catalysis progresses sequentially through intermediate forms 1 to 5′. These steps include the binding of ATP at a catalytic site in the T conformation (1 → 2′), an 80° counter-clockwise rotation (2′ → 3′) driven by an increase in affinity for bound ATP (T → C), which in turn drives a decrease in affinity for ADP and P_i bound at an adjacent site (C → D′), the hydrolysis of ATP at the C site (3′ → 4′), and a 40° counter-clockwise rotation (4′ → 5′) driven by the D′ → D conformational change accompanied by the release of ADP and P_i.

One feature of the mechanism that warrants further comment is the D → D′ conformational transition. The finding that, at physiological concentrations, ADP (18) and P_i (51, 52) can both readily bind at the same catalytic site in presence, but not in the absence, of an electrochemical gradient, suggests that the D → D′ conformational change (1 → 2) is endergonic. Under ATP hydrolysis conditions, the reverse transition, D′ → D, should be exergonic and capable of driving the 40° counterclockwise rotation of γ (4′ → 5′).

Another point of interest concerns alternative substrate binding steps from those depicted in Fig. 4. For example, under conditions of high substrate concentration during ATP synthesis, ADP may bind to form 4 at the D site at a faster rate than the rate of release of ATP from the T site. Likewise, during hydrolysis of high concentrations of ATP, ATP may bind before completion of product release from the D site. In neither case is it anticipated that loading the third site will result in any significant further acceleration of the rate of catalysis. However, as has been noted (44), such binding events at high substrate concentrations may partly explain results from Trp fluorescence measurements (21). Also, with regard to the Cy3-ADP data discussed above, Cy3-ADP may remain bound at the D site (form 5′) until the site is converted to the O conformation in a subsequent step (2′ → 3′).

The ability of F₁ to bind nucleotide at all three catalytic sites simultaneously is not in question. Such a capacity has been well established by earlier studies (e.g., refs. 27 and 53). The question, rather, is whether the main kinetic enhancement occurs upon filling the second or third site. Whatever the answer, we believe it unlikely that this feature of catalysis will be different for MF₁ and EcF₁. Results presented here using a direct measure of nucleotide binding by fully active MF₁ undergoing steady-state catalysis provide evidence that bi-site activation is primarily responsible for the strong positive catalytic cooperativity exhibited by the enzyme.