Cadherin Mechanics and Complexation: The Importance of Calcium Binding

Abstract

E-cadherins belong to a family of membrane-bound, cellular adhesion proteins. Their adhesive properties mainly involve the two N-terminal extracellular domains (EC1 and EC2). The junctions between these domains are characterized by calcium ion binding sites, and calcium ions are essential for the correct functioning of E-cadherins. Calcium is believed to rigidify the extracellular portion of the protein, which, when complexed, adopts a rod-like conformation. Here, we use molecular dynamics simulations to investigate the dynamics of the EC1-2 portion of E-cadherin in the presence and in the absence of calcium ions. These simulations confirm that apo-cadherin shows much higher conformational flexibility on a nanosecond timescale than the calcium-bound form. It is also shown that although the apo-cadherin fragment can spontaneously complex potassium, these monovalent ions are incapable of rigidifying the interdomain junctions. In contrast, removal of the most solvent-exposed calcium ion at the EC1-2 junction does not significantly perturb the dynamical behavior of the fragment. We have also extended this study to the cis-dimer formed from two EC1-2 fragments, potentially involved in cellular adhesion. Here again, it is shown that the presence of calcium is an important factor in both rigidifying and stabilizing the complex.

INTRODUCTION

Cadherins constitute one of the most important families of molecules involved in cell adhesion. They participate in specific cell-cell interactions in many multicellular organisms by forming principally homophilic interactions. Cadherins come in a number of different families, and roughly 100 cadherin genes have been identified within the human genome (1–3). Their expression is crucial for both embryogenesis and tissue morphogenesis. Cadherin damage, or modification of their expression, can lead to a number of disorders and notably plays a major role in the invasive potential of tumor cells and the formation of metastases (4). As their name implies, cadherins (or “calcium-dependent adherent proteins”) require calcium for their activity.

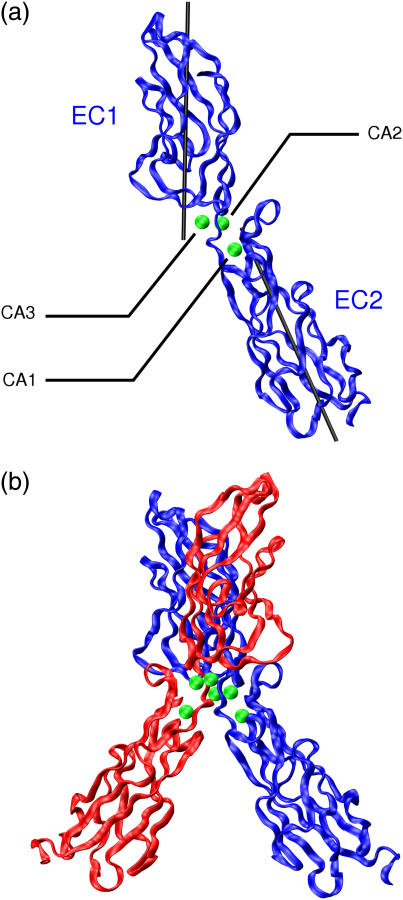
In this study, we have focused our attention on E-cadherin, one of the best-characterized members of the type I (or classical) cadherin family, which also includes C- and N-cadherins. E-cadherins are an important component of epithelial adherens junctions. The interactions mediated by these membrane-spanning glycoproteins involve their extracellular (EC) segments, which comprise five Ig-like Greek key β-strand domains, numbered from the membrane-distal N-terminal domain, EC1–EC5. Each such domain contains roughly 110 amino acids, including a 10 residue interdomain junction which is characterized by three calcium binding sites. Calcium binding is known to control the conformation of the modular EC segment. Electron microscopy studies on both the complete E-cadherin molecule and on the first two domains (hereafter referred to as EC1-2) have shown that a physiological concentration of calcium leads to a rod-like shape, whereas, in the absence of calcium, the structure collapses to a compact form (5,6). Lack of calcium also renders cadherins susceptible to protease attack (2), and the mutation of certain residues directly involved in calcium binding, such as Asp-134, which participates in the CA1 site (see Fig. 1 a), also inactivate E-cadherin (7).

FIGURE 1.

Ribbon diagrams of EC1-2 fragments of E-cadherin. (a) Monomer, showing the three calcium ions (in green) bound at the domain junction and the axes used to characterize the relative position of the two domains. (b) cis-dimer of EC1-2 (PDB file 1FF5, (11)). The images in Figs. 1 and 4 were prepared using VMD (33).

A number of crystallographic studies have provided structures which partly confirm these observations. Thus, a bent rod-like structure has been observed for the complete C-cadherin ectodomain with bound calcium ions (8). For E-cadherin, three crystallographic structures and one NMR structure have been solved. Although the NMR structure only concerns the EC1 domain (Protein Data Bank (PDB) code 1SUH) (9), the x-ray structures contain dimeric structures of two domain EC1-2 fragments. The first such studies (PDB codes 1EDH and 1FF5) (10,11) yielded dimers in which the two EC1 domains interact in a parallel fashion, a conformation now termed a cis-dimer. More recently, a trans-dimer structure, where the two fragments are antiparallel, has been solved (PDB code 1Q1P) (12). One feature distinguishing the two types of dimer concerns the position of a tryptophan side chain of the EC1 domain (Trp-2), which is docked in the hydrophobic pocket of the partner molecule in the trans-dimer while remaining within its own pocket in the cis-dimer. This modification, leading to strand exchange in the trans-dimer, appears to be important for stability (11).

The biological significance of the cis- and trans-dimers is still unknown, and both types of interaction have been considered in building models of intracellular interactions (13). The cis-dimer studied here is thought to play a role in the interaction between cadherin molecules from the same cell as a prerequisite for interactions between cadherins from two distinct cells. It does not thus presuppose an interaction mechanism between the cells. More recently other models have been proposed which use the trans-dimer to explain cell-cell contacts, still with cis interactions, but of another nature. However, at this stage there is no definitive evidence in favor of any of these models. Calcium binding is another important issue concerning cadherins. Electron microscopy has been used by different groups to observe the global shape of cadherin molecules (5,6,11). In the presence of calcium, electron micrographs show elongated molecules exhibiting some modularity, with oligomerization at high protein concentration. In contrast, the cadherin structure collapses in calcium-free media, and the relative orientation of the domains becomes variable. NMR chemical shift changes upon addition of Ca²⁺ to EC1-2 solutions confirm this restructuring (14). These changes have been localized at the interface of EC1 and EC2 domains. Analysis of ¹⁵N T₁ and T₂ relaxation times provides further information on the rigidification of the molecule upon Ca²⁺ binding. At higher protein concentration and in the presence of calcium, NMR data also reveal the formation of dimers and higher order aggregates. The contacts observed between monomers largely agree with the crystallographic data.

Despite these results, the relative importance of the different calcium binding sites at the domain interfaces remains unclear. Pokutta et al. (6) used circular dichroism and tryptophan fluorescence to monitor calcium binding to cadherin. The K_d values obtained by the two techniques differ substantially, but the fluorescence data indicate strong cooperativity between the calcium binding sites (although at the time of these experiments, the number of calcium ions bound to cadherins was not known, and these results should therefore be treated with caution). Alattia et al. (5) also noted enhanced cooperativity after dimer formation. Lastly, equilibrium dialysis measurements of calcium affinity for EC1-2 (15) supported a model with two equivalent binding sites and a third low-affinity site. The authors proposed that the site CA3 (see Fig. 1) was the probable low-affinity site because it was the most solvent-exposed and because the EC1 fragment did not fix calcium ions even though it contained all the necessary chelating amino acids.

Despite the biological and clinical importance of cadherins, and the availability of a wide variety of experimental data, very few computational studies have dealt with this fascinating family of molecules. To our knowledge, there are only two such studies, one dealing with the potential stabilizing role of a disulfide bond between the monomers forming an E-cadherin cis-dimer (16) and, more recently, a steered molecular dynamics study of the trans-dimer of C-cadherin (17) which confirms the mechanistic importance of Trp-2 in dimer stabilization. In recent years, our group has become interested in the mechanical properties of proteins and especially in how these properties are related to structure (18,19). The cadherin exodomains present an interesting mechanical behavior where successful interactions appear to depend on rigid rod-like conformations, which in turn depend on calcium ions being bound at the interdomain junctions. We have therefore attempted to analyze the role of these ions using a series of molecular dynamics simulations which are analyzed from the point of view of conformation and thermodynamics.

The results we have obtained on both monomer and cis-dimer EC1-2 fragments of E-cadherin confirm the impact of calcium binding: with calcium the interdomain junctions are rigid, without calcium they become flexible hinges. The simulations also show that, in the absence of calcium, the calcium binding sites can be occupied by monovalent ions. These interactions are, however, insufficient to rigidify the interdomain junctions. In contrast, there appears to be a distinction in the relative importance of the three calcium sites, and loss of calcium at the most exposed site does not significantly increase the flexibility of the EC1-2 monomer. Lastly, it is shown that calcium binding is essential to cis-dimer formation, both by preorganizing the EC1-2 fragments into a conformation adapted to dimerization and by thermodynamically stabilizing the monomer-monomer interactions.

MATERIALS AND METHODS

Initial configuration

We have chosen to use the 1FF5 structure of the EC1-2 cis-dimer (11) as our starting point, principally because the alternative structure 1EDH (10) lacks the N-terminal residues (and notably the important residue Trp-2) due to molecular disorder within the crystal. We have, however, deleted the first residue Met-1, which is not present in the biologically active molecule. The first chain of the 1FF5 dimer has been used as a starting point for the EC1-2 monomer studies. The pKa of ionizable residues has been calculated using WHATIF software (20). All residues were found to be in a standard ionization state at neutral pH with bound calcium ions. In the absence of calcium, the pKas of several Glu and Asp residues normally chelating calcium were high enough to suggest protonation in the native conformation; however, since the ion binding sites rapidly deform and become solvent accessible in the absence of calcium (see Results section), these residues were left in their anionic form. The monomer and cis-dimer structures were independently solvated in truncated octahedral boxes of TIP3P water molecules (21) whose edges lie at a minimum distance of 10 Å from the solute. K⁺ ions were added to neutralize the cell and further K⁺ and Cl⁻ ions to achieve an ionic concentration close to 0.15 mol/L⁻¹. The monovalent ions were positioned randomly within the simulation cell. This led to systems involving roughly 90,000 atoms.

Molecular dynamics simulations

All the simulations have been carried out using the AMBER 7 program (22) with the parm99 force field (23). Simulations were carried out under periodic boundary conditions, and electrostatic interactions were treated with the particle mesh Ewald method (24,25), using a real-space cutoff of 1 Å. A 2-fs time step was used with SHAKE restraints (26) applied on all bonds involving hydrogen atoms. The systems were equilibrated by starting with 2000 steps of minimization using 25 kcal/mol/Ų quadratic restraints imposed on all the atoms of the protein and the Ca²⁺ ions. The temperature of the systems were then increased during 10 ps to reach 300 K and then held at this temperature during a further 40 ps of constant volume simulation. The restraints on the solute were then gradually relaxed from 5 to 0.5 kcal/mol/Ų during a series of 1000 step minimizations and 25 ps molecular dynamics equilibrations. Finally, 50 ps of unrestrained dynamics were performed before the production phase. With one exception, all production runs were carried out for between 10 and 15 ns.

Structural analysis

Standard analysis of the molecular dynamics simulations was carried out using the Ptraj and Carnal modules from the AMBER 7 package (22). Root mean-square deviations (RMSDs) were calculated using all nonhydrogen atoms. The deformation of calcium binding sites has been studied by analyzing the distance between the axially opposed ligands chelating each ion. These distances refer to the closest oxygen atoms of the Asp, Glu, or Gln residues bound to each calcium. Residue accessible surface areas (ASA) have been computed using a Korobov surface grid with 610 points and a probe radius of 1.4 Å corresponding to a water molecule (27). The residue buried surface area (BSA) is defined as the difference between the ASA of the residue in the EC1-2 monomer and the ASA of the same residue in the cis-dimer. To characterize the relative positions of the EC1 and EC2 domains during the molecular dynamics simulations, we have calculated a bending angle using an optimal helical axis for each domain based on the strands of its β-barrel motif and defined using the approach proposed by Rosenberg et al. (28). An arbitrarily chosen β-strand residue within each domain enabled us to define a vector perpendicular to the domain axis, and thus to also calculate a torsion angle between the two domains. (N.b. residues Tyr-77 and Lys-129 in EC1 and EC2, respectively, were chosen to give a torsion angle close to zero in the reference crystal structure.)

Estimating the free energy of dimerization

Free energy estimates were obtained using the MM-PBSA approach (29). This involved extracting 500 snapshots from the appropriate monomer and dimer simulations (sampling every 10 ps during the last 5 ns of the simulation). Conformational energies were calculated using AMBER parm99 parameters (with a Ca²⁺ Born radius of 1.72 Å, chosen to obtain a correct hydration free energy for this ion (30)), whereas the solvent was modeled as a dielectric continuum using a numerical Poisson-Boltzmann solution with a grid spacing of 0.67 Å, a solute dielectric of 1, a solvent dielectric of 78.5, and a salt concentration of 0.15 mol/L⁻¹. A surface area term with a surface tension of 0.005 kcal/mol/Ų was calculated. All surfaces were obtained using a 1.4 Å probe radius. Conformational entropies were extracted using normal mode calculations (31) for 10 snapshots sampled uniformly from the last 5 ns of each simulation. Conjugate gradient minimizations, carried out before normal mode calculations, were converged to 0.0001 kcal/mol/Å using a 4r distance-dependent dielectric function.

RESULTS AND DISCUSSION

The E-cadherin fragments we have studied (drawn from the PDB file 1FF5), the EC1-2 monomer, and the EC1-2 cis-dimer are shown in Fig. 1. This figure also shows the axes used to define the relative orientation of the monomer domains and the three calcium binding sites, termed CA1, CA2, and CA3, which characterize the junction between the EC1 and EC2 domains. The junction residues involved in chelating the calcium ions are shown in Fig. 2. Note that the CA3 site has only five chelating amino acids and is the most exposed ion binding site.

FIGURE 2.

Geometry of the interdomain calcium binding sites. The histogram at the bottom of the figure shows the evolution of the calcium binding sites in terms of the distance between the chelating atoms of axially opposed amino acid side chains: 1FF5 crystallographic values (solid), C3 (open), C2 (shaded), and C0 (crosshatched). For the values coming from EC1-2 monomer dynamics simulations, the standard deviation of each distance is indicated by error bars.

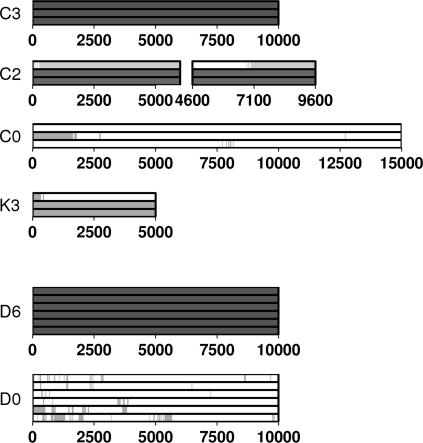
To simplify the presentation of the dynamics simulations we have carried out, each simulation is referred to by a code composed of a letter and a number. Four simulations concern the EC1-2 monomer (C3, C2, C0, K3) and two concern the cis-dimer of EC1-2 (D6, D0). The letters C and K refer to simulations set up with complexing calcium or potassium ions, respectively, and the letter D refers to dimer simulations. The number indicates the total number of ions which complex the EC1-2 junctions. The presence of ions in the interdomain binding sites is summarized in Fig. 3, which will be discussed in more detail below. Ion binding is measured using geometrical criteria: a calcium is considered bound if it lies within 4 Å of at least N − 1 of the N initial chelating side-chain atoms, and a potassium is considered bound, using a more liberal definition, if it lies within 4 Å of at least two of these atoms. With the exception of K3 (see below), the production phase of each simulation was 10−15 ns.

FIGURE 3.

Occupation of the calcium binding sites during the dynamics simulations (time in picoseconds). Solid zones correspond to calcium binding, and shaded zones to potassium binding. Each group of three bars corresponds to the sites CA1, CA2, and CA3 reading from bottom to top.

EC1-2 monomer dynamics

We begin by discussing the influence of ion binding on the conformational fluctuations of the EC1-2 monomer. Our first simulation (C3) had all three junction binding sites occupied by calcium ions, as in the crystallographic conformation of this fragment and in the supposed active form of E-cadherin. During the simulation, the EC1-2 fragment remained close to the experimental structure as shown by the heavy-atom RMSD plot in Fig. 4 a (thin shaded line), which fluctuates between values of 2–3 Å. Removing the most exposed calcium ion from site CA3 does not significantly change this situation, as shown again in Fig. 4 a (simulation C2, thin solid line). Interestingly, during this simulation, the vacant calcium ion binding site was spontaneously occupied by a monovalent potassium ion from the surrounding solvent/counterion shell (see Fig. 3). After 6 ns of simulation, we decided to remove the bound potassium by exchanging it with a distant water molecule. The system was then reequilibrated with 1000 steps of minimization and 100 ps of unrestrained dynamics before restarting the production phase. As seen in Fig. 3, a new potassium ion bound to the site after 2 ns of simulation, but no significant increase in conformational fluctuation was seen either before or after this second binding event (thin solid line in Fig. 4 a). It is remarked in passing that recent simulations (32) show that the diffusion constant of potassium ions with TIP3P water seems to be roughly twice the experimental value; consequently, the speed of the potassium binding events seen here may be somewhat accelerated. Note that the geometry of the ion binding sites shown in Fig. 2 supports the results seen in the overall behavior of the EC1-2 fragment. Removing calcium from the CA3 site has only a limited effect on this site and no visible impact on the two remaining occupied sites.

FIGURE 4.

RMSD with respect to the crystallographic conformation of the EC1-2 monomer. (a) Simulations C3 (thin shaded), C2 (thin solid), C0 (thick solid), and K3 (thick shaded). The break in the C2 line corresponds to restarting the simulation after removing a potassium ion from site CA3. (b) Values for EC1 (shaded) and EC2 (thick solid) during the C0 simulation. The thin solid line corresponds to domain EC2, excluding the loop residues 130–145.

We now turn to the simulation of the apo-EC1-2 fragment (C0). Without any bound calcium ions at the domain junction, the EC1-2 fragment became dramatically more flexible. This is illustrated by the RMSD values in Fig. 4 a (thick solid line), which now fluctuates around 7–14 Å. It is however interesting to note that these strong fluctuations only begin after ∼1.5 ns. This delay seems to be connected to potassium binding, which occurs during this interval at site CA2 (see Fig. 3), suggesting that potassium can, at least momentarily, stabilize the domain junction. To check whether potassium could lead to long-term stabilization, we consequently set up another simulation (K3) with all three calcium binding sites occupied with potassium. The results in Fig. 3 show that although the ion in site CA3 rapidly dissociated, the other two potassium ions remained in place. The loss of the ion at CA3 can be attributed to the deformation of the binding site. This also occurs for site CA2 to a lesser extent, although the ion remains (but we also recall that we have used a relatively lenient measure of binding in the case of potassium). These ions did not, however, stabilize the junction, as shown by the RMSD plot in Fig. 4 a (thick shaded line), with fluctuations rapidly reaching the level seen in the C0 simulation. K3 was consequently not continued beyond 5 ns.

We can now look in more detail at the nature of the conformational fluctuations observed in the absence of calcium. It should first be noted that the increased RMSD values discussed above correspond largely to relative movements of the EC1 and EC2 domains, rather than to deformation within the domains. This is illustrated for the apo-EC1-2 simulation (C0) in Fig. 4 b. The RMSD fluctuations for domains EC1 (thin shaded line) and EC2 (thick solid line) are both below 4 Å. EC2 is, however, somewhat less stable than EC1, for which the fluctuations hardly exceed 2 Å. This difference can be traced to a flexible loop in the EC2 domain involving residues 130–145 (which can be seen at the upper right hand corner of domain EC2 in Fig. 1). Note that residues from this loop (Asp-134, Asp-136, Asn-143) are involved in both the CA1 and CA2 sites. If we remove this loop from the RMSD calculation, Fig. 4 b shows that the remaining part of the EC2 domain (thin solid line) undergoes fluctuations which resemble those of EC1. Since most of the fluctuations in the C0 simulation occur at the domain junction, it is not surprising to note that the geometry of the calcium binding sites is strongly perturbed. This is visible in Fig. 2, where it can be seen that, in contrast to the small effect resulting from the removal of a single calcium ion at the CA3 site, the removal of all three ions leads to a rapid dilation of the distances separating the chelating amino acids.

To characterize the relative movement of the two cadherin domains, we have used the bending angle formed between the axes of the β-barrels within each domain and the torsion defined using a reference residue within each domain (see Materials and Methods). The results for the calcium-bound C3 simulation and the apo-EC1-2 simulation (C0) are given in Table 1 and summarized graphically in Fig. 5. Whether we look at the bending angle or the torsion, the results for the C0 simulation clearly show much more interdomain movement than the calcium-bound C3 case. With calcium ions in place (shaded lines in Fig. 5), the two domains remain roughly coaxial, although the angle between them decreases slightly with respect to the experimental value (152–154°), and only small torsional fluctuations are seen. As expected from the RMSD plots shown in Fig. 4 a, removing a single calcium ion from the most exposed CA3 site has little mechanical impact and does not significantly reduce rigidity of the interdomain junction. In contrast, without calcium (solid lines in Fig. 4 a), the domain junction becomes a strikingly flexible hinge, with an interdomain bending angle which fluctuates between roughly 60° and 120°. This hinging movement is also coupled to increased torsional freedom between the domains as seen in the lower part of the figure, where the fluctuations now cover a roughly 120° range compared to roughly 40° in the presence of calcium ions (see also Table 1). Fig. 6 clearly illustrates the interdomain bending and torsion fluctuations during the C0 simulation with four snapshots taken at 5 ns intervals.

TABLE 1.

Average values and standard deviations (°) of the bending angle and the torsion between the EC1 and EC2 domains during the dynamics simulations

Simulation	Time interval	Bending angle	Torsion
C3	2.5–10	137 ± 6	−18 ± 9
C2	2.5–11	144 ± 7	−31 ± 9
C0	5–15	81 ± 17	27 ± 24
K3	2.5–5	84 ± 10	−26 ± 13
D6	2.5–10	138 ± 7	−16 ± 6
		147 ± 5	−15 ± 7
D0	5–10	107 ± 11	6 ± 9
		139 ± 11	−79 ± 11
Crystal		154	−16
			152	−16

Data from Fig. 4 were used to determine the time intervals (nanoseconds) in which the RMSD in each dynamics simulation was stable enough to allow averaging. The crystallographic results refer to PDB file 1FF5 (11).

FIGURE 5.

Interdomain (a) bending angle and (b) torsion for EC1-2 during the C0 (solid line) and C3 simulations (shaded line).

FIGURE 6.

Snapshots extracted at regular intervals from the C0 simulation showing interdomain flexibility in the absence of bound calcium ions. The axes of the domains are shown in black. The upper (EC1) domains of each snapshot have been placed in identical orientations.

Removing calcium ions clearly destabilizes the EC1-2 junction region and thus represents an additional entropic penalty to be overcome in forming a cadherin dimer. However, this is not the only impact, since the cis-dimer interface extends along the surface of the EC1 domain down to the calcium binding sites. Increased interdomain fluctuations may therefore also deform the dimer interface (14). We will return to this point shortly.

EC1-2 cis-dimer dynamics

The first simulation of the cis-dimer was carried out in the presence of six calcium ions (D6). Under these circumstances the dimer remains stable with both the overall RMSD (shaded line in Fig. 7 a) and the values for the constituent EC1-2 monomers (solid lines) remaining around 2–3 Å. These values are similar to those seen in the simulation of the calcium-bound isolated monomer.

FIGURE 7.

RMSD with respect to the crystallographic cis-dimer structure of EC1-2 (shaded lines) during simulations D6 (a) and D0 (b). Solid lines show the RMSD fluctuations of each EC1-2 fragment with respect to their crystallographic conformation.

If we now remove the bound calcium ions, the situation changes dramatically and the RMSD values increase to ∼6 Å (Fig. 7 b). In this case, it can be seen that the fluctuations influence both the complex (shaded line) and the conformation of the constituent monomers (solid lines). In fact, one of the monomers undergoes less deformation than the other, which may be due to the spontaneous but, in this case, intermittent binding of potassium ions. This occurs mainly in the CA1 and CA2 sites of the monomer illustrated in the lower three lines of the ion-binding plot for simulation D0 in Fig. 3.

We can again look at this dynamic behavior in terms of the angle and the torsion between the β-barrel axes characterizing the EC1 and EC2 domains of each monomer. The results in Fig. 8 show that with six bound calcium ions (shaded lines), both the bending angle and the torsion angle for the D6 simulation remain close to the crystallographic values (see Table 1) and show little fluctuation. In contrast, without bound calcium, the D0 simulation (solid lines in Fig. 8) shows a slow drift toward smaller bending angles and increased torsional fluctuation.

FIGURE 8.

Interdomain (a) bending angle and (b) torsion for EC1-2 during the D6 (shaded line) and D0 simulations (solid line).

To summarize, calcium ion-binding rigidifies the monomers and keeps them in an optimal conformation for cis-dimer formation. Removing the calcium leads to significant deformation of the dimer, although the fluctuations within each monomer are damped to some extent by the existence of the dimer interface.

EC1-2 cis-dimer interface and stability

We now turn to a more detailed look at the cis-dimer interface in the presence or in the absence of bound calcium ions. A first way to characterize this interface is to calculate its interfacial area. The results for the D6 (shaded line) and D0 (solid line) simulations are given in Fig. 9. This measurement confirms the stability of the calcium-bound dimer, with an interfacial area fluctuating around a stable mean value of ∼2400 Ų. In contrast, without calcium, there are large fluctuations, which at times decrease this value by up to 35%. In fact, even when the interfacial area for the D0 simulation increases again to values close to those seen with D6 (after 10 ns of simulation), this corresponds to a strongly modified dimer interface. To analyze these changes, we have looked at how the BSA of each amino acid within the EC1-2 monomers varies (data not shown). The main dimerization zones involve the 25 N-terminal residues, as well as residues around positions 100, 140, and 200. Only minor changes occur in these regions for the D6 dimer, whereas extensive changes are seen with D0, mainly involving a loss of contact at the N-terminal and around residue 100 and the formation of new contacts around residues 90 and 195.

FIGURE 9.

Evolution of the interface area during the simulations D6 (shaded) and D0 (solid).

We have carried out MM-PBSA calculations to get an estimate of the influence of calcium ions on the thermodynamic stability of the EC1-2 cis-dimer. The final results given in Table 2 (details of the various energy terms are available from the authors) show that in the presence of calcium (using snapshots drawn from the D6 and C3 simulations) the dimer has a formation-free energy around −30 kcal/mol, with a strongly favorable enthalpic term largely dominating the entropic loss associated with dimerization. In the absence of bound calcium, using snapshots from the D0 and C0 simulations, the dimer is clearly unstable since although increased flexibility slightly lowers the entropic penalty of association, the enthalpic term is strongly unfavorable. This change can partially be attributed to electrostatic repulsion between the anionic residues of the CA1 and CA2 sites, which are close to the dimer interface. We can estimate this repulsion to be roughly 60 kcal/mol by comparing the 2 × C3 → D6 association in the presence and in the absence of bound calcium (see Table 2). However, this implies that D0 dimerization is further destabilized by roughly 70 kcal/mol due to changes in the apo-monomer conformations and the consequent disruption of the dimer interface. It is lastly interesting to note that without a calcium ion in position CA3, the 2 × C3 → D6 snapshots yield an electrostatic interaction energy that is even slightly stronger than that with CA3 occupied (see last line of Table 2). Although this enthalpic term is likely to be offset by a slightly increased entropic penalty, it supports the idea that the CA3 cation may not be essential for cis-dimerization. The last line of Table 2 shows that a stable complex could, in principle, be formed if potassium ions were substituted for calcium (despite the increased net negative charge of each monomer). This result was, however, obtained using snapshots from trajectories where calcium maintains the geometry of the binding sites at the EC1-2 junctions. In reality, as the simulation K3 shows, the monovalent potassium ions are incapable of providing this stabilization and thus dimerization would, nevertheless, be unfavorable, not because of increased electrostatic repulsion but because of loss of structure.

TABLE 2.

MM-PBSA thermodynamics of EC1-2 cis-dimer formation (kcal/mol)

Dimerization	ΔH	−TΔS	ΔG
2 × C3 → D6	−84	55	−29
2 × C0 → D0	100	48	148
2 × C3 → D6 (without ions)	−27	-	-
2 × C3 → D6 (without CA3)	−99	-	-
2 × C3 → D6 (with K+ ions)	−65	-	-

The last three lines of the table refer to values obtained with snapshots from the C3 and D6 simulations after removal of all the calcium ions, after removal of the calcium at position CA3, or after replacing all the calcium ions with potassium.

CONCLUSIONS

Molecular dynamics simulations have provided a detailed view of the role of calcium ions in determining the mechanical properties of the most important ED domains of E-cadherin. In line with a number of experimental studies, it is found that the junction between the EC1 and EC2 domains behaves like a flexible hinge in the absence of bound calcium. This result is in agreement with the electron microscopy experiments discussed earlier which show the collapse of the cadherin structure under these conditions. The presence of calcium fixes this junction in terms of bending and torsion at a geometry close to that seen in crystallographic studies and is in line with the NMR data. Interestingly, only two out of the three bound calcium ions appear to play a significant role in this rigidification, the absence of the most exposed ion (at the CA3 site) having little impact on the dynamics of the junction. It is also found that vacant calcium sites can be occupied, at least temporarily, by monovalent potassium ions drawn from the surrounding environment. This result appears to be in agreement with the observed nonequivalence of the three binding sites and also supports cooperativity of ion binding, in that CA3 binding requires correctly constituted and bound CA1 and CA2 sites. Calcium ion binding is confirmed to be an essential key to cis-dimer formation, by fixing the monomers in an appropriate conformation for interaction and by hindering fluctuations within the resultant complex. Free energy estimates confirm that dimerization is strongly unfavorable in the absence of bound calcium ions, due to two roughly equal effects: electrostatic repulsion between the anionic amino acids at the empty calcium binding sites and destruction of the monomer binding interface. This is once again in agreement with the experimental observation that Ca²⁺ binding is a prerequisite for the association of two EC1-2 monomers. Studies are currently underway to extend these simulations to the trans-dimer of E-cadherin with the aim of better understanding the conformational and thermodynamic aspects of alternative cadherin interactions and hopefully, via in silico point mutations, the mechanism of their specificity.