Role of Protein Flexibility in Ion Permeation: A Case Study in Gramicidin A

Abstract

Proteins have a flexible structure, and their atoms exhibit considerable fluctuations under normal operating conditions. However, apart from some enzyme reactions involving ligand binding, our understanding of the role of flexibility in protein function remains mostly incomplete. Here we investigate this question in the realm of membrane proteins that form ion channels. Specifically, we consider ion permeation in the gramicidin A channel, and study how the energetics of ion conduction changes as the channel structure is progressively changed from completely flexible to a fixed one. For each channel structure, the potential of mean force for a permeating potassium ion is determined from molecular dynamics (MD) simulations. Using the same molecular dynamics data for completely flexible gramicidin A, we also calculate the average densities and fluctuations of the peptide atoms and investigate the correlations between these fluctuations and the motion of a permeating ion. Our results show conclusively that peptide flexibility plays an important role in ion permeation in the gramicidin A channel, thus providing another reason—besides the well-known problem with the description of single file pore water—why this channel cannot be modeled using continuum electrostatics with a fixed structure. The new method developed here for studying the role of protein flexibility on its function clarifies the contributions of the fluctuations to energy and entropy, and places limits on the level of detail required in a coarse-grained model.

INTRODUCTION

Proteins, and biomolecules in general, are classified as soft condensed matter to distinguish them from the usual hard matter, which is rigid due to crystal structure. Because of the flexibility of the bonding interactions between neighboring atoms, proteins exhibit a rich variety of motions at room temperature ranging from the very fast bond vibrations to very slow breathing and domain motions (1). From a biological perspective, the interesting question is whether these motions play a role in protein function, or they are just thermal noise serving no purpose at all. There are some cases where protein flexibility is known to be important to function: oxygen binding to myoglobin is a classic example (2), and there is a host of allosteric enzymes that change conformation upon binding of a ligand (1). However, for the majority of proteins, the link between flexibility and function is far from obvious.

Molecular dynamics (MD) simulations provide a detailed description of biomolecules at the atomic level, thus they are ideally suited for exploring the role of flexibility in protein function. The flexible nature of proteins was obvious from the first MD simulation of the bovine pancreatic trypsin inhibitor (3), and has been emphasized in countless MD simulations since then. Unfortunately, quantifying the role of flexibility in protein function via MD simulations remains a difficult task, because in most proteins, motions of interest occur beyond the nanosecond time domain that can be currently accessed by MD simulations. Thus, for most proteins, adaptation of coarse-grained models appears to be the only avenue for exploring the role of flexibility in function (4). Membrane proteins that form ion channels offer one of the best candidates for investigating this issue at the level of MD. The function of the channel protein is conductance of ions, and the transit time of ions across membrane channels is of the order of nanoseconds. Any coupling between the motion of a permeating ion and those of protein atoms has to occur at a shorter timescale, which should be accessible with current MD simulations.

The role of flexibility in ion permeation has, indeed, been investigated in several recent articles using the simplest known channel, gramicidin A (gA) (5–7). The choice of gA for this purpose is clear—it is the narrowest known channel with the smallest number of water molecules in the pore. Hence a permeating ion has maximal interaction at close range with the neighboring peptide atoms throughout the channel, whereas the pore water provides minimal amount of screening. If flexibility plays a role in ion permeation, it should appear most conspicuously in the gA channel. One can also make a case for the selectivity filter of potassium channels (8). However, the situation there is not as favorable as gA because the selectivity filter is much shorter and permanently occupied by two K⁺ ions in the functional form of the channel.

In all three articles on the gA channel mentioned above, MD simulations were carried out to obtain snapshots of the protein structure, which were then fed into the Poisson equation to calculate the electrostatic potential energy profiles of a cation along the channel axis. That is, conclusions on the role of protein flexibility were drawn not directly from the MD simulations but from the secondary continuum electrostatics calculations. Failure of continuum electrostatics in the gA channel is fairly well established by now, and hence any conclusions inferred from such calculations are bound to be suspect. Difficulties of describing the single-file water column in gA using a continuum dielectric approach are well known (9,10). More recently, the invalidity of continuum electrostatics in the gA channel was shown conclusively through a comprehensive comparison of the calculated permeation properties with the available experimental data (11). This conclusion was not altered even when the protein flexibility was taken into account in the continuum electrostatics calculations (7).

Clearly, coarse graining of the channel structures obtained from MD simulations via continuum electrostatics is not a viable approach in gA. To obtain a correct assessment of the role of flexibility in ion permeation, one has to stay at the level of MD, at least until some better coarse-grained approach is developed. Since the determination of the KcsA crystal structure (12), the application of MD simulations to ion channels has grown rapidly, displacing some of the more phenomenological methods traditionally used in description of channel properties (for recent reviews, see Kuyucak et al. (13), Tieleman et al. (14), and Roux et al. (15)). Despite some problems with the current force fields (16), MD simulations still provide the most reliable method at present for deciphering complex questions on structure-function relations. Because a direct determination of the channel conductance is not feasible from MD simulations, we use an indirect method for this purpose; namely, the potential of mean force (PMF) of a potassium ion traversing the channel. The PMF summarizes the overall response of the system to the ion's motion and provides a reasonable estimate of the conductance rate. To see the effect of flexibility on the energetics of ion conduction, we consider three structures for gA, i), the peptide is completely flexible, ii), only the C, C_α, and N atoms in the backbone are fixed, and iii), all the peptide atoms are fixed. For each channel structure, the PMF of a permeating potassium ion is determined from MD simulations. We stress that in the second case, the carbonyl oxygens and amide hydrogens are not fixed. Our choice stems from the fact that the carbonyl and amide groups play an important role in ion permeation, and fixing them would lead to a situation similar to the third case, which is not very illuminating. For convenience, we will denote the second case as backbone fixed below although this term is usually understood to mean that only the side chains are flexible.

To see the response of the peptide atoms more directly, we analyze the trajectory data obtained from the MD simulations of the fully flexible structure further. We investigate how the average density of the peptide atoms, and the fluctuations about that average, change as the ion is moved along the channel axis. We also quantify the correlations between the ion's motion and fluctuations of the peptide atoms. Analysis of such correlations is crucial in establishing whether an average protein structure may be used in a coarse-grained model of a channel. Because of the concerns raised above about continuum modeling, this is not of immediate concern for gA. However, such analysis will be of considerable importance for the validation of other coarse-grained channel models such as potassium (17–20) and calcium (21), where use of continuum electrostatics in Brownian dynamics simulations has yielded good agreement with experimental conductance data.

METHODS

Model system

The simulation system is very similar to the one we used previously in calculation of the PMF of potassium ions in the gA channel (16). It consists of the peptide dimer embedded in a bilayer made of 96 dimyristoylphosphatidylcholine molecules and hydrated with ∼3200 water molecules. The only change in the our simulations in this work is that the hybrid peptide structure used in the previous work (one monomer was taken from Ketchem et al. (22) and the other from Koeppe et al. (23)) is replaced with the gA dimer taken from Ketchem et al. (22). This replacement is carried out by ensuring a maximal overlap among the corresponding backbone atoms. In a recent comparison of various NMR structures of gA (24), it has been pointed out that the 1JNO structure (25) provides a better starting point for MD simulations of gA compared to 1MAG (22). Nevertheless, most of the differences between the two NMR structures were observed to disappear after a few nanoseconds of MD simulations (24). Also our purpose here is to study the role of flexibility for a given peptide structure, so the exact starting point is not that important.

The initial structure is placed in an orthorhombic periodic box and equilibrated with surface-tension coupling until the surface area converged to the experimental lipid density of 60 Ų per lipid. (26). In the remaining simulations, the periodic box is fixed in the x and y directions at 60 Å and 52 Å, respectively. A pressure coupling of 1 atm is applied in the z direction, which results in an average box length of 64 Å in that direction. To prevent rotation of the system in long simulations, weak planar restraints of 0.1 kcal/mol/Ų are applied to the lipid phosphate atoms at z = ±17 Å. After lipid preparation, 24 water molecules in the reservoirs are replaced by 12 pairs of potassium and chloride ions to create an electrolyte solution of ∼200 mM. The system structure after the initial equilibration period is shown in Fig. 1.

FIGURE 1.

The model system: gA dimer (green helix) embedded in a dimyristoylphosphatidylcholine bilayer and solvated with ∼3200 water molecules and 12 pairs of KCl ions. K⁺ ions are indicated by blue balls and Cl⁻ ions by red balls. Only the phosphate head groups of lipids (purple balls) are shown for clarity.

Molecular dynamics

MD simulations are carried out using the NAMD code, version 2.5 (27) with the PARAM27 version of the CHARMM force field (28), which provides a complete set of parameters for all the atoms in the system. An NPT ensemble is used with periodic boundary conditions. Pressure is kept at 1 atm using the Langevin piston method with a damping coefficient of 5 ps⁻¹ (29). Similarly, the temperature is maintained at 298 K through Langevin damping with a coefficient of 5 ps⁻¹. Electrostatic interactions are computed using the particle-mesh Ewald algorithm. The list of nonbonded interactions is truncated at 13.5 Å, and a switching cutoff distance of 10 Å is used for the Lennard-Jones interactions. A time step of 2 fs is employed for all simulations. Trajectory data are written at 1 ps intervals during both equilibration and analysis runs.

Initially, a steepest descent minimization of the system with 10,000 steps is carried out, followed by heating to 298 K over 50 ps, whereas the peptide atoms are kept fixed in their original (1MAG) positions. This system with the fixed peptide atoms is then further equilibrated with temperature and pressure coupling for 1 ns. The system thus obtained forms the input for the PMF calculations with a fixed structure. Next, the constraints from all the peptide atoms except the C-C-N atoms forming the backbone are lifted, and the system is equilibrated for 1 ns. This system is used in PMF calculations with a backbone-fixed structure. Finally, the remaining constraints on the backbone atoms are slowly relaxed from 50 to 0.05 kcal/mol/Ų in eight steps during 2 ns of MD simulations. After a further 1 ns equilibration, this system is used in PMF calculations with a flexible structure. We have retained the small restraint of 0.05 kcal/mol/Ų on the C-C-N backbone atoms in subsequent simulations to prevent the drift of the system in long MD runs. Otherwise this restraint has negligible effect on the flexibility of the peptide atoms. For example, in a typical 1 Å excursion of an atom, its effect is only 3% of the kinetic energy, which is too small to have much influence on the dynamics of the system. We have checked this by running a parallel MD simulation with no restraints and comparing the root mean-square (rms) fluctuations. As the restraining force is reduced to zero, the plateau for the rms fluctuations gradually increases from 0 to ∼1 Å. Unlike the other restraints, the rms plateau for 0.05 kcal/mol/Ų is found to be indistinguishable from that of the no-restraint case. Comparison of the current PMF with the earlier ones obtained without restraints (e.g., Allen et al. (16 and 33)) also shows that this restraint has negligible effect, e.g., they all exhibit a central barrier of ∼20 kT.

An interesting question is whether the NMR structure provides a reliable input for the fixed-structure calculations. Equilibration with water usually leads to substantial changes in the peptide structure, which could be quite significant for the energetics of an ion in the narrow lumen of gA. To address this issue, we have performed a further 100 ps simulation of the equilibrated flexible structure, obtaining 100 snapshots of gA. Among these, the one that showed the minimum rms deviation from the averaged structure is selected for a second PMF calculation with a fixed structure.

Potential of mean force

The PMF of potassium ions along the gA channel axis is calculated using umbrella sampling (30) together with the weighted histogram analysis method (31–32). As the method was explained in Allen et al. (16) in some detail, we give a brief account here stressing only the differences from our present work. An ion's position is sampled at various positions along the channel axis using an umbrella potential. The biased ion distributions obtained from the MD production runs are then unbiased and combined using the weighted histogram analysis method. In Allen et al. (16), a potassium ion was dragged along the channel axis in 0.2 Å steps, and the ion was equilibrated for 20 ps at each step using an umbrella potential. A better procedure that avoids potential equilibration problems associated with this method is to replace individual water molecules in the pore with a potassium ion (33). This way, one obtains ∼10 configurations with the ion placed at regular intervals along the channel axis. The ion in each configuration then needs to be pushed by only ∼1 Å to either side to generate the full set of windows required in the PMF calculation. Outside the channel, where equilibration is not a problem, the ion is pushed along the central axis as before.

In each of the four PMF calculations, this procedure is used to generate 161 windows on the channel axis between z = ±20 Å with a window distance of 0.25 Å. A force constant of 25 kT/Ų is employed in the biasing potential, which results in substantial overlapping of ion densities among the neighboring windows. Initially, each of the configurations obtained from ion-water substitution is equilibrated for 200 ps. Next the ion in each configuration is moved to the left and right with umbrella potentials to generate 97 windows between z = ±12 Å. The windows are generated sequentially; that is, the system is equilibrated for 50 ps for each window potential before pushing the ion to the next window position. Finally the ions at z = ±12 Å are pushed out to ±20 Å in 0.25 Å steps with 50 ps equilibration at each step. Each of the 161 windows is equilibrated for a further 100 ps (200 ps in the case of flexible structure) before starting the production runs.

The ion density data for the PMF calculations are produced in two stages. In the first stage, the same umbrella potential as in equilibration is used, and 100 ps of MD data are collected for ion positions at every time step for each window. This 16 ns of MD production run is repeated for all four structures. To reduce the computation time, the number of windows is halved in the second stage. That is, a window size of 0.5 Šwith a force constant of 12.5 kT/Ų is used in the umbrella potential. Another 100 ps of MD data are collected for ion positions again for all four structures but now for 81 windows. Apart from some local fluctuations, the PMFs obtained from two different umbrella potentials are found to be very similar. To ensure adequate sampling, MD simulations for the flexible structure are continued for a further 200 ps. Thus the PMF is determined from 400 ps of MD simulations for the flexible structure and from 200 ps of MD simulations for the other three structures.

The ion coordinates are measured with respect to the center of mass of gA, and the PMF of ions is determined from the ion distributions between z = ±20 Å. We find that neither the initial NMR structure nor the equilibrated structures exhibit a clear symmetry around z = 0. A similar asymmetry is also found in the PMF calculations, which exhibit a few kT shift in energy between the left and right profiles. To understand the nature of this asymmetry, we have performed longer MD simulations using a smaller system (16 lipids instead of 48), which enabled us to extend the PMF calculations up to 1 ns. Our results show that when we use the symmetrized ion densities (i.e., ρ_sym(z) = [ρ(z) + ρ(−z)]/2), the PMF converges already after 0.4 ns to within 1 kT. However, when the raw densities are used, the asymmetry in the PMF persists even after 1 ns. Fluctuations of the center of mass of gA with respect to the lipid bilayer (up to an angstrom) appear to be the major reason for this asymmetry, and hence symmetrizing the ion densities around z = 0 is a reasonable way to deal with this problem in shorter simulations.

Ion-peptide densities, fluctuations, and correlations

Comparison of PMF calculations with fixed and flexible structures allows us to assess the contribution of peptide flexibility to the energetics of ion permeation, but tells us nothing about the actual response of the peptide to a permeating ion, which is needed to judge the feasibility of a coarse-grained model. From the PMF, we know only how much reversible work is needed to move the ion through the channel, but examining the densities and their fluctuations tells us what modes of the peptide contribute to this reversible work. Thus the densities, fluctuations, and correlations provide important complementary information to the PMF. The enormous amount of trajectory data generated during the MD simulations can be harnessed for this purpose using the methods developed for simple fluids (34).

We report the distribution of mass or charge in real space by plotting the distribution as a function of z, which is taken parallel to the channel axis. Fourier analysis provides a convenient means of smoothing the densities. When we compare the mean densities to density fluctuations, we also use a Fourier representation of the functions. Although visualization of functions represented in Fourier space is harder, there are several advantages to the treatment, which we describe below. For now, we note that many methods developed to deal with transport phenomena in simple fluids have proved the usefulness of Fourier analysis (34). Here we describe how these methods can be applied to transport problems in ion channels.

Given the positions of a set of atoms P in a trajectory as {r_i(t), i ∈ P}, the microscopic density for a physical quantity w can be written as

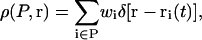(1)

where w can be the mass or charge of the atoms and P could refer to the entire set of the peptide atoms or a selected subset such as carbonyl groups. It is more convenient to deal with the Fourier transform of the density, which is given by

(2)

Here is the total mass or charge of the atoms in the set P. If it vanishes (as in the case of the total charge in gA), we put W_P = 1. The wave vector k is commensurate with the simulation box, and we choose it always parallel to the channel axis (i.e., z), which is the direction of the reaction coordinate for a permeating ion.

Performing the averages in the Fourier space offers several advantages. For example, translations of the protein are automatically removed when considering the absolute square of the density. Also one can easily obtain a smoothed peptide density by damping out the higher wave vectors. This is achieved by multiplying the real-space density in the Fourier space by a Gaussian, , so that the density is smoothed on a scale of α⁻¹. This smoothing removes the detailed, small-scale changes from the density, making the overall changes in the distribution clearer. Gaussian smoothing provides an efficient and convenient method for smoothing wildly fluctuating densities.

The mean structure is obtained by averaging over an ensemble generated during MD simulations. A convenient measure of the extent of the fluctuations about the mean structure is given by the mean-squared density

(3)

The first term here describes the mean structure, and the second describes the fluctuations about that mean structure. The square of the charge density in the Fourier space is related to the electrostatic energy of the charges in the system via the integral

(4)

Here we see the main advantage of the Fourier representation—the Coulomb energy is diagonal, i.e., each Fourier component of the density contributes to the energy independently of the others. Equation 4 gives the instantaneous Coulomb energy. The most important contribution to the PMF comes from the average Coulomb energy, which is obtained from Eqs. 3 and 4:

(5)

The Coulomb energy averaged over an appropriate ensemble has two contributions, one from the mean charge density and one from the fluctuations about the mean density. We see that fluctuations contribute not only to the entropy, but also to the electrostatic energy, and in fact for some wave vectors they dominate the mean density term. Any coarse-grained treatment of the protein must either account for this second fluctuation term, or its applications will be limited to proteins that are sufficiently rigid so that its density fluctuations are negligible compared to the mean density.

A final quantity of interest is the cross correlation between the density of peptide atoms and the ion, which is measured by the function

(6)

where the asterisk denotes complex conjugation, and P and Q refer to peptide and ion densities, respectively. If P and Q were the same density R would be 1. If the two were perfectly anticorrelated it would be −1. A value of 0 indicates the two densities are uncorrelated. Treating the ensemble average as an inner product, these statements follow from Schwarz's inequality. Where R(k) is complex, and it usually is in this case, then we discuss |R(k)|. Note that even when there are no correlations, R would oscillate between positive and negative values due to fluctuations. When we take |R|, this feature is obviously lost. However, as we are interested in the magnitude of correlations (i.e., whether 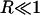or not), this will not be a problem in the interpretation of our results.

Depending on the values of the mean structure 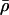, fluctuations about the mean δρ, and cross correlations R, we can identify three possibilities regarding the role of peptide flexibility in ion permeation:

1. As the ion moves across the channel, the mean structure of the peptide changes but the fluctuations about the mean remain negligible or change negligibly. That is, the first term in Eq. 5 dominates. If this were the only effect, the problem is reducible to the motion of a single body. Changes in the static structure of the protein with the ion's motion can be included in the potential governing the ion's motion. If the fluctuations are small, continuum electrostatics may provide a reasonable description of the forces acting on ions.

2. The magnitude of the peptide's fluctuations about its mean structure is significant and changes as the ion moves, but cross correlations remain negligible. In this case, the fluctuations would contribute to the reversible work required to move the ion through the second term of equation (5), through other energy components, and through the entropy. It is important to note that the fluctuations contribute to the energy as well as the entropy, hence the motion of the ion can only be described by a PMF determined from MD simulations. A coarse-grained model of a channel may still be feasible, but any link with continuum electrostatics becomes dubious. Alternatively, one may construct a coarse-grained model that accounts for the fluctuations in the channel structure.

3. The extent of correlations between the ion and peptide is strong, or varies significantly with the motion of the ion. In this case, calculation of the PMF itself may not be sufficient to determine the conductance of a channel, and more sophisticated treatments of the problem using methods from nonequilibrium statistical mechanics may be necessary (35). Naturally, any link with a coarse-grained model would become even more tenuous. However, this extreme situation is unlikely to be realized in ion channels.

RESULTS AND DISCUSSION

Potential of mean force

The results of the PMF calculations obtained using the fixed, backbone fixed, and flexible structures of gA are shown in Fig. 2. The PMF for the flexible structure has been calculated several times before using the CHARMM force field (10,16,33,36). Despite considerable improvements in computational methods and simulation times, the calculated central barrier with respect to the binding well has remained at ∼20 kT. In Allen et al. (33), it was further estimated from continuum electrostatics calculations that inclusion of finite-size effects and polarization of lipid molecules reduced this barrier from 20 to 14 kT. Because our purpose is to study the role of flexibility at the level of MD, we prefer not to include such continuum corrections here. Our present calculation without such corrections also yields a 20 kT barrier, consistent with the earlier findings. The results for the ion binding site show more variations indicating that its description is more sensitive to the system and computational details. For example, of the two binding sites at z = 9.7 and 11.3 Å, we find the former to be deeper with an energy of −7 kT, whereas in Allen et al. (33), the latter is found to be deeper with an energy of −3 kT. Use of a different NMR structure and/or a much smaller number of lipids in Allen et al. (33) compared to our work here (10 vs. 48 lipids on each side) may be responsible for this difference.

FIGURE 2.

PMF profiles of a K⁺ ion along the central axis of the gA channel. The three curves correspond to the fixed, backbone fixed, and flexible structures of gA as indicated on the graph.

The above results may be compared with a recent phenomenological study of the gA properties, where the experimental data for potassium ions are inverted to obtain a PMF of potassium ions consistent with all the available data (11). The results of this study indicate that the barrier height must be less than the absolute value of the well depth to reproduce the observed conductance value, explain the saturation of currents with concentration, and maintain a reasonable binding site (11). By that account, the error in the calculated potassium PMFs remains >11 kT even after some corrections. Thus there are still substantial errors in the calculated properties of the gA channel that need to be understood. A recent calculation of the free energies of ions in the gA channel using a semimicroscopic model has shown that the central barrier can be reduced to a size compatible with experiments by including the polarization interaction (37). Unfortunately, a properly optimized polarizable version of CHARMM (or other force fields) is not available yet.

Returning to the influence of flexibility in energetics of ion permeation, we see substantial increases in the central barrier when the backbone atoms and then all the peptide atoms are fixed. The binding energy of the ion at z = 9.7 Å also increases relative to bulk in proportional amounts. To give quantitative estimates of the changes in the energy, we use the binding site at the pore entrance as a reference as before. The ion binding energy with respect to bulk changes from −7 kT (flexible), to −3 kT (backbone fixed), and +2 kT (fixed). This suggests that flexibility of all the groups in the peptide (i.e., C-O, N-H, side chains, and backbone atoms) plays a role in binding of the ion. The central barrier in the PMF with respect to the binding site, on the other hand, increases from 20 kT in the flexible structure to 29 kT in both the backbone fixed and fully fixed cases. That is, relaxing most of the peptide atoms, while still keeping the backbone atoms fixed, does not help to reduce the barrier. This may be explained by the fact that major contribution to the ion-peptide Coulomb energy comes from the C-O carbonyl and N-H amide dipole groups. These groups form hydrogen bonds that run parallel to the channel axis, with the exception of the C-O groups on the pore mouth, which remain unpaired. When the backbone C and N atoms are fixed, the response of these dipoles to an ion inside the channel is severely restricted, even if the O and H ends are left free. To quantify this statement, we have calculated the average carbonyl dipole-ion energy when the ion is at the center of the channel, which yields −14, −15 and −70 kT, respectively, for the fixed, backbone fixed, and flexible structures. In contrast, when the ion is at the binding site, the same dipole-ion energy is found to be −26, −41, and −81 kT, respectively. In other words, unless they are completely flexible, the carbonyl dipoles forming the channel walls have limited freedom and cannot respond properly to a permeating ion. The carbonyls in the pore mouth, on the other hand, have greater freedom and can respond to a bound ion even when the backbone C atoms are fixed.

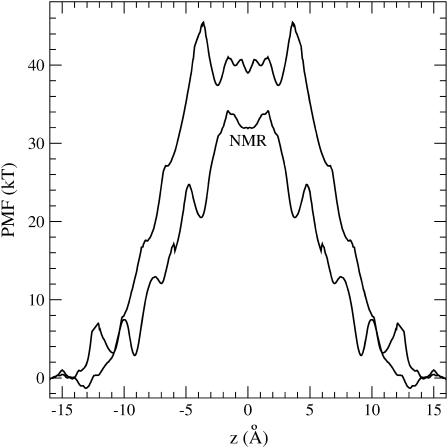
A fair question is whether the 1MAG NMR (22) structure used in the PMF calculation for the fixed peptide provides a representative example. Potential energy calculations using either 1MAG (22) or 1JNO (25) structures yield very similar results (6), so using another NMR structure is likely to yield a similar PMF as well. Therefore, we prefer to address this question using an equilibrated structure obtained from MD simulations as described in Methods. The PMF calculated with this fixed structure is compared to that obtained from the fixed 1MAG structure in Fig. 3. There are definite changes in the new PMF: the central barrier is expanded and is ∼6 kT higher compared to the previous one, and the binding site is shifted to the outer site at ∼11 Å (but the binding energy remains the same). The increase in barrier height may appear counterintuitive—one normally expects a lowering of barriers after equilibration of a crystal structure. However, 1MAG is a solution NMR structure, which is further refined using the CHARMM energy and simulated annealing (22). Ignoring the fine structure, and focusing on the energetics, the new PMF simply reinforces the importance of flexibility and would not change our conclusions.

FIGURE 3.

Comparison of PMFs obtained from two different fixed structures: 1MAG from NMR versus a structure obtained after equilibration with water. The former is indicated on the graph as NMR.

To summarize the results of Fig. 2, the contribution of peptide flexibility to ion binding and to reduction of the central barrier are ∼9 kT each. Thus flexibility helps to stabilize an ion at the center of the gA channel to the tune of 18 kT. Clearly this is a significant contribution to the energetics of an ion, and any model that completely ignores peptide flexibility cannot possibly describe ion permeation in the gA channel. It is instructive to compare the stabilization energy obtained from MD simulations with that from the composite continuum electrostatics calculations, which implement a flexible structure for gA. In Corry and Chung (7), which used 1MAG for the fixed structure and the CHARMM partial charges, the stabilization energy due to flexibility is found to be nearly zero. In Mamonov et al. (5), the same energy is found to be ∼14 kT. The difference between the two calculations arises from the use of the older 1GRM structure for gA (38), the AMBER force field for partial charges (39), and different dielectric coefficients in Mamonov et al. (5). Because the same structure and force field are used in Corry and Chung (7) as in our present work here, it provides a better target for comparison. Thus we estimate that the error committed by using continuum electrostatics in calculation of the flexibility contribution to the stabilization energy of an ion in the gA center is ∼18 kT. Naturally, similar errors are committed in calculation of the other parts of the energy, and there will be some cancellation among errors. However, a precise cancellation of errors is required to obtain the correct PMF profile from continuum electrostatics calculations. Comparison of the PMF profiles obtained by Corry and Chung (7) and Mamonov et al. (5) with the one obtained from the inversion of the experimental data (11) indicates that such a lucky coincidence has not eventuated for gA. To see why this is not possible at all, we turn to an analysis of mean densities and fluctuations.

Ion-peptide densities, fluctuations, and correlations

Here we use the trajectory data obtained from the MD simulations of the fully flexible gA structure to get a better feeling for the actual response of the peptide to a permeating ion. We first consider the case where there are no ions in the channel, which provides a useful reference point. The trajectory data for this calculation are taken from a 100 ps MD simulation before placing ions in the pore. In Fig. 4 A, the Fourier transforms of the square of the mean mass density of the peptide and its fluctuations around that mean (as defined in Eq. 3) are plotted. The three curves that start from a common origin show the original density (dash-dotted line) and its damped versions obtained by multiplying it with a Gaussian, 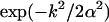. Damping factors of α⁻¹ = 1 Å (solid line) and α⁻¹ = 0.5 Å (dashed line) are employed for this purpose. Several wave vector components that make significant contributions to the density can be identified in Fig. 4 A. The one at 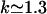Å⁻¹ is associated with the periodic structure of the β-helix, which rises 4.8 Å per turn (24). The fluctuations in the peptide density exhibit an opposite trend to the density, that is, they grow with increasing wave vector. For k < 1.5 Å⁻¹, the magnitude of density fluctuations are quite small compared to the mean densities. Thus for length scales >4 Å, the peptide (in the absence of an ion) can be viewed as a static entity with a mean structure. For larger wave vectors (or smaller length scales), fluctuations are larger than the mean density and the peptide exhibits a fluid-like behavior.

FIGURE 4.

Square of the Fourier transform of the mean mass density and its fluctuations in gA without an ion in the channel (A). The mean density is shown with three curves using different damping factors, α⁻¹ = 1 Å (solid line), α⁻¹ = 0.5 Å (dashed line), and no damping (dash-dotted line). Fluctuations (without damping) are indicated by the dotted line. In B, the mean densities smoothed with damping factors are transformed back to the real space. Here the solid and dashed curves have the same damping factors as those in A.

In Fig. 4 B, the densities with damping factors are transformed back to real space, which provide smoothed distributions of the peptide mass density along the z axis. The original density without damping exhibits wild oscillations, and therefore it is not shown. Nevertheless it can be seen from this figure that the high wave vector components contribute to the finer features of the density, which are not of immediate interest. For example, the ∼1 Å periodic structure seen in the density obtained with α⁻¹ = 0.5 Å smoothing (dashed line) is due to the bond lengths. These modes exhibit fast vibrations and are integrated out when the ion density is averaged over long times to obtain the PMF. Thus use of a damping factor removes the undesired high wave vector components, and provides a clearer picture for the changes occurring in the density. The smoother density distribution obtained using α⁻¹ = 1 Å (solid line) is found to be most suitable for our purposes, and this damping factor is employed in the rest of the calculations. The larger densities at the edges compared to the center of gA is simply due to the presence of the heavier Trp residues there. Otherwise, the smoothed density exhibits a structure as already alluded to in Fig. 4 A. Note that the mass density is not symmetric around z = 0. A similar asymmetry in the mass density is also observed when the ion is at z = 0 (not shown). As noted before, the PMF calculations exhibit a similar asymmetry, which is due to fluctuations in the system and would require much longer simulations to average out. Here we are interested in changes in the density in much shorter MD simulations, and the density in Fig. 4 B provides an adequate reference for that purpose.

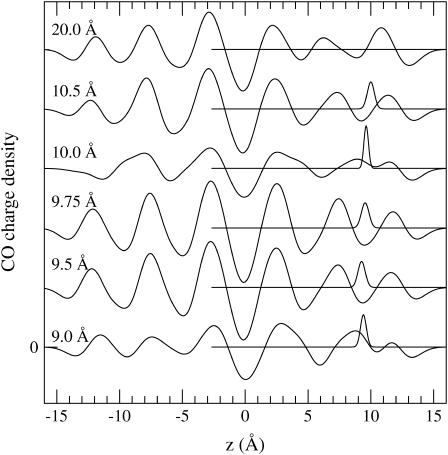
We next consider how the average peptide mass density changes as an ion is moved along the channel axis. Here and in the rest of the density analysis (Figs. 5–10), we employ the same trajectory data that are used in the calculation of the PMF for a flexible gA structure (specifically, the first 100 ps of the production run). Calculation of several mass densities for ion positions between the channel center and the binding site reveals that response of the peptide to the ion's motion is mostly mild. However, some interesting changes in the density occur when the ion is in the vicinity of the binding site, which we discuss in some detail. In Fig. 5, we show the peptide and ion densities for ion positions between 10.5 Å and 9 Å, and at 20 Å, which is the last window used in the PMF calculations. The positions of the umbrella potentials used in each simulation are indicated in the figure with labels. The most important thing to notice is that the natural undulations in the peptide density in the absence of an ion (top) are retained when the ion is near a binding site (z = 9.5, 9.75, and 10.5 Å) but they are washed out once the ion is moved away (z = 9 Å and 10 Å). Thus holding the ion in positions where it feels a large force (cf. PMF in Fig. 2) causes a considerable stress in the whole peptide. There are also significant changes in the immediate neighborhood of the ion, which will be discussed in more detail below.

FIGURE 5.

Mass distribution in gA along the z axis. Each set of distributions has been shifted vertically for clarity, and corresponds to a different simulation with the potassium ion tethered to a different position via a harmonic potential as indicated in the graph. The solid lines give the smoothed mass density of the peptide along the z axis. The sharply peaked, solid lines show the distribution of the potassium ion for each simulation.

FIGURE 10.

Here we show the quantity |R(k)| for the correlations between the ion and peptide masses (A) and ion and carbonyl charges (B) for three ion positions: z = 20 Å (dotted line), z = 9.75 Å (dashed line), and z = 9 Å (solid line). Where R is small, correlation between the ion and the mass density is weak. If |R| = 1, they are perfectly correlated, i.e., one is slave to the other.

FIGURE 6.

Similar to Fig. 5 but for the charge distribution of the peptide atoms along the z axis.

FIGURE 7.

Similar to Fig. 6 but for the charge distribution of the carbonyl atoms only.

FIGURE 8.

Same as Fig. 4 A but for the ion at z = 20 Å (dotted line), z = 9.75 Å (dashed line), and z = 9 Å (solid line). Squares of the densities rapidly fall with increasing k while their fluctuations increase. No damping factors are used in here and the following figures, but the Gaussian damping function used in previous figures is indicated in the lower left-hand side.

FIGURE 9.

Similar to Fig. 8 but for the fluctuations in the charge of the carbonyl atoms (A) and the mass of the backbone atoms (B) for three ion positions: z = 20 Å (dotted line), z = 9.75 Å (dashed line), and z = 9 Å (solid line).

The charge density of the peptide provides information complementary to that from the mass density. We repeat the analysis presented in Fig. 5, replacing mass with charge. Results shown in Fig. 6 replicate those in Fig. 5 for the charge distribution. Because the interaction is more direct and the total charge of the peptide is zero, the charge distribution provides a more sensitive probe for the ion's motion. This is clearly seen in the neighborhood of the ion, where the charge density exhibits significant variations as the ion is moved by small increments. As in the mass density, the largest changes occur when the ion is at z = 9 Å and 10 Å. Due to this sensitivity, it is also more difficult to interpret the changes occurring at the opposite monomer. A possible explanation is that the water column in the channel has a periodic structure, which is sustained while the ion is in one of the binding sites but is perturbed when the ion is moved away (40). The disturbance of the hydrogen bonds between the peptide atoms and water molecules propagates through the channel leading to the changes in the charge density in the opposite monomer.

A much clearer picture that corroborates the above explanation is obtained by restricting the charge distribution to the carbonyl groups (Fig. 7). The small undulations seen in the mass density have now a clear periodic structure and are the main feature of the carbonyl charge density. As in that case, those densities where the ion is near a binding site show the most intense oscillation, and close correspondence with the reference density with no ion (top). This observed lack of change in the peptide structure upon cation binding is in good agreement with the earlier NMR experiments (41,42). Again, as before, moving the ion away from the binding sites (z = 9 Å and 10 Å) results in large distortions of the carbonyl density that propagates throughout the peptide. Also, in these positions, the large overlap of the ion density with the (negative) carbonyl-oxygen density is lost. Contrasting this result with Fig. 6, we see that to maintain charge neutrality in the vicinity of the ion, other charge groups in the peptide respond to the motion of the ion.

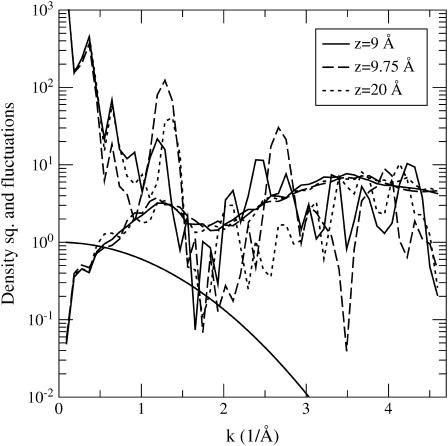
Fluctuations of the mass density exhibit even fewer features compared to the mean density itself. Therefore, we limit their discussion to only three ion positions here: z = 20 Å, 9.75 Å, and 9 Å, which provide a representative sample for the peptide's response to the ion's motion. In Fig. 8, the square of the mean mass density of the peptide and its fluctuations (i.e., the same quantities as in Fig. 4 A) are plotted for these ion positions. The densities are not damped, but the Gaussian damping function used in the previous figures is indicated in the graph. This figure shows that compared to the changes in the mean structure of the peptide, the fluctuations change rather little with the ion's motion. Moreover at lower wave vectors, where density modes survive smoothing (k < 1.5 Å⁻¹), the fluctuations are small compared to the density itself. This result confirms that, on length scales >4 Å, the peptide can be viewed as a static entity with a mean structure even in the presence of an ion. However, at smaller length scales and larger wave vectors (but still within the undamped sector), the fluctuations could make significant contributions to the energetics of a permeating ion.

Averaging over mass washes out some details, which may be picked up by restricting the analysis to certain groups in the peptide (cf. carbonyls in Fig. 7). Indeed, charge fluctuations of the carbonyl groups and the mass fluctuations of the backbone atoms exhibit well-defined structures that are not obvious from Fig. 8. These are shown in Fig. 9, A and B, respectively. The carbonyl fluctuations peak at the k values 1.3–1.4 Å⁻¹ and 2.6–2.8 Å⁻¹, where large changes both in the mean density (not shown but similar to Fig. 8) and the fluctuations occur as a result of the ion's motion. As in the case of densities, these peaks arise from the periodic structure of the β-helix, which rises 4.8 Å per turn. As expected, carbonyl fluctuations are lowered when the ion is in the binding site and increase significantly when it is moved away. The backbone mass fluctuations are relatively smaller in magnitude (when the two are compared to their respective mean-densities squared), and exhibit an opposite behavior—they are suppressed when the ion is moved away from the binding site.

We next examine the extent of correlation of the fluctuations in peptide density with the motion of the ion. However small the fluctuations in the peptide density are, if they are strongly correlated with the motion of the ion, it may not be possible to neglect them. Equation 5 defines a dimensionless measure of this correlation, R(k), and the absolute value of this quantity is plotted in Fig. 10 for the peptide mass (A) and carbonyl charges (B). For simplicity, we use the same ion positions as in Figs. 8 and 9 (using other ion positions yield very similar results). When the ion is at z = 20 Å, we expect no correlations between the ion and peptide, hence the dotted line provides a convenient reference point for the other two cases. As pointed out in Methods, because we take |R|, the positive values here do not signify any correlations but should be interpreted as noise. It is hard to see any simple behavior in the correlation between the peptide mass fluctuations and that of ion, apart from the fact that they are quite small and barely above the noise level (A). Especially for low wave vectors, there is not much difference among the three correlation functions. Because the response of the carbonyl groups to the ion's motion has been the most interesting so far, we also show their correlations with the ion (B). There is not much change in correlations between A and B when the ion is in the binding site (dashed line), but the carbonyl-ion correlations increase above the noise level when the ion is at z = 9 Å (solid line). Ignoring the largest peak at low wave vectors where the fluctuations are negligibly small, the maximum carbonyl-ion correlations can be estimated as R 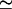0.2. This is not a significant amount and would be even smaller, had we used a more accurate force field (see the discussion below).

Ion-pore water correlations in gA play a significant role in the ion permeation process, which have been discussed in many articles before. We include a brief discussion of ion-water correlations here for completeness and as an example demonstrating the effect of positive correlations in our formalism. The density of water molecules taken across the whole simulation cell will correlate very little with the ion, but that is only because most such water molecules are very far from it. On the other hand, if we take only the water molecules in the channel, the result will be hardly more interesting—the correlation will be very strong because the ion and waters are confined to the channel and it is difficult for one to move without the other. Instead we choose to examine the water molecules within 15 Å of the center of mass of the channel. The cross correlations of the mass and charge of these molecules with the ion in and outside the channel are shown in Fig. 11. As expected, the correlation is intermediate between the two extremes discussed above. There is noticeable correlation over a certain band around k = 2–3 Å⁻¹. As the correlation between the ion and water is stronger than between ion and peptide, a coarse-grained model, which does not include water molecules explicitly, will have difficulty in describing ion permeation in gA.

FIGURE 11.

Similar to Fig. 10 but for the mass (A) and charge (B) correlations between the ion and channel water for three ion positions: z = 20 Å (dotted line), z = 9.75 Å (dashed line), and z = 9 Å (solid line). Only waters within 15 Å of the center of mass of gA are included in the calculations.

Summarizing the above results, the mean density in gA undergoes substantial changes as an ion permeates the channel, and the fluctuations about the mean are important, but the ion-peptide correlations are negligible. This places the gA channel in the second of the three categories identified in the Methods section. That is, the PMF of ions determined from MD simulations is sufficient to characterize the conductance properties of the channel but continuum electrostatics cannot be used for the same purpose.

Because the force field used in the simulations yields a large central barrier, which is not compatible with experiments, we comment on the robustness of the results presented above. Using the PMF obtained from the inversion of the experimental data as a guide (11), we expect a more accurate force field to yield a barrier height that is smaller than the well depth (in absolute value). This will reduce the force acting on the ion as it is moved away from the binding site, which in turn, will reduce the stress applied on the peptide during this motion. Thus we expect the substantial changes seen in the mean density (Figs. 5–7) to be moderated and become less conspicuous. A similar comment applies to the changes in the fluctuations (Fig. 9) and the correlations (Fig. 10). However, as seen in Fig. 8, fluctuations remain in a narrow band regardless of the position of the ion, and hence we don't expect any significant changes in the relative magnitudes of the mean densities and fluctuations. Thus use of a more accurate force field is likely to reinforce our conclusions and make the placement of the gA channel in the second category even firmer.

CONCLUSIONS

The role of protein flexibility in ion permeation is one of the most important issues in modeling of ion channels at present. Due to time limitations, MD simulations cannot be used directly to determine the conductance of an ion channel, which has encouraged the use of coarse-grained models for this purpose. Indeed Brownian dynamics simulations have been applied to several ion channels, providing a successful description of their permeation properties (13). However, a better justification of the assumptions and approximations invoked in such models is required for the acceptance of these results unreservedly. As recently stressed (6), use of a rigid channel structure is one of the most drastic assumptions in coarse-grained models. Therefore, an accurate assessment of the role of protein flexibility in ion permeation is essential for their justification.

In this work, we have investigated this issue in the gA channel from two different perspectives: i), how the energetics of a permeating ion changes as the peptide structure evolves from flexible to fixed, and ii), how the response of the peptide atoms changes as an ion moves in the channel. From the former method, we have found that peptide flexibility contributes ∼18 kT to the stabilization of an ion at the center of the channel. This is a significant contribution, and it is completely missed in continuum electrostatics calculations that otherwise use the same channel structure and force fields. Analysis of the peptide response to the ion's motion has revealed a deeper reason why continuum electrostatics cannot possibly work in gA. The fluctuations in the density is found to be comparable to the mean density at length scales of 4 Å or smaller, which correspond to the coordination shell of the ion and hence are still important in ion permeation (i.e., not integrated out in PMF calculations). Such fluctuations contribute to both the energy and the entropy, which are completely ignored in a continuum electrostatics approach that relies on an average, fixed structure.

For the reasons given in the introduction, the gA channel provides the best example for highlighting the role of flexibility in ion permeation, and our results have largely confirmed this expectation. Consequent failure of continuum electrostatics in gA has already been foreseen from comparisons with experimental data (11), and hence comes as no surprise. A critical question here is the relevance of the results found for gA to other ion channels. Most biological ion channels contain substantially more water molecules, which provide a much better hydration environment for ions compared to the single-file water column in gA. Thus one expects a better screening of the ion-peptide interactions in biological ion channels, which will suppress the changes in the peptide density and fluctuations due to the motion of an ion. Of course, one needs to perform a similar analysis for these channels to show that such expectations are indeed realized, and that the successes of continuum electrostatics in accounting for their permeation properties were not just due to a fortuitous cancellation of errors.

Our treatment of fluctuations could be applied to many other proteins, and the importance of correlations analyzed in the same way. Though our conclusions about the gA channel agree with the previously established picture, we feel that our method has great potential in the analysis of protein function and the development of simple, coarse-grained models, which are increasingly being demanded for description of structure-function relations.