Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells

Abstract

We show that actin filaments, shortened to physiological lengths by gelsolin and cross-linked with recombinant human filamins (FLNs), exhibit dynamic elastic properties similar to those reported for live cells. To achieve elasticity values of comparable magnitude to those of cells, the in vitro network must be subjected to external prestress, which directly controls network elasticity. A molecular requirement for the strain-related behavior at physiological conditionsis a flexible hinge found in FLNa and some FLNb molecules. Basic physical properties of the in vitro filamin–F-actin network replicate the essential mechanical properties of living cells. This physical behavior could accommodate passive deformation and internal organelle trafficking at low strains yet resist externally or internally generated high shear forces.

Mechanical force plays an essential role in the physiology of animal cells. External mechanical forces regulate cell shape, migration, gene expression, and apoptosis (1), and cells generate protrusive and contractile forces during locomotion, phagocytosis, and cytokinesis (2). A peripheral shell of cytoplasm, the cortex, predominately determines a cell’s mechanical properties (3, 4). The dominant structural constituent of the cell cortex is polymeric (F) actin organized as isotropic networks or as parallel bundles by cross-linking actin binding proteins (ABPs), and disruption of F-actin diminishes cellular elasticity (5, 6). Measurements of local displacements of cell surfaces in response to applied forces have revealed that the actin cortex is predominately elastic, although it also exhibits fluid or viscous features (3, 7–10). Moreover, cells are not simply passive responders to applied forces but exert forces of their own on the substratum to which they adhere. Interestingly, the magnitude of this endogenous force correlates with measured cellular elasticity (11). The complexity of a living cell greatly complicates both the measurement and the interpretation of its mechanical properties (8, 9, 11).

One approach has been to measure the mechanical properties of F-actin networks reconstituted in vitro (12–15). Purified actin forms semiflexible filaments many micrometers in length, and entangled solutions of F-actin are viscoelastic (12). However, their elasticity is far lower than the values measured for cellular elasticity (15, 16). Moreover, many motile cells actively maintain their cortical F-actin at contour lengths of 0.5–1 μm (17–19); shortening them makes it more difficult for the filaments to entangle to form a network, further weakening their elasticity at low frequencies (15). Addition of F-actin cross-linking ABPs can stabilize reconstituted F-actin networks and increase their elastic stiffness in vitro (12, 14, 20, 21). But the elasticity of such in vitro actin networks is still orders of magnitude weaker than that found in intact cells. Furthermore, the immense complexity of dynamic actin assemblies within cells responding to stimuli that cause shape changes and motility could prohibit any in vitro system from mimicking cellular elasticity. Thus, an in vitro model that captures the essential mechanical properties of a cell has proven elusive. If a suitable model system were available, it would be of enormous utility, greatly facilitating understanding the mechanical properties of the cell.

In this article, we show that it is in fact possible to replicate essential mechanical behavior of living cells with an in vitro network of F-actin filaments at physiological concentrations and lengths (18), cross-linked with certain ABPs of the filamin (FLN) family. This replication requires that the F-actin network be subject to a large prestress and a specific domain within the filamin molecule.

Results and Discussion

Filamin A (FLNa) is the most widely expressed member of a family of F-actin cross-linking ABPs. It accommodates translational locomotion by cross-linking F-actin into networks, by mediating actin–membrane connections and by serving as a scaffold for numerous cellular components (22, 23). It is the most potent F-actin cross-linking protein as defined by the fact that its minimum gelling concentration, the amount of an ABP required to induce a large consistency increase in an F-actin solution is significantly lower than for other ABPs (24). FLNa’s efficiency in actin gelation presumably resides in its ability to promote high-angle branching of F-actin, meaning that every FLNa molecule can recruit an actin filament into a network, in contrast to ABPs like α-actinin that stabilize parallel actin arrays and therefore accumulate redundantly in the cross-linked complexes. Twenty-four β-pleated sheet repeat segments interrupted by two short “hinge” sequences between repeats 15 and 16 (hinge-1) and repeats 23 and 24 (hinge-2) separate the N-terminal actin-binding domain from the C-terminal dimerization site of the large (180 nm) FLNa subunits (Fig. 1A). This structure is markedly different from the short (100 nm) antiparallel rods comprising α-actinin dimers.

Fig. 1.

The stress–strain relationships of F-actin networks formed with different FLN mutants. (A) A schematic of the hinged and hingeless isoforms of filamin. The filamin molecule is homodimer; each monomer consists of an actin binding domain (rectangles at top), 24 β-sheet repeats (squares), and two unstructured, amino acid sequences between the 15th and 16th repeats and 23rd and 24th repeats (black lines) that serve as flexible hinges. Dimerization occurs at the 24th repeat. The hingeless mutants we study, FLNa h(−) and FLNb h(−), lack the hinge region between the 15th and 16th repeats. (B) The relationship between the stress and the strain at an oscillatory frequency of 0.5 Hz for 48 μM F-actin with 0.12 μM gelsolin cross-linked with 0.48 μM FLNa (filled squares), FLNb (filled triangles), FLNb h(−) (open triangles), and FLNa h(−) (open squares). The stress–strain is approximately linear at all values of stress below 0.5 Pa. In the networks cross-linked with FLNa and FLNb, the stress diverges at stresses above 0.5 Pa and the networks catastrophically break at stresses of 30 Pa and 10 Pa, respectively. In contrast, the networks formed with FLNa h(−) and FLNb h(−) disintegrate at stresses larger than 0.1 Pa and weaken at large strains. (C) A schematic illustration examining the implications of the nonlinearity in the stress–strain relationship. In the linear elastic regime of a material, the relationship between the force per unit area, or stress (ς), and its resulting deformation, or strain (γ), is a simple, linear relationship: ς = G′γ, where G′ is the elastic spring constant. Thus the ratio ς/γ will measure the same spring constant as measuring the differential spring constant, dς/dγ, at a given extension. Typically, materials exhibit linear elasticity over a range of stresses and strains. At larger stresses, nonlinear effects can start to dominate the response. In the nonlinear regime, the relationship between ς and γ is nonlinear and, thus, ς/γ (the slope indicated by the dashed line) will measure a different spring constant than a differential measurement, dς/dγ, (slope indicated by the dotted line) at a fixed stress. Thus, for a nonlinear spring, there are different measures of its spring constant.

We polymerized purified rabbit skeletal muscle F-actin in the presence of human recombinant plasma gelsolin and human endothelial FLNa. To best replicate conditions in the living cytoskeleton, we used gelsolin to shorten the actin filaments to physiological lengths (L = 1–2 μm), physiological concentrations of actin (c_A = 24–72 μM), and typical molar ratios of FLNa:G-actin (R = 1/100–1/50). We polymerized the networks in situ between two parallel plates of a rheometer, where it formed an isotropic, cross-linked F-actin network. We measured the deformation (strain) of the network in response to an applied force per unit area (stress) and determined the force–displacement relationship of the network. For stresses below 1 Pa, the strain, γ, increases in direct proportion to the applied stress, ς, as shown by the filled squares in Fig. 1B. From this relationship, we determined the stiffness or elasticity of the network. However, these FLNa–F-actin networks are not simple elastic networks. Instead, applying a steady shear stress as low as 0.03 Pa results in a sharp rise, followed by a slower evolution of the strain for 150 sec, as shown in Fig. 2A. The strain creep is nearly fully reversible; upon removing the stress, the deformed network returns nearly back to its original position. Full recovery would be characteristic of stably cross-linked viscoelastic gels (20). Instead, the time-dependence of the strain, γ(t), shows power law behavior, γ(t) ∼ t^0.17 in both its response and in its recovery (Fig. 4, which is published as supporting information on the PNAS web site). This may reflect the consequences of the dynamic binding of the cross-linkers, or possibly the effects of filamin unfolding (25). This creep behavior is strikingly similar to the force–displacement relationship of a fibronectin-coated magnetic bead coupled to the actin cytoskeleton of living cells via integrin-mediated connections; such measurements show that γ(t) ∼ t^x, where 0.15 < x < 0.3 (8, 9). Thus, the mechanical relaxation spectrum measured for a living cell strikingly parallels a reconstituted actin network crosslinked by FLNa.

Fig. 2.

The linear mechanical properties of 48μM F-actin network, where filament length is regulated with 0.12 μM gelsolin and cross-linked with 0.48 μM FLNa. Insets schematize the mechanical tests performed. (A) Creep test. We apply a constant stress, or force per unit area (Inset, filled arrow), of 0.03 Pa for 150 sec and measure the resultant displacement (Inset, dashed arrow) over this time. The strain, γ, is the ratio of the plate displacement to the plate separation. The strain slowly evolves with time, increasing from 0.02 to 0.08 over 150 sec, and evolves as a power law such that γ ∼ t^x where x = 0.17 (Fig. 4). Upon removal of the stress, the strain recovers to nearly zero following a power law, γ ∼ t^γ, with γ ≈ 0.17. (B) The dynamic elastic and viscous loss moduli, G′ (filled squares) and G″ (open squares), are determined by measuring the resulting deformation (Inset, dashed arrow) to an applied oscillatory stress (Inset, filled arrow) as a function of frequency. We apply a sufficiently small stress, 0.01 Pa, to stay within the linear elastic regime of the network. A prestress of 15 Pa is applied to this network, and we superpose a small, linear oscillatory stress to measure the differential elastic and loss moduli, K′ (filled triangles) and K″ (open triangles).

Characterization of the linear elastic stiffness, G′, and viscous dissipation, G″, of these networks as a function of frequency, ω, further demonstrates the similarity between the dynamic mechanical response of this in vitro network and that of cells. The FLNa–F-actin network is a soft, viscoelastic gel; G′ is ≈3-fold larger than G″ over the measured frequency range, as shown by the squares in Fig. 2B. The results exhibit a power law scaling, G′ ∼ ω^0.17, and a roughly similar behavior for G″. Cells exhibit a similar scaling, with G′ ∼ ω^x, where 0.15 < x <0.3, and with roughly the same behavior for G″ (9). Thus, the frequency dependence of the viscoelastic behavior of the in vitro network is identical to that of live cells. This congruence further highlights that a purely physical in vitro network, uncomplicated by active remodeling processes, can mimic the mechanical viscoelastic dissipation observed in living cells.

Although the similarities between the dynamic properties of the in vitro network and of live cells are impressive, the absolute magnitudes of their elasticities differ by 10,000-fold. The elasticity of cells is typically 1,000 Pa (9–11), whereas the values measured for in vitro F-actin networks formed under physiological conditions are usually on the order of 0.1 Pa (Figs. 5 and 6, which are published as supporting information on the PNAS web site). Unlike networks formed with some ABPs (26), increasing filament length, filament density or cross-link density by an order of magnitude does not significantly increase the linear elasticity of FLNa–F-actin networks (Fig. 6) and cannot account for the large discrepancy in elasticity values between in vivo and in vitro networks. This discordance appears to be ubiquitous. For example, it is also characteristic for F-actin cross-linked with α-actinin (16) (Fig. 5). Thus, despite the tantalizing similarity in the dynamics of the mechanical response, the linear elasticity of these in vitro cross-linked F-actin networks cannot reproduce the magnitude of that measured in cells.

The key to comparing the elastic properties of reconstituted FLNa–F-actin networks with those of cells is their strain-dependent behavior. The mechanical response of cross-linked F-actin networks can be highly nonlinear at large stresses or strains (20, 21, 26, 27). We find that, at low strains, γ < 0.4, the stress of a FLNa–F-actin network (c_A = 48 μM, L = 1 μm, R = 1/100) increases linearly, behavior expected for a common spring, until a critical stress, ς_crit = 0.2 Pa. By contrast, at increased strains, the stress exhibits a dramatic increase, nearly diverging for a strain of γ ∼ 1, until the network ultimately breaks catastrophically at a stress of ς_max = 30 Pa, as shown by the filled squares in Fig. 1B. The extent of the nonlinear regime of these F-actin networks, characterized by the magnitude of the excess stress that can be applied before the network breaks, ς_max − ς_crit, is roughly 30 Pa. This is substantially larger than previously studied cross-linked F-actin networks with a similar linear modulus, where ς_max − ς_crit ≈ 0.2–1 Pa (21, 26).

The very strong nonlinear behavior demands alternate measurement strategies to fully characterize the behavior. Customarily, the nonlinear behavior is quantified by measuring the engineering modulus, G′ = ς/γ (20, 21), equivalent to measuring the slope of the line from the origin to any given point on a stress–strain plot, indicated by the dashed line in Fig. 1C. However, for sufficiently large stresses, the oscillatory waveforms of the strain response become highly nonlinear and invalidate measurements of G′(ω) (28). We overcame this limitation by measuring the differential modulus, or the local slope of the stress–strain relationship, at a given applied stress, shown by the dotted line in Fig. 1C. When the applied prestress is within the linear elastic regime of the material, the differential mechanical response is identical to the linear viscoelastic response. However, the differential modulus diverges from the engineering modulus in the nonlinear elastic regime, as indicated in the schematic in Fig. 1C. To measure the differential modulus, we applied a time-independent stress and determined the incremental strain response to a superposed small, oscillatory stress. This provides a measure of the frequency-dependent, differential elastic and loss moduli, K′ and K″, as a function of constant prestress. Measuring differential mechanical properties in the highly stress-stiffening networks has been underappreciated and is the only available technique for obtaining a linear measurement in the nonlinear elastic regime.

The differential moduli, K′ and K″ increase significantly with prestress, reflecting the extreme nonlinear behavior. This is shown, respectively, by the filled and open triangles in Fig. 2B, for a FLNa–F-actin network (c_A = 50 μM, L = 2 μm, R = 1/100) subjected to a prestress of ς₀ = 15 Pa. With this applied prestress, the magnitude of K′ increases 100-fold over those at zero prestress, as shown by the filled and open squares in Fig. 2B. However, remarkably, the frequency dependence changes only slightly, and the networks exhibit the same power-law dependence observed in the absence of prestress, with K′ ∼ K″ ∼ ω^x. Moreover, the elastic behavior remains nearly identical to that seen in cells: the networks become more elastic, resulting in a smaller ratio of K″/K′ with corresponding decreases in x. The relationships among K″/K′, x, and K are quantitatively identical to those observed in living cells (9) (unpublished work).

To quantify this variation in network stiffness, we measured the differential stiffness at 0.2 Hz as a function of prestress, ς₀, for physiological FLNa–F-actin networks. For ς₀ < 0.5 Pa, K′ is a constant, as shown by the filled squares in Fig. 3. However, when ς₀ increases above 0.5 Pa, K′ rises sharply, increasing in direct proportion to ς₀ by two orders of magnitude, until the network breaks at ς₀ ≈ 20 Pa. The remarkable linear increase of the differential stiffness with applied stress implies that the network has a very small compliance: no matter how much force is imposed on the network, its elasticity increases just enough to ensure that there is essentially no additional deformation. The linear increase of the differential modulus with prestress suggests that modulus is exponential in applied stress, and this is indeed roughly observed (Fig. 5). Surprisingly, measurements on the modulus of whole tissue reveal similar behavior (29).

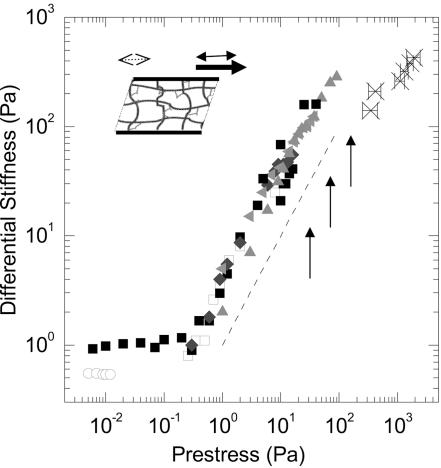
Fig. 3.

We apply a prestress, ς₀, to the network (Inset, single-headed filled arrow) and measure the deformation (Inset, dashed arrow) in response to an additional oscillatory stress (Inset, double-headed filled arrow). We measure the differential elastic stiffness, K′, at 0.2 Hz over a range of concentrations of actin, c_A, and molar ratio of FLNa, R: c_A = 36 μM, R = 1/100 (open squares), c_A = 48μM, R = 1/100 (filled squares), c_A = 74 μM, R = 1/100 (diamonds), c_A = 36 μM, R = 1/50 (left-pointing triangles), and c_A = 53μM, R = 1/50 (upward-pointing triangles). All of the networks have the identical differential stiffness for a given prestress. However, differences between these networks are seen at the maximum stress they can withstand before breaking; the maximum prestress of several networks is indicated by the filled arrows; thus, differences in total protein concentration affect the maximum stress the network can withstand. Under identical network conditions, the hingeless mutants do not exhibit such stress stiffening (open circles); rather, at stresses beyond the linear elastic regime, these networks disintegrate. In vivo measurements where the prestress of the cell is correlated to its stiffness, as measured with twisting bead cytometry from ref. 11, are indicated by the black stars. Thus, there is quantitative comparison between our in vitro measurements of prestressed FLNa–F-actin networks with in vivo measurements of adherent cells.

The behavior of K′ as a function of ς₀ is independent of FLNa and F-actin concentrations, as shown by the overlay of the different symbols in Fig. 3, each of which shows the behavior of a network with different concentrations of constituents. Instead, changes in protein concentrations do lead to significant differences in the maximum stress before the networks break (Fig. 6); the arrows in Fig. 3 denote these values. Moreover, the values of prestress the FLNa–F-actin networks can withstand are >1,000-fold larger than those of F-actin networks crosslinked by other physiological ABPs, such as α-actinin, at similar values of c_A, L, and R, as shown by the open circles in Fig. 3 (Fig. 6). Thus, nonlinear dependence on prestress is the predominant mechanism, aside from buildup and destruction of the network per se, for controlling mechanical properties of FLNa–F-actin networks in vitro.

The critical importance of prestress in setting the elasticity of these networks makes them even more similar to the behavior of living cells as the degree of prestress determines the elasticity of cells (11). The amount of prestress in a cell can be measured by documenting the forces generated by cells grown on compliant substrates (Fig. 7, which is published as supporting information on the PNAS web site). At the same time, magnetic bead twisting cytometry can determine the elastic stiffness of these cells (11, 30, 31) (Fig. 7). We find nearly quantitative agreement between the incremental elasticity as function of prestress for in vitro FLNa–F-actin networks (Fig. 3, filled symbols) and published in vivo measurements for human airway smooth muscle cells (Fig. 3 , crosses). The magnitude of the prestress on the cells is about an order of magnitude larger than that of the FLNa–F-actin networks that may reflect differences in absolute protein concentrations or composition between the in vitro measurements and of cells. Nevertheless, these results demonstrate clearly that an in vitro network consisting of shortened actin filaments cross-linked by FLNa can mimic all of the mechanical properties of a living cell in the absence of additional complex machinery.

To explore the sensitivity of these in vitro networks to their constituents, and to determine their utility as models for the mechanical properties of living cells, we compared their behavior using different filamin isoforms. We measured the mechanical response of F-actin networks cross-linked with a naturally occurring FLN isoform, Filamin B (FLNb), which is expressed in many nonmuscle cells at lower concentrations than FLNa, and which has a similar structure to FLNa, with 80% homology over the entire sequence (32). FLNb–F-actin networks have an identical gel point, network microstructure, and linear elasticity to FLNa–F-actin networks (Fig. 8, which is published as supporting information on the PNAS web site). Moreover, FLNb–F-actin networks exhibit the same nonlinearity in their stress–strain relationship as do FLNa–F-actin networks, as shown by the filled triangles in Fig. 2B. Under similar network conditions, FLNb–F-actin networks can withstand up to 10 Pa of shear stress, similar to that of the FLNa–F-actin networks.

By contrast, another naturally occurring human FLN isoform, FLNb h(−), which lacks a sequence of 24 amino acids that forms the N-terminal flexible hinge (hinge-1), behaves qualitatively differently (Fig. 1A). Networks of FLNb– and FLNb (h−)–F-actin have an identical gel point and, under similar conditions (c_A = 48 μM, L = 2 μm, R = 0.01), have a similar network microstructure and linear elasticity (Fig. 8). However, in marked contrast, the FLNb h(−)–F-actin networks formed at similar conditions of c_A, L, and R exhibit no nonlinearity in its stress–strain relationship, as shown by the open triangles in Fig. 1B. Instead, its elasticity decreases markedly with increased stress, and it breaks at much lower stresses. To establish further the importance of the small hinge-1 sequence for the elasticity of FLN–actin networks, we engineered a recombinant FLNa that lacks hinge-1, FLNa h(−) (Fig. 8). Under similar network conditions, networks of FLNa h(−)–F-actin also do not exhibit nonlinear stiffening, and they break at similarly low stresses, as shown by the open squares in Fig. 1B. Thus, under these physiological network conditions, the hinge-1 of the human filamins appears essential for forming actin networks that exhibit nonlinear stiffening at large stresses and that mimic the mechanical behavior of live cells.

For identical conditions of c_A, L, and R, networks of skeletal muscle α-actinin–F-actin show rheological behavior similar to the hingeless filamins. At these protein concentrations, the α-actinin–F-actin networks break under an applied prestress as low as 0.1 Pa and do not exhibit stress stiffening (Figs 2 and 3). These networks never attain the mechanical stiffness seen in vivo. These findings highlight the importance of the hinge-1 region in dictating the network elastic properties and confirm that this hinge enables the network to withstand large stresses relative to the linear modulus.

Recent work to measure the mechanical response of reconstituted filamin–F-actin networks have focused filamin purified from chicken gizzard (ggFLNa) (28). However, ggFLNa lacks the flexible hinge-1 (33). The ggFLNa–F-actin networks formed with F-actin of unregulated length exhibit a small degree of strain stiffening at sufficiently high values of R (28). We find that networks of FLNb h(−)–F-actin formed with F-actin of unregulated filament length can also demonstrate a degree of strain stiffening similar to those formed with ggFLNa (Fig. 9, which is published as supporting information on the PNAS web site). Similarly, F-actin networks formed with α-actinin can also show a small degree of stress stiffening at large values of R and L (21). The degree of strain stiffening in α-actinin networks can also be altered by variations in temperature (21); this may be attributed to a decreased gel point of the network at lower temperatures (34). It is significant that deletion of the flexible hinge in the filamin does not alter the gel point of the FLN–F-actin networks (Fig. 8), and thus, the variation in the nonlinear mechanical response upon deletion of hinge-1 must be attributed to an alternative mechanism. Moreover, the degree of stress stiffening observed and the ability of the hinged FLN–F-actin networks to withstand such large stresses, ς_max ∼ 100 G′, before rupture is unique to this class of hinged cross-linking molecules.

For any given ABP, the nature of the nonlinear mechanical response of cross-linked F-actin networks depends sensitively on L, c_A, and R (26, 35, 36). Networks of F-actin cross-linked with biotin-avidin, scruin, and ggFLNa all demonstrate stress weakening at low values of R and stress stiffening at larger R values (26, 28). Consistent with these previous findings, we find networks formed with hinged FLN isoforms also exhibit stress weakening when R is substantially reduced to 1/2,000 (data not shown). The absolute values of R required to sustain strain stiffening in cross-linked F-actin networks is highly sensitive to the type of ABP used. We find that, at physiological conditions of F-actin concentration, F-actin length and cross-link density, stress stiffening is observed only in F-actin networks cross-linked with hinged filamins.

We propose that, for small stresses, the role of FLNa or of FLNb is primarily to stabilize short actin filaments into three-dimensional networks with elastic rather than fluid properties. Filamin A is a large and flexible molecule with a persistence length of l_p ≈ 20 nm, the length scale set by the ratio of the bending modulus of the molecule to thermal energy. In contrast, the persistence length of F-actin is ≈17 μm (37) and, thus, has an extensional entropic spring constant ≈10⁶-fold larger than that of a FLN molecule (25). Thus, we hypothesize that the mechanical response of FLNa– or FLNb–F-actin networks at low prestress is principally due to the physical entanglements between F-actin, and the presence or absence of the hinge-1 region does not affect either the ability of the FLNs to stabilize F-actin or the mechanical properties of the F-actin networks (15). By contrast, at higher stresses, both the F-actin filaments and FLNa cross-links can be stretched. We hypothesize that, because of the significantly softer extensional stiffness of the FLNa cross-linkers as compared to the F-actin filaments, the initial nonlinearity in the network mechanical response is due to the nonlinearity in the entropic spring constant of the FLNa molecules as its end-to-end extension approaches its contour length (25, 27). The degree of stretching of individual FLNa crosslinks depends on the distribution of stress within the network, which in turn depends on the detailed structure and connectivity of the filaments (35, 36). The hinge-containing FLN crosslinks are presumably mechanically more effective than the hinge-1-deficient counterparts in response to a steady external shear stress because of flexibility afforded by the hinge. By allowing local reorganization of the network, a larger number of hinged FLNs contribute to the elasticity as effectively stretched cross-links compared with the hingeless FLNs. At significantly higher prestress, we would expect the nonlinearity in the stretching of individual F-actin to also contribute to the mechanical response of the composite network (26, 27).

In this study, we measured the mechanical response of F-actin networks formed at physiological conditions of actin concentration, F-actin length, and cross-linker concentration. When subjected to small stresses, the dynamics of the mechanical response of these networks are similar to those measured in living cells. However, we found that, despite the physiologically similar protein concentrations, the linear elastic modulus of all of the networks formed are significantly weaker than the mechanical stiffness measured for the cellular cytoskeleton in vivo. The networks formed with α-actinin, FLNa h(−), and FLNb h(−) all disintegrated at stresses around 0.3 Pa. In contrast, under identical conditions, the networks formed with FLNa and FLNb withstood up to 100 Pa of shear stress. When a stress larger than 0.3 Pa was applied, these networks exhibited stress stiffening and attained similar magnitudes of elasticity to those seen in cells. The magnitude of the modulus of these networks as a function of prestress compared quantitatively with measurements of living cells.

Our results suggest that all measurements of the elasticity of cells are, in fact, a measurement of the differential elasticity, because the cells themselves are under tension. Any elastic measurement probes the additional force required to induce a deformation. The role of the prestress and stress-dependent stiffening must be properly incorporated in any model for the elastic behavior of cell. Our findings imply that, if at a low value of prestress, cells could respond passively to small mechanical deformations; however, when stressed by internal contractions associated with movement or when exposed to high shear forces, FLNa-actin networks can impart high resistance required to withstand the ambient forces. Our results also have implications for the regulation of cell cytoskeletal mechanics. They suggest that contractile activity mediated by myosin motor proteins that impose internal stresses on cross-linked cytoskeletal actin networks can induce nonlinear stress stiffening of the cytoplasm. This potentially is an additional parameter to regulate cell stiffness above and beyond changes in the absolute concentrations and dynamics of F-actin and associated ABPs. Our results also suggest that the presence or absence of prestress will strongly influence the mechanical consequences of actin network solation by F-actin severing or depolymerization, by dissociation of FLNa or FLNb from F-actin, or by calpain-mediated cleavage of individual FLN cross-links: in the absence of prestress, these events will not markedly affect cellular rheology, whereas under tension they will have major consequences. Finally, these results highlight the importance of FLNa as a cross-linking protein essential in the cytoskeleton networks. Future work must determine the range of possible ABPs that can exhibit similar behavior and must investigate the role of the hinge structure in the macroscopic mechanical behavior. This will provide minimal in vitro models for studies of the mechanical behavior of cells; however, the results presented here suggest that this is a promising route to investigate.

Materials and Methods

Protein Preparation.

Actin was purified from rabbit skeletal muscle, frozen in liquid nitrogen, and stored at −80°C. Chicken gizzard α-actinin was purchased from Sigma (catalog no. A 9776). Recombinant human gelsolin was produced in Escherichia coli (38). Recombinant FLNa was purified from Sf9 cell lysates (24). Deletion of hinge-1 region of FLNa was created by using the QuikChange site-directed mutagenesis kit (Stratagene). The 3.5-kb cDNA was prepared by cutting pFASTBAC FLNa (prepared in Dam⁺ E. coli) with ClaI and XbaI, and subsequently ligated into the pBluescript II SK (+) vector (Stratagene) to generate pBluescript II SK (+)-FLNaCX. The hinge-1 (corresponding to 1740Ala-1771Trp) of FLNa was deleted by using 5′-CAACAGCCCCTTCCAAGTGACGGCCCCGGAGAGGCCCCTGGTG-3′ and 5′-CACCAGGGGCCTCTCCGGGGCCGTCACTTGGAAGGGGCTGTTG-3′ as mutagenic oligonucleotides. The deletion was confirmed by sequencing. After deletion of hinge-1, the 3.4-kb cDNA was prepared by cutting pBluescript II SK (+)-FLNaCXh(−) (prepared in Dam⁺ E. coli) with ClaI and XbaI, and subsequently ligated into the pFASTBAC vector to generate pFASTBAC-FLNa h(−). The cDNAs of human FLNb and FLNb h(−) were kindly provided by Sandor Shapiro (Jefferson Medical College, Philadelphia) and inserted into pFASTBAC vector by using XbaI and HindIII. The full-length FLNa h(−), FLNb, and FLNb h(−) were expressed in Sf9 cells and purified (24).

In Vitro Network Formation.

To form in vitro networks, solutions of gelsolin, Filamin A or α-actinin, and 10× actin polymerization buffer (2 mM Tris·HCl/2 mM MgCl₂/100 mM KCl/0.2 mM DTT/0.2 mM CaCl₂/0.5 mM ATP, pH 7.5) were gently mixed, and G-actin was added last. The solution was loaded in the sample chamber within 10 sec. By varying the actin concentration, c_A, the average distance between filaments, or mesh size, can be changed. By changing the concentration of gelsolin, c_g, relative to c_A, the average filament length, L, can be varied. Previous studies have shown that c_g/c_A = 1/200 results in L ∼ 1 μm (12). Finally, by varying the molar concentration of cross-links, c_xlink, relative to c_A, the degree of cross-linking was varied; we define the ratio, R = c_xlink/c_A. The parameter R varies the average distance between cross-links.

We confirmed that all of the mixtures formed homogeneous networks at length scales on the order of micrometers using multiple particle tracking (39). In this technique, 1-μm colloidal spheres were embedded in the network to probe the microstructure and local mechanical properties around the spheres. We followed the thermally driven dynamics of ≈100 spheres simultaneously to probe spatial variations in the mechanical response. With two-particle microrheology (40), we found that the networks are homogeneous above 3 μm, confirming that a bulk rheological measurement that averages over 100 μm probes the mechanical response of a homogeneous network rather than structural heterogeneities (40).

Bulk Rheology.

The bulk mechanical response of the networks was measured with a stress-controlled rheometer (CVOR, Bohlin Instruments) with a 40-mm-diameter parallel plate geometry and a gap of 140 μm. For the dynamic measurements, we applied a frequency-dependent, sinusoidal stress, ς(ω), and measured the resultant deformation or strain, γ(ω). The in-phase portion of γ(ω) measures the energy storage, or elastic modulus, G′(ω) while the out-of-phase portion of γ(ω) measures the energy loss, or viscous modulus, G″(ω). To measure the mechanical response over a large range of applied stress, we measured G′(ω) and G″(ω) at a single frequency and varied the amplitude of the applied stresses from 0.006 to 100 Pa. Below a critical stress, ς_c, G′(ω), and G″(ω) were independent of the magnitude of the applied stress; this is the linear elastic regime. Typically, ς_c ≈ 0.1 Pa, and to probe the linear mechanical properties, we applied a stress of 0.01 Pa and maintained the strain at <0.02.

For ς > ς_c, G′ and G″ depend on the magnitude of the applied stress, and the waveforms of the strain response often become nonsinusoidal, which can result in errors calculating G′ and G″ (28). Thus, to accurately probe the mechanical properties in this regime, we measured the differential mechanical modulus as a function of applied stress. A steady shear stress, ς₀, was applied to the network, and a small amplitude (<0.1 ς₀), oscillatory stress, ς(ω), was superposed; the resulting oscillatory strain response, δγ(ω), was measured to obtain the frequency-dependent differential complex modulus: K*(ω,ς₀) = [δς(ω)/δγ(ω)]|_ς0. We confirmed that both the applied and measured oscillatory waveforms were sinusoidal. Thus, we measure the linear, differential elastic modulus, K′, and loss modulus, K″, as a function of applied prestress, ς₀. In the linear elastic regime, the differential modulus is equivalent to the elastic modulus, K′(ω) = G′(ω) and K″(ω) = G″(ω); however, there are significant differences in the nonlinear elastic regime. The frequency-dependent differential measurements were performed within 1 min of applying the static prestress.

A third measure of the mechanical properties is a creep test. We measured the creep response of these networks by applying a steady shear stress for 100 sec and measuring the time evolution of the strain. After 100 sec, we removed the applied stress and measured the strain recovery over a period of 150 sec. The creep measurement probes the network response to and recovery from an external steady shear stress. For a purely elastic material, the application of a steady shear stress, ς, will result in a time independent strain, γ = ς/G′. After the stress is removed, the strain will recover quickly to zero, reflecting the stored elastic energy. In contrast, for a viscous fluid with a viscosity η, a constant shear stress will result in a constant strain rate, dγ/dt = ς/η. Furthermore, energy is dissipated in the fluid and thus the strain does not recover after the stress is removed. In a viscoelastic material, an applied stress will lead to a time-dependent strain that reflects the distribution of time scales over which energy is stored and dissipated in the material. Often, this leads to a power law dependence in time, γ(t) ∼ t^α, where 0 < α < 1, over a range of time scales.

Abbreviations

ABP

actin binding protein

FLN

filamin.