Adjustments of prehension synergies in response to self-triggered and experimenter-triggered load and torque perturbations

Abstract

Humans are known to show anticipatory adjustments in the grip force prior to a self-generated or predictable action or perturbation applied to a hand-held object. We investigated whether humans can also adjust covariation of individual finger forces (multi-finger synergies) prior to self-triggered perturbations. To address this issue, we studied adjustments in multi-digit synergies associated with applied load/torque perturbations while the subjects held a customized handle steadily. The main hypothesis was that the subjects would be able to demonstrate the phenomenon of anticipatory covariation, that is changes in covariation patterns among digit forces and moments of force in anticipation of a perturbation, but only when the perturbation was triggered by the subjects themselves. Based on the principle of superposition (decoupled grasping force and resultant torque control), we also expected to see different adjustments in indices of multi-digit synergies stabilizing the total gripping force and the total moment of force. The task for the subjects (n = 8) was to return the initial handle position as quickly as possible after a perturbation, which consisted of removing one of three loads hanging from the handle. There were six experimental conditions: two types of perturbations (self-triggered and experimenter-triggered) by three positions of the load (left, center, and right). Three-dimensional forces and moments of force recorded from each digit contact were used for the analysis. Indices of covariation among digit forces and among moments of force, previously employed for studying motor synergies, were computed across trials. Positive values of the indices reflected negative covariations of individual digit forces and moments of force (their inter-compensatory changes) to stabilize the total force and moment acting on the handle. In steady-state conditions, subjects showed strong positive indices for both digit forces and digit moments. Under the self-triggered conditions, changes in the indices of digit force and moment covariation were seen about 150 ms prior to the perturbation, while such changes were observed only after the perturbation under the experimenter-triggered conditions. Immediately following a perturbation, the indices of force and moment covariation rapidly changed to negative revealing the lack of inter-compensation among the individual digit forces and moments. Later, both indices showed a recovery to positive values; the recovery was faster in the self-triggered conditions than in the experimenter-triggered ones. During the steady-state phase after the perturbation, the indices of force and moment covariation decreased and increased, respectively, as compared to their values during the steady-state phase prior to the perturbation. We conclude that humans are able to adjust multi-digit synergies involved in prehensile tasks in anticipation of a self-triggered perturbation. These conclusions speak against hypotheses on the organization of multi-element actions based on optimal control principles. Different changes in the indices of force and moment covariation after a perturbation corroborate the principle of superposition. We discuss relations of anticipatory covariation to anticipatory postural adjustments.

Introduction

Recent studies of multi-digit interactions in a variety of tasks (Kang et al. 2004; Shim et al. 2004a, b; Olafsdottir et al. 2005a) used a particular view on the control of mechanically redundant systems that considers them not as redundant but as abundant (Gelfand and Latash 1998; Latash 2000). Within this general approach, when the central nervous system faces the problem of producing an action with an apparently redundant motor system, it does not compute a particular solution and implements it, but facilitates families of solutions that are equally adequate to solve the problem such that different solutions may be expected to emerge in different trials. In other words, the controller does not eliminate apparently redundant degrees-of-freedom in a motor system (reviewed in Zatsiorsky and Latash 2004) but instead may use them all to stabilize important aspects of behavior. This approach allows for introducing an operational definition of synergies as neural organizations of elemental variables that stabilize particular performance variables in a task-specific manner. In the case of prehensile actions, elemental variables can be associated with forces and moments of force produced by individual digits, while performance variables may be associated with the total force and total moment of force applied to the hand-held object.

A series of recent experimental studies identified two multi-digit synergies that participate in static prehensile tasks, a synergy that stabilizes the gripping force applied to a hand-held object and a synergy that stabilizes the rotational action of the hand on the object (Shim et al. 2003, 2005a; Zatsiorsky et al. 2004). These two synergies obey the principle of superposition proposed in robotics (Arimoto and Nguyen 2001; Arimoto et al. 2001). This principle assumes that some complex tasks performed by a set of effectors may be decomposed into sub-tasks that are independently controlled with no interference with each other. In other words, one of the sub-tasks may be modified without changing the control of the other sub-tasks.

Hand action has been often used as an object to study feed-forward mechanisms of control in human movements. When a person lifts an object with a pinch grip (using the thumb and the index finger), the gripping force changes in anticipation of the weight (Johansson and Westling 1988; Gordon et al. 1993) and the location of the center of mass (Salimi et al. 2000) of the object. During multi-digit object lifting fairly constant gripping force sharing among individual digits was found before lifting the object (Reilmann et al. 2001). When a person applies force to the bottom of a hand-held object with the other hand, gripping force changes in a feed-forward fashion (Scholz and Latash 1998). All of these studies addressed feed-forward changes in the overall performance of the hand in anticipation of changes in the external forces. In this study, we ask a different question: Can the central nervous system adjust multi-digit synergies in a feed-forward manner, in preparation to a predictable perturbation, without changing the overt behavior of the multi-digit prehension system? Note that investigating only the combined output of all effectors does not allow for addressing possible changes in the synergistic action of individual effectors. However, such changes may be important for planned actions. For instance, a purposeful quick change of the resultant torque during a multi-digit prehensile task may be opposed by negative covariation among individual digit moments of force; therefore, weakening this covariation in preparation to such an action facilitates the action.

There are reasons to believe that feed-forward adjustments of multi-digit synergies exist. In particular, two recent studies documented changes in indices of multi-digit synergies stabilizing the total force generated by a set of digits 100–150 ms prior to a change in the total force from a steady-state force level (Olafsdottir et al. 2005a; Shim et al. 2005b). This phenomenon has been termed anticipatory covariation (ACV). The purpose of ACV has been assumed to weaken a synergy which stabilizes a particular performance variable (the total force) in anticipation of a planned change in the variable.

How general is the ACV phenomenon? Can it be used to prepare a corrective action for a self-triggered perturbation? Can it be observed separately for synergies stabilizing the total grip force and the total moment of forces, as one would expect from the principle of superposition [decoupled controls of the grasping force and the resultant torque during an object prehension (Shim et al. 2004a, 2005a; Zatsiorsky et al. 2004)]? These have been the main questions addressed in experiments with self-triggered (predictable) and experimenter-triggered (unexpected) perturbations applied to a hand-held object. To address these questions, the perturbations were organized in such a way that they could produce different torque perturbations with the same load perturbation. The study also has important implications for competing hypotheses in the area of organization of multi-element synergies. In particular, a purposeful decrease in an index of stabilization of a performance variable in the absence of its change (as in ACV) can be readily incorporated into some of the models (Latash et al. 2005b) but not in others (Harris and Wolpert 1998; Todorov and Jordan 2002).

Methods

Subjects

Eight healthy volunteers (age: 25.2 ± 3.1 years, mass: 71.1 ± 1.2 kg, height: 175.2 ± 3.3 cm, hand length: 19.7 ± 1.4 cm, and hand width: 9.1 ± 0.8) participated in the experiment. The hand length was measured between the distal crease of the wrist and the middle fingertip when a subject positioned the palm side of the right hand and the lower arm on a table with all finger joints extended, and the hand width was measured between the radial side of the index finger metacarpal joint and the ulnar side of the little finger metacarpal joint. All subjects were right-handed according to preferential hand use during daily activities such as eating and handwriting. All the subjects signed an informed consent form approved by the Office for Research Protection of the Pennsylvania State University.

Equipment

Five six-component (three force and three moment components) transducers (four Nano-17s for the fingers and one Nano-25 for the thumb, ATI Industrial Automation, Garner, NC, USA) were attached to an aluminum handle, to which an aluminum beam (3.8 cm × 52.1 cm × 0.6 cm) was affixed, Fig. 1a. A six-component (three position and three angle components) magnetic tracking device (Polhemus FAST-RAK, Rockwell Collins Co., Colchester, VT, USA) was affixed to the top of the handle using a plexiglass base (0.2 cm × 17.0 cm × 13.5 cm). The linearity of recordings about the X-, Y-, and Z-axes was tested using eleven angles with 1° intervals to assure that the magnetic device worked properly while surrounded by metallic objects. The regression analysis on the angles independently measured versus angles recorded yielded coefficients of determination (r²) larger than 0.97.

Fig. 1.

a The customized handle; the force-moment sensors shown as white cylinders were attached to two vertical aluminum bars. Three loads of 0.30 kg each are shown as black cylinders. The loads were attached to the long horizontal aluminum beam; one of them was attached with a cotton thread and the other two with bolt–nut structures. A force sensor was attached to the bottom of the load on the thread. The transmitter of a magnetic position-angle sensor shown as a small black cube was attached to the plastic base affixed to the top of the handle. M_X, M_Y, and M_Z are moments produced by the digits about X-, Y-, and Z-axes. b The subject held the handle while monitoring its angular position about X- and Z-axes, θ_X and θ_Z, respectively. The right wrist and forearm were housed in a wrist–forearm brace and secured with Velcro straps. The left hand could either rest on the knee or positioned just under a load for trials with self-triggered perturbations

The center of mass of the unloaded handle was determined by suspending the handle at different points. Three loads (0.30 kg for each) were attached at three different positions along the beam: left, center, and right, Fig. 1a. One of the loads was attached with a cotton thread (this load was removed during unloading, see Procedure) and the other two were attached with bolt-nut structures. The local x-, y-, and z-axes of each of the sensors were parallel to the global X-, Y-, and Z-axes, respectively. Sandpaper (100-grit) was placed on the contact surface of each transducer to increase the friction between the digits and transducers. The distance between the centers of the finger sensors in the y-direction was 30 mm, and the thumb sensor was placed at the midpoint between the middle and ring fingers along the Y-axis. The grip width, which is the shortest distance between the contact surfaces of thumb and finger sensors in the Z-direction, was 86 mm. The finger pad-sandpaper static friction coefficient was approximately 1.5 [previously measured (Zatsiorsky et al. 2002)]. The sensors were aligned in the Y–Z plane. A piezoelectric one-component force sensor (Model 208A03, Piezotronics, Inc.) was attached to the bottom of the load connected by a thread to the handle.

Thirty-one analog signals of forces and moments (5 force-moment sensors × 6 components + 1 force sensor) from the sensors were routed to the two synchronized 12-bit analog-digital converters (PCI-6031, National Instrument, Austin, TX, USA). The signals from the magnetic device were sent to a serial port at the same time. All the signals were synchronized and processed by a microcomputer (Dell Dimension 8330, Austin, TX, USA). The sampling frequency was 100 Hz. A customized LabVIEW program was used for data acquisition and MATLAB programs were written for data processing.

Procedure

Subjects washed their hands with soap and warm water to normalize the skin condition of the hands. The subjects were given a standardized familiarization session that explained the experimental procedure and apparatus to ensure that they were able to accomplish the experimental tasks properly.

The subjects sat on a chair and placed their right upper arm into a wrist–forearm brace fixed to a table, Fig. 1b. The forearm was positioned on the table and secured with Velcro straps. The angles of the upper arm and the forearm with the frontal plane were ~45° and ~135°, respectively. When the subject held the handle, the angle of the beam attached to the bottom of the handle with the frontal plane was ~45°. The subjects were required to hold the handle upright by watching a 19″ monitor screen, which showed the angular position of the handle about X- and Z-axes.

There were six experimental conditions: two types of perturbation (self-triggered and experimenter-triggered) by three positions of the load lifted for a perturbation (left, center, and right). During trials with self-triggered perturbations, the subjects quickly lifted the load hanging by the thread with the left hand. Prior to this action, the left hand of the subject was placed just under the load, nearly touching its bottom. During trials with experimenter-triggered unloading, a similar action was performed by an experimenter at an unpredictable time. For experimenter-triggered conditions the experimenter’s hand was hidden behind a black curtain (30 × 30 cm) to prevent the subjects from seeing the experimenter’s hand. The tasks for both self-triggered and experimenter-triggered conditions were: (a) prior to the perturbation—minimize the angular deviation of the handle from its nominal vertical orientation while watching the monitor screen, and (b) after the perturbation—restore the original orientation as quickly as possible. The visual feedback on the angular positions was shown on the computer monitor for all experimental conditions. In self-perturbation conditions, the subjects were free to lift the load at any time during the initial 6-s interval after the data collection program started. Each trial involved 10-s of data collection. During experimenter-triggered conditions, the load was lifted unexpectedly within the same time window by an experimenter. Both self-triggered and experimenter-triggered series were performed for each of the three load positions. For a given condition of load position and method of unloading, 12 trials were collected with 20-s intervals between trials. 10-min intervals were given between conditions. The order of six conditions was balanced.

Data processing and statistics

The force and moment data from the force/moment sensors and angular data from the magnetic tracking device were low-pass filtered with a second-order Butterworth filter at 25 Hz (Winter 1990; Shim et al. 2005b). Since each digit makes soft-finger contact with the sensor surface (Mason and Salisbury 1985; Arimoto et al. 2000; Shim et al. 2003), the digit tips could roll on and push against the sensor surfaces, but not pull on them. The position of the points of digit force application with respect to the center of the surface of the sensor was calculated as CoP_x = −m_y/F_Z and CoP_y = m_x/F_Z [CoP stands for the center of pressure of force along Z-axis (F_Z) on the sensor surface; m_x and m_y signify the moments about the local X- and Y-axes with respect to the center of the sensor surface]. The moments of individual finger force (Eq. 1) and the resultant moment (Eq. 1) acting on the handle about the X-axis were calculated with respect to the point where the X and Y coordinates corresponded to the thumb force application point on the X–Y plane and Z coordinate located at the center of mass of the handle along Z-axis.

$$M_X^k=d_Y^k·F_Z^k-d_Z^k·F_Y^k$$ (1)

$$M_X=\sum _K{M}_X^k,$$ (2)

where k stands for all digits including the thumb, i.e. k = {T (thumb), I (index), M (middle), R (ring), and L (little)}, subscripts X, Y, and Z stand for the direction of a force, a moment arm, or a moment. F stands for a force, d stands for a moment arm, and M represents a moment of force.

The time of the initiation (t₀) of force changes recorded by the piezoelectric sensor at the bottom of the load when it was lifted in a trial was defined as the time when the first time derivative of the force reached 5% of its peak level observed during that trial. All trials were aligned by t₀ for further analysis.

The total normal force was calculated as the sum of all finger normal forces at each point in time $\left[F_Z^{\text{TOT}}(t)={\displaystyle \sum _j}{F}_Z^j(t),\text{where}j=\{\text{I},\text{M},\text{R},\text{and}\text{L}\}\right]$. For the 12 trials within each condition, time profiles of the variances of individual finger normal (grasping) forces [VarF^j(t), where j = I, M, R, and L] and of the variance of the total normal force [VarF^TOT(t)] were computed across the trials at each point in time for each subject separately. The time profile of the sum of the variances of individual finger forces [ΣVarF^j(t)] was computed in the same way. The difference between ΣVarF^j(t) and VarF^TOT(t) was computed and normalized by ΣVarF^j(t) for further analyses [Eq. 3 (Shinohara et al. 2003; Shim et al. 2004b)].

$$\mathrm{\Delta }{V}_F(t)=\left[\frac{\sum \text{Var}{F}^j(t)-\text{Var}{F}^{\text{TOT}}(t)}{\sum \text{Var}{F}^j(t)}\right].$$ (3)

Note that when ΔV_F(t) < 0, positive covariations among F^j(t) dominate, and when ΔV_F(t) > 0, negative covariations prevail.

The total/resultant moment about X-axis was calculated as the sum of the moment of each digit including the thumb at each point in time [ $M_X^{\text{TOT}}(t)={\sum }_k{M}_X^k(t)$]. The variances of the moments produced by digits [ $\text{Var}{M}_X^k(t)$] and the variance of the total moment [ $\text{Var}{M}_X^{\text{TOT}}(t)$] were computed across the trials at each point in time for each experimental condition. The time profile of the sum of the variances of individual digit moments [ $\sum \text{Var}{M}_X^k(t)$] was computed in a similar way. The difference between $\sum \text{Var}{M}_X^k(t)$ and $\text{Var}{M}_X^{\text{TOT}}(t)$ was computed and normalized by $\sum \text{Var}{M}_X^k(t)$ for further analyses [Eq. 4 (Shim et al. 2004a, 2005b)].

$$\mathrm{\Delta }{V}_M(t)=\frac{\left[\sum \text{Var}{M}_X^k(t)-\text{Var}{M}_X^{\text{TOT}}(t)\right]}{\sum \text{Var}{M}_X^k(t)}.$$ (4)

In order to determine the time when ΔV_F(t) or ΔV_M(t) started to change with respect to t₀, we computed the first time derivative, i.e., dΔV_F(t)/dt or dΔV_M(t)/dt, and defined the time when the derivative reached 5% of its peak value for that particular series of trials.

For statistical analysis, standard descriptive statistics and repeated-measures ANOVA were used with the factors of Trigger (two levels, experimenter-triggered and self-triggered), Load (three levels, left, center, and right), and Time (the number of levels differed depending on particular comparisons). The significance level was set at P = 0.05.

Results

Mechanical effects of perturbations on the handle

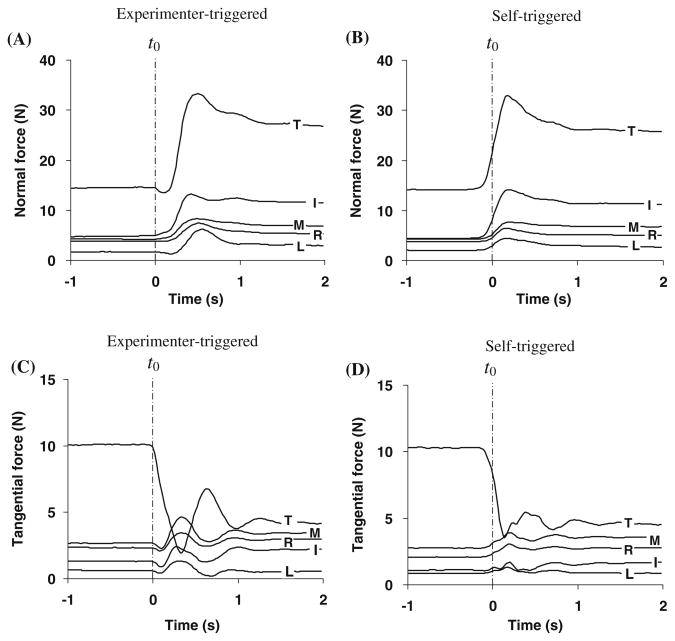
Unexpected removal of one of the three loads by the experimenter (experimenter-triggered condition) resulted in fast changes in normal and tangential forces of all individual digits at contacts with the sensors, Fig. 2.

Fig. 2.

Individual digit a normal and c tangential forces during experimenter-triggered unloading and b normal and d tangential forces during self-triggered unloading. T, I, M, R, and L stand for thumb, index, middle, ring, and little fingers, respectively. The perturbation started at time t = 0 s (t₀). The data are from single trials performed by a representative subject performing a load lifting at the left location. The magnitudes of normal and tangential forces are shown in the figure. Note that thumb normal force direction is opposite to the finger normal forces while all tangential force directions are the same

The changes in forces and moments of individual digits induced a quick motion of the handle involving its translation and rotation, Fig. 3. When the subjects performed the unloading themselves (self-triggered condition), mechanical effects were very different from those seen when a similar unloading was performed by the experimenter. The angular position of the handle after the unloading of the left or right load changed in a manner similar to a step response of an under-damped second-order system and could be modeled as such. However, the modeling will not be discussed in this paper.

Fig. 3.

Linear positions of the magnetic sensor along Y-axis during a experimenter-triggered unloading and b self-triggered unloading. Angular positions of the sensor about X-axis during c experimenter-triggered unloading and d self-triggered unloading. The perturbation started at time t = 0 s (t₀). The data are from single trials performed by a representative subject. Different lines show data during lifting the loads at different locations, left (thin solid line), center (dashed line), and right (thick solid line)

For quantitative analysis of the mechanical effects of the unloadings, the peak linear and angular displacements of the handle were quantified as illustrated in Fig. 3. The magnitudes of both linear and angular displacements of the handle were much smaller under the self-triggered conditions than under the experimenter- triggered conditions, Fig. 4. The peak linear and angular displacements were smaller for the center load conditions, but larger for the right and left perturbations. The angular displacements were especially minimal for the center load conditions. These findings were supported by two-way ANOVA’s (Trigger × Load) which showed significant effects of Trigger [linear: F(1,7) = 69.7 and P < 0.0001; angular: F(1,7) = 328.6 and P < 0.0001], Load [linear: F(2,14) = 29.3 and P < 0.0001, Right > Left > Center (P < 0.05 for all comparisons); angular: F(2,14) = 69.6 and P < 0.0001, Right = Left > Center (P < 0.05)], and a significant Trigger × Load interaction [linear: F(2,14) = 14.3, P < 0.0001; angular: F(2,14) = 49.1, P < 0.0001].

Fig. 4.

Peak linear and angular displacements of the handle under the experimenter-triggered (gray bars) and self-triggered (white bars) conditions. The data were averaged over all 12 trials for each subject and further averaged across all subjects. Mean values are shown with standard error bars

Finger interaction prior to perturbation

We calculated two indices, ΔV_F(t) and ΔV_M(t), to assess quantitative effects of covariation of individual finger forces and moments across trials on stabilization of the total grip force and total moment of forces produced by the digits and acting on the handle. The indices reflect the normalized difference between the variance in the space of elemental variables (digit forces/moments) and the variance in the performance variable (total force or total moment). Their positive values correspond to negative covariation of elemental variables that stabilizes the corresponding performance variable across trials.

When the subject held the handle vertically, both the total grip force and the total moment were stabilized by negative covariation [positive ΔV_F(t) and ΔV_M(t)] of corresponding elemental variables across trials. Figure 5 illustrates the profiles of ΔV_F(t) and ΔV_M(t) over the time interval from 1 s before to 2 s after the perturbation for a typical subject.

Fig. 5.

Indices of finger force covariation, ΔV_F(t) for a experimenter-triggered and b self-triggered conditions and indices of finger moment covariation, ΔV_M(t) for c experimenter-triggered and d self-triggered conditions. The load was removed at time t₀ = 0 s (t₀). The data for a representative subject is shown. Different lines show data during lifting the loads at different locations, left (thin solid line), center (dashed line), and right (thick solid line). Note the early shifts in ΔV indices for self-triggered conditions

Averaged values of ΔV_F(t) and ΔV_M(t) over a 100 ms period 1,000 ms prior to t₀ (steady-state phase) were not different between the experimenter-triggered and self-triggered conditions or among different load locations. This finding was supported by the lack of significant effects of Trigger, Load, or Trigger × Load interactions in corresponding ANOVA. Immediately prior to the perturbation, however, the two conditions differed: There was a drop in both ΔV_F(t) and ΔV_M(t) prior to t₀, but only in the self-triggered conditions. This drop could be seen about −150 ms to −200 ms prior to t₀ (Fig. 6). The time when ΔV_F(t) or ΔV_M(t) started to decrease (t_ΔV) was defined as the time when the first derivative of ΔV_F(t) or ΔV_M(t) reached 5% of its peak level observed in that particular series. Figure 6 shows t_ΔV data averaged across subjects for each condition. Note the consistently positive values (after t₀) in the experimenter-triggered conditions and the consistently negative values, between 150 and 200 ms, in the self-triggered conditions. Two-way ANOVA (Trigger × Load) showed significant effects of Trigger for both ΔV_F(t) [F(1,7) = 94.6, P < 0.0001] and ΔV_M(t) [F(1,7) = 94.6, P < 0.0001], but no effects of Load or Trigger × Load interaction.

Fig. 6.

The times of initiation of a decrease in ΔV_F(t) and ΔV_M(t) with respect to the time of unloading, t₀; negative and positive values represent the times of initiation before and after t₀, respectively. Data averaged across subjects is shown with standard error bars

Finger interaction following a perturbation

Immediately following an unloading (t₀), there was a quick and large drop in both the ΔV_F(t) and ΔV_M(t) indices (Fig. 5), that led to negative values of both indices. Changes in ΔV_F(t) or ΔV_M(t) for each condition were quantified using the difference between the average value of ΔV_F(t) or ΔV_M(t) over the 100 ms period, 1,000 ms prior to the perturbation and its minimum value over the 2,000 ms period after t₀. Figure 7 presents changes in ΔV_F(t) and ΔV_M(t) averaged across subjects. The average values of ΔV_F(t) were larger than ΔV_M(t)in all conditions. In general, the drop in both ΔV_F(t) and ΔV_M(t) was larger for the left and right load perturbations than the center load perturbations although there was no difference between load locations for the experimenter-triggered condition. These findings were supported by two-way ANOVA (Trigger × Load) showed significant effects of Trigger and Load for both ΔV_F(t) [Trigger: F(1,7) = 18.4, P < 0.005; and Load: F(2,14) = 4.6, P < 0.05] and ΔV_M(t) [Trigger: F(1,7) = 10.3, P < 0.05 and Load: F(2,14) = 15.4, P < 0.0001]. No significant interaction was found.

Fig. 7.

Changes in ΔV_F(t) and ΔV_M(t) indices between the steady-state value 1,000 ms prior to t₀ and the minimum value over the 2,000 ms after t₀. The data is shown as averages over subjects with standard error bars

After the steep drop around t₀, ΔV_F(t) and ΔV_M(t) showed a recovery to positive values and stabilized 1–2 s after the perturbation. After 2,500 ms, the former index did not reach the pre-perturbation levels (Fig. 8a), while the latter index reached positive values higher than those prior to the perturbation (Fig. 8b). These findings were supported by three-way ANOVA (Time × Trigger × Load) which showed significant effects of Time for both ΔV_F(t) [F(1,7) = 90.5, P < 0.0001] and ΔV_M(t) [F(1,7) = 8.2, P < 0.05], but no effect of Trigger, Load, or interactions.

Fig. 8.

Averaged values of a ΔV_F(t) and b ΔV_M(t) over the 100 ms, 1,000 ms before and 2,500 ms after the time of perturbation. The data was averaged over subjects and presented as means ± SE

The critical time (t_CR) was calculated as the time after t₀ when a ΔV index, ΔV_F(t) or ΔV_M(t), turned positive, Fig. 9. For both ΔV_F(t) and ΔV_M(t), t_CR was smaller following self-triggered perturbations than following experimenter-triggered perturbations. These findings were supported by two-way ANOVA (Trigger × Load) showed significant effects of Trigger for both ΔV_F(t) [F(1,7) = 5.8, P < 0.05] and ΔV_M(t) [F(1,7) = 5.8, P < 0.05]. There was no significant effect of Load or interactions.

Fig. 9.

Critical times (t_CR) of ΔV_F(t) and ΔV_M(t). The perturbation was given at time 0 s. The data was averaged over subjects and presented as means ± SE

Discussion

Results of the study have confirmed the main hypothesis that the central nervous system is able to prepare a multi-element system for a self-triggered mechanical perturbation by changing the covariation of elemental variables. This hypothesis was originally suggested based on studies of voluntary changes in the total force produced by a set of fingers (Olafsdottir et al. 2005a; Shim et al. 2005b). The current study has extended the hypothesis to more natural tasks (static prehension) involving two performance variables (the total force and the total moment of force), and to preparation of a self-triggered perturbation. Further, we discuss implications of the main findings for the feed-forward control of multi-digit actions and for the principle of superposition [see the Introduction and Arimoto et al. (2001)].

Feed-forward preparation to perturbation

The ability of the central nervous system to produce functionally important changes in control variables in anticipation of an action or a perturbation has been known for a long time (Belen’kiii et al. 1967; Traub et al. 1980; Hugon et al. 1982; Lacquaniti and Maioli 1989). In particular, voluntary movements or manipulations of external objects by a standing person are accompanied by anticipatory postural adjustments [APAs: preparatory changes in the activity of the leg and trunk muscles seen prior to changes in the activity of muscles producing the required action, commonly arm muscles (Riach and Hayes 1990; Massion 1992; Elble and Leffler 2000; Minvielle and Audiffren 2000; Adkin et al. 2002)] Movements in a joint of a multi-joint limb are accompanied by changes in the activity of muscle acting at other joints of the limb that can be seen without a time delay (Koshland et al. 1991). When a person moves a grasped object, changes in the grip force can be seen prior to changes in the force producing the required object motion (Johansson and Westling 1988; Gordon et al. 1993). All these observations suggest that the central controller is capable of predicting mechanical effects of planned actions on parts of the body that are not explicitly involved in these actions.

All of the mentioned studies focused on changes in the activity of particular muscles or mechanical variables. Such overt anticipatory adjustments in the output of particular elements of the human neuromotor system (forces of individual digits) or of a set of effectors as a whole (total grip force) have also been described in experiments with static prehensile tasks (Johansson and Westling 1988; Gordon et al. 1993; Scholz and Latash 1998). In our study, we asked a different question: Can interactions among elemental variables be changed prior to an expected perturbation?

We analyzed patterns of covariation of finger forces and moments similar to how it has been done in studies using the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schoner 1999; Latash et al. 2001). The UCM hypothesis assumes that the controller acts in the space of elemental variables and computes in that space a sub-space (a UCM) corresponding to a desired value of a performance variable. Further, variability in the space of elemental variables across repetitive trials at a task is constrained less within the UCM than orthogonal to the UCM. Several performance variables can be stabilized across repeated trials as long as the number of elemental variables is larger than the number of performance variables.

Our analysis differed from earlier studies using the UCM approach in that we used finger forces and moments rather than finger modes [hypothetical independent variables (Danion et al. 2003; Olafsdottir et al. 2005a)]. This was dictated by practical considerations since computing finger modes requires performing standard tasks with force production one digit at a time. This is impossible to do while holding an object statically, because the object would translate and/or rotate. On the other hand, digit interactions have been shown to change depending on whether the subject acts on a free or a fixed object and also depending on the thumb position (Shim et al. 2004a; Olafsdottir et al. 2005b). Hence, we performed analysis in the space of elemental mechanical variables produced by individual digits.

The five-digit human hand is able to stabilize both the grip force and the total moment exerted simultaneously on a hand-held object (Shim et al. 2005a). In our experiments, the indices of finger interactions (ΔV_F and ΔV_M) were positive for both total force and total moment stabilization when the subjects held the object statically (Fig. 8). These indices did not differ between self- and experimenter-triggered conditions but showed significantly higher values for the total force stabilization (ΔV_F) than for the total moment stabilization (ΔV_M). This finding of stronger total force stabilization contrasts earlier reports of moment stabilization in pressing tasks, even when the tasks did not require stabilizing the moment (Latash et al. 2001, 2002, 2005b).

When the subjects removed one of the loads themselves (self-triggered), early changes in both indices of covariation, ΔV_F and ΔV_M, were observed. These changes started about 150 ms prior to the load removal. They were not observed when the same load manipulation was done unexpectedly by an experimenter. These observations are very similar to the earlier reports on anticipatory changes in multi-finger synergies in preparation for a voluntary quick force change in pressing tasks (Olafsdottir et al. 2005a; Shim et al. 2005b). They suggest that the phenomenon of ACV can be generalized to the more natural prehensile task and to two performance variables, the total grip force and the total moment of forces applied to the handle.

Two components of control of multi-element systems

The results of our experiments suggest that the control of a multi-element system may be viewed as consisting of two components. The first component is related to the production of a required time profile of functionally important performance variables. The second component is related to organizing multi-element synergies that assure certain stability properties of these performance variables. Within this framework, the results suggest that the controller can adjust these two components independently, that is, it can change patterns of covariation of elemental variables without changing the overall performance of the system.

This interpretation fits an earlier model of finger interaction based on central neural back-coupling loops [the CBC-model (Latash et al. 2005b)]. The CBC-model explicitly incorporates a possibility of independent changes in performance variables and in patterns of element interactions. In particular, it allows the controller to destabilize a variable if this is required by the task. The optimal feedback control model (Todorov and Jordan 2002) is able to interpret data that show stabilization of performance variables, but it has no obvious room to accommodate observations of decreased stabilization or destabilization of these variables. Note that following a perturbation, subjects in our experiments typically showed a prolonged time interval when the indices of co-variation dropped to negative values corresponding to destabilization of the total force and the total moment (Fig. 5).

Principle of superposition

The principle of superposition was originally introduced in the field of robotics (Arimoto and Nguyen 2001; Arimoto et al. 2001) and later confirmed for two-dimensional and three-dimensional prehensile actions by human hand (Shim et al. 2003, 2005a). Earlier studies have particularly shown that elemental variables describing the action of the human digits on a hand-held object can form subsets that stabilize the total force acting on the object and the total moment acting on the object, respectively. These observations allowed the authors to conclude that there are two synergies involved in prehensile actions with the purposes of providing required gripping and rotational action components.

In our studies, indices of interaction of elemental variables for stabilization of the total force and total moment showed similarities and differences in their changes. In particular, there were no differences in the timing of changes in ΔV_F and ΔV_M. However, following a perturbation, ΔV_F and ΔV_M showed counter-directional changes as compared to their steady-state values prior to the perturbation: the former index dropped while the latter increased. These findings corroborate the principle of superposition by showing that indices of synergies stabilizing the gripping action (ΔV_F) and the rotational action (ΔV_M) can behave differently. The CNS seems to be more concerned about controlling the stability of the total moment than the total force after the perturbation.

Functional purpose of ACV

One of the observations suggests that ACV may be functionally important in helping the controller regain stabilization of performance variables following a perturbation. In trials with ACV (self-triggered), the subjects returned to positive ΔV values faster than in trials without ACV (experimenter-triggered). This was true for indices of both total force and total moment stabilization. Note that under self-triggered conditions, the subjects avoided the rather large deviations of the orientation of the handle from the initial positions that were seen under experimenter-triggered conditions (Fig. 4).

A somewhat similar conclusion has been reached in a previous study (Olafsdottir et al. 2005a) that compared ΔV_F and ΔV_M changes during the quick force pulse production task under the self-paced and reaction- time instructions. ACV was seen only under the self-paced instruction and it was followed by a smaller drop of ΔV_F and ΔV_M computed for total force stabilization into negative values. In that experiment, the subjects relaxed after producing a force pulse. This did not allow assessing the time taken to return to positive values because ΔV_F and ΔV_M indices could not be defined when the fingers were relaxed.

It is possible that the functional purpose of ACV is similar to that of anticipatory postural adjustments, APAs. These two groups of phenomena have much in common. They both can be seen about 150 ms prior to an action or an expected perturbation (Massion 1992; Olafsdottir et al. 2005a), they both become smaller or disappear under the simple reaction time instruction (Lee et al. 1987; Olafsdottir et al. 2005a), and they both are delayed and decreased in elderly (Woollacott and Manchester 1993; Latash et al. 2005a). We view these commonalities as more than simple coincidences but rather as a suggestion that a significant portion of APAs may actually represent changes in multi-muscle postural synergies (Krishnamoorthy et al. 2003; Ting and Macpherson 2005) with the purpose of destabilizing such variables as the location of the center of pressure (Aruin and Latash 1996; Aruin et al. 1998), the location of the center of mass, and shear forces acting on the body.

We conclude that humans adjust multi-digit synergies involved in prehensile tasks in anticipation of a self-triggered perturbation. These adjustments can be followed by destabilization of performance variable by co-varied changes in individual digit actions. Different changes in the indices of force and moment covariation after a perturbation corroborate the principle of superposition.