Vertical Distribution of Denitrification in an Estuarine Sediment: Integrating Sediment Flowthrough Reactor Experiments and Microprofiling via Reactive Transport Modeling

Abstract

Denitrifying activity in a sediment from the freshwater part of a polluted estuary in northwest Europe was quantified using two independent approaches. High-resolution N₂O microprofiles were recorded in sediment cores to which acetylene was added to the overlying water and injected laterally into the sediment. The vertical distribution of the rate of denitrification supported by nitrate uptake from the overlying water was then derived from the time series N₂O concentration profiles. The rates obtained for the core incubations were compared to the rates predicted by a forward reactive transport model, which included rate expression for denitrification calibrated with potential rate measurements obtained in flowthrough reactors containing undisturbed, 1-cm-thick sediment slices. The two approaches yielded comparable rate profiles, with a near-surface, 2- to 3-mm narrow zone of denitrification and maximum in situ rates on the order of 200 to 300 nmol cm⁻³ h⁻¹. The maximum in situ rates were about twofold lower than the maximum potential rate for the 0- to 1-cm depth interval of the sediment, indicating that in situ denitrification was nitrate limited. The experimentally and model-derived rates of denitrification implied that there was nitrate uptake by the sediment at a rate that was on the order of 50 (± 10) nmol cm⁻² h⁻¹, which agreed well with direct nitrate flux measurements for core incubations. Reactive transport model calculations showed that benthic uptake of nitrate at the site is particularly sensitive to the nitrate concentration in the overlying water and the maximum potential rate of denitrification in the sediment.

Anthropogenic inputs of nitrogen are a major cause of eutrophication in aquatic environments (39). Denitrification, the bacterial dissimilatory reduction of nitrate to gaseous products, counteracts eutrophication by removing inorganic nitrogen and releasing it to the atmosphere and by decomposing organic matter (34). The emissions resulting from denitrification, however, include nitrous oxide, a powerful greenhouse gas (8). Because of its environmental importance, denitrification has been the subject of numerous studies (for reviews, see references 12, 16, and 34). Oxygen and nitrate concentrations, temperature, pH, and the availability of suitable electron donor substrates (mainly organic carbon compounds) are considered the key factors controlling the occurrence and rate of denitrification (6, 22, 38).

In estuarine and coastal environments, the most intense denitrification often occurs in sediments, where reduced solute transport rates enable the establishment of anaerobic conditions. A number of methods have been developed to quantify denitrification and related nitrogen transformations in sediments; these methods include, among others, benthic flux measurement (17), isotope pairing techniques (32), and microprofiling using nitrous oxide (31) or nitrate microsensors (9, 20). The available data show that there are large spatial and temporal variations in denitrification rates in nearshore sediments. Ideally, kinetic models of denitrification should account for these variations.

In this study, we combined potential denitrification rate measurements, N₂O microprofiling in acetylene block core incubations, and reactive transport modeling to quantify the depth distribution of the rate of denitrification in a sediment from the freshwater part of a macrotidal estuary. By combining the various approaches, we were able to verify the predictive capability of the kinetic description of denitrification incorporated into the reactive transport model and to assess the sensitivity of benthic nitrate removal to changes in key model parameters.

MATERIALS AND METHODS

Site description.

Sediment cores were collected in August 2001 and August 2002 at an unvegetated intertidal site in the freshwater part of the Scheldt Estuary near Appels, Belgium. The Scheldt River has a total length of 355 km and flows through France, Belgium, and The Netherlands. The average river discharge is on the order of 120 m³ s⁻¹, while the tidal amplitude in the estuary ranges from 2 to 5 m (3). The Scheldt Estuary is heavily polluted by municipal and industrial discharge and intensive livestock farming. The large input of organic matter sustains high heterotrophic activity in the upper freshwater part of the estuary, which can result in a pronounced oxygen depletion zone extending over a distance of 30 to 70 km (42). Intertidal sediments are the primary site of benthic carbon mineralization in the Scheldt Estuary (36). A detailed description of the site is provided elsewhere (13). All cores used in the experiments described here were collected close to each other (<1 m).

Core incubations.

Sediment was sampled in August 2002 at low tide using Perspex (acrylic glass) cores with a diameter of 7.6 cm and length of 35 cm. To determine the benthic NO₃⁻ flux, two cores containing about 20 cm of sediment collected in August 2002 were incubated for 22 h with river water from the site. The overlying water was gently stirred and sparged with air to avoid development of anoxia. The overlying water of the cores was sampled periodically and analyzed to determine the NO₃⁻ content. The time-averaged nitrate fluxes into the sediment were calculated from the concentration differences measured in the overlying water between the start and end of the incubations, taking into account the known area of the sediment and volume of overlying water.

To assess pore water transport, three additional cores were incubated with 200 ml NaBr-amended river water from the site. The initial bromide concentrations in the overlying water after NaBr addition were on the order of 10 mmol liter⁻¹. The cores were incubated for 36 h. At the end of the incubation, one core was sectioned into 0.5-cm depth intervals, and the two other cores were sectioned into 1-cm intervals. Pore water was separated from the sediment slices by centrifugation (30 min at 1,000 × g) and filtration (0.45-μm-pore-size Whatman filters) and stored at −20°C until it was analyzed to determine the bromide content. Overlying water samples were collected at the beginning and end of the incubations and analyzed to determine the Br⁻ concentrations.

Flowthrough reactors.

Undisturbed, 1-cm-thick sediment slices were collected in August 2002 with a specially designed hand-held corer. Potential nitrate reduction rates were determined with slices corresponding to depth intervals of 0 to 1, 1 to 2, and 2 to 3 cm using flowthrough reactors (FTRs). The corer, coring technique, FTR design, and potential rate determinations are described in detail elsewhere (18, 25). The reactors were supplied with deaerated inflow solutions containing variable nitrate concentrations (2.5, 5, 7.5, and 10 mmol liter⁻¹; four reactors per depth interval) at a flow rate of 4 ml h⁻¹. Steady-state nitrate reduction rates (R_exp) (in nmol cm⁻³ h⁻¹) were calculated after the nitrate concentration in the outflow reached a constant value, as described elsewhere (18). The nitrate reduction rates were fitted to the Michaelis-Menten rate expression:

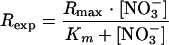(1)

where K_m is the nitrate half-saturation constant and R_max is the maximum nitrate reduction rate. The average nitrate concentration in the reactor ([NO₃⁻]) was estimated to be the midpoint between the inflow and outflow concentrations. The half-saturation constant was assigned a value of 250 μmol liter⁻¹, the average value derived from a large set of FTR experiments with estuarine sediments, which included additional sampling locations, sampling times, and depth intervals (18).

Microprofiling.

Perspex (acrylic glass) cores with a diameter of 4.2 cm and a length of 15 cm were collected at low tide in August 2001 and August 2002. The cores contained about 10 cm of sediment and were incubated at 25°C with river water from the site. The overlying water was gently mixed and sparged with air. Microprofiling was started within 4 h after the cores were collected. Oxygen microprofiles were determined using a miniaturized Clark-type oxygen sensor with an internal reference and a guard cathode (11, 30). Nitrous oxide profiles were determined with a miniaturized Clark-type nitrous oxide sensor with an internal reference and a guard cathode equipped with an oxygen front guard, making it insensitive to oxygen (Unisense, Århus, Denmark). Microprofiles of nitrate were determined only in August 2002, using a Liquid Ion eXchange-type (LIX) electrode (see reference 9) with a calomel reference electrode (Radiometer Copenhagen) and calibrated at the in situ temperature (25°C) and salinity (0‰). Linear two-point calibration of the oxygen and nitrous oxide microsensors was performed with river water from the sampling site. The microelectrodes were mounted on a micromanipulator driven by a computer-controlled motor, making it possible to simultaneously measure vertical distributions of oxygen, nitrate, and nitrous oxide.

Acetylene block experiments.

Conversion of N₂O to N₂ and nitrification were inhibited in sediment cores collected in August 2001 and August 2002 by lateral injection of acetylene-saturated water through silicone-filled holes positioned vertically along the core liner. The holes were positioned every 0.5 cm from the sediment surface to a sediment depth of 5 cm. The injections resulted in a C₂H₂ pore water concentration of 10% (vol/vol). Acetylene-saturated river water from the site was added to the core to obtain a final C₂H₂ concentration of 10% (vol/vol) in the overlying water. After addition of C₂H₂, N₂O profiles were recorded with a depth resolution of 250 μm until 2 cm below the sediment surface. Two to eight profiles were recorded sequentially, approximately every 15 min. Ambient oxygen, nitrous oxide, and nitrate (August 2002 cores only) profiles were determined for sediment cores without C₂H₂ addition to determine background N₂O values and check for matrix effects on the sensor readings.

Additional sediment cores collected in August 2001 and August 2002 were supplied with both nitrate and acetylene. One milliliter of a 10-mmol liter⁻¹ KNO₃ solution saturated with C₂H₂ was injected laterally into each hole along the core liner, producing pore water NO₃⁻ concentrations of ∼1.7 mmol liter⁻¹. Nitrate was also added to the overlying, acetylene-saturated water to a final concentration of ∼2 mmol liter⁻¹ (compared to ambient concentrations on the order of 200 μmol liter⁻¹). Time series microprofiles of N₂O were recorded as described above.

Analytical methods.

Nitrate, nitrite, and ammonium concentrations were determined colorimetrically with a Nutrient Autoanalyzer 3 (Bran and Luebbe), using standard procedures. Bromide concentrations were determined by ion chromatography (IC Waters, Milford MA). Porosity was determined from the weight loss of a core section having a known volume after oven drying at 105°C. Sediment organic C and total N contents were determined with a Carlo Erba CN analyzer. Inorganic C was removed before the analysis by shaking the sample with 1 mol liter⁻¹ HCl twice (12 h and 4 h). Grain size analyses of the bulk sediments were carried out with a Malvern Instruments Mastersizer S. The most probable numbers of denitrifying organisms were determined as described elsewhere (18). Most of the sediment properties reported below were determined using sediment sampled in August 2002; the exceptions were grain size and organic C and total N concentrations, which were determined using sediment collected in May 2002.

Reactive transport modeling.

Model calculations were carried out with the Biogeochemical Reaction Network Simulator, a flexible modeling environment for reactive transport calculations (1, 28; http://www.geo.uu.nl/∼rtm/index). The time-dependent depth profiles of the concentrations of NO₃⁻ and N₂O plus the denitrification rate were described by the non-steady-state mass conservation equation for a pore water solute species (2):

(2)

where x is the depth in the sediment, t is time, C is the concentration of the solute, C₀ is the solute concentration at the sediment-water interface (SWI), D_s is the in situ molecular diffusion coefficient of the solute corrected for tortuosity (5), α is the nonlocal exchange coefficient, and R is the net rate of production of the solute. At 25°C, 0‰ salinity, and a porosity of 0.80, the D_s values were 2.10 × 10⁻⁵ and 1.92 × 10⁻⁵ cm² s⁻¹ for nitrous oxide and nitrate, respectively (5, 33).

The denitrification rate (R_den) was represented via a Michaelis-Menten-type equation (37, 40), taking into account limitation by NO₃⁻ and inhibition by O₂:

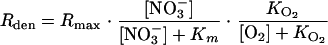(3)

where the default values of K_m and the O₂ inhibition constant () were set at 250 μmol liter⁻¹ (18) and 5 μmol liter⁻¹ (23), respectively. R_max was initially assigned the value derived from the nitrate consumption rate measurements in the flowthrough reactor experiments and then optimized using the time-dependent N₂O profiles. Note that R_max and K_m are apparent kinetic parameters that depend on factors such as organic matter availability and community composition.

The NO₃⁻ and N₂O concentrations measured for the overlying water were used as upper boundary conditions, while zero-concentration gradients were used as lower boundaries. For the transient calculations, the measured ambient NO₃⁻ and N₂O profiles were used as the initial conditions. Pore water O₂ profiles depend on a multitude of reactions (41) and hence were not explicitly computed. Rather, the measured O₂ profiles were used in order to calculate the inhibition term in equation 3. The validity of this approach was confirmed by the time series O₂ microprofiles, which showed that there were no significant changes in the O₂ concentrations over the duration of the incubations (see below).

The depth distributions of N₂O production rates during the acetylene block experiments were estimated from the time series N₂O microprofiles by solving equation 2 for the rate, R(x,t). The second-order spatial derivative in the diffusion term was approximated by the time-averaged change in slope of consecutively measured concentration profiles, whereas the partial derivative of concentration with respect to time was approximated as follows:

(4)

For simplicity, nonlocal exchange was ignored (i.e., α = 0).

RESULTS

Sediment and pore water characteristics.

The uppermost centimeters of sediment at Appels had high porosities and organic carbon contents on the order of 1.5 to 3% (wt/wt) (Table 1). At both sampling times, August 2001 and August 2002, O₂ penetrated approximately 2 to 3 mm below the SWI (Fig. 1). High NO₃⁻ concentrations were found in the river water at the site (around 300 μmol liter⁻¹ and 200 μmol liter⁻¹ in August 2001 and August 2002, respectively). The ambient N₂O concentrations were always below the detection limit of the N₂O microsensor (∼1 μmol liter⁻¹ N₂O). The most probable numbers showed that microorganisms capable of denitrification were present at high densities (∼10⁸ cells cm⁻³ wet sediment) at all depths investigated (0 to 3 cm).

TABLE 1.

Sediment properties

Depth (cm)	Organic C concn (%)	Molar organic C/N ratio	Mean grain size (μm)	Porosity (%)
0-1	1.6	12.3	106	80
1-2	2.5	12.1	67	76
2-3	2.7	13.6	37	66

FIG. 1.

Bromide (A) and oxygen (B) pore water profiles in sediment cores collected in August 2002 at Appels. Note the difference in the vertical scales. The three sets of symbols (measured data) and lines (model calculated) for bromide correspond to three replicate core incubations; the circles, diamonds, and squares correspond to the dotted, dashed, and solid lines, respectively. The calculated bromide profiles assume that there was no enhanced pore water mixing (α = 0). The dotted line in panel B corresponds to a model-predicted steady-state O₂ profile assuming that there was no enhanced mixing, whereas the solid line includes nonlocal pore water transport in the top 0. 75 mm with an α value of 55 h⁻¹. See the text for details.

Enhanced pore water transport.

After 36 h, bromide penetrated to a depth of about 5 cm, and there was good reproducibility for the three replicate cores (Fig. 1A). To quantify pore water mixing in addition to molecular diffusion, the profiles were fitted to solutions of equation 2, taking into account the depletion of Br⁻ in the overlying water with time. Except for the topmost 1 cm of sediment, simulations assuming molecular diffusion only were in good agreement with the measurements, implying that there was no deep (≥1-cm) pore water irrigation. On a vertical scale smaller than that resolved by the bromide measurements, however, a mixed zone in the uppermost 0.75 mm (x_irr) was identified based on the distinct kink in the O₂ microprofiles at that depth (Fig. 1B). An average value for the nonlocal exchange coefficient of 55 h⁻¹ was constrained by fitting the O₂ microprofiles with equation 1, assuming a steady state and a Michaelis-Menten kinetic formulation for the net rate of O₂ consumption. The affinity constant for O₂ was set at 10 μmol liter⁻¹ (41), and the maximum O₂ consumption rate was estimated from 2φD_s(C₀ − C_L)/L², where the O₂ penetration depth (L) corresponds to the depth at which the O₂ concentration drops to 1 μmol liter⁻¹ (i.e., C_L = 1 μmol liter⁻¹) and φ is the porosity. A satisfactory match between measured and predicted O₂ profiles was obtained with α values in the range from 10 to 100 h⁻¹ (Fig. 1B).

The very shallow mixed zone is unlikely to be due to the activity of benthic infauna, which at Appels is dominated by oligochaete worms (35). We believe that this zone reflects an experimental artifact caused by the stirring of the overlying water in the cores. Air sparging and stirring of the overlying water were carried out to avoid progressive chemical stratification and ultimate anoxia of the waters just above the sediment. This would have interfered with the establishment of a steady-state distribution of denitrification activity, hence compromising the interpretation of time series N₂O microprofiles. Enhanced pore water mixing in the upper 0.75 mm of the sediment was accounted for in the reactive-transport calculations by using the same α values for all solute species (55 h⁻¹).

FTR experiments.

The maximum potential nitrate consumption rate obtained in the FTR experiments decreased from 585 nmol cm⁻³ h⁻¹ in the first centimeter of the sediment (0 to 1 cm) to 320 and 225 nmol cm⁻³ h⁻¹ in the two deeper intervals (1 to 2 and 2 to 3 cm, respectively). Because of the high rates of nitrate reduction, relatively high inflow NO₃⁻ concentrations were needed in the FTR experiments in order to recover measurable NO₃⁻ concentrations in the outflow. As a result of the high average nitrate concentrations in the reactors, the measured rates approached the maximum values, and the estimated R_max values were not very sensitive to the value assigned to K_m. In additional acetylene block FTR experiments with Appels sediment, 80 to 100% of the NO₃⁻ consumed was recovered as N₂O (18), implying that under the experimental conditions used, denitrification to N₂ is the dominant pathway of nitrate reduction.

Acetylene block core incubations.

In sediment cores in which C₂H₂ was added to the overlying water, as well as injected laterally into the sediment, increasing pore water concentrations of N₂O occurred as a function of time. A selected number of N₂O depth profiles from a time series experiment carried out in August 2002 are shown in Fig. 2A. The profiles exhibited a distinct maximum at a depth of around 3 mm, with maximum concentrations of ∼35 μmol liter⁻¹ measured after 95 min. The maximum N₂O concentrations occurred below the depth where O₂ penetrated (Fig. 2). Oxygen and NO₃⁻ microprofiles determined alongside the N₂O profiles showed little change during the total time of the incubations (Fig. 2B). As was observed for the ambient O₂ microprofiles (Fig. 1B), the nitrate and O₂ profiles recorded during the C₂H₂ block experiments showed that there was a pronounced change in gradient at a depth of around 0.75 mm (Fig. 2B).

FIG. 2.

Examples of microprofiles of N₂O (A), NO₃⁻ (B), and O₂ (inset) in an acetylene block core incubation experiment carried out in August 2002. The profiles were recorded 30, 59, and 95 min after addition of C₂H₂ to the overlying water and the pore waters via lateral injection ports.

The rate profiles calculated at different times during the acetylene block experiments did not differ significantly over the time scale of the incubations (Fig. 3). The results showed that there was a narrow, 2- to 3-mm-thick layer of denitrification, located between the depths of penetration of O₂ and NO₃⁻ (Fig. 3). The denitrification activity peaked at depths of around 3 mm in both 2001 and 2002, and the maximum rates were in the range from 200 to 400 nmol N cm⁻³ h⁻¹.

FIG. 3.

N₂O production rates for a number of selected time intervals in the same acetylene block core incubation experiment as in Fig. 2. Each rate profile was derived using two successive N₂O profiles (measurement times are indicated), assuming that there was no enhanced pore water transport (α = 0). The shading corresponds to the uppermost sediment layer which exhibits evidence of enhanced pore water transport. See the text for a complete discussion.

The negative rates in the uppermost millimeters were due to the additional removal of N₂O by enhanced pore water transport (see above). When the negative rates were ignored, the integrated N₂O production rates in the sediment were on the order of 60 ± 12 nmol N cm⁻² h⁻¹ for August 2001 and 50 ± 8 nmol N cm⁻² h⁻¹ for August 2002. Note that because acetylene also blocks nitrification, these integrated N₂O production rates should have reflected only denitrification supported by NO₃⁻ uptake from the overlying water.

Addition of NO₃⁻ to the overlying water and sediment pore waters resulted in N₂O concentrations that were more than 1 order of magnitude higher than the values observed in the acetylene block incubations with no added NO₃⁻ (compare Fig. 2A and 4). The maximum concentrations also occurred deeper in the cores, indicating that NO₃⁻ added below the ambient nitrate penetration depth was actively used in denitrification. This observation agreed with the observed presence of denitrifying microorganisms several centimeters below the SWI, as well as the high potential nitrate reduction rates measured with the flowthrough reactors at depths below 1 cm.

FIG. 4.

Examples of N₂O profiles recorded during a core incubation experiment (August 2002) after simultaneous addition of C₂H₂ and NO₃⁻ to the overlying water and pore water. See the text for details.

Nitrate fluxes.

The benthic NO₃⁻ uptake flux, obtained from the measured loss of nitrate from the overlying water in the unamended core incubations in August 2002, was 45 ± 14 nmol N cm⁻² h⁻¹. Diffusive nitrate fluxes were also estimated from the linear portions of the depth profiles for NO₃⁻ concentrations below the zone of enhanced transport, according to the following equation:

(5)

where the concentration gradient was evaluated below 0.75 mm. For the near-steady-state nitrate profiles measured during the acetylene block experiments with no added nitrate in August 2002 (Fig. 2B), equation 5 yielded downward nitrate fluxes into the zone of denitrification of 60 ± 15 nmol N cm⁻² h⁻¹. The nitrate fluxes were thus the same order of magnitude as the integrated N₂O production rate in the August 2002 acetylene block core incubations with no added nitrate.

Reactive transport modeling.

A baseline simulation of the August 2002 acetylene block experiment was carried out using the maximum potential nitrate reduction rate measured for the 0- to 1-cm sediment slice (R_max = 585 nmol cm⁻³ h⁻¹), the default nitrate half-saturation constant (K_m = 250 μM), and the default oxygen inhibition constant (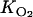= 5 μmol liter⁻¹), plus the mixing parameters derived from the O₂ microprofiles (x_irr = 0.075 cm, α = 55 h⁻¹). Sensitivity analyses were then performed by multiplying or dividing the kinetic parameter values (R_max, K_m, and ) by 2. The results are summarized in Table 2, which also shows the model-predicted effect of the overlying water NO₃⁻ concentration on pore water N₂O production in the acetylene block core incubation experiment.

TABLE 2.

Model sensitivity analyses: effects of the NO₃⁻ concentration in the overlying water and kinetic parameters (R_max, K_m, and 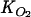) on pore water N₂O buildup during simulated acetylene block core incubations^a

[NO3−]0LW (μmol liter−1)	Rmax (nmol N cm−3 h−1)	Km (μmol lit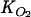er−1)	(μmol liter−1)	[N2O]max (μmol liter−1)	Maximum N2O production rate (nmol N cm−3 h−1)	Integrated N2O production rate (nmol N cm−2 h−1)
188	585	250	5	19.6	135.0	28.7
188	585	125	5	26.7	193.1	35.4
188	585	500	5	12.9	86.6	20.5
188	293	250	5	11.8	76.9	19.0
188	1,170	250	5	28.7	224.8	37.8
188	585	250	2.5	18.9	134.9	27.0
188	585	250	10	20.3	139.5	30.9
94	585	250	5	12.0	76.4	15.8
376	585	250	5	32.2	222.1	50.4

^aIn the model simulations, the observed O₂ profile (Fig. 1 and 2) was imposed to account for inhibition of denitrification by O₂ (equation 3). The maximum N₂O concentrations ([N₂O]_max) and the N₂O production rates were calculated at 59 min. [NO₃⁻]_0LW, NO₃⁻ concentration in the overlying water.

Additional forward reactive transport simulations were carried out to match the measured N₂O concentration buildup in the sediment, by fixing either K_m or R_max to the values derived from FTR experiments. When K_m was set at 250 μmol liter⁻¹, R_max had to be adjusted to 950 nmol cm⁻³ h⁻¹ in order to reproduce the time series N₂O profiles (Fig. 5A). With this set of parameters, the calculated NO₃⁻ concentration profile closely resembled the measured profile (Fig. 5B). As observed, most denitrifying activity was predicted to be restricted to the 1.5- to 4-mm depth interval, although the modeled rates tended to be somewhat lower than the N₂O production rates estimated from the time series N₂O profiles (Fig. 6A). There was also a slight offset of about 0.5 mm between the calculated and observed depths at which the maximum N₂O concentration and production rate were reached.

FIG. 5.

Measured and model-predicted N₂O profiles (A) and measured and predicted NO₃⁻ profiles (B) after 59 min of incubation in an acetylene block core incubation experiment (August 2002) (see Fig. 2 and 3). The dashed lines are the modeled depth distributions obtained using a K_m value of 250 μmol liter⁻¹ and an R_max value of 585 nmol cm⁻³ h⁻¹; the solid lines indicate modeled depth distributions obtained using a K_m value of 250 μmol liter⁻¹ and an R_max value of 950 nmol cm⁻³ h⁻¹. In both simulations, the existence of a thin layer of enhanced pore water transport (x_irr = 0.75 mm) is assumed, with a constant exchange coefficient (α) of 55 h⁻¹. The inset shows the N₂O accumulation after 1, 2, 3, and 4 h. See the text for details.

FIG. 6.

In situ denitrification rates supported by nitrate uptake from the overlying water (A), maximum potential denitrification rates measured in flowthrough sediment reactors (B), and most probable numbers (MPN) of denitrifiers (C) in the top 3 cm of the sediment at Appels (August 2002). The solid line in panel A indicates the model-predicted in situ denitrification rate distribution in an acetylene block core incubation, obtained using a K_m value of 250 μmol liter⁻¹, an R_max value of 950 nmol cm⁻³ h⁻¹, an α value of 55 h⁻¹, and an x_irr value of 0.75 mm. The rectangles in panel A indicate the denitrification rates derived from the time series N₂O microprofiles (negative rates at the top were excluded for clarity).

An equally good fit to the observed values was obtained when we fixed R_max at 585 nmol cm⁻³ h⁻¹ and reduced K_m to 100 μmol liter⁻¹ (results not shown). With both sets of K_m and R_max values, the depth-integrated steady-state rate of N₂O production calculated with the reactive transport model for August 2002 was 37 nmol N cm⁻² h⁻¹. Irrespective of the actual K_m and R_max values used, the reactive transport simulations predicted that the NO₃⁻ concentration profiles should reach steady state shortly after C₂H₂ injection, while the buildup of N₂O in the pore waters should continue for several hours (Fig. 5A, inset). These predictions were consistent with the observations.

DISCUSSION

Rate distribution and nitrate limitation.

The results of the acetylene block experiments performed with cores with no added nitrate indicate that shortly (<15 min) after injection of C₂H₂, the depth profiles for pore water O₂ and NO₃⁻ reach steady state (Fig. 2B). The N₂O production rates derived from the time series N₂O microprofiles also imply that there was little variation in the depth distributions of denitrification activity during the experiments (Fig. 3).

Production of N₂O in the acetylene block experiments started at depths where pore water O₂ concentrations dropped below 50 μmol liter⁻¹ and ended when pore water NO₃⁻ was exhausted (Fig. 2B and 3). As a result, denitrification was restricted to a sediment layer that was about 3 mm thick. The presence of such thin zones of denitrification has been reported previously for stream sediments (6), lake sediments (14, 15, 19), and estuarine sediments (4, 20).

Because of inhibition by O₂ in the uppermost 1 to 2 mm and, more importantly, because of the lack of NO₃⁻ at depths of >5 mm, only a small fraction of the denitrifying capacity of the sediment was utilized. This is shown in Fig. 6, where potential and in situ rates of denitrification are compared (Fig. 6A and B). It is also clearly evident from the instantaneous response of N₂O production to nitrate addition to the pore waters (Fig. 4) and is consistent with the presence of denitrifiers well below the depth of NO₃⁻ penetration (Fig. 6C).

The denitrification rates inferred from the acetylene block core incubations are lower than the maximum potential rate (R_max) measured for the 0- to 1-cm depth interval in the FTR experiments by a factor of about 2 (Fig. 6). Furthermore, the NO₃⁻ concentrations in the overlying water during the two sampling times fall in the range of nitrate half-saturation concentrations (K_m) derived from FTR experiments with estuarine sediments (200 to 600 μmol liter⁻¹) (18). Within the zone of maximum N₂O production (2 to 4 mm), the NO₃⁻ concentrations are well below the K_m.

Taken together, the results indicate that denitrification in the sediment is limited by nitrate. Consequently, the resident denitrifying community rapidly adjusts its level of activity to increased nitrate availability, as shown by the results of the NO₃⁻ addition core incubations (Fig. 4). The excess denitrifying capacity also implies that there is efficient utilization by the denitrifying community of nitrate produced by nitrification. In the mid-Scheldt Estuary downstream from Appels, up to 85% of total denitrification in intertidal sediments may be coupled to nitrification (21). The ability to rapidly respond to changes in the NO₃⁻ concentration should be a useful adaptation in intertidal estuarine sediments where the pore water composition and redox state can vary substantially on short time scales due to tidal flooding and irrigation by benthic infauna.

Microprofiling versus FTR experiments.

Acetylene block and FTR experiments yield different, but complementary, kinetic information. The high-resolution denitrification rate distributions inferred from the N₂O microprofiles provide a precise determination of the in situ reaction zone (Fig. 3). In contrast, FTR experiments are designed to measure potential rates and parameterize predictive rate equations. Furthermore, the spatial resolutions of the two approaches are quite different, as the FTRs integrate the potential denitrifying activity over 1-cm depth intervals. However, as illustrated here, the differences between the two experimental approaches can be bridged through reactive transport modeling.

With the R_max value obtained in the 0- to 1-cm FTR experiment and the baseline K_m value, the model underpredicts the buildup of N₂O; the calculated maximum N₂O pore water concentrations are about one-third lower than the observed values (Table 2). Nonetheless, the forward reactive transport model calculations are able to forecast the general features of the acetylene block core incubation experiments. In particular, the model predicts that production of N₂O is restricted mainly to a narrow 2- to 3-mm zone. In addition, the model-calculated depth distribution of the N₂O production rate rapidly reaches steady state, while the pore water N₂O concentrations keep increasing for several hours.

Better agreement of the magnitudes of the concentrations and production rates of N₂O is obtained with the model by increasing R_max or decreasing K_m (Fig. 5). The significant decrease in the potential denitrification rate with depth (Table 1 and Fig. 6B) suggests that the average R_max for the 0- to 1-cm depth interval (585 nmol cm⁻³ h⁻¹) represents a lower limit for R_max in the zone of denitrification (0.1 to 0.5 cm). Furthermore, matching the N₂O profiles with an R_max value of 585 nmol cm⁻³ h⁻¹ requires a K_m value (100 μM) that is at the extreme low end of the range obtained in a larger set of FTR experiments with Appels sediment (200 to 600 μM) (18). Therefore, by combining the various experimental and model-derived constraints, our best estimates for the ranges of the kinetic parameters in equation 3 are as follows: for K_m, 100 to 500 μM; and for R_max, 585 to 950 nmol cm⁻³ h⁻¹. Note that varying 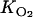by a factor of 2 has only a minor effect on the predicted N₂O concentrations and production rate (Table 2).

The K_m values derived from FTR experiments with natural estuarine sediments (18) are higher than the value determined for a pure culture of a nitrate-reducing bacterium, Paracoccus denitrificans (∼10 μM) (26). They are, however, in line with the typically higher whole-sediment K_m values obtained in slurry or core incubation experiments (10, 17, 24, 27). The great variability of whole-sediment K_m values among different studies, which range from 10 to 600 μmol liter⁻¹, may reflect the great diversity of benthic communities of denitrifiers, which contain organisms exhibiting a wide range of nitrate affinities.

Biogeochemical implications.

The integrated N₂O production rates determined in the acetylene block core incubations, the direct nitrate flux determinations, and the reactive transport modeling results all point to the high capacity for nitrate removal by the intertidal estuarine sediments in the upper Scheldt Estuary (21). High rates of benthic denitrification supported by nitrate uptake from the water column, similar to those at Appels (37 to 60 nmol N cm⁻² h⁻¹), have been reported for nitrate-rich streams (∼120 nmol N cm⁻² h⁻¹) (7) and eutrophic estuaries in Denmark (40 to 140 nmol N cm⁻² h⁻¹) (4, 20).

The experimentally calibrated reactive transport model provides further insight into the role of the kinetic parameters and the overlying water chemistry in denitrification activity in the sediments (Table 2). In particular, the benthic NO₃⁻ uptake and subsequent denitrification are very sensitive to the NO₃⁻ concentration in the overlying water. The water column NO₃⁻ concentrations in the freshwater part of the Scheldt Estuary exhibit large seasonal and interannual variations, with values ranging from a few micromoles per liter to 400 μmol liter⁻¹. For this range of overlying water NO₃⁻ concentrations, the model-predicted depth-integrated denitrification rates increase almost linearly with increasing NO₃⁻ concentrations at the water-sediment interface; that is, benthic nitrate uptake in the upper Scheldt Estuary should directly scale to the water column nitrate concentration.

For maximum potential denitrification rates up to about 1,000 nmol cm⁻³ h⁻¹, the model-calculated integrated rate of denitrification increases with increasing R_max (Table 2). At even greater values of R_max, however, the depth-integrated denitrification rate asymptotically approaches a maximum value (results not shown), reflecting the increasing rate-limiting effect of physical transport of nitrate from the water column to the zone of denitrification. Thus, a benthic denitrifying community exhibiting a potential metabolic capacity much lower than that inferred here from the combined experimental and modeling results (R_max range, 585 to 950 nmol cm⁻³ h⁻¹) would underutilize the high NO₃⁻ concentrations in the Scheldt River water, whereas a community with a much higher R_max would be only marginally more efficient in removing NO₃⁻ from the water column.

Although estuarine sediments are recognized as a sink for reactive nitrogen (3, 34), the role of benthic denitrification is often ignored in estuarine nitrogen models. For example, Regnier and Steefel (29) considered only water column denitrification in their non-steady-state N model of the Scheldt Estuary. The average values for the river discharge (30 m³ s⁻¹) and dissolved inorganic N concentration (600 μmol liter⁻¹) yield a daily input of reactive dissolved inorganic nitrogen (NH₄⁺ plus NO₃⁻) to the upper Scheldt Estuary of around 22 tons N during the summer months. Multiplying the benthic nitrate uptake obtained in this study (∼60 nmol cm⁻² h⁻¹) by the surface area of freshwater tidal sediments (12.2 × 10⁶ m²) (P. Regnier, personal communication) yields a daily benthic uptake of about 2.5 tons of NO₃-N in the upper estuary alone. Although this is a very rough estimate, it indicates that sediments may be responsible for the removal of a considerable fraction of the reactive inorganic N entering the estuary.