Abstract
Cross-talk cancellation is a method for synthesising virtual auditory space using loudspeakers. One implementation is the “Optimal Source Distribution” technique [T. Takeuchi and P. Nelson, J. Acoust. Soc. Am. 112, 2786-2797 (2002)], in which the audio bandwidth is split across three pairs of loudspeakers, placed at azimuths of ±90°, ±15°, and ±3°, conveying low, mid and high frequencies, respectively. A computational simulation of this system was developed and verified against measurements made on an acoustic system using a manikin. Both the acoustic system and the simulation gave a wideband average cancellation of almost 25 dB. The simulation showed that when there was a mismatch between the head-related transfer functions used to set up the system and those of the final listener, the cancellation was reduced to an average of 13 dB. Moreover, in this case the binaural ITDs and ILDs delivered by the simulation of the OSD system often differed from the target values. It is concluded that only when the OSD system is set up with “matched” head-related transfer functions can it deliver accurate binaural cues.
I. INTRODUCTION
Cross-talk cancellation systems have been proposed and described many times (e.g., Bauer, 1961; Atal and Schroeder, 1962; Cooper and Bauck, 1989; Moller, 1989; Kryiakakis, 1998; Ward and Elko, 1999; Foo et al., 1999; Sæbø, 2001; Lentz et al., 2005; Bai et al., 2005; Bai and Lee, 2006). Their performance is often impressive, and they can give compelling demonstrations. In order to be a useful tool for experiments on spatial hearing, however, such systems need to be able to deliver accurately and reliably the interaural-time-difference (ITD) and interaural-level-difference (ILD) cues that underlie binaural analysis. This paper reports a set of computational tests of the degree to which a cross-talk cancellation system can perform binaurally. We conducted these evaluations as we had a requirement for an experimental facility that could replicate in the laboratory the spatial acoustics of real-world scenes; we were planning to study the relationships between spatial hearing and auditory disability or handicap in elderly adults (e.g., Gatehouse and Noble, 2003; Noble and Gatehouse, 2003), and we considered that a cross-talk cancellation system offered a potentially exact and convenient method for doing this.
Damaske (1971) first demonstrated the binaural capability of cross-talk cancellation, using two loudspeakers at azimuths of ±30° placed in an anechoic chamber. The listeners were required to report the location of a virtual source that was generated by binaural recordings using a dummy head of a talker speaking in an anechoic chamber. Localization performance was good, with the mean error being 10° at worst, and remarkably few front-back errors were reported. Performance was impaired if the sounds were reproduced in a reverberant room, and dramatically so if the listener was 17 cm from the optimum position in front of the loudspeakers. Nelson and colleagues (Hill et al., 2000; Takeuchi et al., 2001; Rose et al., 2002) have studied the binaural performance of a cross-talk cancellation system with two loudspeakers placed at azimuths of ±5° in a large anechoic chamber. They found accurate localizations for target azimuths ahead of the listener, although back-to-front errors were again observed, and targets with large azimuths (near ±90°) were often mislocated. Similar results were reported for other two-loudspeaker systems by Foo et al. (1999) and by Sæbø (2001). Bai et al. (2005) observed large numbers of back-to-front errors in their subjective tests of a two-loudspeaker system, although Lentz et al. (2005) found remarkably few back-to-front errors with a four-loudspeaker system, two of which were behind the listener.
Takeuchi (2001) tested the binaural performance of a six-loudspeaker system, placed in three left/right pairs at azimuths of ±90°, ±32°, and ±3.1° presenting frequencies of, respectively, less than 450 Hz, 450 to 3500 Hz, and greater than 3500 Hz. This system — termed the “optimal source distribution” (“OSD”) system (Takeuchi and Nelson, 2002) — showed encouraging results, in that it gave smaller overall localization errors, as well as fewer back-to-front errors, than a standard two-loudspeaker system with ±5° separation. The OSD system also avoids a problem that can be common to two-loudspeaker systems, as at some frequencies the cross-talk cancellation will require more power than the loudspeaker can supply (e.g. Yang et al., 2003; Nelson and Rose, 2005; Orduna-Bustamanate et al., 2005). The values of these frequencies are inversely dependent upon the azimuthal span of the loudspeakers (Takeuchi and Nelson, 2001); they are avoided in the OSD system by a careful choice of loudspeaker spans and the frequencies they reproduce.
In order to perform cross-talk cancellation it is necessary to know what needs to be cancelled. This can be found by measuring the head-related impulse response or “HRIR” (which in the frequency domain is the head-related transfer function or “HRTF”) between the loudspeakers and the ears of the listener. From these HRIRs a set of digital filters can be calculated which will perform the cancellation (see section II.A below). It is well known that the HRIRs of individuals differ considerably (e.g., Wightman and Kistler, 1989; Middlebrooks, 1999a, b). Accordingly, the ideal method would be to measure these HRIRs — and also calculate cross-talk cancellation filters— for each individual listener. In many circumstances, however, it may be more practical to optimize the system in advance using a single set of HRIRs, perhaps from an accurately-placed manikin, calculate from those a set of cross-talk cancellation filters which would be used for all the listeners (e.g., Damaske, 1971; Moller, 1989; Sæbø, 2001; Foo et al., 1999; Takeuchi, 2001; Lentz et al., 2005; Bai et al., 2005). In this situation there will be a difference between the listener/manikin for whom the system is set up and the listener/manikin to whom the final sounds are played back. This distinction is crucial to understanding the actual performance of cross-talk cancellation systems, as it corresponds to a distinction between the HRIRs used to calculate the cross-talk cancellation filters and the HRIRs of whomever is listening to the putatively cancelled sounds. We will refer to the two sets of HRIRs as, respectively, the “setup” and the “playback” HRIRs. The ideal, individualized situation, where both are the same, represents a matched-HRIR system; the other, nonindividualized situation in which the system is optimized in advance is a mismatched-HRIR system. A mismatched cross-talk cancellation system can only be useful for binaural experiments if it can tolerate the differences between the HRIRs of different individuals.
We implemented a computational simulation of the OSD system in order to study the binaural performance of matched-HRIR and mismatched-HRIR systems. First, we validated the simulation against an acoustic system with a manikin (see Section II); next we measured the amount of cancellation it gave in matched and mismatched situations (Section III) and finally we measured its ability to reproduce ITDs and ILDs, again in matched and mismatched situations (Section IV). We used a computational database (Blauert et al, 1998) of seven individual HRIRs to investigate the effects of matching or mismatching the setup and playback HRIRs.
II. VALIDATION OF THE COMPUTATIONAL SIMULATION
In order to validate our computational simulation of the OSD system we compared it to a real acoustic system (Fig. 1). In the initial setup stage, the cross-talk cancellation filters were calculated from a set of HRIRs measured at the ears of the manikin for each of the loudspeakers. Its performance was quantified in the subsequent playback stage using a target signal that was white noise at one ear but silence at the other. Figure 2 shows a schematic illustration of each step involved in playback: first the target signals were digitally convolved with the cross-talk cancellation filters H, then summed to create the left and right signals vL and vR , passed through the frequency-crossover system and so split into three frequency bands. Each band was presented through a separate loudspeaker, and the signals thus obtained at the ears of the manikin were recorded for offline analysis.
FIGURE 1.
Scale diagram of the six-loudspeaker, ±3°/±15°/±90° OSD system. The ±3° loudspeakers were used for frequencies above 3500 Hz, the ±15° loudspeakers between 500 and 3500 Hz, and the ±90°-loudspeakers below 500 Hz.
FIGURE 2.
Schematic illustration of each step involved in the acoustic cross-talk cancellation system. The first step (the cross-talk cancellation processing) was performed on a personal computer while the second step (cross-over filters) was performed on a separate digital-signal processing board; note the D/A and A/D converters between them. The final step was the loudspeaker presentation of the signals to an acoustic manikin, acting as the listener, with a subsequent off-line analysis of the actual signals received at its ears.
The computational system simulated the playback stage by digitally convolving the processed signals with the measured HRIRs of the loudspeakers-to-microphones. Computational simulations have been used before to measure the amount of cancellation and the ITDs of a waveform (e.g., Takeuchi et al., 2001; Hill et al., 2001; Rose et al., 2002; Orduna-Bustamante et al., 2005; Lentz et al., 2005; Bai and Lee, 2006). They tend to predict large amounts of cancellation; for instance, both Takeuchi (2001) and Bai and Lee (2006) predicted over 40 dB. Such performance would have been more than sufficient for binaural experiments, as it is greater than the 25-30 dB of ILD that is the maximum that is usually encountered (e.g., Blauert, 1997).
II.A. Acoustical Methods
Six loudspeakers were used, placed in three pairs at azimuths of ±3°, ±15°, and ±90° and built into two cabinets (Fig. 1, top panel). The cabinets were placed 1 m away from the center of an acoustic manikin (Brüel and Kjaer, model 4100D), and were carefully measured to be left/right symmetric about the manikin. The manikin was fitted with silicone pinnae and with 1/2″ condenser microphones placed at the entrance to each ear canal; the microphones were approximately 1 m above the floor of the room, and were level with the center of the loudspeakers. All the apparatus was placed in the center of a small acoustic chamber (4-m width, 1.8-m depth, 2-m height), whose surfaces were covered with foam wedges. The reverberation time of the room was less than 40 ms between 250 and 8000 Hz. All of the signal presentations were controlled by a host computer (Toshiba P4000). After D-A conversion (using the inbuilt converter of the computer) at a sampling rate of 22050 Hz, the signals were passed through a real-time, digital frequency-crossover system. This consisted of three, 396-sample, 22050-Hz sampling-rate FIR digital filters (Trinder, 1982) running on a digital signal-processing board. The outputs of the crossover system were then amplified individually (three stereo amplifiers, Denon PMA-255UK) to form the feeds to the individual loudspeakers. The three filters were set to 0-500 Hz (“low”; ±90°-loudspeakers), 500-3500 Hz (“mid”; ±15°-loudspeakers), and 3500-11025 Hz (“high”; ±3°-loudspeakers).
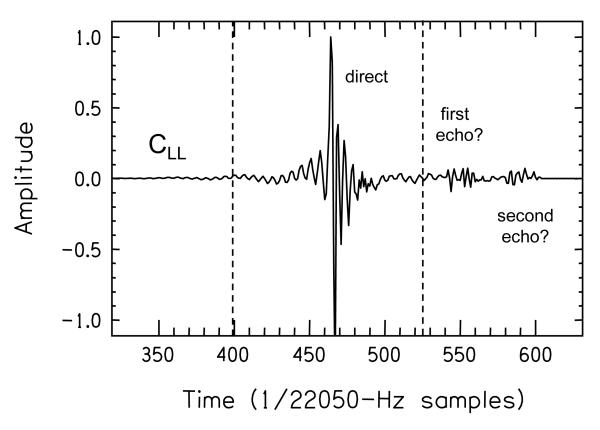
The cross-talk cancellation filters were calculated from measurements of the impulse responses of the transfer functions from the left loudspeakers to the left manikin microphone (“CLL”), left to right (“CLR”), right to left (“CRL”), and right to right (“CRR”).1 The impulse responses were obtained using the maximum-length-sequence (“MLS”) method (e.g., Davies, 1966; for more on our implementation, see Thornton et al., 1991, Thornton et al., 1994, and Chambers et al., 2001). The sampling rate was 44.1 kHz, and, as the MLS signals were passed through the frequency-crossover system and presented simultaneously through the three loudspeakers on the left (or right), the whole of each impulse response was obtained at the same time. Figure 3 shows the MLS recording of the CLL impulse response. The large pulse was the direct sound, and its fine structure is due to both the FIR response of the crossover filters and the HRTF of the manikin, whilst the subsequent, less-intense pulses were probably due to reflections from the loudspeaker cabinets.
FIGURE 3.
The left-loudspeaker-to-left-microphone (“CLL”) impulse response, measured using the MLS method in the ±3°/±15°/±90° cross-talk cancellation system. The direct sound is marked, along with two putative reflections, which were removed in subsequent modifications.
The first step in the calculation of the four cross-talk cancellation filters was to digitially convolve each of the four impulse responses with a sharp, 11-kHz antialiasing digital filter. They were then downsampled to 22050 Hz and edited to a 128-sample (5.8-ms) window, centered on the main pulse in order to remove the subsequent reflections (shown by the dashed lines on Fig. 3). Next, a 4096-point FFT (5.4-Hz resolution) was applied after suitable zero padding, and then the coefficients of the filters were calculated for each of the 4096 frequencies independently using:
| (1) |
(cf. Hill et al., 2000, Eq. 6; Takeuchi and Nelson, 2002, Eq. 17), where k is the frequency index (1-4096), CLL,k, CLR,k, CRL,k, and CRR,k are the Fourier coefficients of the four loudspeaker-microphone transfer functions at the kth frequency, HLL,k, HLR,k, HRL,k, and HRR,k are the Fourier coefficients of the corresponding cross-talk cancellation filters at the kth frequency, D (=1500 samples) is a modelling delay, β (=0.001) is a regularisation parameter for ensuring a stable inversion, and H is the Hermitian operator (i.e., the transpose of the complex conjugate of a matrix).2 The impulse responses of each of the four final cross-talk cancellation filters was obtained by applying an inverse FFT and then, to remove any minor imaginary components due to rounding errors, taking the real part.
The amount of cross-talk cancellation was measured using a 5-second test signal whose right channel dR was a 8-kHz-lowpass filtered white noise and whose left channel dL was silence. These signals (dL and dR) was digitally convolved with the impulse responses of the four cross-talk cancellation filters:
| (2) |
| (3) |
Raised-cosine gates (10-ms duration) were subsequently applied to smooth the onset and offset. The resulting signals were presented by the host computer through the frequency-crossover system and the six-loudspeaker array. The sounds wL and wR reaching the manikin’s microphones were recorded using a digital recorder (Marantz PMD690). They differ from the presented signals by the action of the loudspeaker-microphone transfer functions: i.e.,
| (4) |
| (5) |
If the cross-talk cancellation had been perfect, then wR and wL would have matched dR and dL (i.e., a 8-kHz lowpass-filtered noise and silence).
The majority of analyses were based on the average of ten 10-ms-Hanning windowed DFTs (1920-point, 25-Hz resolution) of the received sounds. The amount of cross-talk cancellation achieved was defined as the difference between the left and right power spectra (in decibels). For convenience, a single-number value was used to summarise performance. Termed the “wideband average cancellation”, it was calculated as the average of the cross-talk cancellation at every discrete spectral frequency between 100 to 8000 Hz.
II.B. Acoustical Results
The top panel of Fig. 4 shows the power spectra of the signals received at the two microphones of the manikin during playback. The spectrum at the right ear was close to the desired 8-kHz lowpass noise, but the spectrum at the left ear was not the desired silence. The bottom panel shows the amount of cross-talk cancellation that was found (i.e., the difference between those power spectra). At some frequencies, as much as 30 dB was obtained, but at other frequencies it was as little as 10 dB. The wideband average cancellation was 20 dB.
FIGURE 4.
The top panel shows the magnitude spectra of the signals delivered to the microphones of the manikin by the ±3°/±15°/±90° cross-talk cancellation system. The right-ear target was a 0-8 kHz white noise, while the left ear target was silence. The bottom panel shows the amount of cross-talk cancellation achieved, which was defined as the difference in those magnitude spectra.
This amount of cancellation was less than we expected from other experimental studies of cross-talk cancellation; for instance, Bai et al. (2005), Lentz et al. (2005), and Bai and Lee (2006) obtained up-to about 30 dB. We noted, however, two possible reflections in the loudspeaker-manikin HRIRs that may have affected performance: one was a reflection from the ±90°-loudspeaker cabinets, corresponding to an additional distance of 1.4 m, or about 90 samples, whilst the other was a reflection from the manikin and then the ±15°/±3°-loudspeaker cabinet, at a distance of 2 m, or 130 samples (see Fig. 3).3 We attempted to reduce both of these by removing the ±90°-loudspeaker cabinets, moving the other cabinet further away, to a distance of 1.6 m, and presenting all the sounds through the middle pair of loudspeakers (which, due to the change in distance, subtended ±9° instead of ±15°; see Fig. 5, top panel). These modifications gave us a minor improvement in wideband cancellation to 23 dB (Fig. 5, bottom panel). The best performance was found between about 2000 and 4000 Hz, where we obtained 30 dB of cancellation.
FIGURE 5.
A scale diagram of the modified acoustic system, using two-loudspeakers at ±9° (c.f. Fig. 1), and the amount of cross-talk cancellation it gave (c.f. Fig. 4).
II.C. Computational methods
Our goal here was to simulate digitally, as closely as possible, the playback operation of the acoustical OSD system. Figure 6 shows a schematic illustration of the method: the same target signals as were used acoustically were defined, they were digitally convolved with the cross-talk cancellation filters (HLL, etc) to get the processed signals vL and vR, and those were then digitally convolved with the playback HRIRs of the four acoustic paths (CLL, etc) to get the signals that would have been received at the manikin microphones. These were then subjected to the same analysis procedures as before.
FIGURE 6.
Schematic illustration of each step involved in the computational simulations of cross-talk cancellation. The steps follow the acoustic system (Fig. 2), except that the loudspeaker presentation is simulated by a set of digital convolution and summations. The illustration represents simulations C, D, and E (Table I), as the digital cross-over filters are not shown; simulations A and B included them.
Table I lists the simulations that we tested. We attempted to predict both the full, six-loudspeaker OSD system (simulations A and B) and the reduced-echo, two-loudspeaker system (C and D). In simulations A and C we set the playback HRIRs to be exactly the same as the setup HRIRs, and so were short enough — 128 samples (5.8 ms) — to encompass only the direct sound. In simulations B and D the playback HRIRs were the full, 731-sample (33.2 ms) MLS recordings from which the setup HRIRs had been extracted; they were long enough to include the earliest reflections from the loudspeaker cabinets and the initial acoustic decay of the room. Simulation E is described later.
TABLE I.
Summary of the computational simulations used in validating the computational model. The sampling rate was 22.05 kHz and so the 5.8-ms duration impulse responses corresponded to 128 points, and the 33.2-ms responses to 751 points.
| Simulation | Loudspeaker azimuths |
Loudspeaker-to- manikin distance |
Duration of set-up HRIRs |
Duration of playback HRIRs |
Relationship of HRIRs |
|---|---|---|---|---|---|
| #A | ±3° ±15° ±90° | 1 m | 5.8 ms | 5.8 ms | Identical |
| #B | ±3° ±15° ±90° | 1 m | 5.8 ms | 33.2 ms | Setup edited from playback |
| #C | ±9° | 1.6 m | 5.8 ms | 5.8 ms | Identical |
| #D | ±9° | 1.6 m | 5.8 ms | 33.2 ms | Setup edited from playback |
| #E | ±9° | 1.6 m | 5.8 ms | 33.2 ms | Independent measurements |
II.D. Computational Results and Discussion
The bold lines on the four panels of Fig. 7 show the amounts of cross-talk cancellation predicted by each of the four simulations, whilst the faint lines show the corresponding results from the acoustic system (Fig. 4). Both simulations A and C gave considerably more cross-talk cancellation than the acoustic measurements; the wideband cancellations were, respectively, 58 dB and 56 dB, whereas the corresponding acoustic values were 20 and 23 dB. In both of these simulations the playback HRIRs included the direct sound only. The results of the two simulations that had also incorporated the initial reflections into the playback HRIRs were a much closer match (simulation B gave 22 dB and simulation D gave 29 dB). Simulation B reproduced with fair accuracy its spectral profile of acoustic cancellation. The fit was less good for simulation D, although it did reproduce the broad dip near 6000 Hz that was seen acoustically.
FIGURE 7.
The results of the five computational simulations of cross-talk cancellation. The parameters of each simulation are reported in Table I. The bold lines in each panel show the amount of cross-talk cancellation predicted by the simulations, and the faint lines show the corresponding acoustical measurements.
The extreme amount of cancellation observed in simulations A and C is of interest. It is likely that it was due to the setup HRIRs being numerically identical to the playback HRIRs as well as to excluding all reflections; this accords with Takeuchi’s (2001) results, who obtained similar ideal performance from simulations which used the same HRIRs (taken from KEMAR; Gardner and Martin, 1995) for setup and playback. We ran another simulation to study this (simulation E). Here the playback HRIRs were taken from a second run of the MLS algorithm; thus both the setup and playback HRIRs were measures of the same loudspeaker-manikin transfer functions, but, being independent recordings, they were numerically slightly different. The results of this simulation are shown in the bottom panel of Fig. 7. The match between the simulated and acoustic spectral profiles was impressive, especially between about 1000 and 6000 Hz (cf. panel D, Fig. 6).
The best matches between the simulation and the acoustic measurements were obtained only after including many of the decay characteristics of the experimental room. This implies that if the goal of a simulation is to predict accurately the performance of a real system, then it is necessary to include in the simulations the acoustics of the room used for playback and, ideally, to ensure that the playback HRIRs are recorded independently of the setup HRIRs. Furthermore, our results indicate that the performance of the real cross-talk cancellation system was probably limited by the reflections and reverberation of the playback room. This is consistent with Damaske (1971), who used a two-loudspeaker, ±30°-azimuth system, and observed near-ideal localization in an anechoic space but an increase in back-to-front confusions in a room with a reverberation time of 0.5 seconds, and also with Sæbø (2001), who found performance compromised by reflections in tests with a system using two closely-spaced loudspeakers placed in an anechoic room with and without additional reflecting surfaces (but it should be noted there are some conflicting data on the effects of reverberation; compare Cooper and Bauck, 1989, to Sæbø, 2001). In another condition Sæbø extended the setup HRIRs — and so the cross-talk cancellation filters — to include a reflection from a wall, and, although this offered some benefit, did not return performance to the anechoic level. Any other fixed extraneous sounds, such as non-frontal radiation from the loudspeakers or any reverberation, would similarly be expected to lead to a reduction in cross-talk cancellation (Takeuchi and Nelson, 2002), and it would always be necessary to exclude any dynamic or random sound from the set-up HRIRs, as a cross-talk cancellation system can only ever remove static sounds.
In summary, it was clear that the acoustical data could be accurately matched by the simulation. The validation procedure was therefore successful, and we felt justified in using the simulation to study the amount of cross-talk cancellation given by and the binaural performance of matched and mismatched systems.
III. AMOUNTS OF CANCELLATION IN MATCHED AND MIS-MATCHED SYSTEMS
We used the computational simulation to investigate the degree to which the cross-talk cancellation system could tolerate the differences between the HRIRs of individuals. These tests were conducted using a database of HRIR recordings from seven individuals (Blauert et al., 1998). We also studied performance when a set of non-individual HRIRs were used for the calculation of the cross-talk cancellation filters, as such methods have been commonly used in subjective tests of the localization performance of cross-talk cancellation, be it either from analytic models of the head (e.g., Hill et al, 2001; Rose et al, 2002) or from manikin measurements (e.g., Foo et al., 1999; Sæbø, 2001; Takeuchi et al., 2001; Lentz et al., 2005; Bai et al., 2005).
III.A. Individual-listener HRIRs
The method followed closely that of the earlier simulations, differing only in that we needed to recreate the HRIRs for each listener as if he or she had been in the OSD system. The basis for this calculation was the seven individual HRIRs in the “AUDIS” database (Blauert et al., 1998), which were recorded in an anechoic chamber at azimuth intervals of 15° around the head, for a loudspeaker-listener separation of 2.5 m. The recordings were taken at both ears, so incorporating the natural asymmetries of real people, and were 9 ms (400 samples @ 44100 Hz) in duration. We took the ±90° and ±15° HRIRs from the database and calculated the ±3° HRIRs by a linear, frequency-domain interpolation of the level and unwrapped phase spectra of the HRIRs at 0° and +15° or 0° and −15° (c.f. Hartung et al., 1999; Langendijk and Bronkhorst, 2000). They were downsampled to 22050 Hz, then convolved with the three digital crossover filters, summed, and finally windowed to 128-samples (7.8 ms) approximately centered on the main impulse. We did not incorporate any reflections or reverberation, and so these simulations represented an ideal situation.
For the first set of simulations, the set-up and playback HRIRs were matched. The top panel of Fig. 8 shows the magnitude spectra of the predicted signals at the ears for one of these simulations (both the setup HRIRs were from listener #5). The spectrum at the right ear was extremely close to the desired 0-8-kHz flat-spectrum noise, and the spectrum at the left ear was at least 40 dB lower, and was over 60 dB lower for frequencies above about 1000 Hz. The wideband average cancellation was 61 dB; the range across all seven matched-HRIR combinations was 61-71 dB.
FIGURE 8.
The magnitude spectra of the signals at the microphones of the manikin calculated from the computational simulation. The top panel shows the results for a matched-HRIR system, the bottom panel for a mismatched-HRIR system.
A second set of simulations studied mismatched HRIRs. The bottom panel of Fig. 8 shows the left and right magnitude spectra for the case when the setup HRIRs came from listener #6 and the playback HRIRs from listener #2. Neither of the signals at the right or left ears were those desired — both were quite modulated — and it is clear that the amount of cross-talk cancellation was far less than that found in the matched-HRIR simulations; the wideband average cancellation was 25 dB. This combination was chosen for illustration as it was the best of the mismatched simulations; the worst value across the 42 combinations was 10 dB, and the group mean was 17 dB (Table II). Figure 9 shows the spectral profile of cancellation for each of 49 combinations of HRIRs in the database. All of the matched combinations (top panel) gave cancellations of 40 dB or more at all frequencies up to 5000 Hz, and some were 70 dB or over at many frequencies. The mismatched combinations (bottom panel) occasionally reached 40 dB but most gave substantially less cancellation than this, and, for a broad band of mid-frequencies (about 800-2500 Hz), the majority gave less than 20 dB of cancellation.
TABLE II.
The values of simulated wideband cancellation for each of the 49 combinations of listener in the AUDIS database. The seven matched-HRIR conditions are along the main diagonal; the others are are the 42 mismatched-HRIR conditions. The row means and column means (both underlined) are for the mismatched conditions only. Also shown are the values when the HRIRs were taken from Gardner and Martin’s (1995) database for the KEMAR manikin.
| Setup HRIR | Playback HRIR | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | Mean | KEMAR | |
| #1 | 68.1 | 16.1 | 14.4 | 14.9 | 16.5 | 13.2 | 13.5 | 14.8 | 12.6 |
| #2 | 10.2 | 62.7 | 17.6 | 13.4 | 24.4 | 21.5 | 17.1 | 17.4 | 21.9 |
| #3 | 11.7 | 21.0 | 64.6 | 16.5 | 21.9 | 19.9 | 17.6 | 18.1 | 17.9 |
| #4 | 12.1 | 16.7 | 16.6 | 62.1 | 17.4 | 14.7 | 12.5 | 15.0 | 13.4 |
| #5 | 10.3 | 24.6 | 18.6 | 14.0 | 60.8 | 21.5 | 17.9 | 17.8 | 22.1 |
| #6 | 10.2 | 24.7 | 19.7 | 14.4 | 24.5 | 70.5 | 17.0 | 18.4 | 21.4 |
| #7 | 12.5 | 22.4 | 19.4 | 14.2 | 23.0 | 19.0 | 62.3 | 18.4 | 17.7 |
|
| |||||||||
| Mean | 11.2 | 20.9 | 17.7 | 14.6 | 21.3 | 18.3 | 15.9 | 17.1 | 18.1 |
|
| |||||||||
| KEMAR | 9.2 | 24.9 | 17.3 | 12.9 | 24.8 | 21.1 | 15.3 | 17.5 | 64.6 |
FIGURE 9.
The amounts of cross-talk cancellation calculated from the computational simulation, for each of the 7 matched-HRIR systems (top panel) and each of the 42 mismatched-HRIR systems (bottom panel). The values of wideband cancellation for each system are reported in Table II.
These simulations were conducted with HRIRs that were recorded in an anechoic room, and which were further windowed to 7.8 ms. We had noted earlier (section II.D) that HRIRs that excluded all of the decay characteristics of the playback room gave unrealistically good cross-talk cancellation performance, and the corresponding values found there (58 and 56 dB) with short, matched HRIRs are only slightly reduced from the range calculated here for matched HRIRs (61-71 dB). It is therefore likely that the present matched-HRIR simulations represent a computational ideal, and so even the reduced performance seen with the mismatched-HRIRs may be difficult to obtain in any real acoustic system operating in a real room.
Table II also reports the row and column means of the cancellations found in the mismatched combinations. It can be seen that the amount of cancellation was relatively constant across setup listener (a range of 3.4 dB) but depended substantially upon playback listener (a range of 10.1 dB). These results suggest that the variations in performance are due more to variations in the playback HRIR than in the setup HRIR. Individual differences in head and ear dimensions can be substantial — heads differ by about ±1 cm, ear sizes by about ±0.5 cm, ear orientations by about ±7° (Algazi et al., 2001; see also Burkhard and Sachs, 1975, and Middlebrooks, 1999a) — and it is likely that the variations across the seven listeners in the AUDIS database represent some of this individuality. Furthermore, unless some form of head-restraint was included listeners may also not place their heads exactly at the required point, and would be unlikely to stay stationary across the course of an experiment. Indeed, it is perhaps not surprising that cross-talk cancellation reduces dramatically when mismatches exist between the setup and playback HRIRs, as successful cancellation requires the signal presented from the right loudspeaker to match accurately, in both phase and amplitude, the signal from the left loudspeaker when both arrive at the ears. Any individual differences in the head or ear dimensions, and any movements or mislocations in position, must lead to differences in the phase or amplitude at the ears.
III.B. Manikin HRIRs
We tested whether a set of non-individual HRIRs would be more successful by rerunning the simulations using Gardner and Martin (1995) database of HRIRs for the KEMAR manikin. These were recorded using its small ears, which are replicas of an individual whose pinna dimensions are similar to the mean of the population (Burkhard and Sachs, 1975; Maxwell and Burkhard, 1978), and were 128 samples in duration. We simulated a matched system, in which the KEMAR HRIRs were used for both set up and playback, and mismatched systems, in which the KEMAR HRIRs were used for set up but the individual HRTFs from earlier were used for playback, or vice-versa.
The results are reported in the last row and column of Table II. When used as the setup HRIR, the overall cancellation (17.5 dB) was as good as that found with many of the AUDIS HRIRs. The range of cancellation seen (11-21 dB) suggests, however, that some listeners — presumably those whose HRIRs are poor matches to KEMAR’s — would gain little benefit. These results support Takeuchi (2001). In some of his experiments on subjective localization with a two-loudspeaker, ±5°-azimuth system, he compared cross-talk cancellation filters calculated from a manikin with those calculated from the individual HRIRs of his listeners. He noted better localization performance and a reduction in back-to-front errors in the individualized conditions, and a subsequent analysis showed that these errors were related to the individual spectral details of the HRIRs.
In summary, the results of these simulations clearly indicate that there is a severe reduction in the amount of cross-talk cancellation when the HRIRs used for setup are mismatched from those used for playback. It is likely that the amount of cancellation — on average, some 10-20 dB, depending upon the choice of setup HRIRs — would be insufficient for most binaural cues to be recreated sufficiently accurately (this is considered in more detail in the next section). Furthermore, the cancellation that is obtained is idiosyncratic to each individual, and so, without a knowledge of someone’s HRIR, it would be impossible to know exactly what sounds were reaching them. But if these HRIRs were measured for each individual using the cross-talk cancellation loudspeakers, then the setup HRIRs would be matched to the playback HRIRs and so performance would be expected to be improved.
IV. BINAURAL PERFORMANCE OF MATCHED AND MIS-MATCHED SYSTEMS
We used the computational simulation to study the accuracy of the delivery of the interaural time delays (ITDs) and interaural level differences (ILDs) that underlie the perception of spatial angle. As the preceding simulations showed that the amount of cancellation dropped considerably in the mismatched-HRIR conditions, we expected that the binaural performance would be similarly compromised. In particular, if the mismatch was sufficiently large that the amount of cancellation was less than the target ILD, we expected that the delivered ITDs and ILDs would bear no resemblance to the target values but would instead be determined by the characteristics of the cross-talking sound (any non-perfect cancellation would, of course, mean that some of the sound intended for one ear would remain, uncancelled, at the other ear, and if this sound was greater than that actually intended for the other ear, it would determine the ITDs and ILDs).
We measured binaural performance in individual frequency channels. For low frequencies, we applied an analysis of ongoing ITDs and ILDs. For high frequencies, we analyzed the envelope ITDs and ILDs, as there is growing evidence from experiments with “transposed stimuli” of the sensitivity of the binaural system to the interaural cues carried by envelopes (e.g., Bernstein and Trahiotis, 2002, 2003).
IV.A Ongoing ITDs and ILDs
The test signal was a white noise with the required target ITD and ILD (see below). This signal was passed through the computational simulation of the six-loudspeaker (azimuths of ±3°, ±15°, and ±90°) system, with HRIRs taken from the AUDIS database. The ITDs and ILDs of the signals that would have been received at the listener’s ears were obtained from a simplified computational model of binaural hearing (e.g. Shackleton et al., 1992; Stern and Trahiotis, 1997; Akeroyd and Summerfield, 2000; Akeroyd, 2001). First, the signals were passed through two gammatone filters, one for the left channel and one for the right channel, each set to the required center frequency (see below) and a bandwidth of 1 ERB (Patterson et al., 1990; Glasberg and Moore, 1999). This filtering approximated peripheral auditory frequency analysis, but excluded any non-linear effects and the action of the inner hair cells. Second, the binaural normalized correlation was computed on the outputs of the filters (Bernstein and Trahiotis, 1996) as a function of a delay applied to one waveform, giving the within-channel cross-correlation function at delays from −750 to +750 μs.4 Third, the largest peak in each cross-correlation function was found, and its position was taken as the delivered value of the ongoing ITD of the test signal. Fourth, the powers of the outputs of the left and right gammatone filters were measured, and the difference between the two was taken as the delivered ILD of the test signal.
For the first set of simulations we tested every combination of target ITD and target ILD in the ranges −600 to +600 μs (in 100-μs steps) and −25 to + 25 dB (in 5 dB steps) for a small number of matched-HRIR and mismatched-HRIR combinations. The auditory-filter frequency was fixed at 1000 Hz. The results are shown in Fig. 10. Each point is for a separate target ITD/ILD combination, with the lines connecting points with the same target ILD. The abscissa of each panel is the delivered ILD, the ordinate is the delivered ITD. The left panel shows the results for one of the matched-HRIR simulations (68-dB wideband average cancellation). The results are near-perfect: the rms errors between the target and delivered values were only 13 μs and 0.1 dB. We took this as a successful validation of the analysis method for ongoing ITDs and ILDs, but it also showed that the OSD system can reliably deliver any combination of ITD and ILD, provided that the setup and playback HRIRs are matched.
FIGURE 10.
The binaural performance of the computational simulation of cross-talk cancellation, calculated for a matched-HRIR system (left panel) and two mismatched-HRIR systems (middle & right panels). Each panel shows the ongoing ITD (ordinate) and ILD (abscissa) delivered by the simulation for a large set of combinations of target ITD and ILDs (parameters); the lines join points with the same target ILD. The analysis was run at an auditory-filter frequency of 1000 Hz.
The middle panel plots the results for one of the mismatched-HRIR simulations, which gave a wideband average cancellation of 16 dB. Here, the OSD system failed to reliably recreate ongoing ITDs and ILDs: the rms errors were 296 μs and 8.5 dB. Furthermore, a “convergence” of ITD was observed, in that for target ILDs less than −5 dB, the delivered ITD was never larger than ±250 μs, despite the target ITDs being as large as ±600 μs. It was as though the delivered ITDs converged on one value — about 0 μs — no matter what the target ITDs were. Both the pattern of the results and the point of convergence varied with the choice of HRIRs in the mismatched simulations. The right panel plots the results for a different mismatched HRIR simulation (14-dB wideband average cancellation), in which the convergent point for negative target ILDs was at about −100 μs.
In a second set of simulations we tested all 42 combinations of mismatched HRIRs for two target ITD and ILDs pairs of −500-μs/0-dB and +500-μs/0-dB. Auditory-filter frequencies between 100 and 1000 Hz were used. The results are shown in Fig. 11. The top-left panel shows the delivered ITDs for the −500-μs/0-dB target. At each frequency most of the combinations gave ITDs in one cluster, for which the solid points and error bars mark the means and standard deviations; those combinations that gave exceptional results — an ITD on the wrong side of the head — are plotted as open circles. The mean ITD (-498 μs) was close to the target value of −500 μs. There was, however, a wide distribution across mismatched-HRIR combination; the standard deviation was, on average, 100 μs. A similar result held for the +500-μs/0-dB target (top-right panel). The delivered ILDs are shown in the bottom-left and bottom-right panels. Again, the mean delivered ILD was almost exactly the target ILD, but the average standard deviation was 4 dB.
FIGURE 11.
The results of the ongoing-ITD and ongoing-ILD analyses of the computational simulation as a function of auditory-filter frequency. Each point plots the mean across all 42 mismatched-HRIR systems (the error bars show the standard deviations). For the top-left & bottom-left panels, the target ITD/ILD was −500-μs/0-dB; for the top-right & bottom-right panels, the target were +500-μs/0-dB. The few mismatched-HRIR systems that gave exceptional ITDs (taken as being on the wrong side) are plotted as open circles.
IV.B Envelope ITDs and ILDs
The test signal was a single-sample click. It was passed through the same OSD simulation and then the same gammatone filters. Next, the envelopes of the outputs of the left and right gammatone filters were found (by calculating the analytic signal via the MATLAB “Hilbert” function and then taking its complex modulus), and the time of the peak of the envelope in each channel was measured. The left-right difference in peak time was taken as the delivered envelope ITD. The heights of the peaks were also measured, and this left-right difference was taken as the delivered value of the envelope ILD. Both binaural models were run at a sampling rate of 48 kHz, giving a time resolution of 21 μs.
Figure 12 shows the delivered envelope ITDs and ILDs at a center frequency of 1000 Hz, plotted in the same format as the earlier ongoing analysis (Fig. 10). The effects that were found there were also found here. First, for the matched-HRIR combination (left panel), the results were again remarkably accurate; the rms error on the measured ITDs was just 14 μs, whilst for the ILDs it was only 0.1 dB. Again, we took this as a successful verification of the analysis method and a demonstration of the ability of the OSD system to deliver the correct envelope ITDs and ILDs when the HRIRs are matched. Second, for the mismatched-HRIR combinations (middle and right panels), the delivered ITDs and ILDs were again quite dissimilar to the target values. There were not, however, any obvious similarities between the delivered ongoing ITDs and the delivered envelope ITDs that were shown in Fig. 10: the envelope ITDs reached much larger values — especially for the more extreme target ILDs — and the points of convergence were different.
FIGURE 12.
The binaural performance of the computational simulations, for the envelope ITD and ILD at 1000 Hz. The format is the same as Fig. 10.
Figure 13 shows the mean and standard deviations, across all the mismatched-HRIR combinations, of the delivered ITDs (top row) and ILDs (bottom row) as a function of frequency and for the three targets of 500-μs/0-dB (left column), 500-μs/10-dB (middle column), and 500-μs/20-dB (right column). The standard deviation of the ITDs, averaged across all conditions, was 430 μs, and so was much larger than that found for the corresponding ongoing analysis shown in Fig. 11. The standard deviation of the ILDs was 4 dB and was therefore comparable to that found earlier. Furthermore, the delivered ITDs and ILDs were inaccurate when the target ILD was 20 dB; the mean errors from the target values of −500 μs and 20 dB were, respectively, +160 μs and −5 dB, respectively.
FIGURE 13.
The results of the envelope-ITD and envelope-ILD analyses of the computational simulation as a function of auditory-filter frequency. Each point plots the mean across all 42 mismatched-HRIR systems (the error bars show the standard deviations). The six panels are for target ITD/ILDs of +500-μs/0-dB (top-left & bottom-left), +500-μs/10-dB (top-middle /& bottom-middle), and +500-μs/20-dB target (top-right & bottom-right).
IV.C Discussion
These simulations show that a cross-talk cancellation system can reliably recreate accurate binaural ITDs and ILDs only when the playback HRIRs were matched to the setup HRIRs. It is likely that this is due to the large amount of cancellation found in the matched conditions — generally over 50 dB (Fig. 9, top panel) — so giving sufficient “headroom” to preserve the ITDs and ILDs of the target (Takeuchi et al., 2001). In mismatched conditions — such as would be found if the system was set up in advance using an accurately-measured HRIR from a manikin, and then used to present sounds to a population of listeners — the delivered ITDs and ILDs were often different from the targets, and it could not be guaranteed that a given target ITD was indeed being delivered. The difference depended on frequency, ILD, whether envelope or ongoing ITDs were being considered, and the set-up vs. playback combination of HRIRs used. The error was largest when the target ILD was 20 dB, which is consistent with the suggestion that the amount of cancellation “headroom” was indeed limiting performance. The standard deviation of the ongoing ITDs, across setup/playback combination, was 100 μs. Only if a random error of this magnitude can be tolerated could a mismatched system be useful for binaural experimentation. Moreover, the convergence phenomenon demonstrates that certain combinations of ITDs and ILDs can never be obtained (e.g., for the middle panel of Fig. 10, a target ITD larger than about 250 μs simultaneously with a target ILD of −10 dB or less). We expect that such effects will occur in any mismatched system; an experimenter would not know in advance quite what ITDs or ILDs were being delivered to a given listener.
It should be noted that all these binaural simulations used a database of short-duration HRIRs measured in an anechoic room. Our experience with the acoustic system described in Section II and our validation of its computational simulation indicated that cancellation performance would be reduced if the acoustic characteristics of the playback were not anechoic or if there were any extraneous reflections or sounds amongst the loudspeakers. We expect the same caution to apply here, and so the binaural simulations probably represent an ideal performance. A real, acoustic cross-talk cancellation system, in which the HRIRs would be changed by room acoustics or listener movement, may deliver binaural cues that bear even less resemblance to the target values, and either would limit the gain to be had from measuring individualized HRIRs and using those to setup the cross-talk cancellation filters.
V. SUMMARY
We used a series of computational simulations to study the binaural performance of a cross-talk cancellation system in order to evaluate its suitability for binaural experimentation. First, we constructed an acoustic system and used that to validate the simulation. This six-loudspeaker system gave a wideband average cancellation of 20 dB, which was improved to 23 dB after modifications to remove the major reflections from the loudspeaker cabinets. A computational simulation of this system showed that when the playback and setup HRIRs were numerically identical, and both were short enough to exclude the acoustical characteristics of the playback room, then the wideband cancellation was over 50 dB. This situation represented a computational ideal, however, and was unrealistic. Instead, a close match between acoustic and computational results was found when the playback HRIRs were longer, so incorporating the early part of the acoustics of the room (and there was no gain in simulated performance from including this in the setup HRIRs). When run with HRIRs from a database of seven listeners, the simulation demonstrated that performance was reduced when the playback HRIR was from a different listener to the setup HRIR; the average amount of cancellation in these “mismatched” simulations was only 17 dB, and varied little with the choice of setup HRIR but depended substantially upon the playback HRIR.
The binaural analyses demonstrated that the cross-talk cancellation system could not be guaranteed to deliver the targeted ITDs and ILDs when the HRIRs were mismatched. The errors in ongoing ITDs and ILDs at low-frequencies were random with a standard deviation of 100 μs or 4 dB, respectively; those for envelope ITDs and ILDs were 430 μs and 4 dB. At the largest ILDs usually encountered, the high frequency envelope ITDs and ILDs had also a systematic error, and, moreover, a “convergence” of delivered ITD was observed: for some values of target ILD, the delivered ITD was always the same value, no matter what the target ITD was. The convergent value differed across playback listener and if envelope or ongoing ITDs were measured.
Although cross-talk cancellation can give impressive demonstrations, and experiments on the angle perception of simple, static noise bursts can often give compelling results, the errors in ITD and ILD demonstrated here will affect any use of mismatched cross-talk cancellation for experiments that rely on accurate binaural cues. Takeuchi et al. (2001) noted that the poorest listeners in their subjective localization experiment were those whose HRIRs had the largest differences to the manikin HRIRs used to set up their system. Our own results support this, confirming that such mismatching of HRIRs is an important source of the inaccuracies in the final delivery of binaural cues.
ACKNOWLEDGEMENTS
We would like to thank Dr Takashi Takeuchi (Institute of Sound and Vibration Research, Southampton) for helping us get started and also in supplying the cross-talk cancellation filters, Dr Jonas Braasch (McGill University, Montreal) for supplying the “AUDIS” HRIR database, the Department of Engineering of the University of Nottingham for allowing us to use their acoustic chamber, Dr Silvia Cirstea for help with the HRTF interpolation, David McShefferty for running some of the simulations, and Helen Lawson for her comments on the manuscript. We also thank the Associate Editor (Dr Armin Kohlrausch) and the three anonymous reviewers for their valuable and insightful comments during the review process. The computational work was performed in MATLAB (www.mathworks.com), The Scottish Section of the IHR is co-funded by the Medical Research Council and the Chief Scientist’s Office of the Scottish Executive Health Department.
Footnotes
Our nomenclature follows that used by Takeuchi and Nelson (2002), where C is the matrix of source-receiver function and H is the matrix of cross-talk-cancellation (inverse) filter.
In our acoustic measurements we did not study the effects of varying the regularization parameter β or the size of the FFT. Subsequent investigations with the one of the computational simulations showed that the chosen value of β (0.001) was well chosen: the wideband average cancellation were 15.5, 21.1, 21.8, 21.8, and 21.4 dB for values of β of 1, 0.1, 0.01, 0.001, and 0.0001, respectively (also, β was frequency-independent; see Bai and Lee (2006) for a frequency-dependent β). Similarly, the chosen FFT size (4096 points) was again justifiable: the cancellations were 11.0, 20.3, 19.2, 20.1, 21.7, and 21.8 dB for sizes of 128, 256, 512, 1024, 2048, and 4096 points, respectively.
The front of the mid/high cabinet was shaped like a segmented arc of circle of 1-m radius. Although not a perfect reflector, it would still be expected to focus some of sound to the center of the circle, which was where the manikin was placed (see Fig. 1). This may contribute to the strength of the reflection, and we found that moving the manikin away from that point reduced it.
The model’s ITD range was slightly larger than the range of the stimuli in order to allow for the possibility that the cross-talk cancellation system might deliver a ITD larger than expected.
PACS 43.66 Pn (binaural hearing);
43.60 Pt (signal processing for inverse problems)
43.38 Md (sound recording and reproducing, general concepts)
REFERENCES
- Akeroyd MA. [last viewed November 6, 2006];A binaural cross-correlogram toolbox for MATLAB. 2001 software downloadable from http://www.ihr.gla.ac.uk/products/matlab.php.
- Akeroyd MA, Summerfield Q. The lateralization of simple dichotic pitches. J. Acoust. Soc. Am. 2000;108:316–334. doi: 10.1121/1.429467. [DOI] [PubMed] [Google Scholar]
- Algazi VR, Duda RO, Thompson DM. The CIPIC HRTF database. Proceedings of the 2001 IEEE Workshop on Applications of Signal Processing to Audio and Electronics; New Paltz, New York: 2001. pp. 99–102. [Google Scholar]
- Atal BS, Schroeder MR. US Patent #3236949. Apparent Sound Source Translator. 1962 [reviewed in J. Acoust. Soc. Am. 41, 263-264 (1967)]
- Bai MR, Tung CW, Lee CC. Optimal design of loudspeaker arrays for robust cross-talk cancellation using the Taguchi method and the genetic algorithm. J. Acoust. Soc. Am. 2005;117:2802–2813. doi: 10.1121/1.1880852. [DOI] [PubMed] [Google Scholar]
- Bai MR, Lee C-C. Development and implementation of cross-talk cancellation system in spatial audio reproduction based on subband filtering. J. Sound Vib. 2006;290:1269–1289. [Google Scholar]
- Bernstein LR, Trahiotis C. On the use of the normalized correlation as an index of interaural envelope correlation. J. Acoust. Soc. Am. 1996;100:1754–1763. doi: 10.1121/1.416072. [DOI] [PubMed] [Google Scholar]
- Bernstein LR, Trahiotis C. Enhancing sensitivity to interaural delays at high frequencies by using ‘transposed’ stimuli. J. Acoust. Soc. Am. 2002;112:1026–1036. doi: 10.1121/1.1497620. [DOI] [PubMed] [Google Scholar]
- Bernstein LR, Trahiotis C. Enhancing interaural-delay-based extents of laterality at high frequencies by using ‘transposed’ stimuli. J. Acoust. Soc. Am. 2003;113:3335–3347. doi: 10.1121/1.1570431. [DOI] [PubMed] [Google Scholar]
- Blauert J. Spatial Hearing: The psychophysics of human sound localization. MIT Press; Cambridge MA: 1997. [Google Scholar]
- Blauert J, Brüggen M, Bronkhorst SW, Drullman R, Reynaud G, Pellieux L, Krebber W, Sottek R. [last viewed November 6, 2006];The AUDIS catalogue of human HRTFs. J. Acoust. Soc. Am. 1998 103:3082. (see also http://www.eaa-fenestra.org/Products/Documenta/Publications/09-de2. [Google Scholar]
- Burkhard MD, Sachs RM. Anthropometric manikin for acoustic research. J. Acoust. Soc. Am. 1975;58:214–222. doi: 10.1121/1.380648. [DOI] [PubMed] [Google Scholar]
- Chambers J, Akeroyd MA, Summerfield AQ, Palmer AR. Active control of the volume acquisition noise in functional magnetic resonance imaging: Method and psychoacoustical evaluation. J. Acoust. Soc. Am. 2001;110:3041–3054. doi: 10.1121/1.1408948. [DOI] [PubMed] [Google Scholar]
- Cooper DH, Bauck JL. Prospects for transaural recording. J. Audio Eng. Soc. 1989;37:3–19. [Google Scholar]
- Damaske P. Head-related two-channel stereophony with loudspeaker reproduction. J. Acoust. Soc. Am. 1971;50:1109–1115. [Google Scholar]
- Davies WT. Generation and properties of maximum-length-sequences. Control. 1966;10:364–365. [Google Scholar]
- Foo KCK, Hawksford MOJ, Hollier MP. Optimization of virtual sound reproduced using two loudspeakers. Proceedings of the 16th AES International Conference: Spatial Sound Reproduction; Rovaniemi, Finland. 1999. pp. 366–378. [Google Scholar]
- Gardner WG, Martin KD. HRTF measurements of a KEMAR. J. Acoust. Soc. Am. 1995;97:3907–3908. [Google Scholar]
- Gatehouse S, Noble W. The speech, spatial, and qualities of hearing scale (SSQ) Int. J. Audiol. 2004;43:85–99. doi: 10.1080/14992020400050014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasberg BR, Moore BCJ. Derivation of auditory filter shapes from notched-noise data. Hear. Res. 1999;47:103–138. doi: 10.1016/0378-5955(90)90170-t. [DOI] [PubMed] [Google Scholar]
- Hartung K, Braasch J, Sterbing S. Comparison of Different Methods for the Interpolation of Head-Related Transfer Functions. Proceedings of the 16th AES International Conference: Spatial Sound Reproduction; Rovaniemi, Finland. 1999. pp. 319–329. [Google Scholar]
- Hill PA, Nelson PA, Kirkeby O. Resolution of front-back confusion in virtual acoustic imaging systems. J. Acoust. Soc. Am. 2000;108:2901–2910. doi: 10.1121/1.1323235. [DOI] [PubMed] [Google Scholar]
- Kirkeby O, Nelson PA, Orduna-Bustamante F, Hamada H. Local sound field reproduction using digital signal processing. J. Acoust. Soc. Am. 1996;100:1584–1593. [Google Scholar]
- Kirkeby O, Nelson P. Local sound field reproduction using two closely spaced loudspeakers. J. Acoust. Soc. Am. 1998;104:1973–1981. [Google Scholar]
- Kyriakakis C. Fundamental and technological limitations of immersive audio systems. Proc. IEEE. 1998;86:941–951. [Google Scholar]
- Langendijk EHA, Bronhorst AW. Fidelity of three-dimensional-sound reproduction using a virtual auditory display. J. Acoust. Soc. Am. 2000;107:528–537. doi: 10.1121/1.428321. [DOI] [PubMed] [Google Scholar]
- Lentz T, Assenmacher I, Sokoll J. Performance of spatial audio using dynamic cross-talk cancellation. Proceedings of the 119th Audio Engineering Society Convention; New York, USA. 2005. preprint 6541. [Google Scholar]
- Maxwell RJ, Burkhard MD. Larger ear replica for KEMAR manikin. J. Acoust. Soc Am. 1979;65:1055–1058. doi: 10.1121/1.382575. [DOI] [PubMed] [Google Scholar]
- Middlebrooks JC. Individual differences in external-ear transfer functions reduced by scaling frequency. J. Acoust. Soc. Am. 1999a;106:1480–1492. doi: 10.1121/1.427176. [DOI] [PubMed] [Google Scholar]
- Middlebrooks JC. Virtual localization improved by scaling nonindividualized external-ear transfer functions in frequency. J. Acoust. Soc. Am. 1999b;106:1493–1510. doi: 10.1121/1.427147. [DOI] [PubMed] [Google Scholar]
- Moller H. Reproduction of artificial-head recordings through loudspeakers. J. Audio Eng. Soc. 1989;37:30–33. [Google Scholar]
- Nelson PA. Active control of acoustic fields and the reproduction of sound. J. Sound. Vib. 1994;177:447–477. [Google Scholar]
- Nelson PA, Rose JFW. Errors in two-point reproduction. J. Acoust. Soc. Am. 2005;118:193–204. doi: 10.1121/1.1928787. [DOI] [PubMed] [Google Scholar]
- Nelson PA, Kirkeby O, Takeuchi T. Sound fields for the production of virtual acoustic images. J. Sound Vib. 1997;204:386–396. [Google Scholar]
- Noble W, Gatehouse S. Interaural asymmetry of hearing loss, speech, spatial, and qualities of hearing (SSQ) disabilities, and handicap. Int. J. Audiol. 2004;43:100–114. doi: 10.1080/14992020400050015. [DOI] [PubMed] [Google Scholar]
- Orduna-Bustamante F, Lopez JJ, Gonzalez A. Prediction and measurement of acoustic crosstalk cancellation robustness. Proc. Acoustics, Speech and Signal Processing; ICASSP; 2001. pp. 3349–3352. 2001. [Google Scholar]
- Patterson RD, Allerhand MH, Giguére C. Time-domain modeling of peripheral auditory processing: A model architecture and a software platform. J. Acoust. Soc. Am. 1995;98:1890–1894. doi: 10.1121/1.414456. [DOI] [PubMed] [Google Scholar]
- Rose J, Nelson P, Rafaely B, Takeuchi T. Sweet spot size of virtual acoustic imaging systems at asymmetric listener locations. J. Acoust. Soc. Am. 2002;112:1992–2002. doi: 10.1121/1.1510532. [DOI] [PubMed] [Google Scholar]
- Sæbø A. Influence of reflections on crosstalk cancelled playback of binaural sound. Norwegian University of Science and Technology; Trondheim, Norway: 2001. Ph.D. thesis. [Google Scholar]
- Shackleton TM, Meddis R, Hewitt MJ. Across frequency integration in a model of lateralization. J. Acoust. Soc. Am. 1992;91:2276–2279. [Google Scholar]
- Stern RM, Trahiotis C. Models of binaural perception. In: Gilkey RH, Anderson TR, editors. Binaural and Spatial Environments. LEA; Mahwah, NJ: 1997. [Google Scholar]
- Takeuchi T. Systems for virtual acoustic imaging using the binaural principle. University of Southampton; Southampton, UK: 2001. Ph.D. thesis. [Google Scholar]
- Takeuchi T, Nelson P. Optimal source distribution for binaural synthesis over loudspeakers. J. Acoust. Soc. Am. 2002;112:2786–2797. doi: 10.1121/1.1513363. [DOI] [PubMed] [Google Scholar]
- Takeuchi T, Nelson P. Robustness to head misalignment of virtual sound imaging systems. J. Acoust. Soc. Am. 2000;109:958–971. doi: 10.1121/1.1349539. [DOI] [PubMed] [Google Scholar]
- Thornton ARD, Folkard TJ, Chambers JD. Technical aspects of recording evoked otoacoustic emissions using maximum length sequences. Scand. Audiol. 1994;23:225–31. doi: 10.3109/01050399409047512. [DOI] [PubMed] [Google Scholar]
- Thornton ARD, Shin K, Hine J. Temporal non-linearities of the cochlear amplifier revealed by maximum length sequence stimulation. Clin. Neurophysiol. 2001;112:768–777. doi: 10.1016/s1388-2457(01)00484-9. [DOI] [PubMed] [Google Scholar]
- Trinder JR. Hardware-software configuration for high-performance digital filtering in real time. Proc. IEEE Conf. Audiol. Speech Signal Process. 1982;2:687–690. [Google Scholar]
- Ward DB, Elko GW. Effect of loudspeaker position on robustness of acoustic crosstalk cancellation. IEEE Sig. Proc. Let. 1999;6:106–108. [Google Scholar]
- Wightman FL, Kistler DJ. Headphone simulation of free-field listening. I: stimulus synthesis. J. Acoust. Soc. Am. 1989;85:858–867. doi: 10.1121/1.397557. [DOI] [PubMed] [Google Scholar]
- Yang J, Gan W-S, Tan S-E. Improved sound separation using three loudspeakers. ARLO. 2003;4:47–52. [Google Scholar]