Allosteric Transitions in the Chaperonin GroEL are Captured by a Dominant Normal Mode that is Most Robust to Sequence Variations

Abstract

The Escherichia coli chaperonin GroEL, which helps proteins to fold, consists of two heptameric rings stacked back-to-back. During the reaction cycle GroEL undergoes a series of allosteric transitions triggered by ligand (substrate protein, ATP, and the cochaperonin GroES) binding. Based on an elastic network model of the bullet-shaped double-ring chaperonin GroEL-(ADP)₇-GroES structure (R″T state), we perform a normal mode analysis to explore the energetically favorable collective motions encoded in the R″T structure. By comparing each normal mode with the observed conformational changes in the R″T → TR″ transition, a single dominant normal mode provides a simple description of this highly intricate allosteric transition. A detailed analysis of this relatively high-frequency mode describes the structural and dynamic changes that underlie the positive intra-ring and negative inter-ring cooperativity. The dynamics embedded in the dominant mode entails highly concerted structural motions with approximate preservation of sevenfold symmetry within each ring and negatively correlated ones between the two rings. The dominant normal mode (in comparison with the other modes) is robust to parametric perturbations caused by sequence variations, which validates its functional importance. Response of the dominant mode to local changes that mimic mutations using the structural perturbation method technique leads to a wiring diagram that identifies a network of key residues that regulate the allosteric transitions. Many of these residues are located in intersubunit interfaces, and may therefore play a critical role in transmitting allosteric signals between subunits.

INTRODUCTION

Molecular chaperones play an essential role in helping proteins that have low spontaneous yield reach their native states by mediating their productive folding. Among this class of nanomachines, the most extensively studied is the Escherichia coli chaperonin GroEL, which has two heptameric rings stacked back-to-back (for review see Sigler et al. (1)). GroEL is among a wide variety of allosteric proteins that have the intrinsic capacity to undergo conformational changes in response to ligand binding (for review see Swain and Gierasch (2)). In the biological context allostery is widely used as a regulation mechanism of enzymes. During the reaction cycle GroEL goes through a number of allosteric states that are triggered by ATP binding and interactions with the cochaperonin GroES (1,3). The substrate protein (SP), which also affects the allosteric transitions, is most efficiently recognized when GroEL is in the T state, and ATP binding shifts the equilibrium to the R state. Binding of GroES and subsequent ATP hydrolysis result in the formation of the R″ state. The T → R → R″ allosteric transitions result in the formation of the cis-ring. When ATP or SP binds to the opposite or trans-ring the ligands (the inorganic phosphate, ADP, and GroES) are ejected from the cis-ring. Because the two rings are out of phase in their function, just as in a two-stroke motor, it is likely that the symmetric complex in which GroES is bound to both rings (the football complex) is rarely if ever populated. It has been appreciated that the dramatic allostery observed in GroEL is intimately related to its function (4). Indeed, in the course of the allosteric transitions the polarity of the inner lining of the cavity changes from hydrophobic in the T state to hydrophilic in the R″ state. The SP-GroEL interaction is attractive when GroEL is in the T state and becomes less so as the T → R → R″ transitions occur. The change in polarity of the inner cavity is required for the annealing function of the GroEL machinery (3).

The crystal structures of GroEL (TT state), the double-ring GroEL-GroES (R″T state) and the cryo-electron microscopy (cryo-EM) map of the ATP-GroEL complex (RR state) have given us a glimpse of the working mechanism of GroEL. Comparison of the structures of the three states has provided insights into the global motions that GroEL undergoes during the reaction cycle (1). The ATP hydrolyzed GroEL-GroES complex (Protein Data Bank (PDB) code, 1AON) describes the R″T state, in which the cis-ring has bound ADP and GroES (R″ state) and the trans-ring is unliganded (T state). The R″T → TR″ transition involves a series of large-scale conformational changes that eventually invert the bullet configuration (trans to cis, and cis to trans) as GroEL completes one-half of its working cycle. During the functional cycle, the cis-ring releases the SP and ADP, while the trans-ring binds ATP and encapsulates SP. The cycle of ATP and GroES binding and subsequent ATP hydrolysis is repeated until the folding reaction is near completion (1,3).

Although the outlines of the reaction cycle and the mechanism of assisted folding have been clear (1,3) the pathways and the dynamics connecting the allosteric states have not been fully elucidated. A number of intriguing questions remain. For instance, is a football-shaped conformation (R″R″ state) an obligatory step during the transition? What is the right sequence of structural changes in the individual domains (E, equatorial domain; A, apical domain; I, intermediate domain; see below) along the path? In principle, the dynamics of allosteric transitions are best studied using detailed all-atom models of GroEL in explicit water. However, the long timescales and uncertainties in the force fields prevent straightforward applications of all-atom dynamics simulations to address the nature of events that control allosteric regulations in biological enzymes in general and GroEL in particular. Several simplifications have been used to provide insights into the allosteric transitions in GroEL. Normal mode calculations (5) and the targeted molecular dynamics simulations (6) of a part of the GroEL complex have led to key insights to the allosteric transitions in GroEL. The CONCOORD method (7), which yields low frequency collective fluctuations for proteins by generating different conformations based on distance restrictions, has been used to probe the allosteric mechanism in GroEL. de Groot and co-workers have identified global motions involved in the overall allostery of GroEL. More importantly, they showed that, upon ATP and GroES binding, structural fluctuations in the nucleotide binding domain are involved in the intra-ring communications (7). In addition, elastic network model (ENM) of GroEL has also been used in exploring the normal modes that may describe the transitions between known structures (8). Recently, a self-organized polymer model of GroEL has been used to probe the dynamics of allosteric transitions in a single ring (9). These authors identified a network of salt bridges whose formation and breakage trigger many of the observed large-scale domain movements. Bahar and co-worker proposed a novel approach based on Markov propagation of information to study the potential pathways of allosteric communication in GroEL-GroES (10).

Although these computational models have provided key insights into the global conformational changes in GroEL (5–10), the correlation between the low frequency modes and the structural changes (at the residue level) in the 14-mer for the R″T → TR″ transition has not been fully explored. The complexity of the dynamic changes associated with the allosteric transitions of GroEL has forced many of the studies to focus on the conformational changes in a single subunit. It is clear that concerted transitions within one ring and communication between rings are crucial to the GroEL function (4). Here, we build on previous studies of various proteins based on ENM (11–18) by performing extensive normal mode analysis for the double ring GroEL-(ADP)₇-GroES (R″T state) complex (where the cis-ring is in the R″ state, the trans-ring is in the T state, and GroES is not included). In particular, we address the following key questions: 1), Can a small number of normal modes be used to describe the allosteric transitions in GroEL? Do these modes lead to anticlockwise movement of the apical domains upon ATP binding? 2), Are the structurally based normal modes robust to perturbations from sequence variations? This is an important issue because from an evolutionary perspective structures are more conserved whereas there are large sequence variations. 3), Are there key (mechanically “hot”) residues that transmit allosteric signals as GroEL undergoes transitions from T → R → R″ states in response to ATP, SP, and GroES binding? The answer to this question provides a link between globally important motions and local fluctuations at the residue level.

To answer the above questions, we employ a combination of a bioinformatics technique, which utilizes the evolutionary information of sequences that are homologous to GroEL, and ENM, which captures the shape and topology of the GroEL structure (19,20). By comparing each normal mode with the observed R″T → TR″ conformational changes, we show that there is a single dominant normal mode that offers insights into the complex dynamics governing the R″T → TR″ transition. Surprisingly, the dominant mode accounts qualitatively for the puzzling allosteric couplings within and between the two rings. Analysis of the dominant mode reveals a dynamic asymmetry between the cis- and the trans-rings that tidily explains the positive cooperativity within one ring and the negative inter-ring cooperativity. To assess the functional significance of the seemingly high frequency mode we show that this dominant mode is most robust to sequence variations. The response of the mode to structural perturbations, which is in silico mimic of mutations, allows us to construct the allostery wiring diagram that gives a network of distant residues that are involved in the allosteric transitions. Many of the residues that are involved in the large conformational changes are at the interface of two subunits. Our study shows that understanding the function of complex biological nanomachines in general and GroEL in particular requires reliable models of the intact particle made up of all the subunits. Simulations of single subunit are likely to miss important roles played by residues at the interfaces in executing the complex collective motions that drive allostery in biological nanomachines.

METHODS

Elastic network model

In the simplest ENM (21,22) the structure of a protein is represented using only the coordinates of the C_α atoms. A harmonic potential is used to account for pairwise interactions between the C_α atoms that are within a cutoff distance R_C. The energy in the elastic network representation of a protein is

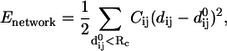(1)

where 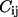is the force constant for contact (i, j), which is usually taken to be a constant ( 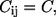independent of i and j) for all contacts, d_ij is the distance between the C_α atoms i and j, and 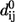is the corresponding distance in the folded structure. For the potential energy in Eq. 1 we can compute its second-order expansion near the basin conformation as follows:

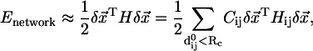(2)

where 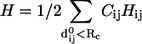is the Hessian matrix. The eigenvectors of the lowest frequency normal modes of the Hessian matrix, obtained by a normal mode analysis (NMA), are used to compute the overlap (or similarity) of a given mode m with the conformational changes between two states with known structures (denoted as 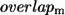; see Zheng and Doniach (18)). To preserve the sevenfold symmetry of GroEL during the ENM construction, we do the following symmetry operation: if the pair (i, j) satisfies 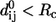and are therefore connected by a spring, then all those pairs related to (i, j) by sevenfold rotational symmetry are also connected by a spring even if their distance is slightly larger than R_c in the structure. In other words, a slight tolerance in R_c is allowed that enables us to produce an ENM with a strict sevenfold symmetry.

Fitting B-factors to calibrate the cutoff distance R_c

The ENM has two parameters, namely, the R_C and the force constant C. The normal mode spectrum depends on R_C whereas C merely sets a uniform scaling factor for the eigenvalues. We calibrate R_C by fitting the isotropic crystallographic B-factors 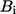of the C_α atoms of given crystal structure using (see Eyal et al. (23))

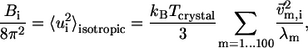(3)

where 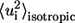is the isotropic mean square displacement (from rest position) of C_α atom i, k_B is Boltzmann constant, 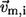is the three-dimensional component of the eigenvector of mode m at position i, 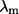is the eigenvalue of mode m, and T_crystal is the temperature at which the structure was determined. The quality of the fit is evaluated by the cross-correlation coefficient between the experimental and the calculated B-factors. In most previous studies a physically reasonable value of R_C is used, and typically the normal mode spectrum is relatively insensitive to the precise R_C values. Application to GroEL shows that the maximal overlap is sensitive to R_C. Therefore, it is crucial to choose R_C that reproduces experimental B-factors as closely as possible.

Structural perturbation method

To decipher the network of residues that transmit allostery (allostery wiring diagram) in biological nanomachines, we introduced a structural perturbation method (SPM) (19). The basic premise of SPM is that, for a given mode M, the dynamic importance of the i^th position can be assessed by the response to a local perturbation at i. The perturbation, which in the context of ENM is realized by small changes in the force constant of those springs that connect i to its neighbors, is akin to a point mutation in experiments. The response is measured in terms of a normalized score given by

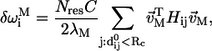(4)

where 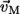() is the eigenvector (eigenvalue) of mode M, and 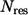is the total number of residues in the protein. The residues with high are dynamically critical (with values ≫1) to the motion of mode M. Such residues constitute mechanical “hot-spot residues” that may be involved in controlling the domain movements (19). The set of high 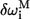residues, which are dispersed throughout the structure, form the allostery wiring diagram.

Assessing mode robustness: combined structural and bioinformatic approach

We showed in a previous study (20) that normal modes that most accurately describe the motions between two specific structures, in a number of biological nanomachines, are most robust to sequence variations. The variations in sequences are evaluated using the evolutionary imprints within a given family. To assess the robustness of a mode we first used PSI-BLAST (www.ncbi.nlm.nih.gov/blast) to obtain homologous sequences (search nr database with E cutoff, 10; j = 1). Subsequently, we used clustalW to align the sequences. We retain only sequences with >30% sequence identity to the query sequence. In this study, we do multiple sequence alignment for a single-chain sequence of GroEL structure 1AON because all the chains have the same sequence.

Evaluation of the probability of nonconservation at a position based on MSA

Following our previous study (20), we define the residue-similarity score for an amino-acid substitution (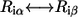) at position i using

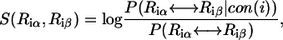(5)

where is the probability of the substitution if position i is conserved (“conserved” means position i maintains its interactions with its neighbors). We use the PAM250 score to evaluate residue similarity in Eq. 5. The probability of the i^th position not being conserved, if the substitution 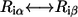is allowed, is given by

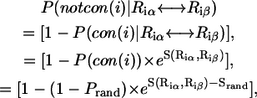(6)

where P_rand = 0.5. We compute the average 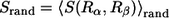for two randomly generated residues (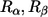) (both are randomly chosen from all 20 types of amino acids). The probability of nonconservation of position i is given by

(7)

where the average is over all possible () for the given position i in the MSA.

The robustness score of mode M (20) based on its eigenvalue (fractional variation of its eigenvalue 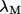) is assessed using

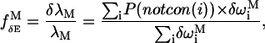(8)

where is computed using Eq. 4, and is given in Eq. 7.

Robustness score for the eigenvector of a normal mode

Given a perturbation to the Hessian matrix δH, as a result of variations in the force constants C_ij, the first-order correction to the eigenvector of mode M is

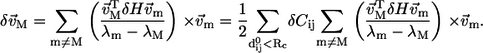(9)

For simplicity, we assume that the distributions of δC_ij are centered at zero, and are independent of the residue pairs. As a result, the mean square average of the amplitude of 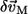is

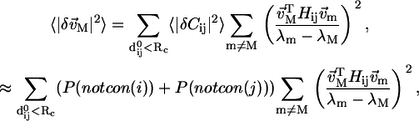(10)

where we estimate as the sum of probability of nonconservation at position i and j. For improved efficiency without loss of accuracy, in Eq. 10 we only sum over mode m with 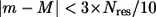rather than all the modes. The robustness score of mode M based on its eigenvector (fractional variation of its eigenvector's amplitude) is

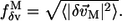(11)

Here we have used 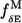(Eq. 8) and 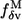(Eq. 10) to assess the robustness of functionally relevant modes.

RESULTS

B-factors fitting calibrates the cutoff distance R_c

The only essential parameter in the ENM is R_c (see Methods), which determines the maximal distance between two C_α atoms of residues that are considered in contact in a given structure. Previous studies have used R_c in the range 7 Å < R_c <20 Å depending on the system (11–18). We choose an “optimal” R_c so that the computed and measured B-factors are maximally correlated (see Eq. (3)). Comparison of the B-factors for the GroEL structure at R″T state as a function of R_c (Fig. 1) show that for R_c = 10 Å we obtain the highest cross-correlation coefficient between the B-factors computed using ENM and the crystallographic B-factors. Interestingly, with R_c = 10 Å the maximal overlap between the dominant mode and the observed R″T → TR″ conformational change is also at maximum. For other R_c values the maximal overlap decreases sharply (Fig. 1). This observation suggests that the allosteric transitions in GroEL may hinge on a delicate balance between interactions over a range of distance scales. Allosterically coordinated multidomain motions are best described if the interaction range is optimally chosen. Within the ENM description, the range R_c can be adjusted so as to obtain the best correlation between the experimental and the computed B-factors. This procedure for choosing R_c can be used for other systems as well.

FIGURE 1.

Dependence of B-factors fitting and the maximal overlap on R_c. The cross-correlation coefficient between the calculated B-factors based on the ENM and the crystallographic B-values is shown by the top line. The bottom line shows the maximal overlap between each mode and the observed R″T → TR″ conformational changes in GroEL, which is defined as 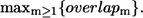Interestingly, for both quantities, R_c = 10 Å is the optimal value.

R″T → TR″ transition is captured by a single dominant normal mode 18

To assess the relevance of various modes we compare each normal mode for the R″T state (PDB code, 1AON) with the observed transitions R″T → TR″, R″T → TT, and R″T → RR. The PDB codes for TT and RR structures are 1GR5 and 2C7E, respectively. The R″T → TR″ transition, which is the last step in the reaction cycle of GroEL, is dominated by a single mode 18 (with overlap = 0.68). Several subdominant modes, namely, 3, 8, 17, 38–39, also have lower but relatively significant overlaps (Fig. 2 top). In contrast, the other two transitions are spread over multiple modes. The maximal overlap per mode for the R″T → TT transition is 0.49, and for the transition R″T → RR it is 0.43. In both these transitions the dominant mode is 18. Because R″T → TR″ transition is best captured by a single dominant mode, we focus on this transition. The other two states (TT and RR) appear to be less favorable for GroEL to visit during the R″T → TR″ transition. Even if these two other transitions are also functionally important, the lower overlap values would probably render the analysis based on a single mode less accurate. The results for R″T → TR″ support the functional importance of mode 18, which warrants a more detailed analysis.

FIGURE 2.

Mode-dependent variations of key factors in the allosteric transitions in GroEL. The top panel shows the overlap with the observed R″T → TR″ transition for the lowest 50 modes. The middle panel gives the robustness score based on the eigenvalue (f_δE) for the lowest 50 modes. The bottom panel displays the robustness score based on the eigenvector (f_δv) for the lowest 50 modes. Nonzero mode number starts from 1. Low values of the dimensionless robustness scores mean high robustness (see Methods for details). The coincidence of the modes that are important to the allosteric transition (with high overlap values) and the modes that are most robust (with low values of the robustness scores) is shown by the arrows (including modes 3, 8, 17, 18).

Mode 18 is most robust to perturbations from sequence variations

The finding that mode 18, with a relatively high frequency, is functionally the most relevant to the GroEL double ring, seems to contradict previous studies that usually found that the lowest two to 10 modes are sufficient to capture the functional motions of protein complexes (14). Indeed, an earlier ENM study of GroEL (8) was limited to the lowest 10 modes based on the assumption that the higher modes are less likely to be relevant. We use the robustness to sequence variations as a criterion to justify the importance of mode 18 in addition to the retrospective validation by computing the overlap values. The robustness is determined by f_δE, which is the fractional variation of the eigenvalue of each mode in response to the random perturbations to the force constants caused by sequence variations (19). By combining the robustness criterion with the low-frequency criterion, we can accurately select the functionally significant modes that should be robust to sequence variations.

Mode 18 has the highest robustness score (or lowest value in f_δE), and modes 19 and 20 rank second and third, respectively (see Fig. 2 middle). Therefore, the robustness score f_δE allows us to precisely predict the dominant mode, although the subdominant modes (3, 8, 17, 38–39) are not as accurately predicted.

In addition to the eigenvalue-based robustness analysis, we performed a similar analysis based on the eigenvectors. The small perturbation in the Hessian matrix can be captured using the first-order correction to the eigenvector of a normal mode as a linear combination of the eigenvectors from the other modes (see Methods). We computed the fractional variation of the amplitude of an eigenvector f_δv, i.e., the amplitude of the above first-order correction averaged over random perturbations to the force constants caused by sequence variations (Methods). The results for f_δv pinpoint four most robust modes (3, 8, 17, 18) as nearly degenerate global minima, and several other highly robust modes (say 39) as local minima (Fig. 2 bottom). All of these modes correspond to either the dominant mode (18) or subdominant modes (3, 8, 17, 38–39). Because the motions from one allosteric state to another takes place along the eigenvectors, f_δv appears to be a more effective indicator of functional relevance than f_δE. These results suggest that for a large system, such as the 14-mer GroEL at R″T state, multiple modes are required to fully capture the functionally relevant motions that drive allosteric transitions.

Mode 18 reveals a dynamic asymmetry between cis- and trans-rings

The identification of a single dominant mode allows us to describe the initial structural changes that occur during the R″T → TR″ transition. By comparing the motions in the dominant mode with the observed structural differences between the two allosteric states, we tentatively identify two types of regions in the GroEL structure. First, the regions of good fit where the selected mode overlaps well with the observed changes between the end states. The motions in these regions may describe the initial structural changes of the transition. Second, the regions of discrepancy where the selected mode fails to fit well to the observed differences. Such deviations may determine late-stage structural changes in the transition that are not encoded in the initial-state structure. By distinguishing between these two types of regions and their associated structural changes, we can achieve a qualitative (or even semiquantitative) view of the complex dynamic transitions connecting the R″T and TR″ states.

The structural displacements of mode 18 for all seven trans-ring subunits are found to be nearly symmetric (obeying sevenfold rotational symmetry). They overlay well along the polypeptide chain of 524 residues (Fig. 3). The sevenfold symmetry is preserved in the cis-ring for mode 18. Therefore, this mode indeed describes a highly symmetric and concerted set of motions in both the cis- and the trans-rings. However, there are substantial differences between the two rings. In the trans-ring, mode 18 matches well in amplitude with the observed T → R″ changes in the E and I domains, but in the A domain mode 18 predicts significantly reduced motions than is observed (see Fig. 3). Therefore, the preferred motions of the trans-ring in the T state, as described by 18, can quantitatively account for the moderate movements of the I and E domains but not the very large-amplitude motions of the A domain. This is consistent with the global two-stage T → R″ transition where the I domain moves into the R″-state configuration (clamping downward to close the nucleotide binding site) before the A domain fully opens (twisting in the clockwise direction and swinging upward) for GroES binding (6,9,24).

FIGURE 3.

Amplitude of the eigenvector of mode 18 (green for trans-ring, red for cis-ring) and the observed trans-cis-swapping transition (blue) as a function of residue position. Displacement amplitudes at seven subunits of trans- and cis-rings are overlaid in the same panel. The locations of the domains are: A domain (191–376), E domain (6–133, 409–548), I domain (134–190, 377–408). The superposition of the amplitudes for the seven subunits is indicative of the concerted nature of the allosteric transitions (see a similar plot in Yang 2006 (42)).

In the cis-ring, however, mode 18 predicts larger-amplitude motions in the A and E domains of the cis-ring than in the trans-ring (see Fig. 3). The substantial differences in motions between the two rings have the following consequences. First, the inter-ring interface may be structurally distorted due to the unequal motions in E domains between the trans- and cis-rings, which may then facilitate the transmission of allosteric signals from the cis-ring to the trans-ring. Second, the observation that the motion in the A domain is much larger in the cis-ring than in the trans-ring, indicates that large-scale closing motions of the A domain probably occur early in the cis-ring. This is subsequently followed by the large-scale opening motions of the A domain in trans-ring. These observations are also suggestive of a two-stage R″ → T transition in the cis-ring that qualitatively reverses the T → R″ transition in the trans-ring. This also points to a possible on-path intermediate state with the A domains in both rings adopting a closed conformation. The analysis seems to rule out the presence of a football-shape intermediate state where the A domains in both rings are in open/elevated conformation. These conclusions, based on the ENM model, should be viewed as tentative because of the absence of explicit dynamics. It is likely, as shown by using the self-organized polymer model of GroEL, that there are multiple paths that connect the various allosteric states (9). The existence of parallel pathways for the ATP-induced allosteric transition in GroEL was also supported by an experimental Φ-value analysis (25).

Coordinated interdomain structural changes are revealed by mode 18

To visualize the detailed structural motions in the A, E, and I domains of both rings, we show in Fig. 4 the deformed structural model along mode 18 superimposed on the initial structure of a subunit from each ring as given in the PDB structure 1AON. In a trans-ring subunit, the E domain tilts slightly downward near its N- and C-terminals, which face the interior of the central cavity (Fig. 4 c; see arrows, lower right). In the E domain, there is an axial-translation in helix C and a shift at the tip of the stem loop away from where the ADP is located (Fig. 4 c; see arrows, middle). The helices F and M of the I domain shift down toward the E domain (the distances between helices M/F and the stem loop decrease). The A domain swings slightly upward, and twists in the counterclockwise direction, which is consistent with the EM study (24). When viewed along the central axis from outside the cavity, the A domains in all seven subunits rotate in the counterclockwise direction, while the seven E domains rotate in the clockwise direction.

FIGURE 4.

Structural displacements (from blue to red) as predicted by mode 18. (a) This shows the side view (perpendicular to the central axis) for one trans-ring subunit (chain H). (b) The side view for cis-ring subunit of chain A is shown using the ribbon diagram. (c) Structural representation of the double-ring complex is displayed. The boxes enclose a single subunit from cis- and trans-ring as shown in panels a and b. The arrows give the two viewing directions for panels d and e. (d) The structure shows the top view (along the central axis) for the apical domains of cis-ring. The clockwise rotation of the A domains are indicated. (e) We show a bottom view for the apical domains of trans-ring with explicit counterclockwise rotation of the A domains.

In a cis-ring subunit, the E domain tilts slightly upward near its N- and C-terminals (Fig. 4 d; see arrows, lower right). The ADP pocket remains closed by helices F and M of the I domain and the stem loop (although there is an overall shift in them, the distances between helices F and M and the stem loop remain unchanged). The A domain swings downward significantly, and twists in the clockwise direction. Viewing along the central axis from outside the cavity, the seven A domains rotate in the clockwise direction, while all the E domains rotate in the counterclockwise direction.

At the interface between the two rings, two inter-ring contacts (A109, A109) and (V464, V464) are slightly closer as a result of unequal tilting of the cis-ring and trans-ring. Therefore, the structural changes of mode 18 may result in stronger inter-ring interactions that may reverse the weakening effect of ATP binding (24).

In summary, mode 18 predicts anticorrelated motions between the trans- and cis-rings together with highly symmetric motions within each ring, therefore suggesting an intrinsic coupling between the negative inter-ring cooperativity and the positive intra-ring cooperativity (26). Such a coupling was also found in experiments that showed that a mutation (E461K) at the inter-ring interface causes the intra-ring cooperativity to be abolished (27). The predicted structural changes in the trans-ring are compatible with ATP binding (28), which are coupled via mode 18, to the large-scale downward motions in the A domains of the cis-ring. The downward motions of the A domains may disfavor binding with GroES and cause its release. This explains the observed allosteric coupling between ATP binding in the trans-ring and GroES release in the cis-ring (29). The E domains of the trans-ring and the cis-ring tilt in opposite directions, which agrees with the crystallographic observations (30). However, unequal amplitudes in the E domain's motions (larger amplitude in cis-ring than trans-ring) most likely result in structural distortions at the inter-ring interface, which is consistent with the EM study (24) that found that the E domains of the T ring (trans-ring) have a smaller tilt opposing that of the R ring (cis-ring).

Allostery wiring diagram identified by the structural perturbation method reveals the importance of residues at the interface of subunits

In a recent article (20), we generated the allostery wiring diagram (see Methods) for the subunit A of GroEL cis-ring by performing the SPM analysis (19). For the cis-ring subunit A, mode 1 has maximal overlap with the R″ → T transition. For the reverse T → R″ transition in subunit H of the trans-ring, mode 3 was found to give the maximal overlap. Using the SPM we obtained the network of cis-ring residues that encode the dynamics described by mode 1, many of which were found to be important to GroEL functions by mutational studies. In a previous article (20), we made comparisons between our computational study and genetic experiments (31) that identified key residues. Because our previous work was restricted to a single subunit, we could not pinpoint the allostery wiring diagram that describes intra- and inter-ring couplings. With the identification of mode 18 for the double-ring GroEL as being the most relevant for the allostery in the whole complex, we use SPM to identify additional residues that encode the interactions between subunits. Comparisons of the allosterically relevant residues for a single subunit and for the 14-mer (see Table 1) allow us to infer the wiring diagram that describes allostery in the whole “two-stroke” nanomachine.

TABLE 1.

List of high-δω residues for mode 18 of the double-ring versus mode 3 of the trans-ring subunit (chain H)

Mode	Residue numbers (normalized δω score)
Mode 3 subunit H	26 (2.7)	29 (2.2)	38 (12.2)	39 (22.3)	40 (11.3)
	41 (9.5)	42 (6.7)	43 (4.3)	45 (3.3)	46 (2.3)
	47 (18.7)	48 (12.6)	49 (3.8)	50 (13.6)	51 (2.4)
	55 (32.0)	56 (2.9)	83 (32.8)	85 (2.1)	86 (3.0)
	136 (2.3)	139 (3.2)	147 (2.1)	171 (4.1)	173 (3.1)
	176 (2.5)	189 (4.4)	206 (7.9)	207 (16.4)	209 (53.7)
	210 (3.9)	211 (8.3)	214 (3.5)	215 (2.2)	327 (23.7)
	328 (11.3)	333 (2.2)	374 (3.5)	404 (2.2)	407 (2.6)
	492 (2.9)
Mode 18 trans-ring	109 (3.3)	110 (3.3)	145 (3.3)	146 (3.3)	147 (2.7)
	148 (2.7)	171 (3.9)	172 (3.9)	173 (3.0)	174 (3.0)
	175 (2.4)	176 (2.4)	267 (2.1)	268 (2.1)	279 (2.1)
	280 (2.1)	369 (2.4)	370 (2.4)	373 (3.6)	374 (3.6)
	385 (2.1)	386 (2.1)	411 (2.1)	412 (2.1)	463 (3.0)
	464 (3.0)	491 (4.7)	492 (4.7)	493 (2.7)	494 (2.7)

New high-δω residues only present in mode 18 are underlined. The cutoff value of δω is 2.

The results in Tables 1 and 2 show that many high-δω residue positions are shared between the single subunit mode (20) and the double-ring mode 18. Several of the identified residues have been found to be functionally important by experiments or in computational studies (20). There are also a number of new high-δω residues (Tables 1 and 2) due to intersubunit couplings, which are mostly located at intersubunit interfaces (some are intra-ring, others are between rings). These residues are predicted to be involved in the signal transmissions between different subunits of the two rings. Many of the relevant residues that are identified using SPM are displayed in Fig. 5.

TABLE 2.

List of high-δω residues for mode 18 of the double-ring versus mode 1 of the cis-ring subunit (chain A)

Mode	Residue numbers (normalized δω score)
Mode 1 subunit A	83 (10.5)	141 (2.1)	144 (2.5)	161 (2.6)	164 (2.6)
	165 (4.2)	166 (7.4)	167 (7.9)	168 (16.1)	169 (4.9)
	170 (4.7)	171 (9.3)	172 (15.4)	173 (5.6)	174 (16.8)
	175 (12.8)	176 (10.9)	177 (3.5)	187 (2.6)	188 (2.8)
	189 (4.2)	190 (7.0)	191 (25.3)	192 (10.2)	193 (8.2)
	194 (14.0)	195 (8.2)	288 (11.2)	291 (7.4)	295 (7.5)
	331 (6.1)	332 (2.5)	333 (2.1)	346 (3.7)	347 (4.2)
	349 (2.6)	352 (4.0)	353 (2.5)	357 (2.1)	359 (12.5)
	360 (3.0)	361 (2.3)	363 (8.1)	364 (3.2)	365 (5.3)
	366 (6.5)	367 (5.8)	368 (32.1)	369 (6.0)	370 (2.5)
	371 (4.6)	372 (2.6)	373 (18.1)	374 (9.6)	375 (7.4)
	376 (20.5)	377 (4.4)	378 (8.4)	379 (2.8)	397 (3.9)
	400 (6.1)	404 (3.2)
Mode 18 cis-ring	87 (2.1)	88 (2.1)	109 (2.7)	110 (2.7)	165 (5.9)
	166 (5.9)	167 (3.3)	168 (3.3)	169 (3.0)	170 (3.0)
	171 (24.9)	172 (24.9)	175 (9.2)	176 (9.2)	187 (2.1)
	188 (2.1)	189 (9.5)	190 (9.5)	191 (6.8)	192 (6.8)
	193 (6.2)	194 (6.2)	195 (3.3)	196 (3.3)	203 (3.3)
	204 (3.3)	207 (4.4)	208 (4.4)	209 (2.1)	210 (2.1)
	263 (2.1)	264 (2.1)	305 (5.0)	306 (5.0)	307 (3.6)
	308 (3.6)	309 (2.4)	310 (2.4)	331 (5.6)	332 (5.6)
	333 (3.0)	334 (3.0)	343 (3.0)	344 (3.0)	345 (7.1)
	346 (7.1)	347 (6.8)	348 (6.8)	349 (6.5)	350 (6.5)
	351 (4.7)	352 (4.7)	353 (6.5)	354 (6.5)	361 (2.1)
	362 (2.1)	365 (2.1)	366 (2.1)	367 (4.2)	368 (4.2)
	369 (16.9)	370 (16.9)	371 (3.0)	372 (3.0)	373 (5.9)
	374 (5.9)	375 (9.5)	376 (9.5)	377 (3.9)	378 (3.9)
	379 (2.1)	380 (2.1)	381 (3.3)	382 (3.3)	383 (12.5)
	384 (12.5)	385 (2.4)	386 (2.4)	397 (3.0)	398 (3.0)
	401 (2.1)	402 (2.1)	403 (6.2)	404 (6.2)	407 (15.7)
	408 (15.7)	463 (3.0)	464 (3.0)	465 (3.0)	466 (3.0)
	505 (3.3)	506 (3.3)

New high-δω residues only present in mode 18 are underlined. The cutoff value of δω is 2.

FIGURE 5.

Some key residues in the allostery wiring diagram for GroEL determined using the SPM are overlaid in the structure. Residues with high-δω for mode 18 (spheres in red and orange) involved in intersubunit contacts in trans-ring subunits (green) and cis-ring subunits (blue) are explicitly shown. For clarity, only three subunits from each ring are shown.

In what follows, we discuss the intersubunit contacts involving the high-δω residues with reference to the structure and their relevance to experiments.

A domains

In the cis-ring residues Y203, F204, T210 form contacts with I305, G306, Q351 of the adjacent subunit. Residues V263 and V264 also form contact with I305 and G306 of the neighboring subunit. In the trans-ring, residues G269 and I270 form contact with residue E257 of the neighboring subunit. Experiments have shown that mutants Y203E and F204E both do not show GroES or SP bindings (32). Residue T210 is at the hinge of the loop (199–204) between strands 6 and 7 that binds SP in the T state. Residue E209 was proposed to contact R58 in E domain (note S55 and V56 are high-δω residues of mode 3 of subunit H) (28) and may affect the hinge motion between the E and A domains. Residues V263 and V264 bind to SP in the T state, and form part of the GroEL-GroES interface in the R″ state (30). Mutant V263S shows no GroES/SP binding, and V264S shows reduced ATPase activity and no GroES/SP bindings (32). Residue R268 is also a potential SP-binding site (33). Mutants L309K and L314K show reduced SP folding (32). Residues I301–K311 were found to be indirectly involved in peptide binding (34). Danziger and co-workers found that E257 is a sensor involved in coupling polypeptide substrate binding to stimulation of ATP hydrolysis (35). E257 was also shown to be involved in the unfolding action of GroEL on a protein substrate in a recent computational study (36). Stan et al. have also emphasized the role of E257 in the release of SP using all-atom simulations (37). R58 and M267 were previously found as part of the wiring diagram in a bioinformatic study by Kass and Horovitz (38).

E domains of both rings

Residues A109 and G110 are involved in inter-ring contacts, as are residues S463 and V464.

Between E and I domains

In the cis-ring residue Y506 forms contacts with residues A384 and T385 of neighboring subunit. Mutants A503V and A507T were found to give active single-ring GroEL (39).

Between A and I domains A

In the trans-ring, residue F281 forms contact with residues T181 and A383–E386 of neighboring subunit. Experimentally, the F281D mutant has decreased ATPase activity and decreased SP folding (32). Mutant A383E has no ATPase activity, no GroES binding, and no SP refolding (32). A salt bridge forms between R197 and E386 in the T state and a new E386–K80 salt bridge may be formed in the ATP-bound state (24). Mutants T385I, E388K, M389I were found to give active single-ring GroEL (39).

Among the above high-δω residues, A109, G110, Y203, F204, V263, R268, P279, G280, A383, T385, and E386 are highly conserved (40) with conservation score 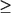8 (using conservation scores from ConSurf-HSSP ranging from 1 to 9, where 1 means most variable and 9 most conserved) (41). The overlap between the dynamically key residues and SP binding residues suggest that SP binding is closely coupled with the allosteric transitions and the associated large-scale structural changes.

CONCLUSIONS

We have performed an ENM-based normal mode analysis on the R″T state of the GroEL structure to explore the preferred collective motions encoded in the 14-mer GroEL complex. For the R″T → TR″ conformational transition, we have found a single dominant normal mode 18 that offers a simplified glimpse into this highly intricate allosteric transition. An in-depth analysis of mode 18 has revealed the structural and dynamic details that underlie the positive intra-ring and negative inter-ring allosteric couplings. This mode predicts that the structural motions are highly concerted within each ring, and are anticorrelated between the two rings. By assessing the robustness of this dominant mode (in comparison with the other modes) to parametric perturbations caused by sequence variations, we have validated its functional importance. Finally, we have applied the structural perturbation method technique to this dominant mode to identify the allostery wiring diagram, namely, a network of key residues that control its motions. Many of these residues are located at intersubunit interfaces and are therefore predicted to play critical roles in transmitting allosteric signals between subunits. These results also show that to obtain insights into the conformational changes in multimodular structures it is important to study the entire complex. By merely focusing on a single subunit and appealing to symmetry, the important consequences of dynamic symmetry breaking and the role played by interface contacts may be missed.

The combination of structural and bioinformatics methods proposed here is general enough that it can be used to examine allostery in other biological systems as well. It is important to assess if the dynamics in a mode is also robust enough to evolutionary sequence variations because it is believed that it is the structure, rather than the sequence, that is more conserved for functional reasons.

The SPM tool is available at http://enm.lobos.nih.gov.