Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2007 Nov;16(11):2564–2569. doi: 10.1110/ps.073124507

On the role of structural class of a protein with two-state folding kinetics in determining correlations between its size, topology, and folding rate

Andrei Y Istomin 1,2, Donald J Jacobs 1, Dennis R Livesay 2
PMCID: PMC2211710  PMID: 17962408

Abstract

The time it takes for proteins to fold into their native states varies over several orders of magnitude depending on their native-state topology, size, and amino acid composition. In a number of previous studies, it was found that there is strong correlation between logarithmic folding rates and contact order for proteins that fold with two-state kinetics, while such correlation is absent for three-state proteins. Conversely, strong correlations between folding rates and chain length occur within three-state proteins, but not in two-state proteins. Here, we demonstrate that chain lengths and folding rates of two-state proteins are not correlated with each other only when all-α, all-β, and mixed-class proteins are considered together, which is typically the case. However, when considering all-α and all-β two-state proteins separately, there is significant linear correlation between folding rate and size. Moreover, the sets of data points for the all-α and all-β classes define asymptotes of lower and upper limits on folding rates of mixed-class proteins. By analyzing correlation of other topological parameters with folding rates of two-state proteins, we find that only the long-range order exhibits correlation with folding rates that is uniform over all three classes. It is also the only descriptor to provide statistically significant correlations for each of the three structural classes. We give an interpretation of this observation in terms of Makarov and Plaxco's diffusion-based topomer-search model.

Keywords: protein folding, folding rate, contact order, long-range order, folding kinetics, topomer-search model

Relationships between protein-folding rates and their basic characteristics (e.g., chain length, topology, and amino acid composition) have been considered for about a decade due to the insight they provide into underlying folding mechanisms (Jackson 1998; Plaxco et al. 1998, 2000; Mirny and Shakhnovich 2001; Gromiha 2003; Naganathan and Munoz 2005). The pioneering work of Plaxco et al. (1998) demonstrated that a “relative contact order” (RCO) parameter is linearly correlated to logarithm of folding rates, k f, of small two-state proteins. Since then, a number of other measures of protein topology and size have been analyzed (Grantcharova et al. 2001; Gromiha and Selvaraj 2001; Mirny and Shakhnovich 2001; Zhou and Zhou 2002; Ivankov et al. 2003; Ivankov and Finkelstein 2004). An “absolute contact order” (ACO) was shown to have stronger correlation with folding rates than RCO when chain lengths vary over a wide range: from about 16 (β-hairpin peptide) to 322 residues (α-helical protein) (Ivankov et al. 2003). In Gromiha and Selvaraj (2001), a “long-range order” (LRO) parameter was also found to correlate strongly with folding rates. Other measures considered include the fraction of local contacts (Mirny and Shakhnovich 2001), total contact distance (TCD) (Zhou and Zhou 2002), chain length (Galzitskaya et al. 2003), local secondary structure content (Gong et al. 2003), and effective chain length (Ivankov and Finkelstein 2004), and n-order contact distance (Zhang and Sun 2005).

A significant effort of the field has been to find the most adequate descriptors of protein folding rates capable of predicting them for proteins of any structural class (i.e., all-α, all-β, and mixed class) that obey either two-state or multistate (three-state) folding kinetics. One of the most interesting, yet counterintuitive conclusions from those studies is that for small proteins obeying two-state kinetics, structure topology is the main determinant of the folding rate, and that there is virtually no correlation between chain length and the folding rate (Galzitskaya et al. 2003). For proteins with observable intermediates the opposite was found (i.e., chain length is the main determinant of folding rates, while there is little correlation between them and contact order [Galzitskaya et al. 2003]). The lack of correlation between size and folding rates of two-state proteins has been subsequently reproduced and emphasized in a number of other analyses (see, e.g., Makarov and Plaxco 2003), including several very recent ones (Galzitskaya and Garbuzynskiy 2006; Prabhu and Bhuyan 2006; Huang et al. 2007).

The aim of this paper is not to construct a new descriptor of protein-folding rates, nor is it to provide improved means for folding-rate prediction. Rather, we illustrate how considerations of structural class within two-state proteins drastically affect scaling between folding rates and existing descriptors. Moreover, we attempt to use these results to gain insight into the underlying protein-folding mechanisms.

Results and Discussion

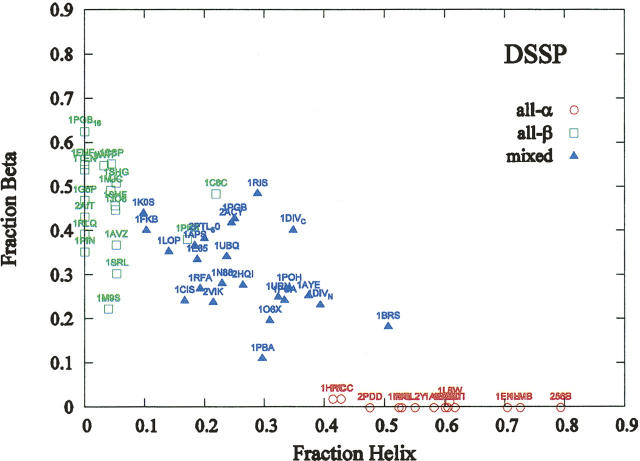
For our analyses, we have compiled a set of 56 nonredundant two-state proteins with experimentally measured folding rates (cf. Table I in the Supplemental material). Our set includes proteins whose chain length varies from 16 residues (the C-terminal β-hairpin peptide of the B1 domain of protein G) to 322 residues (4 α-helix bundle of the VlsE antigen protein [PDB id: 1L8W]). The distribution of relative secondary structure content calculated using the DSSP approach (Kabsch and Sander 1983) in our protein set, which was partitioned into structural classes according to SCOP with two exceptions (cf. Materials and Methods), is shown in Figure 1. A key point from Figure 1 is that the fractions of residues in the β-like and helical conformations within all-α and all-β proteins, respectively, are rather small. Moreover, mixed-class proteins appear as an intermediate phase. Because our data set cleanly partitions into all-α and all-β proteins, we expect that a correlation between ln k f and chain length L may exist individually, even though it does not exist globally. Further, if linear correlations within these two classes are revealed, it is likely that the slopes in linear regression models for all-α and all-β proteins would be substantially different. This is expected because folding of helical and β-like structures occur on significantly different timescales, as folding of β-like structures involves a greater exploration of conformation space.

Figure 1.

Figure 1.

Open in a new tab

Distribution of α-helical and β-like secondary structure content in two-state proteins included in the data set. All-α proteins are shown by red circles, all-β proteins by green squares, and mixed-class proteins by blue triangles.

In the following, we have adopted the original definitions for all topological parameters. The relative contact order (Plaxco et al. 1998) is defined by:

graphic file with name 2564equ1.jpg

where L is the chain length, N c is the total number of contacting atoms (using a 6 Å distance threshold), and dij is the number of residues separating those two residues to which atoms i and j belong. The absolute contact order (ACO) is defined as in Ivankov et al. (2003): ACO = L × RCO. Long-range order (LRO) (Gromiha and Selvaraj 2001), is defined by:

graphic file with name 2564equ2.jpg

where

graphic file with name 2564equ3.jpg

Two residues are considered to be in contact if the closest distance between their Cα atoms is less than or equal to 8 Å. The LRO parameter thus gives the average number of structural contacts separated by 12 or more sequence positions per residue.

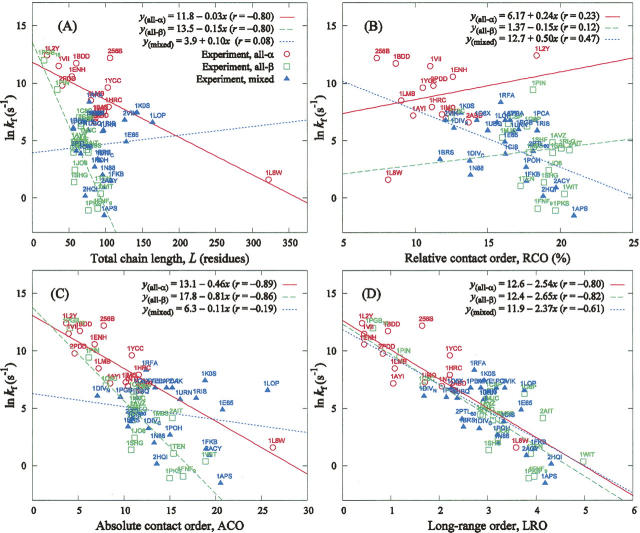
We start by comparing the logarithmic folding rate, lnk f, to the simplest of the considered descriptors, namely the chain length. Figure 2A demonstrates that in contrast to the findings of Galzitskaya et al. (2003) and many other subsequent reports, chain length is linearly correlated to folding rates when considering all-α and all-β two-state proteins separately. These two sets of data points are well described with high correlation (the correlation coefficients are r all-α = −0.80 and r all-β = −0.80) and statistical significance (the t-distribution P-values are p all-α = 5.7 × 10−4 and p all-β = 6.0 × 10−5) by two linear regression equations with two substantially different pairs of regression coefficients. However, collapsing the structural classes into one data set lowers the correlation coefficient to r = −0.29. Further, it is clear from Figure 2A that the sets of data points for all-α and all-β classes serve as asymptotic lower and upper limits for proteins of the mixed class, which can be naturally expected. (We note that correlation between lnk f and chain length of seven two-state mainly β proteins was found in Kuznetsov and Rackovsky [2004], where it was, however, considered not statistically significant.) For mixed-class proteins, there is almost no correlation between chain length and lnk f (r = 0.10), which we believe points to a higher complexity and variability of their folding mechanisms. It should be pointed out that the data point corresponding to protein 1L8W in Figure 2A has a relatively large Cook's distance, d = 0.68, which significantly affects the correlation for all-α proteins. The leverage for this data point is large (0.85); however, its standardized residual is small (0.5). While excluding 1L8W from the data set decreases the correlation to −0.53, its effect on regression coefficients is not dramatic; the regression equation becomes y all-α = 12.4 − 0.04x, compared with the original y all-α = 11.7 − 0.03x. The second significant outlier, 256B, has a Cook's distance of 0.19 with small leverage (0.075), but relatively large residual (2.2).

Figure 2.

Figure 2.

Open in a new tab

Correlation between natural logarithmic folding rates, ln kf, and basic structural and topological parameters for proteins belonging to three structural classes. In regression equations, x and y stand for abscissa and ordinate axes quantities; r is the correlation coefficient. (A) ln kf versus protein chain length, L (the t-test P-values are p all-α = 5.7 × 10−4, p all-β = 6.0 × 10−5, and p mixed = 0.71). (B) ln kf versus relative contact order, RCO (the t-test P-values are p all-α = 0.43, p all-β = 0.65, and p mixed = 0.021). (C) ln kf versus absolute contact order, ACO (the t-test P-values are p all-α = 2.3 × 10−5, p all-β = 5.5 × 10−6, and p mixed = 0.38). (D) ln kf versus long-range order, LRO (the t-test P-values are p all-α = 6.4 × 10−4, p all-β = 2.6 × 10−5, and p mixed = 1.5 × 10−3). Structural classes for experimental data and regression lines are defined as in A.

The relative contact order, RCO, as reported previously, is capable of describing lnk f for small two-state proteins of all three structural classes together (Plaxco et al. 1998) and separately (Kuznetsov and Rackovsky 2004). It fails, however, when short peptides or large two-state proteins are included in the data set (Ivankov et al. 2003). Note that in Kuznetsov and Rackovsky (2004), the two linear regression lines describing seven mainly α- and 19 β-sheet-containing proteins have similar slopes and exhibit statistically significant correlation. In our Figure 2B, however, use of the significantly expanded data set resulted in the complete failure of the RCO, similarly to findings of Ivankov et al. (2003). Specifically, inclusion of the 20-residue Trp-cage miniprotein construct TC5b (PDB: 1L2Y), of the 322-residue VlsE protein (PDB: 1L8W), as well as of several others, has completely disrupted correlations among all-α proteins. In the set of all-β proteins, inclusion of the 16-residue C-terminal β-hairpin of protein G, of the 34-residue subdomain of peptidyl-prolyl cis-trans isomerase (PDB: 1PIN), and a number of other proteins has also diminished the correlation.

On the other hand, the absolute contact order, ACO, correlates with high statistical significance with the folding rates of all-α and all-β proteins (cf. Fig. 2C). The slopes of the corresponding regression equations are closer to each other than in Figure 2A, where lnk f is compared with the chain length. This indicates that, as pointed out in Ivankov et al. (2003), both chain length and structural topology significantly affect two-state folding rates.

The situation is clarified even more by considering the long-range order parameter, LRO (Gromiha and Selvaraj 2001) (cf. Fig. 2D). Remarkably, the linear regression equations, separately describing each of the three data sets, have almost identical coefficients. That is, of all descriptors considered herein, only LRO provides a uniformly accurate description of folding rates for proteins over all three structural classes. The corresponding correlation coefficients, r all-α = −0.80, r all-β = −0.82, and r mixed = −0.61 are, however, slightly lower than those for the ACO. Nevertheless, LRO is the only topological descriptor considered herein that provides statistically significant correlations for all three structural classes. Consistent with the results of Galzitskaya et al. (2003), none of the topological parameters (RCO, ACO, or LRO) correlate with lnk f for any of the structural classes (data not shown) in proteins with multistate folding kinetics.

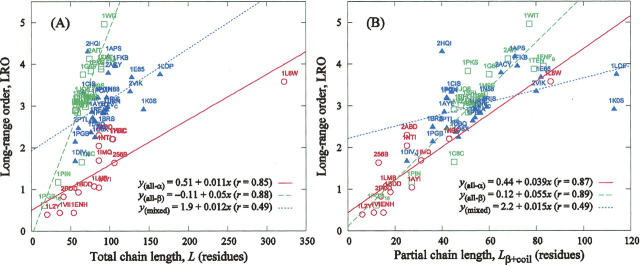
We believe that the observed uniform correlation of the LRO parameter with lnk f for two-state proteins stems from (1) characteristic features of their folding kinetics and (2) the similarity of description of lnk f in terms of LRO to the one by topomer-search model (Makarov and Plaxco 2003). On one hand, as Huang et al. (2007) have recently pointed out, for two-state proteins of all three structural classes, the rate-limiting step is the formation of β-sheet and loop structures, i.e., formation of contacts that are long range in sequence, whose rate is limited by cooperative diffusion (Makarov and Plaxco 2003). (In α-helical and mixed-class, two-state protein formation of helices is generally the fastest step of folding, while for all-β proteins, it is simply absent.) Therefore, by explicitly taking into account the number of long-range contacts, the LRO parameter exhibits uniform correlation with protein-folding rates of all three classes. On the contrary, for proteins with multistep folding kinetics, the fast step is the nonspecific hydrophobic collapse with formation of loops, while formation of helical and β-like structures represents the rate-limiting step, so that lnk f correlates well with the sum of numbers of residues in α-helical and β conformations (Huang et al. 2007). It is evident from Figure 3A that total chain length, L, can be considered a proxy for the LRO within all-α and all-β proteins. As in the case of lnk f versus L correlation (cf. Fig. 2A), the linear models in Figure 3A have substantially different proportionality coefficients. However, the correlation of LRO with the number of residues in the β-like and coil conformations, L β + coil, is more uniform (cf. Fig. 3B). Further, if five proteins with unusually high folding rates (all-α: 1L8W; mixed class: 1LOP, 1K0S, 1E65, and 2VIK) are eliminated, the correlation between LRO and L β+coil becomes uniform over all three structural classes (data not shown). (Note: These five proteins were not in the data set of Huang et al. [2007].) Finally, we find that the correlation between lnk f and the number of residues in the coil conformation is significant only for all-α proteins. The correlation should be strong for all three classes if all local secondary structure elements folded fast, as suggested by a hierarchical view of folding (e.g., Gong et al. 2003). We believe this again indicates that the slow step of two-state folding is the organization of β-like and coil structures, which are both likely to be limited by diffusion.

Figure 3.

Figure 3.

Open in a new tab

Correlation of the LRO with total and partial chain lengths. (A) LRO versus the total number of residues (the t-test P-values are p all-α = 1.3 × 10−4, p all-β = 1.3 × 10−6, and p mixed = 1.5 × 10−2). (B) LRO versus the number of residues in the β-like or coil-like conformations (the t-test P-values are p all-α = 4.4 × 10−5, p all-β = 5.6 × 10−7, and p mixed = 1.6 × 10−2).

On the other hand, the meaning of the LRO parameter is directly related to the number of sequence-distant pairs, Q d, introduced in the diffusion-based topomer search model that was found highly successful in describing folding rates of 24 two-state proteins (Makarov and Plaxco 2003). Within this model, the folding rate is described by the relation:

graphic file with name 2564equ4.jpg

where κ ≈ 108 s −1 is the attempt frequency for forming a single contact, γ ≈ 3.8 × 10−5 accounts for the chain entropy reduction associated with forming few first contacts, and K is the equilibrium constant less than unity (Makarov and Plaxco 2003). By noticing that QD = L × LRO, where L is the chain length (cf. Equations 2 and 3), we rewrite Equation 4 as follows:

graphic file with name 2564equ5.jpg

Next, because in the 24-protein set in Makarov and Plaxco (2003) the chain length variation is relatively small, we replace L in Equation 5 by its average value over the data set in Makarov and Plaxco (2003), L ≈ 85, and neglect the term ln LRO, whose absolute value is small compared with other terms in Equation 5. Finally, by setting K ≈ 0.97 and evaluating numerical values, Equation 5 becomes:

graphic file with name 2564equ6.jpg

in excellent agreement with all three regression equations in Figure 2D. We note that our value of the equilibrium constant, K ≈ 0.97, is comparable to the one obtained by fitting to a smaller data set (K ≈ 0.86) in Makarov and Plaxco (2003).

To summarize, we have demonstrated that for two-state all-α and all-β proteins considered separately, there is significant linear correlation between logarithmic folding rates and chain length. The lack of such correlation reported in many previous works exists only when proteins of different structural classes are considered together. Further, by analyzing correlation of folding rates with topological parameters for two-state proteins of three structural classes separately, we have found that only the long-range order parameter provides a uniformly accurate description of folding rates for proteins over all three structural classes. First, this observation supports the argument of Huang et al. (2007) that the rate-limiting step in folding of two-state proteins is the formation β-sheet and loop structural elements (i.e., of long-range contacts). Second, it supports the hypothesis of diffusion-limited folding for two-state proteins that is behind the topomer-search model of Makarov and Plaxco (2003), with which our regression equations for all three structural classes are in excellent agreement.

Materials and Methods

The protein set for our analyses contains 56 two-state proteins and was compiled based on experimental data available in the literature. In particular, it includes data two-state proteins reported in Maxwell et al. (2005), where folding rates were measured under “standard” experimental conditions. Following Maxwell et al. (2005), our goal was to compile a set containing exact structural information that was often lacking in previous reports. These data are included in the Supplemental material.

Secondary structure assignment for all proteins in our set (cf. Fig. 1) was performed using the DSSP approach (Kabsch and Sander 1983). The secondary structure elements α-helix, 310 -helix, and π-helix were classified as an α-helical conformation; β-strand and β-bridge were classified as β-conformation; hydrogen-bonded turns and loop structures were not included in Figure 1. We note that performing secondary structure assignment using the PROSS approach (Srinivasan and Rose 1999) that is based on binning a backbone dihedral angles' plane, results in a similar distribution in which, however, there are more overlaps between structural classes (data not shown).

Structural class assignment was performed using the SCOP database, with two exceptions. First, the protein domain CheW (PDB id: 1K0S), annotated as all-β in SCOP, contains a nine-residue C-terminal α-helix and a five-residue α-helix, and was therefore assigned to a mixed class. We believe that the presence of these α-helices may be partly responsible for the extraordinarily high folding rate of this 151-residue-long mainly β protein. (We note that the experimental folding rate value for this protein reported in Maxwell et al. [2005] is the only one available in the literature.) Second, a cyclophilin A protein (PDB id: 1LOP), classified as all-β in SCOP, contains two α-helices that are 13 and nine residues long, and has also been assigned to the mixed class. The unusually high folding rate for this 164 residue long protein has been attributed to its unique hydrophobic core with a phenylalanine cluster (Ikura et al. 2000).

The presented P-values, Cook's distances, leverages, and standardized residuals were calculated using R and R Commander statistical packages (R Development Core Team 2006). The t-test P-value gives the probability that in a sample of data drawn from the t-distribution, the ratio of the slope to the variance will be as high or higher than that observed in our data set. Cook's distance quantifies the effect of a single data point on the regression model, and depends on both leverage and residual. The leverage of a data point characterizes its distance from the centroid of the data set along the independent variable axis, while the residual characterizes its distance along the dependent variable axis from the value predicted by the model.

Electronic supplemental material

Experimental data on folding rates of proteins in our protein set, their structural information, and the corresponding calculated topological parameters, can be found in Table I in the Electronic supplemental material on the Protein Science Web site.

Acknowledgments

We thank M. Michael Gromiha for stimulating discussions. This work is supported by NIH grant R01 GM073082-01A1 to D.J.J. and D.R.L.

Footnotes

Supplemental material: see www.proteinscience.org

Reprint requests to: Andrei Y. Istomin, Department of Computer Science and Bioinformatics Research Center, University of North Carolina at Charlotte, 9201 University City Boulevard, Charlotte, NC 28223, USA; e-mail: ayistomi@uncc.edu; fax: (704) 687-8197.

References

  1. Galzitskaya O.V. and Garbuzynskiy, S.O. 2006. Entropy capacity determines protein folding. Proteins 63: 144–154. [DOI] [PubMed] [Google Scholar]
  2. Galzitskaya O.V., Garbuzynskiy, S.O., Ivankov, D.N., and Finkelstein, A.V. 2003. Chain length is the main determinant of the folding rate for proteins with three-state folding kinetics. Proteins 51: 162–166. [DOI] [PubMed] [Google Scholar]
  3. Gong H., Isom, D.G., Srinivasan, R., and Rose, G.D. 2003. Local secondary structure content predicts folding rates of simple, two-state proteins. J. Mol. Biol. 327: 1149–1154. [DOI] [PubMed] [Google Scholar]
  4. Grantcharova V., Alm, E.J., Baker, D., and Horwich, A.L. 2001. Mechanisms of protein folding. Curr. Opin. Struct. Biol. 11: 70–72. [DOI] [PubMed] [Google Scholar]
  5. Gromiha M.M. 2003. Importance of native-state topology for determining the folding rate of two-state proteins. J. Chem. Inf. Comput. Sci. 43: 1481–1485. [DOI] [PubMed] [Google Scholar]
  6. Gromiha M.M. and Selvaraj, S. 2001. Comparison between long-range interactions and contact order in determining the folding rate of two-state proteins: Application of long-range order to folding rate prediction. J. Mol. Biol. 310: 27–32. [DOI] [PubMed] [Google Scholar]
  7. Huang J.-T., Cheng, J.-P., and Chen, H. 2007. Secondary structure length as a determinant of folding rate of proteins with two- and three-state kinetics. Proteins 67: 12–17. [DOI] [PubMed] [Google Scholar]
  8. Ikura T., Hayano, T., Takahashi, N., and Kuwajima, K. 2000. Fast folding of Escherichia coli cyclophilin A: A hypothesis of a unique hydrophobic core with a phenylalanine cluster. J. Mol. Biol. 297: 791–802. [DOI] [PubMed] [Google Scholar]
  9. Ivankov D.N. and Finkelstein, A.V. 2004. Prediction of protein folding rates from the amino acid sequence-predicted secondary structure. Proc. Natl. Acad. Sci. 101: 8942–8944. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ivankov D.N., Garbuzynskiy, S.O., Alm, E., Plaxco, K.W., Baker, D., and Finkelstein, A.V. 2003. Contact order revisited: Influence of protein size on the folding rate. Protein Sci. 12: 2057–2062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Jackson S.E. 1998. How do small single-domain proteins fold? Fold. Des. 3: R81–R91. doi: 10.1016/S1359-0278(98)00033-9. [DOI] [PubMed] [Google Scholar]
  12. Kabsch W. and Sander, S. 1983. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22: 2577–2637. [DOI] [PubMed] [Google Scholar]
  13. Kuznetsov I.B. and Rackovsky, S. 2004. Class-specific correlations between protein folding rate, structure-derived, and sequence-derived descriptors. Proteins 54: 333–341. [DOI] [PubMed] [Google Scholar]
  14. Makarov D.E. and Plaxco, K.W. 2003. The topomer search model: A simple, quantitative theory of two-state protein folding kinetics. Protein Sci. 12: 17–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Maxwell K.L., Wildes, D., Zarrine-Afsar, A., De Los Rios, M.A., Brown, A.G., Friel, C.T., Hedberg, L., Horng, J.-C., Bona, D., Miller, E.J., et al. 2005. Protein folding: Defining a “standard” set of experimental conditions and a preliminary kinetic data set of two-state proteins. Protein Sci. 14: 602–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Mirny L. and Shakhnovich, E. 2001. Protein folding theory: From lattice to all-atom models. Annu. Rev. Biophys. Biomol. Struct. 30: 361–396. [DOI] [PubMed] [Google Scholar]
  17. Naganathan A.N. and Munoz, V. 2005. Scaling of folding times with protein size. J. Am. Chem. Soc. 127: 480–481. [DOI] [PubMed] [Google Scholar]
  18. Plaxco K.W., Simons, K.T., and Baker, D. 1998. Contact order, transition state placement and the refolding rates of single domain proteins. J. Mol. Biol. 277: 985–994. [DOI] [PubMed] [Google Scholar]
  19. Plaxco K.W., Simons, K.T., Ruczinski, I., and Baker, D. 2000. Topology, stability, sequence, and length: Defining the determinants of two-state protein folding kinetics. Biochemistry 39: 11177–11183. [DOI] [PubMed] [Google Scholar]
  20. Prabhu N.P. and Bhuyan, A.K. 2006. Prediction of folding rates of small proteins: Empirical relations based on length, secondary structure content, residue type, and stability. Biochemistry 45: 3805–3812. [DOI] [PubMed] [Google Scholar]
  21. 2006. R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, http://www.R-project.org.
  22. Srinivasan R. and Rose, G.D. 1999. A physical basis for protein secondary structure. Proc. Natl. Acad. Sci. 96: 14258–14263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Zhanga L. and Sun, T. 2005. Folding rate prediction using n-order contact distance for proteins with two- and three-state folding kinetics. Biophys. Chem. 113: 9–16. [DOI] [PubMed] [Google Scholar]
  24. Zhou H. and Zhou, Y. 2002. Folding rate prediction using total contact distance. Biophys. J. 82: 458–463. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES