Abstract
A pharmacokinetic–pharmacodynamic mathematical model is developed for cellular pharmacology of chemotherapeutic drugs for which the decisive step towards cell death occurs at a point in the cell cycle, presumably corresponding to a cell cycle checkpoint. For each cell, the model assumes a threshold level of some intracellular species at that checkpoint, beyond which the cell dies. The threshold level is assumed to have a log-normal distribution in the cell population. The kinetics of formation of the lethal intracellular species depends on the drug, and on the cellular pharmacokinetics and binding kinetics of the cell. Specific models are developed for paclitaxel and for platinum drugs (cisplatin, oxaliplatin and carboplatin). In the case of paclitaxel, two separate mechanisms of cell death necessitate a model that accounts for two checkpoints, with different intracellular species. The model was tested on a number of in vitro cytotoxicity data sets for these drugs, and found overall to give significantly better fits than previously proposed cellular pharmacodynamic models. It provides an explanation for the asymptotic convergence of dose-response curves as exposure time becomes long.
Key words: carboplatin, cellular pharmacodynamics, chemotherapy, cisplatin, dose-response, mathematical model, oxaliplatin, paclitaxel, pharmacology, Taxol
INTRODUCTION
Mathematical models for cellular pharmacology of anticancer drugs have several applications in the optimization and individualization of therapy, and in screening for new drug combinations. Given the expense and time-consuming nature of clinical trials and animal studies, quantitative predictive models are useful in assessing different possible choices of dose and schedule for drug administration. Even for single agents, optimal therapeutic choices are not always known. For example, Briasoulis et al. (1) noted that the optimal schedule and dosage for administration of paclitaxel has not yet been defined. The use of drugs in combination, the development of complicated drug delivery systems such as liposomes or nanoparticles, and the administration of drug therapy in conjunction with other modalities such as hyperthermia, all further complicate the question of optimal delivery. These systems introduce new variables that can be adjusted in a clinical setting in order to achieve the most favorable response: for drugs in combination, the ratio of doses and sequence of delivery. While these additional variables represent new opportunities to optimize therapy, they also lead to an increased need for a rational basis for deciding among the possibilities, given limited data and the infeasibility of exploring more than a very small sample of available treatments through clinical trials or animal models. Mathematical models predicting response for a given cellular drug exposure over time provide an important part of such a rational basis.
Mechanistic models for drug pharmacology also offer potential for improved understanding of differences in response between in vitro and in vivo conditions. In vitro assays are used to screen for new drug combinations, and are regarded as having great potential as a means for individualizing therapy (2). A key aspect in realizing the potential of this approach will be improved methods for predicting in vivo response based on in vitro data. It is known that cells in vivo generally have a lower proliferation rate, an altered rate of drug uptake, and a different level of target expression than cultured cells. The distribution of sensitivity in vivo may be altered, and may shift in time, as resistance develops. In mechanistic models for pharmacodynamics, the effect of these separate factors on response can be tested explicitly, offering the potential for predicting how in vitro-in vivo differences will affect response.
Several mathematical models for cellular pharmacology have been proposed in the literature. Some models are drug-nonspecific (intended to apply to all drugs), while others are drug-specific. El-Kareh and Secomb (3) reviewed the drug-nonspecific models including the AUC model, which has both an exponential form (4) and a Hill equation form (5,6), the CnT model (7–9), the model of Levasseur et al. (10) and the exponential-kill model of Gardner (11). Several of these models are summarized in Table I. As noted by El-Kareh and Secomb (6,12), these models have in common that they predict that dose-response curves for a given exposure time continue to shift towards lower concentration (i.e., IC50 continues to decrease) as the exposure time increases. In other words, they predict that response at any concentration continues to improve as the exposure time gets longer. This assumption appears to be contradicted by experimental data for most chemotherapeutic drugs in widespread clinical use, as can be seen from the data of Au et al. (13) for paclitaxel, Eliaz et al. (14) and Vrignaud et al. (15) for doxorubicin, Minderman et al. (16) for irinotecan, and Parsons (17) for melphalan. All these data sets show the response asymptotically approaching a limit as exposure time becomes long.
Table I.
Summary of Literature Models for Cellular Pharmacodynamics of Chemotherapeutic Drugs
| Name of Model | Reference | Equations | No. of Fitted Parameters | Fitted Parameters |
|---|---|---|---|---|
| Extracellular AUC model—Hill form | (4) |

|
2 | A, m |
| Extracellular AUC model—exponential form | (5) |

|
1 | K |
| Extracellular C n T model | (7,76) |

|
3 | A,n,m |
| Levasseur et al. model | (10) |
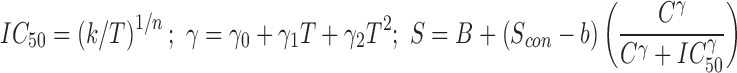
|
7 | B, S con, k, n, γ 0, γ 1, γ 2 |
| Peak bound intracellular model (cisplatin) | (12) |
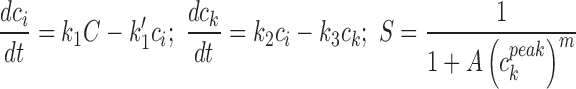 where where  is the peak value of ck over the period of exposure is the peak value of ck over the period of exposure |
4 or 2a | A, m, k 1′, k 3 (k 1 and k 2 are not independent; can be set to 1) |
| Cell cycle checkpoint model (paclitaxel) | Present study |
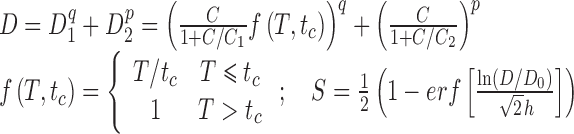
|
7; 3–6 in certain casesb | D 0, h, q, p, C 1, C 2, t c |
| Cell cycle checkpoint model (platinum drugs) | Present study |
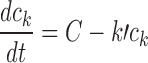 for t < T; for t < T; 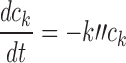
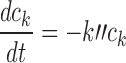 for t > T for t > T
|
5; 2–4 in certain casesc | k′, k″, D 0, h, t c |
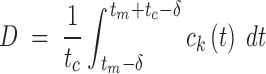 ; δ chosen to maximize integral ; δ chosen to maximize integral 
| ||||
Peak intracellular model (k″ = 0 case): 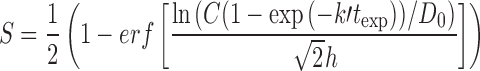
| ||||
Extracellular AUC model lognormal form (k′=k″ = 0 case): 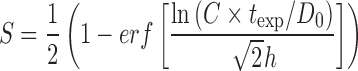
|
C or C(t) (if time varying) extracellular concentration, t time, T total exposure time, S survival relative to untreated controls
aThe two parameters relating to cellular uptake may be obtained separately if cellular uptake data is available
bIn some cases, the cell cycle time t c and the saturation parameter C 1 are obtainable from separate experimental data. Also, for some data sets saturation for the second mechanism occurs outside the observed range of concentrations, effectively reducing C 2 to zero or infinity (see text)
cExperimental values of the cell cycle time may be available; the model may reduce to one of the simplified forms
Drug-specific models have included the transit compartment model of Lobo and Balthasar (18) for methotrexate, the DNA crosslink model of Miyagi et al. (19) for nedaplatin, and the peak concentration models of El-Kareh and Secomb (6,12) for cisplatin and doxorubicin. The model of Lobo and Balthasar (18) involves a rate of cell kill that depends on the concentration of a cellular drug species. This concentration is related through a series of linear kinetic equations to the extracellular concentration; therefore, in common with the above-mentioned drug-nonspecific models, the Lobo and Balthasar (18) model predicts continually increasing response with increasing exposure time. A similar transit-compartment model has successfully fit in vivo data (20), where response depends on a number of additional factors besides cellular pharmacodynamics, including drug transport and plasma pharmacokinetics. Of these models, only the peak concentration models of El-Kareh and Secomb (6,12) and the DNA crosslink model of Miyagi et al. (19) are able to reproduce the asymptotic convergence to a single limiting dose-response curve at long exposure time.
The peak concentration models of El-Kareh and Secomb (6,12) are able to satisfactorily describe a number of literature data sets, but they offer no means of predicting how shifts in the distribution of cells over the cell cycle affect response. Understanding such cell cycle effects is important in modeling response to drug combinations, as many chemotherapeutic drugs cause accumulation of cells in one cell cycle phase, often resulting in a significant effect on response to another drug used in combination. This effect may take the form of schedule dependence and possibly antagonism (21), if cells fail to reach the cell cycle phase where the second drug is active. Further, proliferative status appears to be an important factor in drug-induced cell kill, even for drugs not generally classified as “cell-cycle specific” or “cell-cycle phase-specific”, such as cisplatin (22,23). Quiescent and slowly proliferating cells have significantly lower response to nearly all conventional chemotherapeutic drugs (24,25). Given this importance of cell cycle progression, there is a need for cellular pharmacologic models that include the effects of distribution of cells over the cell cycle. In this paper, the simultaneous cellular pharmacokinetic-pharmacodynamic approach adopted by El-Kareh and Secomb (6,12) will be applied to develop mathematical models for cellular pharmacology that include cell cycle effects, for the anticancer drugs paclitaxel, cisplatin, oxaliplatin and carboplatin.
The cell cycle phase-specific models of Gardner (11), Lobo and Balthasar (18), as well as several other mathematical models developed to describe tumor response to cell cycle specific drugs (26–29), have in common the assumption that during a specific phase of the cell cycle of finite duration, cells are drug sensitive. They assume a rate of cell kill that depends on the instantaneous concentration of either extracellular drug or (in the Lobo and Balthasar (18) transit compartment model case) some intracellular species, and that applies throughout this phase. The data of Donaldson et al. (30) offer a different picture of cell cycle effects for the drugs cisplatin and paclitaxel. There, the IC50 is plotted vs. length of time between resumption of cycling, for cells that were initially quiescent, after a pulse exposure of 1 h. For cisplatin, the IC50 shows a single minimum over the cell cycle time, and for paclitaxel, there are two minima, apparently corresponding to two mechanisms of paclitaxel cell kill (31,32). As Donaldson et al. (30) noted, this data is suggestive not of a sensitive phase during which cell kill occurs, but rather that cell death is associated with traversal of a particular point in the cell cycle while cellular drug is present. This observation of a critical point in the cell cycle at which the cell embarks on a lethal pathway forms the basis for cell cycle effects in the models developed below. Because the critical point probably corresponds to what is generally called a “cell cycle checkpoint” (a point in the cell cycle at which a cell either continues cycling or embarks on the apoptosis pathway), the models developed here will be referred to as “cell cycle checkpoint models”.
MATERIALS AND METHODS
Model Assumptions
The basic assumptions of the pharmacokinetic–pharmacodynamic model are as follows: (1) death of an individual cell occurs if some measure D of drug-induced damage exceeds a threshold level for that cell; (2) the thresholds are heterogeneously distributed in the cell population, with a probability density P(D); (3) the damage D is defined as the maximal value of intracellular concentration ck of the lethal form of the drug that is reached at a specific point (checkpoint) in the cell cycle. The model is a generalization of the peak-concentration models of El-Kareh and Secomb (6,12), in which the damage D was defined as the peak value over time of the concentration, independent of the cell cycle, i.e., D = ck(tm) where tm is the time of maximum concentration. Model notation is summarized in Table II.
Table II.
Notation
| Symbol | Meaning |
|---|---|
| AUC | Area under the extracellular concentration-time curve |
| C | Extracellular concentration during exposure |
| C 1 | Cellular pharmacodynamic parameter for paclitaxel giving concentration at which binding of lethal species for first cell kill mechanism reaches saturation |
| C 2 | Cellular pharmacodynamic parameter for paclitaxel giving concentration at which binding of lethal species for second cell kill mechanism reaches saturation |
| c i | Total intracellular concentration of drug |
| c k | Concentration of the lethal cellular species, that is, the cellular species giving rise to cell kill |
| δ | Time shift used to obtain limit of integration interval for integral average of lethal species concentration, chosen so as to obtain the interval over which the exposure level was highest |
| D | Drug-induced cellular damage |
| D 0 | Model parameter, depends on cell line; measure of average drug sensitivity of cell line |
| D 1 | Damage from first mechanism of cell kill, when two mechanisms are present |
| D 2 | Damage from second mechanism of cell kill, when two mechanisms are present |
| F | Function appearing in paclitaxel model; fraction of cells that were exposed to drug during critical point of cell cycle |
| h | Model parameter, depends on cell line; measure of heterogeneity in drug sensitivity of cell line |
| IC50 | Drug concentration required for 50% survival relative to controls |
| k | Cellular pharmacokinetic parameter giving rate constant for aquation of cisplatin |
| k′ | Cellular pharmacokinetic parameter giving rate constant for equilibration of extracellular and intracellular concentrations |
| k″ | Cellular pharmacokinetic parameter giving rate constant for repair of DNA platinum lesions |
| M | In C n T model: exponent describing steepness of dose-response curve, that is, heterogeneity of the chemosensitivity of the cell population |
| n | Exponent in C n T model, weighting the importance of concentration vs. exposure time for drug response |
| P(D) | Probability density function for the lethal threshold damage level |
| p | In additive damage model for two cell kill mechanisms, exponent weighting damage term corresponding to second mechanism. |
| q | In additive damage model for two cell kill mechanisms, exponent weighting first damage term corresponding to first mechanism. |
| S(D) | Survival relative to controls as a function of cellular damage |
| T | Duration of extracellular drug exposure at constant concentration |
| t c | Cell cycle time (depends on cell line) |
| t m | Time at which maximum value of c k occurs |
These model assumptions are based on observed features of experimental in vitro dose-response data. In such experiments, all cells are subjected to the same growth conditions and drug exposure. The fact that the resulting cell kill is a smooth, sigmoidal function of drug exposure implies heterogeneity in cellular response, represented here by the distribution P(D) of the damage threshold. If all cells succumbed at the same drug exposure levels, dose-response curves would be step functions. For several drugs including paclitaxel (13) and cisplatin (33), the dose-response curves converge to a limiting curve as exposure time becomes large. Such behavior is inconsistent with models in which cell kill depends on the time integral of a function of concentration, because increasing exposure time would then always increase cell kill. However, the convergence of dose-response curves at long exposure times is predicted by peak-concentration models in which intracellular drug concentration approaches a limiting value with prolonged exposure (6,12).
Distribution of Threshold for Cell Kill
If the threshold damage level D for cell kill has a probability distribution P(D), the survival fraction (relative to controls) is given by
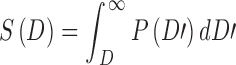 |
1 |
Previously, survival curves have frequently been represented using Hill-type equations (6,10,12):
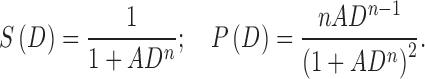 |
2 |
However, these equations have the unrealistic property that the probability density goes to infinity rather than to zero as D approaches zero, if n < 1. Low values of n correspond to highly heterogeneous populations. To avoid this problem, a lognormal probability density is assumed here, so that P(D) → 0 as D → 0 for all parameter values:
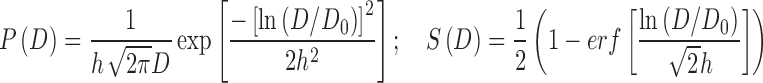 |
3 |
where D0 is a constant such that ln(D/D0) has zero mean, and h2 is the variance of ln(D/D0), a measure of population heterogeneity. This distribution gives sigmoidal dose-response curves similar to those given by the Hill-type equation.
Effect of Cell Cycle
In an asynchronous cell population, cells pass through the checkpoint at different times, which do not generally coincide with the instant of maximum concentration. To take this into account, the damage D is defined as the average over all cells of the maximum value of ck(t) occurring at a checkpoint. Under the assumptions that all cells cycle with a fixed cycle time tc, that the phase shifts of cells are uniformly distributed over the cell cycle, and that ck(t) rises to a maximum at tm and then decays, it follows that
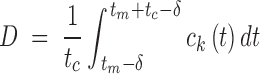 |
4 |
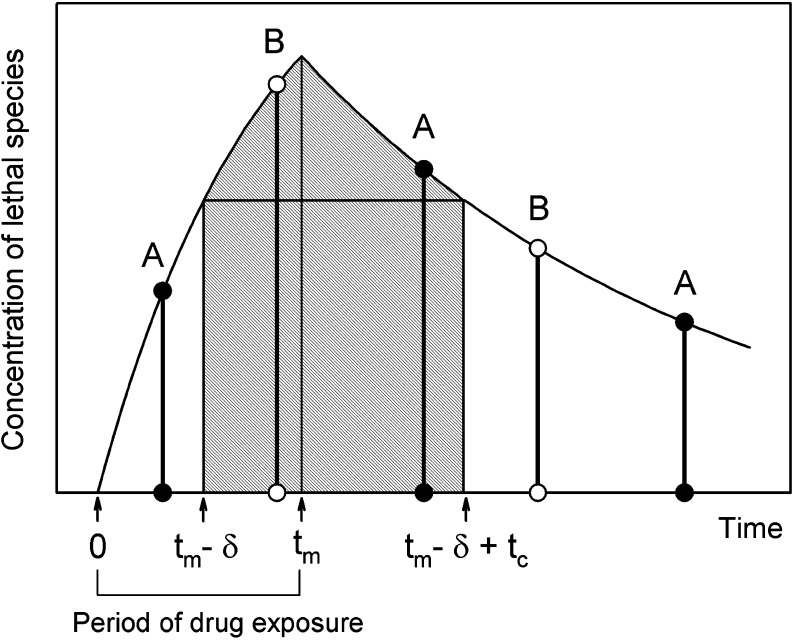
where δ is chosen to maximize the integral, or, equivalently, to satisfy the condition that ck(tm − δ) = ck(tm + tc − δ). Typically, tm = T, the exposure time, under in vitro conditions. As illustrated in Fig. 1, ck(t) is averaged over an interval that includes all possible checkpoints at which ck is maximal for some cell in the population.
Fig. 1.
Schematic diagram illustrating definition of cell damage in the checkpoint model. The y-axis represents the concentration of the cellular bound species giving rise to the cytotoxic effect; because of the kinetics of uptake and binding this is not the same as extracellular concentration. A and B: times at which cells A and B pass through successive cell cycle checkpoints. Hatched region: interval of integration in Eq. 3. This interval includes all possible checkpoints at which the concentration c k of the lethal species is maximal for a particular cell. The time t m at which lethal species concentration peaks is equal to the exposure time T for the cases modeled in this study, because intracellular concentrations decay rapidly when extracellular exposure is stopped. For a general drug, however, t m may be larger than T, depending on the cellular pharmacokinetics. Notation in Table II
Cellular Pharmacokinetics for Paclitaxel
Kuh et al. (34) examined the uptake of paclitaxel by human breast MCF tumor cells in monolayer cultures and found that the intracellular concentration reached a plateau within 3 h of exposure. The cytotoxicity data sets considered here (13,35,36) are for exposure times of 3 h or longer, for which this equilibration can be approximated as instantaneous. The observed plateau level depended nonlinearly on extracellular concentration, implying that the uptake was saturable. Based on these observations, the relationship between intracellular concentration ci and the extracellular concentration C is here assumed to be:
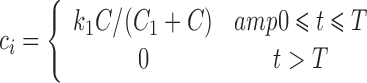 |
5 |
where k1 and C1 are constants that are determined by fitting cytotoxicity data and T is the exposure time. This is a simplified version of the model developed by Kuh et al. (34), assuming equilibrium conditions and neglecting depletion and protein binding of the drug in the extracellular medium and paclitaxel-induced amplification of the expression of its own cellular target tubulin. Information regarding the kinetics of formation of the active bound intracellular species of paclitaxel is not available. Here, we assume for simplicity that the concentration of this lethal species is proportional to the total intracellular concentration. The constant of proportionality can be absorbed into other unknown constants, so we let ck = ci. From Eq. 4, the damage is:
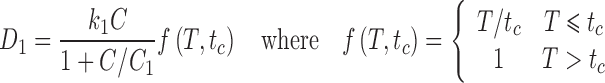 |
6 |
Several studies show that paclitaxel has two major mechanisms of action (31,32,37,38), corresponding to blocks occurring at checkpoints in the G1 and G2M phases of the cell cycle. Torres and Horwitz (38) found that these mechanisms were concentration-dependent, with a transition at an extracellular concentration around 9 nM. Sena et al. (31) found that the G2M block mechanism did not become significant until the concentration was at least 50 nM. The dose-response curves of Au et al. (13) show a substantial decline in survival with increasing extracellular concentration in the range 10–50 nM. This decline occurs at all the observed exposure times (3–96 h), suggesting that the G2M block mechanism is not strongly dependent on exposure time. The study of Donaldson et al. (37) offers an explanation for this. It was found that additional washes significantly increased the IC50 of G1/S populations, but had no effect on G2M populations, implying that the lesions formed in mitotic cells were stable. In such a case, the effect of the exposure is the same whether it occurs before or during the critical cell cycle point in an actively cycling cell. Averaging over phase shift of the cell population is not required. A damage term consistent with this is
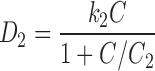 |
7 |
Multiple Damage Mechanisms
The pharmacodynamic model for paclitaxel requires a method to estimate the combined effect of two damage mechanisms, Eqs. 6 and 7. As in our study of doxorubicin (6), we assume that the effect can be described by the “additive damage” model, in which total damage is represented as an exponent-weighted sum of damage from the two mechanisms:
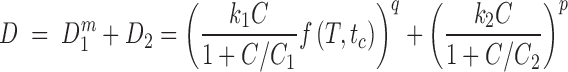 |
8 |
with survival again given by Eq. 3. The rationale for the exponents q and p in this expression is that they allow for different levels of heterogeneity in the thresholds for the two mechanisms. The final model equation obtained by combining Eqs. 8 and 3 is shown explicitly in Table I. An alternative “independent damage” model was also considered:
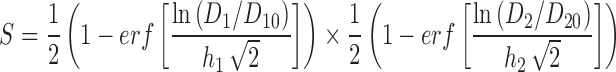 |
9 |
where D10, D20, h1 and h2 are constants. This model predicts cell kill if the two damage mechanisms act completely independently: That is, not only do they have no target in common, but also each damage mechanism does not weaken the cell in a way that creates greater susceptibility to the other damage mechanism. With this assumption, the probability of survival from both damage mechanisms is, by basic probability theory, the product of the survivals for each one by itself. Therefore, S = S1 × S2, where S1 and S2 are the survival if only damage D1 or damage D2, respectively, is present, from Eq. 3. This independent survival model was used by Kern (39) for describing the combined effect of two different drugs.
Cellular Pharmacokinetics for Platinum Drugs
To determine ck(t) for platinum drugs, cellular pharmacokinetic models are used, based on cell uptake data of Troger et al. (33) for cisplatin. In the cases of oxaliplatin and carboplatin, no comparable data set for cellular uptake including a range of exposure times and concentrations could be found. However, there is much evidence for similarity in the mechanisms of uptake of platinum drugs. Hector et al. (40) and Mishima et al. (41) found that cellular uptake of oxaliplatin, like that of cisplatin, is linear with extracellular concentration. The aquated species of cisplatin and carboplatin that are assumed active (the positively charged diaquo compound) are identical. Binks and Dobrota (42) found that uptake of carboplatin and cisplatin was nonsaturable up to a concentration of 1.0 mM. Based on these considerations, we assume here that a single cellular pharmacokinetic model applies to all three platinum drugs. This is further supported by Ghezzi et al. (43) who studied the three platinum drugs and concluded that the data primarily supported the same mechanism of passive diffusion through the membrane for all three drugs.
We previously developed a model for cisplatin uptake (12) in which rates of uptake and efflux are linearly dependent on the extracellular concentration C and the unbound intracellular concentration ci:
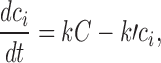 |
10 |
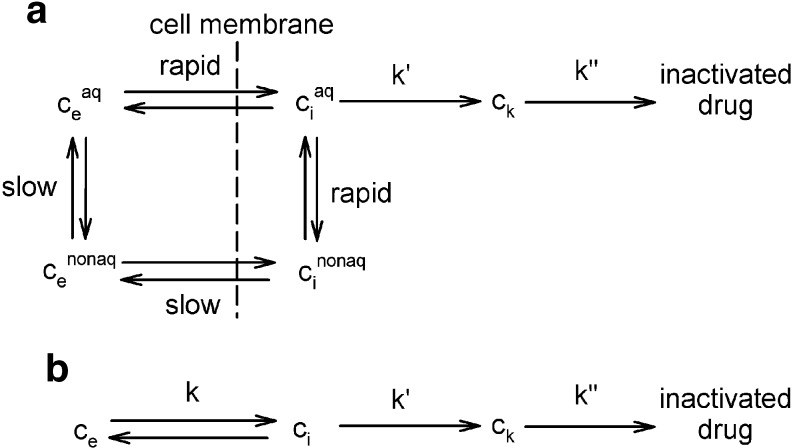
based on the assumption that cisplatin uptake occurs by passive diffusion. While this assumption has been questioned (44), the linearity of cisplatin uptake with extracellular concentration is nevertheless experimentally well-established (12). Cisplatin is active in its aquated form; the aquation reaction is the rate-limiting step (44) and occurs slowly at physiological (i.e., extracellular) pH, but more rapidly at intracellular pH. The aquated form crosses the cell membrane much faster than neutral cisplatin. These kinetics are summarized in Fig. 2a. The success of Eq. 10 in describing cisplatin uptake (12) suggests the use of simplified kinetics for total cisplatin (Fig. 2b). Figure 2a shows that intracellular non-bound platinum concentrations rapidly go to zero once extracellular concentration goes to zero, firstly because the aquated species crosses the membrane rapidly, and secondly because intracellular platinum is readily aquated. Thus, it is assumed here that ci goes instantaneously to zero when ce goes to zero. This assumption was also made in our previous study (12), although a detailed explanation was not provided there.
Fig. 2.
a Schematic depiction of cellular pharmacokinetics of cisplatin. Aquated form is active. Aquation is slow in the extracellular environment at physiological pH, but rapid intracellularly. Non-aquated cisplatin is exchanged more slowly than the aquated form. b Simplified kinetics assumed in present model. Total cisplatin is considered
With Eq. 10 representing the kinetics of the rate-limiting step of cisplatin aquation, the subsequent formation of the lethal intracellular platinum species (through binding with DNA and adduct formation) occurs much faster, so that the concentration ck of this lethal species is essentially proportional to the intracellular free drug concentration. As before, we let ck = ci. Once drug exposure is discontinued, the kinetics governing the lethal species concentration ck is no longer described by Eq. 10, since the process is now dominated not by formation of the hydrolyzed species, but rather by the repair of DNA lesions. As in our previous model, this repair is assumed to be governed by first-order kinetics:
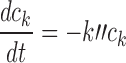 |
11 |
The DNA repair after exposure is relevant to the response because some cells may reach the critical cell cycle phase after exposure is discontinued. Their response depends on the length of the interval between cessation of exposure and the critical cell cycle point, during which DNA lesions are being repaired. Eqs. 10 and 11 lead to the following equation for the lethal species concentration:
 |
12 |
Equations 3, 4 and 12 form the cellular pharmacokinetic–pharmacodynamic model for the platinum drugs in the case of exposure at constant extracellular concentration C for a period T followed by washing and drug-free incubation. The case of variable extracellular concentration, such as occurs in vivo, can be modeled by integrating Eqs. 10 and 11 with the time-varying function C(t) substituted for constant C.
In the special case where the parameter k″ is very small, so that the time scale 1/k″ for repair is very long compared to the cell cycle time, this model simplifies to a “peak intracellular” model similar to the one discussed by El-Kareh and Secomb (12), the only difference being that the log normal form of Eq. 3 is used here instead of a Hill equation (Eq. 2). In this special case, cytotoxicity depends only on the peak intracellular concentration achieved over the entire exposure, and this peak is reached at t = texp. A further reduction of the model occurs in the case when the time scale for equilibration of cellular uptake (1/k′) is much longer than the exposure times texp. In such cases the model reduces to an extracellular AUC model. The equations for these cases are shown explicitly in Table I along with the full cell cycle checkpoint model for platinum drugs.
Parameter Estimation
The mathematical models for cellular pharmacology described above were fit to a number of data sets, including those of Troger et al. (33), Rupniak et al. (45) and Kurihara et al. (46) for cisplatin; Kornmann et al. (47) for oxaliplatin, Levasseur et al. (10) for cisplatin and paclitaxel; Mohammed and Retsas (48) for all three platinum drugs; and Au et al. (13), Riccardi et al. (35) and Hassan et al. (36) for paclitaxel. The data points were extracted from these publications by manually reading the plots, with the exception of the data of Hassan et al. (36), which the author provided in numerical form. In that data set, the relative survival values for several exposure times were significantly above 1 at low concentrations. This unrealistic behavior was interpreted as resulting from random errors in the measured control survival values at zero concentration. Therefore, the relative survival values for the five lowest concentrations were averaged and this value was used to renormalize the data.
Not all the parameters used in the derivation of the above models are independent. In the case of the independent model, it can be shown that the parameters D10 and D20 in Eq. 9 can be set to 1 without loss of generality, for the case here in which the kinetic parameters k1 and k2 appearing in Eqs. 6 and 7 are estimated from cytotoxicity data, because cellular uptake data is unavailable. For the additive damage model, it can be shown that k1 and D0 are not independent. Therefore, the choice was made to set k1 = 1, and the notation of the additive damage model was simplified to that of Table I. For paclitaxel, then, in the most general case, seven parameters remain to be fit. However, for all but one cell line, the parameter h could be set to 1. The rationale for this simplification is that if at any exposure time and concentration, one of the two cell damage mechanisms is dominant, the parameter h becomes redundant because it can be absorbed into the values of the exponents q and p. Only in the transition regime where both mechanisms are of the same magnitude must h be fitted as an independent parameter. This transition regime was found in all but one case to not contribute significantly. Further, for several cell lines, experimental values of the cell cycle could be used so that tc was not fitted. Finally, an experimental value for the parameter C1 (the saturation parameter for cellular uptake of paclitaxel) is given by Kuh et al. (34) as 4.93 nM for MCF-7 cells. While this parameter can be expected to vary across cell lines, it was found that this value applied to many of the cell lines considered here. For some cell lines, the data lay in a regime where saturation of the second mechanism was never observed (meaning that effectively C2 = infinity), or occurred at a concentration lower than the range sampled (effectively C2 = 0). Following on these various considerations, the number of fitted parameters for the paclitaxel model ranged from three to seven.
For the platinum drugs, k/k′ in Eq. 12 was set equal to 1 without loss of generality, leaving five fitted parameters. For most cell lines, an experimental value of tcyc from the literature was used, leaving only four parameters to be fit. The parameters were estimated from the cytotoxicity data using the minimization routine “NMinimize” in the software package Mathematica 5.0 (Wolfram Research, Inc., Champaign, IL, USA). The criterion for best-fit was minimization of the root-mean-square deviation of the predicted from the experimental values for survival relative to controls. Because the values for survival relative to controls lie between 0 and 1, and all data sets used here did not include the very low survival regime, no weighting was used. In some cases, convergence to the best fit values could be accelerated by first using the Hill-type model, and then using the pharmacokinetic parameters obtained from this fit as initial estimates for the lognormal model.
Confidence regions at 95% confidence level were obtained for all parameter fits using the log-likelihood method discussed by Vugrin et al. (49). For multiparameter nonlinear regression, the confidence regions are in general not rectangular (49). To obtain a confidence interval for each parameter, first the parameter was varied alone, with the values of other parameters fixed, and the log-likelihood test was applied. Because the residual error function is nonlinear, the confidence interval obtained by this method was generally not symmetrical about the best-fit value of the parameter. To account for the non-rectangular shape of the confidence region, a second estimate of the confidence interval was obtained as follows. The residual error was linearized about the point of best fit in parameter space; as discussed by Vugrin et al. (49), this approximates the confidence region as ellipsoidal. The matrix of second derivatives of the residual error function with respect to the parameters was computed. The eigenvectors of this matrix represented the major and minor axes of the ellipsoidal linearized confidence region. The extreme values of the parameters at the vertices of the ellipsoid were then estimated by determining the point in parameter space along the line determined by each eigenvector at which the residual error equaled its 95% confidence value. The final confidence interval for each parameter reported in the tables represents the maximum of the ranges determined by the two methods described. This approach corresponds to projecting the multidimensional confidence region onto the parameter axes. It is important to note that reporting ranges on individual parameters represents a very conservative estimate, since the resulting rectangular confidence region is much larger than the ellipsoidal region obtained by the log-likelihood method (49).
RESULTS
Results for Paclitaxel
Table III shows RMS (root mean square) deviations between model values and experimental data for paclitaxel, for 12 different cell lines, including a resistant one. The corresponding parameter values are shown in Table IV. The experimental data are from the studies of Au et al. (13), Levasseur et al. (10), Riccardi et al. (35) and Hassan et al. (36). The models considered are the cell cycle checkpoint model with the additive damage (Eq. 8) and the independent damage (Eq. 9) assumptions, the extracellular AUC Hill model for which S = 1/(1 + A (CT)m), the CnT Hill model for which S = 1/(1 + A (CnT)m) and the single Hill model of Levasseur et al. (10). [The cell-cycle phase-specific model of Gardner (11) was not included because inconsistencies in the mathematical formulation could not be readily resolved.] In virtually every case, the cell cycle checkpoint model with additive damage gives the lowest RMS deviation from the corresponding experimental data.
Table III.
RMS Deviations between Experimental Data and Model Predictions for Paclitaxel Acting on Different Tumor Cell Lines
| Tumor Cell Line | Data Source | Cell Cycle Checkpoint Additive Damage | Cell Cycle Checkpoint Independent Damage | Extracellular AUC (Hill) | C n T (Hill) | Levasseur et al. (10) single Hilla |
|---|---|---|---|---|---|---|
| RT4 bladder (33 h) | (13) | 0.0444 (33 h) | 0.0445 (35.2 h) | 0.0913 | 0.0900 | 0.0510 |
| MCF-7 breast (30 h) | (13) | 0.0401 (12.3 h) 0.0521 (30 h) | 0.0465 (24.3 h) | 0.101 | 0.101 | 0.0647 |
| SKOV-3 ovarian (25 h) | (13) | 0.0345 (36.3 h) 0.0501 (25 h) | 0.0371 (35.1 h) | 0.0806 | 0.0788 | 0.0561 |
| FaDu pharynx (22 h) | (13) | 0.0312 (32.9 h) 0.0476 (22 h) | 0.0295 (29.2 h) | 0.0818 | 0.0782 | 0.0640 |
| DU145 prostate (24 h) | (13) | 0.0384 (40.8 h) 0.0878 (24 h) | 0.0547 (73.0 h) | 0.0735 | 0.0733 | 0.0461 |
| PC3 prostate (24 h) | (13) | 0.0402 (24 h) | 0.0309 (27.5 h) | 0.200 | 0.0867 | 0.0567 |
| BE(2)M17 neuroblastoma | (35) | 0.0577 (41.4 h) | 0.0589 (45.6 h) | 0.127 | 0.119 | 0.0961 |
| CHP100 neuroblastoma | (35) | 0.0503 (63.5 h) | 0.0922 (46.3 h) | 0.154 | 0.154 | 0.116 |
| SH-SY5Y neuroblastoma | (35) | 0.0623 (>80.0 h) | 0.0685 (132.4 h) | 0.193 | 0.0774 | 0.146 |
| U937 GTB lymphoma | (36) | 0.0944 (37.1 h) | 0.0956 (30 h) | 0.135 | 0.134 | 0.0782 |
| A2780 human ovarian wild type (18 h) | (10) | 0.227 (18 h) | 0.270 (1.94 h) 0.233 (18 h) | 0.261 | 0.249 | 0.158 |
| A2780/DX5B human ovarian resistant (20 h) | (10) | 0.0899 (20 h) | 0.0871 (20 h) | 0.198 | 0.136 | 0.136 |
When an experimental value for the cell cycle time of untreated cells in vitro is available from the literature, it is listed in parentheses after the cell line name. For the cell cycle checkpoint models, which include cell cycle time tc as a parameter, the value of t c corresponding to the RMS deviation is indicated in parentheses. In some cases, the RMS deviation was lower at a fitted cell cycle time than at the experimentally measured value, and both results are indicated.
aOne parameter (E con) of the Levasseur et al. (10) model was set equal to 1 to ensure that survival at zero concentration equals 1. A different value could be used to correct for errors in the control value used to normalize the data
Table IV.
Summary of parameter values for cellular pharmacodynamic model for paclitaxel
| Cell Line | Cell Cycle Checkpoint Model RMS Deviation | No. of Fitted Parameters | C 1 (nM) | C 2 (nM) | q | p | log D 0 | h | t c (h) | Source for t c Estimate |
|---|---|---|---|---|---|---|---|---|---|---|
| RT4 bladder (33 h) | 0.0444 | 4 | 4.93a | 207.1 (71.0,492.) | 1.841 (1.39,2.51) | 0.5570 (0.412,0.715) | 2.259 (1.81,2.93) | 1b | 33.0b | (13) |
| MCF-7 breast (30 h) | 0.0401 | 6 | 0.04999 (0.0497, 0.0503) | 0.2061 (0.106,0.207) | 35.84 (35.8,35.9) | 68.27 (68.1,68.5) | −108.2 (−108.4,−108.1) | 1b | 12.3 (12.1,12.5) | Fit |
| SKOV-3 ovarian (25 h) | 0.0345 | 5 | 4.93a | 2576. (740,∞) | 1.888 (1.59,2.24) | 0.3439 (0.313,0.378) | 1.519 (1.41,1.63) | 1b | 36.3 (29.4,46.3) | Fit |
| FaDu pharynx (22 h) | 0.0312 | 5 | 4.93a | 1.007 (1.00,1.01) | 0.8533 (0.743,0.983) | 85.48 (36.7,147) | −0.1417 (−0.230,−0.0543) | 1b | 32.9 (28.2,38.4) | Fit |
| DU145 prostate (24 h) | 0.0384 | 4 | 4.93a | ∞c | 2.497 (2.27,2.67) | 0.5242 (0.459,0.552) | 2.205 (2.07,2.27) | 1b | 40.8 (35.2,49.9) | Fit |
| PC3 prostate (24 h) | 0.0402 | 3 | 4.93a | ∞ c | 2.418 (2.11,2.79) | 0.3941 (0.321,0.485) | 1.342 (1.24,1.48) | 1b | 24.0b | (13) |
| BE(2)M17 neuroblastoma | 0.0577 | 6 | 11.00 (5.00,18.7) | 0.2416 (0.0,2.81) | 1.116 (0.586,1.60) | 0.5393 (0,16.0) | 1.091 (0.234,2.04) | 1b | 41.4 (28.0,59.0) | Fit |
| CHP100 neuroblastoma | 0.0503 | 5 | 4.93a | 0.8882 (0.375,1.37) | 2.563 (1.04,8.83) | 1.744 (0.471,4.16) | −0.004584 (−0.929,1.13) | 1b | 63.5 (37.2,87.2) | Fit |
| SH-SY5Y neuroblastoma | 0.0623 | 7 | 2.258 × 10−7 (9.24 × 10−8, 2.99 × 10−7) | 236.4 (25.1,∞) | 0.00052551 (0.00050,0.000563) | 0.0001666 (0.0000999,0.000270) | 0.6891 (0.68907,0.68922) | 0.0002204 (0.000126, 0.000428 | >80d | Fit |
| U937 GTB lymphoma | 0.0944 | 6 | 80.24 (34.7,135) | 2.065 (1.49,2.65) | 2.244 (1.26,3.18) | 4.781 (3.10,6.27) | 3.888 (2.27,5.31) | 1a | 37.1 (25.2,57.2) | Fit |
| A2780 human ovarian wild type (18 h) | 0.227 | 3 | 4.93a | 0e | 0.7168 (0.422,1.24) | 0.8342 (0.0494,∞) | −0.1464 (−0.461,0.168) | 1a | 18.0b | (10) |
| A2780/DX5B human ovarian resistant (20 h) | 0.0899 | 4 | 603.10 (478,833) | ∞c | 1.877 (1.73,1.97) | 0.8598 (0.783,0.923) | 10.64 (10.1,11.1) | 1b | 20.0b | (10) |
Units of parameters are chosen so that extracellular concentration C is in nanomolars, time t is in hours, and D and D 0 are dimensionless. The 95% confidence intervals are given below the fitted value in parentheses
aParameter value from (34)
bParameter was specified, not fit
cSaturation did not occur over the range of concentrations sampled, making C 2 effectively infinity
dAsymptotic convergence of dose-response curves did not occur within the range of exposure times sampled by the data; therefore only lower bound on t c could be obtained
eSaturation occurred at a concentration lower than the entire range sampled, making C 2 effectively 0
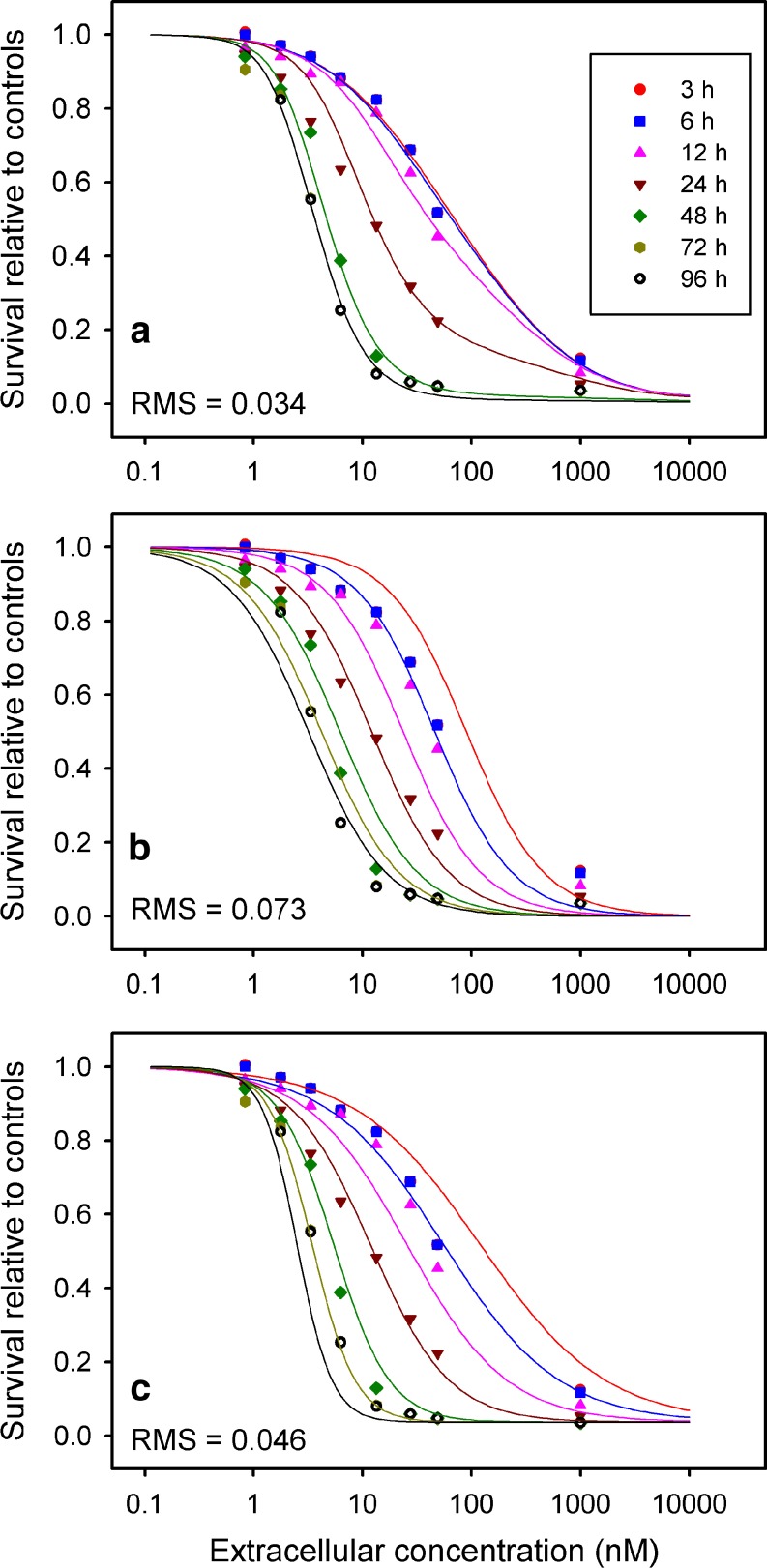
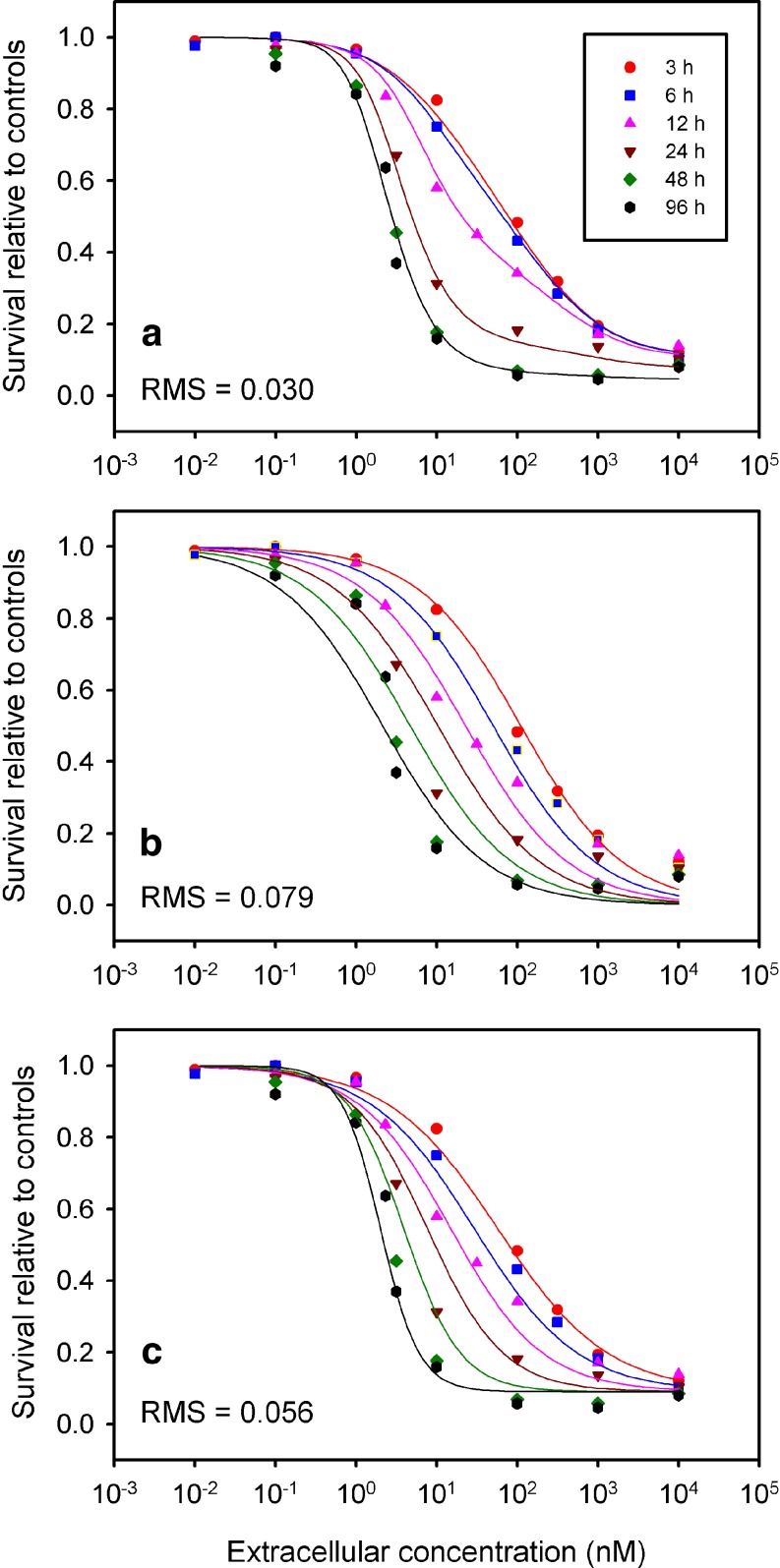
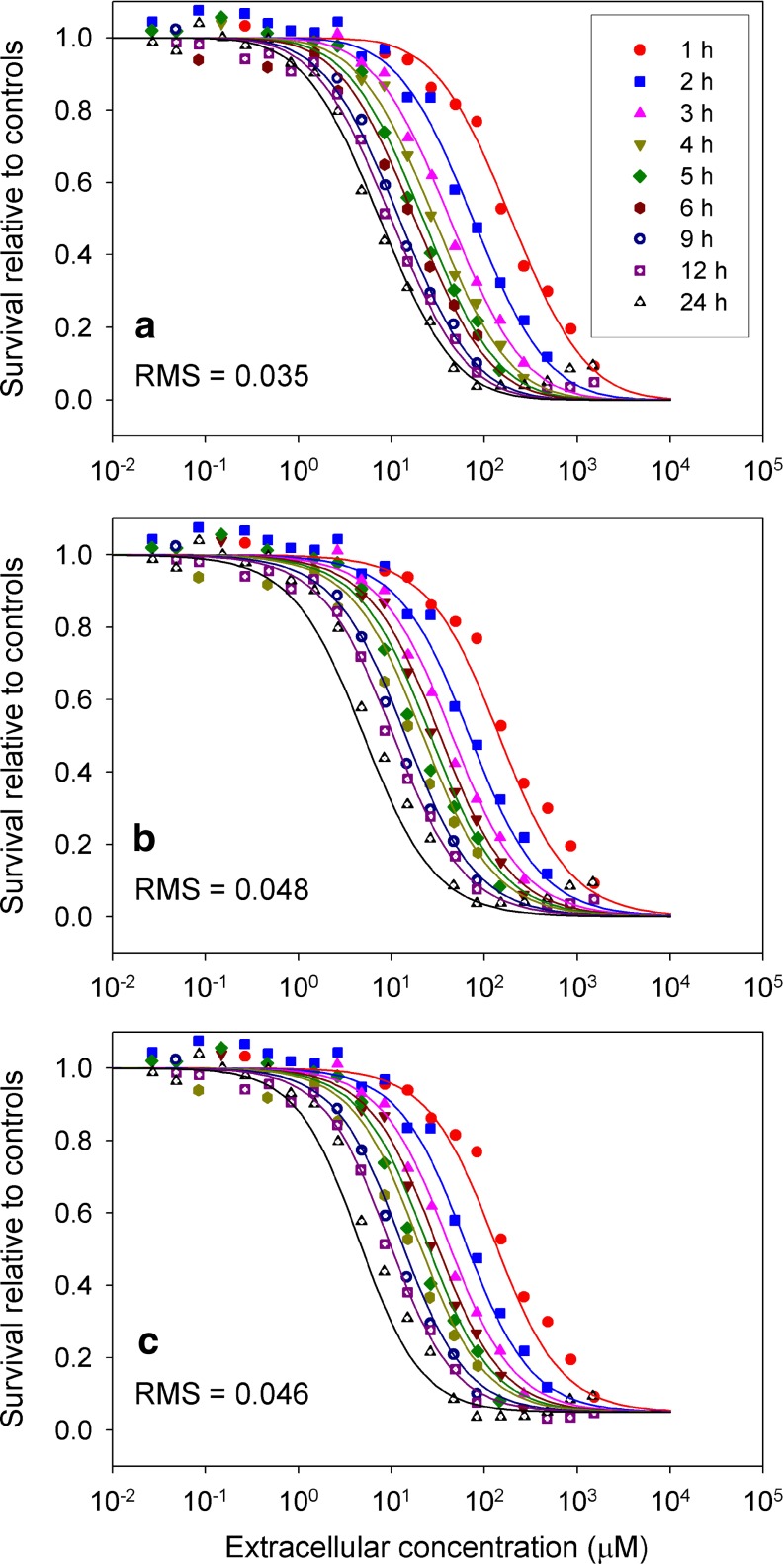
Figures 3 and 4 show fits to data of Au et al. (13) for the DU-145 and SKOV-3 (ovarian) human cell lines, respectively, for the cell cycle checkpoint model, as well as the two next best performing models (CnT and Levasseur et al. (10)). The cell cycle checkpoint model provides a much closer fit to the experimental dose-response behavior at short exposure times, and is better able than the other models to represent the changes in steepness of the dose-response data with exposure time.
Fig. 3.
Comparison of model fits to experimental data of Au et al. (13) for paclitaxel acting on the DU145 human cell line. a Cell cycle checkpoint model. b C n T Hill model. c Single Hill model of Levasseur et al. (1998)
Fig. 4.
Comparison of model fits to experimental data of Au et al. (13) for paclitaxel acting on the SKOV-3 human ovarian carcinomia cell line. a Cell cycle checkpoint model. b C n T Hill model. c Single Hill model of Levasseur et al. (10)
The cell cycle checkpoint model was also tested assuming a single mechanism of damage, as in Eq. 6. The resulting dose-response curves showed plateaus at high concentration that varied with exposure time, and could not provide a satisfactory fit to the experimental data of Au et al. (13) (Figs. 3 and 4) which show a tendency to converge at a relative survival that is at or near zero, with this downward tendency becoming evident at concentrations around 50 nM or more. Introduction of a second mechanism for damage is therefore essential to this model.
Results for Platinum Drugs
Tables V, VIII and IX compare the RMS deviations between model values and experimental data for the three platinum drugs cisplatin, oxaliplatin and carboplatin, for cytotoxicity data sets (10,33,45–48), with the corresponding parameter values shown in Tables VI, VII and XI, respectively. Cell cycle times for many of the cell lines could be estimated from doubling times obtained from literature studies (50–57). In addition to the models considered for paclitaxel, the cell-cycle phase-nonspecific version of the exponential kill model of Gardner (11) is included in the comparison.
Table V.
RMS deviations between experimental data and model predictions, for cisplatin acting on different tumor cell lines
| Tumor cell line | Data source | Cell cycle checkpoint | Peak bound intracellular (Hill) | Extracellular AUC (Hill) | C n T (Hill) | Gardner 2000 cell-cycle non-phase specific | Levasseur et al. (10) single Hilla |
|---|---|---|---|---|---|---|---|
| CAL 27 head and neck cancer | (33) | 0.0378 (13.5 h) 0.0400 (20 h) | 0.0536 | 0.117 | 0.091 | 0.122 | 0.0886 |
| C32 human melanoma (33 h) | (48) | 0.0376 | 0.0360 | 0.0629 | 0.0397 | 0.0742 | 0.0347 |
| G361 human melanoma (33.6 h) | (48) | 0.0556 (25 h) 0.0607 (33.6 h) | 0.0579 | 0.0632 | 0.0547 | 0.0812 | 0.0447 |
| COLO 205 colon carcinoma (62 h) | (45) | 0.0798 (62 h) | 0.0790 | 0.100 | 0.0970 | 0.0997 | 0.0687 |
| Ovarian carcinoma cells (from patient) | (45) | 0.0866 | 0.0855 | 0.0973 | 0.0829 | 0.107 | 0.0864 |
| A2780 human ovarian wild type cells (18 h) | (10) | 0.0321 (18 h) | 0.0287 | 0.0491 | 0.0386 | 0.0613 | 0.0367 |
| A2780/CP3 human ovarian resistant (29 h) | (10) | 0.0354 (4.41 h) 0.0447 (29 h) | 0.0365 | 0.0491 | 0.0484 | 0.0584 | 0.0459 |
| MKN45 gastric cancer (22.9 h) | (46) | 0.0330 (22.9 h) | 0.0331 | 0.0645 | 0.0562 | 0.169 | 0.0337 |
| MKN74 gastric cancer (44 h) | (46) | 0.0463 (44 h) | 0.0417 | 0.0543 | 0.0503 | 0.163 | 0.0398 |
When an experimental value for the cell cycle time of untreated cells in vitro is available from the literature, it is listed in parentheses after the cell line name. For the cell cycle checkpoint models, which include cell cycle time t c as a parameter, the value of t c corresponding to the RMS deviation is indicated in parentheses. In some cases, the RMS deviation was lower at a fitted cell cycle time than at the experimentally measured value, and both results are indicated
aOne parameter (E con) of the Levasseur et al. (10) model was set equal to 1 to ensure that survival at zero concentration equals 1. A different value could be used to correct for errors in the control value used to normalize the data.
Table VIII.
RMS Deviations between Experimental Data and Model Predictions, for Oxaliplatin Acting on Different Tumor Cell Lines
| Tumor Cell Line | Data Source | Cell cycle checkpoint | Peak Bound Intracellular (Hill) | Extracellular AUC (Hill) | C n T (Hill) | Gardner 2000 Cell-cycle Phase Non-specific | Levasseur et al. (10) Single Hilla |
|---|---|---|---|---|---|---|---|
| C32 human melanoma | (48) | 0.0403 (33 h) | 0.0395 | 0.0498 | 0.0385 | 0.0709 | 0.0292 |
| G361 human melanoma | (48) | 0.0505 (33.6 h) | 0.0529 | 0.0889 | 0.0482 | 0.0851 | 0.0270 |
| Colo357 human pancreatic cancer | (47) | 0.0587 (21 h) | 0.0610 | 0.114 | 0.0585 | 0.139 | 0.0432 |
| HT29 human colon cancer | (47) | 0.0497 (25.9 h) | 0.0492 | 0.0614 | 0.0548 | 0.135 | 0.0471 |
| NMG64/84 human colon cancer | (47) | 0.0481 (20 h) | 0.0437 | 0.0904 | 0.0588 | 0.134 | 0.0585 |
| MIAPaCa2 human pancreatic cancer | (47) | 0.0828 (23.9 h) | 0.0777 | 0.0986 | 0.0935 | 0.0782 | 0.212 |
| PMH2/89 human pancreatic cancer | (47) | 0.0668 (20 h) | 0.0641 | 0.0671 | 0.0671 | 0.122 | 0.0523 |
When an experimental value for the cell cycle time of untreated cells in vitro is available from the literature, it is listed in parentheses after the cell line name. For the cell cycle checkpoint models, which include cell cycle time t c as a parameter, the value of t c corresponding to the RMS deviation is indicated in parentheses. In some cases, the RMS deviation was lower at a fitted cell cycle time than at the experimentally measured value, and both results are indicated
aOne parameter (E con) of the Levasseur et al. (10) model was set equal to 1 to ensure that survival at zero concentration equals 1. A different value could be used correct for errors in the control value used to normalize the data
Table IX.
RMS Deviations between Experimental Data and Model Predictions, for Carboplatin Acting on Two Different Tumor Cell Lines
| Tumor Cell Line | Data Source | Cell Cycle Checkpoint | Peak Bound Intracellular (Hill) | Extracellular AUC (Hill) | C n T (Hill) | Gardner 2000 Model Cell-cycle Phase Nonspecific | Levasseur et al. (10) Single Hilla |
|---|---|---|---|---|---|---|---|
| C32 human melanoma | (48) | 0.0397 (33 h) | 0.0391 | 0.0390 | 0.0387 | 0.0403 | 0.0263 |
| G361 human melanoma | (48) | 0.0822 (33.6 h) | 0.0806 | 0.0805 | 0.0802 | 0.0936 | 0.0451b |
When an experimental value for the cell cycle time of untreated cells in vitro is available from the literature, it is listed in parentheses after the cell line name. For the cell cycle checkpoint models, which include cell cycle time t c as a parameter, the value of t c corresponding to the RMS deviation is indicated in parentheses. In some cases, the RMS deviation was lower at a fitted cell cycle time than at the experimentally measured value, and both results are indicated
aOne parameter (E con) of the Levasseur et al. (10) model was set equal to 1 to ensure that survival at zero concentration equals 1. A different value could be used correct for errors in the control value used to normalize the data
bDose-response curves crossed each other, which is not possible for a drug that is not self-inhibiting
Table VI.
Summary of Parameter Values for Cellular Pharmacodynamic Model for Cisplatin
| Tumor Cell Line | Data Source | Cell Cycle Checkpoint Model RMS Deviation | No. of Fitted Parameters | k′ (h−1) | k″ (h−1) | log(D 0) | h | t c (h) | Source for t c Estimate |
|---|---|---|---|---|---|---|---|---|---|
| CAL 27 head and neck cancer | (33) | 0.0378 | 5 | 0.1641 (0.115,0.243) | 0.5402 (0.330,0.878) | −2.368 (−2.55,−2.08) | 2.373 (1.93,2.87) | 13.5 (11.2,16.2) | Fitted |
| C32 human melanoma | (48) | 0.0376 | 3 | 0.06618 (0.0519,0.0860) | 0c | −1.099 (−1.27,−0.924) | 1.271 (1.02,1.55) | 33a | (50) |
| G361 human melanoma | (48) | 0.0607 | 3 | 0.03054 (0.0217,0.0440) | 0c | −1.962 (−2.25,−1.68) | 1.288 (0.865,1.81) | 33.6a | (51) |
| COLO 205 colon carcinoma | (45) | 0.0798 | 3 | 1.710 (0.500,infinity) | ∞b | −4.236 (−4.68,−3.72) | 2.540 | 62a | (52) |
| Ovarian carcinoma cells (from patient) | (45) | 0.0866 | 3 | 0.01216 (0.00610,0.0260) | 0c | −3.198 (−3.75,−2.64) | 1.347 (0.578,2.66) | – | – |
| A2780 human ovarian wild type cells (18 h) | (10) | 0.0321 | 3 | 1.67 (1.27,2.16) | ∞b | −2.646 (−2.74,−2.56) | 0.8636 (0.768,0.966) | 18a | (10) |
| A2780/CP3 human ovarian resistant (29 h) | (10) | 0.0447 | 3 | 2.580 (1.34,6.19) | ∞ b | 1.3913 (1.27,1.54) | 1.484 (1.33,1.66) | 29a | (10) |
| MKN45 gastric cancer | (46) | 0.0330 | 3 | 0.1396 (0.0882,0.274) | 0c | 0.5512 (0.295,0.804) | 2.872 (2.36,3.57) | 22.9a | (53) |
| MKN74 gastric cancer | (46) | 0.0463 | 3 | 0.06763 (0.0394,0.131) | 0c | 0.8681 (0.463, 1.27) | 3.362 (2.52,4.81) | 44a | (54) |
The 95% confidence intervals are given below the fitted value in parentheses
aParameter was specified, not fit
bRepair was rapid relative to cell cycle time, making k″ effectively ∞
cRepair was slow relative to cell cycle time, reducing model to the peak intracellular model (see Table I)
Table VII.
Summary of Parameter Values for Cellular Pharmacodynamic Model for Oxaliplatin
| Tumor Cell Line | Data Source | Cell cycle Checkpoint RMS Deviation | No. of Fitted Parameters | k′ (h−1) | k″ (h−1) | log(D 0) | h | t c (h) | Source for t c Estimate |
|---|---|---|---|---|---|---|---|---|---|
| C32 human melanoma | (48) | 0.0403 | 4 | 0.4443 (0.297,0.706) | 0.8956 (0.542,1.70) | −0.1796 (−0.419,0.0616) | 1.608 (1.26,2.01) | 33a | (50) |
| G361 human melanoma | (48) | 0.0505 | 4 | 0.2717 (0.187,0.412) | 1.148 (0.642,2.53) | −2.350 (−2.94,−1.95) | 1.078 (0.731,1.52) | 33.6a | (51) |
| Colo357 human pancreatic cancer | (47) | 0.0587 | 3 | 0.4298 (0.151,19.7) | 0b | −1.055 (−1.77,1.37) | 1.983 (1.15,3.11) | 21a | (55) |
| HT29 human colon cancer | (47) | 0.0497 | 3 | 0.07961 (0.0323,0.241) | 0b | −0.6980 (−1.42,0.560) | 2.791 (1.90,3.96) | 25.9a | (56) |
| NMG64/84 human colon cancer | (47) | 0.0481 | 3 | 0.1919 (0.0792,0.490) | 0b | −0.4312 (−1.04,0.178) | 2.042 (1.33,2.98) | 20a | Assumed based on other colon lines |
| MIAPaCa2 human pancreatic cancer | (47) | 0.0828 | 3 | 1.178 (0.914,infinity) | Infinityc | 0.1568 (−0.949,1.27) | 1.933 (0.815,3.81) | 23.9a | (57) |
| PMH2/89 human pancreatic cancer | (47) | 0.0668 | 3 | 0.003810 (0.00133,0.0109) | 0b | 2.670 (−3.90,−1.88) | 2.922 (1.63,4.85) | 20a | Assumed based on other pancreatic lines |
The 95% confidence intervals are given below the fitted value in parentheses
aParameter was specified, not fit
bRepair was slow relative to cell cycle time, simplifying to the peak intracellular model
cRepair was rapid relative to cell cycle time, making k″ effectively ∞
Table XI.
Summary of Parameter Values for Cellular Pharmacodynamic Model for Carboplatin
| Tumor Cell Line | Data Source | Cell Cycle Checkpoint Model RMS Deviation | No. of Fitted Parameters | k′ (h−1) | k″ (h−1) | log(D 0) | h | t c (h) | Source for t c Estimate |
|---|---|---|---|---|---|---|---|---|---|
| C32 human melanoma | (48) | 0.0397 | 2a | 0b | 0b | 5.190 (5.02, 5.37) | 1.383 (1.11, 1.69) | 33b | (50) |
| G361 human melanoma | (48) | 0.0787 | 2a | 0b | 0b | 4.804 (4.40, 5.22) | 1.809 (1.18, 2.66) | 33.6b | (51) |
The 95% confidence intervals are given in parentheses.
aIn the special case of k′ = 0, k″ = 0 the full cell cycle checkpoint model simplifies to an extracellular AUC model; see Table I
bParameter was specified, not fit
Because of similarities in drug uptake and intracellular target among the platinum drugs, it was speculated that all drugs in this class could be described by the same cell cycle checkpoint model, and Tables V, VIII and IX confirm this. In all cases, the model gives relatively low RMS deviations from experimental data, and describes the data much more satisfactorily than the AUC (area under the concentration-time curve) model which is often mentioned in the literature as the appropriate model for cell cycle nonspecific drugs such as cisplatin (5,58). In some cases, a lower RMS deviation from the data can be achieved using the model of Levasseur et al. (10); however, the predicted dose-response curves for different exposure times cross each other, which is physically impossible for a drug that is not self-inhibiting. This behavior of the Levasseur et al. (10) model was also found in the previous study of doxorubicin (6).
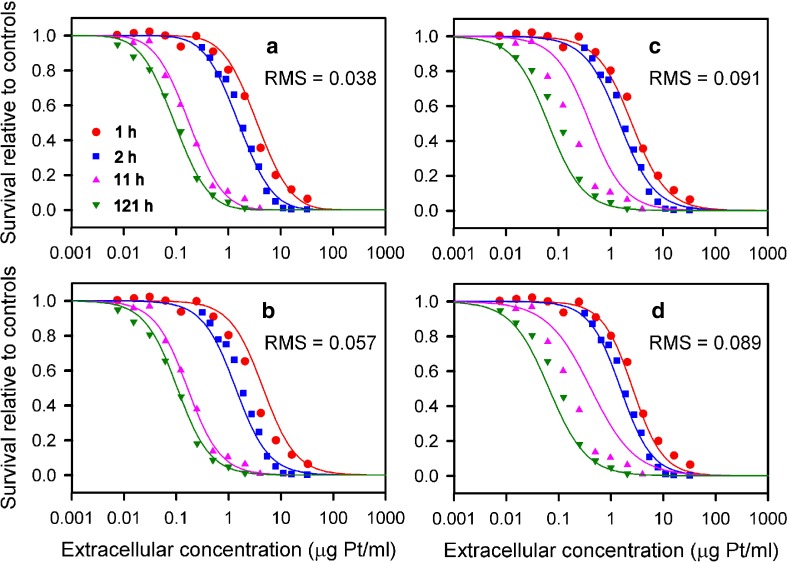
Figures 5 and 6 compare predictions of the cell cycle checkpoint model with data for cisplatin acting on two human cell lines including the resistant A2780/CP3 line (10,33). Relative to other models, this model provides a closer fit to these experimental data particularly at the extremes of short and long exposure times. Figure 5b includes results of a previous model that assumed cytotoxicity depended on peak concentration (12). The present model performs similarly at long exposure times, but shows improved agreement at short exposure times.
Fig. 5.
Comparison of model fits to experimental data of Troger et al. (33) for cisplatin acting on a human cell line. a Cell cycle checkpoint model. b Peak bound intracellular model of El-Kareh and Secomb (3). c C n T Hill model. d Single Hill model of Levasseur et al. (10)
Fig. 6.
Comparison of model fits to experimental data of Levasseur et al. (10) for cisplatin acting on the resistant A2780/CP3 human cell line. a Cell cycle checkpoint model. b C n T Hill model. c Single Hill model of Levasseur et al. (10)
The Wilcoxon signed rank test was performed using the RMS deviation values from Tables V, VIII and IX, to assess whether the improved results provided by the cell cycle checkpoint model had statistical significance. The Levasseur et al. (10) model yields low RMS deviations in some cases, but shows nonphysical behavior with dose-response curves at different exposure times crossing each other, and was not included. For paclitaxel, the cell cycle checkpoint additive damage model was superior to the AUC Hill model, the CnT model, and the cell cycle checkpoint independent model (p < 0.001 in all cases). For all three platinum drugs considered together, the cell cycle checkpoint model was superior to the AUC Hill model, the CnT model, and the Gardner (11) cell cycle phase non-specific model (p < 0.005 in all cases), but it was not statistically different from the peak bound intracellular model (12).
As a further test of model performance, mean predictive errors (MPE; 59) were computed for all cases; MPE is a measure of the bias of the model fit rather than its closeness to the data. For paclitaxel, the magnitudes of the MPE for the cell cycle checkpoint model (with additive damage) lay in the range 0.00076–0.0243 which compares favorably to the scale of survival relative to controls which lies between 0 and 1. For the platinum drugs nearly all the MPE magnitudes were quite small; for 12 cell lines they were less than 0.01, and the remainder were less than 0.02 with the exception of the PMH2/89 pancreatic cell line, for which the MPE was 0.0651. The Wilcoxon signed rank test performed on the MPE magnitudes indicated that the cell cycle checkpoint model was superior to the AUC Hill model (p < 0.05), the CnT model (p < 0.05), and the cell cycle checkpoint independent model (p < 0.05). In the case of the platinum drugs, the Wilcoxon signed rank test showed a statistically significant advantage based on MPE magnitudes of the cell cycle checkpoint model over the Gardner model (p < 0.005), but not over the other models.
DISCUSSION
An important feature of the models developed here is that they are based on mechanistic assumptions regarding cell responses to chemotherapeutic drugs. Although these assumptions are simplified relative to the actual mechanisms of drug action, such an approach has several advantages over purely empirical models. Mechanistic models can yield useful predictions for parameter ranges outside those for which data are available to test the model. In contrast, purely empirical models may yield physically unreasonable results when extrapolated outside the fitted range. Further, mechanistic models have the potential to distinguish factors affecting response or leading to resistance, such as cellular drug uptake and efflux kinetics, target expression, inactivation of drug intracellularly through binding to inactive sites or sequestration, sensitivity at a given intracellular drug level, and doubling time. This can help in the interpretation of experimental studies that relate sensitivity with these factors. For example, Tseng et al. (60) in a study of glioma and medulloblastoma cell lines, observed that “Paradoxically, we found a statistically significant inverse correlation between LD10 and doubling time for our lines (i.e., greater resistance is associated with faster growth).” The model presented here suggests that, while increased cell cycle time does indeed by itself reduce paclitaxel cytotoxicity, this effect may be obscured by other differences between cell lines such as drug uptake rate and intracellular binding kinetics. Welters et al. (61) studied cellular doubling time and cisplatin sensitivity in human head and neck cancer cell lines, and found that IC50 did not correlate with cellular doubling time. The present study suggests that a relatively slow rate of repair of platinum-DNA lesions could explain such a lack of correlation.
Basis for Model Assumptions
The present models assume that measured growth inhibitory effects are primarily due to cell kill. While the assays used (Table X) do not distinguish between cytotoxic and cytostatic drug effects, other studies support the assumption that the drugs considered here mainly exert a cytotoxic effect. Jäckel and Köpf-Maier (62) studied the cytokinetic effects of cisplatin on human head and neck carcinoma xenografts. They observed a weak G2 delay, but noted that this was associated with non-responding tumors whose growth remained nearly unaltered by therapy. The much more significant G1/S blocks they observed were irreversible and associated with cytotoxicity. A similar correlation between cytokinetic effects and cell kill was observed in vitro by Jäckel et al. (63). Pasquier et al. (64) contrasted the cytostatic mechanism of action of paclitaxel on endothelial cells at low doses with the cytotoxic effect at higher doses, only the latter being similar to that observed in tumor cells. They state “To our knowledge, it has never been described in cancer cells that a high inhibition of cell proliferation induced by microtubule-damaging agents involves only a cytostatic effect. Indeed, in cancer cells, microtubule-damaging agents generally induce G2–M arrest and subsequent apoptosis.” These studies suggest that growth inhibition by the drugs considered here is due mainly to drug-induced cell kill.
Table X.
Assay Methods Used to Determine Growth Inhibition
| Study | Assay Used to Assess Cytotoxicity or Growth Inhibition |
|---|---|
| (13) | One to three washes; SRB assay |
| (36) | Four washes; fluorometric microculture cytotoxicity assay |
| (47) | HTCA (human tumor colony-forming assay) |
| (46) | MTT assay |
| (10) | Two or four washes; SRB protein dye assay |
| (48) | SRB assay |
| (35) | Wash; Trypan blue dye exclusion test |
| (45) | Soft-agar assay |
| (33) | MTT assay |
The present models assume constant drug activity during the treatment period. A potential concern is that the observed asymptotic approach of the dose-response curves to a single curve at long exposure times might reflect declining activity of drug in the cell culture medium (65). In the study of Troger et al. (33), which included the longest exposure time for cisplatin (121 h), a change in the 121 h dose-response curve was detected when drug was renewed at 24, 48 and 72 h, compared with no renewal; however, the relative shift in the dose-response curve is not very large, and the results still suggest a strong deviation from AUC-dependent cytotoxicity. Further, Troger et al. (33) observed that intracellular platinum concentrations reached a plateau after approximately 16 h of exposure, and remained stable for up to 64 h. Their drug efflux data shows that when the extracellular drug is removed, the cellular platinum starts to decline; the plateau in intracellular concentration is therefore suggestive of a constant extracellular concentration. Given that cell survival was related to intracellular platinum content, it appears more likely that the diminishing response they observed at 121 h compared to 11 h did not result primarily from degradation of extracellular drug over this time period. Degradation of paclitaxel is also unlikely to affect the data analyzed here: Ringel and Horwitz (66) found that taxol converts to 7-epitaxol in cell culture medium, but that this compound had an effect on cells similar to taxol, and they concluded that this conversion process did not significantly alter the overall biological activity of taxol. Further studies with either periodic drug renewal or sampling of the medium would be helpful in resolving the issue of whether drug instability affects dose-response data.
The assumption of dependence of cytotoxicity on peak concentration rather than cumulative exposure is the key feature of the present models that allows them to reproduce the asymptotic convergence of dose-response curves evident in most of the data sets considered here, and particularly evident in the paclitaxel data of Au et al. (13). Predictions for optimal therapy can be highly dependent on the model used to predict cell kill. If cell death depends on peak concentration, it cannot be predicted adequately if it is assumed that the rate of cell death depends on instantaneous concentration. Such an assumption forms the basis of a number of mathematical models for chemotherapy (11,18,29,67,68). The models presented here performed satisfactorily not only for wild type cells but also for two resistant cell lines (Tables III and V; Fig. 6). This suggests that resistant cells may be described by the same pharmacological models as sensitive cells, but with different parameter values.
Comparison with Previous Models
The present models for paclitaxel and platinum drugs give significantly better fits overall to literature dose-response data than any previously proposed model, as evidenced by the results of Tables III, V, VIII, IX and the Wilcoxon signed rank test. The CnT Hill and Levasseur et al. (10) models, both of which are empirical, performed best among the previous models, but exhibited significant systematic deviations from the data. A limitation of the CnT Hill model in fitting the paclitaxel data is that the steepness of the dose-response curve cannot change with exposure time, whereas the data show a significant variation in this steepness (Figs. 3 and 4). In a Hill equation model, the Hill exponent n determines the slope of the dose-response curve; the Levasseur et al. (10) model allows this exponent to vary as a quadratic function of exposure time, resulting in an improved ability to fit the data over the range of exposure times considered. However, it should be noted that this polynomial dependence on exposure time causes the model to break down for exposure times outside the fitted range, because the exponent changes sign. Further, it is difficult to interpret the dependence of the Hill equation exponent on exposure time. This exponent represents the heterogeneity in sensitivity of the population. In the model presented here for paclitaxel, the changes in steepness of the dose-response curves are explained in terms of two separate mechanisms of cell kill, each having a different degree of heterogeneity in the population’s sensitivity. As the concentration and exposure time changes, the relative importance of the two mechanisms shifts, causing variations in the steepness of the dose-response curve.
The data of Au et al. (13) for paclitaxel show a change in steepness of the dose-response curve at an extracellular concentration around 50 nM, an indication of a shift from one mechanism to another at this concentration corroborated by other experimental studies (31,38). The cell cycle checkpoint model represents this effect through the shift in dominance from one mechanism to the other (Figs. 3 and 4). The Levasseur et al. (10) model, with a Hill exponent that can vary with exposure time but not concentration, has difficulty reproducing this behavior. Levasseur et al. (10) also proposed a double Hill model which could result in changes in steepness with concentration; they interpret the need for superposition of two Hill equations as resulting from population heterogeneity rather than two cell kill mechanisms. The improvement in fit using the double Hill model (results not shown) was found insufficient to give satisfactory fits or to justify the much greater number of fitted parameters. Both the CnT and the Levasseur et al. (10) model predict that dose-response curves continue to shift left as exposure time increases, resulting in a poor fit at long exposure times, when the data in fact show asymptotic convergence of these curves to a single high-exposure time limit (Figs. 3, 4, 5 and 6). The cell cycle checkpoint model for the platinum drugs had from three to five independent fitted parameters (only one cell line required all five), which compares favorably with the six fitted parameters of the Levasseur et al. (10) model. In the case of paclitaxel, the cell cycle checkpoint model had from three to seven fitted parameters (only one cell line required all seven).
The cell cycle checkpoint model also performed significantly better than previously proposed mechanistic models, which include the AUC model of Ozawa et al. (5) and the Gardner (11) exponential kill model. The Ozawa et al. (5) theoretical development, which assumes linear cellular uptake of cisplatin over time, predicted that cytotoxicity would depend only on AUC, although the exact form of the mathematical dependence was not specified. We tested this model using both a Hill equation and an exponential relation between relative survival and AUC. While the Hill equation gave better results, it was inferior to the CnT Hill model.
The models developed here retain the central assumption of the peak concentration models developed by El-Kareh and Secomb (6,12) for cisplatin and doxorubicin, namely that cytotoxicity depends not on measures of cumulative exposure such as extracellular or intracellular AUC, but rather on the peak concentration of a particular cellular drug species that is associated with cell death. The previous models represent special cases of the cell cycle checkpoint model, applicable when repair or reversal of formation of the lethal cellular drug species is relatively slow or negligible. In such cases, the lethal species remains in the cell until the critical cell phase is reached, at which point it causes the cell to embark on a pathway to death, if the lethal species concentration exceeds the threshold. The time at which exposure occurs then has little effect on the response. For some cell lines, the fit of the cell cycle checkpoint model to the cisplatin data was relatively insensitive to the cell cycle time parameter over a range of physically reasonable values. This may reflect a slow rate of DNA repair, so that repair of lethal lesions between exposure and the critical cell cycle point is rare.
The inclusion in the present models of both cellular pharmacokinetics and cell cycle kinetics is an important feature that accounts for the delay time between extracellular exposure and intracellular exposure and response. This concept, missing in most previously proposed models, is included in the model of Lobo and Balthasar (18). Mathematically, their sequence of first-order kinetic equations is analogous to the kinetic processes of cellular uptake, binding, and cell cycle progression, although certain nonlinear effects such as saturation cannot fit within their first-order linear kinetic framework. The success of the Lobo and Balthasar model in describing in vivo data (20) may reflect a dominance of processes that are not at the cellular level, such as plasma pharmacokinetics, extravasation of drug and transport of drug within the tumor interstitial spaces.
Parameter Values
The goodness of fit was more sensitive to the value of the cell cycle time parameter for paclitaxel than for the platinum drugs. For a number of cell lines exposed to platinum drugs, repair was slow relative to the cell cycle time, so that the model simplified to a peak intracellular model, which is independent of tc. In the case of paclitaxel the best fit values of tc were generally in the same range as the experimentally measured values for untreated cells (for those cell lines for which such measurements were available), although the RMS deviation was sometimes significantly higher if the experimentally measured value was used. This discrepancy is not unexpected, since cell cycle times for the same cell line often show a range, depending on the exact medium and growth conditions and the number of times they have been passaged, which may differ between the cytotoxicity study and the study where doubling time was determined. Further, the experimental estimates of cell cycle time taken from the literature are in fact in vitro doubling times. Population doubling times are generally longer than cell cycle times, since the proliferating fraction is less than 1. It is also conceivable that drug-induced cell cycle perturbations in sensitive cells may result in a different cell cycle time compared to untreated cells. For the cell lines for which no experimentally measured cell cycle time was provided, the best fit values generally fell within the range of 12–60 h, which is typical for untreated cells.
The values of C1 and C2 in Table IV reflect the concentrations at which paclitaxel uptake and binding saturate. These parameters can be compared to the saturating concentration parameter Kd,c of Kuh et al. (34), which was estimated at 4.93 nM for MCF-7 cells. In most cases the fitted values of C1 are close to this experimentally measured value. The fitted values of C2 are generally larger and vary more. There are several reasons that this is plausible. The Kuh et al. (34) study considers only a single saturability parameter, because that study looked at total intracellular concentration, whereas in the present model two distinct cellular drug species are accounted for, and saturability can occur at different concentrations for these two species. Variations in C1 or C2 also reflect variations in cellular drug uptake kinetics and target expression among the cell lines. In some cases C2 was effectively 0 or infinity; this reflects the fact that the concentration range in the data lay either well below or well above the saturation regime. Essentially, this means that the concentration range of the data set was not complete enough to obtain an estimate of C2.
For the platinum drugs, the model parameter k′ corresponds to the rate constant for equilibration of intracellular and extracellular concentrations. Data of Troger et al. (33) for cisplatin uptake of the CAL-27 cell line show that the time scale for this equilibration is on the order of 15–30 h, which corresponds to a value of k′ on the order of 0.1 h−1. There do not appear to be any data in the literature for kinetics of carboplatin and oxaliplatin cellular uptake. For the majority of cell lines, Table VI gives values of k′ consistent with the Troger et al. data. However, for some cell lines the values are significantly larger. Reduced uptake of platinum is known to be a cause of resistance, and active efflux systems for cisplatin have been identified in some tumor cell types. Significant variation in the kinetics of cisplatin uptake among cell lines is therefore not unexpected. Differences in the range of k′ values among the platinum drugs in Tables VI, VII and XI are also to be expected, given studies showing differences in the mechanism of drug uptake among platinum drugs, e.g. Zhang et al. (69).
The model parameter k″ for the platinum drugs is intended to represent DNA repair of platinum lesions. The kinetics of repair of cisplatin-DNA adducts has been measured in several studies. Fichtinger-Schepman et al. (70) observed DNA repair in white blood cells of cisplatin-treated patients and noted that 75% of the adducts formed during the first cycle of treatment were removed after 24 h. This gives an estimate of the rate constant for repair of k″ = 0.058 h−1. Köberle et al. (71) measured the fraction of remaining platinated DNA relative to the initial for several testis and bladder cell lines. Their data give a range for k″ from 0.005 to 0.03 h−1 showing that at least an order of magnitude variation can be expected among different cell lines. By comparison, the model-fitted values from Table VI include a number of cases where k″ is effectively 0, and the model simplified to the peak intracellular model. This corresponds to DNA repair that is slow, so that no significant repair occurs over a cell cycle. For a few cell lines, k″ was found to effectively be infinite. This is unlikely to be attributable solely to DNA repair; more likely it results from other physical processes that would give an effectively higher value of k″. Such processes could include intracellular sequestration, a phenomenon documented by Samimi et al. (72); strong intracellular binding to inactivating thiolate ligands such as glutathione and metallothionein (73); and active efflux of cisplatin. Since these have all been invoked as mechanisms of resistance, they are particularly plausible in explaining the higher value of k″ for the resistant cell line A2780/CP3.
Potential for Application of Models to In Vivo and Combination Therapy
While the models presented here were developed using in vitro data, several features should make them useful for application to predicting cellular drug response under conditions encountered in vivo. Cell cycle time appears explicitly as a model parameter; as a tumor grows, the cell cycle may be lengthened due to cells spending a longer period of time in G0. Indeed, cell cycle time, like growth fraction, is likely to vary spatially within a tumor. Cellular drug uptake is affected by pH and by the extent of contact with neighboring cells, and may be significantly different in vivo than in vitro; this can be accounted for through the parameter values for cellular pharmacokinetics. It is possible to experimentally simulate such effects to some extent in vitro, for example by using three-dimensional cell cultures, and the models presented here could be applied to such in vitro data generated under conditions more closely resembling tumor microenvironment. Unlike the model of Levasseur et al. (10), the present models can readily be generalized to cases involving time-varying extracellular concentrations as occur in vivo. Because they relate response to tumor cell extracellular concentration, not plasma concentration, they need to be integrated with models describing plasma pharmacokinetics and tumor drug transport, and possibly, in addition, tumor microenvironment variables such as pH, to make predictions for in vivo response.
The additive damage model, used in this study to describe the resultant effect of the two distinct cell kill mechanisms of paclitaxel, provides a framework that could potentially be used to model the effects of drug combinations in a mechanistic manner. For paclitaxel, the additive damage model gives consistently better fits than the independent model (Table III), suggesting that the two assumed cell kill mechanisms do not operate independently, even though they occur at distinct points of the cell cycle. In the additive damage model, the combined effect of the two damage mechanisms can exceed the threshold for cell death, even when each mechanism individually is below the threshold. Such a synergistic interaction may occur when damage inflicted by one mechanism weakens the cell, making it less able to recover from damage resulting from the other mechanism. The additive damage model can be considered a mechanistic generalization of the isobologram method (74), where damage is assumed additive, instead of assuming additivity based on drug concentrations. Steel and Peckham (74) and Loewe (75) warned that defining synergy without reference to a model for drug interaction that has some physical basis would be misleading. The additive damage approach addresses this issue, since additivity of damage has a physical interpretation that is lacking when additivity is based on concentration.
Cellular pharmacodynamic models developed to date have been validated using data for natural cell populations in which the cells are presumably uniformly distributed over the cell cycle. In vivo, cells are often subject to fractionated doses or combination therapy, and either pretreatment or simultaneous treatment with another drug may significantly skew the distribution of the cell population over the cell cycle. The cell cycle checkpoint models presented here are unique in their ability to make predictions for cell populations with an arbitrary, not necessarily uniformly distributed, distribution of cells over the cell cycle. As such, they can reproduce the sinusoidal dependence of IC50 on the cell cycle position at which pulse exposure occurred, for the synchronized cells observed by Donaldson et al. (30). It is often stated that cells must be actively proliferating to be sensitive to many chemotherapeutic agents, but Donaldson et al. (30) found somewhat more complex behavior. They state that “The results presented here also related drug toxicity to the two major regulatory points in the cell cycle, G1 to S-phase and G2 to M-phase transition, rather than a correlation between proliferation and sensitivity.” In the cell cycle checkpoint model, it is the ability of the cell to reach the critical cell cycle point, while still containing enough lethal cellular drug, that determines cell kill; beyond this, proliferative status is irrelevant. The model is consistent with another observation of Donaldson et al. (30): “With either cis-DDP or taxol exposure a period of cell cycle progression following removal of the drug is required to bring about cell killing.” That is, since most cells are not at the critical phase at the time of exposure, they must continue to cycle until the critical phase is reached.
Conclusion
The cell cycle checkpoint models developed here represent a continuation of the general approach of simultaneous pharmacokinetic–pharmacodynamic mechanistic modeling, in which the kinetics of drug uptake and binding are accounted for, and cell kill is related to concentrations of lumped intracellular or bound drug species. They provide significantly improved descriptions of dose-response data for paclitaxel and platinum drugs and represent a framework for modeling drugs that show asymptotic convergence of dose-response curves at long exposure times, a property apparently shared by most chemotherapeutic drugs in wide clinical use. The validity of a single model for all three platinum drugs offers the hope that models may be developed with broad applicability to other drug classes. In addition to the practical application of these models for prediction of in vivo response and optimization of therapy, they offer a new picture of chemotherapeutic drug action and its relation to the cell cycle.
Acknowledgement
We thank Saadia Hassan for sending us digitized dose-response data for paclitaxel corresponding to the published figures in Hassan et al. (36). This work was supported by NIH grants CA098671 and CA040355.
References
- 1.Briasoulis E., Karavasilis V., Tzamakou E., Haidou C., Piperidou C., Pavlidis N. Pharmacodynamics of non-break weekly paclitaxel (Taxol) and pharmacokinetics of Cremophor-EL vehicle: results of a dose-escalation study. Anticancer Drugs. 2002;13(5):481–489. doi: 10.1097/00001813-200206000-00006. [DOI] [PubMed] [Google Scholar]
- 2.Schrag D., Garewal H. S., Burstein H. J., Samson D. J., Von Hoff D. D., Somerfield M. R. American Society of Clinical Oncology technology assessment: chemotherapy sensitivity and resistance assays. J. Clin. Oncol. 2004;22(17):3631–3638. doi: 10.1200/JCO.2004.05.065. [DOI] [PubMed] [Google Scholar]
- 3.El-Kareh A. W., Secomb T. W. Theoretical analyses and simulations of anticancer drug delivery. In: Brown D. M., editor. Drug Delivery Systems in Cancer Therapy. Clifton, NJ: Humana Press; 2003. pp. 25–41. [Google Scholar]
- 4.Eichholtz-Wirth H. Dependence of the cytostatic effect of adriamycin on drug concentration and exposure time in vitro. Br. J. Cancer. 1980;41(6):886–891. doi: 10.1038/bjc.1980.165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ozawa S., Sugiyama Y., Mitsuhashi Y., Kobayashi T., Inaba M. Cell killing action of cell cycle phase-non-specific antitumor agents is dependent on concentration–time product. Cancer Chemother. Pharmacol. 1988;21(3):185–190. doi: 10.1007/BF00262767. [DOI] [PubMed] [Google Scholar]
- 6.El Kareh A. W., Secomb T. W. Two-mechanism peak concentration model for cellular pharmacodynamics of doxorubicin. Neoplasia. 2005;7(7):705–713. doi: 10.1593/neo.05118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Skipper H. E. The effects of chemotherapy on the kinetics of leukemic cell behavior. Cancer Res. 1965;25(9):1544–1550. [PubMed] [Google Scholar]
- 8.Adams D. J. Invitro pharmacodynamic assay for cancer drug development—application to crisnatol, a new Dna intercalator. Cancer Res. 1989;49(23):6615–6620. [PubMed] [Google Scholar]
- 9.Millenbaugh N. J., Wientjes M. G., Au J. L. S. A pharmacodynamic analysis method to determine the relative importance of drug concentration and treatment time on effect. Cancer Chemother. Pharmacol. 2000;45(4):265–272. doi: 10.1007/s002800050039. [DOI] [PubMed] [Google Scholar]
- 10.Levasseur L. M., Slocum H. K., Rustum Y. M., Greco W. R. Modeling of the time-dependency of in vitro drug cytotoxicity and resistance. Cancer Res. 1998;58(24):5749–5761. [PubMed] [Google Scholar]
- 11.Gardner S. N. A mechanistic, predictive model of dose-response curves for cell cycle phase-specific and -nonspecific drugs. Cancer Res. 2000;60(5):1417–1425. [PubMed] [Google Scholar]
- 12.El-Kareh A. W., Secomb T. W. A mathematical model for cisplatin cellular pharmacodynamics. Neoplasia. 2003;5(2):161–169. doi: 10.1016/s1476-5586(03)80008-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Au J. L. S., Li D., Gan Y. B., Gao X., Johnson A. L., Johnston J., et al. Pharmacodynamics of immediate and delayed effects of paclitaxel: role of slow apoptosis and intracellular drug retention. Cancer Res. 1998;58(10):2141–2148. [PubMed] [Google Scholar]
- 14.Eliaz R. E., Nir S., Marty C., Szoka F. C. Determination and modeling of kinetics of cancer cell killing by doxorubicin and doxorubicin encapsulated in targeted liposomes. Cancer Res. 2004;64(2):711–718. doi: 10.1158/0008-5472.CAN-03-0654. [DOI] [PubMed] [Google Scholar]
- 15.Vrignaud P., Londosgagliardi D., Robert J. Cellular pharmacology of doxorubicin in sensitive and resistant rat glioblastoma cells in culture. Oncology. 1986;43(1):60–66. doi: 10.1159/000226106. [DOI] [PubMed] [Google Scholar]
- 16.Minderman H., Cao S. S., Rustum Y. M. Rational design of irinotecan administration based on preclinical models. Oncology (New York) 1998;12(8):22–30. [PubMed] [Google Scholar]
- 17.Parsons P. G. Dependence on treatment time of melphalan resistance and Dna cross-linking in human-melanoma cell-lines. Cancer Res. 1984;44(7):2773–2778. [PubMed] [Google Scholar]
- 18.Lobo E. D., Balthasar J. P. Pharmacodynamic modeling of chemotherapeutic effects: Application of a transit compartment model to characterize methotrexate effects in vitro. AAPS PharmSci. 2002;4(4):42–44. doi: 10.1208/ps040442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Miyagi Y., Kawanishi K., Miyagi Y., Yamada S., Yamamoto J., Kodama J., et al. Cytocidal effect and DNA damage of nedaplatin: a mathematical model and analysis of experimental data. Cancer Chemother. Pharmacol. 2001;47(3):229–235. doi: 10.1007/s002800000237. [DOI] [PubMed] [Google Scholar]
- 20.Simeoni M., Magni P., Cammia C., De Nicolao G., Croci V., Pesenti E., et al. Predictive pharmacokinetic–pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 2004;64(3):1094–1101. doi: 10.1158/0008-5472.CAN-03-2524. [DOI] [PubMed] [Google Scholar]
- 21.Shah M. A., Schwartz G. K. Cell cycle-mediated drug resistance: an emerging concept in cancer therapy. Clin. Cancer Res. 2001;7(8):2168–2181. [PubMed] [Google Scholar]
- 22.Evans D. L., Tilby M., Dive C. Differential sensitivity to the induction of apoptosis by cisplatin in proliferating and quiescent immature rat thymocytes is independent of the levels of drug accumulation and Dna adduct formation. Cancer Res. 1994;54(6):1596–1603. [PubMed] [Google Scholar]
- 23.Jackson R. C. The problem of the quiescent cancer cell. Adv. Enzyme Regul. 1989;29:27–46. doi: 10.1016/0065-2571(89)90092-7. [DOI] [PubMed] [Google Scholar]
- 24.Dimancheboitrel M. T., Garrido C., Chauffert B. Kinetic resistance to anticancer agents. Cytotechnology. 1993;12(1–3):347–356. doi: 10.1007/BF00744672. [DOI] [PubMed] [Google Scholar]
- 25.Masunaga S., Ono K., Hori H., Akaboshi M., Kawai K., Suzuki M., et al. Enhancement of cisplatin sensitivity of quiescent cells in solid tumors by combined treatment with tirapazamine and low-temperature hyperthermia. Radiat. Med. 1998;16(6):441–448. [PubMed] [Google Scholar]
- 26.Swierniak A., Polanski A., Kimmel M. Optimal control problems arising in cell-cycle-specific cancer chemotherapy. Cell Prolif. 1996;29(3):117–139. doi: 10.1046/j.1365-2184.1996.00995.x. [DOI] [PubMed] [Google Scholar]
- 27.Jusko W. J. Pharmacodynamic model for cell-cycle-specific chemotherapeutic agents. J. Pharmacokinet. Biopharm. 1973;1(3):175–200. doi: 10.1007/BF01062346. [DOI] [Google Scholar]
- 28.Ozawa S., Sugiyama Y., Mitsuhashi J., Inaba M. Kinetic-analysis of cell killing effect induced by cytosine-arabinoside and cisplatin in relation to cell-cycle phase specificity in human-colon cancer and Chinese-hamster cells. Cancer Res. 1989;49(14):3823–3828. [PubMed] [Google Scholar]
- 29.Fister K. R., Panetta J. C. Optimal control applied to cell-cycle-specific cancer chemotherapy. SIAM J. Appl. Math. 2000;60(3):1059–1072. doi: 10.1137/S0036139998338509. [DOI] [Google Scholar]
- 30.Donaldson K. L., Goolsby G. L., Wahl A. F. Cytotoxicity of the anticancer agents cisplatin and taxol during cell-proliferation and the cell-cycle. Int. J. Cancer. 1994;57(6):847–855. doi: 10.1002/ijc.2910570614. [DOI] [PubMed] [Google Scholar]
- 31.Sena G., Onado C., Cappella P., Montalenti F., Ubezio P. Measuring the complexity of cell cycle arrest and killing of drugs: kinetics of phase-specific effects induced by Taxol. Cytometry. 1999;37(2):113–124. doi: 10.1002/(SICI)1097-0320(19991001)37:2<113::AID-CYTO4>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 32.Trielli M. O., Andreassen P. R., Lacroix F. B., Margolis R. L. Differential taxol-dependent arrest of transformed and nontransformed cells in the G1 phase of the cell cycle, and specific-related mortality of transformed cells. J. Cell Biol. 1996;135(3):689–700. doi: 10.1083/jcb.135.3.689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Troger V., Fischel J. L., Formento P., Gioanni J., Milano G. Effects of prolonged exposure to cisplatin on cytotoxicity and intracellular drug concentration. Eur. J. Cancer. 1992;28(1):82–86. doi: 10.1016/0959-8049(92)90391-E. [DOI] [PubMed] [Google Scholar]
- 34.Kuh H. J., Jang S. H., Wientjes M. G., Au J. L. Computational model of intracellular pharmacokinetics of paclitaxel. J. Pharmacol. Exp. Ther. 2000;293(3):761–770. [PubMed] [Google Scholar]
- 35.Riccardi A., Servidei T., Tornesello A., Puggioni P., Mastrangelo S., Rumi C., et al. Cytotoxicity of paclitaxel and docetaxel in human neuroblastoma cell-lines. Eur. J. Cancer. 1995;31A(4):494–499. doi: 10.1016/0959-8049(95)00056-O. [DOI] [PubMed] [Google Scholar]
- 36.Hassan S. B., Jonsson E., Larsson R., Karlsson M. O. Model for time dependency of cytotoxic effect of CHS 828 in vitro suggests two different mechanisms of action. J. Pharmacol. Exp. Ther. 2001;299(3):1140–1147. [PubMed] [Google Scholar]
- 37.Donaldson K. L., Goolsby G., Kiener P. A., Wahl A. F. Activation of P34(Cdc2) coincident with taxol-induced apoptosis. Cell Growth Differ. 1994;5(10):1041–1050. [PubMed] [Google Scholar]
- 38.Torres K., Horwitz S. B. Mechanisms of taxol-induced cell death are concentration dependent. Cancer Res. 1998;58(16):3620–3626. [PubMed] [Google Scholar]
- 39.Kern D. H., Morgan C. R., Hildebrandzanki S. U. Invitro pharmacodynamics of 1-beta-d-arabinofuranosylcytosine—synergy of antitumor-activity with cis-diamminedichloroplatinum(Ii) Cancer Res. 1988;48(1):117–121. [PubMed] [Google Scholar]
- 40.Hector S., Bolanowska-Higdon W., Zdanowicz J., Hitt S., Pendyala L. In vitro studies on the mechanisms of oxaliplatin resistance. Cancer Chemother. Pharmacol. 2001;48(5):398–406. doi: 10.1007/s002800100363. [DOI] [PubMed] [Google Scholar]
- 41.Mishima M., Samimi G., Kondo A., Lin X., Howell S. B. The cellular pharmacology of oxaliplatin resistance. Eur. J. Cancer. 2002;38(10):1405–1412. doi: 10.1016/S0959-8049(02)00096-5. [DOI] [PubMed] [Google Scholar]
- 42.Binks S. P., Dobrota M. Kinetics and mechanism of uptake of platinum-based pharmaceuticals by the rat small-intestine. Biochem. Pharmacol. 1990;40(6):1329–1336. doi: 10.1016/0006-2952(90)90400-F. [DOI] [PubMed] [Google Scholar]
- 43.Ghezzi A., Aceto M., Cassino C., Gabano E., Osella D. Uptake of antitumor platinum(II)-complexes by cancer cells, assayed by inductively coupled plasma mass spectrometry (ICP-MS) J. Inorg. Biochem. 2004;98(1):73–78. doi: 10.1016/j.jinorgbio.2003.08.014. [DOI] [PubMed] [Google Scholar]
- 44.Pereira-Maia E., Garnier-Suillerot A. Impaired hydrolysis of cisplatin derivatives to aquated species prevents energy-dependent uptake in GLC4 cells resistant to cisplatin. J. Biol. Inorg. Chem. 2003;8(6):626–634. doi: 10.1007/s00775-003-0458-3. [DOI] [PubMed] [Google Scholar]
- 45.Rupniak H. T., Whelan R. D., Hill B. T. Concentration and time-dependent inter-relationships for antitumour drug cytotoxicities against tumour cells in vitro. Int. J. Cancer. 1983;32(1):7–12. doi: 10.1002/ijc.2910320103. [DOI] [PubMed] [Google Scholar]
- 46.Kurihara N., Kubota T., Hoshiya Y., Otani Y., Kumai K., Kitajima M. Antitumor activity of cis-diamminedichloroplatinum (II) depends on its time x concentration product against human gastric cancer cell lines in vitro. J. Surg. Oncol. 1995;60(4):238–241. doi: 10.1002/jso.2930600405. [DOI] [PubMed] [Google Scholar]
- 47.Kornmann M., Fakler H., Butzer U., Beger H. G., Link K. H. Oxaliplatin exerts potent in vitro cytotoxicity in colorectal and pancreatic cancer cell lines and liver metastases. Anticancer Res. 2000;20(5A):3259–3264. [PubMed] [Google Scholar]
- 48.Mohammed M. Q., Retsas S. Oxaliplatin is active in vitro against human melanoma cell lines: comparison with cisplatin and carboplatin. Anticancer Drugs. 2000;11(10):859–863. doi: 10.1097/00001813-200011000-00010. [DOI] [PubMed] [Google Scholar]
- 49.K. W. Vugrin, L. P. Swiler, R. M. Roberts, N. J. Stucky-Mack, and S. P. Sullivan. Confidence region estimation techniques for nonlinear regression: three case studies. SAND2005–6893. 1–10–2005. Albuquerque NM, Sandia National Laboratories. Sandia Report.
- 50.Siwak D. R., Shishodia S., Aggarwal B. B., Kurzrock R. Curcumin-induced antiproliferative and proapoptotic effects in melanoma cells are associated with suppression of I kappa B kinase and nuclear factor KB activity and are independent of the B-Raf/mitogen-activated/extracellular signal-regulated protein kinase pathway and the Akt pathway. Cancer. 2005;104(4):879–890. doi: 10.1002/cncr.21216. [DOI] [PubMed] [Google Scholar]
- 51.Photiou A., Sheikh M. N., Bafaloukos D., Retsas S. Antiproliferative activity of vinorelbine (navelbine) against 6 human-melanoma cell-lines. J. Cancer Res. Clin. Oncol. 1992;118(4):249–254. doi: 10.1007/BF01208613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Derenzini M., Montanaro L., Trere D., Chilla A., Tazzari P. L., Dall’Olio F., et al. Thymidylate synthase protein expression and activity are related to the cell proliferation rate in human cancer cell lines. J. Clin. Pathol.: Mol. Pathol. 2002;55(5):310–314. doi: 10.1136/mp.55.5.310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ma T., Zhu Z. G., Ji Y. B., Zhang Y., Yu Y. Y., Liu B. Y., et al. Correlation of thymidylate synthase, thymidine phosphorylase and dihydropyrimidine dehydrogenase with sensitivity of gastrointestinal cancer cells to 5-fluorouracil and 5-fluoro-2′-deoxyuridine. World J. Gastroenterol. 2004;10(2):172–176. doi: 10.3748/wjg.v10.i2.172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Akiyama S., Amo H., Watanabe T., Matsuyama M., Sakamoto J., Imaizumi M., et al. Characteristics of 3 human gastric-cancer cell-lines, Nu-Gc-2, Nu-Gc-3 and Nu-Gc-4. Jpn. J. Surg. 1988;18(4):438–446. doi: 10.1007/BF02471470. [DOI] [PubMed] [Google Scholar]
- 55.Morgan R. T., Woods L. K., Moore G. E., Quinn L. A., Mcgavran L., Gordon S. G. Human cell-line (Colo 357) of metastatic pancreatic adenocarcinoma. Int. J. Cancer. 1980;25(5):591–598. doi: 10.1002/ijc.2910250507. [DOI] [PubMed] [Google Scholar]
- 56.Yao K., Gietema J. A., Shida S., Selvakumaran M., Fonrose X., Haas N. B., et al. In vitro hypoxia-conditioned colon cancer cell lines derived from HCT116 and HT29 exhibit altered apoptosis susceptibility and a more angiogenic profile in vivo. Br. J. Cancer. 2005;93(12):1356–1363. doi: 10.1038/sj.bjc.6602864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chen Z. H., Olopade O. I., Savarese T. M. Expression of methylthioadenosine phosphorylase cDNA in p16(-), MTAP(-) malignant cells: Restoration of methylthioadenosine phosphorylase-dependent salvage pathways and alterations of sensitivity to inhibitors of purine de novo synthesis. Mol. Pharmacol. 1997;52(5):903–911. doi: 10.1124/mol.52.5.903. [DOI] [PubMed] [Google Scholar]
- 58.Tacka K. A., Szalda D., Souid A. K., Goodisman J., Dabrowiak J. C. Experimental and theoretical studies on the pharmacodynamics of cisplatin in Jurkat cells. Chem. Res. Toxicol. 2004;17(11):1434–1444. doi: 10.1021/tx0498760. [DOI] [PubMed] [Google Scholar]
- 59.Sheiner L. B., Beal S. L. Some suggestions for measuring predictive performance. J. Pharmacokinet. Biopharm. 1981;9(4):503–512. doi: 10.1007/BF01060893. [DOI] [PubMed] [Google Scholar]
- 60.Tseng S. H., Bobola M. S., Berger M. S., Silber J. R. Characterization of paclitaxel (Taxol) sensitivity in human glioma- and medulloblastoma-derived cell lines. Neuro-oncol. 1999;1(2):101–108. doi: 10.1093/neuonc/1.2.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Welters M. J. P., FichtingerSchepman A. M. J., Baan R. A., Hermsen M. A. J. A., VanderVijgh W. J. F., Cloos J., et al. Relationship between the parameters cellular differentiation, doubling time and platinum accumulation and cisplatin sensitivity in a panel of head and neck cancer cell lines. Int. J. Cancer. 1997;71(3):410–415. doi: 10.1002/(SICI)1097-0215(19970502)71:3<410::AID-IJC18>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- 62.Jackel M., Kopfmaier P. Influence of cisplatin on cell-cycle progression in xenografted human head and neck carcinomas. Cancer Chemother. Pharmacol. 1991;27(6):464–471. doi: 10.1007/BF00685161. [DOI] [PubMed] [Google Scholar]
- 63.Jackel M. C., TauschTreml R., Kopfmaier P. Cytokinetic effects of cisplatin on diverse human head and neck carcinomas in vitro: dependence on the tumor sensitivity to cisplatin. J. Cancer Res. Clin. Oncol. 1996;122(10):596–602. doi: 10.1007/BF01221191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Pasquier E., Carre M., Pourroy B., Camoin L., Rebai O., Briand C., et al. Antiangiogenic activity of paclitaxel is associated with its cytostatic effect, mediated by the initiation but not completion of a mitochondrial apoptotic signaling pathway. Mol. Cancer Ther. 2004;3(10):1301–1310. [PubMed] [Google Scholar]
- 65.Schuldes H., Bade S., Knobloch J., Jonas D. Loss of in vitro cytotoxicity of cisplatin after storage as stock solution in cell culture medium at various temperatures. Cancer. 1997;79(9):1723–1728. doi: 10.1002/(SICI)1097-0142(19970501)79:9<1723::AID-CNCR13>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- 66.Ringel I., Horwitz S. B. Taxol is converted to 7-epitaxol, a biologically-active isomer, in cell-culture medium. J. Pharmacol. Exp. Ther. 1987;242(2):692–698. [PubMed] [Google Scholar]
- 67.Iliadis A., Barbolosi D. Optimizing drug regimens in cancer chemotherapy by an efficacy-toxicity mathematical model. Comput. Biomed. Res. 2000;33(3):211–226. doi: 10.1006/cbmr.2000.1540. [DOI] [PubMed] [Google Scholar]
- 68.Martin R. B., Fisher M. E., Minchin R. F., Teo K. L. A mathematical model of cancer chemotherapy with an optimal selection of parameters. Math. Biosci. 1990;99(2):205–230. doi: 10.1016/0025-5564(90)90005-J. [DOI] [PubMed] [Google Scholar]
- 69.Zhang S. Z., Lovejoy K. S., Shima J. E., Lagpacan L. L., Shu Y., Lapuk A., et al. Organic cation transporters are determinants of oxaliplatin cytotoxicity. Cancer Res. 2006;66(17):8847–8857. doi: 10.1158/0008-5472.CAN-06-0769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Fichtinger-Schepman A. M., Dijt F. J., Bedford P., van Oosterom A. T., Hill B. T., Berends F. Induction and removal of cisplatin-DNA adducts in human cells in vivo and in vitro as measured by immunochemical techniques. IARC Sci. Publ. 1988;89:321–328. [PubMed] [Google Scholar]
- 71.Koberle B., Grimaldi K. A., Sunters A., Hartley J. A., Kelland L. R., Masters J. R. W. DNA repair capacity and cisplatin sensitivity of human testis tumour cells. Int. J. Cancer. 1997;70(5):551–555. doi: 10.1002/(SICI)1097-0215(19970304)70:5<551::AID-IJC10>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 72.Samimi G., Howell S. B. Modulation of the cellular pharmacology of JM118, the major metabolite of satraplatin, by copper influx and efflux transporters. Cancer Chemother. Pharmacol. 2006;57(6):781–788. doi: 10.1007/s00280-005-0121-5. [DOI] [PubMed] [Google Scholar]
- 73.Sadler P. J., Guo Z. J. Metal complexes in medicine: design and mechanism of action. Pure Appl. Chem. 1998;70(4):863–871. doi: 10.1351/pac199870040863. [DOI] [Google Scholar]
- 74.Steel G. G., Peckham M. J. Exploitable mechanisms in combined radiotherapy-chemotherapy - concept of additivity. Int. J. Radiat. Oncol. Biol. Phys. 1979;5(1):85–91. doi: 10.1016/0360-3016(79)90044-0. [DOI] [PubMed] [Google Scholar]
- 75.Loewe S. The problem of synergism and antagonism of combined drugs. Arzneimittelforschung. 1953;3(6):285–290. [PubMed] [Google Scholar]
- 76.Adams D. J., Watkins P. J., Knick V. C., Tuttle R. L., Bair K. W. Evaluation of arylmethylaminopropanediols by a novel in vitro pharmacodynamic assay: correlation with antitumor activity in vivo. Cancer Res. 1990;50(12):3663–3669. [PubMed] [Google Scholar]