Allostery and cooperativity revisited

Abstract

Although phenomenlogical models that account for cooperativity in allosteric systems date back to the early and mid-60's (e.g., the KNF and MWC models), there is resurgent interest in the topic due to the recent experimental and computational studies that attempted to reveal, at an atomistic level, how allostery actually works. In this review, using systems for which atomistic simulations have been carried out in our groups as examples, we describe the current understanding of allostery, how the mechanisms go beyond the classical MWC/Pauling-KNF descriptions, and point out that the “new view” of allostery, emphasizing “population shifts,” is, in fact, an “old view.” The presentation offers not only an up-to-date description of allostery from a theoretical/computational perspective, but also helps to resolve several outstanding issues concerning allostery.

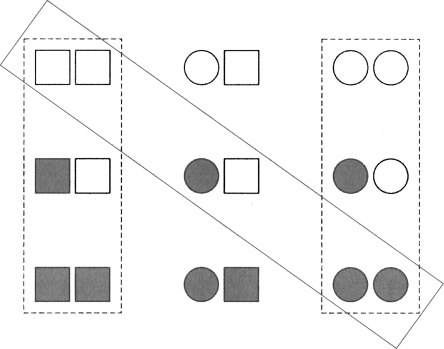
Control at the molecular level is one of the essential elements of cellular function, and is exercised both within molecules and between molecules. Intramolecular control often involves the effect of one ligand on the binding or catalysis of another with no direct interaction between the two ligands. To describe such interaction at a distance, the adjective “allosteric”¹ was introduced in 1961 by Jacques Monod and François Jacob in their summary article for the Cold Spring Harbor Symposium on Cellular Regulatory Mechanisms (Monod and Jacob 1961). They coined the term to characterize the experiments of Jean-Pierre Changeux, who was at the time a student in Monod's laboratory, on end-product inhibition of the enzyme, L-threonine deaminase (Changeux 1961). Since the end product, in this case L-isoleucine, differs sterically from the reactant, L-threonine, the proposal was made that by binding at a different, nonoverlapping (regulatory) site, the former could inhibit the enzyme without competing with the latter.² Although the term allosteric was coined only in 1961, more than 25 years before (in 1935) Pauling (Pauling 1935) had proposed a model for intramolecular control in hemoglobin to explain the positive cooperativity observed in the binding of oxygen molecules. The Pauling model was taken up in 1966 by Koshland et al. (1966) and is now generally referred to as the KNF model (see Fig. 1).

Figure 1.

Models for allostery. Pictorial representation of Pauling-KNF model and MWC model for a homodimer. Tertiary t and r states are indicated by squares and circles, respectively; liganded and unliganded states by filled and empty symbols, respectively. The states along the diagonal dotted line correspond to the Pauling-KNF model, in which there are only tertiary structural changes, and the left and right vertical columns to the MWC model, in which only quaternary structural changes occur. (The left column refers to the T state and the right column to the R state.) More complex models include all the states. Partition function for Pauling-KNF model: Ξ = 1 + 2Kλ + αK² λ ². K is the ligand binding constant for an individual subunit and α is the interaction constant; α is greater (less than) unity for positive (negative) cooperativity. Partition function for MWC model: Ξ = L(1 + cKλ)² + (1 + Kλ)². L is the equilibrium constant between the unligand T and R structures (L = [T]/[R]), K is the binding constant for a subunit in the R state and c is the reduction factor for binding to the T state.

In 1965, the view of allostery was revolutionized when Monod, Wyman, and Changeux published their landmark paper (referred to here, and generally, as the MWC model) (Monod et al. 1965), which is as important today as it was then. (See also, the surprisingly precise definition in the Merriam-Webster's Collegiate Dictionary [10th edition], p. 31: “of, relating to, or being a change in the shape and activity of a protein [as an enzyme] that results from combination with another substance at a point other than the chemically active site.) Monod et al. (1965) described allostery as follows:

“… indirect interactions between distinct binding sites (allosteric effects) … these interactions are mediated by some kind of molecular transition (allosteric transition) which is induced or stabilized by the protein when it binds an allosteric ligand.”

This statement concerning allostery implies that the entire molecule can undergo a conformational transition even when it is only partially liganded. The MWC paper developed an elegant model for allostery based on specific postulates, which codify this idea (see Fig. 1): (1) Allosteric proteins are oligomers made of identical monomers in a symmetric arrangement; and (2) the allosteric effect is produced by binding of a ligand that leads to a change in the quaternary structure by rotation of the subunits about an axis so as to preserve the symmetry of the oligomer. A corollary of the model is that the different quaternary structures are accessible in both the liganded and unliganded form and that the change in the equilibrium between the conformers on ligand binding leads to the allosteric effect. In the model, cooperative (homotropic) effects between the primary ligands and signaling (heterotropic) effects involving secondary ligands are distinguished. The MWC model has found widespread applications in biology (for a recent review, see Brunori et al. 2006), from the classic case of hemoglobin (Eaton et al. 1999) to membrane receptors (Changeux and Edelstein 2005), and it has been generalized in many ways, including an extension to infinite arrays (Duke and Bray 1999).

Forty years after MWC and 70 years after Pauling, it is useful to examine what the intervening time has taught us concerning allostery. We focus initially on the MWC model in part because it has been shown for a number of well-studied systems, such as hemoglobin, to be the correct zero-order model, and in part because the original formulation is very precise and can best serve as a basis for introducing the developments in our understanding that have taken place since its original formulation. The rigor of the MWC model has been important in its widespread applications, but when it is interpreted in a literal sense, there are limitations. It appears that the investigators recognized this and decided not to sacrifice elegance for completeness (Changeux and Edelstein 2005; Brunori et al. 2006; J-P. Changeux, pers. comm.). The first assumption that allosteric effects can occur only in oligomeric proteins has to be revised; i.e., many monomeric proteins show allosteric effects to be of functional importance. The second assumption of symmetry is also not satisfied by numerous allosteric proteins. Further, a quaternary structural change is not always required for allostery in oligomeric systems. Negative cooperativity, which is more rarely observed, is not treated by the simple MWC model with equivalent subunits, and an alternative description (e.g., that supplied by the Pauling-KNF model) appears to be required. However, it should be noted that an extended MWC model can yield negative cooperativity (as defined by a Hill coefficient less than unity) (Kister et al. 1987). Finally, the implied assumption that the oligomers behave as rigid units prevents the transition from the mathematical MWC model to an atomic level description. Both the MWC and the Pauling-KNF models are phenomenological, and so do not answer the fundamental question of how the binding of a ligand or its modification yield the observed allosteric effect at an atomic level of detail. Present day applications of computational methods to biomolecular systems, combined with structural, thermodynamic, and kinetic studies, make possible an approach to that question, so as to provide a deeper understanding of the requirements for allostery. The primary purpose of this review is to describe specific examples, mainly from our own work, germane to these points and, secondarily, to comment on the relation of so-called “new views” of allostery (see, for example, Gunasekaran et al. 2004), which emphasize “population shifts,” to the understanding derived from these examples.

Knowledge of the mechanism by which conformational change occurs in biomolecules is essential for a fundamental analysis of allostery. The prescient statement in Richard Feynman's Lectures in Physics published in 1963, “… everything that living things do can be understood in terms of the jigglings and wigglings of atoms” serves as the basis for atomic-level descriptions of conformational change (Feynman et al. 1963). However, the proposal of Feynman had to wait nearly 25 years before the first molecular dynamics simulation of a protein provided a quantitative measure of the motions involved (McCammon et al. 1977). The simulation made clear that proteins are relatively soft polymers and, consequently, have significant structural fluctuations at room temperature; i.e., the static view of the structure of biomolecules (Phillips 1981) had to be replaced by a dynamic picture. It is now recognized that the atoms of which biomolecules are composed are in a state of constant motion at ordinary temperatures. The X-ray structure of a protein provides the average atomic positions, but the atoms exhibit fluid-like motions of sizable amplitudes about these averages. Average atomic positions make possible a discussion of many aspects of biomolecular function in the language of structural chemistry. Inclusion of the atomic fluctuations opens the way to a more sophisticated and accurate interpretation of protein activity that is essential for understanding the mechanism of allostery (Brooks II et al. 1988). It is now clear that there is a complementarity between structure and dynamics in that the conformational changes that play a functional role in allostery, as well as in protein more generally (the molecular machines of which a cell is composed) (Alberts 1998), are coded into the structure (Karplus and Gao 2004). This has been demonstrated explicitly by normal mode studies (Cui and Bahar 2006), which show that the functional motions are generally well described by a few low-frequency modes (Cui et al. 2004). Many allosteric proteins are, in fact, constructed from semi-rigid domains or subdomains with hinges and/or semi-rigid subunits, which can move relative to each other, so that the “jigglings and wigglings” (Brownian motion, which is always present at physiological temperatures) can be harnessed through biasing of the free energy surface by ligand binding, modification, and release.⁴

Tetrametric hemoglobin—the allosteric paradigm

Hemoglobin has long been the prototype system for the investigation of allostery and cooperativity in macromolecules. We, therefore, describe the development of our understanding of this molecule in some detail. It was the first allosteric protein for which an X-ray structure (at 5.5 Å resolution) demonstrated that it was a symmetric tetramer (Muirhead and Perutz 1963), and it has been studied more than any other allosteric protein by structural, thermodynamic, kinetic, and computational methods. The review of Eaton et al. (1999) shows convincingly that the MWC model, albeit in a somewhat elaborated form, can provide a very accurate description of the cooperative thermodynamics and kinetics. Given the phenomenological characterization based on the MWC model, it is now possible to go beyond that description and determine how allostery “works” in tetrameric hemoglobin. The essential aim of such an analysis is to find the detailed relationship at the atomic level between structural changes induced by ligation and the thermodynamic and kinetic manifestations of allostery and cooperativity.

The X-ray structures of unliganded and liganded hemoglobin solved by Perutz and his collaborators (Perutz 1970) indicated that there exists two quaternary structures (deoxy, T, and oxy, R) for the tetramer and two tertiary structures for each individual chain (liganded r and unliganded t). Based on the structural results and other data, Perutz proposed a stereochemical mechanism for cooperativity, in which salt bridges (some with ionizable protons in the neutral pH range) provide the link between ligand-induced tertiary structural changes and the relative stability of the two quaternary forms. The elements of the Perutz mechanism were incorporated into a structure-based statistical–mechanical model (Szabo and Karplus 1972) that utilizes a partition function to describe the influence of homotropic (oxygen) and heterotropic (protons and 2,3-bisphosphoglycerate) effectors on the set of contributing structures. An essential element in the model is the quantitative evaluation of the effects of specific tertiary structural changes induced by ligand binding on the stability of the T and R quaternary structures; this provides a basis for the shift of the equilibrium between them, which leads to the sigmoidal (cooperative) ligand binding as a function of concentration. The model provides a satisfactory description of the cooperativity in ligand binding, the alkaline Bohr effect, the effect of 2,3-bisphosphoglycerate on ligand affinity, and the influence of chemical modifications and certain mutations on these properties (Szabo and Karplus 1975). Importantly, the values of the model parameters, which correspond to physically meaningful quantities, were in the range suggested by independent estimates, thus providing support for the basic postulates of the Perutz mechanism. Comparisons of a series of crystal structures of unliganded T and liganded R tetramers with liganded R tetramers and unliganded T tetramers (Perutz 1970; Fermi and Perutz 1981) showed that there is significant coupling between the tertiary conformation of a subunit and the quaternary structure of the tetramer. These results led to an improved model with two tertiary structures (unliganded and liganded) in both the T and R tetramers (Lee and Karplus 1983; Henry et al. 2002). The new model introduced ligand-binding restraints coupled to both tertiary and quaternary structural change. This is in accord with the more detailed description based on empirical energy function calculations (Gelin et al. 1983), which have demonstrated that the low affinity of the deoxy quaternary structure arises not only from the perturbation of salt bridges but also from steric constraints imposed by contacts at the α₁β₂ and α₂β₁ interfaces that transmit the ligation-induced strain in the “allosteric core” (the heme, proximal histidine, F helix, and the FG corner of each subunit) from one subunit to another.

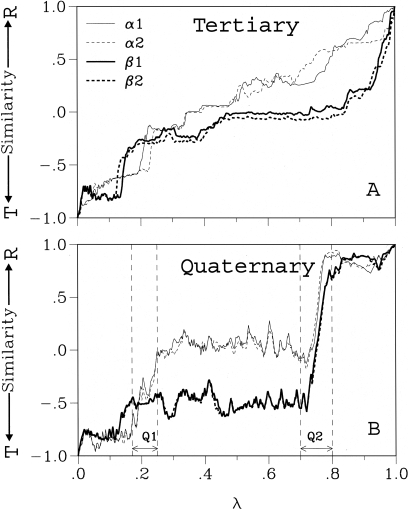
Reaction path calculations from the T state to the R state (Olsen et al. 2000) indicate that tertiary structural changes precede the quaternary transition; i.e., tertiary changes induced by ligand binding are required to stabilize the R state in accord with the above discussion (Fig. 2). Although the rate of the T to R transition has not been measured (there is no single obvious “trigger” to obtain a synchronized T to R transition in an ensemble of molecules, although single molecule experiments could, in principle, be used), we can estimate it from the experimentally determined R to T transition rates and the R/T equilibrium constant. For the unliganded hemoglobin tetramer, indicated by the subscript “o,” the R_o to T_o rate is about 20 μsec (Sawicki and Gibson 1976; Jones et al. 1992). With the equilibrium constant of [T_o/R_o] ≈ 5 × 10⁶, the T_o to R_o rate is calculated to be very slow, on the order of seconds, with the major contribution to the activation barrier coming from the equilibrium free energy difference between T_o and R_o. Since this equilibrium shift toward R with ligand binding (it changes from T_o/R_o ≈ 10⁵ to 10⁶ in the unligand state to T₄/R₄ ≈ 10⁻³ in the fully liganded state), the intrinsic free energy activation barrier for the quaternary change is expected to dominate for T₃ to R₃; a reasonable hypothesis is that the rate is similar to the R_o to T_o transition (i.e., on the microsecond timescale). The major tertiary structural change on photodissociation of the ligand is on the nanosecond timescale in myoglobin (Kuczera et al. 1993; Lim et al. 1993) and hemoglobin (P. Anfinrud, pers. comm.). Again, there is no value for the transition rate on ligand binding, but the type of local relaxation involved suggests it is also on the nanosecond timescale. Thus, although the T and R state are in equilibrium in both the unliganded and liganded tetramer, the transition between the two is likely to be slow compared to the tertiary structure changes. Once a tertiary structural change takes place as each ligand binds, the tetramer has a higher probability of diffusing from the T state toward the R state (Karplus 2000), which is now relatively more stable.

Figure 2.

Tertiary and quaternary structural change in hemoglobin. The similarity to both end states (R and T) are plotted for structures obtained along the path (measured as the normalized root-mean-square deviation [RMSD] from the R[1] and T[−1] structures). For example, a value close to 1 (respectively, +1) indicates that the structure is very similar to the T state (respectively, R state); a value of zero indicates that the structure is equidistant from the two end states. Before calculating the RMSD, the two structures are superimposed by using a least-square fit. This makes possible a separation of the tertiary from the quaternary changes. For the tertiary change the least-square fit is done with respect to the atoms of each subunit, whereas for the quaternary change the least-square fit involves all atoms of the protein. Contributions from intrasubunit change were removed approximately from the quaternary similarity by substituting the internal coordinates of each subunit with those of a constant structure (chosen here as the average of T and R). The reaction coordinate λ is the normalized sum along the path of the change in all atomic coordinates. (A) The tertiary (i.e., intrasubunit) and (B) the quaternary (i.e., intersubunit) similarity are shown separately for each of the four subunits. The first (Q1) and second (Q2) major quaternary events are indicated (see Olsen et al. 2000).

It has been suggested recently, based on NMR data for dihydrofolate reductase (Boehr et al. 2006), that ligand binding does not take place in the dominant conformer but rather in a higher energy configuration that is present to a small degree in the unliganded state but has a greater affinity; a corresponding proposal was made for catalysis in this system. Although further studies are required to prove this interesting suggestion, one aspect of it can be tested for hemoglobin; i.e., that ligand binding occurs not to the T_o state but rather to the small population of R_o state that is present. The equilibrium between T_o and R_o (see above) and the kinetic rate constants for ligand binding to the T_o and R_o states have been measured (Eaton et al. 1999). They show that binding of the first ligand is to the low-affinity state (T_o) and not to the high-affinity (R_o) state; the fourth oxygen does bind to the R state because that is now the predominant species. Whether there are fluctuations in the tertiary structure of a subunit in the T state that favor ligation at the time a ligand binds is not known.

The overview presented here indicates that we do know how allostery “works” in vertebrate tetrameric hemoglobins. Coupling between fast tertiary structural changes and a slow quaternary structural transition are essential elements of the mechanism, demonstrating the importance of relaxing the requirement for a pure quaternary transition inherent in the original MWC model.

Cooperativity in dimeric hemoglobin: Water-mediated allostery without quaternary change

Dimeric hemoglobin of the blood clam Scapharca (HbI) is composed of two subunits with the myoglobin fold (Royer Jr. et al. 1990). However, the assembly of the subunits is very different from that in HbA; i.e., the interface in HbI is formed by the E and F helices, which face the solvent in HbA. As a result, the two heme groups are nearly in direct contact. Also unlike HbA, no major quaternary changes occur upon binding of oxygen to HbI (the heavy-atom RMSD between the liganded and unliganded structure of HbI is 1.3 Å), and the tertiary structural changes are small and localized near the heme group. Nevertheless, HbI is highly cooperative; the binding of oxygen to its two equivalent binding sites has a Hill coefficient of 1.5 (Chiancone et al. 1981; Ikeda-Saito et al. 1983), similar to the value (1.36–1.72) for human hemoglobin (HbA) when two of the Fe⁺² are replaced by nonreactive Ni⁺² (Shibayama et al. 1993). Thus, the mechanism of cooperativity must be very different from that of the vertebrate hemoglobins described above.

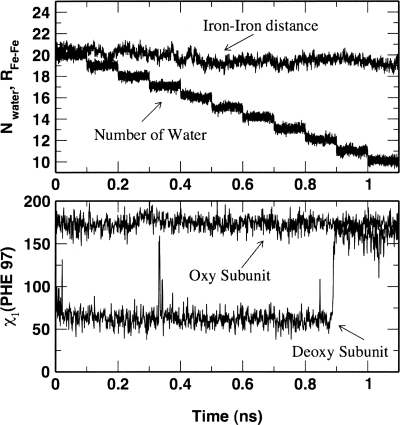
The most significant tertiary change between deoxy and oxy HbI is the reorientation of the side chain of Phe 97 (Royer Jr. et al. 1990; Royer Jr. 1994). As a result, the phenyl group is displaced from the neighborhood of the heme pocket into the interface between the two subunits. Further, 17 (ordered) waters observed between the two subunits in deoxy HbI are reduced to only 11 in oxy HbI. Mutation of Phe 97 to Leu leads to a reduction of the Hill coefficient to 1.2 (Pardanani et al. 1997), supporting an important role for Phe 97 in cooperativity. Both the reorientation of Phe 97 in the binding pocket and the change in the number of interfacial waters have been implicated in the cooperative mechanism. To obtain further insight into the origin of the structural changes and their role in the cooperative mechanism, an intermediate with one liganded and one unliganded subunit was constructed and investigated by molecular dynamics simulations (Zhou et al. 2003). Such an intermediate corresponds to the doubly liganded intermediates in HbA, which have played an important role in understanding cooperativity in that molecule; e.g., it is the concentration of double-liganded intermediates that distinguishes between the MWC (Monod et al. 1965) and Pauling-KNF models (Pauling 1935; Koshland et al. 1966). Since, unlike HbA, no structures for intermediates or their analogs are available, they were constructed by combining subunits from the unliganded and liganded dimers; because of the small structural changes between the two species, little relaxation was required to obtain a stable structure. A recent time-resolved X-ray study of the allosteric transition in HbI (Knapp et al. 2006) gives some information about the intermediate and it is hoped that a structure for it will be forthcoming (W. Royer Jr., pers. comm.). The major structural changes (repositioning of the ring of Phe 97 and the change of iron–iron distance) found by comparing the unliganded and fully liganded X-ray structures are stable in molecular dynamics simulations of the half-liganded intermediate. The number of interfacial waters was then used as an umbrella sampling coordinate for the hybrid system, and it was shown that reduction in their number (a drier, oxy-like interface) promotes the conformational change of Phe 97 from its deoxy to oxy position (Fig. 3). Moreover, the latter leads to a higher-binding affinity as a result of stronger H-bonding of the heme to the proximal histidine (Zhou et al. 2003). Thus, HbI represents a very different cooperative mechanism from that in vertebrate hemoglobins; it is a dimeric system, in which tertiary structural changes, without quaternary changes, and the number of waters in the dimer interface play the essential role.

Figure 3.

Role of water in allostery of the dimeric Scarpharca hemoglobin. (Top) The number of interfacial water molecules and the distance between irons as a function of time in the constrained molecular dynamic simulation. (Bottom) The corresponding dihedral angle χ1 for Phe 97 side chains (see Zhou et al. 2003).

GroEL: Tertiary structural changes of the subunits lead to cooperativity of the symmetric heptamer ring

Although many proteins fold spontaneously in dilute solution (Anfinsen 1973), the folding process is complicated in the cellular medium due to the high concentration of other molecules (Ellis and Hartl 1999). They can interfere with the folding to the native state and may cause misfolding or aggregation of denatured proteins, leading to disease and death in some cases (Dobson 2002). One mechanism to prevent such problems in the cell is the protection of the newly synthesized protein chains by chaperones (Hartl 1996; Saibil 2000). The best-studied chaperone is the bacterial chaperonin, GroEL, a large protein shaped like a double-ring (Boisvert et al. 1996; Xu et al. 1997; Grallert and Buchner 2001). The rings are composed of seven identical subunits, which enclose a central cavity. Each subunit consists of three domains: the large equatorial domain, which contains the adenosine triphosphate (ATP) binding site, and couples the two rings; the apical domain, which forms the ring entrance and is important for substrate binding (Fenton et al. 1994); and the smaller intermediate domain, which connects the equatorial and apical domains.

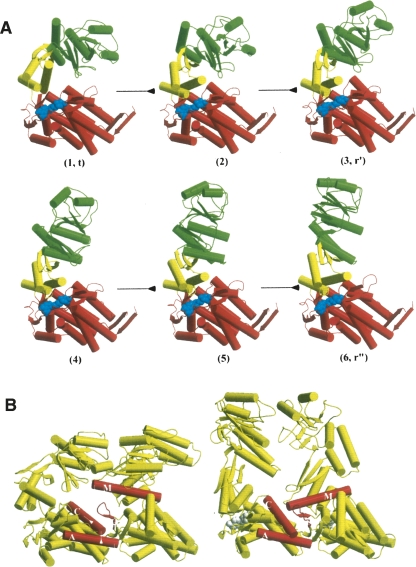
Experiments have shown that the chaperone function involves large conformational changes in each of the two rings, which alternate between two conformations in the GroEL cycle. There is cooperativity of ATP binding and hydrolysis within one ring and anti-cooperativity between the rings. The denatured protein substrate is first bound to the apical domains of one of the rings (called the cis ring) (Weissman et al. 1996; Rye et al. 1997, 1999) in the closed (or t tertiary) state. The GroEL transition, which is initiated by ATP binding to the equatorial domains of the cis ring (Inobe et al. 2001) first goes to an intermediate structure, called r′ (see Fig. 4), that has been visualized by simulations and cryoelectron microscopy. It has been shown by simulations (Ma et al. 2000; van der Vaart et al. 2004; Hyeon et al. 2006) and confirmed by cryoelectron microscopy (Ranson et al. 2001) that the first step in the t to r′ transition after binding of ATP is a downward twisting motion of the intermediate domain that is the trigger for the major conformational changes (Fig. 4). The intermediate domain is pulled down by its interaction with ATP to close the ATP binding pocket. This releases its coupling to the apical domain of a neighboring subunit so as to permit its upward motion. Simultaneously, the intermediate domain pushes downward on the equatorial domain in the enlarged GroEL cavity (Ma et al. 2000; van der Vaart et al. 2004). The r′ state is reached by an upward motion and, looking down from the top of the cis ring, a clockwise rotation of the apical domains. Interestingly, recent cryoelectron microscopy studies (Ranson et al. 2001) and simulations (Ma et al. 2000; van der Vaart et al. 2004) have shown that the initial motion is actually anticlockwise. Binding of the co-chaperone GroES to the cis ring results in a large upward, twisting motion of the apical domains to achieve the fully open structure called r″. The essential cooperativity of the motion within the cis ring has been demonstrated experimentally by cross-linking (Thirumalai and Lorimer 2001) and mutation (Danziger et al. 2003) experiments. The simulations have demonstrated that the cooperativity is due to both steric and electrostatic effects (Ma et al. 2000; van der Vaart et al. 2004). The steric effects arise from van der Waals repulsions, which can be avoided only by a concerted “opening” motion of the apical domains of the seven subunits in the cis ring. The electrostatic effects involve an intraring, intersubunit salt bridge between Glu386 and Arg197, which is broken by the intermediate domain motion. Anti-cooperativity between the rings is primarily due to steric effects. The twisting of the equatorial domains upon ATP binding would result in severe van der Waals clashes if binding occurred simultaneously in both rings (Ma et al. 2000); this is analogous to the fact that in tetrameric hemoglobin, the unligand T quaternary conformation is not strained and strain is introduced by the tertiary conformational change induced by ligation. Overall, the observed allosteric pathway of GroEL, which is understood from simulations and mutant studies, is the result of coupled tertiary structure changes, rather than quaternary structural effects in this symmetric molecule (van der Vaart et al. 2004; Horowitz and Willison 2005). Nevertheless, a phenomenal description in terms of a mixture of the MWC model for the intraring cooperativity and the Pauling-KNF model for the interring anti-cooperativity is applicable (Yifroch and Horovitz 1995).

Figure 4.

Conformational change in the GroEL cycle. (A) A set of structures on the path showing the behavior of a single subunit (apical domain in green, intermediate domain in yellow, equatorial domain in red; the nucleotide is shown in blue): (1) through (3) correspond to the first stages associated with nucleotide binding; (4) through (6) correspond to the second stage involving GroES binding. The early downward motion of the intermediate domain (compare [1,t] with [2] and [6,r″]) is the trigger for the overall transition. (B) The mechanism of the intermediate domain trigger. Two adjacent subunits from the crystal structures are shown in a view looking out from the inside. The key structural elements are in red; they are helices A, C, M, and the stem loop. The downward motion of helix M of the intermediate domain frees the apical domain for its upward movement and twist and also stabilizes the inclination of the equatorial domain. The arrows indicate the direction of the motion of the helices; the arrow along the axial direction of the C helix corresponds to an axial translation (see Ma et al. 2000).

Allostery in monomeric systems: CheY, a response regulator in bacterial chemotaxis

It is increasingly clear that allostery occurs in many monomeric systems. Examples include small signaling proteins, various molecular motors (Vale and Milligan 2000), ion pumps (Stokes and Green 2003), and even small ribozymes (Rueda et al. 2004). The small size of some of the systems makes them suitable for detailed NMR and simulation studies, which have provided detailed insights concerning the mechanism.

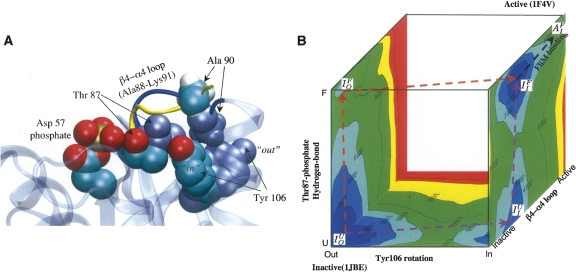
Chemotaxis protein Y (CheY) is a prototypical response regulator in bacterial chemotaxis (Stock et al. 2000), and is highly homologous to the protein NtrC studied by recent NMR experiments (Volkman et al. 2001). The structure of CheY undergoes rather subtle changes upon phosphorylation of Asp 57 (Volz and Matsumura 1991; Simonovic and Volz 2001): The β4−α4 loop (Ala 88 to Lys 91) undergoes a displacement (root-mean-square deviation for the backbone and all non-hydrogen atoms are 1.9 and 3.6 Å, respectively), and the side chain of Tyr 106 switches from a solvent-exposed position to being buried in a cavity under the β4−α4 loop. The distance between Tyr 106 and the phosphorylation site (Asp 57) is >9.5 Å, which makes CheY a prototypical single-domain protein that exhibits allosteric behavior.

The highly conserved Thr 87 spatially separates Asp 57 and Tyr 106 and the traditional activation mechanism of CheY is the so-called “Y-T” coupling scheme (Cho et al. 2000; Lee et al. 2001a,b): Phosphorylation of Asp 57 causes Thr 87 to move toward the phosphorylation site due to enhanced hydrogen-bonding interactions, which leaves more space for Tyr 106 to occupy the buried rotameric state. Although logical, the “Y–T” coupling scheme seems oversimplified considering the observations that CheY is partially active even in the absence of phosphorylation or when the Thr 87 is mutated to Ala (Karak and Eisenbach 1992; Appleby and Bourret 1998). In fact, multiple orientations of Tyr 106 have been observed in different high-resolution X-ray structures of CheY in the absence of phosphorylation (Simonovic and Volz 2001). The various conformations of the β4−α4 loop are correlated with different Tyr 106 orientations, which suggests that the loop plays a role in the activation process (Ma and Cui 2007).

To gain further mechanistic insights into the activation of CheY, as an example of monomeric protein allostery, molecular dynamics and free energy simulations were used to explore the coupling between various conformational transitions (e.g., the β4−α4 loop transition, Tyr 106 rotation, and Thr 87 displacement) and phosphorylation in both the wild-type CheY and the T87A mutant (Formaneck et al. 2006; Ma and Cui 2007). Using the transition path sampling technique (Bolhuis et al. 2002), it has been shown (Ma and Cui 2007) that the isomerization of Tyr 106 does not require the displacement of Thr 87 and that the hydrogen bond between Thr 87 and Asp 57 phosphate, an essential element of the “Y–T” scheme, is not formed. Free energy simulations (Ma and Cui 2007) further showed that the isomerization of Tyr 106 and formation of the Thr 87-phosphate hydrogen bond have similar barriers and are thermodynamically coupled; i.e., kinetically, either event can occur first and facilitate the other (Fig. 5). The free energy results also showed that the β4−α4 loop transition has substantially higher barriers, and therefore is unlikely to gate the Tyr 106 rotation; rather, the rotation of Tyr 106 stabilizes the active configuration of this loop, which is consistent with a statistical analysis of all CheY structures in the PDB (Dyer and Dahlquist 2006; Stock and Gunhaniyogi 2006). Thus, the CheY simulations show that structural transition at the response site (Tyr 106 isomerization) can occur prior to the so-called activation event (Thr 87–phosphate hydrogen-bond formation). This suggests that the Tyr orientations are in equilibrium, and that the active conformation is stabilized by Thr 87–phosphate hydrogen-bond formations; kinetically, either event can occur first. We note that in the NMR study of the closely related NtrC, the relaxation measurement found that motion of the corresponding Tyr residue persists in both the unphosphorylated and phosphorylated forms (Volkman et al. 2001), which led to the interpretation that the Tyr rotation is “uncoupled” from phosphorylation. Although the computational study of CheY also indicates that the Tyr rotation can occur in the absence of phosphorylation, the results of the free energy simulations indicate that the Tyr rotation toward the buried configuration is indeed stabilized by phosphorylation through energetic coupling with Thr87–phosphate hydrogen-bond formation. In other words, these studies suggest that the mechanism of CheY activation has features of both the MWC and Pauling-KNF descriptions: The rotation of Y106 can occur with a low barrier prior to Thr87 displacement, although the two processes are coupled thermodynamically, which is reminiscent of the MWC model; on the other hand, the displacement of the β4−α4 loop is energetically feasible only following the Y106 rotation, reflecting the Pauling-KNF model.

Figure 5.

Study of allosteric coupling in CheY. (A) Comparison of the inactive and active structures of CheY. Overlay of key residues between the phosphorylation (Asp 57) and response sites (Tyr 106). Residues in the active structure are colored according to atom types, while those in the inactive structure are colored as ice-blue. The inactive and active configurations of the β4–α4 loop are colored as dark blue and yellow, respectively. (B) A three-dimensional scheme that illustrates the energetics and possible pathways for CheY activation based on computed two-dimensional potentials of mean force along the key degrees of freedom. The expected fully active state, A^F _I, is not a local free-energy minimum in the simulations, presumably due to the absence of the FliM peptide in the model (see Ma and Cui 2007).

Homodimer with negative cooperativity: CAP protein

Allostery leading to negative cooperativity (e.g., that the binding constant decreases with the number of bound ligands) is of interest for several reasons. It has been documented in a number of systems (Abeliovich 2005), although fewer than for those with positive cooperativity (for a recent discussion of this point, see Koshland Jr. and Hamadani 2002). An important aspect is that, in contrast to positively cooperative systems like the hemoglobins (see the analysis of the dimeric Scapharca hemoglobin, above), intermediate states are significantly populated in negatively cooperative systems and so can be studied directly in the wild-type protein. Also, negative cooperativity is not described by the original MWC model, while the Pauling-KNF model is applicable (see Fig. 1). We consider here a specific system, the CAP protein and its ligand c-AMP, for which structural, thermodynamic, and dynamic data have become available recently (Popovych et al. 2006).

The CAP dimer has a C-terminal DNA binding domain and an N-terminal domain, CAP^N, which is responsible for the dimerization and negative cooperativity of cAMP binding. CAP^N, which can be isolated as a cooperative, cAMP binding dimer, is the subject of the present analysis. The measured values of the cAMP binding constants are K_D ¹ = 0.04 μM and K_D ² = 4 μM, which clearly shows negative cooperativity (K_D ² >> K_D ¹). These values correspond to an interaction coefficient α in the Pauling-KNF model generating function (see Fig. 1) equal to 0.01; the (negative) cooperative free energy is equal to 2.8 kcal/mol. Calorimetric measurements have shown that the enthalpic interaction term actually corresponds to positive cooperativity (1.1 kcal/mol), and that the negative cooperativity arises entirely from an entropic interaction contribution of 3.9 kcal/mol; the free energy of binding of the first cAMP ligand is also dominantly entropic (ΔH ₁ = −1.8 kcal/mol and TΔS ₁ = −8.5 kcal/mol at 300 K). The importance of the entropic contribution is of interest, although positively cooperative systems, such as the dimeric HbI and the vertebrate Hb tetramer, also have entropy dominated cooperative transitions.

That large changes in configurational entropy can be involved in ligand binding processes is not surprising, given that the residual configurational entropy in a small folded protein, such as BPTI, which is made up of 58 residues, has been estimated to be −602 kcal/mol at 300 K by normal mode simulations with quantum corrections (Brooks and Karplus 1983). This value is approximately an order of magnitude larger than the estimated configurational entropy of denaturation of the protein. It should be noted also, that the phrase “dynamics” has been used rather loosely in many discussions of experimental thermodynamic studies. Rigorously, “dynamics” should be reserved to refer to time-dependent processes, while “motion” or more exactly, the average magnitude of the fluctuation (independent of their timescale), characterizes the equilibrium behavior of a system and are correlated with thermodynamic quantities such as entropy.

NMR techniques (relaxation and amide exchange) have been used (Popovych et al. 2006) to analyze the structural and dynamic properties of the monomers in dimeric CAP with different numbers (0, 1, and 2) of bound c-AMP ligands. Although only the high-resolution structure of the symmetric dimer cAMP₂-CAP^N is known, chemical shift data indicate that unliganded CAP^N is also a symmetric dimer. The monoliganded species, cAMP–CAP^N, appears to be asymmetric with the unliganded and liganded subunits having structures approximating those of CAP^N and (cAMP)₂ CAP^N, respectively.

Interestingly, microsecond-millisecond scale motions appeared in both monomers with the binding of the first c-AMP, while they were largely quenched upon the binding of the second c-AMP. Motions on the picosecond-nanosecond scale, by contrast, were not changed with the first c-AMP binding; these fast motions were quenched in (c-AMP)₂ CAP^N. Since the binding of the first c-AMP does not alter the mean conformation of the second binding site, the investigators concluded that the negative cooperativity in CAP is due almost entirely to changes in the protein “dynamics” rather than in the average structure upon ligand binding, in accord with the proposal put forward many years ago by Cooper and Dryden (1984).

Although the analysis by Popovych et al. (2006) is suggestive, it does not prove that the origin of the negative cooperativity is the quenching of motion, or better, the reduction in configuration entropy, in (c-AMP)₂–CAP^N versus cAMP-CAP^N. A deficiency in the argument is that the contribution from the monomer–monomer interaction to the apparent binding free energies for the two c-AMP binding steps is not considered. Since the binding of c-AMP causes significant structural changes in the liganded monomer, the entropic contributions from the changed monomer–monomer interactions between the first and second binding of c-AMP could play a role in the cooperativity. To describe the situation, we refer to the Pauling-KNF model in Figure 1. There the intrinsic first and second binding constants are assumed to be the same and the entire cooperativity arises from the interaction constant α, which is ∼0.01. Although the Pauling-KNF model is phenomenological in character, for the present system it is possible that it describes the microscopic mechanism, based on the observation that the conformational changes within each monomer produced by c-AMP binding appear to be essentially identical for the two binding steps. This suggests that the difference in the apparent binding free energies may be due, in part, to the change in the monomer–monomer interactions at the dimer interface. The chemical shift data for the singly liganded species indicate that the unliganded subunit is not altered in its average conformation, except at the interface, while the liganded monomer has changes throughout the entire subunit and has a structure similar to that in the doubly liganded species. Consequently, the dimer interface is expected to be perturbed in the ligation process and could be an important source for the negative cooperativity. The observed reduction in the magnitude of the fluctuations and the concomitant entropy decrease could also play a significant role, as Popovych et al. (2006) suggest. Clearly, a full understanding of allostery in CAP will have to await the determination of the missing unliganded and single-liganded dimer structures and comparative simulations for the three species (see Note added in proof).

What do “new views” add to our understanding?

Based particularly on recent NMR studies of small- to medium-sized proteins, a “new view” of allosteric transitions, often referred to as the “population-shift” model, has become very popular (Kern and Zuiderweg 2003; Gunasekaran et al. 2004; Swain and Gierasch 2006; Bahar et al. 2007; see also an earlier review, Jardetzky 1996). The model emphasizes that the activated conformation (i.e., the dominant conformation after the allosteric transition, such as the R state of hemoglobin) has a nonnegligible population prior to activation, and that the allosteric event (i.e., homotropic or heterotropic binding) shifts the preexisting equilibrium between the low- and high-activity conformations toward the latter. As discussed in the introduction, a “population shift” is the basis of the original MWC model, and therefore can hardly be considered new. To make this clear we quote (Changeux and Edelstein 2005): “A critical statement of the MWC theory was that, in essence, the conformational transition that links the multiple sites present on the allosteric oligomer and mediates signal transduction involves states that are populated in the absence of ligand and may spontaneously interconvert with each other.” Moreover, as for the MWC model itself, a “population shift” is a thermodynamic description and does not provide mechanistic details regarding how the population shift is induced by ligand binding. Arguably, the most important aspect of the “new view” is that it has revived an interest in allostery, which had been a neglected field in biophysics for some years. (As Francis Crick is supposed to have remarked long ago, “Hemoglobin has a ‘bore’ effect”). In analogy to the “new view” of protein folding (Karplus 1997), there appears to have been a paradigm shift in how allostery is described. The “new view” emphasizes the intrinsic dynamic nature of proteins and nucleic acids, which have been studied over many years (McCammon et al. 1977; Frauenfelder et al. 1979; Brooks II et al. 1988). What is new is that a variety of measurements (e.g., NMR, FRET, and single molecule studies) are providing additional data beyond that available previously from structural, thermodynamic, and kinetic results. These should serve to continue to improve our understanding of the molecular mechanism of allostery, particularly when supplemented by simulations and theoretical analyses. One suggestion from the dynamic view is that the binding of a ligand anywhere has an effect throughout the protein, including the active site and so induces “allosteric” behavior. It has been argued, “all proteins are allosteric” (Gunasekaran et al. 2004). This is analogous to the results for human hemoglobin, for which mutants with nearly every amino acid replaced individually are known, in part because they often cause diseases by their effect on oxygenation, and in part from the more general screening of hemoglobins of patients in hospitals (Morimoto et al. 1971). The effect of many mutations has been difficult to interpret, in spite of the considerable available data, including X-ray structures of the mutants (Morimoto et al. 1971; Fermi and Perutz 1981). This raises the question of whether the perturbation introduced by generalized binding should be considered a manifestation of allostery or whether the term should be reserved for cases where the allosteric effect has a biological function. If the latter, one expects that binding to positions that are functionally important will yield larger changes in activity than from nonspecific perturbations. A recent analysis compares structural changes induced by ligand binding between two tertiary states of a set of proteins known to have functional allostery (e.g., “any protein that binds an effector molecule at one site with a function change at a second site”) with a set that does not; structural changes in the former are twice as large, on average, than those in the latter (Daily and Gray 2007).

An extreme incarnation of the “dynamic” picture is the early proposal by Cooper and Dryden (1984), already mentioned, that a change in the average structure (or “population”) is not required for allostery; rather, it is the distribution around the average structure that changes, which in turn, affects the subsequent (binding) affinity at a distant site. Such a model focuses on the vibrational contribution to the entropy as the origin of cooperativity, as discussed for the CAP^N dimer. More generally, NMR measurements have found significant global changes in the side-chain motions upon ligand binding (Igumenova et al. 2005), although the quantitative relation of such effects to the change in the system entropy is not straightforward (Wrabl et al. 2000). Wall and coworkers (Ming and Wall 2005, 2006) have codified this idea in terms of an “allosteric potential” for a given site in a protein as the difference between protein conformational distributions (approximated by a harmonic model) with and without a test (“binding”) perturbation at that site. An analysis of protein structures from a standard small-molecule docking test set suggested that the natural binding sites tend to have elevated “allosteric potentials” (Ming and Wall 2006), although no quantitative estimate of the energetic importance of these changes was made. The intrinsic structural flexibility of proteins, as reflected by low-frequency normal modes, is important in allostery, as for conformational changes in general (Karplus and Gao 2004). However, low-frequency modes are collective in nature and have been found to be rather insensitive to the level of detail of the method used for their calculation (Kondrashov et al. 2007). It therefore seems unlikely that ligand binding (in the absence of significant average structural change) can alter the character or frequency of the modes and the resulting population distributions sufficiently to explain the free energy changes observed in allostery. This does not exclude the possibility that mode perturbations can be used to determine regions that are important for allosteric effects (Ming and Wall 2006; Taly et al. 2006).

Is allostery fully understood 70 years after Pauling and 40 years after MWC?

The large bodies of experimental and computational studies now available have made possible a mechanistic understanding of a number of allosteric systems. As described in this review, the well-studied examples show that a wide range of mechanisms have been developed by evolution to transmit information from one part of a molecule (the allosteric site) to another (the effector site). Many allosteric systems consist of semi-rigid domains or subunits interacting via flexible regions, such that local events can propagate over a long distance to affect activities elsewhere. Tetrameric hemoglobin and motor proteins, like GroEL and myosin (Yu et al. 2007), are striking examples. The involvement of both flexible and semi-rigid parts is likely to be a result of evolution, which serves to encode a balance between sensitivity (or specificity) and robustness for effects of functional importance. However, more subtle allosteric mechanisms exist and only a few of these have been fully characterized; the dimeric clam hemoglobin and CheY described here are key examples. Clearly, both enthalpic and entropic effects can and do contribute to allostery. Whether effects on the vibrational entropy alone (and/or other entropic effects, including that involving the solvent) can make the primary contribution, as has been suggested for the CAP^N protein, is not clear at this time, but hopefully will be resolved before long.

A combination of experiments and simulations has recently led to an understanding of many aspects of the molecular mechanism of allostery. These results complement the phenomenological MWC and Pauling-KNF descriptions. However, additional studies are needed to apply the available methods for obtaining a detailed mechanistic description of the large number of systems involved in biological control. Of particular interest will be a functional analysis of the allosteric properties that arise from protein–protein interactions encoded in cellular networks. We hope that this review of examples that have been studied in detail, as well as alternative approaches (Suel et al. 2003; Whitten et al. 2005), will aid in the search for the mechanisms of the ever-increasing number of allosteric proteins for which the necessary data are becoming available.

Note added in proof

After the paper was accepted for publication, a simulation study on the CAP system was published (Li et al. 2007). The binding of cAMP was found to have a significant impact on the structure of CAP, especially the DNA binding modules, although no detailed analysis was given of the monomer–monomer interface. Results from principal component analysis and approximate binding calculations suggest that the negative cooperativity has contributions from both structural changes of the ligand-binding domain and changes in the low-frequency modes of the protein with different numbers of ligands.