Abstract
This work is motivated by experimental observations that cells on stretched substrate exhibit different responses to static and dynamic loads. A model of focal adhesion that can consider the mechanics of stress fiber, adhesion bonds, and substrate was developed at the molecular level by treating the focal adhesion as an adhesion cluster. The stability of the cluster under dynamic load was studied by applying cyclic external strain on the substrate. We show that a threshold value of external strain amplitude exists beyond which the adhesion cluster disrupts quickly. In addition, our results show that the adhesion cluster is prone to losing stability under high-frequency loading, because the receptors and ligands cannot get enough contact time to form bonds due to the high-speed deformation of the substrate. At the same time, the viscoelastic stress fiber becomes rigid at high frequency, which leads to significant deformation of the bonds. Furthermore, we find that the stiffness and relaxation time of stress fibers play important roles in the stability of the adhesion cluster. The essence of this work is to connect the dynamics of the adhesion bonds (molecular level) with the cell's behavior during reorientation (cell level) through the mechanics of stress fiber. The predictions of the cluster model are consistent with experimental observations.
INTRODUCTION
Experiments on tissue cells, including fibroblasts, smooth-muscle cells, endothelial cells (ECs), and stem cells, have shown that cells can sense the mechanical properties of their environment and actively respond to mechanical stimuli through actin cytoskeleton remodeling. Adhered cells cultured on a cyclically stretched substrate tend to reorient themselves away from the stretching direction for high frequencies (∼1 Hz) (1–6). Dartsch and Hammerle (2) found that cells do not respond to small stretch amplitudes (<2%), suggesting that there exists a threshold stretch amplitude at which cell reorientation is initiated. Above this threshold, an increasing number of cells begin to respond to substrate deformation by reorienting themselves away from the stretching direction. The larger the stretch amplitude, the more cells reorient. Neidlinger-Wilke and co-workers (7) reported that most of the cells joined the reorientation process once the stretch amplitude exceeded a second threshold level around 5–6%. However, it has been found that the picture is not the same for static or quasistatic stretching, i.e., the adhered cells always align parallel to the stretching direction (8,9).
Recent studies have shown that stretch-induced cell reorientation is a function of the interplay between the magnitude of stretching and Rho pathway activity (10). The small GTPase Rho regulates the formation of actin stress fibers of adherent cells through activation of its effector proteins Rho kinase and mDia. When the Rho signaling pathway is intact, stress fibers are randomly organized independent of the level of Rho activity in the absence of stretching. In contrast, cyclic stretch can induce perpendicular orientation of stress fibers to an extent dependent on both the level of Rho activity and the magnitude of stretch (10). When the Rho pathway is inhibited, stress fibers orient parallel, rather than perpendicular, to the loading direction. Kaunas et al. (10) proposed that the active orientation of the actin cytoskeleton mediated by Rho may represent a mechanism by which cells reduce the increase in intracellular tension generated by cyclic stretching. It is shown that although Rho GTPase plays the main role in the formation of focal adhesions (FA) and associated stress fibers, the GTPase Rac plays a crucial role in the formation of focal complexes by regulating the activation of actin polymerization (11–16).
Besides the force-induced cell reorientation, experiments also show that FAs exhibit an interesting feature of force-induced growth (17–20). In particular, the applied force correlates linearly with lateral size of FAs, with a stress constant around 5 nN/μm2 that is remarkably similar among different cell types (18,19,21,22). These experiments have stimulated several theoretical studies on the physical mechanisms governing FA mechanosensing and dynamics. In a series of studies, Safran and Geiger and their co-workers (23–25) modeled focal adhesions as two-layered structures in which the front edge of the mechanosensitive layer undergoes compression, resulting in an increased affinity for the plaque proteins and leading to FA enlargement. From a different viewpoint, Kozlov and co-workers (26–28) showed that FA mechanosensitive behavior can be explained by a thermodynamic principle governing self-assembly of molecules into an aggregate subjected to pulling force. Wagner and co-workers (29) studied the shear-stress profile along individual FAs and suggested that the shape of stress profiles might be the mechanism for biochemical feedback activity of the adhesion growth.
It is worth noting that the principle mechanisms of force-induced cell orientation are different from those of force-induced growth of FAs. In this study, we intend to focus on the molecular mechanisms of force-induced cell orientation. We will show that these two kinds of cell responses are dominated by different kinds of molecular interactions and activated by different force scales. We assume that the force scale inducing cell orientation should be much larger than that inducing growth of FAs. This assumption will be justified later, in the Results section.
Wang and co-workers (6,30) showed that despite the complex underlying biological responses, the final aligning angle of cells under cyclic stretching can be calculated based on the principle of minimum strain energy. Gao and Chen (31,32) demonstrated that models based on contact mechanics may also be useful for understanding the behaviors of cells on stretched substrates. Their prediction of the critical strain for cell reorientation is consistent with experimental data. More recently, an elastic force-dipoles model was introduced by De et al. (33,34) to predict the dynamics and orientation of cells in both the absence and presence of applied stress. These works gave helpful insights into the response of adhered cells to the external stimulus by using continuum mechanics without explicitly considering the mechanics of subcellular structures. However, it is important to achieve a full understanding of the underlying mechanisms at the subcellular level.
In recent years, the stability of adhesion clusters of cells under external force has been of increasing interest to investigators. Rapid progress in the development of experimental techniques to study single or multiple bond rupture (35–37) has provided us with valuable experimental data for theoretical modeling of the adhesion cluster. Erdmann and Schwarz (38–40) presented a stochastic model for rupture and rebinding dynamics of clusters of parallel adhesion molecules subjected to a constant force or to a linearly increasing force, as commonly used in experiments. Li and Leckband (41) proposed a theoretical analysis of the forced separation of two adhesive surfaces linked via a large number of parallel adhesion bonds. The clustering instability in adhesive contact between elastic solids via diffusive molecular bonds was studied by Wang and Gao (42) using a perturbation method. They found that the instability of the cluster can be attributed primarily to elastic deformation energies of cell and matrix. With the intention of studying stick-slip motion in friction dynamics, Filippov et al. (43) proposed a microscopic model to establish the relationship between the dynamics of formation and rupture of individual bonds and the macroscopic frictional phenomena. These studies are helpful for our understanding of the mechanics of cell adhesion at the subcellular level. However, despite significant progress in experimental studies and theoretical modeling in cell mechanics during the past decades, some basic questions remain for the research community: what are the underlying physics of the reorientation of cells at the critical external strain, and why do cells respond differently to static and dynamic loads at the molecular level?
In this work, we aim to address these problems by developing a focal adhesion model on the molecular level, i.e., an adhesion cluster of hundreds of adhesion bonds in parallel between cell and substrate. The dynamic response of the cluster to external strain at various parameters of bonds, substrate, and stress fiber is analyzed. Different from previous continuum models (31–34), our model in essence relates the macroscopic response of adhered cells to their intrinsic properties at the subcellular level, i.e., it can consider the elastic deformation of bonds and substrate, as well as intrinsic stiffness and viscoelastic properties of stress fibers. The structure of this article is as follows. In the next section, the adhesion cluster model is developed and the master equations of the system are given. The numerical scheme is introduced in the third section. In the fourth section, the coordinated responses of the bonds of the cluster to external stimulus are studied by analyzing the evolution of the mean fraction of bound bonds. Comparison of our predictions with experiments and physics-based explanations of experimental observations are presented in the fifth section. The last section is devoted to conclusions and discussion.
MODEL DEVELOPMENT
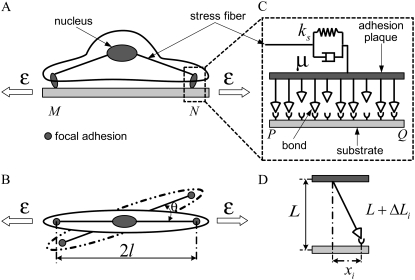
Focal adhesions are large, multiprotein complexes that provide a mechanical link between the cytoskeletal contractile machinery and the extracellular matrix (28). In this work, we treat a single focal adhesion as an adhesion cluster consisting of stress fiber, substrate, and integrin-ligand bonds between the adhered cell and the substrate. Fig. 1, A and B, depicts the side and top views, respectively, of a sketch of the cell, represented by a minimal system for contractile activity of adherent cells consisting of one stress fiber connecting two focal adhesions. The dashed line in Fig. 1 B denotes the reoriented cells with orientation 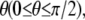 where θ is defined as the angle between the major axis of the cell and the loading direction. Fig. 1 C shows a magnification of the adhesion cluster, including the stress fiber, the adhesion plaque connecting the adhesion bonds and the stress fiber, the adhesion bonds, and the substrate. For simplicity, the adhesion plaque is assumed to be undeformable, as modeled by Ward and Hammer in their study of the effect of focal adhesion on the fracture and peeling strength of cells (44). The substrate in the model is the “local” area of the total substrate where the adhesion cluster is located. When the total substrate is loaded by external tension, the local substrate will be moved relative to the center of the cell due to the deformation of the total substrate (see Fig. 1). Since the bonds are adhered to the local substrate, they will be extended and develop bond force when the local substrate is moved.
where θ is defined as the angle between the major axis of the cell and the loading direction. Fig. 1 C shows a magnification of the adhesion cluster, including the stress fiber, the adhesion plaque connecting the adhesion bonds and the stress fiber, the adhesion bonds, and the substrate. For simplicity, the adhesion plaque is assumed to be undeformable, as modeled by Ward and Hammer in their study of the effect of focal adhesion on the fracture and peeling strength of cells (44). The substrate in the model is the “local” area of the total substrate where the adhesion cluster is located. When the total substrate is loaded by external tension, the local substrate will be moved relative to the center of the cell due to the deformation of the total substrate (see Fig. 1). Since the bonds are adhered to the local substrate, they will be extended and develop bond force when the local substrate is moved.
FIGURE 1.
Schematic illustration of the side view (A) and top view (B) of the adhered cell under external strain. The dashed line in B denotes the adhered cell with a different orientation, characterized by angle θ. (C) Magnification of the adhesion cluster showing how the adhesion plaque (upper plate) couples the adhesion bonds and the stress fiber. The semimajor axis of the adhered cell is kept constant at l = 10 μm. (D) Illustration of the bond deformation under lateral force.
A viscoelastic model of stress fiber
The stress fiber is the primary structure associated with intracellular tension. We describe the mechanical properties of stress fibers at a conceptual level by using a viscoelastic model,
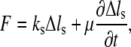 |
(1) |
where F is the tension force, 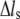 is the extension, and
is the extension, and  and μ are elastic and damping coefficients of the stress fiber, respectively. There exists an intrinsic relaxation time of the stress fiber,
and μ are elastic and damping coefficients of the stress fiber, respectively. There exists an intrinsic relaxation time of the stress fiber,  which defines how quickly the stress fiber recovers its equilibrium configuration. Typical relaxation time of the stress fiber is on the order of seconds (45).
which defines how quickly the stress fiber recovers its equilibrium configuration. Typical relaxation time of the stress fiber is on the order of seconds (45).
Adhesion bonds in the adhesion cluster
We assume that the adhesion bonds are uniformly distributed in parallel between the cell surface and the substrate. All the bonds are normal to the surface at the beginning, and will be extended in an oblique direction by lateral external force, as shown in Fig. 1 D. The upper ends of the integrins are anchored on the adhesion plaque, and the bottom ends can make contact with the substrate to form closed bonds. In our model, individual integrins do not have their own binding sites (ligands) and the integrin of a ruptured bond can rebind to any binding site available on the substrate. Due to the relative slip between cell surface and substrate, the bonds undergo deformation and then develop bond force that can vary from site to site because of different binding states (open or closed) and extension of molecular bonds. Each bond is modeled as an elastic spring,  where
where  is the stiffness of the bond, and
is the stiffness of the bond, and 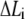 is the extension of the ith bond. For simplicity, we neglect the interaction between bonds. The applied bond force,
is the extension of the ith bond. For simplicity, we neglect the interaction between bonds. The applied bond force, 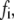 will lower the energy barrier for bond rupture, and thus shorten the bond lifetimes (46). The reverse rate of bonds is given by Bell (46) as,
will lower the energy barrier for bond rupture, and thus shorten the bond lifetimes (46). The reverse rate of bonds is given by Bell (46) as,
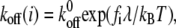 |
(2) |
where  is the reverse rate constant in the absence of force, λ is the compliance length, which can be viewed as the range of the energy well that defines the bound state, and
is the reverse rate constant in the absence of force, λ is the compliance length, which can be viewed as the range of the energy well that defines the bound state, and 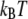 is the thermal energy. The Bell model is commonly used to analyze single bond rupture experiments, due to the explicit coupling between the reverse rate and the applied force.
is the thermal energy. The Bell model is commonly used to analyze single bond rupture experiments, due to the explicit coupling between the reverse rate and the applied force.
The forward rate,  is given by (43)
is given by (43)
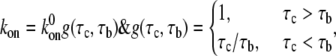 |
(3) |
where  is the forward rate constant of bond formation for an immobile contact,
is the forward rate constant of bond formation for an immobile contact,  is the contact time, and
is the contact time, and 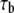 is the intrinsic association time of integrin and ligand molecules (i.e., the average time to form a closed bond). The contact time,
is the intrinsic association time of integrin and ligand molecules (i.e., the average time to form a closed bond). The contact time, 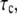 is defined as the time during which the free end of integrin is exposed to a contact area that moves with respect to it. The intrinsic association time,
is defined as the time during which the free end of integrin is exposed to a contact area that moves with respect to it. The intrinsic association time, 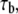 is on the order of 0.01 – 1 s in magnitude (47,48), and we choose
is on the order of 0.01 – 1 s in magnitude (47,48), and we choose  in our calculations. The larger the ratio of contact time to association time,
in our calculations. The larger the ratio of contact time to association time, 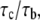 the higher is the probability of bond formation. The contact time,
the higher is the probability of bond formation. The contact time, 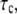 is inversely proportional to the relative velocity between the adhesion plaque and substrate:
is inversely proportional to the relative velocity between the adhesion plaque and substrate: 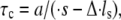 where a is a characteristic length of the contact area (the spacing between adhesion bonds in the focal adhesion) on the order of tens of nanometers (49–51) (
where a is a characteristic length of the contact area (the spacing between adhesion bonds in the focal adhesion) on the order of tens of nanometers (49–51) (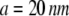 in our calculations), and
in our calculations), and  and
and 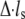 denote the derivatives of the substrate displacement, s, and the extension of the stress fiber,
denote the derivatives of the substrate displacement, s, and the extension of the stress fiber, 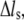 respectively, with respect to time. In the derivation, we have assumed that the substrate is much stiffer than the stress fiber. Equation 3 defines a contact-time-dependent forward rate that is crucial for study of the effect of stretching frequency on the stability of the adhesion cluster. The mechanism is that the stretching frequency controls the velocity of the relative slip between the plaque and substrate, which then determines the contact time.
respectively, with respect to time. In the derivation, we have assumed that the substrate is much stiffer than the stress fiber. Equation 3 defines a contact-time-dependent forward rate that is crucial for study of the effect of stretching frequency on the stability of the adhesion cluster. The mechanism is that the stretching frequency controls the velocity of the relative slip between the plaque and substrate, which then determines the contact time.
Adhesion plaque and substrate
The local substrate, PQ (see Fig. 1 C; we call it substrate for short in the following sections), will move cyclically due to the dynamic external tension applied on substrate MN. Assuming that the substrate is much stiffer than the stress fiber and adhesion bonds, we can obtain a simple formula for the displacement of substrate PQ along the major axis of the cell, i.e., 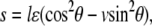 which depends on angle θ, Poisson ratio v, and applied strain ɛ. ɛ is a cyclically dynamic strain given by
which depends on angle θ, Poisson ratio v, and applied strain ɛ. ɛ is a cyclically dynamic strain given by  where
where  is the strain amplitude, and ω is the frequency. Although the magnitude of the applied strain can change cyclically, the direction of strain is only in the stretching direction. It is noted that the increase of orientation angle θ from θ = 0 will decrease the magnitude of the substrate displacement, s, along the major axis of the cell until it reaches a specific location at which the magnitude of s is at its minimum (Fig. 1 B, dashed line). Therefore, the reorientation of the cell away from the loading direction will alleviate the tension stress of the bonds in the adhesion cluster.
is the strain amplitude, and ω is the frequency. Although the magnitude of the applied strain can change cyclically, the direction of strain is only in the stretching direction. It is noted that the increase of orientation angle θ from θ = 0 will decrease the magnitude of the substrate displacement, s, along the major axis of the cell until it reaches a specific location at which the magnitude of s is at its minimum (Fig. 1 B, dashed line). Therefore, the reorientation of the cell away from the loading direction will alleviate the tension stress of the bonds in the adhesion cluster.
The adhesion plaque will move along the stretching direction due to the bond forces of the cluster when the substrate is moved under the cyclic external strain. In this work, the adhesion plaque consists of plaque proteins and the intracellular domains of integrins (23,24,28), i.e., the adhesion plaque does not include the extracellular domains of integrins. Although the intracellular domains of integrins are embedded in the rigid adhesion plaque, the extracellular domains of integrins can undergo extension (for closed bonds) or relaxation (for open bonds) due to the applied force. The forces acting on the adhesion plaque include the bond forces of adhesion molecules and the force of the stress fiber. Please note that the force of the stress fiber, which is a passive force (in this work, the active contractility of stress fibers due to myosin motor activity is not considered), is induced by the pulling of the bonds through the adhesion plaque. Considering the equilibrium of the adhesion plaque, we have
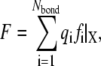 |
(4) |
where F is the tension force of the stress fiber, and the righthand term of Eq. 4 is the summation of all adhesion bond forces along the loading direction, X. 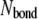 is the total bond number, and the subscript i denotes the ith bond. A state index,
is the total bond number, and the subscript i denotes the ith bond. A state index, 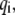 is introduced to characterize the state (open or closed) of the ith bond, i.e.,
is introduced to characterize the state (open or closed) of the ith bond, i.e.,  corresponds to the state of a closed bond that connects the adhesion plaque and substrate, and
corresponds to the state of a closed bond that connects the adhesion plaque and substrate, and 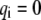 corresponds to the state of an open bond attached only to the adhesion plaque.
corresponds to the state of an open bond attached only to the adhesion plaque.
NUMERICAL METHODS
We now introduce the numerical scheme used in the calculations. For simplicity, the variables are normalized as  and
and  All these variables are listed in Table 1 . We begin with the calculation of the bond extension,
All these variables are listed in Table 1 . We begin with the calculation of the bond extension, 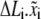 is defined as the projection of the bond length of the ith bond in the lateral direction, as shown in Fig. 1 D. The rate of
is defined as the projection of the bond length of the ith bond in the lateral direction, as shown in Fig. 1 D. The rate of  is
is
 |
(5) |
As we can see from the above equation, as long as a bond is closed, it is stretched in the lateral direction at a velocity equal to the relative velocity between the adhesion plaque and the substrate. However, an open bond relaxes along the direction to its equilibrium state, characterized by its intrinsic relaxation time, 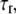 normalized by
normalized by 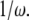 Since the relaxation time of molecules is much smaller than the time step in our simulation, the bond can reach its equilibrium state quickly in one time step. The projection of the bond length is calculated by the forward difference scheme,
Since the relaxation time of molecules is much smaller than the time step in our simulation, the bond can reach its equilibrium state quickly in one time step. The projection of the bond length is calculated by the forward difference scheme,
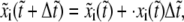 |
(6) |
where 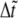 is the dimensionless time step. The bond extension is calculated as
is the dimensionless time step. The bond extension is calculated as  and the lateral component of the bond force is calculated by
and the lateral component of the bond force is calculated by 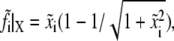 according to the normalization. Then, the reverse rate of the bond can be obtained from the normalized forms of Eq. 2:
according to the normalization. Then, the reverse rate of the bond can be obtained from the normalized forms of Eq. 2:
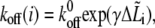 |
(7) |
where 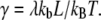 The forward rate can be calculated using Eq. 3, where
The forward rate can be calculated using Eq. 3, where 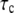 and
and  are normalized as
are normalized as  and
and  respectively. Thus, the force of the stress fiber is
respectively. Thus, the force of the stress fiber is
 |
(8) |
where 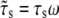 and
and 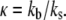 The superscript
The superscript 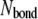 is the bond number (
is the bond number (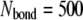 in our calculations). The mechanical equilibrium equation (Eq. 8) is discretized by using the typical forward difference scheme for the time derivative,
in our calculations). The mechanical equilibrium equation (Eq. 8) is discretized by using the typical forward difference scheme for the time derivative,
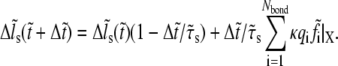 |
(9) |
The parameters used in our calculation come directly from experimental measurements or theoretical estimation based upon experiments. The physiological ranges of the main parameters and their values, as well as the reference sources, are listed in Table 2.
TABLE 1.
Nomenclature of symbols
| Abbreviation | Definition |
|---|---|
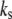 |
Stress fiber stiffness |
| μ | Stress fiber viscosity |
 |
Bond stiffness |
| L | Bond rest length |
| a | Bond spacing |
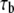 |
Bond association time |
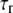 |
Bond relaxation time |
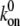 |
Forward rate constant |
 |
Reverse rate constant |
| λ | Compliance length |
| kB | Boltzmann constant |
| T | Absolute temperature |
| γ |  |
 |
Substrate displacement |
 |
Semimajor axis |
| θ | Orientation angle |
| ls | Stress fiber length |
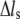 ( (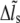 ) ) |
Stress fiber extension |
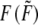 |
Stress fiber tension |
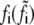 |
Bond force |
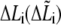 |
Bond extension |
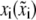 |
Bond length projection in the lateral direction |
 |
Bond state index |
| ξ | Random number generated uniformly between (0,1) |
The subscript i denotes the ith bond.
TABLE 2.
Physiological ranges of the main parameters and their values chosen in the calculations
| Abbreviation | Definition | Physiological range | Used value | Source |
|---|---|---|---|---|
| a | Bond spacing | 20 nm | (49–51) | |
 |
Stress fiber stiffness | 45 nN/μm | (16,54) | |
| μ | Stress fiber viscosity | 45 nN s/μm | (45,54) | |
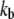 |
Bond stiffness | 10−2–101 nN/μm | 10 nN/μm | (56) |
| L | Bond length | 10–100 nm | 20 nm | (56,57) |
 |
Bond association time | 10−2–1 s | 0.01 s | (47,48) |
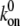 |
Forward rate constant | 1–100 s−1 | 100 s−1 | (47,48) |
 |
Reverse rate constant | 1–10 s−1 | (46,48) | |
| λ | Compliance length | 0.01–1 nm | 0.05 nm | (38,58) |
During each time step, the state (open or closed) of each integrin-ligand bond is checked. An equation governing bond rupture and formation is introduced for calculating the state index of the bond as follows (43):
 |
(10) |
where ξ is a random variable generated uniformly in (0,1), and H is a Heaviside step function that accounts for a stochastic rupture (formation) of a bond. An open state will close if  and a closed state will open if
and a closed state will open if 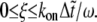 The time step,
The time step, 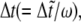 should be smaller than a critical value for numerical stability (although we cannot give a rigorous analysis for the critical time step due to the stochastic character of the system). That is, the smaller the time step,
should be smaller than a critical value for numerical stability (although we cannot give a rigorous analysis for the critical time step due to the stochastic character of the system). That is, the smaller the time step, 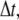 the more stable is the simulation. In our simulation, we choose
the more stable is the simulation. In our simulation, we choose 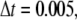 at which the simulation is very stable and also has a reasonable simulation time.
at which the simulation is very stable and also has a reasonable simulation time.
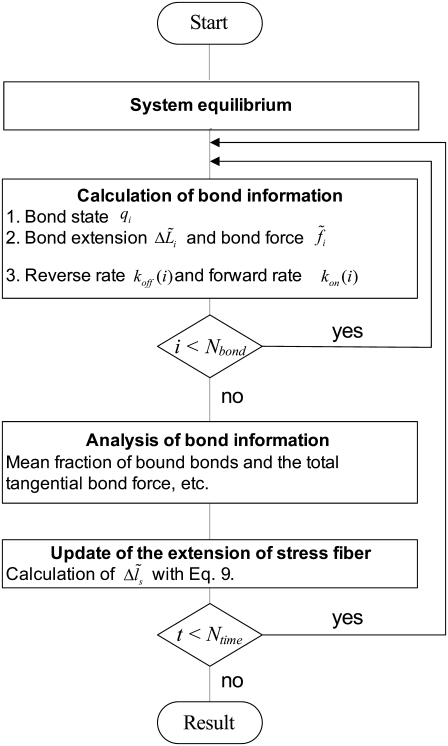
A numerical iteration scheme is illustrated in Fig. 2. At the initial time, all the adhesion bonds are in parallel and perpendicular to the substrate, and are in ideal equilibrium with each state index,  We first run a simulation of 2000 time steps to equilibrate the system, then another
We first run a simulation of 2000 time steps to equilibrate the system, then another 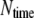 (here,
(here,  ) time steps calculation for collection of the results with a constant time step
) time steps calculation for collection of the results with a constant time step 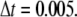 During each time step, the bond information is first calculated for each bond in a loop from
During each time step, the bond information is first calculated for each bond in a loop from  to
to  which includes three parts (see Fig. 2): 1), calculation of bond state
which includes three parts (see Fig. 2): 1), calculation of bond state 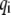 using Eq. 10; 2), calculation of bond extension
using Eq. 10; 2), calculation of bond extension 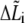 and bond force
and bond force  ), calculation of the reaction rates,
), calculation of the reaction rates,  and
and 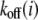 with Eqs. 3 and 7, respectively. Then, the bond information, e.g., the fraction of bound bonds and the total tangential bond force, is calculated. Afterward, the extension of the stress fiber,
with Eqs. 3 and 7, respectively. Then, the bond information, e.g., the fraction of bound bonds and the total tangential bond force, is calculated. Afterward, the extension of the stress fiber, 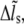 is updated for the next time step according to Eq. 9. The force and deformation of the individual adhesion bond and the stress fiber are tracked in all calculation steps. At last, the mean fraction of bound bonds is obtained by averaging the fractions of bound bonds (number of bound bonds divided by total bond number) of all the time steps during the time of the collection of results. According to our simulations, having the fraction of closed bonds very low or near zero will not cause problems for the stability and convergence of the calculation. We do not need special approaches to deal with the calculation when the fraction of closed bonds equals zero.
is updated for the next time step according to Eq. 9. The force and deformation of the individual adhesion bond and the stress fiber are tracked in all calculation steps. At last, the mean fraction of bound bonds is obtained by averaging the fractions of bound bonds (number of bound bonds divided by total bond number) of all the time steps during the time of the collection of results. According to our simulations, having the fraction of closed bonds very low or near zero will not cause problems for the stability and convergence of the calculation. We do not need special approaches to deal with the calculation when the fraction of closed bonds equals zero.
FIGURE 2.
Flow chart of the numerical scheme for calculations of the mean fraction of bound bonds of the adhesion cluster under cyclic lateral force.
RESULTS
Threshold value of external strain for the stability of the cluster
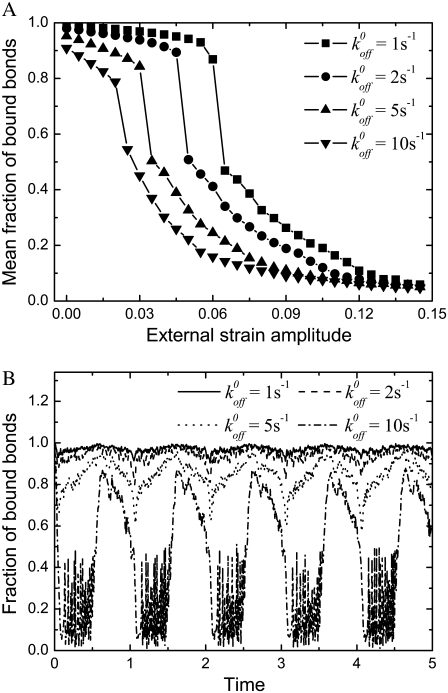
The stability of the adhesion cluster is studied by examining the change in the number of bound bonds under the external load. Fig. 3 A shows the evolution of the mean fraction of bound bonds as a function of external strain amplitude, 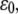 at different reverse rate constants,
at different reverse rate constants,  It is noted that for each curve, particularly those with small
It is noted that for each curve, particularly those with small  value, there is an apparent threshold value of the stretching strain,
value, there is an apparent threshold value of the stretching strain, 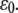 The mean fraction of bound bonds is insensitive to
The mean fraction of bound bonds is insensitive to  when
when  is smaller than the threshold value, but decreases quickly when
is smaller than the threshold value, but decreases quickly when  is larger than the threshold, causing disassembly of the adhesion cluster. In this way, the adhered cells can reorient themselves away from the stretch direction when the applied strain is higher than a critical value. The threshold value of external strain is on the order of a few percent, depending on
is larger than the threshold, causing disassembly of the adhesion cluster. In this way, the adhered cells can reorient themselves away from the stretch direction when the applied strain is higher than a critical value. The threshold value of external strain is on the order of a few percent, depending on  e.g., ∼2–6% when
e.g., ∼2–6% when 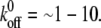 Our results are consistent with the experimental results (2,7,52,53), suggesting that the disassembly of the focal adhesion is correlated with the reorientation of cells.
Our results are consistent with the experimental results (2,7,52,53), suggesting that the disassembly of the focal adhesion is correlated with the reorientation of cells.
FIGURE 3.
(A) Dependence of the mean fraction of bound bonds on the external strain, 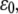 at a different reverse rate constant,
at a different reverse rate constant,  In the calculation, we chose
In the calculation, we chose 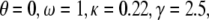 and
and  (B) Evolution of the fraction of bound bonds as a function of time at
(B) Evolution of the fraction of bound bonds as a function of time at 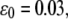 with
with  and 10 (top to bottom). The larger the
and 10 (top to bottom). The larger the 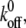 the larger is the fluctuation of the fraction of bound bonds.
the larger is the fluctuation of the fraction of bound bonds.
The equilibrium state of the adhesion cluster is the result of the balance between formation and rupture of the adhesion bonds, characterized by the forward rate and reverse rate, respectively. Our results show that only sufficiently large external load can break the balance and change the state of the adhesion cluster. This can be understood by looking at the behavior of a specific bond in the cluster. When the external load is small, the forward rate is much larger than the reverse rate, as the bond force,  is small, and therefore the bond is very stable, with a high formation probability. However, as the applied external strain is increased, the developing bond force,
is small, and therefore the bond is very stable, with a high formation probability. However, as the applied external strain is increased, the developing bond force, 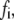 will enlarge the reverse rate according to Eq. 2. There should be a critical value of
will enlarge the reverse rate according to Eq. 2. There should be a critical value of 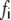 at which the reverse rate will be equal to the forward rate of the bond. Before
at which the reverse rate will be equal to the forward rate of the bond. Before  reaches this critical value, the bond formation process is dominant, and the bond is therefore stable. When
reaches this critical value, the bond formation process is dominant, and the bond is therefore stable. When  becomes larger than the critical value, the bond rupture process will dominate and the bond will have a spontaneous transition from a stable to an unstable state. The physical mechanism is that the action of external force lowers the energy barrier and makes it easier for the bonds to escape from their energy well. Therefore, when the amplitude of external strain,
becomes larger than the critical value, the bond rupture process will dominate and the bond will have a spontaneous transition from a stable to an unstable state. The physical mechanism is that the action of external force lowers the energy barrier and makes it easier for the bonds to escape from their energy well. Therefore, when the amplitude of external strain, 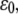 is larger than a threshold value, it will cause the bond force of a large fraction of bonds to reach the critical value, which induces a significant decrease in the number of bound bonds.
is larger than a threshold value, it will cause the bond force of a large fraction of bonds to reach the critical value, which induces a significant decrease in the number of bound bonds.
Fig. 3 B shows the evolution of the fraction of bound bonds with time for different reverse rate constants, 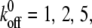 and 10, at
and 10, at  For a clear expression, we only plot a partial time region (0–5) of the total calculation time (0–20). From the difference of fluctuation in amplitudes of these four curves, we can see that the interplay of bond formation and bond rupture determines the stability of the adhesion cluster, i.e., the fluctuation in the number of bound bonds is determined by the competition between the two reaction rates. Therefore, for a given forward rate constant,
For a clear expression, we only plot a partial time region (0–5) of the total calculation time (0–20). From the difference of fluctuation in amplitudes of these four curves, we can see that the interplay of bond formation and bond rupture determines the stability of the adhesion cluster, i.e., the fluctuation in the number of bound bonds is determined by the competition between the two reaction rates. Therefore, for a given forward rate constant, 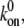 an increase in the reverse rate constant,
an increase in the reverse rate constant, 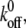 will make the cluster more sensitive to the external force with larger fluctuation (see Fig. 3 B), i.e. the cluster is prone to losing stability at smaller external strain (see Fig. 3 A).
will make the cluster more sensitive to the external force with larger fluctuation (see Fig. 3 B), i.e. the cluster is prone to losing stability at smaller external strain (see Fig. 3 A).
Effect of the frequency of external load
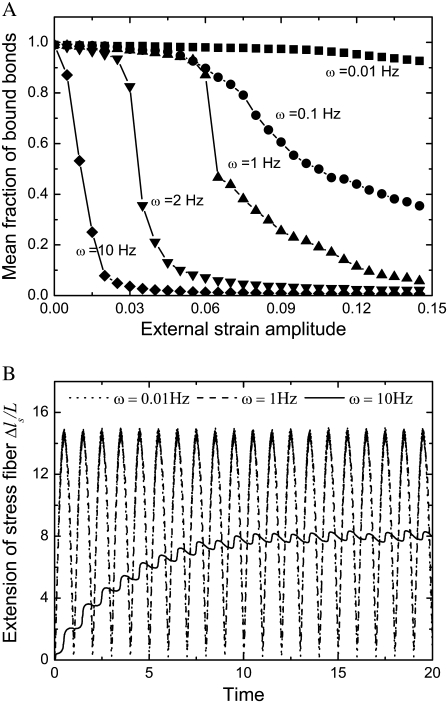
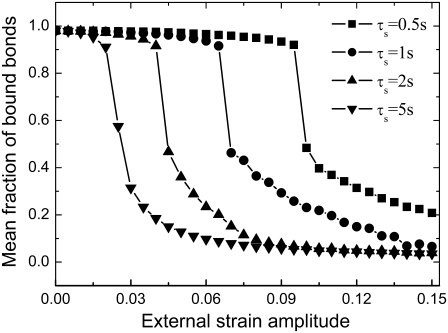
In this section, we study the effect of loading frequency, ω, on the stability of the adhesion cluster by examining the evolution of the fraction of bound bonds under different stretching frequencies. At medium frequency, e.g., 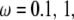 and 2 Hz, there is a distinct external strain threshold value of a few percent for the adhesion cluster's transition from a stable to an unstable state (Fig. 4 A). The threshold values agree with both experimental observations (2–7) and theoretical analysis (33,34). In addition, the experiments (10) showed that the adhered cells with a normal Rho pathway tend to reorient themselves away from the stretch direction at frequencies of 1 Hz. However, at a very high frequency of strain amplitude, i.e.,
and 2 Hz, there is a distinct external strain threshold value of a few percent for the adhesion cluster's transition from a stable to an unstable state (Fig. 4 A). The threshold values agree with both experimental observations (2–7) and theoretical analysis (33,34). In addition, the experiments (10) showed that the adhered cells with a normal Rho pathway tend to reorient themselves away from the stretch direction at frequencies of 1 Hz. However, at a very high frequency of strain amplitude, i.e.,  the adhesion cluster disassembles quickly under smaller external strain without a distinct threshold value (see Fig. 4 A). In contrast, at a very low frequency,
the adhesion cluster disassembles quickly under smaller external strain without a distinct threshold value (see Fig. 4 A). In contrast, at a very low frequency,  the cluster can have a stable state at very large external strain. This suggests that the cell will likely not respond to static/quasistatic loading, which is in agreement with experiments (8,9) and theoretical predictions (33,34).
the cluster can have a stable state at very large external strain. This suggests that the cell will likely not respond to static/quasistatic loading, which is in agreement with experiments (8,9) and theoretical predictions (33,34).
FIGURE 4.
(A) Dependence of the mean fraction of bound bonds on the external strain, 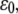 at different frequency, ω. (B) Extension of the stress fiber as a function of time. In the calculation, we chose
at different frequency, ω. (B) Extension of the stress fiber as a function of time. In the calculation, we chose 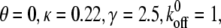 and
and 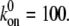
The effect of the loading frequency on the stability of the cluster can be explained by two mechanisms. 1), The loading frequency determines the contact time (which is inversely proportional to the deformation rate) between the free end of adhesion bonds and the substrate surface, which in turn influences the probability of bond formation, i.e. the forward rate, according to Eq. 3. Rapid deformation of the substrate is not likely to occur from the association of integrin and ligand molecules, since these adhesion molecules do not have enough contact time to form adhesion complexes. 2), The deformability of the stress fiber is rate-dependent due to its intrinsic viscosity. The stress fiber becomes stiffer at high frequency, as it does not have time to relax, and therefore its deformation is much smaller in comparison with that at low frequency (see Fig. 4 B). Therefore, to accommodate the deformation of the substrate at high frequency, the bond extension, and thus the bond force, should be increased, which consequently increases the reverse rate of the bonds. In contrast, the static or quasistatic load of frequency approaching zero will be very helpful for bond formation, and at the same time allow enough relaxation of the stress fiber to accommodate deformation of the cell, and therefore induce a very small bond force.
Effect of stiffness and relaxation time of the stress fiber
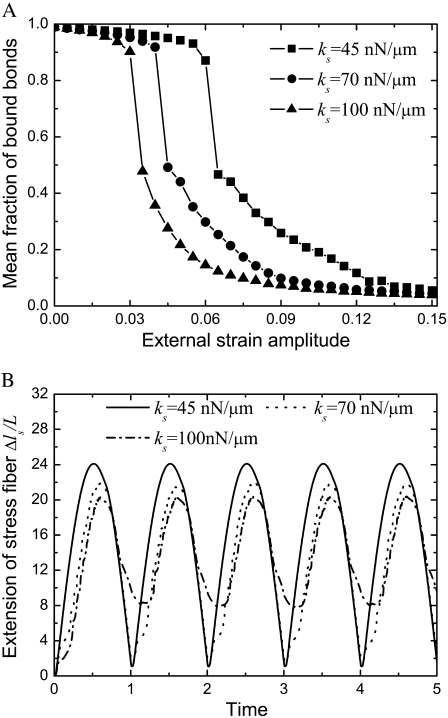
Stress fibers play an important role in the formation and stability of focal adhesions (10). Although the mechanical properties of the stress fiber are not well defined, some of its mechanical properties have been tested in recent experiments (45,54), including, e.g., the stiffness, relaxation time, and breaking force. Here, we are interested in the effect of its elastic stiffness,  and relaxation time,
and relaxation time,  on the stability of the adhesion cluster. Fig. 5 A shows the mean fraction of bound bonds as a function of strain amplitude at different stiffnesses of the stress fiber,
on the stability of the adhesion cluster. Fig. 5 A shows the mean fraction of bound bonds as a function of strain amplitude at different stiffnesses of the stress fiber,  with the relaxation time,
with the relaxation time, 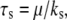 kept constant. Note that increasing
kept constant. Note that increasing 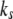 decreases the extension of the stress fiber (see Fig. 5 B), then increases the extension of bonds and the bond force (because it is the combination of the deformation of stress fiber and the bonds to accommodate the deformation of cell induced by the stretched substrate), which will consequently reduce the stability of the adhesion cluster. Fig. 5 A also shows that the external strain threshold value decreases with the increase of stiffness of the stress fiber. Since the relaxation time of the stress fiber is an important timescale, we also calculate the effect of
decreases the extension of the stress fiber (see Fig. 5 B), then increases the extension of bonds and the bond force (because it is the combination of the deformation of stress fiber and the bonds to accommodate the deformation of cell induced by the stretched substrate), which will consequently reduce the stability of the adhesion cluster. Fig. 5 A also shows that the external strain threshold value decreases with the increase of stiffness of the stress fiber. Since the relaxation time of the stress fiber is an important timescale, we also calculate the effect of 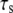 on the stability of the adhesion cluster while keeping the stiffness of the stress fiber constant. Fig. 6 shows the effect of
on the stability of the adhesion cluster while keeping the stiffness of the stress fiber constant. Fig. 6 shows the effect of 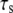 on the mean fraction of bound bonds at constant stiffness of the stress fiber and constant loading frequency. We can see that the larger the
on the mean fraction of bound bonds at constant stiffness of the stress fiber and constant loading frequency. We can see that the larger the 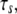 the stiffer the stress fiber (because it needs more time to relax and respond to the external force of constant loading frequency), and therefore the more unstable is the adhesion cluster. In addition, we find that the simulation results are not sensitive to small changes of the two parameters
the stiffer the stress fiber (because it needs more time to relax and respond to the external force of constant loading frequency), and therefore the more unstable is the adhesion cluster. In addition, we find that the simulation results are not sensitive to small changes of the two parameters 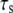 and
and 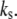
FIGURE 5.
(A) Effect of the stiffness of the stress fiber on the stability of the adhesion cluster. In the calculation, we chose 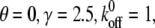 and
and  (B) Extension of the stress fiber as a function of time at
(B) Extension of the stress fiber as a function of time at 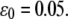
FIGURE 6.
Effect of the relaxation time of the stress fiber on the stability of the adhesion cluster. In the calculation, we chose 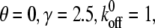 and
and 
As stress fiber is a kind of polymer, according to polymer physics its stiffness will increase with internal tension. Since stress fiber is the primary structure associated with intracellular tension, it is possible that cells control the stiffness and relaxation time of stress fiber by adjusting its tension through a Rho pathway, and a polymerization and depolymerization process, respectively, to respond to external force. This suggests a potential mechanism in which the cell controls its adhesion strength on the extracellular matrix (ECM) by changing the tension and then the stiffness of the stress fiber, which controls the stability of focal adhesion. As a result, the cell can respond effectively to the external load. Mogilner et al. (15) formulated a mathematical model in their pioneer work to describe the coupled dynamics of cell adhesions, small GTPases Rac and Rho, and actin stress fibers in a directional reorganization of the actin cytoskeleton under shear stress. Recently, Besser and Schwarz (16) modeled a feedback loop for the contractibility of stress fibers coupled with Rho regulatory pathways by a system of reaction-diffusion equations. Although in this study we did not consider the biochemical aspects of regulatory pathways of stress fiber mechanical properties, we intend to do so in future work.
Comparison with experiments
In this section, we try to compare our predictions with the experimental and theoretical studies to explain the underlying mechanisms of cell reorientation. Our calculations predict that there is a threshold value of external strain for the stability of the focal adhesion. The threshold value of external strain is on the order of a few percent. Our results are generally consistent with experimental observations (2–7,52,53). We also show that loading frequency plays a crucial role in the stability of the focal adhesion, which is in agreement with both experimental observations (1–5) and theoretical analysis (33,34). For example, adhered cells with a normal Rho pathway tend to reorient themselves away from the stretch direction at comparably high loading frequencies (∼1 Hz).
Researchers have observed that cells respond differently to static and dynamically varying strains. In the case of static or quasistatic strain, cells align parallel to the direction of the applied strain (8,9), whereas for cyclic strain, cells align away from the direction of the applied stretch; for comparably high frequencies (∼1 Hz), cells/stress fiber align nearly perpendicular to the strain direction (10,52,53). Our calculations (see Fig. 4) are consistent with those observations. The underlying mechanism is that both the dynamics of bond formation and the viscoelastic properties of the stress fiber are responsible for the different responses of cells to static and dynamic strain. Under static or quasistatic load, the forward rate of bond formation is much higher than the reverse rate, and also the stress fiber is softer, which can accommodate most of the deformation of the cell to alleviate the bond force of adhesion bonds. Therefore, the focal adhesion is stable at static and quasistatic loading. In contrast, the forward rate becomes lower than the reverse rate at higher loading frequency, and at the same time the stress fiber becomes stiffer, which induces larger bond force in adhesion bonds, which accelerates the disassembly of the focal adhesion.
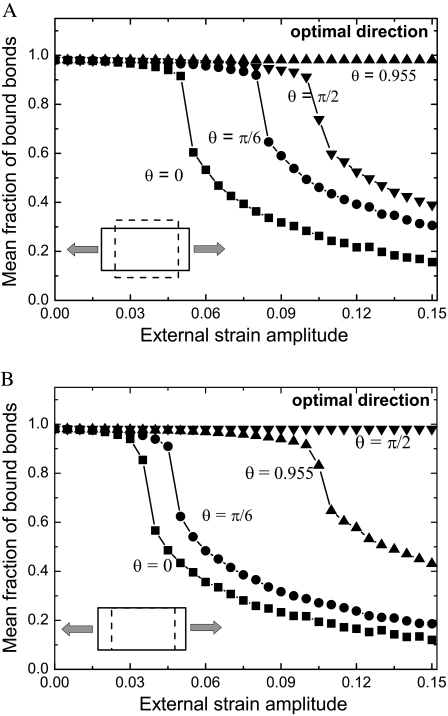
To explain why the cell and stress fiber always reorient themselves away from the stretching direction to some specific locations at high loading frequency (34,55), we analyze the stability of the adhesion cluster at different cell orientations. Under external strain, ɛ, the displacement of the substrate (PQ), s, along the major axis of the cell depends on the angle, θ, and Poisson's ratio, v, of the substrate, i.e., 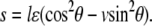 When the cell is aligned along the loading direction (
When the cell is aligned along the loading direction ( ), the displacement of the substrate is at its maximum, and the mean fraction of bound bonds is most sensitive to the applied external strain. Therefore, the cell is prone to reorient away. The final configuration of the reoriented cells depends on the magnitude of the applied stretch and Poisson's ratio, v, as well as on other aspects, e.g., the level of Rho activity. In this study, we focus on the mechanical aspects of cell responses and assume that the biochemical controlling pathways function normally. The relationship between the mean fraction of bound bonds and the applied strain amplitude at different θ angles is shown in Fig. 7 A, where Poisson's ratio is v = 0.5. We find that the mean fraction of bound bonds does not decrease under the external load when
), the displacement of the substrate is at its maximum, and the mean fraction of bound bonds is most sensitive to the applied external strain. Therefore, the cell is prone to reorient away. The final configuration of the reoriented cells depends on the magnitude of the applied stretch and Poisson's ratio, v, as well as on other aspects, e.g., the level of Rho activity. In this study, we focus on the mechanical aspects of cell responses and assume that the biochemical controlling pathways function normally. The relationship between the mean fraction of bound bonds and the applied strain amplitude at different θ angles is shown in Fig. 7 A, where Poisson's ratio is v = 0.5. We find that the mean fraction of bound bonds does not decrease under the external load when  implying that
implying that  is the optimal direction along which the adhesion cluster is most stable. This result (v = 0.5) is consistent with the simple elongation stretching experiment of Wang et al. (55), which shows that the cells align along an optimal direction defined by
is the optimal direction along which the adhesion cluster is most stable. This result (v = 0.5) is consistent with the simple elongation stretching experiment of Wang et al. (55), which shows that the cells align along an optimal direction defined by 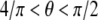 (i.e.,
(i.e.,  ). However, it is shown that the optimal direction becomes
). However, it is shown that the optimal direction becomes 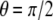 when v = 0, i.e., the cells are prone to align perpendicular to the stretching direction, as shown in Fig. 7 B. This result (v = 0) is consistent with pure uniaxial stretching experiments (lateral deformation of the substrate is constrained and in this case Poisson's ratio, v, is effectively equal to zero) of Wang et al. (55). Our results are also consistent with the theoretical studies of De et al. (34).
when v = 0, i.e., the cells are prone to align perpendicular to the stretching direction, as shown in Fig. 7 B. This result (v = 0) is consistent with pure uniaxial stretching experiments (lateral deformation of the substrate is constrained and in this case Poisson's ratio, v, is effectively equal to zero) of Wang et al. (55). Our results are also consistent with the theoretical studies of De et al. (34).
FIGURE 7.
Dependence of the mean fraction of bound bonds on the external strain, 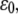 at different angle θ. In the calculation, we chose
at different angle θ. In the calculation, we chose 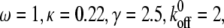 and
and 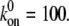 (A) v = 0.5. (B) v = 0. Insets show the stretching modes, i.e., simple elongation and pure uniaxial stretching, respectively.
(A) v = 0.5. (B) v = 0. Insets show the stretching modes, i.e., simple elongation and pure uniaxial stretching, respectively.
In summary, in addition to the biochemical aspects, active reorientation of the cell/stress fiber may represent a mechanism by which cells reduce the increase in intracellular tension generated by cyclic stretching (10). In this way, the cells reorient themselves in an optimal direction along which the intra- and extracellular tension exerted on them by ECMs is less than in the former direction. We explain this reorientation mechanism by using the adhesion cluster model, i.e., through disassembly of the focal adhesion along the loading direction ( ), the adhered cell can establish new contacts away from the loading direction and form stable focal adhesions there.
), the adhered cell can establish new contacts away from the loading direction and form stable focal adhesions there.
DISCUSSIONS
We find that there is a threshold value of external strain amplitude for the stability of the adhesion cluster, beyond which the cluster disrupts quickly, and this is in agreement with experimental observations of cell reorientation on the cyclically stretched substrate. The existence of the threshold value is explained by analyzing the competition between bond formation and rupture under external strain. When the external strain is smaller than the threshold value, bond formation is dominant, but when it is larger than the threshold value, bond rupture is dominant. The frequency of external strain can influence both the bond contact time and the instantaneous stiffness (related to the viscoelasticity) of the stress fiber. At the higher frequency, the contact time becomes shorter and the stress fiber becomes stiffer, both of which will induce more bonds to rupture. Of particular interest is the effect of stress fiber stiffness, which is assumed to be used by the cell to control the stability of the focal adhesion. The stiffness of the stress fiber can be manipulated by the cell itself through, e.g., prestress, polymerization, and depolymerization of the stress fiber. We explain cell reorientation using a simple model that takes into account the effect of cell orientation on the stability of the adhesion cluster. Different from previous studies, this work provides a new way of understanding the different responses of adhered cells to external load at a subcellular level, and its predictions are in good agreement with experimental results.
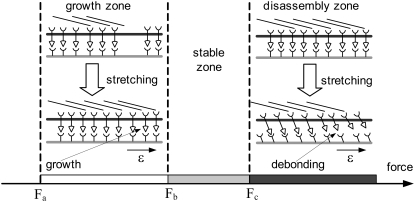
It is noteworthy that the molecular mechanisms of force-induced instability of FAs studied in this work are different from those of force-induced growth of FAs. Disassembly of FAs is caused by disassociation of the adhesion molecules on cells (integrins) from their ligands on the ECM (a “cell-ECM” interaction). However, force-induced growth of FAs originates from the addition of new integrin molecules and associated intracellular proteins (called a “protein complex” by Nicolas et al. (23) and “FA proteins” by Shemesh et al. (28), it is here renamed “integrin complex” (integrinC) for convenience) to the FA through an “integrinC-integrinC” interaction (23,28) (“intracelluar” interaction). In other words, the “integrin-ligand” interaction dominates the disassembly of FAs in our study, whereas the “integrinC-integrinC” interaction dominates force-induced growth of FAs (see schematic illustration in Fig. 8). Based on the analysis of the disassembly of focal adhesions in this work, and on comparisons with the experimental and theoretical studies of force-induced growth of FAs, we outline a map of force scales for the dynamics of FAs. According to Nicolas et al. (23), there exists a range of stress for FA growth, i.e., when the stress is smaller than a minimum value or larger than a maximum value, it cannot induce FA growth. The minimum force threshold is determined by the balance of the assembly rate at the front and the disassembly rate at the rear of the FA, and the maximum force threshold is ∼5.5 nN/μm2 (22). We show that the characteristic force for disassembly of the FA is much larger than the force for FA growth. The characteristic force can be estimated by a summation of the horizontal component of bond force at the threshold value of the cyclic strain amplitude. For example, according to Fig. 5 B, the characteristic force is as high as 48 nN/μm2 at  We can see that the characteristic force for FA disassembly is one order of magnitude larger than the force for inducing FA growth. Thus, we suggest that there exists a force scale diagram for the dynamics of FA, as shown in Fig. 8. The force scale in the growth zone can induce FA growth, and the force scale in the stable zone can induce neither growth nor disassembly of FAs, but the force scale in the disassembly zone will induce disassembly of FAs.
We can see that the characteristic force for FA disassembly is one order of magnitude larger than the force for inducing FA growth. Thus, we suggest that there exists a force scale diagram for the dynamics of FA, as shown in Fig. 8. The force scale in the growth zone can induce FA growth, and the force scale in the stable zone can induce neither growth nor disassembly of FAs, but the force scale in the disassembly zone will induce disassembly of FAs.
FIGURE 8.
Force scale diagram for the growth and disassembly of focal adhesions. The growth zone denotes the force range for FA growth,  described by Nicolas et al. (23), and the disassembly zone corresponds to
described by Nicolas et al. (23), and the disassembly zone corresponds to  (the force range
(the force range  corresponds to the stable zone) in the model described here. In the growth zone, the force-induced growth of FA originates from the addition of a new integrin molecule and its associated intracellular proteins to the FA through an “integrinC-integrinC” interaction (“intracelluar” interaction). However, in the disassembly zone, disassembly of the FA is caused by disassociation of the adhesion molecules on cells (integrin receptors) from their ligands on the ECM (“cell-ECM” interaction).
corresponds to the stable zone) in the model described here. In the growth zone, the force-induced growth of FA originates from the addition of a new integrin molecule and its associated intracellular proteins to the FA through an “integrinC-integrinC” interaction (“intracelluar” interaction). However, in the disassembly zone, disassembly of the FA is caused by disassociation of the adhesion molecules on cells (integrin receptors) from their ligands on the ECM (“cell-ECM” interaction).
The adhesion cluster model captures many generic features of focal adhesion, e.g., the viscoelastic properties of the stress fiber, the dynamics of formation and rupture of integrin-ligand bonds, and deformation of the substrate. The essence of this model is that it connects the dynamics of the adhesion bonds (at subcelluar and molecular levels) with the behaviors of the reorientation of the cell (macroscopic cell level) through the mechanics of the stress fiber. Although it may be oversimplified (e.g., integrin molecules are assumed to be fixed on the cell surface, which does not allow for the effects of adhesion molecule diffusion, and the model is one-dimensional, which does not take into account the effects of two-dimensional distribution of molecular bonds), it will still help us to understand different cell behaviors in response to mechanical forces. We intend to develop more sophisticated and realistic models of focal adhesions, e.g., a two-dimensional model that combines biochemistry and mechanics with multiscale modeling, in future work.
Acknowledgments
The work reported here was supported by the key project of Chinese Academy of Sciences through grants KJCX2-YW-M04 and KJCX-SW-L08. B.J. is grateful for support from the National Natural Science Foundation of China through grants 10502031, 10628205, and 10732050, and to the National Basic Research Program of China grant 2004CB619304. The support of super computing center of the Chinese Academy of Sciences is acknowledged. We are highly grateful to three anonymous reviewers for their helpful comments, which have improved our manuscript significantly.
Editor: Denis Wirtz.
References
- 1.Buck, R. C. 1980. Reorientation response of cells to repeated stretch and recoil of the substratum. Exp. Cell Res. 127:470–474. [DOI] [PubMed] [Google Scholar]
- 2.Dartsch, P., and H. Hammerle. 1986. Orientation response of arterial smooth muscle cells to mechanical stimulation. Eur. J. Cell Biol. 41:339–346. [PubMed] [Google Scholar]
- 3.Wang, J. H. C., E. S. Grood, J. Florer, and R. Wenstrup. 2000. Alignment and proliferation of MC3T3-E1 osteoblasts in microgrooved silicone substrata subjected to cyclic stretching. J. Biomech. 33:729–735. [DOI] [PubMed] [Google Scholar]
- 4.Neidlinger-Wilke, C., E. S. Grood, J. H. C. Wang, R. A. Brand, and L. Claes. 2001. Cell alignment is induced by cyclic changes in cell length: studies of cells grown in cyclically stretched substrates. J. Orthop. Res. 19:286–293. [DOI] [PubMed] [Google Scholar]
- 5.Moretti, M., A. Prina-Mello, A. J. Reid, V. Barron, and P. J. Prendergast. 2004. Endothelial cell alignment on cyclically-stretched silicone surfaces. J. Mater. Sci. Mater. Med. 15:1159–1164. [DOI] [PubMed] [Google Scholar]
- 6.Wang, H. C., W. Ip, R. Boissy, and E. S. Grood. 1995. Cell orientation response to cyclically deformed substrates: experimental validation of a cell model. J. Biomech. 28:1543–1552. [DOI] [PubMed] [Google Scholar]
- 7.Neidlinger-Wilke, C., H.-J. Wilke, and L. Claes. 2005. Cyclic stretching of human osteoblasts affects proliferation and metabolism: a new experimental method and its application. J. Orthop. Res. 12:70–78. [DOI] [PubMed] [Google Scholar]
- 8.Collinsworth, A. M., C. E. Torgan, S. N. Nagda, R. J. Rajalingam, W. E. Kraus, and G. A. Truskey. 2000. Orientation and length of mammalian skeletal myocytes in response to a unidirectional stretch. Cell Tissue Res. 302:243–251. [DOI] [PubMed] [Google Scholar]
- 9.Eastwood, M., V. C. Mudera, D. A. McGrouther, and R. A. Brown. 1998. Effect of precise mechanical loading on fibroblast populated collagen lattices: morphological changes. Cell Motil. Cytoskeleton. 40:13–21. [DOI] [PubMed] [Google Scholar]
- 10.Kaunas, R., P. Nguyen, S. Usami, and S. Chien. 2005. Cooperative effects of Rho and mechanical stretch on stress fiber organization. Proc. Natl. Acad. Sci. USA. 102:15895–15900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Geiger, B., and A. Bershadsky. 2001. Assembly and mechanosensory function of focal contacts. Curr. Opin. Cell Biol. 13:584–592. [DOI] [PubMed] [Google Scholar]
- 12.Burridge, K., and K. Wennerberg. 2004. Rho and Rac take center stage. Cell. 116:167–179. [DOI] [PubMed] [Google Scholar]
- 13.Ridley, A. J., and A. Hall. 1992. The small GTPbinding protein rho regulates the assembly of focal adhesions and actin stress fibers in response to growth factors. Cell. 70:389–399. [DOI] [PubMed] [Google Scholar]
- 14.Ridley, A. J., H. F. Paterson, C. L. Johnston, D. Diekmann, and A. Hall. 1992. The small GTP-binding protein rac regulates growth factor-induced membrane ruffling. Cell. 70:401–410. [DOI] [PubMed] [Google Scholar]
- 15.Civelekoglu-Scholey, G., A. Wayne Orr, I. Novak, J. J. Meister, M. A. Schwartz, and A. Mogilner. 2005. Model of coupled transient changes of Rac, Rho, adhesions and stress fibers alignment in endothelial cells responding to shear stress. J. Theor. Biol. 232:569–585. [DOI] [PubMed] [Google Scholar]
- 16.Besser, A., and U. S. Schwarz. 2007. Coupling biochemistry and mechanics in cell adhesion: a model for inhomogeneous stress fiber contraction. New J. Phys. 9:425. [Google Scholar]
- 17.Riveline, D., E. Zamir, N. Q. Balaban, U. S. Schwarz, T. Ishizaki, S. Narumiya, Z. Kam, B. Geiger, and A. D. Bershadsky. 2001. Focal contacts as mechanosensors: externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J. Cell Biol. 153:1175–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bershadsky, A. D., N. Q. Balaban, and B. Geiger. 2003. Adhesion-dependent cell mechanosensitivity. Annu. Rev. Cell Dev. Biol. 19:677–695. [DOI] [PubMed] [Google Scholar]
- 19.Balaban, N. Q., U. S. Schwarz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky, L. Addadi, and B. Geiger. 2001. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 3:466–472. [DOI] [PubMed] [Google Scholar]
- 20.Kaverina, I., O. Krylyshkina, K. Beningo, K. Anderson, Y.-L. Wang, and J. V. Small. 2002. Tensile stress stimulates microtubule outgrowth in living cells. J. Cell Sci. 115:2283–2291. [DOI] [PubMed] [Google Scholar]
- 21.Tan, J. L., J. Tien, D. M. Pirone, D. S. Gray, K. Bhadriraju, and C. S. Chen. 2003. Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc. Natl. Acad. Sci. USA. 100:1484–1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schwarz, U. S., N. Q. Balaban, D. Riveline, L. Addadi, A. Bershadsky, S. A. Safran, and B. Geiger. 2003. Measurement of cellular forces at focal adhesions using elastic micro-patterned substrates. Mater. Sci. Eng. C. 23:387–394. [Google Scholar]
- 23.Nicolas, A., B. Geiger, and S. A. Safran. 2004. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc. Natl. Acad. Sci. USA. 101:12520–12525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Besser, A., and S. A. Safran. 2006. Force-induced adsorption and anisotropic growth of focal adhesions. Biophys. J. 90:3469–3484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nicolas, A., and S. A. Safran. 2006. Limitation of cell adhesion by the elasticity of the extracellular matrix. Biophys. J. 91:61–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bershadsky, A. D., C. Ballestrem, L. Carramusa, Y. Zilberman, B. Gilquin, S. Khochbin, A. Y. Alexandrova, A. B. Verkhovsky, T. Shemesh, and M. M. Kozlov. 2006. Assembly and mechanosensory function of focal adhesions: experiments and models. Eur. J. Cell Biol. 85:165–173. [DOI] [PubMed] [Google Scholar]
- 27.Kozlov, M. M., and A. D. Bershadsky. 2004. Processive capping by formin suggests a force-driven mechanism of actin polymerization. J. Cell Biol. 167:1011–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shemesh, T., B. Geiger, A. D. Bershadsky, and M. M. Kozlov. 2005. Focal adhesions as mechanosensors: a physical mechanism. Proc. Natl. Acad. Sci. USA. 102:12383–12388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Aroush, D. R.-B., and H. D. Wagner. 2006. Shear-stress profile along a cell focal adhesion. Adv. Mater. 18:1537–1540. [Google Scholar]
- 30.Wang, J. H. C. 2000. Substrate deformation determines actin cytoskeleton reorganization: a mathematical modeling and experimental study. J. Theor. Biol. 202:33–41. [DOI] [PubMed] [Google Scholar]
- 31.Chen, S., and H. Gao. 2006. Non-slipping adhesive contact between mismatched elastic spheres: a model of adhesion mediated deformation sensor. J. Mech. Phys. Solids. 54:1548–1567. [Google Scholar]
- 32.Chen, S., and H. Gao. 2006. Non-slipping adhesive contact of an elastic cylinder on stretched substrates. Proc. R. Soc. A Math. Phys. Eng. Sci. 462:211–228. [Google Scholar]
- 33.De, R., A. Zemel, and S. A. Safran. 2007. Dynamics of cell orientation. Nat. Phys.. 3:655–659. [Google Scholar]
- 34.De, R., A. Zemel, and S. A. Safran. 2008. Do cells sense stress or strain? Measurement of cellular orientation can provide a clue. Biophys. J. 94:L29–L31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Evans, E. A., and D. A. Calderwood. 2007. Forces and bond dynamics in cell adhesion. Science. 316:1148–1153. [DOI] [PubMed] [Google Scholar]
- 36.Marshall, B. T., M. Long, J. W. Piper, T. Yago, R. P. McEver, and C. Zhu. 2003. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 423:190–193. [DOI] [PubMed] [Google Scholar]
- 37.Zarnitsyna, V. I., J. Huang, F. Zhang, Y.-H. Chien, D. Leckband, and C. Zhu. 2007. Memory in receptor ligand-mediated cell adhesion. Proc. Natl. Acad. Sci. USA. 104:18037–18042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Erdmann, T., and U. S. Schwarz. 2004. Stability of adhesion clusters under constant force. Phys. Rev. Lett. 92:108102. [DOI] [PubMed] [Google Scholar]
- 39.Erdmann, T., and U. S. Schwarz. 2004. Adhesion clusters under shared linear loading: a stochastic analysis. Europhys. Lett. 66:603–609. [Google Scholar]
- 40.Erdmann, T., and U. S. Schwarz. 2004. Stochastic dynamics of adhesion clusters under shared constant force and with rebinding. J. Chem. Phys. 121:8997–9017. [DOI] [PubMed] [Google Scholar]
- 41.Li, F., and D. Leckband. 2006. Dynamic strength of molecularly bonded surfaces. J. Chem. Phys. 125:194702. [DOI] [PubMed] [Google Scholar]
- 42.Wang, J., and H. Gao. 2008. Clustering instability in adhesive contact between elastic solids via diffusive molecular bonds. J. Mech. Phys. Solids. 56:251–266. [Google Scholar]
- 43.Filippov, A. E., J. Klafter, and M. Urbakh. 2004. Friction through dynamical formation and rupture of molecular bonds. Phys. Rev. Lett. 92:135503. [DOI] [PubMed] [Google Scholar]
- 44.Ward, M. D., and D. A. Hammer. 1993. A theoretical analysis for the effect of focal contact formation on cell-substrate attachment strength. Biophys. J. 64:936–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kumar, S., I. Z. Maxwell, A. Heisterkamp, T. R. Polte, T. P. Lele, M. Salanga, E. Mazur, and D. E. Ingber. 2006. Viscoelastic retraction of single living stress fibers and its impact on cell shape, cytoskeletal organization, and extracellular matrix mechanics. Biophys. J. 90:3762–3773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 47.Lawrence, M. B., and T. A. Springer. 1991. Leukocytes roll on a selectin at physiologic flow rates: distinction from and prerequisite for adhesion through integrins. Cell. 65:859–873. [DOI] [PubMed] [Google Scholar]
- 48.Rinko, L. J., M. B. Lawrence, and W. H. Guilford. 2004. The molecular mechanics of P- and L-selectin lectin domains binding to PSGL-1. Biophys. J. 86:544–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Cavalcanti-Adam, E. A., T. Volberg, A. Micoulet, H. Kessler, B. Geiger, and J. P. Spatz. 2007. Cell spreading and focal adhesion dynamics are regulated by spacing of integrin ligands. Biophys. J. 92:2964–2974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cavalcanti-Adam, E. A., A. Micoulet, J. Blummel, J. Auernheimer, H. Kessler, and J. P. Spatz. 2006. Lateral spacing of integrin ligands influences cell spreading and focal adhesion assembly. Eur. J. Cell Biol. 85:219–224. [DOI] [PubMed] [Google Scholar]
- 51.Arnold, M., E. A. Cavalcanti-Adam, R. Glass, J. Blummel, W. Eck, M. Kantlehner, H. Kessler, and J. P. Spatz. 2004. Activation of integrin function by nanopatterned adhesive interfaces. ChemPhysChem. 5:383–388. [DOI] [PubMed] [Google Scholar]
- 52.Neidlinger-Wilke, C., E. Grood, L. Claes, and R. Brand. 2002. Fibroblast orientation to stretch begins within three hours. J. Orthop. Res. 20:953–956. [DOI] [PubMed] [Google Scholar]
- 53.Kurpinski, K., J. Chu, C. Hashi, and S. Li. 2006. Anisotropic mechanosensing by mesenchymal stem cells. Proc. Natl. Acad. Sci. USA. 103:16095–16100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Deguchi, S., T. Ohashi, and M. Sato. 2006. Tensile properties of single stress fibers isolated from cultured vascular smooth muscle cells. J. Biomech. 39:2603–2610. [DOI] [PubMed] [Google Scholar]
- 55.Wang, J. H. C., P. Goldschmidt-Clermont, J. Wille, and F. C. P. Yin. 2001. Specificity of endothelial cell reorientation in response to cyclic mechanical stretching. J. Biomech. 34:1563–1572. [DOI] [PubMed] [Google Scholar]
- 56.Bell, G. I., M. Dembo, and P. Bongrand. 1984. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys. J. 45:1051–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Ward, M. D., M. Dembo, and D. A. Hammer. 1994. Kinetics of cell detachment: peeling of discrete receptor clusters. Biophys. J. 67:2522–2534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Krasik, E. F., and D. A. Hammer. 2004. A semianalytic model of leukocyte rolling. Biophys. J. 87:2919–2930. [DOI] [PMC free article] [PubMed] [Google Scholar]