Abstract
Event-related brain potentials (ERP) are important neural correlates of cognitive processes. In the domain of language processing, the N400 and P600 reflect lexical-semantic integration and syntactic processing problems, respectively. We suggest an interpretation of these markers in terms of dynamical system theory and present two nonlinear dynamical models for syntactic computations where different processing strategies correspond to functionally different regions in the system’s phase space.
Keywords: Computational psycholinguistics, Language processing, Event-related brain potentials, Dynamical systems
Introduction
How are symbolic processing capabilities such as language realized by neural networks in the human brain? This is one of the most important problems in cognitive neurodynamics. Although methods such as event-related brain potentials (ERPs), event-related fields (ERFs), and functional magnetic resonance imaging (fMRI) have yielded considerable experimental evidence relating to the neural correlates of language processing, very little is known about the computational neurodynamical processes occurring at mesoscopic and microscopic scales that are responsible for macroscopically measurable effects.
Existing attempts to model language-related brain potentials are macroscopic-phenomenological, successfully relating particular ERP components to particular computational steps on the one hand, and to distinct cortical areas, on the other hand (Friederici 1995, 1998, 1999, 2002; Grodzinsky and Friederici 2006; Hagoort 2003, 2005; Bornkessel and Schlesewsky 2006; Frisch et al. 2008). However, these models are presently unable to relate ERPs to underlying neurodynamical systems.
In this paper we attempt to provide such an account for syntactic language processing. (A first step towards the modeling of the mismatch negativity ERP (MMN) for word recognition has recently been suggested by Wennekers et al. (2006) and Garagnani et al. (2007)). Using a particular ERP experiment on the processing of German subject–object ambiguities (Friederici et al. 1998, 2001; Bader and Meng 1999; beim Graben et al. 2000; Vos et al. 2001; Frisch et al. 2002, 2004; Schlesewsky and Bornkessel 2006), a locally ambiguous context-free grammar and two appropriate deterministic pushdown recognizers are constructed from a Government and Binding (Chomsky 1981; Haegeman 1994) representation of the stimulus material. Subsequently, we present two different implementations of these automata by nonlinear dynamical systems, resulting from universal tensor product representations (Dolan and Smolensky 1989; Mizraji 1989; Smolensky 1990; Mizraji 1992; Smolensky and Legendre 2006; Smolensky 2006). The first model is a parallel distributed processing (PDP) model (Rumelhart et al. 1986) in a high-dimensional activation vector space. Local ambiguity is processed in parallel (Lewis 1998) and model ERPs are obtained from principal components in the activation space. The second model generalizes previous work of beim Graben et al. (2004) on nonlinear dynamical automata (NDAs), where generalized shifts in symbolic dynamics (Moore 1990, 1991; Siegelmann 1996) are mapped onto a bifurcating two-dimensional dynamical system. In this model, local ambiguity is processed serially according to a diagnosis and repair account (Lewis 1998). Model ERPs are then described by the parsing entropy, obtained from a measurement partition.
Both models aim at a dynamical system interpretation of language-related ERPs (Başar 1980, 1998): The application of different processing strategies to ambiguous sentences is reflected by the exploration of different regions (probably with different volumes as well) in the processor’s phase space. These regions can be functionally related to differents ways of symbol manipulation (Fodor and Pylyshyn 1988; Smolensky 1991).
We begin with overview of language-relevant ERP components and how they could be interpreted in terms of dynamical system theory and other existing models of language processing. Then we describe a pilot study of a language processing ERP experiment and present two dynamical system models of the empirical data. This is followed by preliminary results of the ERP analysis to illustrate the dynamics of the two models in the light of their ERP correlates.
Event-related potentials in language studies
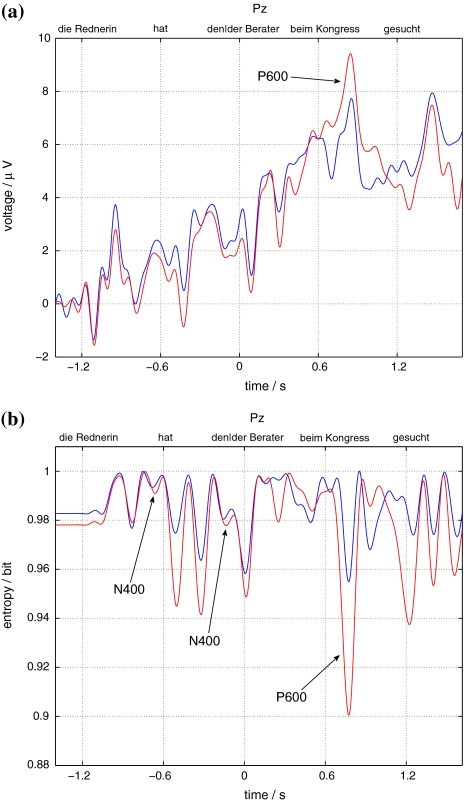
Event-related brain potentials (ERPs) are transient changes in the ongoing electroencephalogram (EEG) which are time-locked to the perception or processing of particular stimuli or cognitive events (Başar 1980, 1998; Regan 1989; Niedermeyer and da Silva 1999). ERPs differ with respect to their amplitude, polarity, latency (usually regarded as the time of maximal amplitude), duration, morphology, spatial topography, and, eventually, their putative neural generators. Some of these parameters vary depending on experimental manipulations that might be physical, such as pitch or volume for acoustic stimuli, size or color for visual stimuli, in the domain of psychophysics; or instructions or unexpectedness in the domain of cognitive neuroscience (Coles and Rugg 1995). As the ERP signal is about one order of magnitude smaller than the amplitude of the spontaneous EEG, signal analysis methods, such as ensemble averaging, source separation, or nonlinear techniques have to be employed (Regan 1989; Niedermeyer and da Silva 1999; Friederici et al. 2001; Makeig et al. 2002; Marwan and Meinke 2004; beim Graben et al. 2000, 2005; Allefeld et al. 2004; Schinkel et al. 2007). In the conventional averaging paradigm, the resulting waveforms are labeled by the polarities and latencies of peaks, such as N100, P300, N400, P600, denoting negativities around 100 and 400 ms, and positivities around 300 and 600 ms, respectively.
Since the pioneering work of Kutas and Hillyard (1980, 1984), ERPs have become increasingly important for the investigation of online language processing in the human brain. In this paper we focus on two important measures from the psycholinguistic perspective, the N400 and the P600.
The N400 component in language processing
Kutas and Hillyard (1980) reported a parietally distributed negativity around 400 ms after stimulus onset for semantically anomalous sentence continuations (shown in bold) such as (1), compared to semantically normal control sentences (2).
 |
1 |
 |
2 |
In subsequent work, Kutas and Hillyard (1984) reported that this N400 component is also sensitive to semantic priming, not only in sentence processing but also in lexical decision tasks (Osterhout and Holcomb (1995); see also Kutas and van Petten (1994) and Coles and Rugg (1995) for further reviews). According to Coles and Rugg (1995, p. 23), “the N400 appears to be a ‘default’ component, evoked by words whose meaning is unrelated to, or not predicted by, the prior context of the words” (Dambacher et al. 2006). This view is further supported by recent experimental findings on N400s evoked by purely semantic and thematic-syntactic manipulations (Frisch and Schlesewsky 2001; Bornkessel et al. 2004; Frisch and beim Graben 2005; beim Graben et al. 2005). For example, in the (extended) Argument Dependency Model (eADM) of Bornkessel and Schlesewsky (2006), the N400 reflects a mismatch with previous prominence information held in working memory (eADM is discussed in section “Introduction/Phenomenological models”).
The P600 component in language processing
The first syntax-related ERP component, observed by Neville et al. (1991), was the left anterior negativity (LAN). It is often more pronounced at left-hemispheric recording sites (hence the name). The LAN is related to phrase structure or word category violations 1 such as at the critical verb ‘of’ in2
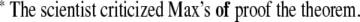 |
3 |
The LAN was accompanied by a sustained parietal positivity around 600 ms, which turned out to be a very reliable indicator of syntactic processing problems. Osterhout and Holcomb (1992) found this P600 [or Syntactic Positivity Shift (SPS; Hagoort et al. (1993)] for phrase structure violations, such as (4), and for local garden path sentences (5).
 |
4 |
 |
5 |
When reading the sentence (5) from left to right, the preposition ‘to’ (in bold) renders the sentence temporarily ungrammatical because the comprehender expects the verb ‘persuaded’ to be followed by an object noun phrase. However, further downstream, when the phrase ‘was sent…’ is encountered, the sentence is recognized as grammatical: the verb ‘persuaded’ is a contraction of the full form ‘who was persuaded’, in other words, a reduced relative construction. Such local ambiguities thus lead the reader temporarily down a garden path; hence the name (Fodor and Ferreira 1998).
The P600 does not only reflect ungrammaticality or ambiguity. Its amplitude and latency varies with syntactic complexity and reanalysis costs (Osterhout et al. 1994; Kaan et al. 2000). Mecklinger et al. (1995); Friederici et al. (1998) and Frisch et al. (2004) reported an earlier positivity (P345) for sentences where syntactic reanalysis was easier to perform than for those evoking a P600. Late positivities which co-vary also with semantic and pragmatic contexts have been reported e.g. by Drenhaus et al. (2006). For this reason, Bornkessel and Schlesewsky (2006) propose distinguishing between the P600 and late positivites in their model.
The dynamical system approach
The brain is a complex dynamical system whose high-dimensional phase space is spanned by the activation space of its neural network. Measuring EEG, MEG or neuroimaging characteristics comprises a spatio-temporal coarse-graining that maps the phase space in an observable space spanned by multivariate time series (Amari 1974; Atmanspacher and beim Graben 2007; Freeman 2007). This observable space is explored by trajectories representing e.g. EEG time series, such as individual ERP epochs, that start from randomly scattered initial conditions.
Following Başar (1980, 1998), the experimental manipulations of an ERP experiment can be regarded as control parameters in the sense that individual ERP epochs recorded under different conditions will explore different regions of the observable space thereby revealing different topologies of the system’s flow. Changing the control parameters critically then causes bifurcations of the dynamics, that can be assessed by suitable order parameters, such as the averaged ERP, coherence, synchronization or information measures (Başar 1980, 1998; Allefeld et al. 2004; beim Graben et al. 2000).
Applying methods from information theory to ERP data requires a further coarse-graining of the continuous time series into a symbolic representation. Symbolic dynamics (Hao 1989; Lind and Marcus 1995) deals with dynamical systems of discrete phase space and time where trajectories are given by bi-infinite (for invertible maps) “dotted” symbol sequences
 |
6 |
with symbols 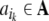 taken from a finite set, the alphabetA. In Eq. (6) the dot denotes the
observation time t0 such that the symbol right to the dot,
taken from a finite set, the alphabetA. In Eq. (6) the dot denotes the
observation time t0 such that the symbol right to the dot,
 displays the current state. The dynamics is
given by the left shift
displays the current state. The dynamics is
given by the left shift
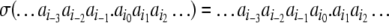 |
7 |
resulting to a new sequence with current state
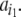
In order to get a symbolic dynamics from a continuous system
(X,Φt) with phase space X and flow  one must first discretize time, such that Φt = Φt are the iterations of a map
one must first discretize time, such that Φt = Φt are the iterations of a map 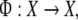 and secondly, one has to partition the
observable space X into a
finite number I of mutually
disjoint sets: {Ai|i = 1, 2,…,
I} which cover the whole
phase space X, i.e.
and secondly, one has to partition the
observable space X into a
finite number I of mutually
disjoint sets: {Ai|i = 1, 2,…,
I} which cover the whole
phase space X, i.e.
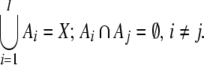 The index set A = {1, 2,…, I}
of the partition can then be interpreted as the alphabet of
symbols ai = i. Thus, the
current state
The index set A = {1, 2,…, I}
of the partition can then be interpreted as the alphabet of
symbols ai = i. Thus, the
current state  contained in cell Ai is mapped onto the dotted symbol “. ai”. Accordingly, its successor x1 = Φ (x0) is mapped onto the symbol aj if
contained in cell Ai is mapped onto the dotted symbol “. ai”. Accordingly, its successor x1 = Φ (x0) is mapped onto the symbol aj if 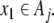 On the other hand, the left shift σ brings
aj onto the “surface” of the sequence s = … ak . aiaj… by σ(… ak . aiaj…) = … akai . aj….
On the other hand, the left shift σ brings
aj onto the “surface” of the sequence s = … ak . aiaj… by σ(… ak . aiaj…) = … akai . aj….
Partitioning the observable space of ERP time series, beim
Graben et al. (2000, 2005), Frisch et al. (2004) and Drenhaus et al.
(2006) were
able to describe ERP components by suitable order parameters
obtained from a symbolic dynamics of the time series. In this
approach, each ERP epoch is represented by a string of length
L of a few symbols
{ai|i = 1, 2,…,
I} which form an
epoch ensemble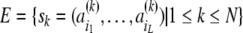 of N
sequences for each experimental condition. A subset of these
epochs that agree at a certain time t in a particular building block, a word
of N
sequences for each experimental condition. A subset of these
epochs that agree at a certain time t in a particular building block, a word of n = |w|
symbols,
of n = |w|
symbols,
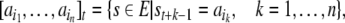 |
8 |
is called a cylinder
set. Counting the members of cylinder sets (i.e.
determing their probability measure) yields the word statistics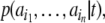 from which event-related cylinder entropies
from which event-related cylinder entropies
 |
9 |
can be obtained.
Language processing models in psycholinguistics
In this section we provide a brief overview of language processing models discussed in the psycholinguistic literature (see e.g., Lewis (2000), Vasishth and Lewis (2006b), Lewis et al. (2006)). These can be classified into three broad types (some models cut across these broad categories, of course). The first type is the phenomenological model. Such a model pursues a top-down approach, accounting for macroscopic, phenomenological evidence from neuroimaging techniques, EEG, MEG, behavioral data and clinical studies; this type of model is usually neither algorithmically nor mathematically codified. The second type is the symbolic computational model; this class of model follows the classical cognitivistic account of formal language theory and automata theory (Newell and Simon 1976; Fodor and Pylyshyn 1988). The third type is the dynamical systems approach to cognition; these models attempt to bridge the gap between symbolic computation and continuous dynamics on the one hand, and between qualitative descriptions and quantitative predictions on the other.
These types of models can be classified along another dimension as well: they can be either serial or parallel (Lewis 1998). In a serial model, when a temporary ambiguity is encountered, only one possibility is pursued until a valid representation is computed, or the computation breaks down. In case of a breakdown, either the immediately preceding computational steps have to be retraced until a viable alternative can be found (backtracking), or the search space of possible continuations is locally modified such that the processing trajectory jumps into another admissible track (repair). By contrast, in a parallel model, the entire search space is globally explored by the processor. We study the implications of these two strategies by developing a parallel processing model (section “Methods/Tensor product top-down recognizer”) and a serial diagnosis and repair model (section “Methods/Nonlinear dynamical automaton”).
Phenomenological models
Based on the Wernicke-Geschwind model (Kandel et al. 1995, Chapt. 34), Friederici (1995, 1999, 2002) proposed her serial neurocognitive model of language processing (see also Grodzinsky and Friederici (2006)) that comprises three different phases: In a first phase around 200 ms, only word category information is taken into account to construct a preliminary syntactic representation of a sentence. Word category violations elicit the early left anterior negativity (ELAN) in the ERP (see section “Introduction/Event-related potentials in language studies”). In the second phase from 300 to 500 ms, semantic and thematic information such as the verb’s subcategorization frames are used to compute the argument dependencies and a first semantic interpretation. Violations of subcategorization information or semantic plausibility are related to the left anterior negativity (LAN) and the N400 component, respectively. Finally, in the third phase (between 500 and 800 ms), syntactic reanalysis of phrase structure violations and garden-path interpretations are accompanied by the P600 component.
This model became supplemented by a diagnosis and repair mechanism (Friederici 1998), which describes the recovery of the human language system from weak garden paths without backtracking. After diagnosing the need of reanalysis, the search space of possible grammatical continuations is modified by a local repair operation, into which the system moves directly afterwards (Lewis 1998). Friederici (1998) provides evidence that the diagnosis process is reflected by the onset of the “P600” which might appear as a P345 in constructions where only binding relations have to be recomputed (Friederici et al. 1998, 2001; Vos et al. 2001; Frisch et al. 2004). In contrast, amplitude and duration of the P600 reflect the amount of reanalysis costs. This view has been challenged by Hagoort (2003) who reported ERP results on weak and strong syntactic violations (11, 12) compared to a correct sentence (10) as in
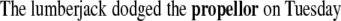 |
10 |
 |
11 |
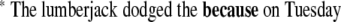 |
12 |
where the weak violation (11) does not evoke an early positivity as it would have to be expected upon the diagnosis and repair model predicting that the weak violation would be easier to diagnose and to repair. However, this interpretation is at variance with the model because the weak violation (11) is morphosyntactic, which might be harder to diagnose than the strong word category violation (12) which in fact evoked an early starting, large and sustained P600.
Relying on Friederici’s (1995, 1999, 2002) neurocognitive model of language processing, Bornkessel and Schlesewsky (2006) have recently proposed their (extended) Argument Dependency Model, where only a syntactic core consisting of word category and argument structure information is maintained (van Valin 1993). The model accounts for cross-linguistic differences in ERP and neuroimaging patterns solely attributed to computational steps in the processing of semantic and thematic dependencies (Friederici’s phase 2). However, the third phase in the eADM comprises a generalized mapping and well-formedness checks that are reflected by late positivities in the ERP.
At the edge between the phenomenological and computational/dynamical models lies Hagoort’s Memory, Unification and Control (MUC) model (Hagoort 2003, 2005). It shares the property of a syntactic core (lexicalized structure frames) with the eADM and was computationally implemented by Vosse and Kempen (2000). The MUC attributes ERP and neuroimaging findings to a binding mechanism between lexical frames. The ELAN is evoked by a failure to bind lexical frames together, whereas the P600 is related to the time required to establishing such bindings. However, the MUC differs from the neurocognitive model and the eADM with respect to the priority of syntactic computation. While the former are serial/hierarchical, presupposing a syntax first mechanism, the latter is fully parallel where all kinds of information (word category, argument structure, semantics) are used as they become available.
Computational symbolic models
Classical cognitive science rests on the physical symbol system hypothesis that any cognitive process is essentially symbol manipulation that can be achieved by a Turing machine (or less powerful automata) (Newell and Simon 1976; Fodor and Pylyshyn 1988; beim Graben 2004). It is obvious that formal language theory provides the natural framework for treating such systems (Hopcroft and Ullman 1979; Aho and Ullman 1972).
Formal languages. A
formal language is a subset of finite words 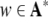 over an alphabet A. Formal languages can be generated by formal
grammars and recognized or translated by automata. Although
natural languages are not context-free (Shieber 1985), context-free
grammars (CFGs) and pushdown automata provide useful tools
for the description of natural languages. A context-free
grammar is a tuple G = (T,
N, P, S) where T is
the (terminal) alphabet of a language, N is an alphabet of auxiliary nonterminal
symbols,
over an alphabet A. Formal languages can be generated by formal
grammars and recognized or translated by automata. Although
natural languages are not context-free (Shieber 1985), context-free
grammars (CFGs) and pushdown automata provide useful tools
for the description of natural languages. A context-free
grammar is a tuple G = (T,
N, P, S) where T is
the (terminal) alphabet of a language, N is an alphabet of auxiliary nonterminal
symbols, 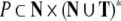 is a set of rewriting rules
is a set of rewriting rules
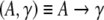
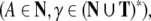 and
and 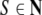 is a distinguished start symbol.
is a distinguished start symbol.
In the framework of Government and Binding Theory (GB) (Chomsky 1981; Haegeman 1994) the X-bar module supplies a context free grammar
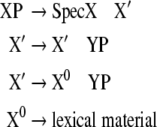 |
where X and Y, respectively, denote one of the syntactic categories C (complementizer), I (inflection), D (determiner), N (noun), V (verb), A (adjective), or P (preposition). The start symbol of this grammar is usually CP or IP. The first rule determines that a maximal projection is formed from a specifier, SpecX, and an X′ phrase. The second rule allows for recursive adjunction and the third rule indicates that a head X0 takes a complement YP to form an X′ phrase. The head X0projects over its complements and adjuncts to the maximal projection. We use this framework in section “Methods/Processing models” to construct our particular language processing model.
Automata. Context-free
languages can be parsed
(i.e. recognized or translated) by serial pushdown automata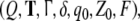 where Q
is a finite set of internal states, T is the input alphabet matching with the
terminal alphabet of a context-free language, Γ is a finite
stack alphabet,
where Q
is a finite set of internal states, T is the input alphabet matching with the
terminal alphabet of a context-free language, Γ is a finite
stack alphabet, 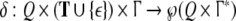 is a partial transition function,
is a partial transition function,
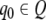 is the distinguished initial state,
is the distinguished initial state,
 is the initial stack symbol, and
is the initial stack symbol, and
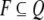 is the set of final (accepting) states. An
automaton with no final states:
is the set of final (accepting) states. An
automaton with no final states:  is said to accept
by empty stack. Given a context-free grammar
G, one can construct
a pushdown automaton accepting the language generated by
G by simulating rule
expansions. Such an automaton is called a top-down recognizer. Formally,
if G = (N, T, P,
S) is a context-free
grammar, then the pushdown automaton
is said to accept
by empty stack. Given a context-free grammar
G, one can construct
a pushdown automaton accepting the language generated by
G by simulating rule
expansions. Such an automaton is called a top-down recognizer. Formally,
if G = (N, T, P,
S) is a context-free
grammar, then the pushdown automaton 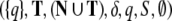 is a top-down
recognizer for G, where δ is defined for all
is a top-down
recognizer for G, where δ is defined for all
 and all
and all  as follows:
as follows:
 |
13 |
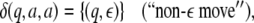 |
14 |
where 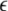 denotes the empty
word of the language. For further discussion,
see Aho and Ullman (1972); Hopcroft and Ullman (1979) and beim Graben
et al. (2004).
denotes the empty
word of the language. For further discussion,
see Aho and Ullman (1972); Hopcroft and Ullman (1979) and beim Graben
et al. (2004).
For a deterministic top-down
recognizer, the sets 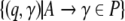 in Eq. 13 always contain only one element as the
grammar G must be
locally unambiguous.
This can, however, be achieved by decomposing the grammar
G into its locally
unambiguous parts (beim Graben et al. (2004), see also Hale and
Smolensky (2006) for a related approach). A
deterministic top-down recognizer can be more conveniently
characterized by its state
descriptions
in Eq. 13 always contain only one element as the
grammar G must be
locally unambiguous.
This can, however, be achieved by decomposing the grammar
G into its locally
unambiguous parts (beim Graben et al. (2004), see also Hale and
Smolensky (2006) for a related approach). A
deterministic top-down recognizer can be more conveniently
characterized by its state
descriptions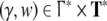 where
γ = γ0γ1…γk−1 is
the content of the stack while w = w1w2…wl is a finite word at the input tape. It follows
from the definition of the transition function δ that the
automaton has access only to the top of the stack
γ0 and to the first symbol of the
input tape w1 at each instance of time. Hence, we
can define a map
where
γ = γ0γ1…γk−1 is
the content of the stack while w = w1w2…wl is a finite word at the input tape. It follows
from the definition of the transition function δ that the
automaton has access only to the top of the stack
γ0 and to the first symbol of the
input tape w1 at each instance of time. Hence, we
can define a map  acting on pairs of the topmost symbols of
stack
acting on pairs of the topmost symbols of
stack 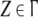 and input tape
and input tape 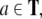 respectively, by the transition function
δ
respectively, by the transition function
δ
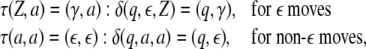 |
15 |
where γ = γ0…γk−1 if
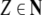 and if P contains a rule
and if P contains a rule 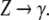
Computational psycholinguistics does not only attempt to describe the grammar of natural languages, it also seeks to identify the mechanisms underlying human sentence processing (Lewis 2000). The existence of garden-paths is evidence that natural languages have local ambiguities; in addition, garden-paths have occasionally been taken to motivate serial processing theories (for contrasting parallel processing accounts, see section “Methods/Tensor product top-down recognizer” and Hale (2003, 2006), Boston et al. (in press)). One of the first serial processing models for human languages was Frazier and Fodor’s Sausage Machine (1978). It comprises two modules: the “sausage machine” generates phrase packages by looking a few symbols ahead into the input, while the “sentence structure supervisor” incrementally builds the phrase structure tree according to a context-free grammar. The model also accounts for particular processing strategies which minimize computational effort. Frazier and Fodor’s (1978) Minimal Attachment Principle favors phrase structure trees with a minimal number of nodes. Additionally, it has been shown that the model cannot be represented by a simple top-down recognizer (Fodor and Frazier 1980). However, there are proposals in the literature that the human parser may be a kind of a deterministic left-corner automaton with finite look-ahead (Marcus 1980; Staudacher 1990), as suggested by the sausage machine.
Generalized shifts. Of
special interest for our exposition in
section “Methods/Nonlinear dynamical automaton” is that any
automaton (even Turing machines and super Turing devices)
can be reconstructed by a particular kind of symbolic
dynamics, called generalized
shifts (Moore 1990; 1991; Siegelmann 1996). These are given
by sets of bi-infinite dotted strings Eq. 6 which evolve under the left
shift Eq. 7
augmented with a word replacement mechanism. Let
 be a number of digits around the dot, i.e.
d = 2, then the words
w = a−1. a0 of length d lie in a domain of
dependence (DoD). The generalized shift is
given by
be a number of digits around the dot, i.e.
d = 2, then the words
w = a−1. a0 of length d lie in a domain of
dependence (DoD). The generalized shift is
given by
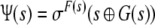 |
16 |
 |
17 |
 |
18 |
where F(s) = l
dictates a number of shifts to the right (l < 0), to the left
(l > 0) or no
shift at all (l = 0),
G(s) is a word w′ of length e in the domain of effect (DoE) to be
replacing the content w
in the DoD of s, and
 denotes this replacement function.
denotes this replacement function.
A deterministic top-down recognizer as described by Eq. 15 can be easily represented by such a generalized shift, choosing
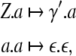 |
19 |
where the stack content γ had to be reverted to γ′ = γk−1… γ0 in order to bring the topmost symbol γ0 into the DoD of the generalized shift (beim Graben et al. 2004).
Although the repair procedure of Lewis (1998) goes beyond the domain of top-down parsing, it can be straightforwardly embedded into the framework of generalized shifts by a table of additional maps, such as
 |
20 |
where γk could be a (reversed) string in the stack with arbitrary length |γk|. As the repair operation can only take place within the stack, the input string w remains unaffected. We exploit this possibility in our serial diagnosis and repair model in section “Methods/Nonlinear dynamical automaton”.
Cognitive architectures. To conclude this section we shall also consider computational models that are partly hybrid architectures of symbolic and dynamic systems (Vosse and Kempen 2000; Hale 2003, 2006; Hale and Smolensky 2006; van der Velde and de Kamps 2006). One particular type of these models is based on cognitive architectures such as ACT-R, which we discuss next as an illustration.
The cognitive theory ACT-R (Anderson et al. 2004) is implemented as a general computational model and incorporates constraints developed through considerable experimental research on human information processing. The ACT-R theory relevant for the present discussion and the parsing model are outlined next, and its empirical coverage is briefly discussed. For details of the architecture the reader should consult the article mentioned above.
In its essence, ACT-R consists of two distinct systems, declarative memory and procedural memory. Declarative memory consists of items (chunks) identified by a single symbol. Each chunk is a set of feature–value pairs; the value of a feature may be a primitive symbol or the identifier of another chunk, in which case the feature–value pair represents a relation. In addition to the memory systems, focused buffers hold single chunks. There is a fixed set of buffers, each of which holds a single chunk in a distinguished state that makes it available for processing. Items outside of the buffers must be retrieved to be processed. The three important cognitive buffers are: the goal buffer, the problem state buffer, and the retrieval buffer. The goal buffer serves to represent the current control state information, and the problem state buffer represents the current problem state. The retrieval buffer serves as the interface to declarative memory, holding the single chunk from the last retrieval.
The retrieval-buffer structure has much in common with conceptions of working memory and short-term memory that posit an extremely limited focus of attention of one to three items, with retrieval processes required to bring items into the focus for processing (McElree and Dosher 1993). All procedural knowledge is represented as production rules—asymmetric associations specifying conditions and actions. Conditions are patterns to match against buffer contents, and actions are taken on buffer contents. All behavior arises from production rule firing; the order of behavior is not fixed in advance but emerges in response to the dynamically changing contents of the buffers. The sentence processing model critically depends on the built-in constraints on activation fluctuation of chunks as a function of usage and delay. Chunks have numeric activation values that fluctuate over time; activation reflects usage history and time-based decay. The activation affects a chunk’s probability and latency of retrieval. ACT-R also assumes that associative retrieval is subject to interference. Chunks are retrieved by a content-addressable, associative retrieval process (McElree 2000). Similarity-based retrieval interference arises as a function of retrieval cue-overlap: the effectiveness of a cue is reduced as the number of items associated with the cue increases. Associative retrieval interference arises because the strength of association from a cue is reduced as a function of the number of items associated with the cue.
The sentence processing model embedded in ACT-R consists of a definition of lexical items in permanent memory defined in terms of feature–value pairs, and a set of production rules specifying a left-corner parser (Aho and Ullman 1972). The model has been applied to several different published reading experiments involving English (Lewis and Vasishth 2006), German (Vasishth et al. 2008), and Hindi (Vasishth and Lewis 2006a), using the self-paced reading and eyetracking methodologies. The simulations provide detailed accounts of the effects of length and structural interference on both unambiguous and garden path structures.
An important result in this model is that all fits were obtained with most of the quantitative parameters set to default values in the ACT-R literature. The remaining theoretical degrees of freedom in the model are the production rules that embody parsing skill, and these rules represent a straightforward realization of left-corner parsing conforming to one overriding principle: compute the parse as quickly as possible. This approach thereby considerably reduces theoretical degrees of freedom; both the specific nature of the strategic parsing skill and the mathematical details of the memory retrieval derive from existing theory, plus the assumption of fast, incremental parsing.
Dynamical system models
The dynamical systems approach to cognition claims that cognitive computation is essentially the transient behavior of nonlinear dynamical systems (Crutchfield 1994; Port and van Gelder 1995; van Gelder 1998; Beer 2000; beim Graben et al. 2004).
Connectionist models.
Most attempts for such models of syntactic language
processing (see Christiansen and Chater (1999); Lewis
(2000) for
surveys), were made using local
connectionist representations. These are
given by activation patterns in neural networks which are
either extended over many processors (“neurons”), for
distributed
representations, or localized to single
processors for local representations. All N network processors
 together span a finite vector space
together span a finite vector space
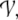 the activation space, in which the
representational states of a connectionist network are
situated. Formally, a representation
the activation space, in which the
representational states of a connectionist network are
situated. Formally, a representation
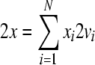 |
21 |
is local if
exactly one processor  is activated at a certain time, i.e.
xi = 1, xj = 0, for all
is activated at a certain time, i.e.
xi = 1, xj = 0, for all  On the other hand, every other
representation is distributed (Smolensky and Legendre 2006).
On the other hand, every other
representation is distributed (Smolensky and Legendre 2006).
In his seminal work, Elman (1995) suggested a simple recurrent neural network (SRN) architecture that predicts word categories of an input string. This model was elaborated by Tabor et al. (1997) and Tabor and Tanenhaus (1999) using a gravitational clustering mechanism to account for reading time differences. However, local representations have been criticized by Fodor and Pylyshyn (1988) as being cognitively implausible because they lack the required compositionality and causality properties.
In response to these criticisms, Dolan and Smolensky (1989); Smolensky (1990) and independently Mizraji (1989, 1992) suggested a unifying framework for distributed representations of structured symbolic information such as lists or phrase structure trees. According to Smolensky (1990), this approach comprises three steps:
decomposing symbolic structures via fillers and roles,
representing conjunctions,
superimposing conjunctions formed by tensor products of filler/role bindings.
A distributed connectionist representation of symbolic
structures s in a set
S is a mapping ψ from
S to activation
vector space 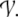 The set S contains strings, binary trees, or other
symbol structures. Smolensky (1990) called the
mapping ψ faithful if ψ
is injective and no symbolic structure is mapped onto the
zero vector.
The set S contains strings, binary trees, or other
symbol structures. Smolensky (1990) called the
mapping ψ faithful if ψ
is injective and no symbolic structure is mapped onto the
zero vector.
In order to prescribe the desired representation, Smolensky (1990) defined the role decomposition F/R for the set of symbolic structures S as a cartesian product of sets F × R, where the elements of F are called fillers and those of R are dubbed roles. The role decomposition is then defined by the following mapping:
 |
22 |
where each  is associated to the set β(s) of filler/role bindings in
(Smolensky 1990, p.169) .3 The mapping β is referred to as the filler/role representation of
S which provides the
first step of decomposing symbolic structures via fillers
and roles.
is associated to the set β(s) of filler/role bindings in
(Smolensky 1990, p.169) .3 The mapping β is referred to as the filler/role representation of
S which provides the
first step of decomposing symbolic structures via fillers
and roles.
Consider, e.g., a finite sequence (a word)
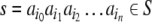 |
23 |
of n symbols ai from a finite alphabet T. Following Smolensky, the symbols can be identified with the fillers, i.e. F = T. On the other hand, the roles are given by the n string positions, R = {0, 1,…, n}. Then, we obtain from Eq. 22,
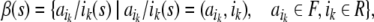 |
where the expression 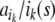 tells that filler
tells that filler  is bound at role ik in forming s.
is bound at role ik in forming s.
A connectionist representation ψ comprises three different
maps. First, all elements  and
and 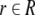 are mapped onto different vectors
are mapped onto different vectors
 of two finite-dimensional vector spaces
of two finite-dimensional vector spaces
 respectively. Second, tensor product representations
of the filler/role bindings are introduced by another
function from β(s) to
respectively. Second, tensor product representations
of the filler/role bindings are introduced by another
function from β(s) to
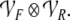 Therefore, Smolensky (1990, p. 174) defined
the maps:
Therefore, Smolensky (1990, p. 174) defined
the maps:
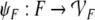 |
24 |
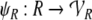 |
25 |
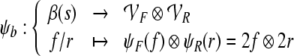 |
26 |
The Eqs. 24 and 25 map the fillers and roles onto the corresponding vector spaces. The filler/role binding is then formed by algebraic tensor products in Eq. 26.
The second step, representing conjunctions, is achieved by pattern superposition, which is basically vector addition. If two vectors are each represented in one connectionist system by an activation pattern, then the representation of the conjunction of these patterns is the pattern resulting from superimposing the individual patterns. Smolensky (1990, p. 171) defined that a connectionist representation ψ employs the superpositional representation of conjunction if and only if:
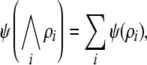 |
27 |
where 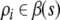 are the filler/role bindings for s conceived as propositions:
“filler f binds to role
r”. Thus, the
connectionist representation of a conjunction of filler/role
bindings is the sum of the representations of the individual
bindings.4 The connectionist representation ψ restricted to
β(s) is defined in
Eq. 26 as ψb, such that we arrive eventually at
are the filler/role bindings for s conceived as propositions:
“filler f binds to role
r”. Thus, the
connectionist representation of a conjunction of filler/role
bindings is the sum of the representations of the individual
bindings.4 The connectionist representation ψ restricted to
β(s) is defined in
Eq. 26 as ψb, such that we arrive eventually at
 |
28 |
The string  from example (23) is thus represented by
the sum of tensor products
from example (23) is thus represented by
the sum of tensor products
 |
29 |
Depending on the dimensionality of the filler and role vector spaces, the representation Eq. 28 is faithful, if the filler and role vectors are both linearly independent. Contrarily, if this is not the case, the tensor product representation Eq. 28 describes graceful saturation of activation (Smolensky 1990; Smolensky and Legendre 2006). Note that a faithful tensor product representation allows the projection of activation patterns back into the respective filler and role spaces, thus enabling the unbinding of constituent structures. We shall use such a faithful representation for phrase structures trees in section “Methods/Tensor product top-down recognizer” for modeling our massively parallel top-down recognizer. Such models are important as they possess a compositional architecture whose representations by patterns of distributed activation are in fact causally efficacious for cognitive computations, thereby disproving Fodor and Pylyshyn (1988).
On the other hand, tensor product representations that are
not faithful are interesting for other reasons. One example
for such representations are fractal
encodings, proposed by Tabor (1998, 2000) for constructing
dynamical automata in
case of 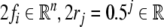 (Smolensky and Legendre 2006; Smolensky
2006).
Also Gödel encodings
(Moore 1990,
1991;
Siegelmann 1996; beim Graben et al. 2004) are special,
namely, one-dimensional tensor product representations, for
integer fillers and real-valued roles:
(Smolensky and Legendre 2006; Smolensky
2006).
Also Gödel encodings
(Moore 1990,
1991;
Siegelmann 1996; beim Graben et al. 2004) are special,
namely, one-dimensional tensor product representations, for
integer fillers and real-valued roles: 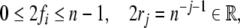 where n
is the number of fillers.
where n
is the number of fillers.
Dynamical recognizers.
Pollack (1991)
introduced dynamical recognizers and implemented them
through cascaded neural networks in order to describe
classification tasks for formal languages. A dynamical
recognizer is a quadruple 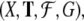 where
where 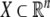 is a “phase space”, T is a finite input alphabet of symbols
ai,
is a “phase space”, T is a finite input alphabet of symbols
ai, 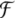 is an iterated function system,
parameterized by the symbols from
is an iterated function system,
parameterized by the symbols from 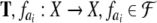 and
and  is a “decision function”. The recognizer
accepts a finite string
is a “decision function”. The recognizer
accepts a finite string 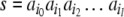 as belonging to a certain formal language,
when
as belonging to a certain formal language,
when
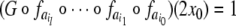 |
for a particular initial condition
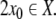 Note that this dynamical system is
completely non-autonomous as there is no intrinsic dynamics
Note that this dynamical system is
completely non-autonomous as there is no intrinsic dynamics
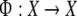 prescribed generating trajectories from
initial conditions as itineraries
prescribed generating trajectories from
initial conditions as itineraries  These systems have been further developed
by Moore (1998); Moore and Crutchfield (2000), and especially by
Tabor (1998,
2000)
towards “quantum automata” and dynamical automata,
respectively. We exploit these ideas in
section “Methods/Nonlinear dynamical automaton” to present a
“quantum representation theory for dynamical automata”.
These systems have been further developed
by Moore (1998); Moore and Crutchfield (2000), and especially by
Tabor (1998,
2000)
towards “quantum automata” and dynamical automata,
respectively. We exploit these ideas in
section “Methods/Nonlinear dynamical automaton” to present a
“quantum representation theory for dynamical automata”.
Nonlinear dynamical automata. The simplest variant of the tensor product representation is the Gödel encoding, where a one-sided string (Eq. 23) is mapped onto a real number in the unit interval [0, 1] by a bT-adic expansion
 |
30 |
Here,  is an arbitrary encoding of the bT symbols in T
by the integers from 0 to bT − 1, and
is an arbitrary encoding of the bT symbols in T
by the integers from 0 to bT − 1, and 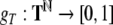 denotes its extension to sequences from
denotes its extension to sequences from
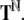
The Gödel encoding Eq. 30 has the advantage that also dotted
bi-infinite strings (Eq. 6) can be described by numeric values, simply
by splitting the string at the dot and representing the
left-hand-side from the dot by one number 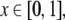 and the right-hand-side from the dot by
another number
and the right-hand-side from the dot by
another number 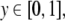 such that
such that
 |
31 |
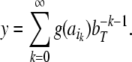 |
32 |
Thus, a bi-infinite string is mapped onto by a point (x, y) in the unit square [0, 1]2. This “symbologram” provides a phase space representation of a symbolic dynamics (Cvitanović et al. 1988; Kennel and Buhl 2003).
Next, consider a generalized shift with DoD of length
d as in
section “Introduction/Computational symbolic models”. Then,
the word contained in the DoD at the left-hand-side of the
dot, partitions the x-axis of the symbologram, while the word
contained in the DoD at the right-hand-side of the dot
partitions its y-axis. In
our case, for d = 2, the
DoD is formed by the words w = a−1. a0, such that the symbol a−1 produces a partition of the
x-axis and the symbol
a0 of the y-axis. Taken together, the DoDs partition the
unit square into rectangles which are the corresponding
domains of the symbologram dynamics. Moore (1990, 1991) has proven that
this dynamics is given by piecewise affine linear (yet,
globally nonlinear) maps. In contrast to the non-autonomous,
forced dynamical recognizers and automata (Pollack
1991; Tabor
1998,
2000), the
nonlinear symbologram dynamics, 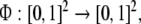 resulting from generalized shifts is
autonomous and intrinsic. Therefore, we shall refer to these
systems as to nonlinear dynamical
automata (NDA). It is obvious that rectangles
in the NDA’s phase space, which correspond to cylinder sets
of the underlying generalized shift, are symbolic
representations and that these are causally efficacious as
they are contained in the cells of the partition defining
the NDA’s dynamics (beim Graben 2004). Less obvious is
yet, that these rectangles are also constituents obeying
compositionality demands (Fodor and Pylyshyn 1988). However, this
becomes clear by considering the symbolic dynamics of the
NDA: constituents form admissible words of generalized
shifts (Atmanspacher and beim Graben 2007).
resulting from generalized shifts is
autonomous and intrinsic. Therefore, we shall refer to these
systems as to nonlinear dynamical
automata (NDA). It is obvious that rectangles
in the NDA’s phase space, which correspond to cylinder sets
of the underlying generalized shift, are symbolic
representations and that these are causally efficacious as
they are contained in the cells of the partition defining
the NDA’s dynamics (beim Graben 2004). Less obvious is
yet, that these rectangles are also constituents obeying
compositionality demands (Fodor and Pylyshyn 1988). However, this
becomes clear by considering the symbolic dynamics of the
NDA: constituents form admissible words of generalized
shifts (Atmanspacher and beim Graben 2007).
In sum, we realize that faithful high-dimensional tensor product representations as well as two-dimensional NDAs fulfill Fodor and Pylyshin’s (1988) constraints on dynamical system architectures for cognitive computation, where different regions in phase space represent different symbolic contents with different causal effects.
Methods
In this section we present two different models of syntactic language processing both comprised by Smolensky’s universal tensor product representations. The first model makes explicit use of a high-dimensional and faithful filler/role binding architecture that allows the description of syntactic parsing as a massively parallel process in the phase space of a nonlinear dynamica l system. The second model, on the other hand, generalizes the nonlinear dynamical automata approach of Gödel encoded generalized shifts. It is a serial diagnosis and repair model, augmented with a non-autonomous forcing to describe incoming sentence material. Both models will be developed on the basis of a context-free grammar that describes the processing difficulties in a pilot experiment on language-related brain potentials. The models are able to describe, at least qualitatively, the obtained ERP results by trajectories that explore different regions in phase space in pursuing different processing steps.
ERP experiment
In an ERP experiment on the processing of locally ambiguous German sentences, 14 subjects were asked to read 120 sentences each, belonging to two different condition classes:
 |
33 |
 |
34 |
Sentences were visually presented phrase-by-phrase with 500 ms (plus 100 ms blank screen resulting in 600 ms interstimulus interval) at the screen of a computer monitor. The sentences were presented in pseudo-randomized order and subjects had to answer probe questions after each sentence to control for their attendance.
The sentences (33) and (34) began with a feminine noun phrase
(NP) die Rednerin (‘the
speaker’), ambiguous with respect to its grammatical role
(either subject or direct object). The disambiguating
information was provided by the determiner of the second noun
phrase:  Berater (‘the advisor’) is
explicitly marked as accusative case, therefore assigned to the
direct object role in sentence (33). By contrast,
Berater (‘the advisor’) is
explicitly marked as accusative case, therefore assigned to the
direct object role in sentence (33). By contrast,
 Berater bears nominative
case, hence indicating that this NP must be interpreted as the
subject of the sentence. Correspondingly, die Rednerin has to be
disambiguated towards the direct object role of the sentence
(34).
Berater bears nominative
case, hence indicating that this NP must be interpreted as the
subject of the sentence. Correspondingly, die Rednerin has to be
disambiguated towards the direct object role of the sentence
(34).
According to psycholinguistic principles such as the minimal attachment principle, discussed in section “Introduction/Computational symbolic models”, a subject interpretation of the ambiguous NP is preferred against the alternative direct object interpretation. This preference, the subject preference strategy, leads to processing problems for object-first sentences such as (34). These difficulties are reflected by changes in the event-related brain potential.
In order to measure ERPs, subjects were attached to an EEG recorder by means of 25 Ag/AgCl electrodes mounted according to the 10–20 system (Sharbrough et al. 1995). EEG was recorded with a sampling rate of 250 Hz (impedances < 5kΩ) and was referenced to the left mastoid (re-referenced to linked mastoids offline). Additionally, EOG was monitored to control for eye-movement artifacts.
For the ERP analysis only artifact-free trials (determined by visual inspection) with correct answers to the probe questions were selected. Epochs covering the whole sentence from −1,400 to 2,500 ms relative to the presentation of the critical second NP were baseline corrected by subtracting the time-average of a pre-sentence interval of 200 ms. Mean ERPs were computed for each subject and condition and subsequently averaged into the grand averages.
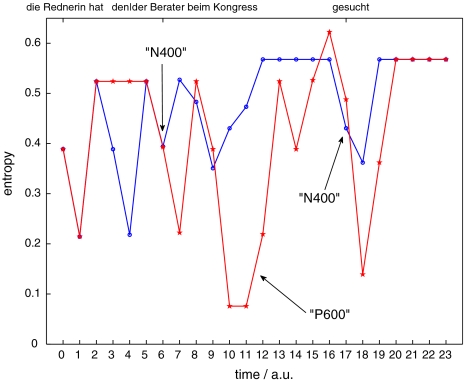
Moreover, a symbolic dynamics analysis (section “Introduction/The dynamical system approach”) was performed. As ERPs are strongly nonstationary over a whole sentence, the binary half-wave encoding (beim Graben 2001; beim Graben and Frisch 2004; Frisch et al. 2004) was employed with parameters: width of secant slope window, T1 = 70 ms; width of moving average window, T2 = 10 ms; dynamic encoding lag, l = 8 ms. This symbolization technique detects local maxima and minima of the EEG time series, mapping time intervals between their successive inflection points onto words consisting of only “0”s and “1”s, respectively. Note that the half-wave encoding resembles the first sifting step of the empirical mode decomposition (Huang et al. 1998; Sweeney-Reed and Nasuto 2007). Due to its local operations, the half-wave encoding technique is able to reduce baseline problems and nonstationary drifts. From the symbolically encoded ERP epochs, event-related cylinder entropies Eq. 9 were computed.
As the ERP results have only illustrative purpose in this study, we do not perform statistical analyses here. A follow-up of this provisional pilot experiment is currently scheduled; and comprehensive results will be published later.
Processing models
In order to construct a formal representation of our ERP
language stimuli, we present the phrase structure trees of the
sentences 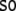 (33) and
(33) and 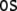 (34) according to Government and Binding
Theory (GB) (Chomsky 1981; Haegeman, 1994) in Fig. 1. Figure 1a shows the tree of (33) and
1b that for
(34).
(34) according to Government and Binding
Theory (GB) (Chomsky 1981; Haegeman, 1994) in Fig. 1. Figure 1a shows the tree of (33) and
1b that for
(34).
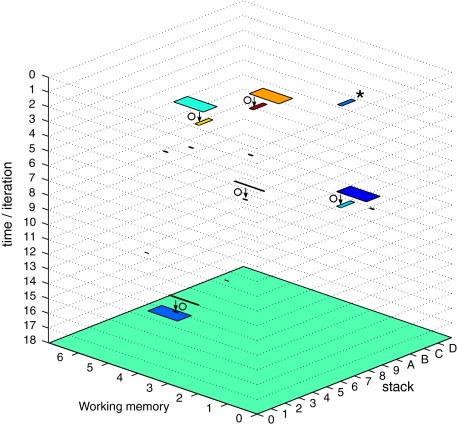
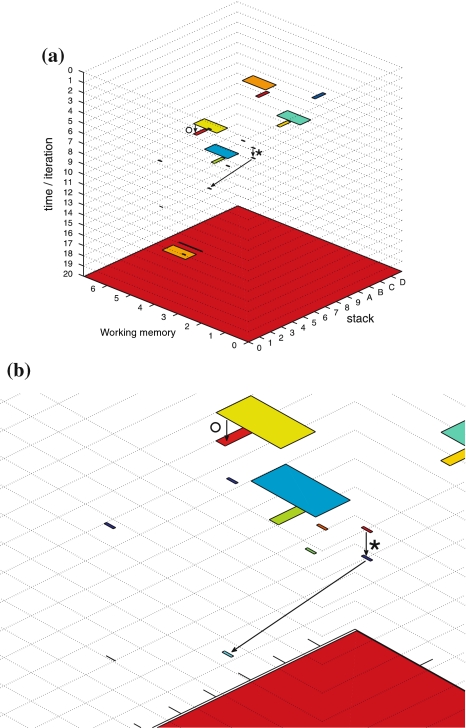
Fig. 1.
GB phrase structure trees. (a) For the
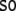 sentence (33). (b) For the
sentence (33). (b) For the
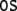 sentence (34)
sentence (34)
These trees are derived on the basis of the X-bar module of GB (section “Introduction/Computational symbolic models”). Their binding relations result from movement operations that are represented by co-indexed nodes (hence the nodes DPk and DPi are essentially the same, they only differ in their binding partners, the tracestk, ti). Note that binding and movement cannot be captured within the framework of context-free grammars; one possibility to do so are minimalist grammars (Stabler 1997; Michaelis 2001; Stabler and Keenan 2003; Hale 2003; Gerth 2006).
From the trees in Fig. 1, a context-free grammar is readily obtained. Though, for the sake of simplicity, we first discard the lexical material regarding the next to last nodes in the trees as the terminal symbols T = {DP1, C0, t, DP2, DP3, V0, I0} where:
 |
Additionally, only binary branches of the trees are taken into account such that the expansion of I0 is also abandoned. The corresponding nonterminal alphabet is then given by N = {CP, C′, I1, I2, VP, IP, V′} where we have introduced two categories I1, I2 for the I′ nodes in Fig. 1b. The grammar G = (T, N, P, CP) comprises the rewriting rules
 |
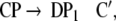 |
35 |
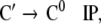 |
36 |
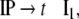 |
37 |
 |
38 |
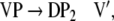 |
39 |
 |
40 |
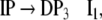 |
41 |
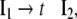 |
42 |
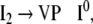 |
43 |
 |
44 |
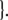 |
The grammar G is locally ambiguous for there is more than one rule to expand the nonterminals IP, I1, VP, respectively. Following beim Graben et al. (2004), the grammar can be decomposed into two locally unambiguous grammars G1, G2, resulting in the production systems
 |
45 |
for generating sentence (33), and
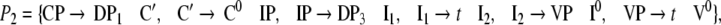 |
46 |
for generating sentence (34), (this decomposition is analogue to the harmonic normal form decomposition suggested by Hale and Smolensky (2006)).
Each of the languages produced by the disambiguated grammars G1, G2, can be deterministically parsed with a suitable top-down recognizer as explained in section “Introduction/Computational symbolic models”. In the following two subsections, we use Smolensky’s tensor product representations in order to construct two different top-down recognizers. The first, a parallel, high-dimensional dynamical system using faithful filler/role bindings (Dolan and Smolensky 1989; Smolensky 1990, 2006; Smolensky and Legendre 2006); the second, a serial diagnosis and repair NDA based on a Gödel encoding of generalized shifts (Moore 1990, 1991; Siegelmann 1996) combined with a non-autonomous update dynamics (Pollack 1991; Moore 1998; Tabor 2000; Moore and Crutchfield 2000).
Tensor product top-down recognizer
Following Dolan and Smolensky (1989), Smolensky (1990, 2006) and Smolensky and Legendre (2006), hierarchical structures can be represented in activation space of neural networks by filler/role bindings through tensor products. A labeled binary tree supplies three role positions: Parent, LeftChild, and RightChild which can be identified with basis vectors of a three-dimensional role vector space,
 |
47 |
To each of these roles, either a simple or a complex filler can be attached. Simple fillers are terminal and nonterminal symbols of the grammar G, which in turn are also identified with basis vectors of another, 14-dimensional space:
 |
48 |
The binding of a category to a tree position is expressed
by a tensor product 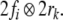 A simple tree is then given by the sum
over all filler/role bindings
A simple tree is then given by the sum
over all filler/role bindings  Since tree positions can be occupied by
subtrees, a recursive application of tensor products, as
e.g. in
Since tree positions can be occupied by
subtrees, a recursive application of tensor products, as
e.g. in  instantaneously increases the
dimensionality of the respective subspaces. Therefore, the
sum has to be replaced by a direct sum over tensor product
spaces leading to
instantaneously increases the
dimensionality of the respective subspaces. Therefore, the
sum has to be replaced by a direct sum over tensor product
spaces leading to
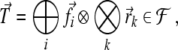 |
49 |
where  is the infinite-dimensional Fock space generated by the
finite-dimensional filler
is the infinite-dimensional Fock space generated by the
finite-dimensional filler  and role vector spaces
and role vector spaces 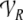 (Smolensky and Legendre 2006, p. 186, footnote
11). In fact, a faithful representation of infinitely
recursive phrase structures would demand the complete Fock
space (beim Graben et al. 2007).
(Smolensky and Legendre 2006, p. 186, footnote
11). In fact, a faithful representation of infinitely
recursive phrase structures would demand the complete Fock
space (beim Graben et al. 2007).
However, the grammar G
is fortunately not recursive thus making Smolensky’s
approach tractable with finite means. In the following, we
shall devise a tensor product
top-down recognizer. Its state description at
time t comprises two Fock
space elements 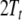 and
and 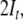 corresponding to the stack and the input
of the automaton defined in Eq. 15, respectively.
corresponding to the stack and the input
of the automaton defined in Eq. 15, respectively. 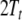 denotes the tensor product tree at
processing time t, while
the tensor
denotes the tensor product tree at
processing time t, while
the tensor  is of the form
is of the form  i.e. all fillers, which correspond only to
terminals, are assigned to the root position. Thereby,
i.e. all fillers, which correspond only to
terminals, are assigned to the root position. Thereby,
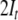 encodes the input being processed. Because
the direct sum in these expressions is commutative and
associative, we additionally require two pointers,
encodes the input being processed. Because
the direct sum in these expressions is commutative and
associative, we additionally require two pointers, 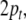 to the next, not yet expanded, nonterminal
filler in the stack
to the next, not yet expanded, nonterminal
filler in the stack 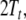 and
and 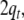 to the topmost position in the input.
Therefore, a tensor product top-down recognizer τi for processing grammar Gi (i = 1, 2)
is characterized by a semi-symbolic state
description
to the topmost position in the input.
Therefore, a tensor product top-down recognizer τi for processing grammar Gi (i = 1, 2)
is characterized by a semi-symbolic state
description
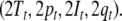 |
50 |
The parser recursively expands the nonterminal filler
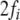 beneath
beneath  into an elementary tree
into an elementary tree 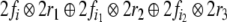 when there is a rule corresponding to
when there is a rule corresponding to
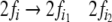 in the grammar. Thereafter, it looks into
the expanded tree, whether
in the grammar. Thereafter, it looks into
the expanded tree, whether  or
or 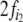 agrees with the terminal symbol in
agrees with the terminal symbol in
 pointed to by
pointed to by  If this is the case, the particular filler
will be removed only from the input, readjusting
If this is the case, the particular filler
will be removed only from the input, readjusting
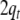 to the next input symbol.
to the next input symbol.
Since filler/role bindings can be established recursively,
we introduce four additional roles 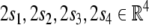 indicating the positions in the state
description list above. Binding
indicating the positions in the state
description list above. Binding 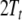 to
to 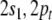 to
to 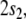 etc., yields the representation of a state
description of τi
etc., yields the representation of a state
description of τi
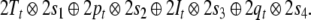 |
51 |
As there are two sentences, 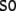 (33) and
(33) and 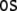 (34), which can be processed by two
deterministic tensor product top-down recognizers
τ1 and τ2,
there are four different parses,
(34), which can be processed by two
deterministic tensor product top-down recognizers
τ1 and τ2,
there are four different parses, 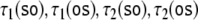 to be examined. Parsing trajectories are
presented in the Appendix.
to be examined. Parsing trajectories are
presented in the Appendix.
For numerical implementation of the model, we chose the
arithmetic vector spaces 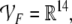 and
and 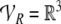 and identify the fillers
and identify the fillers 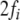 and roles
and roles 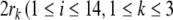 ) with their canonical basis vectors
) with their canonical basis vectors
 respectively. Thus, e.g. the role for the
parent position in vector space
respectively. Thus, e.g. the role for the
parent position in vector space 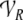 is
is 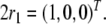 This leads to a local and faithful
representation of these symbols.
This leads to a local and faithful
representation of these symbols.
In this representation, the tensor products are then given
by Kronecker products
(Mizraji 1989,
1992) of
filler and role vectors, 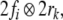 where
where
 |
Generally, the calculation of iterated tensor products
leads to a vast number of subspaces of different dimensions.
Consider, e.g., the tree representation attached to
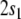 for state 2 of the
for state 2 of the 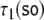 parse,
parse,
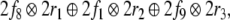 |
saying that CP is attached to Parent,
DP1 to LeftChild and C′ to RightChild. Since the filler
 is beneath the “stack pointer” in
is beneath the “stack pointer” in
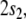 rule (36),
rule (36), 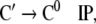 corresponding to the state
transition
corresponding to the state
transition
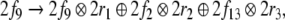 |
applies next. This results into state 3 of the trajectory with
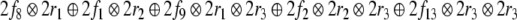 |
in  position.
position.
Obviously, the first two direct summands 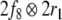 and
and 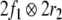 in this term belong to another, lower
dimensional, subspace of the Fock space than the remaining
ones. Therefore, usage of direct sums is crucially required
for proper tensor product representations. However, as our
model grammars are not recursive at all, we know that the
representation of the last phrase structure tree for
well-formed parses is an element of a finite tensor product
space
in this term belong to another, lower
dimensional, subspace of the Fock space than the remaining
ones. Therefore, usage of direct sums is crucially required
for proper tensor product representations. However, as our
model grammars are not recursive at all, we know that the
representation of the last phrase structure tree for
well-formed parses is an element of a finite tensor product
space  with maximal dimension M. Therefore, we take
with maximal dimension M. Therefore, we take
 as an embedding
space, interpreting the direct sums as those
of finite subspaces in
as an embedding
space, interpreting the direct sums as those
of finite subspaces in  Technically, we achieve this by
multiplying all vectors from lower-dimensional subspaces
Technically, we achieve this by
multiplying all vectors from lower-dimensional subspaces
 with tensor powers of the root role
with tensor powers of the root role
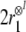 from the right, where
from the right, where 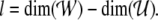
For the example above, we hence obtain the correct expression
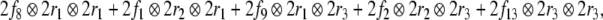 |
where the usual vector addition is now admissible.
Since all representations are now activation vectors from
the same high-dimensional vector space 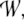 we can easily construct the desired
parallel parser from
the four trajectories obtained by
we can easily construct the desired
parallel parser from
the four trajectories obtained by 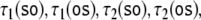 respectively, simply by superimposing the
state descriptions of
respectively, simply by superimposing the
state descriptions of 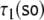 and
and  for each processing step separately. This
entails the parallel parse of the
for each processing step separately. This
entails the parallel parse of the 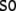 sentence (33). On the other hand,
superimposing the instantaneous state descriptions of
sentence (33). On the other hand,
superimposing the instantaneous state descriptions of
 and
and  yields the parallel parse of the
yields the parallel parse of the
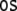 sentence (34). Note that the trajectories
of the parses have to be filled up with zero vectors to
adjust their different durations.
sentence (34). Note that the trajectories
of the parses have to be filled up with zero vectors to
adjust their different durations.
At the end, our construction yields a time-discrete
dynamical system  with phase space
with phase space and flow
and flow , representing a parallel tensor product
top-down recognizer. The iterates
, representing a parallel tensor product
top-down recognizer. The iterates 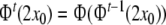 generate the parsing trajectory for
t = 0, 1, 2… starting
with initial condition
generate the parsing trajectory for
t = 0, 1, 2… starting
with initial condition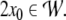
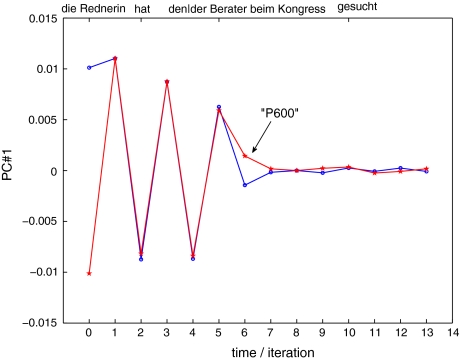
The results of this model are presented in section “Results/Tensor product top-down recognizer”. Here, we have standardized the numerical data by the z-transform in order to make the different parses comparable. Additionally, we employ a principal component analysis (PCA) for reducing the dimensions of the activation vector space in order to facilitate visualization. In short, the PCA is an orthogonal linear transformation that rotates the data into a new coordinate system such that the greatest variance of the data has the direction of the first principal component, PC#1, the second greatest variance of the second principal component and so on.
Nonlinear dynamical automaton
In this section, we construct an NDA top-down recognizer for the stimulus material of the ERP experiment along the lines of beim Graben et al. (2004). Given the two, locally unambiguous grammars G1, G2 with productions Eqs. 45, 46, we first construct two generalized shifts τ1,τ2 for recognizing the context-free languages generated by them.
Pushdown automata generally process finite words
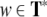 , whereas generalized shifts are operating
on bi-infinite strings
, whereas generalized shifts are operating
on bi-infinite strings 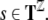 Therefore, we first have to describe
finite words through infinite means. This can be achieved by
forming equivalence classes of bi-infinite sequences that
agree in a particular building block around the separating
dot. Yet, such classes of equivalent bi-infinite sequences
are exactly the cylinder sets introduced in
section “Introduction/The dynamical system approach”. Thus,
every state description γ′ . w of a generalized shift emulating a top-down
recognizer, with
Therefore, we first have to describe
finite words through infinite means. This can be achieved by
forming equivalence classes of bi-infinite sequences that
agree in a particular building block around the separating
dot. Yet, such classes of equivalent bi-infinite sequences
are exactly the cylinder sets introduced in
section “Introduction/The dynamical system approach”. Thus,
every state description γ′ . w of a generalized shift emulating a top-down
recognizer, with  (γ′ denotes γ in reversed order, again)
and
(γ′ denotes γ in reversed order, again)
and  corresponds to a cylinder set
corresponds to a cylinder set
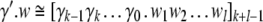 |
52 |
in 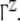 For the sake of subsequent modeling and
numerical implementation, we regard the finite strings γ in
the stack and w in the
input as one-sided infinite strings, continued by random
symbols
For the sake of subsequent modeling and
numerical implementation, we regard the finite strings γ in
the stack and w in the
input as one-sided infinite strings, continued by random
symbols 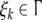 and
and 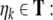
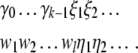 |
53 |
Next, we address the Gödel encoding to construct the NDAs.
Because the stack alphabet 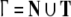 and the input alphabet T of the pushdown automata differ
in size, two separate Gödel encodings, one for the x- and another one for the
y-axis of the
symbologram are recommended. Using the random continuations
Eq. 53, we
obtain from Eq. 30
and the input alphabet T of the pushdown automata differ
in size, two separate Gödel encodings, one for the x- and another one for the
y-axis of the
symbologram are recommended. Using the random continuations
Eq. 53, we
obtain from Eq. 30
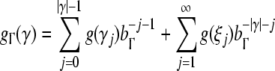 |
54 |
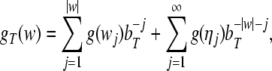 |
55 |
where bT is the number of terminal symbols in T, bΓ = bT + bN is the number of stack symbols in
 is the number of nonterminal symbols in
N,), and g is the arbitrary Gödel
encoding of these symbols.
is the number of nonterminal symbols in
N,), and g is the arbitrary Gödel
encoding of these symbols.
Fixing the prefixes γ0…γk−1 of
the stack and w1w2…wl of the input, results to a cloud of points
randomly scattered across a rectangle in the unit square of
the symbologram. These rectangles are compatible with the
symbol processing dynamics of the NDA, while individual
points  do not have an immediate symbolic
interpretation. We shall refer to arbitrary rectangles
do not have an immediate symbolic
interpretation. We shall refer to arbitrary rectangles
 as to macrostates, distinguishing them from the
microstates
as to macrostates, distinguishing them from the
microstates of the underlying dynamical system.
of the underlying dynamical system.
In order to achieve our modeling task, we first determine the Gödel codes of the context-free grammar derived in section “Methods/Processing models” by arbitrarily introducing the integer numbers
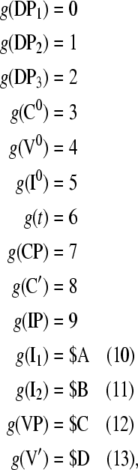 |
56 |
where we have used “hexadecimal” notation for numbers 10 to 13.
Disregarding the numerical values of these codes for a moment, we can prescribe the two generalized shifts τ1,τ2 by their transition functions. For the shift that emulates the top-down recognizer τ1, processing the productions P1 (Eq. 45), this function is
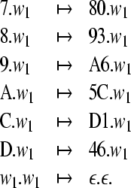 |
57 |
Here, w1 always stands for the topmost
symbol in the input. The last transition describes any
attachment of a successfully predicted terminal. All other
transitions describe the prediction by expanding a rule in
P1. Table 1 presents the dynamics of this generalized
shift processing the sentence  (33).
(33).
Table 1.
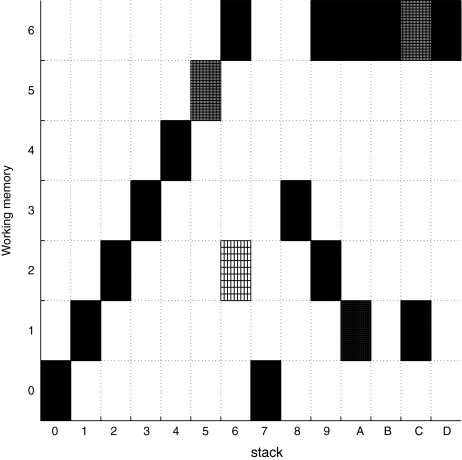
Sequence of state transitions of the generalized shift τ1, processing the well-formed string 0361645
| Time | State | Operation |
|---|---|---|
| 0 | 7 · 0361645 |
 
|
| 1 | 80 · 0361645 | 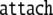 |
| 2 | 8 · 361645 |
 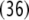
|
| 3 | 93 · 361645 |  |
| 4 | 9 · 61645 |
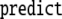 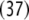
|
| 5 | A6 · 61645 | 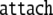 |
| 6 | A · 1645 |
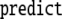 
|
| 7 | 5C · 1645 |
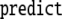 
|
| 8 | 5D1 · 1645 | 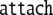 |
| 9 | 5D · 645 |
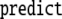 
|
| 10 | 546 · 645 |  |
| 11 | 54 · 45 |  |
| 12 | 5 · 5 | 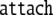 |
| 13 |  |
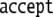 |
The operations are indicated as follows:
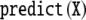 means prediction according to
rule (X) in the productions Eq. 45 of a
context-free grammar;
means prediction according to
rule (X) in the productions Eq. 45 of a
context-free grammar;  means cancelation of
successfully predicted terminals both from stack
and input; and
means cancelation of
successfully predicted terminals both from stack
and input; and 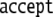 means acceptance of the string
as being well-formed
means acceptance of the string
as being well-formed
Accordingly, the generalized shift
τ2 for recognizing the
well-formedness of the string 0326645, which encodes
sentence  (34), with respect to the productions
P2 is constructed. Table 2 displays the resulting
symbolic dynamics.
(34), with respect to the productions
P2 is constructed. Table 2 displays the resulting
symbolic dynamics.
Table 2.
Sequence of state transitions of the generalized shift τ2, processing the well-formed string 0326645
| Time | State | Operation |
|---|---|---|
| 0 | 7 · 0326645 |
 
|
| 1 | 80 · 0326645 |  |
| 2 | 8 · 326645 |
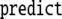 
|
| 3 | 93 · 326645 | 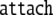 |
| 4 | 9 · 26645 |
 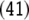
|
| 5 | A2 · 26645 | 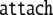 |
| 6 | A · 6645 |
|
| 7 | B6 · 6645 |  |
| 8 | B · 645 |
|
| 9 | 5C · 645 |
 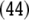
|
| 10 | 546 · 645 |  |
| 11 | 54 · 45 | 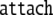 |
| 12 | 5 · 5 | 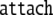 |
| 13 | 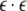 |
 |
The operations are indicated as above
In order to describe the processing problem arising from
parsing the  string 0326645 by
τ1, we present this dynamics in
Table 3.
string 0326645 by
τ1, we present this dynamics in
Table 3.
Table 3.
Sequence of state transitions of the generalized shift τ1, processing the unpreferred string 0326645
| Time | State | Operation |
|---|---|---|
| 0 | 7 · 0326645 |
 
|
| 1 | 80 · 0326645 |  |
| 2 | 8 · 326645 |
|
| 3 | 93 · 326645 |  |
| 4 | 9 · 26645 |
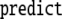 
|
| 5 | A6 · 26645 | 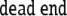 |
| 6 | A6 · 26645 |
The operations are indicated as above,
yet  refers to the processing
problem that a predicted VP is not present in
the input
refers to the processing
problem that a predicted VP is not present in
the input
A possible solution for describing diagnosis and repair processes (Lewis 1998; Friederici 1998) in generalized shifts was proposed by beim Graben et al. (2004). Comparing step 6 in Table 3 with step 5 in Table 2, suggests the construction of a third generalized shift τ3 with only one nontrivial transition
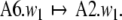 |
58 |
This repair shift replaces the stack content A6 by another content A2 which now lies at the admissible trajectory of τ2 shown in Table 2, steps 5 to 13.
Now, we brought all necessary ingredients together to construct the NDA. The DoD of the generalized shifts τ1, τ2 has width d = 2 such that both symbols next to the dot partition the x- and the y-axis of the unit square symbologram through the Gödel encoding, Eqs. 54, 55. Note that the DoD of the repair shift has width d = 3, as the two most significant symbols in the stack have to be replaced. Because there are bΓ = 14 stack symbols and bT = 7 input symbols, the x-axis is divided into 14 intervals whereas the y-axis is covered by 7 intervals. The resulting partitioning of the phase space is depicted in Fig. 7 below.
Fig. 7.
Measurement partition of the NDA phase space. Grid density is shown logarithmically
The top-down recognizers that are emulated by the
generalized shifts τp (p = 1, 2)
can either  categories according to a uniquely given
rule in their production systems Pp if the topmost symbol γ0
in the stack is a nonterminal which is subsequently expanded
into the right-hand-side of the production since the
grammars are locally unambiguous by construction.
Correspondingly, the NDA dynamics Φp maps a point
categories according to a uniquely given
rule in their production systems Pp if the topmost symbol γ0
in the stack is a nonterminal which is subsequently expanded
into the right-hand-side of the production since the
grammars are locally unambiguous by construction.
Correspondingly, the NDA dynamics Φp maps a point 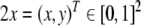 to its image
to its image  if x
belongs to one of the intervals labeled by 7 to D in Fig. 7. These points are translated parallel to
the x-axis. Moreover, a
point
if x
belongs to one of the intervals labeled by 7 to D in Fig. 7. These points are translated parallel to
the x-axis. Moreover, a
point 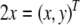 with
with  is subjected to the numerical counterpart
of
is subjected to the numerical counterpart
of  Summarizing these effects, all points
contained within one rectangle of the partition are
equivalently transformed by the piecewise linear map Φp acting as
Summarizing these effects, all points
contained within one rectangle of the partition are
equivalently transformed by the piecewise linear map Φp acting as
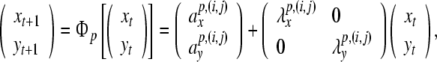 |
59 |
where (xt, yt)T is a state at time t, (xt+1,
yt+1)T is its successor at time t + 1, and (i, j) indicates the ith rectangle along the x-axis and the jth rectangle along the y-axis, given by the Gödel numbers i = g(γ0), j = g(w1) of the topmost symbols of stack
and input tape. The coefficients 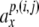 and ap, (i,j)y of the flow Φp (p = 1, 2)
describe a parallel translation of a state whereas the
matrix elements λp,(i,j)x and λp,(i,j)y mediate the stretching (λ > 1) or squeezing
(λ < 1) of a rectangular macrostate.
and ap, (i,j)y of the flow Φp (p = 1, 2)
describe a parallel translation of a state whereas the
matrix elements λp,(i,j)x and λp,(i,j)y mediate the stretching (λ > 1) or squeezing
(λ < 1) of a rectangular macrostate.
Thus, the Gödel encoding provides three different functions Φp (p = 1, 2, 3) assigned to the generalized shifts τp. It is therefore obvious to regard the index p as a control parameter of only one dynamical system living at the unit square. Doing so, relates diagnosis and repair processes in language processing to bifurcations in dynamical systems, namely qualitative changes in their global behavior.
Nevertheless, the NDA model constructed so far exhibits serious disadvantages concerning psycholinguistic plausibility. Since it is a deterministic, autonomous dynamical system, the complete future of the system’s evolution is already encoded in its initial conditions, which is clearly at variance with psycholinguistic evidence. First, psycholinguistic experiments are generally conducted either acoustically or visually in a word-by-word (or phrase-by-phrase) presentation paradigm. In both cases, the human language processor is an open, non-autonomous system that is continuously perturbed by new information supplied from the environment (beim Graben 2006). Therefore, an interactive computational account appears to be more appropriate (Wegner 1998). Second, predictions of the human parsing module are often incorrect. Garden path interpretations (Osterhout and Holcomb 1992; Hagoort et al. 1993; Mecklinger et al. 1995; Osterhout et al. 1994; Fodor and Ferreira 1998; Kaan et al. 2000) or the failure of particular processing strategies, as exemplified in section “ERP experiment”, clearly demonstrate the non-determinacy of the human language processor.
In order to remedy these shortcomings, we suggest the
following solution: First, restrict the automaton’s input to
a working memory, or
look-ahead, of finite length (Frazier and Fodor 1978), say, l = 2, such that w = w1w2. Second, after each attachment
(i.e. when w = w2), the next symbol 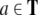 is scanned from the environment, that is
regarded as an information
source (Shannon and Weaver 1949; beim Graben
2006).
Third, define a map
is scanned from the environment, that is
regarded as an information
source (Shannon and Weaver 1949; beim Graben
2006).
Third, define a map 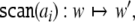 such that w′ = w2ai. I.e.,
such that w′ = w2ai. I.e.,  inserts ai into the second-most significant position of
the working memory. A generalized shift described in this
way, is not longer an autonomous system. Now, it is
interacting with its environment which non-deterministically
perturbs its state descriptions (Wegner 1998).
Table 4
illustrates the parsing of the string 0361645 by the
generalized shift τ1 augmented with
the
inserts ai into the second-most significant position of
the working memory. A generalized shift described in this
way, is not longer an autonomous system. Now, it is
interacting with its environment which non-deterministically
perturbs its state descriptions (Wegner 1998).
Table 4
illustrates the parsing of the string 0361645 by the
generalized shift τ1 augmented with
the  operation.
operation.
Table 4.
Sequence of state transitions of the
generalized shift τ1
supplemented by the  operation, processing the
well-formed string 0361645
operation, processing the
well-formed string 0361645
| Time | State | Operation |
|---|---|---|
| 0 | 7 · 03 | 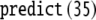 |
| 1 | 80 · 03 |  |
| 2 | 8 · 3 |  |
| 3 | 8 · 36 |
 
|
| 4 | 93 · 36 |  |
| 5 | 9 · 6 |  |
| 6 | 9 · 61 |
 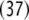
|
| 7 | A6 · 61 |  |
| 8 | A · 1 |  |
| 9 | A · 16 |
 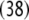
|
| 10 | 5C · 16 |
 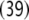
|
| 11 | 5D1 · 16 |  |
| 12 | 5D · 6 |  |
| 13 | 5D · 64 |
|
| 14 | 546 · 64 |  |
| 15 | 54 · 4 |  |
| 16 | 54 · 45 |  |
| 17 | 5 · 5 |  |
| 18 | ϵ · ϵ | 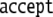 |
The operations are indicated as above;
additionally 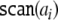 denotes the non-autonomous
action of the scanned new input symbol ai upon the state description of the
shift. In contrast to Table 1 the initial
state contains only the symbols 03 in the
working memory
denotes the non-autonomous
action of the scanned new input symbol ai upon the state description of the
shift. In contrast to Table 1 the initial
state contains only the symbols 03 in the
working memory
How does the 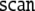 operation affect the corresponding NDAs? A
possible solution to this problem is offered by the
dynamical recognizers, discussed in
section “Introduction/Dynamical system models” (Pollack
1991; Moore
1998; Tabor
1998,
2000;
Moore and Crutchfield 2000), where functions
operation affect the corresponding NDAs? A
possible solution to this problem is offered by the
dynamical recognizers, discussed in
section “Introduction/Dynamical system models” (Pollack
1991; Moore
1998; Tabor
1998,
2000;
Moore and Crutchfield 2000), where functions  acting on the phase space X are assigned to symbols
acting on the phase space X are assigned to symbols
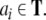 However, the assumption of an arbitrarily
parameterized iterated function system is apparently
inconvenient in the present context, where the Gödel
encoding Eqs. 31,
32 already
provides a suitable interface between the symbolic and the
numeric levels of description. Fortunately, the mathematical
discipline of algebraic representation theory (van der
Waerden 2003),
and its physical counterpart, algebraic quantum theory (Haag
1992),
supply adequate concepts for formulating a proper solution.
However, the assumption of an arbitrarily
parameterized iterated function system is apparently
inconvenient in the present context, where the Gödel
encoding Eqs. 31,
32 already
provides a suitable interface between the symbolic and the
numeric levels of description. Fortunately, the mathematical
discipline of algebraic representation theory (van der
Waerden 2003),
and its physical counterpart, algebraic quantum theory (Haag
1992),
supply adequate concepts for formulating a proper solution.
Taking the word
semigroup (T*,
·) as our starting point5 we can “represent” the individual symbols
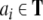 by “quantum operators”
by “quantum operators”  acting on the phase space through
acting on the phase space through
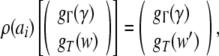 |
60 |
where w′ = w2 ·ai. That is, the scanned input ai only acts at the y-coordinate of the state 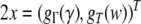 in the symbologram according to
in the symbologram according to
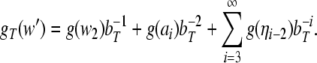 |
61 |
This mapping is indeed a semigroup homomorphism and hence a representation as is proven in the appendix. Numerically, Eqs. 60, 61 lead to the functions
 |
62 |
where  denotes the Gaussian integer function.
Thereby, a dynamical recognizer with iterated function
system
denotes the Gaussian integer function.
Thereby, a dynamical recognizer with iterated function
system  is implemented upon the phase space of a
nonlinear dynamical automaton (X, Φp). Supplementing the generalized shifts
τ1,τ2 with
the
is implemented upon the phase space of a
nonlinear dynamical automaton (X, Φp). Supplementing the generalized shifts
τ1,τ2 with
the  operation and representing it by
Eqs. 60,
61,
62 in the NDA’s
phase space, yields a non-autonomous, interactive dynamical
system. Each
operation and representing it by
Eqs. 60,
61,
62 in the NDA’s
phase space, yields a non-autonomous, interactive dynamical
system. Each  operation is now reflected by a vertical
squeezing of rectangular macrostates in phase space.
operation is now reflected by a vertical
squeezing of rectangular macrostates in phase space.
Finally, we have to address the measurement of the NDA’s states at macroscopic scales. Can we find a suitable “order parameter” accounting for the occurrence of processing problems? In our ERP analysis (sections “Introduction/The dynamical system approach”, “Methods/ERP experiment”) we used information-theoretic entropies as indicators of disorder–order transitions in language-related brain dynamics. The key concept for this analysis is the cylinder entropy Eq. 9. Obviously, this quantity is also appropriate for assessing the dynamics of generalized shifts and NDAs, since the symbolically meaningful states of the generalized shifts are essentially cylinder sets and these are given by rectangular macrostates in the phase space X = [0, 1]2 of the NDA.
In order to measure the cylinder entropy of the processing states, we equip the phase space with a measurement partition whose mesh width determines the probability
 |
63 |
that a rectangle R is covered by a cell Bi of the partition. Here, the geometrical function area(R) = (x2−x1) · (y2−y1) determines the area of the rectangle R = [x1, x2] × [y1, y2] (beim Graben et al. 2004).
Results
In this section, we present the results of our dynamical system simulations on syntactic language processing and the qualitative findings of the illustrative ERP experiment for comparison.
ERP data
Figure 2 displays the
voltage grand averages of the sentence processing ERPs (a) and
the running cylinder entropy resulting from the half-wave
encoding (b) at parietal electrode site Pz. The blue waveforms
were obtained for the control condition  (33). The critical
(33). The critical  (34) condition exhibits a P600 ERP
(Fig. 2a), evoked by
the crucial determiner der
versus den in the second NP.
The P600 is reflected by a large drop in the cylinder entropies
(Fig. 2b).
Additionally, Fig. 2b
shows the N400 deflections elicited by each integration of
incoming lexical material. The comparison of Fig. 2a and b also reveals a strong
nonstationary drift in the averaged ERPs that became completely
suppressed by the local algorithm of the half-wave
encoding.
(34) condition exhibits a P600 ERP
(Fig. 2a), evoked by
the crucial determiner der
versus den in the second NP.
The P600 is reflected by a large drop in the cylinder entropies
(Fig. 2b).
Additionally, Fig. 2b
shows the N400 deflections elicited by each integration of
incoming lexical material. The comparison of Fig. 2a and b also reveals a strong
nonstationary drift in the averaged ERPs that became completely
suppressed by the local algorithm of the half-wave
encoding.
Fig. 2.
Event-related brain potentials for the
 (blue) and
(blue) and 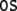 (red) sentences ((33 and 34),
respectively) at the parieto-central electrode
Pz. (a) ERP
voltage averages. (b) Event-related cylinder entropies
obtained from a half-wave symbolic encoding with
parameters T1 = 70ms, T2 = 10ms, and l = 8ms. Waveforms
are digitally low-pass filtered with a cut-off
frequency of 10Hz for better visibility. The
disambiguating words der versus den appeared at t0 = 0s. Language-related
ERPs, N400 and P600, are indicated by
arrows
(red) sentences ((33 and 34),
respectively) at the parieto-central electrode
Pz. (a) ERP
voltage averages. (b) Event-related cylinder entropies
obtained from a half-wave symbolic encoding with
parameters T1 = 70ms, T2 = 10ms, and l = 8ms. Waveforms
are digitally low-pass filtered with a cut-off
frequency of 10Hz for better visibility. The
disambiguating words der versus den appeared at t0 = 0s. Language-related
ERPs, N400 and P600, are indicated by
arrows
Parsing dynamics
Tensor product top-down recognizer
First, we present the successive increase of subspace
dimensions of the tensor product top-down recognizer,
constructed in section “Methods/Tensor product top-down
recognizer”. Table 5
displays these dimensions for the parsing trajectories per
time step. Starting with an initially 224-dimensional space,
the final embedding space has dimension 
Table 5.
Dimensions of the subspaces for
parsing the  and the
and the  sentences, by a tensor
product top-down recognizer,
respectively
sentences, by a tensor
product top-down recognizer,
respectively
| Iteration |  |
 |
|---|---|---|
| 1 | 224 | 224 |
| 2 | 224 | 224 |
| 3 | 224 | 224 |
| 4 | 896 | 896 |
| 5 | 896 | 896 |
| 6 | 3,584 | 3,584 |
| 7 | 3,584 | 3,584 |
| 8 | 14,336 | 14,336 |
| 9 | 57,344 | 14,336 |
| 10 | 57,344 | 57,344 |
| 11 | 57,344 | 229,376 |
| 12 | 229,376 | 229,376 |
| 13 | 229,376 | 229,376 |
| 14 | 229,376 | 229,376 |
Applying the PCA, entailed a remarkable result: The very
high-dimensional dynamics shown in Table 5, turned out to be
effectively one-dimensional. Only the first principal
component, PC#1, of the standardized trajectories exhibits
considerable variance. Figure 3 depicts a return plot of xt = PC#1 for a given iteration at the x-axis plotted against its next
iteration, xt+1 at
the y-axis, for both
parallel parses. Blue lines represent the  sentence (33), while red lines stand for
the
sentence (33), while red lines stand for
the  sentence (34). Additionally, the green
line shows the identity function xt+1 = xt.
sentence (34). Additionally, the green
line shows the identity function xt+1 = xt.
Fig. 3.
Return plot of the first principal
component, PC#1, of the tensor product
top-down recognizer processing the
 (blue) and
(blue) and  (red) sentences (33 and
34), respectively
(red) sentences (33 and
34), respectively
As Fig. 3 reveals,
both parses start with different initial conditions in phase
space, reflecting the initially different inputs to be
processed: for the  sentence (blue), it is
DP1C0t DP2t
V0 I0
and for the
sentence (blue), it is
DP1C0t DP2t
V0 I0
and for the 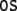 sentence (red), DP1
C0 DP3ttV0
I0. The map Φ, whose action is
indicated by the lines connecting the points, is obviously
nonlinear in phase space. For the first iterations, the
trajectories converge. However, they are significantly
diverging after the fifth iteration. Eventually, both
trajectories settle down in a stable
fixed point attractor (0, 0)T approaching the accepting states of the
automaton.
sentence (red), DP1
C0 DP3ttV0
I0. The map Φ, whose action is
indicated by the lines connecting the points, is obviously
nonlinear in phase space. For the first iterations, the
trajectories converge. However, they are significantly
diverging after the fifth iteration. Eventually, both
trajectories settle down in a stable
fixed point attractor (0, 0)T approaching the accepting states of the
automaton.
The surprising finding that the dynamics is effectively one-dimensional, can be easily explained by looking at the core transformation of the tensor product top-down recognizer. Consider again the transition from state
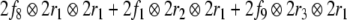 |
to its successor
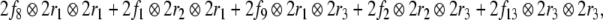 |
where we provisionally assume that the last vector belongs to the embedding space. Because all fillers and roles are represented through canonical basis vectors in their respective vector spaces, their Kronecker tensor products are rather sparse vectors, consisting mostly of zeros and only a few ones. The parser’s action expanding a grammatical rule is therefore described by inserting more and more ones into the state vector as the processing evolves. In the limit such dynamics would reach the—though not well-formed—vector (1, 1,…,1)T which is given by the identity line in the high-dimensional embedding space. Accordingly, also approaching the accepting states of the tensor product top-down recognizer appears as convergence towards such limit ray. Its direction is obtained by the PCA.
Finally, we present the first principal component PC#1 depending on time as the parser’s “time series” in Fig. 4.
Fig. 4.
Time series of the first principal
component of the tensor product top-down
recognizer in phase space processing the
 (blue) and
(blue) and 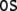 (red) sentences (33 and
34), respectively. The model “P600” is
indicated by the arrow
(red) sentences (33 and
34), respectively. The model “P600” is
indicated by the arrow
Again, we see that both parses start from different initial conditions, subsequently converging for a number of iterations. At step 6, the time series diverge significantly from each other. At this point one path of the processes maintained in parallel, breaks down due to the garden path and becomes abandoned. Afterwards, only successful paths are continued, thereby correctly parsing the subject–object sentence with grammar G1 and the object–subject sentence with its appropriate grammar G2. The behavior of the first principal component exhibits considerable resemblance with the reanalysis P600 observed in the ERP data in section “Results/ERP data”. Therefore, we propose this observable as model EEG and consider its behavior as a “model P600”.
Nonlinear dynamical automaton
The NDA model was constructed as a dynamical system
(X, Φp). The phase space X = [0, 1]2 is
partitioned into rectangles given by the cartesian products
of 14 intervals at the x-axis and 7 intervals at the y-axis labeled by the syntactic
categories of the grammar as discussed in
section “Methods/Processing models”. The control parameter
p distinguishes two
syntactic processing strategies, subject preference by default (p = 1) and object-first (p = 2). A third value
(p = 3) is assigned
to a repair map, connecting those strategies with each
other. The intrinsic dynamics 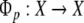 is augmented with a non-autonomous
counterpart, a representation ρ of the word semigroup by
phase space operators
is augmented with a non-autonomous
counterpart, a representation ρ of the word semigroup by
phase space operators  establishing the
establishing the  operation. Incoming linguistic material
thereby interactively perturbs the autonomous evolution of
the NDA.
operation. Incoming linguistic material
thereby interactively perturbs the autonomous evolution of
the NDA.
Figure 5 presents
the macroscopic evolution of the NDA processing the string
0361645 according to subject preference strategy p = 1. Each horizontal layer
corresponds to one processing step in Table 4. Initial conditions are 700
points randomly scattered over the blue rectangle indicated
by the star “*” which corresponds to row 0 in
Table 3. After
each attachment, the NDA’s state covers exactly one domain
of the piecewise linear maps Eq. 59 given by the partition. Then, the next
word is scanned from the external information source, acting
as a quantum operator at X. These transitions are indicated by “°”s.
Obviously, only the extend of the rectangles in the
y-axis is influenced
by a squeezing operation described through Eq. 62. The parsing process ends
when the states are spread across the whole unit square.
Then, the stack and the working memory both contain the
empty word 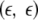 which corresponds to the 0-cylinder
[].
which corresponds to the 0-cylinder
[].
Fig. 5.
Phase space dynamics of input-driven
nonlinear automaton processing the
 sentence (33). Each layer
displays one iteration of the NDA top-down
recognizer. The initial condition is
indicated by “*”; non-autonomous
sentence (33). Each layer
displays one iteration of the NDA top-down
recognizer. The initial condition is
indicated by “*”; non-autonomous
 operations are indicated
by “°”
operations are indicated
by “°”
Correspondingly, Fig. 6 displays the NDA dynamics starting from 700
randomly distributed initial conditions comprising the first
macrostate in Table 3. Again, the non-autonomous  operations are indicated by “°”s. Now the
“*” depicts the failure of the subject preference strategy applied to the
operations are indicated by “°”s. Now the
“*” depicts the failure of the subject preference strategy applied to the
 sequence 0326645. State 5 is invariant
under the action of Φ1 which is
diagnosed during the transition to state 6. At this time, an
external control system intervenes into the dynamics by
tuning the control parameter to p = 3 for one iteration (steps 6 to 7), thus
destabilizing the unwanted invariant state. Here, the repair
map replaces the stack content A6 by A2. After repair, the
control system intervenes again by setting p = 2 such that the NDA now
emulates the object-first strategy. The processing is
completed when the whole phase space is occupied by the
cloud of microstates at time 20.
sequence 0326645. State 5 is invariant
under the action of Φ1 which is
diagnosed during the transition to state 6. At this time, an
external control system intervenes into the dynamics by
tuning the control parameter to p = 3 for one iteration (steps 6 to 7), thus
destabilizing the unwanted invariant state. Here, the repair
map replaces the stack content A6 by A2. After repair, the
control system intervenes again by setting p = 2 such that the NDA now
emulates the object-first strategy. The processing is
completed when the whole phase space is occupied by the
cloud of microstates at time 20.
Fig. 6.
Phase space dynamics of input-driven
nonlinear automaton processing the
 sentence (34). Here, only
one non-autonomous
sentence (34). Here, only
one non-autonomous  operation is indicated by
“°”. The diagnosis and repair transitions
are indicated by “*”. (a) Global view. (b)
Enlargement
operation is indicated by
“°”. The diagnosis and repair transitions
are indicated by “*”. (a) Global view. (b)
Enlargement
In order to assess the cylinder entropy as the NDA’s order parameter, the measurement partition Fig. 7 is used. The partition is constructed in such a way, that fine-grained meshes lead to high cylinder entropy, while coarse-grained meshes give rise to low entropy values. Note the relatively coarse partitioning of cell 6 × 2 accounting for the garden path in Fig. 6.
Figure 8
eventually, presents the cylinder entropies for both
sentences  (blue) and
(blue) and  (red). In order to synchronize the
respective
(red). In order to synchronize the
respective  operations, some idling cycles have been
introduced. Therefore, processing time is now measured in
arbitrary units instead of iterations.
operations, some idling cycles have been
introduced. Therefore, processing time is now measured in
arbitrary units instead of iterations.
Fig. 8.
Time series of the cylinder entropy
of the NDA top-down recognizer processing
the  (blue) and
(blue) and  (red) sentences (33 and
34), respectively. The model “N400’s and the
“P600” are indicated by arrows
(red) sentences (33 and
34), respectively. The model “N400’s and the
“P600” are indicated by arrows
Figure 8 shows
that the unwanted invariant state processing  according to subject preference has low
entropy similar to the P600 in the ERP data
(Fig. 2b). This
is due to the measurement partition Fig. 7 whose grid in the cell
6 × 2 is too coarse to capture the
invariant state. Moreover, Fig. 8 reveals that each
according to subject preference has low
entropy similar to the P600 in the ERP data
(Fig. 2b). This
is due to the measurement partition Fig. 7 whose grid in the cell
6 × 2 is too coarse to capture the
invariant state. Moreover, Fig. 8 reveals that each  operation is reflected by a drop in
cylinder entropy as well, because the volumes of the
macrostates are reduced by the vertical squeezing. Hence the
probabilities to cover these states by the cells of the
measurement partition are lowered as well. Thus, we suggest
to consider entropy drops in the NDA dynamics as “model
ERPs” as in section “Results/Tensor product top-down
recognizer”. Our “model P600” is now reflected by a drop in
entropy caused by arriving at an unwanted invariant
macrostate in phase space, a region that has no functional
significance for the processing of the input. Likewise, our
“model N400s” are elicited by the integration of incoming
new material into working memory, which reduces the
available phase space volume each time.
operation is reflected by a drop in
cylinder entropy as well, because the volumes of the
macrostates are reduced by the vertical squeezing. Hence the
probabilities to cover these states by the cells of the
measurement partition are lowered as well. Thus, we suggest
to consider entropy drops in the NDA dynamics as “model
ERPs” as in section “Results/Tensor product top-down
recognizer”. Our “model P600” is now reflected by a drop in
entropy caused by arriving at an unwanted invariant
macrostate in phase space, a region that has no functional
significance for the processing of the input. Likewise, our
“model N400s” are elicited by the integration of incoming
new material into working memory, which reduces the
available phase space volume each time.
Discussion
In this paper, we presented two psycholinguistically plausible nonlinear dynamical system models for language-related brain potentials. In a paradigmatic ERP experiment on the processing of local object–subject ambiguities in German, we found a strong P600 at the disambiguating clausal region for dispreferred object-first sentences in comparison with subject-first sentences which are more easily understood due to the subject preference strategy for the interpretation of ambiguous noun phrases (Bader and Meng 1999; Friederici et al. 2001; Frisch et al. 2004). Consistently, a symbolization analysis of the ERP data revealed a large drop in event-related cylinder entropy in the same time window as the P600. Smaller drops in entropy reflected the N400 component for integrating incoming new lexical material into working memory (Coles and Rugg 1995; Dambacher et al. 2006).
For our models, we first described the stimulus material of the experiment by phrase structure trees according to Government and Binding theory (Chomsky 1981; Haegeman 1994), and derived a locally ambiguous context-free grammar from these trees. This grammar was subsequently decomposed into its unambiguous parts, following a technique suggested by beim Graben et al. (2004). These unambiguous grammars represented the two alternative processing strategies, namely subject preference against object preference. Processing both stimulus sentences, either subject–object or object–subject by deterministic top-down recognizers (Aho and Ullman 1972; Hopcroft and Ullman 1979) for both grammars, respectively, lead to four different parses for subsequent modeling.
Both dynamical system processing models were essentially grounded in Smolensky’s and Mizraji’s tensor product representations of symbolic content in neural activation spaces (Dolan and Smolensky 1989; Mizraji 1989, 1992; Smolensky 1990). The first model represented the syntactic categories of the disambiguated grammars as linearly independent filler vectors and positions in a labeled binary tree as a basis of three-dimensional space. Hence, our tensor product top-down recognizer was obtained as a nonlinear function from the high-dimensional activation space onto itself. The four different parses corresponded to itineraries of this nonlinear map. In order to build a parallel processor (Lewis 1998), the two parses for the subject–object sentence and the other two for the object–subject sentence were linearly superimposed in activation space. In each of these superpositions one process leading into a garden path extinguished.
For this parallel processing model we found that the dynamics was essentially one-dimensional, as revealed by a principal component analysis. The trajectories of the parser, starting from different initial conditions which represented the subject–object and object–subject order, respectively, settled down into one stable fixed point in PCA space. During its transient computation, the trajectories diverged exactly when the garden path was encountered. Regarding the first principal component as our model EEG, its time series showed a remarkable resemblance with the P600 effect in averaged ERPs.
Our second model deployed a two-dimensional, linearly dependent, representation of the tensor product scheme through a Gödel encoding. The two deterministic top-down recognizers corresponding to subject preference and object preference strategy were first translated to generalized shifts (Moore 1990, 1991; Siegelmann 1996). In order to cope with the garden path, a third repair shift was constructed. Using the symbologram method (Cvitanović et al. 1988; Kennel and Buhl 2003), a nonlinear dynamical automaton, i.e. a time-discrete dynamical system at the unit square depending on a control parameter was obtained. This model implemented a serial diagnosis and repair processor (Lewis 1998; Friederici 1998) where the garden path corresponds to an unwanted invariant set which became destabilized by a bifurcation into the repair mode.
The intrinsic, autonomous parsing dynamics was supplemented by a non-autonomous counterpart, inspired by dynamical recognizers (Pollack 1991; Moore 1998; Tabor 1998, 2000; Moore and Crutchfield 2000), where the environment interactively perturbs the states of the dynamics by incoming new words (Wegner 1998; beim Graben 2006). We implemented these interactions using algebraic representation theory of quantum operators (Haag 1992; van der Waerden 2003), or in other words, by representations of the “phrase space” on the phase space. Since symbolic content is represented by a partition of the model’s phase space into rectangular macrostates, symbolic dynamics provides appropriate measures for this system in terms of information theory (Shannon and Weaver 1949; beim Graben et al. 2000). Therefore, we considered the cylinder entropy with respect to a particular measurement partition as our model ERP. Making the measurement partition rather course-grained in the phase space region of the garden path thus entailed an entropy drop corresponding to the P600 component. On the other hand, integrating new words into the model’s working memory shrinks the volume of the macrostates thus leading to lower entropy as well. Therefore our model is also able to reflect the N400 component, at least partially.
Both dynamical systems models have their respective advantages and disadvantages. First of all, they are both consistent with the dynamical system interpretation of event-related brain potentials (Başar 1980, 1998; beim Graben et al. 2000). According to this view, the brain is a high-dimensional, complex dynamical system whose trajectories transiently explore different regions in phase space when performing different computational tasks. On the other hand, these regions are functionally significant and therefore causally distinguished (Fodor and Pylyshyn 1988). Neurophysiological measurements, such as EEG/ERP, MEG, fMRI, or others map this high-dimensional phase space to a less dimensional observable space by spatio-temporal coarse-graining, i.e. by taking signal averages over space, time and trial dimensions (Amari 1974; Freeman 2007; Atmanspacher and beim Graben 2007). However, robust, general features of the underlying dynamics might be preserved in this observable representation. This is especially the case using symbolic dynamics (Hao 1989; Lind and Marcus 1995; beim Graben et al. 2000) for modeling and analysing experimental data. Atmanspacher and beim Graben (2007) have shown that spatio-temporal coarse-grainings generally lead to a coarse-graining, namely a partitioning of the system’s phase space into equivalence classes as well.
The same holds actually for our models. The parallel tensor product top-down recognizer lives in a 229,376-dimensional embedding space. However, as “meaningful” symbols are only represented by sparse vectors of zeros and ones (i.e. by vertices in a 229,376-dimensional hypercube), most of the available space is a meaningless vacuum. After choosing the PCA as coarse-graining method, the one-dimensional observable space spanned by PC#1 turned out to be a viable description. We saw that the effectively one-dimensional dynamics is due to the representation of grammatical rules where more and more ones are introduced in the state vector.
By contrast, the non-autonomously driven nonlinear automaton lives in a two-dimensional partitioned phase space by construction. Also by construction, these rectangular cells of the partition are the domains of the intrinsic piecewise affine linear map that represents the symbol processing of the NDA. Therefore, these regions are in fact functionally significant and causally distinguished. On the other hand, we had to introduce a further coarse-graining by means of a measurement partition. Two microstates belonging to the same cell of this partition are epistemically indistinguishable with respect to a particular observable, which could hence be regarded as the model EEG (Atmanspacher and beim Graben 2007).
In sum, we presented two nonlinear dynamical language processors where ERP effects are reflected by functionally and causally different regions in phase space. Nevertheless, we are acutely aware that these models are only a first step towards a proper understanding of the neurophysiological bases of linguistic computation. We shall conclude this discussion by addressing some open problems and an outlook to ongoing and future research.
Concerning the tensor product top-down recognizer, we were in the lucky situation that our context-free model grammar was not recursive. Yet, recursion is an important property of natural languages allowing, e.g., for center embedding of clauses. In such cases, using linearly independent filler and role vectors would lead to an explosion of the dimension of embedding space. One possible resort for this problem has recently been suggested by beim Graben et al. (2007) making use of the full-fledged Fock space of tensor product representations instead of finite-dimensional embeddings thereof. This line of research might lead to a field-theoretical account to computational psycholinguistics (Amari 1977; Jirsa and Haken 1996; Thelen et al. 2001; Erlhagen and Schöner 2002; Wright et al. 2004). By contrast, Smolensky (2006) and Smolensky and Legendre (2006) argue in favor of linearly dependent representations in order to account for processing problems of center embeddings by graceful saturation in activation space.
Another issue is that natural languages are definitely not context-free (Shieber 1985) and that language processing is certainly not simply top-down (Fodor and Frazier 1980; Marcus 1980; Staudacher 1990). However, since our model grammar is based on Government and Binding theory (Chomsky 1981; Haegeman 1994) and includes at least the necessary traces resulting from the non-context-free movement operations, it was suited in its restricted domain describing only the two stimulus sentences of our ERP experiment. More appropriate grammars are e.g. minimalist grammars (Stabler 1997; Michaelis 2001; Stabler and Keenan 2003; Hale 2003). A minimalist tensor product parser has meanwhile been constructed by Gerth (2006).
Although Moore (1990, 1991) proved that any Turing machine can be implemented by an NDA, this two-dimensional representation might actually not be sufficient for such minimalist grammars. The last proposal of Stabler and Keenan (2003) indicates that a multiprocessor system where each processor would be one NDA could be better for this aim. Therefore, neural network or neural field implementations suggest themselves for NDA and tensor product automata as well.
This leads to our final issue. In the present paper, we have formally constructed time-discrete nonlinear systems in phase space without explicitly devising neural networks. In this sense, we presented training patterns for connectionist models of language processing. The remaining step of implementing these models would be important to provide continuous-time dynamical models (Vosse and Kempen 2000; van der Velde and de Kamps 2006; Wennekers et al. 2006; Garagnani et al. 2007). Such models are also required for predicting latencies of ERP components and to bridge the gap to other dependent measures such as reading times and eye movements (Lewis and Vasishth 2006; Vasishth and Lewis 2006a; Vasishth et al. 2008; Boston et al. in press).
Acknowledgements
We thank Stefan Frisch for support conducting the ERP experiment and for helpful comments on the manuscript. We also thank Leticia Pablos Robles, Roland Potthast, and Slawomir Nasuto for inspiring discussions. The ERP pilot study was funded through grant FOR 375/1-4 by Deutsche Forschungsgemeinschaft.
Appendix
Trajectories of the tensor product top-down recognizer
The processing trajectory for the  sentence (33) according to grammar G1 (
sentence (33) according to grammar G1 (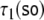 ) comes out to be
) comes out to be
 |
On the other hand, processing the 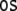 sentence (34) with grammar
sentence (34) with grammar 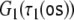 leads into the garden path. Its trajectory is
then
leads into the garden path. Its trajectory is
then
 |
Here, the parser expands the first two rules of grammar
G1 without any difficulty, since they are
the same as the two first rules of the appropriate grammar
G2. After processing rule (37), IP →
t
I1, the first symbol on the input stack
is the filler  which represents the category
DP3. However the upcoming filler to be
handled is
which represents the category
DP3. However the upcoming filler to be
handled is  At this point the parser breaks and does not
reach the accepting final state by its trajectory. Similarly,
another garden path occurs for processing the
At this point the parser breaks and does not
reach the accepting final state by its trajectory. Similarly,
another garden path occurs for processing the  sentence (33) according to grammar
sentence (33) according to grammar
 while
while 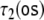 accepts the
accepts the 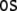 sentence (33) as being well-formed regarding
G2 in the end.
sentence (33) as being well-formed regarding
G2 in the end.
Proof of the word semigroup representation theorem
What finally remains is to prove the assertion stated in
section “Nonlinear dynamical automaton” that the quantum operators provide a semigroup homomorphism and hence a
representation of the word semigroup in the phase space
X of an NDA (X, Φ). To this end, we have to
generalize the definition Eqs. 60, 61
to proper words.
provide a semigroup homomorphism and hence a
representation of the word semigroup in the phase space
X of an NDA (X, Φ). To this end, we have to
generalize the definition Eqs. 60, 61
to proper words.
Let therefore 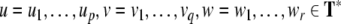 be words over the terminal alphabet T of the NDA (X, Φ) with lengths
be words over the terminal alphabet T of the NDA (X, Φ) with lengths  As defined in Eq. 55, the Gödel code of the input word
w of (X, Φ) with respect to the terminal
number base bT is given as
As defined in Eq. 55, the Gödel code of the input word
w of (X, Φ) with respect to the terminal
number base bT is given as
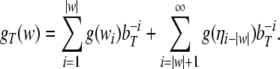 |
Call ρ′(u) the operator ρ (u) (Eq. 60) projected onto the y-component of the phase space. Its impact is then given by Eq. 61
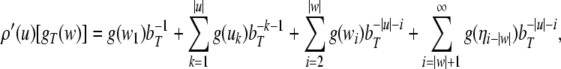 |
which can be written as
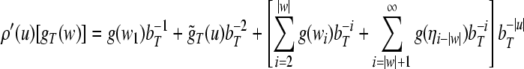 |
after introducing the function
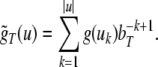 |
For the proof we calculate
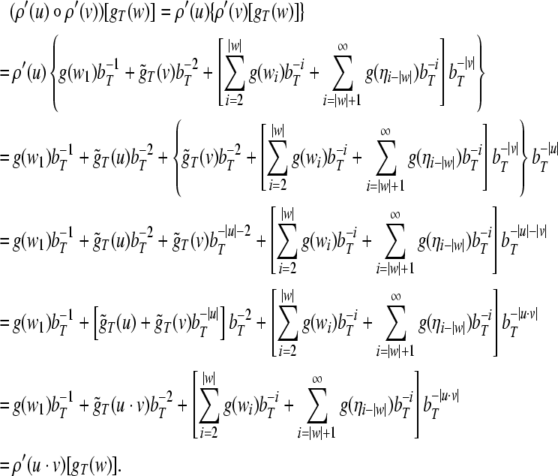 |
QED.
Footnotes
Ungrammatical sentences are usually denoted by the * in linguistic examples.
Also an early left anterior negativity (ELAN) was observed for such violations (Friederici et al. 1993).
Note that we modified Smolensky’s original definition slightly: The ordered pairs (f, r) are the definiens of the filler/role binding f/r(s), the definiendum, which therefore has to stand in front of the set definition symbol “|”.
We shall see below, that the sum in Eq. 27 has to be replaced by the direct sum over tensor product spaces for a proper treatment of recursion.
Words u = u1,…, up, v = v1,…, vq of finite length formed from symbols in
T, can be
concatenated to form a new word 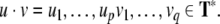 This concatenation product is
associative: u
·(v
·w) = (u ·v)
·w, such that
(T*,·) forms a
semigroup. Note that the concatenation is generally
not commutative, thus justifying the notion of a
“quantum operator”.
This concatenation product is
associative: u
·(v
·w) = (u ·v)
·w, such that
(T*,·) forms a
semigroup. Note that the concatenation is generally
not commutative, thus justifying the notion of a
“quantum operator”.
References
- Aho AV, Ullman JD (1972) The theory of parsing, translation and compiling, vol i: parsing. Prentice Hall, Englewood Cliffs (NJ)
- Allefeld C, Frisch S, Schlesewsky M (2004) Detection of early cognitive processing by event-related phase synchronization analysis. NeuroReport 16(1):13–16 [DOI] [PubMed]
- Amari SI (1974) A method of statistical neurodynamics. Kybernetik 14:201–215 [DOI] [PubMed]
- Amari SI (1977) Dynamics of pattern formation in lateral-inhibition type neural fields. Biol Cybernet 27:77–87 [DOI] [PubMed]
- Anderson JR, Bothell D, Byrne MD, Douglass S, Lebiere C, Qin Y (2004) An integrated theory of the mind. Psychol Rev 111(4):1036–1060 [DOI] [PubMed]
- Atmanspacher H, beim Graben P (2007) Contextual emergence of mental states from neurodynamics. Chaos Complex Lett 2(2/3):151–168
- Başar E (1980) EEG-brain dynamics. Relations between EEG and brain evoked potentials. Elsevier/North Holland Biomedical Press, Amsterdam
- Başar E (1998) Brain function and oscillations. Vol I: brain oscillations. Principles and approaches. Springer series in synergetics. Springer, Berlin
- Bader M, Meng M (1999) Subject–object ambiguities in German embedded clauses: an across-the-board comparison. J Psycholinguist Res 28(2):121–143 [DOI]
- Beer RD (2000) Dynamical approaches to cognitive science. Trends Cogn Sci 4(3):91–99 [DOI] [PubMed]
- Bornkessel I, Schlesewsky M (2006) The extended argument dependency model: a neurocognitive approach to sentence comprehension across languages. Psychol Rev 113(4):787–821 [DOI] [PubMed]
- Bornkessel I, McElree B, Schlesewsky M, Friederici AD (2004) Multi-dimensional contributions to garden path strength: dissociating phrase structure from case marking. J Mem Lang 51:494–522 [DOI]
- Boston MF, Hale JT, Kliegl R, Patil U, Vasishth S (in press) Parsing costs as predictors of reading difficulty: an evaluation using the Potsdam Sentence Corpus. J Eye Mov Res 1
- Chomsky N (1981) Lectures on goverment and binding. Foris
- Christiansen MH, Chater N (1999) Connectionist natural language processing: the state of the art. Cogn Sci 23(4):417–437 [DOI]
- Coles MGH, Rugg MD (1995) Event-related brain potentials: an introduction. In: Coles MGH, Rugg MD (eds) Electrophysiology of mind: event-related brain potentials and cognition, chap 1. Oxford University Press, Oxford
- Crutchfield JP (1994) The calculi of emergence: computation, dynamics and induction. Physica D 75:11–54 [DOI]
- Cvitanović P, Gunaratne GH, Procaccia I (1988) Topological and metric properties of Hénon-type strange attractors. Phys Rev A 38(3):1503–1520 [DOI] [PubMed]
- Dambacher M, Kliegl R, Hofmann M, Jacobs AM (2006) Frequency and predictability effects on event-related potentials during reading. Brain Res 1084:89–103 [DOI] [PubMed]
- Dolan CP, Smolensky P (1989) Tensor product production system: a modular architecture and representation. Connect Sci 1(1):53–68 [DOI]
- Drenhaus H, beim Graben P, Saddy D, Frisch S (2006) Diagnosis and repair of negative polarity constructions in the light of symbolic resonance analysis. Brain Lang 96(3):255–268 [DOI] [PubMed]
- Elman JL (1995) Language as a dynamical system. In: Port, van Gelder (eds), pp 195–223
- Erlhagen W, Schöner G (2002) Dynamic field theory of movement preparation. Psychol Rev 109(3):545–572 [DOI] [PubMed]
- Fodor JD, Ferreira F (eds) (1998) Reanalysis in sentence processing. Kluwer, Dordrecht
- Fodor JD, Frazier L (1980) Is the human sentence parsing mechanism an ATN? Cognition 6:417–459 [DOI] [PubMed]
- Fodor J, Pylyshyn ZW (1988) Connectionism and cognitive architecture: a critical analysis. Cognition 28:3–71 [DOI] [PubMed]
- Frazier L, Fodor JD (1978) The sausage machine: a new two-stage parsing model. Cognition 6:291–326 [DOI]
- Freeman WJ (2007) Definitions of state variables and state space for brain-computer interface. Part 1. Multiple hierarchical levels of brain function. Cogn Neurodyn 1:3–14 [DOI] [PMC free article] [PubMed]
- Friederici AD (1995) The time course of syntactic activation during language processing: a model based on neuropsychological and neurophysiological data. Brain Lang 50:259–281 [DOI] [PubMed]
- Friederici AD (1998) Diagnosis and reanalysis: two processing aspects the brain may differentiate. In: Fodor, Ferreira (eds), pp 177–200
- Friederici AD (1999) The neurobiology of language comprehension. In: Friederici AD (ed) Language comprehension: a biological perspective, 2nd edn. Springer, Berlin, pp 265–304
- Friederici AD (2002) Towards a neural basis of auditory language processing. Trends Cogn Sci 6:78–84 [DOI] [PubMed]
- Friederici AD, Pfeifer E, Hahne (1993) Event-related brain potentials during natural speech processing: effects of semantic morphological and syntactic violations. Cogn Brain Res 1:183–192 [DOI] [PubMed]
- Friederici AD, Steinhauer K, Mecklinger A, Meyer M (1998) Working memory constraints on syntactic ambiguity resolution as revealed by electrical brain responses. Biol Psychol 47:193–221 [DOI] [PubMed]
- Friederici AD, Mecklinger A, Spencer KM, Steinhauer K, Donchin E (2001) Syntactic parsing preferences and their on-line revisions: a spatio-temporal analysis of event-related brain potentials. Cogn Brain Res 11:305–323 [DOI] [PubMed]
- Frisch S, beim Graben P (2005) Finding needles in haystacks: symbolic resonance analysis of event-related potentials unveils different processing demands. Cogn Brain Res 24(3):476–491 [DOI] [PubMed]
- Frisch S, Schlesewsky M (2001) The N400 reflects problems of thematic hierarchizing. NeuroReport 12(15):3391–3394 [DOI] [PubMed]
- Frisch S, Schlesewsky M, Saddy D, Alpermann A (2002) The P600 as an indicator of syntactic ambiguity. Cognition 85:B83–B92 [DOI] [PubMed]
- Frisch S, beim Graben P, Schlesewsky M (2004) Parallelizing grammatical functions: P600 and P345 reflect different cost of reanalysis. Int J Bifurcat Chaos 14(2):531–549 [DOI]
- Frisch S, Kotz SA, Friederici AD (2008) Neural correlates of normal and pathological language processing. In: Ball MJ, Perkins M, Müller N, Howard S (eds) Handbook of clinical linguistics. Blackwell, Boston
- Garagnani M, Wennekers T, Pulvermüller F (2007) A neuronal model of the language cortex. Neurocomputing 70:1914–1919 [DOI]
- van Gelder T (1998) The dynamical hypothesis in cognitive science. Behav Brain Sci 21(5):615–628 [DOI] [PubMed]
- Gerth S (2006) Parsing mit minimalistischen, gewichteten Grammatiken und deren Zustandsraumdarstellung. Master’s thesis, Universität Potsdam
- beim Graben P (2001) Estimating and improving the signal-to-noise ratio of time series by symbolic dynamics. Phys Rev E 64:051104 [DOI] [PubMed]
- beim Graben P (2004) Incompatible implementations of physical symbol systems. Mind Matter 2(2):29–51
- beim Graben P (2006) Pragmatic information in dynamic semantics. Mind Matter 4(2):169–193
- beim Graben P, Frisch S (2004) Is it positive or negative? On determining ERP components. IEEE Trans Biomed Eng 51(8):1374–1382 [DOI] [PubMed]
- beim Graben P, Saddy D, Schlesewsky M, Kurths J (2000) Symbolic dynamics of event-related brain potentials. Phys Rev E 62(4):5518–5541 [DOI] [PubMed]
- beim Graben P, Jurish B, Saddy D, Frisch S (2004) Language processing by dynamical systems. Int J Bifurcat Chaos 14(2):599–621 [DOI]
- beim Graben P, Frisch S, Fink A, Saddy D, Kurths J (2005) Topographic voltage and coherence mapping of brain potentials by means of the symbolic resonance analysis. Phys Rev E 72:051916 [DOI] [PubMed]
- beim Graben P, Gerth S, Saddy D, Potthast R (2007) Fock space representations in neural field theories. In: Biggs N, Bonnet-Bendhia AS, Chamberlain P, Chandler-Wilde S, Cohen G, Haddar H, Joly P, Langdon S, Lunéville E, Pelloni B, Potherat D, Potthast R (eds) Proc. waves 2007. The 8th international conference on mathematical and numerical aspects of waves. Dept. of Mathematics, University of Reading, Reading, pp 120–122
- Grodzinsky Y, Friederici AD (2006) Neuroimaging of syntax and syntactic processing. Curr Opin Neurobiol 16:240–246 [DOI] [PubMed]
- Haag R (1992) Local quantum physics: fields, particles, algebras. Springer, Berlin
- Haegeman L (1994) Introduction to goverment & binding theory, Blackwell textbooks in linguistics, vol 1, 2nd edn. Blackwell Publishers, Oxford, 1st edition 1991
- Hagoort P (2003) How the brain solves the binding problem for language: a neurocomputational model of syntactic processing. NeuroImage 20:S18–S29 [DOI] [PubMed]
- Hagoort P (2005) On Broca, brain, and binding: A new framework. Trends Cogn Sci 9(9):416–423 [DOI] [PubMed]
- Hagoort P, Brown CM, Groothusen J (1993) The syntactic positive shift (SPS) as an ERP measure of syntactic processing. Lang Cogn Process 8:439–483 [DOI]
- Hale JT (2003) The information conveyed by words in sentences. J Psycholinguist Res 32(2):101–123 [DOI] [PubMed]
- Hale JT (2006) Uncertainty about the rest of the sentence. Cogn Sci 30(4) [DOI] [PubMed]
- Hale JT, Smolensky P (2006) Harmonic grammar and harmonic parsers for formal languages. In: Smolensky, Legendre (eds), chap 10, pp 393–415
- Hao BL (1989) Elementary symbolic dynamics and chaos in dissipative systems. World Scientific, Singapore
- Hopcroft JE, Ullman JD (1979) Introduction to automata theory, languages, and computation. Addison–Wesley, Menlo Park, California
- Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q, Yen NC, Tung CC, Liu HH (1998) The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc Lond A 454:903–995
- Jirsa VK, Haken H (1996) Field theory of electromagnetic brain activity. Phys Rev Lett 77(5):960–963 [DOI] [PubMed]
- Kaan E, Harris A, Gibson E, Holcomb P (2000) The P600 as an index of syntactic integration difficulty. Lang Cogn Process 15(2):159–201 [DOI]
- Kandel ER, Schwartz JH, Jessel TM (eds) (1995) Essentials of neural science and behavior. Appleton & Lange, East Norwalk, Connecticut
- Kennel MB, Buhl M (2003) Estimating good discrete partitions from observed data: Symbolic false nearest neighbors. Phys Rev Lett 91(8):084–102 [DOI] [PubMed]
- Kutas M, Hillyard SA (1980) Reading senseless sentences: brain potentials reflect semantic incongruity. Science 207:203–205 [DOI] [PubMed]
- Kutas M, Hillyard SA (1984) Brain potentials during reading reflect word expectancy and semantic association. Nature 307:161–163 [DOI] [PubMed]
- Kutas M, van Petten CK (1994) Psycholinguistics electrified. Event-related brain potential investigations. In: Gernsbacher MA (ed) Handbook of psycholinguistics. Academic Press, San Diego, pp 83–133
- Lewis RL (1998) Reanalysis and limited repair parsing: leaping off the garden path. In: Fodor, Ferreira (eds), pp 247–285
- Lewis RL (2000) Computational psycholinguistics. In: Encyclopedia of cognitive science, Macmillan Reference Ltd
- Lewis RL, Vasishth S (2006) An activation-based model of sentence processing as skilled memory retrieval. Cogn Sci 29:375–419 [DOI] [PubMed]
- Lewis RL, Vasishth S, Van Dyke J (2006) Computational principles of working memory in sentence comprehension. Trends Cogn Sci 10:447–454 [DOI] [PMC free article] [PubMed]
- Lind D, Marcus B (1995) An introduction to symbolic dynamics and coding. Cambridge University Press, Cambridge (UK), reprint 1999
- Makeig S, Westerfield M, Jung TP, Enghoff S, Townsend J, Courchesne E, Sejnowski TJ (2002) Dynamic brain sources of visual evoked responses. Science 295:690–694 [DOI] [PubMed]
- Marcus M (1980) A theory of syntactic recognition for natural language. MIT Press, Cambrigde (MA)
- Marwan N, Meinke A (2004) Extended recurrence plot analysis and its application to ERP data. Int J Bifurcat Chaos 14(2):761–771 [DOI]
- McElree B (2000) Sentence comprehension is mediated by content-addressable memory structures. J Psycholinguist Res 29(2):111–123 [DOI] [PubMed]
- McElree B, Dosher BA (1993) Serial retrieval processes in the recovery of order information. J Exp Psychol Gen 122(3):291–315 [DOI]
- Mecklinger A, Schriefers H, Steinhauer K, Friederici AD (1995) Processing relative clauses varying on syntactic and semantic dimensions: an analysis with event-related potentials. J Mem Lang 23:477–494 [DOI] [PubMed]
- Michaelis J (2001) Derivational minimalism is mildly context-sensitive. In: Moortgat M (ed) Logical aspects of computational linguistics. Lecture notes in artificial intelligence, vol 2014, Springer, Berlin, pp 179–198
- Mizraji E (1989) Context-dependent associations in linear distributed memories. Bull Math Biol 51(2):195–205 [DOI] [PubMed]
- Mizraji E (1992) Vector logics: the matrix-vector representation of logical calculus. Fuzzy Sets Syst 50:179–185 [DOI]
- Moore C (1990) Unpredictability and undecidability in dynamical systems. Phys Rev Lett 64(20):2354–2357 [DOI] [PubMed]
- Moore C (1991) Generalized shifts: unpredictability and undecidability in dynamical systems. Nonlinearity 4:199–230 [DOI]
- Moore C (1998) Dynamical recognizers: Real-time language recognition by analog computers. Theor Comput Sci 201:99–136 [DOI]
- Moore C, Crutchfield JP (2000) Quantum automata and quantum grammars. Theor Comput Sci 237:275–306 [DOI]
- Neville HJ, Nicol J, Barss A, Forster K, Garrett M (1991) Syntactically based sentence processing classes: Evidence from event-related potentials. J Cogn Neurosci 6:233–244 [DOI] [PubMed]
- Newell A, Simon HA (1976) Computer science as empirical inquiry: symbols and search. Commun Assoc Comput Mach 19:113–126
- Niedermeyer E, da Silva FHL (eds) (1999) Electroencephalography. Basic principles, clinical applications, and related fields, 4th edn. Lippincott Williams and Wilkins, Baltimore
- Osterhout L, Holcomb PJ (1992) Event-related brain potentials elicited by syntactic anomaly. J Mem Lang 31:785–806 [DOI]
- Osterhout L, Holcomb PJ (1995) Event-related potentials and language comprehension. In: Coles MGH, Rugg MD (eds) Electrophysiology of mind: event-related brain potentials and cognition, chap 6. Oxford University Press, Oxford
- Osterhout L, Holcomb PJ, Swinney DA (1994) Brain potentials elicited by garden-path sentences: evidence of the application of verb information during parsing. J Exp Psychol Learn Mem Cogn 20(4):786–803 [DOI] [PubMed]
- Pollack JB (1991) The induction of dynamical recognizers. Mach Learn 7:227–252. Also published in Port and van Gelder (1995), pp 283–312.
- Port RF, van Gelder T (eds) (1995) Mind as motion: explorations in the dynamics of cognition. MIT Press, Cambridge (MA)
- Regan D (1989) Human brain electrophysiology: evoked potentials and evoked magnetic fields in science and medicine. Elsevier, New York
- Rumelhart DE, McClelland JL, the PDP Research Group (eds) (1986) Parallel distributed processing: explorations in the microstructure of cognition, vol I. MIT Press, Cambridge (MA) [DOI] [PubMed]
- Schinkel S, Marwan N, Kurths J (2007) Order patterns recurrence plots in the analysis of ERP data. Cogn Neurodyn. doi:10.1007/s11571-007-9023-z [DOI] [PMC free article] [PubMed]
- Schlesewsky M, Bornkessel I (2006) Context-sensitive neural responses to conflict resolution: electrophysiological evidence from subject–object ambiguities in language comprehension. Brain Res 1098:139–152 [DOI] [PubMed]
- Shannon CE, Weaver W (1949) The mathematical theory of communication. University of Illinois Press, Urbana, reprint 1963
- Sharbrough F, Chartrian GE, Lesser RP, Lüders H, Nuwer M, Picton TW (1995) American Electroencephalographic Society guidelines for standard electrode position nomenclature. J Clin Neurophysiol 8:200–202 [PubMed]
- Shieber SM (1985) Evidence against the context-freeness of natural language. Linguist Philos 8:333–343 [DOI]
- Siegelmann HT (1996) The simple dynamics of super Turing theories. Theor Comput Sci 168:461–472 [DOI]
- Smolensky P (1990) Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artif Intell 46:159–216 [DOI]
- Smolensky P (1991) Connectionism, constituency, and the language of thought. In: Loewer B, Rey G (eds) Meaning in mind. Fodor and his critics, chap 12. Blackwell, Oxford, pp 201–227
- Smolensky P (2006) Harmony in linguistic cognition. Cogn Sci 30:779–801 [DOI] [PubMed]
- Smolensky P, Legendre G (2006) The harmonic mind. From neural computation to optimality-theoretic grammar, vol 1: cognitive architecture. MIT Press, Cambridge (MA)
- Stabler EP (1997) Derivational minimalism. In: Retoré C (eds) Logical aspects of comutational linguistics, Springer lecture notes in computer science, vol 1328. Springer, New York, pp 68–95
- Stabler EP, Keenan EL (2003) Structural similarity within and among languages. Theor Comput Sci 293:345–363 [DOI]
- Staudacher P (1990) Ansätze und Probleme prinzipienorientierten Parsens. In: Felix SW, Kanngießer S, Rickheit G (eds) Sprache und Wissen. Westdeutscher Verlag, Opladen, pp 151–189
- Sweeney-Reed CM, Nasuto SJ (2007) A novel approach to the detection of synchronisation in EEG based on empirical mode decomposition. J Cogn Neurosci. doi:10.1007/s10827-007-0020-3 [DOI] [PubMed]
- Tabor W (1998) Dynamical automata. Technical report TR98-1694, Cornell Computer Science Department, Department of Psychology, Uris Hall, Cornell University, Ithaca, NY 14853
- Tabor W (2000) Fractal encoding of context-free grammars in connectionist networks. Expert Syst Int J Knowl Eng Neural Networ 17(1):41–56
- Tabor W, Tanenhaus MK (1999) Dynamical models of sentence processing. Cogn Sci 23(4):491–515 [DOI]
- Tabor W, Juliano C, Tanenhaus MK (1997) Parsing in a dynamical system: an attractor-based account of the interaction of lexical and structural constraints in sentence processing. Lang Cogn Process 12(2/3):211–271 [DOI]
- Thelen E, Schöner G, Scheier C, Smith LB (2001) The dynamics of embodiment: a field theory of infant perseverative reaching. Behav Brain Sci 24:1–86 [DOI] [PubMed]
- van Valin R (1993) A synopsis of role and reference grammar. In: van Valin R (eds) Advances in role and reference grammar. Benjamins, Amsterdam
- Vasishth S, Lewis RL (2006a) Argument-head distance and processing complexity: explaining both locality and antilocality effects. Language 82
- Vasishth S, Lewis RL (2006b) Human language processing: symbolic models. In: Brown K (eds) Encyclopedia of language and linguistics, vol 5. Elsevier, Amsterdam, pp 410–419
- Vasishth S, Brüssow S, Lewis RL, Drenhaus H (2008) Processing polarity: how the ungrammatical intrudes on the grammatical. Cogn Sci 32(4) [DOI] [PubMed]
- van der Velde F, de Kamps M (2006) Neural blackboard architectures of combinatorial structures in cognition. Behav Brain Sci 29:37–108 [DOI] [PubMed]
- Vos SH, Gunter TC, Schriefers H, Friederici AD (2001) Syntactic parsing and working memory: the effects of syntactic complexity, reading span, and concurrent load. Lang Cogn Process 16(1):65–103 [DOI]
- Vosse T, Kempen G (2000) Syntactic structure assembly in human parsing: a computational model based on competitive inhibition and a lexicalist grammar. Cognition 75:105–143 [DOI] [PubMed]
- van der Waerden BL (2003) Algebra, vol 2. Springer, New York
- Wegner P (1998) Interactive foundations of computing. Theor Comput Sci 192:315–351 [DOI]
- Wennekers T, Garagnani M, Pulvermüller F (2006) Language models based on hebbian cell assemblies. J Physiol (Paris) 100:16–30 [DOI] [PubMed]
- Wright JJ, Rennie CJ, Lees GJ, Robinson PA, Bourke PD, Chapman CL, Gordon E, Rowe DL (2004) Simulated electrocortical activity at microscopic, mesoscopic and global scales. Int J Bifurcat Chaos 14(2):853–872 [DOI]