Abstract
Image-based computational models for atherosclerotic plaques have been developed to perform mechanical analysis to quantify critical flow and stress/strain conditions related to plaque rupture which often leads directly to heart attack or stroke. An important modeling issue is how to determine zero stress state from in vivo plaque geometries. This paper presents a method to quantify human carotid artery axial and inner circumferential shrinkages by using patient-specific ex vivo and in vivo MRI images. A shrink-stretch process based on patient-specific in vivo plaque morphology and shrinkage data was introduced to shrink the in vivo geometry first to find the zero-stress state (opening angle was ignored to reduce the complexity), and then stretch and pressurize to recover the in vivo plaque geometry with computed initial stress, strain, flow pressure and velocity conditions. Effects of the shrink-stretch process on plaque stress/strain distributions were demonstrated based on patient-specific data using 3D models with fluid-structure interactions (FSI). The average artery axial and inner circumferential shrinkages were 25% and 7.9%, respectively, based on a data set obtained from 10 patients. Maximum values of maximum principal stress and strain increased 349.8% and 249% respectively with 33% axial stretch. Influence of inner circumferential shrinkage (7.9%) was not very noticeable under 33% axial stretch, but became more noticeable under smaller axial stretch. Our results indicated that accurate knowledge of artery shrinkages and the shrink-stretch process will considerably improve the accuracy of computational predictions made based on results from those in vivo MRI-based FSI models.
Keywords: Atherosclerosis, vulnerable plaques, carotid artery, blood flow, artery shrinkage, fluid-structure interactions
1. Introduction
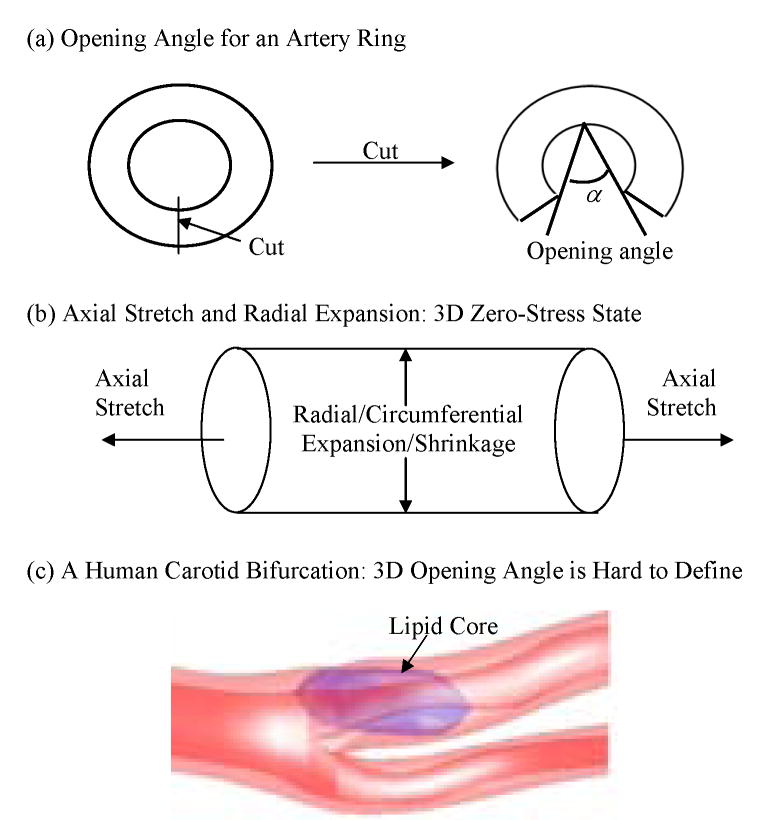
Magnetic resonance image (MRI)-based computational models (2D/3D structure only, 3D fluid-only, 3D models with fluid-structure interactions) for atherosclerotic plaques have been introduced to perform mechanical analysis to quantify critical flow and stress/strain conditions related to plaque rupture which often leads directly to heart attack or stroke [3, 8–11, 13–19, 22, 24]. An important modeling issue is how to determine zero stress state from in vivo plaque geometry. Dr. Fung wrote in his celebrated three-book “Biomechanics” series: “A body in which there is no stress is at the zero stress state. If strain is calculated with respect to the zero stress state, then the strain is zero when the stress is zero, and vice versa. This is an important feature of the constitutive equation. Hence the analysis of stress and strain begins with the identification of the zero stress state” [5, p.351]. Fung and his colleagues introduced the zero-stress state concept for living organs in 1983 [4, 5] and the opening angle for artery rings to investigate zero-stress state under 2D assumption [4]. Some earlier work included opening angles in pulmonary arteries [6], in the aorta of the pig and dog [7, 21], systemic and pulmonary veins [23], and trachea [7]. For computational atherosclerotic plaque models based on in vivo MRI data, it is important to develop a practical process to obtain the zero-stress geometry of the plaque from the in vivo geometry so that solution process could start from there and accurate stress/strain predictions could be obtained. It should be noted that opening angle is only one of the quantities needed to determine artery zero stress state. For 3D artery models, Fig. 1 indicates that patient-specific artery opening angle, axial and radial shrinkages should be quantified and used in the model construction process.
Figure 1.
Schematic drawing of 3 elements concerning zero stress state in 3D models. (a) Opening angle; (b) Axial shrinkage/stretch and circumferential shrinkage/expansion; (c) 3D reconstructed geometry of a human carotid plaque showing its nonuniform geometry and plaque components.
In this paper, a shrink-stretch process for in vivo MRI-based human carotid artery models was introduced to partially address the zero stress state issue. Effects of the shrink-stretch process on plaque stress/strain distributions were demonstrated based on patient-specific data using 3D models with fluid-structure interactions (FSI). Human carotid plaque morphologies reconstructed from in vivo/ex vivo MRI data were compared and plaque morphological features were used to quantify artery axial and radial shrinkages. The shrinkage data was used to shrink the in vivo plaque geometry to get the computational zero-stress geometry which was used as the starting geometry of the model. Axial stretch and pressure conditions were then imposed so that the in vivo plaque morphology could be recovered, together with proper initial stress/strain conditions. This process gave us the proper plaque morphology and initial flow and stress/strain conditions so that we could start the simulation of blood flow under physiological pulsating pressure conditions. Opening angle was omitted in our shrink-stretch process because: a) complex structure and inhomogeneous plaque materials cause the opening angle vary from slice to slice, and very difficult to quantify; b) computational effort is huge if we cut open the artery to different angles for different slices and then bend and “glue” (a numerical technique to put two edges or surfaces together) it again; c) for in vivo MRI-based models, data will not be available since we cannot take the artery from the patient. This (opening angle) remains to be one of our future topics to be added to our models.
Figure 1 gives some sketches to demonstrate opening angle, axial and radial shrinkages related to the zero stress state determination process. Fig. 1(c) gives a human carotid artery with bifurcation showing that it would be hard to define opening angle for carotid arteries with plaque components and bifurcation. Combination of in vivo/ex vivo MR images enables us to quantify the patient-specific artery shrinkage in axial and cross-section directions between in vivo state and ex vivo state. To our knowledge, this is the first report demonstrating human carotid artery shrinkage using in vivo and ex vivo MR Images.
2. Data acquisition and artery shrinkage
2.1 Multi-contrast MRI data acquisition
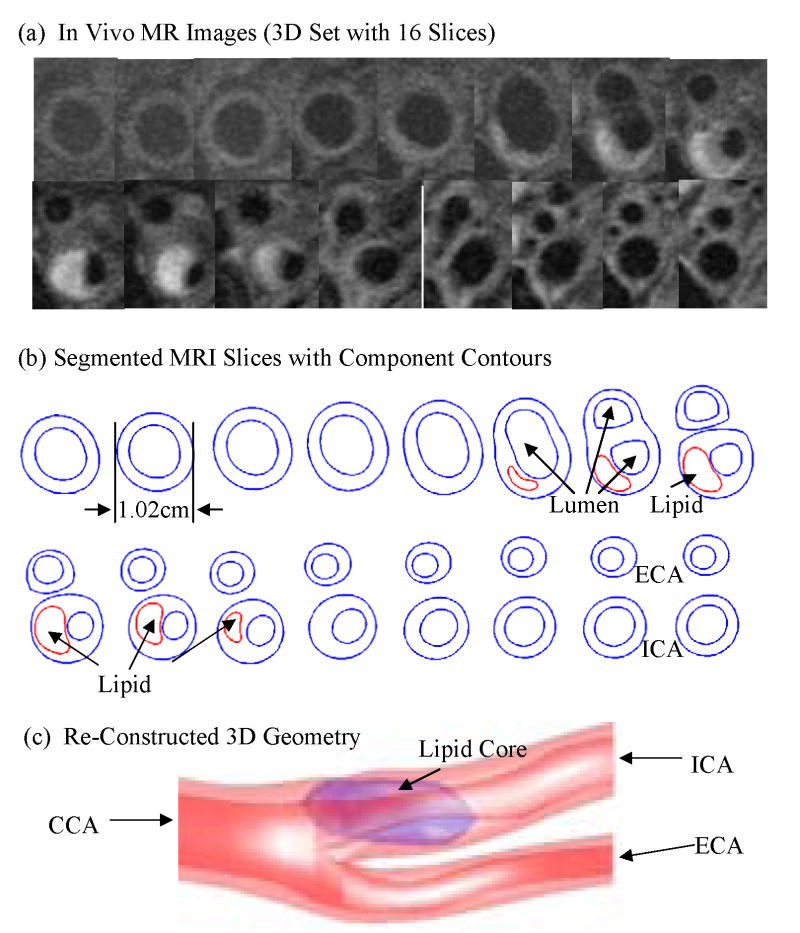
3D In vivo/ex vivo MR images of human carotid atherosclerotic plaques from ten (10) patients (age: 51–82, average: 65; 9 male; 1 female) were acquired by Dr. Yuan’s group (9 patients) at University of Washington using protocol approved by University of Washington Institutional Review Board, and by Dr. Woodard and Dr. Zheng’s group (1 patient) at Washington University using protocol approved by Washington University Institutional Review Board, with informed consent obtained at both locations. Multi-contrast images in T1, T2, proton density (PD), time-of-fight (TOF), and contrast-enhanced (CE) T1 weightings of carotid atherosclerosis were generated to characterize plaque tissue composition, luminal and vessel wall morphology. A computer package CASCADE (Computer-Aided System for Cardiovascular Disease Evaluation) developed by the Vascular Imaging Laboratory (VIL) at the University of Washington (UW) was used by Yuan’s group to perform image analysis and segmentation [12]. CASCADE analysis tools has been validated by histological studies and are able to accurately identify specific plaque features, including the lumen, wall boundary, lipid rich necrotic core, calcifications and other components. Upon completion of a review, an extensive report is generated and segmented contour lines for different plaque components for each slice are stored as digital files for 3D geometry reconstruction. MRI data acquired at the Washington University site was segmented by Woodard and Zheng’s group using a self-developed software package Atherosclerotic Plaque Imaging Analysis (APIA) written in Matlab (Math Works, MATLAB, Natick, MA) and also validated by histological analysis. Fig. 2 gives 16 MRI slices from a human carotid plaque sample, the segmented component contour plots, re-constructed 3D geometry. Some smoothing, which was kept to minimum, was applied to correct numerical and MRI artifacts.
Figure 2.
In vivo 3D MRI images of a human carotid plaque and re-constructed 3D geometry. (a) 16 MRI (T1) slices (S1–S16), slice spacing: 3mm. Each image shown here was cut from the whole neck image; (b) Segmented contour plots showing plaque components; (c) The reconstructed 3D geometry showing a lipid core.
2.2 Artery shrinkage in axial and circumferential direction
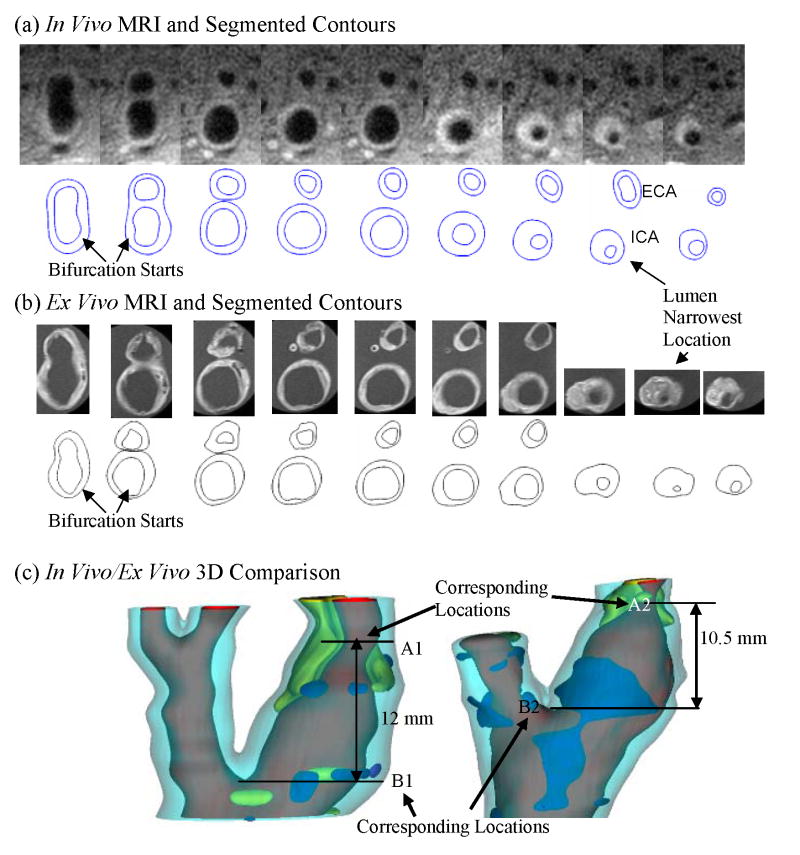
In vivo/ex vivo MRI Images of carotid atherosclerotic plaques were used to construct in vivo/ex vivo geometries. Both 3D geometries and 2D slices were carefully examined and compared to identify “corresponding locations” to quantify patient-specific artery shrinkage. This is called “registration” in MRI terminology. The bifurcation point is a natural choice for registration. Other plaque morphological features such as lumen narrowing and shape change, plaque component size, shape and location were all considered. There are considerable differences between ex vivo and in vivo images due to: a) image resolution difference; b) plaque sample changes once it was taken out of human body (loss of blood, water, lipid leakage, etc.); c) deformation caused by manual handling. Among various morphological features, lumen size and shape are more reliable and easier to compare between ex vivo and in vivo images. So using lumen size to register became our preferred choice. The luminal bifurcation and narrowest location were selected as marking points for registration. Fig. 3 gives the registration results using both 2D slices and the matching 3D view. Locations A1, A2 mark the corresponding lumen narrowest location and B1, B2 indicate the corresponding beginning position of luminal bifurcation at in vivo and ex vivo state respectively. There are 5 slices of MRI image at in vivo state and 6 slices of MRI image at ex vivo state between these two locations respectively. The slice thickness of in vivo MRI data set is 2 mm, so the length of the two marking points at in vivo state is 12 mm. The slice thickness of ex vivo MRI images is 1.5 mm, the distance of the two marking points is 10.5 mm at ex vivo state. Assuming the shrinkage of the artery in axial direction was uniform and defining the axial shrinkage as λz,
Figure 3.
In vivo and ex vivo MR images and 3D geometries of a human carotid plaque (Example #1) were compared to quantify axial and inner circumferential shrinkages. (a) In vivo MRI images and segmented contour plots; (b) Ex vivo MRI images and segmented contour plots; (c) 3D geometries and identified corresponding locations.
| (1) |
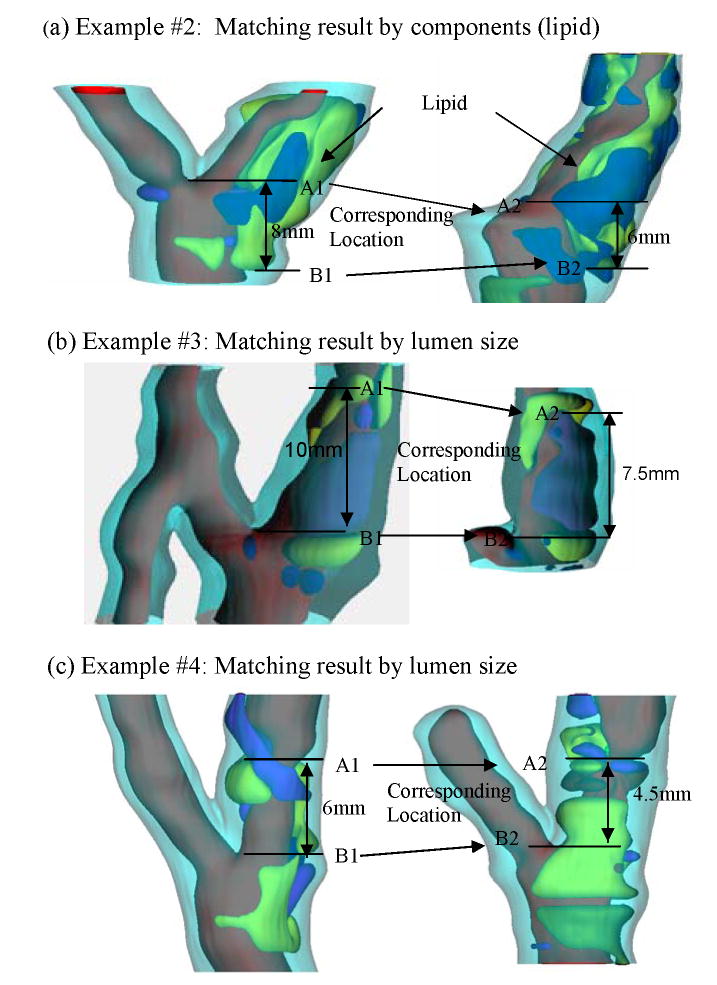
where Lin and Lex are the distance between the two marking points of in vivo and ex vivo state respectively, we got the axial shrinkage for this plaque sample which is 12.5%. Fig. 4 gives 3 more examples showing site registrations using lumen and plaque component features.
Figure 4.
Three more examples showing plaque registration results, 3D view.
To quantify radial shrinkage, we choose to use plaque inner circumference for the following reasons: a) most plaque cross sections are of very irregular shape and not circular. It is not possible to define “radius” for those cross sections. On the other hand, circumference can be calculated easily and used to measure circumferential shrinkage. b) When plaque is taken out of human body during endarterectomy surgery, the media and adventitia layers of the artery are kept in patient’s body. Therefore, while in vivo MR images include the artery with all its layers, ex vivo samples and MR images do not include the media and adventitia layers of the vessel. So the outer boundary is not suitable for use in determining circumferential shrinkage. The circumferential shrinkage for a cross-section of the artery (represented by a cross-section MRI slice) is defined as λc,
| (2) |
Where Cin and Cex are the lumen circumference corresponding to in vivo and ex vivo state, respectively. When the in vivo and ex vivo MRI images were not matched slice by slice, linear interpolation was used to calculate the inner circumference of corresponding slice at ex vivo state. The average shrinkage value from all slices of a plaque sample was used as the circumferential shrinkage for the plaque.
3. Models and methods
3.1 The computational solid and fluid models
The artery wall and plaque components were assumed to be hyperelastic, isotropic, incompressible and homogeneous. The 3D nonlinear modified Mooney-Rivlin (M-R) model was used to describe the material properties of the vessel wall and plaque components [18–19, 24]. Blood flow was assumed to be laminar, Newtonian, viscous and incompressible. The incompressible Navier-Stokes equations with arbitrary Lagrangian-Eulerian (ALE) formulation were used as the governing equations which are suitable for problems with fluid-structure interactions and frequent mesh adjustments. Flow velocity at the flow-vessel interface was set to move with vessel wall (no-slip condition) for unsteady flow. Natural traction equilibrium boundary conditions and continuity of displacement were specified on all interfaces between all components and the interface between solid and fluid. With all of these, we come to the following FSI model:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
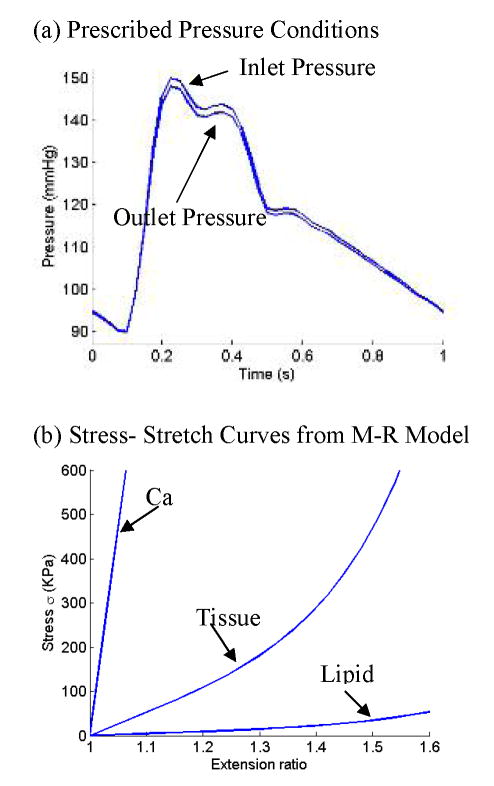
A typical cardiac pressure profile was specified at the inlet and the outlet pressure (see Fig. 5(a)). Strain energy function for M-R model is given by,
Figure 5.
Pressure conditions and material stress-stretch curves used in the multi-component plaque FSI model. (a) Pressure conditions specified at the inlet (CCA) and outlet (ICA and ECA); (b) Stress-stretch curves derived from the modified Mooney-Rivlin model. The parameters are (c2=0 for all materials; the unit for c1 and D1 is: dyn/cm2): vessel and fibrous tissue: c1=368000, D1=144000, D2=2.0; lipid: c1=20000, D1=20000, D2=1.5; Ca: C1=3680000, D1=1440000, D2=2.0.
| (11) |
| (12) |
where I1 and I2 are the first and second strain invariants, C =[Cij] = XTX is the right Cauchy-Green deformation tensor, X=[Xij] = [∂xi/∂aj], (xi) is current position, (ai) is original position, ci and Di are material parameters chosen to match experimental measurements [18] and ex vivo/in vivo shrinkage data. The 3D stress/strain relations can be obtained by finding various partial derivatives of the strain energy function with respect to proper variables (strain or stretch components) [1, 2]. In particular, setting material density =1 g • cm−3 and assuming,
| (13) |
where λ1, λ2 and λ3 are stretch ratios in the (x,y,z) directions respectively, the uni-axial stress/stretch relation for an isotropic material is obtained from (11),
| (14) |
The parameter values and stress-stretch curves for the baseline model are given by Fig. 5(b).
3.2 3D geometry re-construction and mesh generation
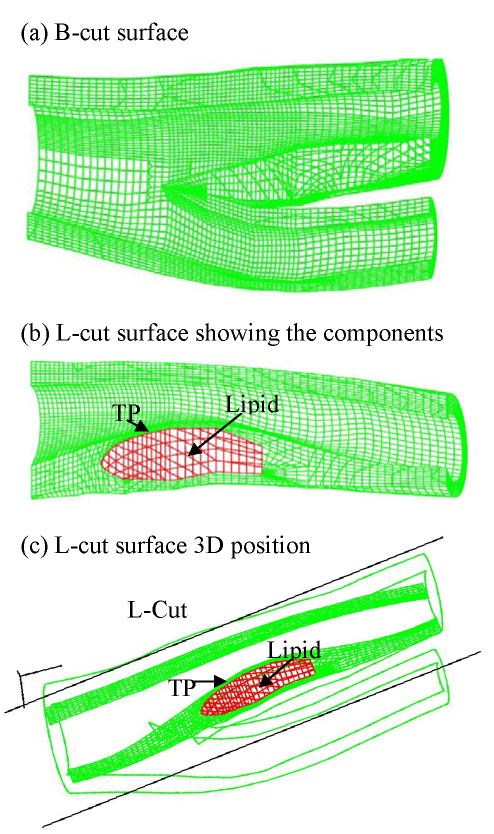
In vivo MRI geometry data points were shrunk initially using patient-specific shrinkage data (25% axially, 8% inner circumference). Outer circumference shrinkage rate was determined so that the total 3D volume of the geometry was conserved. The final circumferential shrinkage was adjusted numerically so that the lumen geometry from the FSI model would have a best match with MRI lumen dimensions. All segmented 2D slices were read into ADINA input file, pixel by pixel. 3D surfaces, volumes and computational mesh were made under ADINA computing environment. The procedure is explained as follows. For each object (made of one material) such as the vessel itself, lipid core, calcification, or the fluid domain, we first divide its geometry into enough volumes so that each volume has a more regular shape for mesh/element generation. We next specify an element group for each volume, which includes element style, material and other information (such as indications assuming large-strain or large-displacement for the kinematic formulation for the element group). After that, we specify mesh density and mesh style for each volume. Elements of all the volumes were generated using the ADINA command “Gvolume”. The key here is the proper division of each physical object into computational volumes so that mesh/elements can be generated. This step has a strong influence on the element shape and convergence of the model. For a multi-component FSI plaque model with bifurcation, many volumes are needed. Fig. 6 gives a bifurcation cut (B-cut) surface and longitudinal cut (L-cut) surface showing meshes used in our computations. Volumes and elements used for this patient-specific models are: Normal (fibrous) tissue: volumes: 298, elements: 95,296; lipid core: volumes: 5, elements: 2688; Fluid: volumes: 30, elements: 315,648. Total volumes for the whole model: 333; total elements: 413,632.
Figure 6.
Finite element meshes for the computational model showing different cut-surfaces. (a) Mesh for the solid domain showing the position of a bifurcation-cut (B-cut) surface; (b) A longitudinal-cut (L-cut) surface showing the lipid core and thin plaque cap; (c) Location of the L-cut surface.
With the initial geometry, a 33% axial stretch (33% stretch is needed to recover the 25% shrinkage) and a physiological pressure condition were imposed to recover the in vivo geometry with stress/strain distributions obtained for the sample. It should be noted that axial stretch makes the artery shrink in radial direction and pressure leads to radial expansion. The initial radial shrinkage often needs to be adjusted several times until the geometry with stretch and pressure reaches best agreement with original in vivo geometry. Then we are ready to solve the FSI model given by (3)–(10).
3.3 Solution method
The coupled fluid and structure models were be solved by ADINA (ADINA R & D, Inc., Watertown, MA, USA). ADINA uses unstructured finite element methods for both fluid and solid models. Nonlinear incremental iterative procedures are used to handle fluid-structure interactions. The governing finite element equations for both the solid and fluid models are solved by the Newton-Raphson iteration method. Proper mesh will be chosen to fit the shape of each component, the vessel, and the fluid domain. Finer mesh will be used for thin plaque cap, bifurcation, and components with sharp angles to get better resolution and handle high stress concentration behaviors (Fig. 6). Using the axial and circumferential shrinkage results obtained from 2.2, the stretch ratio in axial direction and expansion in circumferential direction were calculated. The artery was stretched axially and pressurized gradually to specified conditions. Mesh analysis was performed until differences between solutions from two consecutive meshes were negligible (less than 1% in L2-norm). Two cardiac cycles were needed to obtain periodic solutions. More details of the computational models and solution methods can be found from Tang et al [18–19] and Bathe [1,2].
4. Results
Simulations were conducted using the plaque sample given by Fig. 2. Six 3D FSI multi-component models obtained from the base plaque model with specified pressure (Fig. 6(a)) were used to investigate the effects of different axial stretch ratio and circumferential shrinkage/expansion: Case 1 (base model) and Case 2: 0% axial stretch, with/without circumferential shrinkage; Cases 3 & 4: 10% axial stretch, with/without circumferential shrinkage; Cases 5 & 6: 33% axial stretch, with/without circumferential shrinkage. Due to the complexity of 3D solutions, two sagittal cut surfaces (B-cut and L-cut as given in Fig. 6) were chosen to present flow velocity, shear stress, pressure and plaque stress/strain distribution solution behaviors (Figures 7–9).
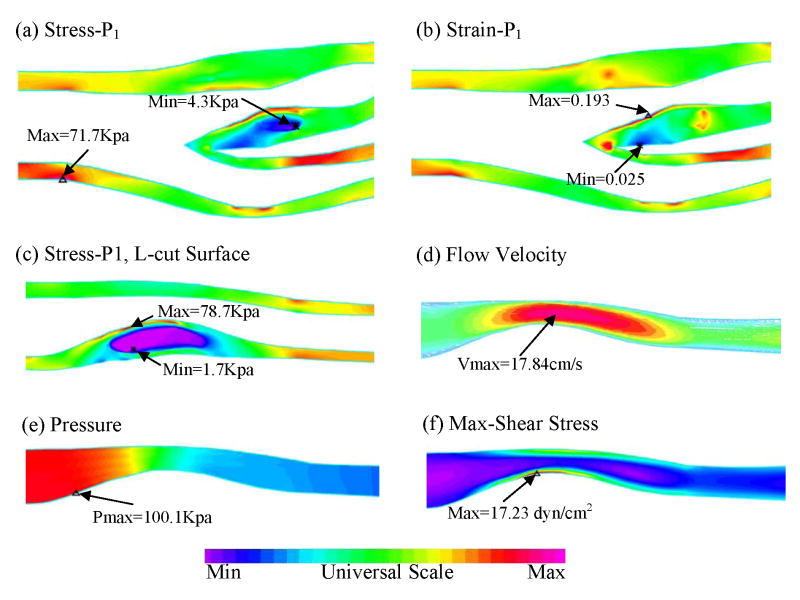
Figure 7.
Stress/strain distributions and flow characteristics from the 3D FSI model (Case 3, 10% axial stretch, 7.8 inner circumferential shrinkage), Pin=100 mmHg. (a) Plot of maximum principal stress (Stress-P1) distribution on B-cut surface; (b) Plot of maximum principal strain (Strain-P1) distribution on B-cut surface; (c) Stress-P1 on L-cut surface; (d) Flow velocity reaching its maximum in the stenotic region; (e) Pressure band plot on L-cut surface; (f) Flow maximum shear stress band plot on L-cut surface showing a maximum at the stenosis throat.
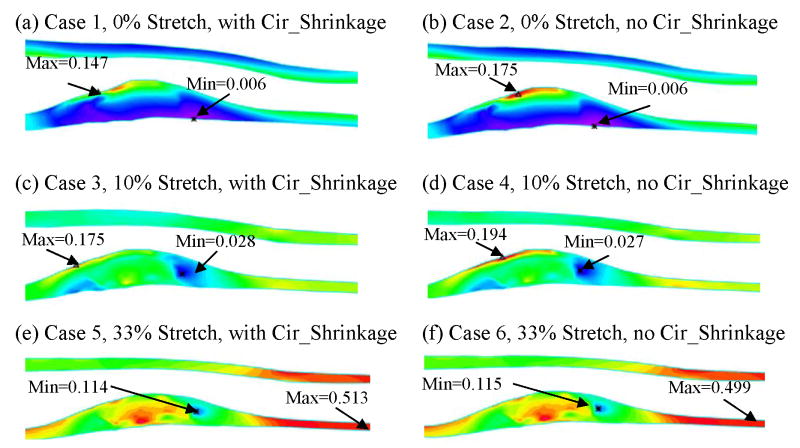
Figure 9.
Plots of Strain-P1 distribution on L-cut surface from 6 case studies showing effects of axial stretch and circumferential shrinkage.
4.1 Artery axial and circumferential shrinkage
Table 1 gives axial and circumferential shrinkage results from the 10 patients who participated in this study. From this 10 patient data set, it was found that the average value of axial shrinkage was 25% and inner circumferential shrinkage was 7.9%.
Table 1.
The results of axial and circumferential shrinkage for carotid artery determined from comparisons of in vivo and ex vivo MR images and re-constructed 3D geometries. Data was obtained from 10 participating patients.
| Patient | Circumferential Shrinkage (%) | Axial Shrinkage (%) |
|---|---|---|
| Patient 1 | 3.3 | 25 |
| Patient 2 | 9.2 | 25 |
| Patient 3 | 12.3 | 25 |
| Patient 4 | 11.9 | 25 |
| Patient 5 | 5.7 | 25 |
| Patient 6 | −5.3 | 13 |
| Patient 7 | 10.3 | 25 |
| Patient 8 | 5.7 | 25 |
| Patient 9 | 16.7 | 25 |
| Patient 10 | 9.1 | 33 |
| Average | 7.9 | 25 |
4.2 Overview of plaque stress/strain, flow velocity and shear stress behaviors
Fig. 7 presents maximum principal stress (Stress-P1) and maximum principal strain (Strain-P1) distributions, flow velocity, pressure and maximum-shear-stress (MSS) on two sagittal cut surfaces for Case 3. On the B-cut surface, maximum Stress-P1 value was found at a healthy site of the vessel where the vessel wall was thin (Fig. 7(a)) and minimum value was found at the lipid pool. Fig. 7(b) shows that maximum Strain-P1 value was located at plaque cap where the plaque may rupture. Fig. 7(c)–(f) give band plots of both structure and flow features on L-cut surface which shows lipid pool and cap thickness much better than the bifurcation cut. Fig. 7(c) presents distribution of Stress-P1 showing maximum value located at the lipid cap position. Flow velocity is higher at the stenosis narrowing of internal carotid artery (ICA). A maximum value of Maximum-Shear Stress (MSS) was also found at the plaque throat (narrowing). 3D FSI results contain rich information which can serve as the basis for many further investigations.
4.3 Effects of axial stretch
Cases 1, 3, and 5 (with 0%, 10%, and 33% axial stretch, all with circumferential shrinkage) were compared to investigate the stress/strain variation with axial stretch. The L-cut surface is chosen to present the results for the comparative case studies because it has simpler geometry and shows the lipid core and plaque cap better. Figures 8 & 9 give band plots of Stress-P1/Strain-P1 distributions for all six cases corresponding to 100 mmHg inlet pressure conditions. Maximum Stress-P1 and Strain-P1 values were summarized in Table 2. Using Model 1 numbers as the base, maximum Stress-P1 values increased from 62.6 to 78.7 KPa (Case 3, 25.7% increase) and 281.6 KPa (Case 5, 349.8% increase), and maximum Strain-P1 values increased from 0.147 to 0.175 (Case 3, 19% increase) and 0.513 (Case 5, 249% increase), when axial stretch increased from 0% to 10% and 33%, respectively. Stress/Strain distribution patterns and locations of maxima were different for the 3 cases. Greater axial stretch moved the location of maximum stresses to healthy part of the vessel where the vessel wall is thin.
Figure 8.
Plots of Stress-P1 distribution on L-cut surface from 6 case studies showing effects of axial stretch and circumferential shrinkage.
Table 2.
Maximum values of Stress-P1 and Strain-P1 increased 349.8% and 249% respectively with 33% axial stretch: Comparison of maximum Stress-P1 and Strain-P1 values from 6 cases showing axial stretch has considerable effects on stress/strain predictions.
| Case | Defining Conditions | Stress-P1 (Kpa) | % of Base | Strain-P1 | % of Base | |
|---|---|---|---|---|---|---|
| Axial Stretch | Circumferential Shrinkage | |||||
| Case1 | 0% | YES | 62.6 | 100.0 | 0.147 | 100.0 |
| Case2 | 0% | NO | 77.9 | 124.4 | 0.175 | 119.0 |
| Case3 | 10% | YES | 78.7 | 125.7 | 0.175 | 119.0 |
| Case4 | 10% | NO | 89.9 | 143.6 | 0.194 | 132.0 |
| Case5 | 33% | YES | 281.6 | 449.8 | 0.513 | 349.0 |
| Case6 | 33% | NO | 284.3 | 454.2 | 0.499 | 339.5 |
The plaque cap location was also chosen to be examined because that is a site where plaque rupture would likely occur. Table 3 summarizes Stress-P1 and Strain-P1 values tracked at the plaque cap location (position of the tracking point was shown in Fig. 6(b)) for all 6 cases. Significant variations of Stress-P1/Strain-P1 values at the tracking point were found. Still using Model 1 numbers as the base, Stress-P1 values at plaque cap increased from 39.6 to 61.5 KPa (Case 4, 55% increase) and 167.9 KPa (Case 6, 324% increase), and maximum Strain-P1 values increased from 0.105 to 0.116 (Case 4, 10.5% increase) and 0.271 (Case 6, 158% increase), when axial stretch increased from 0% to 10% and 33%, respectively. These results demonstrate that the axial stretch also has considerable effects on plaque cap stress/strain conditions which are more closely related to plaque rupture and vulnerability assessment [20].
Table 3.
Stress-P1 and Strain-P1 values at the plaque cap increased 324% and 158% respectively with 33% axial stretch: Comparison of Stress-P1 and Strain-P1 values tracked at plaque cap.
| Case | Defining Conditions | Stress-P1 (Kpa) | % of Base | Strain-P1 | % of Base | |
|---|---|---|---|---|---|---|
| Axial Stretch | Circumferential shrinkage | |||||
| Case1 | 0% | YES | 39.6 | 100.0 | 0.105 | 100.0 |
| Case2 | 0% | NO | 59.1 | 149.2 | 0.148 | 141.0 |
| Case3 | 10% | YES | 61.5 | 155.3 | 0.116 | 110.5 |
| Case4 | 10% | NO | 76.1 | 192.2 | 0.146 | 139.0 |
| Case5 | 33% | YES | 167.9 | 424.0 | 0.271 | 258.1 |
| Case6 | 33% | NO | 166.3 | 419.9 | 0.261 | 248.6 |
4.4 Effects of circumferential stretch
Figures 8 & 9 and Tables 2 & 3 give Stress-P1/Strain-P1 plots as well as maximum values for the 6 cases considered which form three groups (0%, 10%, and 33% axial stretches) to investigate the variation of stress/strain behavior due to circumferential stretch. Table 4 calculated the percentage differences using Cases 1, 3, & 5 as base numbers. Cases 2 and 4 gave higher stress/strain values (plaque cap Stress-P1 was 49.2% higher for 0% case, and 23.7% higher for the 10% case), while the 33% axial stretch group (Cases 5 & 6) only had very small differences with/without circumferential shrinkage. This is understandable because the large axial stretch suppressed the changes caused by the much smaller circumferential shrinkage. These results indicate that when the axial stretch is more significant, the effects of circumferential shrinkage on stress/strain are less noticeable. When axial stretch is smaller (<10%), effects from the circumferential shrinkage become more noticeable and should be taken into account.
Table 4.
Comparison and percentage increase (no circumferential shrinkage vs. with circumferential shrinkage, i.e., Cases 2,4,6 vs, Cases 1,3,5) of maximum and plaque cap Stress-P1 and Strain-P1 values on L-cut surfaces showing the circumferential shrinkage affects.
| Axial Stretch | Max Stress-P1 Increase (%) | Cap Stress-P1 Increase (%) | Max Strain-P1 Increase (%) | Cap Strain-P1 Increase (%) |
|---|---|---|---|---|
| 0% | 24.4 | 49.2 | 19.0 | 41.0 |
| 10% | 14.2 | 23.7 | 10.9 | 25.9 |
| 33% | 0.96 | −1.0 | −2.7 | −3.7 |
5. Discussion and Conclusion
The method presented here is the first attempt quantifying human carotid artery axial and inner circumferential shrinkages by comparing ex vivo and in vivo MRI images. To our knowledge, this is also the first time such human artery shrinkage data has been reported. The shrink-stretch process based on patient-specific shrinkage data and in vivo MRI images takes artery axial and circumferential shrinkages into account to find a zero-stress state (opening angle was ignored to reduce the complexity), and then recover the in vivo plaque geometry with computed initial stress, strain, flow pressure and velocity conditions. This will improve the accuracy of in vivo MRI-based FSI models and predictions made based on results from those models.
The effects of axial stretch and circumferential shrinkage/expansion were quantified by six FSI models in this paper. These fill a gap in the current literature. From the observations, the effects of axial stretch are not only in stress/strain value but also in their distribution patterns, especially when axial stretch is large (33% stretch case). The average value of axial shrinkage from the 10 patient data is 25%. This is significant and should be taken into consideration in computational modeling. Average circumferential shrinkage was smaller (7.9%) and its effect was more noticeable when axial stretch was smaller.
While our in vivo MRI-based plaque model with fluid-structure interactions represents clear advances in the modeling process, some limitations and model simplifications should be acknowledged: a) Opening angle was not included due to lack of data and consideration of computational effort; b) Tissue tethering is the mechanical force that keeps the artery in its in vivo shape. It was not included in our model so our model geometries tend to become rounder when pressured. This may lead to increased stress/strain concentration level at large curvature sites. Including tethering in FSI models represents a big challenge to all modeling researchers. c) Non-Newtonian effect was not included because it has been recognized that differences between Newtonian and Non-Newtonian flow models for large arteries are small and can be ignored [24]. d) Different tissue and plaque components may have different shrinkage and may affect the artery shrinkage. For example, calcification may shrink much less and lipid core may have leakage and shrink more. This should be taken into consideration by shrinking individual component separately, if data is available.
Another non-modeling limitation of this study was the resolution of in vivo/ex vivo MRI images. The slice thickness was 2 mm for in vivo MRI images and 1.5 mm for ex vivo MRI images, respectively. The resolutions of in vivo and ex vivo MRI images were not the same. Ex vivo images had better resolution and could “see” plaque components better, which made it hard to compare in vivo and ex vivo geometries. These issues limited the accuracy of our shrinkage results. This could be improved when MRI images with better resolution become available.
Acknowledgments
This research was supported in part by NIH grant NIH/NIBIB, 1 R01 EB004759 and in part by NSF grant DMS-0540684.
References
- 1.Bathe KJ. Finite Element Procedures. Prentice Hall, Inc; New Jersey: 1996. [Google Scholar]
- 2.Bathe KJ, editor. ADINA and ADINA-F. I & II. ADINA R & D, Inc; Watertown: 2002. Theory and Modeling Guide. [Google Scholar]
- 3.Cheng GC, Loree HM, Kamm RD, Fishbein MC, Lee RT. Circulation. 1993;87:1179–1187. doi: 10.1161/01.cir.87.4.1179. [DOI] [PubMed] [Google Scholar]
- 4.Fung YC. In: What Principle Governs the Stress Distribution in Living Organs. Fung YC, Fukada E, Junjian W, editors. Biomechanics; China, Japan and USA: Science; Beijing, China: 1983. pp. 1–13. [Google Scholar]
- 5.Fung YC. Biomechanics: Mechanical Properties of Living Tissues. Springer; New York: 1993. pp. 349–352. [Google Scholar]
- 6.Fung YC, Liu SQ. in Changes of zero stress state of rat pulmonary arteries in hypertrophy. J Appl Physiol. 1991;70:2455–2470. doi: 10.1152/jappl.1991.70.6.2455. [DOI] [PubMed] [Google Scholar]
- 7.Han HC, Fung YC. J Biomech Eng. 1991;113:446–451. doi: 10.1115/1.2895425. [DOI] [PubMed] [Google Scholar]
- 8.Holzapfel GA, Stadler M, Schulze-Bause CAJ. Ann Biomed Eng. 2002;30(6):753–767. doi: 10.1114/1.1492812. [DOI] [PubMed] [Google Scholar]
- 9.Huang H, Virmani R, Younis H, Burke AP, Kamm RD, Lee RT. Circulation. 2001;103:1051–1056. doi: 10.1161/01.cir.103.8.1051. [DOI] [PubMed] [Google Scholar]
- 10.Joshi AK, Leask RL, Myers JG, Ojha M, Butany J, Ethier CR. Arterioscler Thromb Vasc Biol. 2004;24(12):2408–13. doi: 10.1161/01.ATV.0000147118.97474.4b. [DOI] [PubMed] [Google Scholar]
- 11.Kaazempur-Mofrad MR, Isasi AG, Younis HF, Chan RC, Hinton DP, Sukhova G, Lamuraglia GM, Lee RT, Kamm RD. Ann Biomed Eng. 2004;32(7):932–946. doi: 10.1023/b:abme.0000032456.16097.e0. [DOI] [PubMed] [Google Scholar]
- 12.Kerwin W, Hooker A, Spilker M, Vicini P, Ferguson M, Hatsukami T, Yuan C. Circulation. 2003;107(6):851–856. doi: 10.1161/01.cir.0000048145.52309.31. [DOI] [PubMed] [Google Scholar]
- 13.Lee RT, Grodzinsky AJ, Frank EH, Kamm RD, Schoen FJ. Circulation. 1991;83(5):1764–70. doi: 10.1161/01.cir.83.5.1764. [DOI] [PubMed] [Google Scholar]
- 14.Lee RT, Schoen FJ, Loree HM, Lark MW, Libby P. Arterioscler Thromb Vasc Biol. 1996;16:1070–3. doi: 10.1161/01.atv.16.8.1070. [DOI] [PubMed] [Google Scholar]
- 15.Long Q, Xu XY, Ariff B, Thom SA, Hughes ADAV. J Magn Reson Imaging. 2000;11:299–311. doi: 10.1002/(sici)1522-2586(200003)11:3<299::aid-jmri9>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 16.Loree HM, Kamm RD, Stringfellow RG, Lee RT. Circ Res. 1992;71:850–8. doi: 10.1161/01.res.71.4.850. [DOI] [PubMed] [Google Scholar]
- 17.Steinman DA. Ann Biomed Eng. 2002;30(4):483–97. doi: 10.1114/1.1467679. [DOI] [PubMed] [Google Scholar]
- 18.Tang D, Yang C, Kobayashi S, Ku DN. J Biomech Eng. 2004;126:363–370. doi: 10.1115/1.1762898. [DOI] [PubMed] [Google Scholar]
- 19.Tang D, Yang C, Zheng J, Woodard PK, Sicard GAA, Saffiz JE, Yuan C. Ann Biomed Eng. 2004;32:947–960. doi: 10.1023/b:abme.0000032457.10191.e0. [DOI] [PubMed] [Google Scholar]
- 20.Tang D, Yang C, Zheng J, Woodard PK, Saffiz JE, Petruccelli JD, Sicard GA, Yuan C. Annals of Biomedical Engineering. 2005;33(12):1789–1801. doi: 10.1007/s10439-005-8267-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vaishnav RN, Vossoughi J. In: Biomedical Engineering II, Recent Developments. Hall CW, editor. Pergamon Press; New York: 1983. pp. 330–333. [Google Scholar]
- 22.Williamson SD, Lam Y, Younis HF, Huang H, Patel S, Kaazempur-Mofrad MR, Kamm RD. J Biomech Eng. 2003;125:147–155. doi: 10.1115/1.1537736. [DOI] [PubMed] [Google Scholar]
- 23.Xie JP, Liu SQ, Yang RF, Fung YC. J Biochem Eng. 1991;113:36–41. doi: 10.1115/1.2894083. [DOI] [PubMed] [Google Scholar]
- 24.Yang C, Tang D, Yuan C, Hatsukami TS, Zheng J, Woodard PK. CMES: Comput Model Eng Sci. 2007;19(3):233–245. [PMC free article] [PubMed] [Google Scholar]