REPETITA: detection and discrimination of the periodicity of protein solenoid repeats by discrete Fourier transform

Abstract

Motivation: Proteins with solenoid repeats evolve more quickly than non-repetitive ones and their periodicity may be rapidly hidden at sequence level, while still evident in structure. In order to identify these repeats, we propose here a novel method based on a metric characterizing amino-acid properties (polarity, secondary structure, molecular volume, codon diversity, electric charge) using five previously derived numerical functions.

Results: The five spectra of the candidate sequences coding for structural repeats, obtained by Discrete Fourier Transform (DFT), show common features allowing determination of repeat periodicity with excellent results. Moreover it is possible to introduce a phase space parameterized by two quantities related to the Fourier spectra which allow for a clear distinction between a non-homologous set of globular proteins and proteins with solenoid repeats. The DFT method is shown to be competitive with other state of the art methods in the detection of solenoid structures, while improving its performance especially in the identification of periodicities, since it is able to recognize the actual repeat length in most cases. Moreover it highlights the relevance of local structural propensities in determining solenoid repeats.

Availability: A web tool implementing the algorithm presented in the article (REPETITA) is available with additional details on the data sets at the URL: http://protein.bio.unipd.it/repetita/.

Contact: silvio.tosatto@unipd.it

1 INTRODUCTION

Proteins can adopt a wide range of structures uniquely determined by sequence, with the vast majority being globular and stabilized by a unique cooperative hydrophobic core formed upon folding. It is long known that not all structures follow this general schema, e.g. fibrous proteins in silk (Kajava et al., 2006). There has been an increasing interest over the last years for such cases that apparently do not fold in the same way as globular proteins (Main et al., 2005). Several proteins fold into conformations with repeated structural regions (Andrade et al., 2000). Such repeat proteins are present in 14% of known protein sequences with specific functions generally associated to higher organisms (Marcotte et al., 1999). Protein repeats can be broadly divided in three different classes, depending on their length (Kajava, 2001). Short repeats of up to four residues have crystalline structures or form fibrous structures, while domain-forming repeats are longer than about 45 residues and behave like short globular proteins. In between are the so-called solenoid proteins forming peculiar protein folds (Kobe and Kajava, 2000). Solenoids are modular assemblies of identical units, containing secondary structure elements, which are coiled along a common axis or direction in space with a fixed curvature. Secondary structure varies from β-strand to α-helix with increasing repeat length (Fig. 1). Recently it has been experimentally established that folding of solenoid repeats is sequential (Kajander et al., 2005). A distinctive subclass is formed by the β-propeller proteins with 44–60-residue repeats arranged like the blades of a propeller: unlike solenoid repeats, these apparently have to form a closed circular structure.

Fig. 1.

Cartoon representation of sample solenoid structures. Rainbow coloring from blue to red shows the topology from the N- to the C-terminus. (A) Antifreeze protein (PDB 1EZG), (B) Pectate Lyase(PDB 1AIR), (C) Leucine Rich Repeat (LRR) variant (PDB 1JL5), (D) LRR (PDB 1YRG) and (E) Armadillo (PDB 2BCT). All pictures were drawn using PyMol (URL: http://pymol.sourceforge.net/).

Short repeats can be easily identified due to their low sequence complexity and regularity (Wootton, 1994). Domain-forming repeats are generally of sufficient length to allow recognition with sensitive database search tools, e.g. PSI-BLAST (Altschul et al., 1997). Solenoid proteins are more difficult to predict, as the single repeat can be quite degenerate in sequence and vary widely in number of repeat units (Kobe and Kajava, 2000). In fact, conservation appears more related to certain characteristics of the protein sequence, e.g. hydrophobicity, than to any given amino-acid type. This makes application of tools like PSI-BLAST difficult, since it relies on clear conservation patterns. A number of methods for solenoid repeat detection have been published over the years to overcome this limitation. Most methods are based on the self-alignment of the sequence (Biegert and Soding, 2008; George and Heringa, 2000; Gruber et al., 2005; Heger and Holm, 2000; Soding et al., 2006; Szklarczyk and Heringa, 2004). Ideally, repeated parts of the sequence should appear as off-diagonal regions of similarity, allowing identification of the basic repeat unit and the number and location of units along the sequence. Sequence conservation remains an issue, as highly degenerate repeat units may escape detection. Alternative approaches based on spectral analysis have been recently proposed (Murray et al., 2002; Murray et al., 2004; Gruber et al., 2005). The method of Murray and coworkers (Murray et al., 2002; Murray et al., 2004) is mainly aimed at the automated detection of repeats in known protein structures, in itself a highly non-trivial problem. REPPER (Gruber et al., 2005) implements a Fourier transform of the sequence using a hydrophobicity scale, but was not extensively benchmarked and has been tested to detect mainly periodicities of fibrous proteins. One of the most sensitive methods to detect degenerated repeats of solenoid proteins is based on sequence profiles (Lupas et al., 1997). The profile can identify tandem repeats of solenoids as well as protein domains, i.e. autonomously folding parts of the protein with distinct functions, if it spans more than one repeat (Kajava et al., 2004).

The present study aims to detect solenoid repeats and discriminate them from globular proteins, using the information coming from sequence profiles together with the discrete Fourier transform (DFT), based on the assumption that few characteristics of sequence repeats uniquely identify structural repeats. The Fourier transform is a mathematical tool capable of highlighting latent periodicities in a protein sequence given one or more adequate metrics used to characterize the amino-acid sequence efficiently. For this purpose, we employ the five numeric scales proposed by Atchley and coworkers after a rigorous statistical analysis of almost 500 different attributes associated with each amino acid (Atchley et al., 2005). In the following, we describe the development of a new DFT-based method and relevant statistical parameters for the identification of solenoid repeats and their periodicities in protein sequences. The REPETITA algorithm is compared to published methods and the implications are discussed.

2 METHODS

2.1 Datasets used

An initial set of 32 proteins with solenoid repeats was taken from the website (URL: http://www.crbm.cnrs.fr/∼kajava/solenoidtable.html) of a previous review (Kobe and Kajava, 2000). The TESE server (Sirocco and Tosatto, 2008) was used to find more protein domains belonging to the same solenoid folds as the initial set. TESE allows the user to generate ad hoc non-redundant sets of proteins with known structure, by limiting the maximal residual structural similarity according to the CATH classification (Pearl et al., 2003). Choosing representatives with at most 35% pairwise sequence identity (i.e. CATH ‘S’ level) yielded the final set of 105 solenoid domains. The set of non-solenoid protein domains was generated with TESE by randomly choosing X-ray structures with different topologies and no detectable sequence similarity (i.e. CATH ‘T’ level), for a total of 247 domains. The rationale for having a larger number of non-solenoid proteins is that the method should work well over all known protein folds. Both sets are shown on the web site. The RADAR (Heger and Holm, 2000) and TRUST (Szklarczyk and Heringa, 2004) methods were downloaded and run locally on the two datasets. Solenoid predictions for both were considered when at least two consecutive repeat units were detected.

The overall set of 105 solenoid repeat proteins and 247 non-solenoid protein domains was randomly split into a training set of 50 solenoid proteins and 119 non-solenoid domains and a test set of 55 solenoid proteins and 128 non-solenoid domains, with the constraint that solenoid structures of low similarity fall in the same partition. Sequence profiles for use with the DFT method are generated with PSI-BLAST (Altschul et al., 1997). The non-redundant database is searched for four interactions with standard parameters and an e-value threshold for inclusion in the profile of 0.001. The final alignments are used to derive the frequency profiles by counting each amino-acid type while ignoring gaps.

2.2 DFT formulation

We first translate the sequence profile of the candidate solenoid repeat into the numerical functions derived by Atchley and collaborators (Atchley et al., 2005). These five functions summarize 494 attributes of amino acids obtained from an online database (Kawashima et al., 1999), and characterize polarity, secondary structure, molecular volume, codon diversity and electrostatics charge, etc. In the following step, the five functions measuring amino-acid properties are normalized, to allow a straightforward comparison between the numerical values of the direct functions and the corresponding Fourier transforms. Normalization is performed on the squares of the functions, so that they sum up to 1:

(1)

where X=[A, C, D, E,…, W, Y] is the one-letter code corresponding to each of the 20 amino acids, and g_a are the five normalized sequence metrics. We are then ready to measure the sequence profile of the candidate solenoid repeat with the newly normalized functions. A sequence profile p_k(X) of length N, giving the probability of finding amino acid X in the profile at position k along the sequence, will be described by means of the set of five discrete functions, whose values are given according to the previously defined metrics:

(2)

The problem related to the detection of the periodicities hidden along the sequence is then mapped on the frequency space, using the DFT. It is applied to each function separately to obtain the corresponding transform F_a=F [f_a], whose values Fⁿ_a are needed to expand the original functions as a sum of trigonometric functions with angular frequencies and corresponding periods given by Equation (3):

(3)

The DFT is computed for each n=0,…, N−1 according to Equation (4):

(4)

The five-sequence functions are real, so that Fⁿ_a=(F^N−n_a)^* and the resulting spectrum has only N_sp<N spectral amplitudes. The latter are normalized in such a way that their height is not increased with sequence length, thus making comparison easier among different sequences:

(5)

The amplitude with n=0 is related to the average of the function f_a. The number of independent spectral lines is:

(6)

In this way we are not considering the information coming from the N−N_sp independent phases associated to the Fⁿ_a.

2.3 Confidence estimates

In order to identify the existence of a periodicity in the DFT signal of a candidate solenoid repeat sequence it is necessary to locate peaks in the spectra that should correspond to the exact period or to higher harmonics. In practice, the DFT spectra of protein sequence profiles display a quite noisy background, so that in order to correctly discriminate significative peaks we found it useful to employ a two-dimensional analysis based on the two parameters ρ_θ and z_max defined below.

We first introduce a threshold σ_θ=θσ_a to select spectral amplitudes above the threshold μ_a + θσ_a where the real number θ is the only fitted parameter of REPETITA, μ_a is the average and σ_a is the standard deviation of each spectrum (a=1,…, 5). The spectrum of each function of the metric is separately checked to count the number of spectral amplitudes above the threshold. The use of z-scores zⁿ_a of the amplitudes makes the check straightforward, since z-scores are defined as:

(7)

so that the threshold condition becomes zⁿ_a > θ.

Averages μ_a and standard deviations σ_a for the five metric functions are computed discarding A⁰_a (a=1,…, 5), which are the averages of the function f_a. These numbers depend on the overall sequence composition and are not meaningful to detect periodicities. We then proceed by counting the number of amplitudes in the spectrum of all the five functions, which have z-scores larger than θ, which we call N_θ: N_θ=N(zⁿ_a> θ), where a=1,…, 5 and n=1,…, N_sp − 1. Note that z⁰_a is discarded from the procedure, since it has no meaning, after having discarded A⁰_a from the computation of averages and standard deviations used to obtain the z-scores.

This number is then normalized by dividing by the number of spectral amplitudes considered for all five metric functions. The quantity obtained will give the percent ratio of spectral amplitudes above the selected threshold, which we will shortly call θ-ratio and write as ρ_θ:

(8)

The θ-ratios of the test sequences are computed for different values of θ ranging from 1 to 5. More information might be obtained from further analysis of the spectra, and a second parameter which strengthens the significance of the detected periodicity within the sequences under analysis is the maximum z-score found among all spectral amplitudes (z_max), for all the five metric functions.

In summary, a signal in sequence periodicity should be reflected in large enough spectral amplitudes (after proper normalization z-scores are used in place of raw amplitudes). We use two different parameters to extract as much information as possible from our data: z_max, the largest spectral amplitude; ρ_θ, the percent ratio of spectral amplitudes with z-score larger than θ.

2.4 Evaluation criteria

In order to derive a simple confidence estimate, we begin by testing different values of θ ranging from 1 to 5. For any given value of θ we proceed systematically deriving separating lines in the z_max–ρ_θ plane. For each separating line with slope m and intercept q, the sets of solenoid (actual positives, a_p) and globular sequences (actual negatives, a_n) are scanned to check the number of correct and wrong predictions. This procedure is similar to linear discriminant analysis. A prediction is correct if a solenoid (globular) sequence has a positive (negative) sign of

(9)

which tells whether the sequence under consideration lies above (predicted solenoid) or below (predicted globular) the separating line. The number of sequences predicted to be solenoid (predicted positives, p_p) or to be globular (predicted negatives, p_n) are then checked against the actual positives, a_p, and actual negatives, a_n. The outcome of the comparison are the number of true and false positives (t_p, f_p) and the number of true and false negatives, which may be obtained from the previous ones (t_n=a_n − f_p, f_n=a_p − t_p). For each separating line we compute the Matthews correlation coefficient

(10)

C_M values lie in the range [−1, 1], with 1 representing perfect agreement between predictions and actual values. For a given θ, we select the optimal separating line (m, q) as the one maximizing C_M. Sensitivity (true positive rate, t_p/a_p) and specificity (true negative rate, t_n/a_n) are also computed. A further optimization of C_M is carried out on the training set upon varying θ. The final values obtained will be then left fixed in the implementation of the REPETITA algorithm.

3 RESULTS

3.1 DFT calculation

From the homology profile of a given protein sequence, DFT spectra are calculated with standard techniques, as described in Section 2. The DFT provides the representation of the original function in the frequency domain, highlighting its periodicities with peaks at the corresponding frequencies computed according to Equation (3). Rather than using a single function to transform the amino-acid profile at each sequence position into a numerical value used in the DFT, we use the five scales introduced by Atchley and co-workers (Atchley et al., 2005). An example of the frequency amplitudes obtained from the five spectra is shown in Figure 2 for the 82 residue antifreeze protein (PDB code 1EZG). This protein forms a regular β solenoid repeat (see Fig. 1A) with a period of 12 residues. The peak above threshold with the lowest frequency rank (i.e. longest periodicity) reads 7 on scale 2. This transforms to a correctly predicted period of about 12 residues, as a result of the substitution of N = 82 and n = 7 in Equation (3). Notice that looking at other scales peaks above threshold correspond roughly to higher harmonics (ranks 27, 41). However, it is clear from these spectra that the determination of the correct period is not a trivial task, since the corresponding peaks are not always very pronounced for all scales, higher harmonics do not always appear, and there is a strong background noise which makes the analysis quite complicated. In order to overtake this problem we perform an analysis as described in the Section 2 by using the two parameters z_max and ρ_θ.

Fig. 2.

Fourier spectral amplitudes of Atchley's functions of the 3-solenoid domain of the antifreeze protein with sequence length N = 82 (PDB identifier: 1EZG). The peaks around frequencies n = 14, 21, 28, 35 belong to the harmonic series of the fundamental frequency rank n = 7, which appears as global maximum in the spectrum of Atchley's function 2 (top right) and as local maximum in the others. It corresponds to a periodic repeat T = 12 [computed using Equation (3)], in agreement with the actual structural repeat.

In order to assess the validity of the DFT predictions on a representative set, 352 protein sequences were selected among solenoid repeats (105) and globular proteins (247) without structural repeats from CATH (Pearl et al., 2003).

The proteins belonging to the two sets are listed on the web site. The solenoid repeats were chosen to cover the main repeat classes (all-α, α/β and all-β) with available structural information. Other known repeats are structurally and evolutionarily related to these major folds, e.g. HEAT and ARM repeats (Andrade et al., 2001). The large class of β-propeller proteins was excluded as these have to form closed structures and are not true solenoids. The representative set was divided into a training set and a test set (see Section 2).

3.2 Detection of solenoid repeats

For all the proteins in the training and test sets we computed the values of z_max and ρ_θ, as θ was varied from 1 to 5. The scatter plot in Figure 3 shows the θ-ratios for the final value θ = 2.1, obtained from our optimization procedure on the training set, versus the maximum z-scores for the sequences in the joint training and test sets, where solenoid proteins are represented by red crosses and non-solenoid protein domains by green crosses.

Fig. 3.

Maximum z-score of the amplitudes (z_max, x-axis) and optimal θ- ratio (ρ_θ, y-axis) are shown in the scatter plot for the joint training and test set of sequences. The separation of the regions with mainly non-solenoids (green crosses, bottom left) and solenoid repeat sequences (red crosses, top right) is remarkable, even if few proteins lay on the opposite side, in the vicinity of the optimal line separating the two sets. The result corresponding to the 3-solenoid domain of the antifreeze protein (PDB identifier: 1EZG) is shown as a blue square.

The large majority of solenoid proteins are characterized by high values of z_max and ρ_θ and are therefore found in the upper-right part of the diagram. As explained in Methods, in order to make this observation more quantitative we estimate an optimal line which discriminates between solenoid and non-solenoid sequences that can be used to make our algorithm predictive. We compute the signed distance of each representative point in the plot of Figure 3 from a set of lines, identified by the values of their slope and intercept (see Section 2). A positive distance will be interpreted as a solenoid-repeat sequence; while a negative distance will mark a non-solenoid one. The Matthews correlation coefficient C_M is then computed for each line in the set and the whole procedure is repeated for different values of θ. The procedure returns an optimal line (drawn in Fig. 3) corresponding to an overall Matthews correlation coefficient C_M=0.52, which allows for a very accurate determination of the existence of repeated motifs. In particular for the training set we obtain the optimal values θ=2.1, m=−0.787, q=6.591. In order to assess the predictive power of the algorithm introduced so far, we have considered its outcome on the test set (Table 1). It is remarkable to notice that the optimal line is again separating the region of solenoid proteins from the region of globular proteins with a very good accuracy.

Table 1.

REPETITA benchmark results for the training and test sets

	Training set	Test set	Overall
Sensitivity	70%	69%	70%
Specificity	85%	83%	84%
CM	0.54	0.51	0.52

In order to investigate the effect of the sequence profiles, we have repeated the experiments without the PSI-BLAST search. As expected, the results are far worse with overall 19% sensitivity and 81.4% specificity using the previously established optimal values (θ=2.1). Re-optimizing the parameters without profiles (new θ=3.4) does not improve the results sufficiently, with 57.5% sensitivity and 63% specificity overall.

While our approach combining sequence profiles and DFT gives remarkable results, DFT methods are able to identify well mainly tandem repeats with approximately the same size and sufficient number of copies. Many solenoid structures have repeats of variable lengths that reduce the height of the corresponding DFT peaks. Therefore, the method is not able to identify correctly few sequences which appear in fact as false positives in the plots of Figure 3. However, the stability of the results obtained with the two sets of proteins shows the robustness and the validity of the method which can then be used as predictor. For any new protein the position on the z_max–ρ_θ plane can be used to estimate the existence of repeat units. The distance from the optimal line will be used as a measure of the confidence of the estimation (see next section). As an example of the application of the algorithm, Figure 3 also shows the output of the REPETITA method for the 3-solenoid domain of the antifreeze protein (PDB code: 1EZG). The data for the 82 residue sequence of 1EZG has been computed using the web server.

3.3 Comparison to available methods

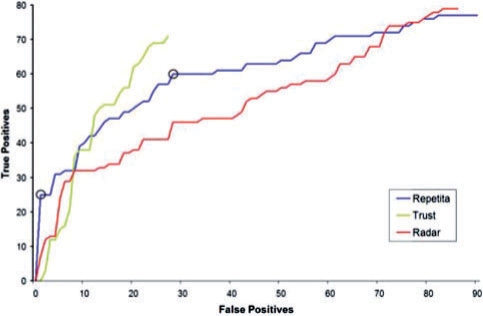
We compared the predictions of REPETITA for the total set, obtained by joining the training and the test set together, of sequences against two computational tools for the detection of protein repeats: RADAR (Heger and Holm, 2000) and TRUST (Szklarczyk and Heringa, 2004). Given the limited number of solenoid sequences, the full set was used to benchmark on a larger sequence database, as performance on both subsets is similar for REPETITA. It is also unknown whether RADAR and TRUST have been trained on some of the sequences. Both make use of self-alignment and while the first one validates repeats by iterative profile alignment, the second one improves the predictions applying the concept of transitivity in order to detect missed sub-optimal self-alignments. We chose to compare our method to these two algorithms in order to have a reference against a classical algorithm (RADAR) and a state of the art one (TRUST), both capable of addressing solenoid repeats without introducing gaps within or between repeats and not using a priori knowledge of repeat families. Results of this comparison are summarized in Figure 4: for every method predictions are ranked according to the parameter assessing how good the latter are. In the case of REPETITA, this parameter is the signed distance from the optimal line [given by Equation (9)]. In the case of TRUST and RADAR, we consider predictions where at least two repeat units have been detected. Figure 4 shows the number of false positives vs. true positives. Among all methods, REPETITA has the unique remarkable feature of yielding a virtual certainty in identifying solenoid repeats when the distance from the optimal line is larger than 1.0. On the other hand, if one wishes to identify a larger number of solenoid repeats, false positives are more and more present. Under these conditions, TRUST is performing better than REPETITA.

Fig. 4.

Comparison of REPETITA, RADAR and TRUST on the total set of sequences: the number of false positives (x-axis) is plotted against the number of true positives (y-axis). Predictions are ranked according to the values of the parameter measuring the reliability of the methods (for REPETITA, it is the signed distance from the optimal line of Fig. 3). Two black circles are drawn to highlight REPETITA predictions with signed distance thresholds at +1 and 0, respectively. Note that the first 25 predictions of REPETITA are all true positives.

3.4 Estimating repeat periodicities

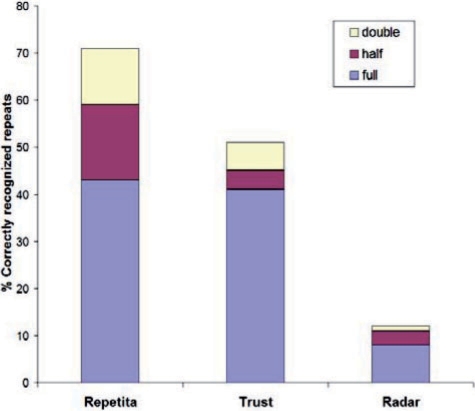
Once the presence of a solenoid repeat has been established for a given protein sequence, the next issue to address is periodicity. Within the DFT method, the estimation of the period is straightforward and can be derived from the frequency number of the peak with the largest amplitude z_max. The periods which would be estimated from nearby peaks naturally yield the confidence window for period prediction, which is defined as the interval [N/(n + 1),N/(n – 1)] if the frequency with the largest amplitude is n. The results for the set of 105 solenoid repeat sequences are summarized in Figure 5, together with their comparison with the predictions yielded by REPPER and TRUST on the same sequences. A given period is said to have been recognized correctly if it falls within the confidence window defined above. Results are shown for predictions based on recognition of full period and adding the possibility of recognizing just half or double periodicity. REPETITA performs much better than RADAR and at least as good as TRUST in recognizing full periods. REPETITA, however, scores better than TRUST if we allow for recognition also of half or double periodicity, which might prove meaningful for the periodicity of physicochemical properties of the sequence.

Fig. 5.

Detection of periodicity of repeats: comparison of REPETITA, RADAR and TRUST. Predictions were counted as correct if they were respectively within one residue of the full, half or double of the structural repeat length. REPETITA outperforms both RADAR and TRUST.

We observed the fact that the second function (scale 2) of (Atchley et al., 2005), which represents local conformational propensity, is most frequently seen corresponding to the predicted repeat period (shown in Fig. 5). An example of the peak list with corresponding estimated periods for the 3-solenoid antifreeze protein (PDB code: 1EZG) is shown on the web page. It is interesting to note that the method identifies the correct period for short repeats of up to 28 residues and after that breaks down the period in two halves. From a structural point of view, this corresponds to α-helix proteins where each helix, rather than pair, is seen as the structural repeat. Arguments can be brought in favor of this view being correct, as LRR repeats for example are known to sometimes contain half repeats at the N- or C-terminus. Taken together, periodicity results for the DFT method correspond to a substantially correct prediction.

4 DISCUSSION

4.1 Implications

The DFT method combined with sequence profiles has been shown to be competitive with other state of the art methods in recognizing difficult structural repeats. Furthermore, it definitely outperforms the existing methods tested in this work in the identification of the repeat length, once the solenoid sequence has been detected.

This is of relevance as DFT methods alone have, so far, not been widely used mainly due to the difficulty in discriminating globular from solenoid structures and to the difficulty of identifying repeats with variable length. Given a protein's power spectrum, it is often difficult to judge whether there is any signal coming from tandem repeats or rather just the presence of spurious internal similarity. The three novel strategies that we have adopted here proved instead to be promising.

The first is to use the five different similarity metrics proposed by Atchley, which cover a wider range of amino-acid characteristics, while most methods using the power spectrum are limited to hydrophobicity (Gruber et al., 2005; Murray et al., 2002). Depending on the protein sequence we find interesting signals in other features, which yield a wider range of spectra from which to choose.

The second innovation is the proposal of two mathematical parameters, the maximum z-score z_max and the θ-ratio ρ_θ, that allow an immediate and systematic comparison across different proteins and make possible to identify with a good reliability the periodicity of the repeats, employing the properties of DFT.

Finally, the third relevant improvement to the method comes from the inclusion of sequence profiles in place of the single protein sequence as input to the DFT of Atchley's functions. The use of a database search method such as PSI-BLAST (Altschul et al., 1997) to derive a sequence profile helps considerably to remove spurious hits. Solenoid proteins, even if degenerate in sequence, appear to be significantly more conserved in terms of amino-acid characteristics at any given position. Previous DFT methods used only the single query sequence to derive the features on which the power spectrum is calculated.

4.2 Possible improvements

In the present implementation, the DFT method considers the entire protein sequence at once. While this is justified for single domain proteins, it is an obvious disadvantage for long multi-domain proteins. In such cases the repeat signal is averaged through the different regions and likely to fall below the detection threshold. This issue can be addressed in future developments of the current implementation of REPETITA by running the DFT method with different sliding window sizes over the sequence. The choice of sliding window size will require some optimization, as will the threshold values required to discriminate globular from solenoid sequences. Intuitively, the longer the sliding window, the clearer the signal may become, at the expense of detecting shorter solenoid domains.

4.3 Reassessing local conformations

One of the most striking conclusions that emerge from our work is the evidence that the propensity to form repeated proteins is mainly encoded in the function shown by Atchley to be related to local conformational properties (scale 2). The importance of local information is a well established concept in molecular biology and it is underscored by the fact that many schemes for secondary structure prediction do well using just local sequence information. However in the last years there is a growing body of evidence that also global folding is strongly dictated by short range information: it was observed that in folding models [such as Go-models (Go and Scheraga, 1976)] which rely on the knowledge of the native state, a complete and successful folding can be achieved only by biasing the sampling of dihedral angles towards their native values (Hoang and Cieplak, 2000).

More recently, the importance of local interactions in determining protein structure was the basis of the ROSETTA structure prediction algorithm (Simons et al., 1999) which is possibly the best performing method in de novo structure prediction. This is also consistent with recent work by Fang and Shortle (Fang and Shortle, 2005) on knowledge-based local potentials. Chikenji et al. have shown that local structure preferences strongly shape up the protein folding funnel (Chikenji et al., 2006), whereas Tosatto has elucidated that when applied to model selection in protein structure recognition, torsion angle potentials present the strongest correlation with model quality (Tosatto, 2005; Tosatto and Battistutta, 2007). Our conclusion that even the presence of repetitive motifs in protein structures can be inferred by local properties is another step to understand their relevance for determining protein structure.

5 CONCLUSION

We have presented a novel method for the detection of solenoid repeats from their amino-acid sequence. The method is based on a DFT of the sequence using five different metrics and sequence profiles. Parameters and thresholds were derived to allow the reliable discrimination of solenoid repeats from globular structures and the identification of their periodicities. The comparison with two established methods demonstrates the performance of the method and highlights the relevance of local conformational preferences in solenoid repeats.