Learning partially directed functional networks from meta-analysis imaging data

Abstract

We propose a new exploratory method for the discovery of partially directed functional networks from fMRI meta-analysis data. The method performs structure learning of Bayesian networks in search of directed probabilistic dependencies between brain regions. Learning is based on the co-activation of brain regions observed across several independent imaging experiments. In a series of simulations, we first demonstrate the reliability of the method. We then present the application of our approach in an extensive meta-analysis including several thousand activation coordinates from more than 500 imaging studies. Results show that our method is able to automatically infer Bayesian networks that capture both directed and undirected probabilistic dependencies between a number of brain regions, including regions that are frequently observed in motor-related and cognitive control tasks.

1 Introduction

Since the advent of functional neuroimaging, the number of experimental studies published each year has grown exponentially, with a total of approximately 9500 fMRI studies published so far in English language journals alone (Derrfuss and Mar, 2009). Despite the use of standardized co-ordinate systems, scanning parameters, and analysis techniques, this wealth of imaging data still conveys a variable picture, in particular with respect to higher-order brain functioning. The need to consolidate results across studies thus calls for analysis techniques on the meta-level. Moreover, neuroimaging research is currently advancing from “simple” function–structure mapping in the brain to the analysis of complex cognitive processes and interdependencies between brain regions. These research questions cannot be addressed by isolated imaging experiments, but again require the concerted evaluation of imaging results across different cognitive tasks and experimental setups.

In recent years, a number of quantitative meta-analysis techniques have emerged. These methods facilitate the identification and modelling of individual brain regions that show a consistent response across experiments as well as the search for functional networks that capture multivariate co-activations patterns across several brain regions (Turkeltaub et al., 2002; Chein et al., 2002; Wager et al., 2003; Nielsen and Hansen, 2004; Nielsen, 2005; Laird et al., 2005a; Lancaster et al., 2005; Neumann et al., 2005, 2008; Eikhoff et al., 2008). Some of the most recently developed techniques thereby capitalize on the ability to simultaneously evaluate activation patterns across several experimental paradigms (Robinson et al., 2009; Smith et al., 2009; Toro et al., 2008).

In this paper we propose a new method for the discovery of partially directed networks of brain regions from meta-analysis data. Our method builds on the use of Bayesian networks for the representation of statistical dependencies. It takes as observational data co-activation patterns of brain regions across imaging studies and performs structure learning for directed acyclic graphs.

The detection of interdependencies between brain regions has recently become one of the most researched methodological questions. A number of network analysis techniques have been proposed both on the level of individual imaging experiments, including structural equation modelling (SEM) and dynamic causal modelling (DCM), and on the meta-analysis level, including fractional similarity network analysis (FSNA) and replicator dynamics (McIntosh and Gonzalez-Lima, 1994; Büchel and Friston, 1997; Goncalves and Hall, 2003; Friston et al., 2003; Neumann et al., 2005; Lancaster et al., 2005).

Our new method presented in this paper differs from these techniques in several aspects. First, unlike confirmatory methods such as SEM and DCM that require strong a priori hypotheses about interdependencies between brain regions, we follow an exploratory approach. That is, in the absence of any pre-defined model, we infer with our method possible functional interdependencies between brain regions from observational data alone.

Secondly, we wish to determine interdependencies between brain regions on the most general level possible, and thus employ a meta-analysis technique. Since the collective evaluation of individual fMRI time series is not workable on this level of analysis, we consider as observational data the co-activation of brain regions across several functional imaging studies.

Thirdly, existing network analysis techniques on the meta-level so far explore activation co-ordinates in search of undirected functional networks that represent multivariate co-activation patterns across brain regions. Going beyond these approaches, with our new method we focus on the directionality of multivariate relations between functional regions.

Fourthly, results of our method represent probabilistic dependencies between brain regions rather than functional or effective connectivities (as determined with SEM and DCM) or the mere co-activation of brain regions (as represented in FSNA and replicator dynamics networks). In other words, with our method we can infer from observational data whether and how the activation of one functional region statistically depends on the activation of others.

Mathematically, probabilistic dependencies are characterized by the concept of conditional probabilities. Multivariate probabilistic dependencies can be conveniently represented by graphical models where nodes in a graph represent random variables and links between nodes represent their statistical interdependencies. Out of the rich family of graphical models, we confine our investigations to the use of Bayesian networks. Although this choice restricts the application of our method to acyclic graphs, it was made for the following two reasons. Firstly, Bayesian networks belong to the class of directed graphical models, which enables us to investigate directed interdependencies between the activation of different brain regions. Secondly and most importantly, the structure of Bayesian networks can be inferred from observational data. In other words, we can learn the statistical interdependencies between the brain regions from activations observed across a number of imaging experiments. While for less restrictive graphical models, learning the underlying structure from observational data is impossible or requires a prohibitive amount of data, algorithms for learning the structure of Bayesian networks are well researched (Verma and Pearl, 1990; Chickering et al., 1995; Buntine, 1996; Krause, 1998; Pearl, 2000; Acid and de Campos, 2003; Steyvers et al., 2003; Chen et al., 2006, among others) and, as we will show in this paper, operate to a satisfactory level even when applied to relatively few observations.

However, the amount of available data remains a critical issue in the use of structure-learning algorithms, even for Bayesian networks. In our context, we face the problem of data sparsity, as every imaging study in our meta-analysis approach provides only a single data sample for the structure-learning algorithm. The investigation of the number of data sets required for learning a Bayesian network from observational data is therefore one of the key issues when assessing the feasibility of this method for our domain. As this question cannot be answered on theoretical grounds, we have addressed it with an extensive series of simulations, before applying the method to data obtained in real fMRI experiments.

A second question, specific to our context, pertains to the results of learning Bayesian networks when supplied with observational data collected from different experimental tasks. Although brain regions are generally assumed to exhibit a very specific functionality, their role in functional brain networks might differ across experimental paradigms and interdependencies between brain regions might vary accordingly. It is thus of great interest to investigate whether Bayesian networks can be extracted from meta-analysis data representing several experimental tasks. We addressed this question in a second set of simulations, investigating network learning from observational data that represent a ’mixture’ of partially overlapping Bayesian networks.

In the following we will provide the theoretical background of our work, introducing Bayesian networks and the principle of structure learning. We will then present the results of our simulations. Finally, we will demonstrate the application of the method in a coordinate-based meta analysis of a large cohort of fMRI studies automatically extracted from a neuroimaging database BrainMap (Fox and Lancaster, 2002; Laird et al., 2005b).

2 Methods

In this section we only introduce the basic principles of Bayesian networks and structure learning that are essential for the understanding of the paper. More comprehensive introductions are provided, for example, by Pearl (2000); Jensen (2001); Bishop (2006).

2.1 Bayesian networks

Bayesian networks are probabilistic graphical models representing a set of random variables and their probabilistic interdependencies. More formally, a Bayesian network is a directed acyclic graph (DAG) 𝒢 that comprises

• a set of nodes or vertices V in a one-to-one correspondence with a set of random variables X = {X_v : v ∈ V}

• a set of directed links or edges connecting these nodes.

Each variable X_i is assigned a conditional probability distribution P(x_i| Pa(X_i)), where Pa(X_i) denotes the set of parents of X_i. A variable X_j is said to be a parent of X_i in 𝒢 if there is a direct link pointing from X_j to X_i. If X_i has no parents, then this probability distribution reduces to the unconditional probability distribution P(x_i). In case of discrete random variables, the conditional probability distributions are typically represented in a conditional probability table (CPT). A Bayesian network then represents the joint probability distribution

$$P(x_1,\dots ,x_k)={\displaystyle \prod _{i=1}^{k}P(x_i|\text{Pa}(X_i)).}$$

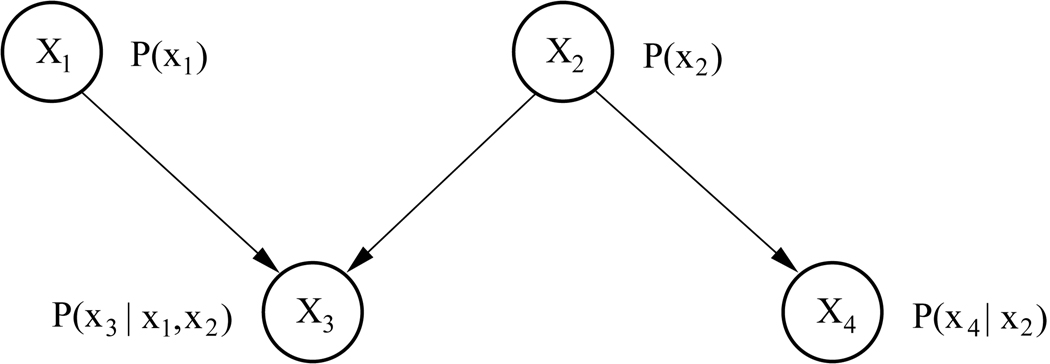
Consider for example the network in Figure 1, representing the joint probability distribution of four random variables X₁,…,X₄. Here, the probability distributions of X₁ and X₂ are unconditional, given that these two nodes do not have any parents. The probability distribution of X₃ is conditioned on its parents X₁ and X₂, and the probability distribution of X₄ is conditioned on X₂. Applying the product rule of probability, the joint probability distribution of all four variables represented in this network can be written as

$$P(x_1,x_2,x_3,x_4)=P(x_1)P(x_2)P(x_3|x_1,x_2)P(x_4|x_2).$$

Figure 1.

A simple Bayesian network representing four variables.

Thus, a Bayesian network represents a particular factorization of the joint probability distribution of a set of random variables.

2.2 Learning the structure of Bayesian networks

With our method we wish to identify interdependencies between functional regions given information about their common activation across experiments. This problem amounts to learning the structure of a Bayesian network, i.e. its underlying DAG, where the nodes represent the functional regions of interest and links encode their statistical interdependencies.

The theory for learning Bayesian networks from observational data has been described in the literature in great detail. For a discussion and comparison of the various approaches see, e.g., Verma and Pearl (1990); Chickering et al. (1995); Buntine (1996); Krause (1998); Pearl (2000); Spirtes et al. (2000); Friedman and Koller (2003); Steyvers et al. (2003); Acid and de Campos (2003); Acid et al. (2004); Chen et al. (2006).

In our implementation we used a so-called search-and-score method for network learning. In these methods a scoring function is used to describe the fit of the network to the observed data, and a particular search heuristic is employed to find networks with a high score. We employed the Bayesian score (Cooper and Herskovits, 1992; Heckerman et al., 1995; Chickering et al., 1995) which evaluates the log posterior probability of a network structure 𝒢 with parameters Θ, given observational data D. According to Bayes’ rule, this is

$$\text{log}P(𝒢|D)=\text{log}P(D|𝒢)+\text{log}P(𝒢)+c,$$

where c is a constant independent of the network structure, and log P(D | 𝒢 ) is the log marginal likelihood, averaging the probability of the data over all possible parameters of 𝒢. Specifically,

$$P(D|𝒢)={\displaystyle \int P(D|\mathrm{\Theta },𝒢)}P(\mathrm{\Theta }|𝒢)d\mathrm{\Theta }.$$

Note that including log P(D| 𝒢 ) into the scoring function has the effect of penalizing structures with too many parameters, leading the algorithm to choose the most parsimonious model that fits the data.

As search heuristic, we employed the Metropolis-Hastings algorithm (Metropolis et al., 1953; Hastings, 1970) to search the space of all possible network structures¹. In this approach, a new sample structure 𝒢^t+1 is uniformly sampled from a proposal density which contains the neighborhood of the current sample structure 𝒢^t. This neighborhood is defined as the set of all structures that differ from 𝒢^t by a single edge deletion, addition, or reversal. Thus, by administering small changes to an already examined graph structure, new candidate structures are derived and scored according to the available data.

2.3 The problem of network equivalence

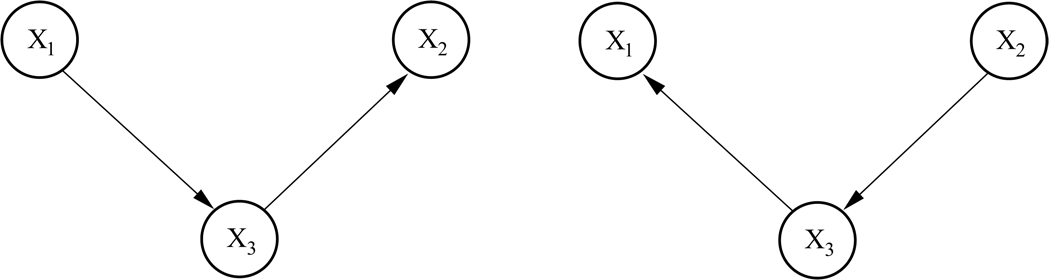
Learning the structure of a Bayesian network is limited by a property of Bayesian networks referred to as Markov equivalence. Consider, for example, the two networks given in Figure 2. The probability distribution P(x₁, x₂, x₃) factorizes according to the left graph as

$$P(x_1,x_2,x_3)=P(x_1)P(x_3|x_1)P(x_2|x_3).$$ (1)

Figure 2.

Two Markov-equivalent networks describing interdependencies between three variables.

Repeatedly applying Bayes’ rule, this factorization can be transformed:

$$\begin{array}{cc}P(x_1)P(x_3|x_1)P(x_2|x_3)\hfill & =P(x_1)\frac{P(x_1|x_3)P(x_3)}{P(x_1)}P(x_2|x_3)\hfill \\ \hfill & =P(x_1|x_3)P(x_3)P(x_2|x_3)\hfill \\ \hfill & =P(x_1|x_3)P(x_3)\frac{P(x_3|x_2)P(x_2)}{P(x_3)}\hfill \\ \hfill & =P(x_2)P(x_3|x_2)P(x_1|x_3),\hfill \end{array}$$

which is the factorization according to the right graph in Figure 2. Thus, both networks are consistent with the same joint probability distribution and, in other words, determine the same statistical model (Andersson et al., 1997). They are said to fall within the same Markov equivalence class. This is problematic for learning Bayesian networks from observational data, as without further knowledge, two networks modeling the same joint probability distribution cannot be distinguished on the grounds of observing this joint probability distribution alone. Differentiating between such networks would require either some prior knowledge, prohibiting certain directions in the graph, or the application of external interventions which would allow us to probe the network in order to test specific hypotheses about the structure (Steyvers et al., 2003).

Given the nature of our data, such external intervention is not possible and prior knowledge might often not be available. Thus, if we set out to infer directed interdependencies between cortical regions from observational data alone, what we can safely determine is a partially directed acyclic graph representing a Markov equivalence class of Bayesian networks. Specifically, in the absence of additional prior information, a particular graph resulting from structure learning needs to be converted into its corresponding Markov equivalence class, in order to rule out erroneous over-interpretation of some directed interdependencies between regions. Only directed connections surviving this conversion can be interpreted as directed statistical dependencies between cortical regions that are truly reflected in the training data.

A Markov equivalence class can be represented by a completed partially directed acyclic graph (CPDAG). In a CPDAG, all links that can be reversed without changing the equivalence class of the graph are represented as undirected links. Note that an entirely undirected graph that results from ignoring the directionality in some directed graph 𝒢 is referred to as skeleton of 𝒢.

The method for converting a DAG into its corresponding CPDAG that we employed in our implementation is described in detail by Chickering (2002).

2.4 Data preprocessing

The presented method for learning the structure of Bayesian networks requires as input a data set capturing the common occurrences of the events that are represented by the network nodes. For example, if we wish to learn a Bayesian network representing the statistical dependencies between cloudy weather, rain, and low air pressure, we will have to record for a number of time points or days, whether or not it was cloudy, and/or rainy, and whether or not this was accompanied by low air pressure.

In the context of fMRI meta-analyses, our input data set should contain information about whether or not, in a set of fMRI experiments, the brain regions of interest were found jointly activated. This requires the definition of such brain regions and the collection of information regarding their co-activation across experiments prior to network learning.

Different sources for obtaining the required information are conceivable. In some cases, regions of interest might be pre-defined by the research question addressed, and co-activation of these brain regions might already be discussed in the literature. However, we might also face situations where we want to investigate one or more particular cognitive tasks without specific prior knowledge about all brain regions involved and their typical activation patterns. This would require some additional preprocessing steps transforming what data is available into co-activation patterns of functional regions.

A number of meta-analysis techniques are available to perform this data transformation. The most commonly used data available for meta-analyses are lists of activation coordinates collected from a number of fMRI experiments. From such coordinate lists, functional brain regions can be modelled using variants of kernel density estimation for fMRI meta-analysis data, such as Activation Likelihood Estimation (ALE) (Turkeltaub et al., 2002; Chein et al., 2002; Laird et al., 2005a), Kernel Density Analysis (KDA) (Wager et al., 2004) or multilevel KDA (Wager et al., 2007). Where necessary, activation coordinates falling within the resulting regions can be further sub-clustered, e.g. by model-based clustering (Fraley and Raftery, 1998, 2002; Neumann et al., 2008) to gain a finer-grained segregation of functional brain regions. From a set of functional regions, a subset of the most frequently activated and hence most ’important’ regions can be automatically determined using, e.g., replicator dynamics (Schuster and Sigmund, 1983; Lohmann and Bohn, 2002; Neumann et al., 2005) or Fractional Similarity Network Analysis (FSNA) (Lancaster et al., 2005). Finally, a co-activation matrix can be formed for a set of functional regions by simply counting the number of pairwise activations of these regions across the investigated experiments.

2.5 Computational issues

In recent years, Bayesian networks have received great interest in a wide range of research areas such as machine learning, logic, and engineering. Thus, a wealth of academic as well as commercial software tools is available for the implementation of the described methods. Our particular structure-learning approach was implemented in Matlab making use of the open-source Matlab package Bayes Net Toolbox (Murphy, 2001). The package contains routines for different network scoring functions, search strategies, data sampling, and network transformations. As mentioned above, in all simulations and real-world applications further described, we used the Metropolis-Hastings algorithm for network search, the Bayesian score as scoring function, and the method proposed by Chickering (2002) for the conversion of DAGs into CPDAGs as the three building blocks of Bayesian network learning. Computation times for all experiments was in the range of seconds or minutes on a standard Linux workstation, depending on the size of the training data set and the number of nodes in the DAG.

3 Simulations

Prior to the application of the method to real-world data, we performed a set of simulations to assess the feasibility of the approach for the application to functional meta-analysis imaging data. We first focussed on the number of data sets that is sufficient for learning the structure of a Bayesian network from observational data. Data sets for simulations were generated as follows: For a particular number of nodes, a network was randomly chosen from all possible Bayesian networks. Data sets of different sizes were sampled from this network, and the CPDAG corresponding to the chosen network was determined. The sampled data sets then served as input data to the structure-learning algorithm. This way, we could assess whether or not the CPDAG corresponding to the original network could be fully or partially recovered by the network-learning process. Test-retest reliability of structure learning was assessed by repeated application to newly sampled data sets.

3.1 Small networks

Three Bayesian networks with 3, 4, and 5 nodes were randomly generated and data sets containing between 50 and 5000 observations were sampled from them. The CPDAGs of the randomly generated networks are shown in Figure 3.

Figure 3.

Equivalence classes (CPDAGs) of three randomly generated small Bayesian networks.

Although structure learning for Bayesian networks is a well-researched field, no general theoretical statement can be made about the size of the training data set required for a structure-learning algorithm to return a network of acceptable quality. One reason for this is that successful recovery of a network structure not only depends on the amount of available data, it is also crucially depended on the specific joint probability distribution underlying the network. In general, for networks encoding strong dependencies between random variables, structure learning up to the correct equivalence class should be straightforward, as such strong dependencies already become obvious from observing relatively few data sets. However, as the relationships between variables become more stochastic, i.e. less predictable from observational data, more training data will be necessary.

In our simulation we accounted for this fact by sampling the entries in the conditional probability tables for each network node with k parents from a Dirichlet distribution with parameter vector {α₁,…, α_2k} where α₁ = α₂ = … = α_2k = α. Specifically, for all random variables X_i represented in a network, P(x_i| Pa(X_i)) ~ Dir(α) where α > 1 encourages ’weak’ or more random dependencies between the variables and α ≤ 1 leads to CPTs encoding ’strong’ or more deterministic dependencies. For illustration, the CPTs of the randomly generated network consisting of three nodes X₁, X₂, and X₃ with more stochastic (α = 2) and the more deterministic (α = 0.7) dependencies are presented in Table 1.

Table 1.

Randomly generated CPTs encoding more deterministic (left) and more stochastic (right) dependencies between three nodes in a Bayesian networks. Entries in the table were sampled from a Dirichlet distribution with parameter α = 0.7 and α = 2, respectively.

	α = 0.7			α = 2
	P(X3)	True	False	P(X3)	True	False
		0.92	0.08		0.56	0.44
	P(X3)	True	False	P(X3)	True	False
P(X1|X3)
True		0.85	0.15		0.75	0.25
False		0.12	0.88		0.30	0.70
	P(X3)	True	False	P(X3)	True	False
P(X2|X3)
True		0.05	0.95		0.82	0.18
False		0.94	0.06		0.55	0.45

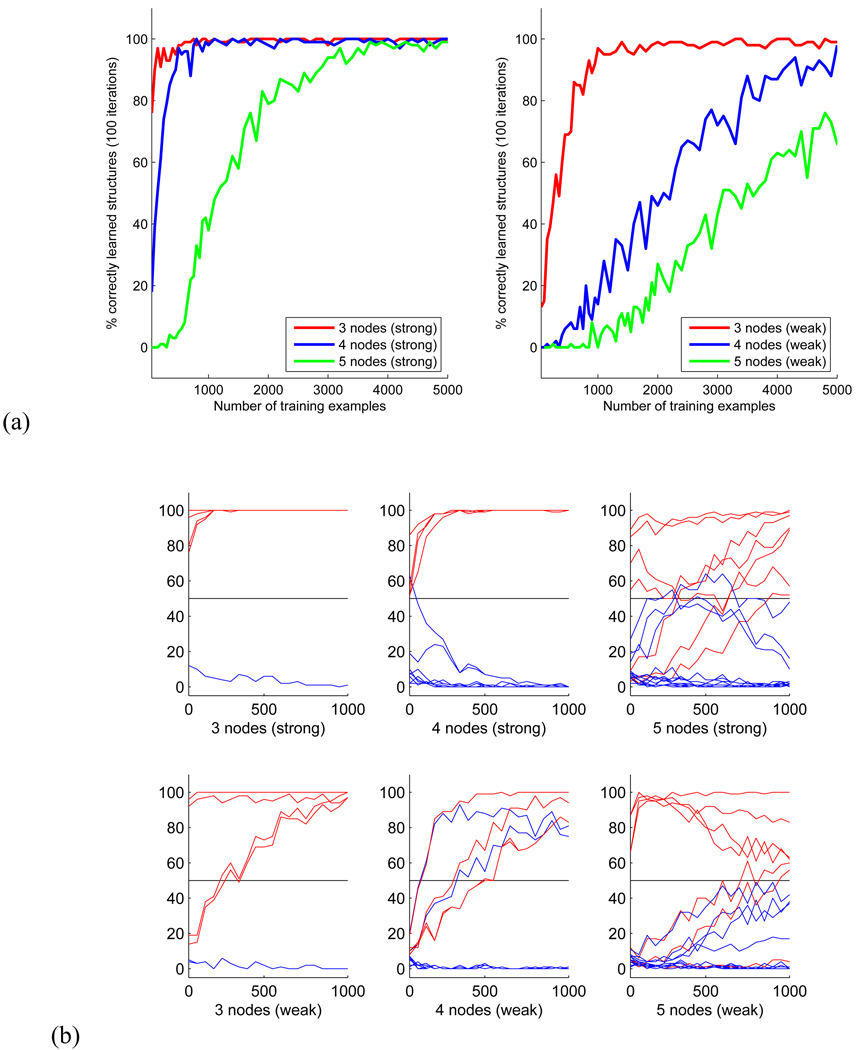
For each size of the data set, sampling and structure learning was repeated 100 times. Test-retest reliability of the structure recovery is presented in Figure 4a, where the number of correctly discovered CPDAGs is plotted against the size of the observational data set for networks with ’stronger’ and ’weaker’ dependencies between nodes. As expected, successful and reliable structure recovery required considerably more data for networks with more stochastic dependencies (Figure 4a, right) than for networks with more deterministic dependencies (left).

Figure 4.

(a) Size of training data sets required for learning a graph structure with up to 5 nodes. (b) Number of times each network connection was detected out of 100 trials of structure learning from randomly generated networks with 3 to 5 nodes. Connections belonging to the correct CPDAG are plotted in red.

Somewhat surprisingly, the simulations revealed that even for small Bayesian networks with 3 or 4 nodes, several hundred data sets are required to fully learn the correct CPDAG from observational data. Note that in addition to the use of the MH-algorithm, we performed a full search for the best-fitting network structure with 3 and 4 nodes. For all training data sets, the number of correctly discovered CPDAGs was identical with results obtained from the MH-algorithm.

We further analyzed the individual network connections of the recovered structures. Figure 4b pictures the number of times each connection was detected as part of the network structure plotted against the size of the data sets, again for networks with stronger and weaker dependencies. Connections belonging to the correct structures are plotted in red. In the following we consider a connection as correctly detected part of the topology, if it was part of the recovered CPDAG in more than half of the 100 trials, i.e. the relative frequency of detection was above chance.

In the 3-node network with strong dependencies, all connections were correctly detected even for the smallest data set of 50 observations. In the same network with weaker dependencies, detecting the connections between nodes 2 to 3 required at least 250 observations.

In the strong network with 4 nodes, all connections were correctly recovered from data sets of all sizes, with a single false positive connection from node 1 to 4 detected from the smallest data set only. In case of the weak dependencies, the recovery of correct connections required more data. The connections from node 4 to 1, 2 to 1, and between nodes 3 and 4 required data sets with at least 150, 350 and 500 observations, resp. In addition, the algorithm detected two false positive connections from node 1 to 2 and from node 1 to 4. Although these nodes were connected in the correct equivalence class, the direction of these connections was reversed after structure recovery.

In the network with 5 nodes, 2 out of 5 connections were correctly detected already from the smallest data set with both strong and weak dependencies between the nodes. These were the connections between nodes 1 and 3 and between nodes 2 and 4. The correct recovery of the remaining connections required considerably more data for both networks. However, the edge between node 4 and 5 in the network with weak dependencies was the only connection that could not be correctly recovered from less than 1000 observations.

Although these results convey a rather variable picture at first, we can draw two important conclusions. First, with the exception of one missing link, all connections could be detected with a reliability above chance from 1000 observations, with the majority of connections recovered from much smaller data sets. Second, for all small networks and data sets, no connection was falsely detected that did not belong to the skeleton of the correct structure. False positive connections that were detected in some trials were part of the skeleton of the correct CPDAG but with reversed directionality. Thus, for small networks, our method is able to detect the correct skeleton of a Bayesian network and at least some directionality of relations between the network nodes from data sets as small as 50 observations. This makes the method in principle suitable for the search of small partially directed functional networks from meta-analysis imaging data.

3.2 Larger networks

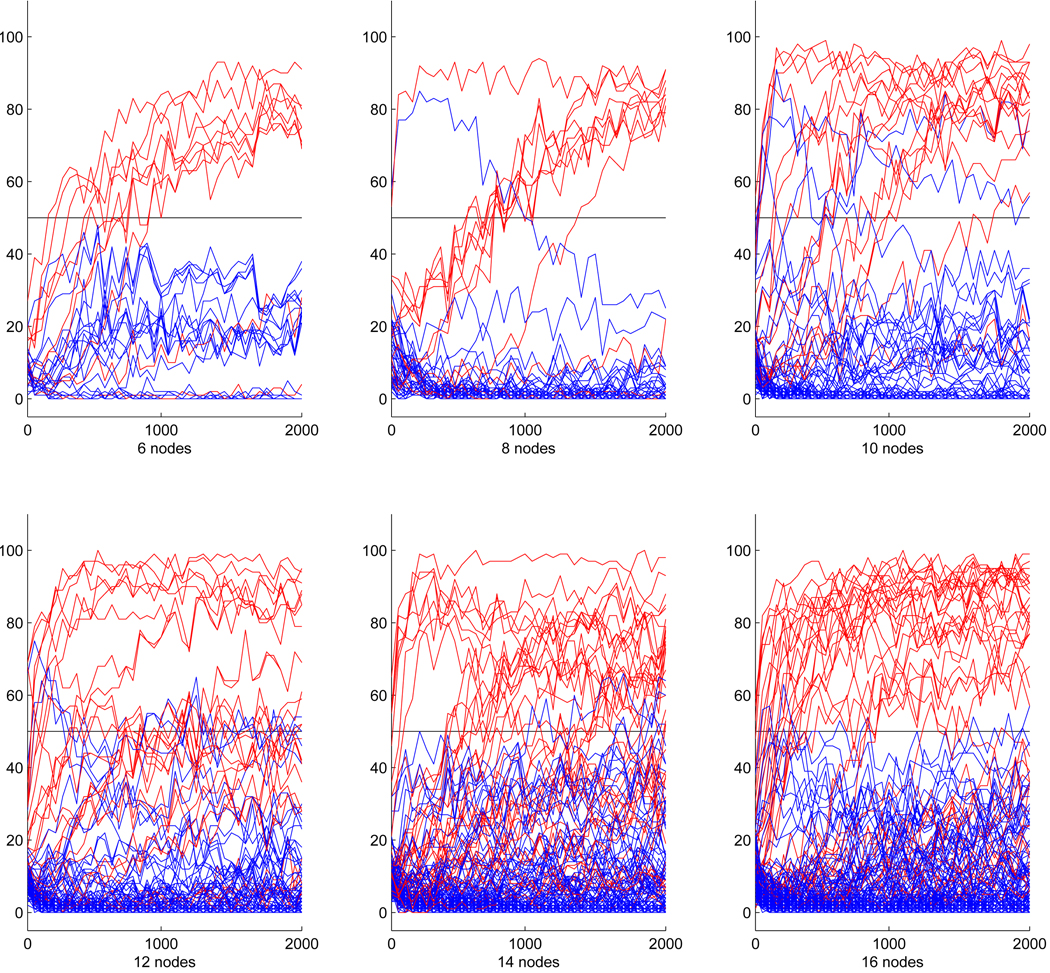
For randomly generated networks of 6 or more nodes, overall performance of the learning algorithm declined even in networks with strong dependencies. The complete correct equivalence class could not be detected even with up to 2000 data samples. This is not entirely surprising given the results from smaller networks and the super-exponential increase of the number of possible network structures with growing network size. However, despite this decline in overall performance, in networks encoding strong relationships between nodes, a considerable number of directed connections in the correct CPDAG could still be detected from under 2000 data sets with very few false positives. Example results for randomly generated networks with up to 16 nodes are presented in Figure 5. Red lines again mark edges that belong to the correct CPDAG.

Figure 5.

Number of times each network connection was detected out of 100 trials of structure learning from randomly generated networks with up to 16 nodes. Connections belonging to the correct CPDAG are plotted in red.

Like for smaller networks, the vast majority of connections in the CPDAG were correctly recovered for networks with up to 10 nodes, though in most cases several hundred observations were required to do so. A single false positive edge in the network with 8 nodes was only wrongly detected for data sets smaller than 1000 observations. In the 10-node network, two false positive connections were part of the solution even for larger data sets. Again, these were connections that belonged to the skeleton of the CPDAG, but their direction was reversed.

With growing network size, we observed a relative increase in the number of true connections that were not detected by the algorithm. Still, the learning algorithm only very rarely produced false positive answers: 5 out of 132 possible connections for the 12-node network, 3 out of 182 possible connections for the 14-node network, and 5 out of 240 possible connections for the 16-node network. All of these false positive connections belonged to the skeleton of the network.

In summary, our simulations for both smaller and larger networks show that essential parts of a Bayesian network can be detected from a few hundred observational data sets. Moreover, no connection that did not belong to the skeleton of the original CPDAG was falsely detected. Thus, even if we cannot expect a structure learning algorithm to fully recover a large Bayesian network from sparse observational data alone, major connections representing strong relationships between brain areas are still reliably detectable.

3.3 Partially overlapping network

In a second set of simulations, we investigated the behavior of the network-learning algorithm when supplied with data representing a mixture of different partially overlapping Bayesian networks. This situation is of particular importance in the context of fMRI meta-analyses, as the same brain regions might be involved in different brain networks, depending on the experimental paradigm. With the following simulations we thus wanted to investigate, whether network learning yields meaningful and interpretable results in situations where training data comes from such different sources. As will be seen in the following section, we faced such a situation in our real-world application, taking as input data activation coordinates obtained in different experimental paradigms.

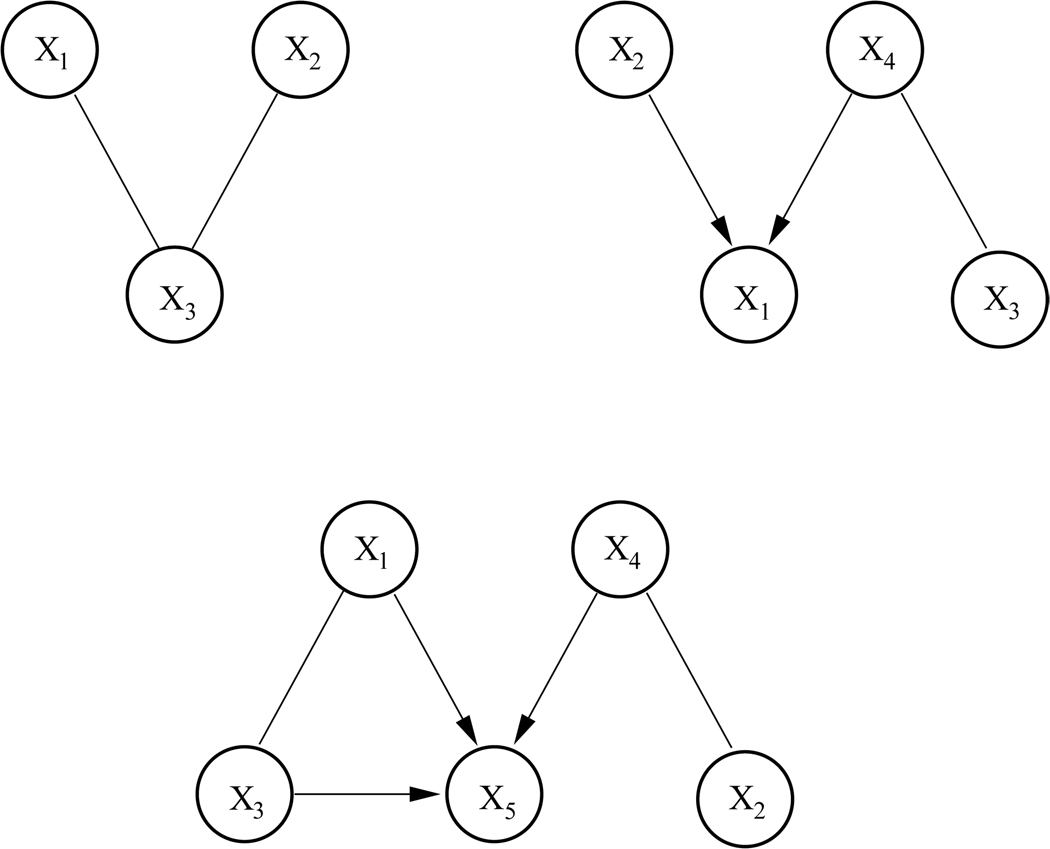
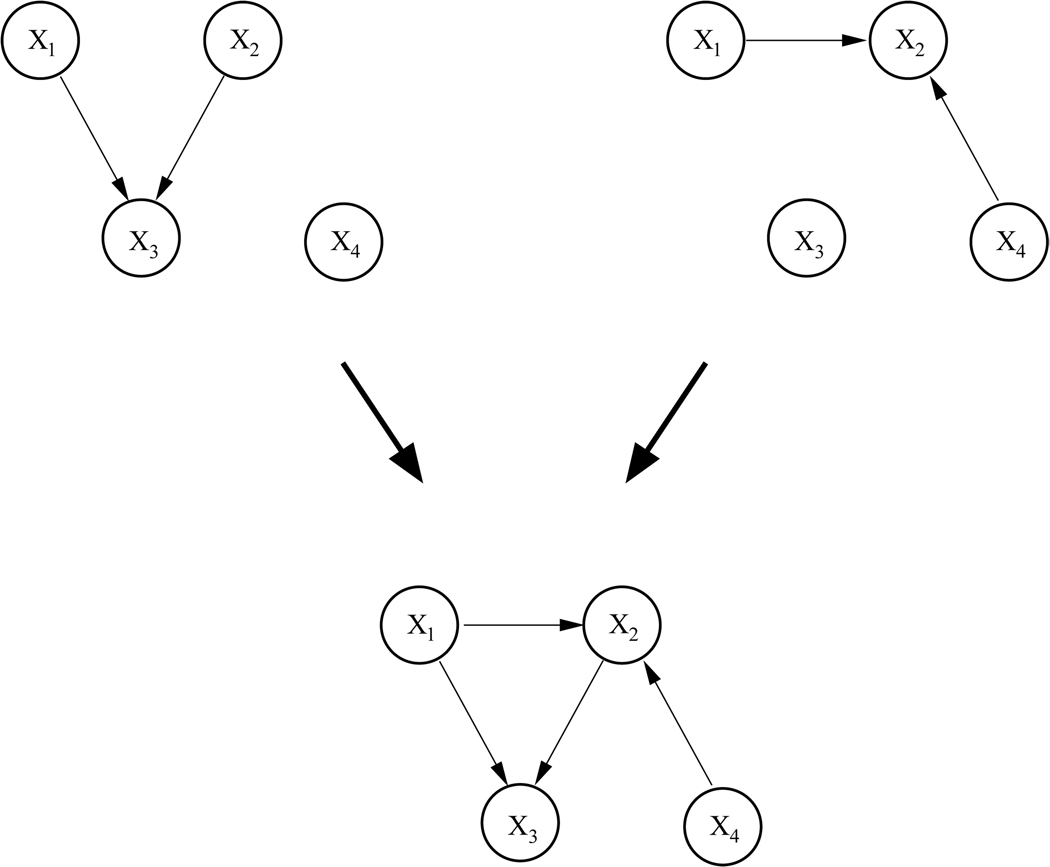
Two pairs of networks of four nodes were generated. They are shown in the top rows of Figure 6 and Figure 7, resp. The networks in the first pair have two nodes but no connections in common. Moreover, the union of the two networks yields a valid DAG, depicted in the bottom row of Figures 6. Note that for all three graphs the structure of the DAG and the corresponding CPDAG are identical. Thus, with this pair of networks we simulate a straightforward situation where data from two sources are not contradictory and the network structures could in principle be fully recovered.

Figure 6.

Top: Two Bayesian networks encoding non-contradictory statistical dependencies between 4 nodes. Bottom: ’Mixture’ of the two networks.

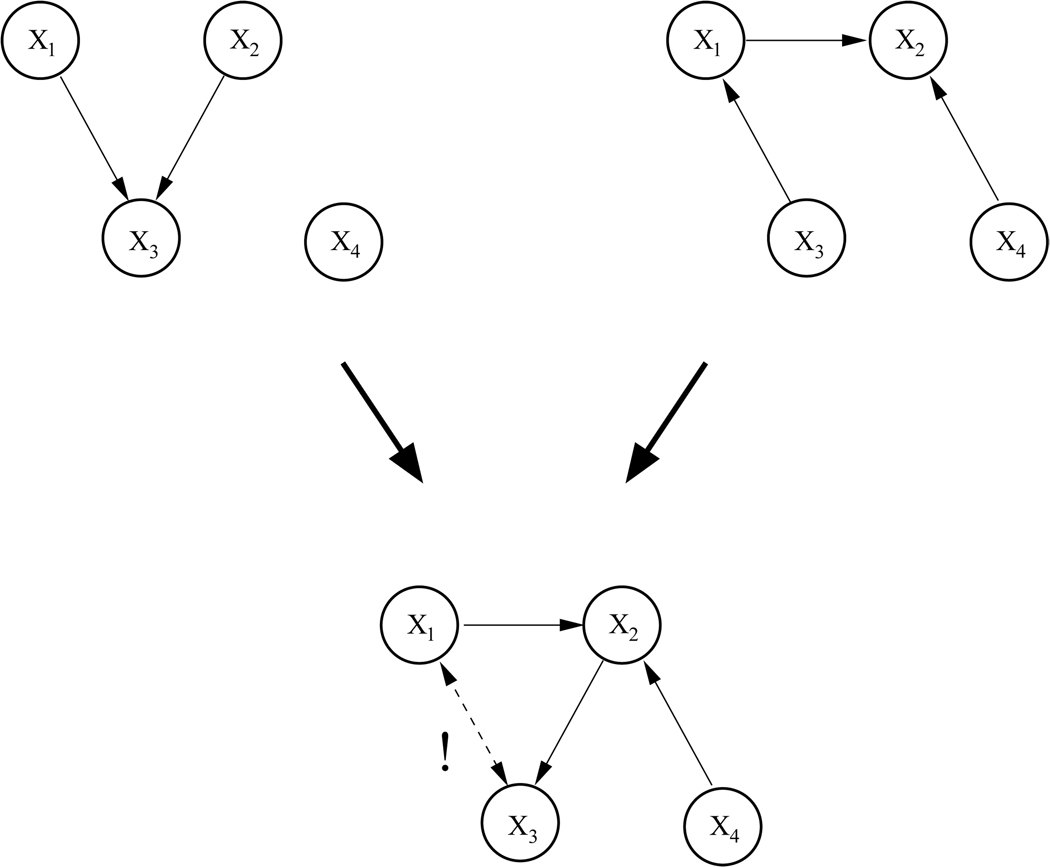
Figure 7.

Top: Two Bayesian networks encoding partially contradictory statistical dependencies between 4 nodes. Bottom: ’Mixing’ the two networks results in a graph that does not meet the requirements of a DAG.

The networks in the second pair have three nodes and one connection in common. However, this common connection between nodes X₁ and X₃ is of opposite directionality in the two graphs. Moreover, the union of the two networks yields a structure that is not a valid DAG, as it contains a cycle between X₁, X₂, and X₃. Note further that for the second network (right) the CPDAG differs from the DAG in that the connection between X₁ and X₃ is undirected. The directionality of this connection would therefore not be detectable by network learning. Thus, we are now facing a more complex situation where the training data contains contradictory information, network structures are not fully recoverable due to Markov equivalences, and the complete mixture of the two graphs contains loops.

Five datasets of 1000 observations were sampled from each pair with different mixing proportions. Specifically, in the first data set, 10% of the data points were drawn from the first (left) network, and 90% from the second (right) network. The other four data sets contained sample points at a ratio of 30 :70, 50 :50, 70 :30 and 90 :10 samples from the first and second network, resp.

For data sets with a very unequal ratio, one would expect the network-learning algorithm to return the network that is primarily represented in the input data set. For data sets with more equal proportion, one would hope for a learning result that, for the first pair of networks, represents the correct ’mixed’ graph. For the second pair, the resulting network should ideally contain all connections from both graphs that do not contradict each other or violate the validity of a DAG structure.

As in the previous simulations, network learning was repeated 100 times with newly sampled data sets and a connection were regarded as successfully detected, if the test-retest reliability of its detection was above 50%.

For the first pair, learning yielded the expected results. From the two data sets with a ratio of 70 :30 and 90 :10, the left DAG was fully recovered. From the two data sets with a ratio of 30 :70 and 10 :90, the right DAG was fully recovered. For the equal ratio, structure learning resulted in the correct ’mixed’ graph (Figure 6, bottom row).

For the second pair, learning performance was as follows: From the two data sets with a ratio of 90 :10 and 10 :90, the CPDAGs corresponding to the left and right DAG, respectively, were correctly recovered. Learning from the remaining data sets resulted in a graph containing the correct connections between X₁ and X₂, between X₄ and X₂, and between X₂ and X₃, that would be expected to be part of a correct ’mixture’. Moreover, a directed connection between X₁ and X₃ was detected. This result seems plausible, given that the connection with this directionality is present in the first graph and thus part of all input data sets, and the reversed directionality could not have been learned from the second graph due to graph equivalences. Thus, the algorithm recovered a DAG that comes closest to the true ’mixture’ of the graphs but, by omission of a single connection, does not validate the DAG property of an acyclic structure.

From these simulations we can draw the following conclusions: Learning the structure of a Bayesian network can yield meaningful results, even if the input data used for learning is drawn from different sources. If one source dominates others in the input data set, the Bayesian network underlying this dominating source will likely be discovered. If information from different sources is more equally distributed and not contradictory, the learned structure is likely to represent this information equally in the learning results. In case of contradictory information, network learning is likely to result in a structure containing all non-contradictory information of the different sources. Most notably, network learning from mixed sources did not introduce any connections that did not belong to the skeleton of the expected network or, indeed, return any false positive connection. Applied to our context, we would thus argue that Bayesian network learning can be meaningfully employed with data representing different experimental paradigms, even if the full brain network underlying this observational data might not always be completely detectable.

4 Application to functional imaging data

In order to apply our method to real-world imaging data, fMRI activation coordinates were extracted from the BrainMap database (Fox and Lancaster, 2002; Laird et al., 2005b). BrainMap provides results from published functional neuroimaging experiments as coordinate-based (x,y,z) activation locations in Talairach space, together with detailed information on the experimental setup. This facilitates the search for pre-defined regions of interest as well as for specific experimental paradigms, stimulus types, imaging modalities etc.

Given the results of our simulations, that is, the need for relatively large amounts of data for reliable structure learning, we aimed at the most extensive test data set possible, restricting the database search initially by imaging modality and experimental paradigm used. However, no data set representing an individual experimental paradigm in the database was sufficiently large to match the required size of a data set for reliable structure learning, as determined by our simulations. Specifically, the largest amount of data (296 experimental contrasts including 2475 activation coordinates) was available for the n-back paradigm. However, the number of data points surviving the necessary preprocessing steps as described below was not yet sufficient for the network learning algorithm to extract a Bayesian network with a test-retest reliability above chance. We therefore formed our test data set from a larger pool of data, namely all activation coordinates that were obtained by searching the database for imaging modality ’fMRI’. Coordinates that were already results of a meta-analysis were excluded. This procedure yielded 21136 activation coordinates from 2505 individual contrasts published in over 500 peer-reviewed papers.

4.1 Data preprocessing

As stated above, if only lists of activation coordinates are available, these lists need to be transformed into data sets representing the co-activation of brain regions. In the following we describe the particular methods used in our application. All preprocessing steps were implemented in C as part of the image analysis software Lipsia (Lohmann et al., 2001) with additional use of the software package MCLUST for model-based clustering (Fraley and Raftery, 1999, 2003). As previously mentioned, it is important to note that network learning does not intrinsically depend on these particular preprocessing steps and some of the following methods could be easily replaced by alternative approaches. Moreover, as a complete description of the applied techniques is beyond the scope of this paper, we will only illustrate the main principles of our preprocessing methods together with the results of their application. For a more comprehensive description we would like to refer the reader to the provided literature.

Activation coordinates were transformed into functional regions by a sequence of meta-analysis processing steps consisting of Activation Likelihood Estimation (ALE) (Turkeltaub et al., 2002; Chein et al., 2002; Laird et al., 2005a), model-based clustering (Fraley and Raftery, 1998, 2002; Neumann et al., 2008) and replicator dynamics (Schuster and Sigmund, 1983; Lohmann and Bohn, 2002; Neumann et al., 2005). Aim of this preprocessing sequence was the extraction of functional regions which form a potential network of manageable and interpretable size, and yet contain sufficient information about their co-activation to enter the structure-learning algorithm.

ALE

In ALE, activation coordinates are first modeled by 3-dimensional Gaussian probability distributions centered at their Talairach coordinates. Specifically, the probability that a given activation maximum lies within a particular voxel is

$$p=\frac{1}{(2\pi {)}^{3/2}{\sigma }^3}\text{exp}\left[\frac{-d^2}{2{\sigma }^2}\right],$$ (2)

where σ is the standard deviation of the distribution and d is the Euclidean distance of the voxel to the activation maximum. For each voxel, the union of these probabilities calculated for all activation coordinates yields the ALE value. In regions with a relatively high density of reported activation coordinates, voxels will be assigned a high ALE value in contrast to regions where few and widely spaced activation coordinates have been reported.

From the resulting ALE maps, one can infer whether activation coordinates reported from different experiments are likely to represent the same functional activation. A non-parametric permutation test is utilized to test against the null hypothesis that the activation coordinates are spread uniformly throughout the brain. Given some desired level of significance α, ALE maps are thresholded at the 100(1−α)th percentile of the null distribution. Topologically connected voxels with significant ALE values are then considered activated functional regions.

In our application ALE maps were thresholded at α = 0.0001. This α-level was already suggested in the original ALE work (Turkeltaub et al., 2002) and later shown to correspond to the application of FDR-corrected thresholding at p = 0.05 (Laird et al., 2005a).

In contrast to most previous meta-analyses, we chose a relatively small standard deviation ( σ = 3 mm) of the Gaussian, as it was previously observed that for very large numbers of activation coordinates, a small standard deviation is necessary to achieve the desired noise reduction and to reduce the list of activation coordinates to a number feasible for further processing (Neumann et al., 2008). Using the typically employed width of 10 mm FWHM in the present data set would in fact result in a single continuous ALE region covering almost the entire brain.

Applying ALE with σ = 3 mm and σ = 0.0001 resulted in 13 ALE regions containing 4769 of the original activation coordinates spread across different parts of the brain. Results are exemplified in Figure 8. Despite the small standard deviation of the Gaussian, most of the detected ALE regions were clearly too large to represent only a single functional region. The largest region had a volume of 76, 545 mm³ and spanned almost the entire left lateral cortex. For a meaningful application of the network learning algorithm, the ALE regions thus needed further sub-clustering, which was realized by means of model-based clustering.

Figure 8.

Axial and sagittal views exemplifying the result from ALE as first meta-analysis processing step.

Model-based clustering

Model-based clustering builds on the idea that clusters of points in 3-dimensional space can be represented by a mixture of 3-dimensional Gaussian probability distributions. In the context of neuroimaging meta-analyses, these points are activation coordinates in Talairach space. A mixture of Gaussians can thus be fitted to activation coordinates falling within the same ALE region in order to find a sub-clustering that best represents the spatial distribution of these coordinates. Fitting is performed by expectation maximization (EM) (Dempster et al., 1977), and the best fitting model is determined by means of the Bayesian information criterion (BIC) (Fraley and Raftery, 2002). Mathematical details of the method and its application in neuroimaging meta-analyses are provided by Fraley and Raftery (2002), and Neumann et al. (2008).

We applied the method to all 4769 activation coordinates that survived ALE, using 10 different model parameterizations and up to 50 possible clusters. The best model resulted in a sub-clustering of the ALE regions into 49 functional regions. However, since a partially directed network with 49 nodes would hardly be interpretable and, as our simulations suggested, structure-learning performance gradually declines with growing network size, we needed to further reduce the number of functional regions entering the learning algorithm. Thus, the final step of data preprocessing in our application was the selection of functional regions that should constitute the nodes of our network structures.

Recall that structure learning is based on the analysis of co-activation patterns. We would thus expect regions that are most frequently co-activated across the included experiments to provide the most informative data for the network learning algorithm. Such regions can be found as follows. From the coordinates falling within the 49 regions obtained, a co-occurrence matrix can be formed, recording for each pair of regions the number of co-occurrences across the individual experiments. This matrix can then be subjected to a replicator process.

Replicator dynamics

Based on the principles of natural selection, a replicator process determines a so-called dominant network or group of regions with the property that every region included in the group co-occurs more often with every other group member than with non-members. Using this mechanism we can select the most frequently co-occurring functional regions from our imaging data, providing the most informative data set to enter the structure-learning mechanism. Details on replicator dynamics and its application to fMRI single-subject data and in meta-analyses are provided by Schuster and Sigmund (1983); Lohmann and Bohn (2002); Neumann et al. (2005, 2006).

Figure 9 shows all coordinates falling within the most frequently co-occurring functional regions. These regions were determined by three consecutive applications of the replicator process to the co-occurrence matrix. Coordinates falling within the same region are displayed in the same color. The regions include part of the posterior medial frontal cortex (PMFC) primarily covering supplementary and presupplementory motor areas, anterior cingulate cortex (ACC), posterior parts of the lateral prefrontal cortex (LPFC) bilaterally, dorsal premotor cortex (PMC) bilaterally, left and right anterior insula (Ins) and thalamus (Thal), left and right anterior intraparietal sulcus (IPS), in the right hemisphere extending into precuneus, and the left cerebellum (Cer). For reasons of symmetry we additionally included the right cerebellum into the subsequent network learning. Note that determining these regions was a fully automatic process applied to data which were not pre-selected according to any specific experimental paradigm. It is thus not surprising that anatomical localization is somewhat blurred and some regions extend into neighboring areas.

Figure 9.

Axial and sagittal views of the 13 most often co-occurring regions determined by the replicator process, plus right anterior insula. Slices correspond to those presented in Figure 8.

In the first application, the replicator process identified a fronto-parietal network consisting of ACC, left and right LPFC, left anterior insula, and left IPS, regions that are regularly found in the investigation of cognitive control tasks such as Stroop or task switching and decision making paradigms (Vincent et al., 2008; Koechlin et al., 2003; Ridderinkhof et al., 2004; Forstmann et al., 2005; Zysset et al., 2001, 2006; Derrfuss et al., 2005, e.g.). The second replicator network primarily contained areas related to motor tasks: PMFC, left and right dPMC, left cerebellum. Additionally, the network contained right anterior insula and right IPS. The left and right thalamus formed the third network.

4.2 Bayesian network learning

Building on the results of the replicator process, four groups of different sizes were formed to enter the learning algorithm. Group 1, the smallest group, contained the 4 motor-related regions identified by the replicator process. As a 5th region the right cerebellum was added. Group 2 was formed based on the fronto-parietal network determined by the replicator process and consisted of ACC, left and right LPFC, left and right insula and left and right IPS. In group 3 all cortical regions from the first two groups were combined to form a network of 10 nodes. Finally, all 14 regions were combined to form group 4. For each group the data set was assembled containing all co-activation patterns of the group members from the individual experiments. Note that only patterns containing at least two of the group members were included in the training sets. This lead to data sets of 218, 377, 524, and 633 examples for groups 1 to 4 respectively. In 100 trials, 196, 339, 471, and 569 samples, corresponding to 90% of the total sample size, were randomly selected from each group, respectively, to form the training set. This way training conditions were comparable to those of the simulated data, with several hundred observations in each data set and 100 trials for each group to assess the reliability of the learning results.

Given our simulation results, we expected the structure-learning algorithm to perform with a high test-retest reliability at least for the two smallest networks. We again regarded a connection as successfully detected, if the test-retest reliability of its detection was above 50%. If not stated otherwise, connections with a detection reliability of 50% or higher are included in the graphs presented in the Figure 10 to Figure 12.

Figure 10.

Most reliably detected connections in the CPDAG of cortical areas determined from data set 1.

Figure 12.

Most reliably detected connections in the CPDAG of cortical areas determined from data set 3. Connections that were detected in 50%, 35%, and 25% of all trials are plotted in bold, medium, and thin lines, respectively.

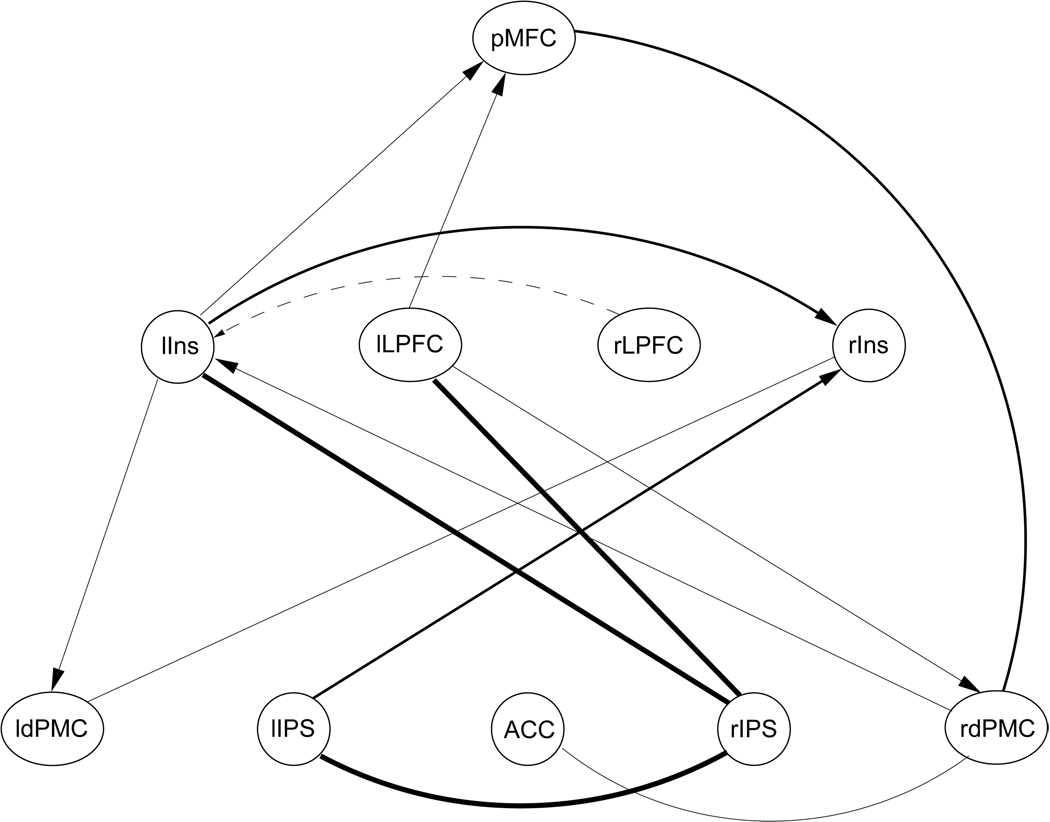
Learning the structure of the smallest motor-related network yielded a tightly and strongly connected graph in the majority of the 100 trials. The network structure is presented in Figure 10. Specifically, 6 out of 10 possible connections were detected with a reliability between 64% and 87%, with the most reliable detection rate of 84% and 87% for the directed connections between pMFC and left and right cerebellum, respectively. This high performance of the structure-learning algorithm is not entirely surprising, given that the members of the graph had been identified by the replicator process as frequently co-activated as an entire group. In fact, in about one quarter of all experiments included in the data set for group 1, at least three of the five regions were found co-activated. This data set can thus be expected to encode strong statistical dependencies between the individual nodes which, according to our simulations, can be reliably detected from data sets of even less than 100 observations. Note that the directionality between rdPMC and cerebellum bilaterally could not be determined due to graph equivalence.

Results for learning the structure of graph 2 and 3 are presented in Figure 11 and Figure 12, respectively. Both graphs primarily contained functional regions frequently found activated by cognitive control processes. As in our simulations, network learning performance declined with network size, despite an increase in the number of observations. In the second graph, 6 out of 21 possible connections were detected with a reliability of more than 50%, (maximum 68%). These include directed connections between left and right LPFC and right and left insula, respectively, connections between left and right insula and right and left IPS, respectively, whereby directionality between lIns and rIPS could not be determined, and a directed connection between left and right IPS. Interestingly, the ACC was not part of the learned topology, although it was activated in 37% of all experiments included in data set 2. In contrast, left and right IPS were only activated in 26% and 19% of all experiments, respectively. However, the network learning algorithm determined the statistical dependencies between these regions as well as their interdependencies with other network members. This nicely demonstrates that results of structure learning do not merely reflect activation frequencies but functional dependencies arising from co-activation of functional regions. Note that the strongest possible dependency on the ACC in the network was detected for the left IPS, but only with a reliability of 40% (dashed line in Figure 11).

Figure 11.

Most reliably detected connections in the CPDAG of cortical areas determined from data set 2.

Only very few interdependencies could be detected in group 3 with a test-retest reliability of 50% or higher. These dependencies include the connections between rIPS and lIns (64%), between rIPS and lIPS (59%), and between rIPS and lLPFC (60%). Reassuringly, these connections were also included in the graph learned from group 2, although directionality could no longer be determined in the larger network due to network equivalences. Figure 12 presents a graph containing all connections detected from group 3 with a test-retest reliability of at least 25%. Connections that were detected in 50%, 35%, and 25% of all trials are plotted in bold, medium, and thin lines respectively. Note that the right LPFC was not included in the graph even for an acceptance threshold of 25% reliability. Its strongest dependency was determined in relation to the left insula (dashed line in Figure 12), however, this connection was part of the learned topology in only 20% of all trials.

Reliability of structure learning further declined for the largest network. Only two connections could be detected with a reliability above chance: between rLPFC and pMFC and between rIPS and rCer. While these connections do not contradict any findings in the smaller networks, reliability of detection was as low as 54% and 51%, respectively. In contrast to our simulations, where in a network with 14 nodes, a subset of connections could still be detected with a reliability of well above 70%, this was not possible in our real-world application.

5 Discussion

In a series of simulations and a real-world application, we have demonstrated that structure learning for Bayesian networks can be used to infer partially directed functional networks from fMRI meta-analysis data. For small numbers of functional regions, directed and undirected statistical interdependencies can be reliably detected from a few tens or hundreds of observations. In larger networks, at least a subset of expected interdependencies is reliably detectable given sufficient amounts of data.

Our method has a number of advantages over existing network-analysis techniques. Most importantly, Bayesian network learning is exploratory in nature. This is in contrast to network analysis techniques commonly applied on the level of individual subject data. These methods, including SEM and DCM, rely on a confirmatory approach. That is, the structure of a connectivity model is not inferred from the data, but proposed a priori and subsequently tested against the available data. This facilitates the incorporation of prior knowledge, for example about existing anatomical connections, into the connectivity model. However, the number of possible networks grows super-exponentially with the number of nodes. For example, the number of network models capturing all possible connectivity patterns between five brain regions already exceeds one million. The application of confirmatory methods thus requires very strong hypotheses about probable connectivity patterns between brain regions, in order to rule out the vast majority of all theoretically possible network configurations and test the remaining ones against the available data.

We wish to point out, however, that in our real-world example, one non-exploratory step was introduced in the presented processing chain by manually grouping brain regions into groups that defined the search space for the network learning algorithm. While this was done for demonstration purposes, as it allowed us to investigate learning of differently sized networks, this manual step can of course be omitted in other applications, rendering the entire processing chain purely data-driven.

Secondly, our method captures the directionality in the association between functional regions by way of conditional dependencies, a well-defined statistical concept. This goes beyond earlier meta-analysis techniques which so far resulted in network structures only capturing undirected, though multivariate, co-activation patterns.

It is important to be clear that conditional dependencies between regions do not encode connectivity in the sense of directed information flow via direct or indirect anatomical links, or in the sense of temporal precedence of activation. Whether or not we can gain such information from fMRI measurements alone is still subject of a heated debate, given for example the low temporal resolution of fMRI time series and the complex and still not fully understood coupling between the obtained measurements and the underlying neural activity. However, even if such information is not attainable, from the results of our method we can derive important conclusions. For example, in a Bayesian network learned with our approach a directed link from node A to node B represents a statistical dependency such that activation of node B statistically depends on activation of node A. It is thus more likely that activation of region A has a direct or indirect effect on activation of region B in the investigated experimental setups than vice versa.

Further, it is important to note that directionality in a Bayesian network does not imply causal relationships. In fact, causal relationships in general cannot be inferred from observational data alone. This requires the application of external intervention (Pearl, 2000), a fact that holds true for all directed network models. One conceivable intervention in the context of functional imaging is the application of transcranial magnetic stimulation (TMS) which transiently alters the neuronal behavior in the stimulated circuitry. An example of this approach was recently presented by Laird et al. (2008), applying structural equation modelling to PET data acquired during TMS. Lesions in patient data could also be viewed as a form of external intervention, though this would not be controlled by the experimenter.

Recently, Zheng and Rajapakse (2006) employed structure-learning for Bayesian networks to extract directed connectivities from single-subject data. The method is comparable to ours except for the nature of the input data, fMRI time series averaged across voxels in pre-defined regions of interest. Using fMRI time series as observational data circumvents the problem of data sparsity, but conclusions drawn from such analyses are only supported by a single or a small number of subjects and are specific to the employed experimental paradigm and setup. Zheng and Rajapakse (2006) present applications of the method in the domains of natural language processing and cognitive control. Surprisingly though, the authors do not address the question of Markov equivalence, and the structure of their exemplified graphs suggest the existence of further graphs that fall within the same Markov equivalence classes. The extensive graphs presented in the example analyses might thus be over-specific in some of the directed connections they contain.

Our simulations suggest that a considerable number of dependencies between regions can be reliably learned even for networks with more than 10 nodes. However, for real meta-analysis data, learning larger networks resulted in relatively few connections and reduced reliability. This apparent discrepancy was most likely caused by two factors. Firstly, the number of observations was comparatively low in the real-world data sets: 471 and 569 observations were available in our meta analysis data sets for networks of 10 and 14 nodes. However, for a large proportion of connections determined in simulated networks of comparable size, reliability increased to a satisfactory level only with data sets of 1000 observations or more. Secondly, in our simulations training data for larger networks were sampled from networks encoding strong statistical dependencies between the nodes. In contrast, training data sets derived in our fMRI meta-analysis are more likely to only weakly capture the statistical dependencies between the individual regions. This is due to the broad and unconstrained selection of training data. While statistical dependencies between functional regions are most certainly different across different experimental paradigms, we included data from all experimental paradigms available in the database. This approach yields reasonably large data sets, yet it comes at a cost of less specific information captured in the training data. While our simulations provided reassuring results for Bayesian network learning from data of different origin, we would still expect the reliability of the learning to further improve when applied to data sets of comparable size but encoding a single or very closely related experimental paradigms and hence containing more specific information. At the time of writing, no experimental paradigm encoded in the database provided enough data points to allow for such learning with sufficient reliability. However, with the exponentially growing number of imaging studies published each year, this will be possible in the very near future.

In agreement with others, we regard the possibility to apply functional image analysis techniques simultaneously to several experimental paradigms as one of the major strength of meta-analyses (Costafreda, 2009; Robinson et al., 2009; Derrfuss and Mar, 2009; Smith et al., 2009). This way, research questions can be addressed that cannot be answered on the grounds of isolated imaging experiments alone. For example, Derrfuss et al. (2005) applied meta-analyses to directly compare activation patterns across tasks. Toro et al. (2008) and Robinson et al. (2009) developed new meta-analysis techniques for the detection of task-independent co-activation patterns for anatomically defined regions of interest. Most recently, Smith and colleagues applied independent component analysis to meta-analysis data in order “…to identify the major functional networks in the brain as estimated, and hence representative of, a significant proportion of all functional activation studies carried out to date” (Smith et al., 2009, p.1). Thus, such meta-analysis techniques, including ours, might provide a further step in the identification of the general principles of brain processing.

It is important to note that network learning in general is dependent on some starting assumptions, most notably the selection of regions entering the network learning process. Just like in confirmatory approaches where networks can only contain regions that are present in the a priori hypotheses, network learning in our approach can only assess interdependencies between regions that are represented in the input data. In both confirmatory and exploratory approaches, leaving out pivotal brain areas will lead to spurious or oversimplified results. For demonstration purposes, we chose a fully automated meta-analysis processing chain as means to select our input regions. While this approach includes large amounts of data and is not biased by human subjectivity, it is relatively uninformed and does not allow for the inclusion of specific regions of interest. Nevertheless, despite its “blindness”, the procedure selected and grouped together a highly plausible set of regions that are frequently found activated in motor-related and cognitive control tasks, tasks that make up large parts of the database the data was extracted from. Other selection strategies are conceivable based on prior knowledge derived from individual imaging experiments, anatomical knowledge or alternative meta-analysis techniques. For example, the method for the derivation of co-activations from meta-analysis data proposed by Toro et al. (2008) is comparable to our selection strategy, but additionally facilitates the search of co-activations between specific seed regions. In any case, well informed pre-selection strategies will prove essential for extracting neuro-anatomically realistic networks.

Finally, we wish to point out a number of current limitations of our method that will be subject of future research. Firstly, Bayesian networks encode partially directed statistical dependencies and thus, by definition, can only have acyclic topologies. Functional loops present in the brain will therefore not be detectable with our method. An alternative approach was recently presented by Storkey et al. (2007) who proposed to learn structural equation models including loops from fMRI time series. Other approaches such as the use of chain graphs that facilitate directed acyclic together with undirected cyclic structures are conceivable. However, learning these or even more complex graphical models requires considerable more sample points for the learning algorithm (Storkey et al., 2007; Ma et al., 2008) and is thus, at present, not applicable to meta-analysis data.

A second limitation of structure learning pertains to the inability to distinguish between graphs falling within the same Markov equivalence class. This means that, typically, the directionality of some connections in the learned graph cannot be resolved. Structure learning alone might thus not be sufficient to infer a full connectivity model from functional imaging data. Our future research will therefore be directed towards approaches that inform network learning about interdependencies that can be ruled out or defined, for example, on anatomical grounds, thus reducing the number of graphs within the same Markov equivalence class.

Conclusions

We have presented a new method for the detection of interdependencies between brain regions from functional imaging data. To our best knowledge, this is the first method on the meta-analysis level that provides information about the directionality of possible relationships between regions, drawing on the concepts of conditional probability distributions and structure learning in Bayesian networks. Our method thus represents a useful exploratory data analysis tool complementing existing approaches to the meta-analysis of functional imaging data.