The Shape of Motile Cells

Abstract

Motile cells — fan-like keratocytes, hand-shaped nerve growth cones, polygonal fibroblasts, to name but a few — come in different shapes and sizes. We discuss the origins of this diversity as well as what shape tells us about the physics and biochemistry underlying cell movement. We start with geometric rules describing cell-edge kinetics that govern cell shape, followed by a discussion of the underlying biophysics; we consider actin treadmilling, actin–myosin contraction, cell-membrane deformations, adhesion, and the complex interactions between these modules, as well as their regulation by microtubules and Rho GTPases. Focusing on several different cell types, including keratocytes and fibroblasts, we discuss how dynamic cell morphology emerges from the interplay between the different motility modules and the environment.

Introduction

Cells come in different shapes and sizes. The beautifully changing cell shape reflects dynamic cellular processes, most importantly remodeling of the cytoskeleton underlined by biochemical signaling. Cell geometry affects cell fate in processes such as cell growth and death [1], development [2] and tumor growth [3]. In this review, we focus on individual migrating cells [4] and do not discuss other phenomena, such as the shapes of dividing cells [5] or interacting cells within tissues [6].

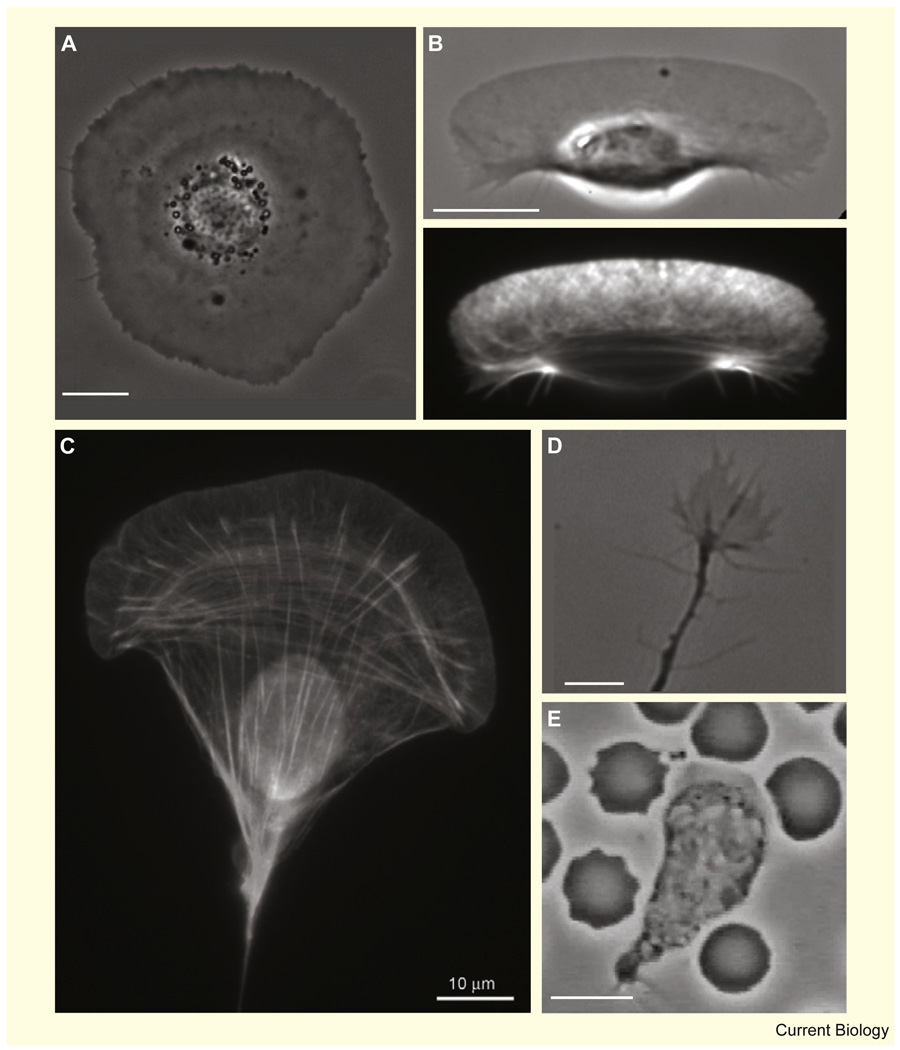
The diverse migratory behavior of different cell types is manifested by the spectrum of their shapes (Figure 1), from the simple circular shape of stationary cells spread on a flat surface [7] (Figure 1A) and the half-moon shape of motile fish keratocytes [8] (Figure 1B), through to more elongated fibroblasts [9] (Figure 1C) and the hand-like shape of neuronal growth cones [10] (Figure 1D), and on to the pulsating amoeboid shape of neutrophils [11] (Figure 1E). In the influential treatise On Growth and Form [12], D’Arcy Thomson suggested that the diversity of structures in morphogenesis can be explained by forces and motion and that biological forms correlate with mechanical phenomena. Here we attempt to apply this idea to individual cells.

Figure 1. Diverse shapes of motile cells.

(A) Phase contrast image of a live stationary keratocyte. The cell body is at the center, surrounded by a flat lamellipodium. (B) Phase contrast (top) and fluorescence (bottom) images of a motile keratocyte fixed and stained with phalloidin to visualize actin filaments. The broad lamellipodium at the front has a characteristic criss-cross pattern of actin staining, while bundles of actin appear near the cell body at the rear. (C) Fluorescence image of a cultured mouse embryo fibroblast fixed and stained with phalloidin. Fluorescence signal from the lamellipodial actin meshwork and from linear actin structures, including arcs at the base of the lamellipodium, linear stress fibers and peripheral bundles [94] is visible, together with auto-fluorescence from the cell nucleus (copyright: Tatyana Svitkina, courtesy of the Biology Image Library: http://biologyimagelibrary.com/imageID=48799). (D) A neural growth cone from a live rat commissural neuron. (Image courtesy of P.T. Yam, McGill University.) (E) A human neutrophil surrounded by red blood cells chasing a bacterium (image taken from a movie by D. Rogers, Vanderbilt University). Bars, 10 µm.

We begin this review by analyzing cell geometry and boundary kinetics phenomenologically, followed by a brief overview of the different types of motile appendages created by dynamic actin structures. We then present keratocytes and fibroblasts as relatively simple model systems for whole-cell motility research and discuss what is known about cell-shape determination in these cells. This is followed by a discussion of the role of biochemical regulators and microtubules in cell-shape regulation. Finally, we focus on motile cells in a 3D environment and highlight the similarities and differences between crawling in 2D and movement in 3D.

Geometry: Boundary Kinetics of a Motile Cell

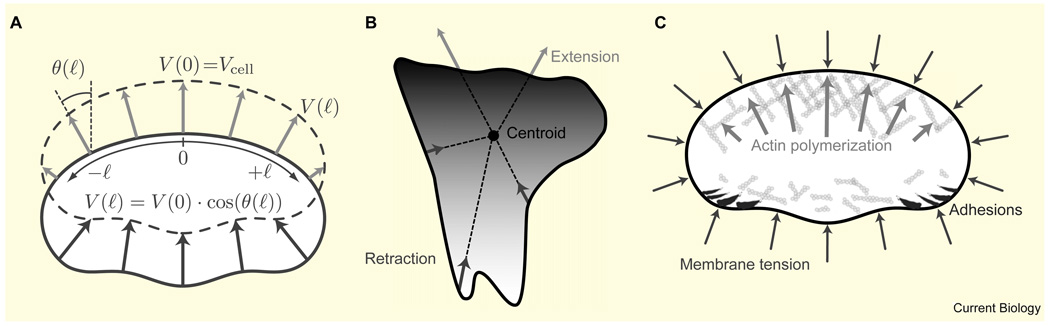
The shape of migrating cells (Figure 1) is defined by their dynamic boundaries, which, in turn, are determined by the local balance between expansion and retraction. Before diving into the details of the biochemical and biophysical processes governing the kinetics of the cell’s boundary, let us consider phenomenological descriptions of cell shape dynamics that are based on simple geometric principles. An elegant example is the graded radial extension (GRE) model [13], which describes the movement of one of the simplest migrating cells — a fish keratocyte. The GRE model describes a steady-state situation in which local extension of the cell boundary is perpendicular to the cell’s edge. To maintain steady shape, the magnitude of extension must be graded, from a maximum at the center of the leading edge to zero at the sides (Figure 2A). Similarly, at the rear the retraction rate is maximal at the midpoint and decreases towards the sides. According to a simple trigonometric formula (Figure 2A), this graded extension rate defines the cell’s shape. The question of how a cell regulates the extension rates along its boundary in such a coordinated fashion is left unanswered by this model.

Figure 2. Geometric and dynamic models of motile cell shape.

(A) The graded radial extension model [13]. The cell boundary of a keratocyte is shown before (solid) and after (dashed) displacement. In order to maintain constant shape, the locally normal protrusion (light) and retraction (dark) have to be graded along the boundary as shown. The extension rate as a function of arc length, l, is denoted V(l). Cell shape is determined from the local angle between the vector normal to the boundary and the direction of crawling, θ(l), which is given by the trigonometric equation shown. (B) The ‘rule-based’ model for cell shape [14]. At each position along the perimeter of the cell, the boundary extends/retracts (light/dark arrows) along radial spokes from the centroid of the cell. The extension and retraction rates are defined by a reaction–diffusion system with positive feedback for the protrusion signal and global inhibition of the retraction signal. Shading corresponds to the sum of protrusion–retraction signals, which at the edge is proportional to the local protrusive activity (dark, high protrusion; light, high retraction). (C) Force balance model of keratocyte shape [42]. Membrane tension generates a constant load along the cell boundary. The density of actin filaments is graded along the leading edge, so the force-per-filament varies. This force is minimal in the high-density regions at the center and increases toward the sides of the cell where filament density is low and filament growth is stalled. The disassembled actin network is pushed forward at the rear by membrane tension. The adhesion complexes at the rear sides inhibit the lamellipodial actin network and thus contribute indirectly to a higher actin density at the center front.

More complex movements and shapes, which are not necessarily in steady state, can be described by a rule-based geometric model, in which a cell is modeled by its perimeter [14] (Figure 2B). The local rates of protrusion and retraction are regulated by a model that incorporates local stimulation and global inhibition of protrusive activity. Evolution of local protrusion is calculated from lateral propagation and decay of protrusion signals, with a stochastic positive feedback loop accounting for increased protrusion in already-protruding regions. The retraction signal is specified by a simple global inhibition rule, in which the retraction rate is constant along the boundary and proportional to the total protrusive activity. For computational simplicity, rather than extending in a direction locally normal to the boundary, the points along the cell perimeter either protrude or retract along imaginary spokes radiating from the centroid of the cell (Figure 2B). This rule-based model was able to reproduce the characteristic shape and trajectory of amoeboid Dictyostelium cells. Furthermore, by simply varying the parameters, the model was also able to mimic other motile cell shapes with surprising reliability; addition of focal adhesions, which were modeled as anchorage points resisting retraction, resulted in wedge-shaped cells with tails, characteristic of fibroblasts. Alternatively, an increase in the protrusive positive feedback was able to produce stable and persistent half-moon keratocyte-like shapes.

These models illustrate that dynamic cell shapes can emerge from relatively simple boundary kinetics and that few changes in the distribution of protrusion/retraction along the boundary are sufficient to recapitulate the observed diversity in cell shapes. To advance beyond these phenomenological descriptions we need to consider the underlying biophysics and biochemistry and, in particular, the dynamics of the actin cytoskeleton.

Shape and Movement on Fine Scales

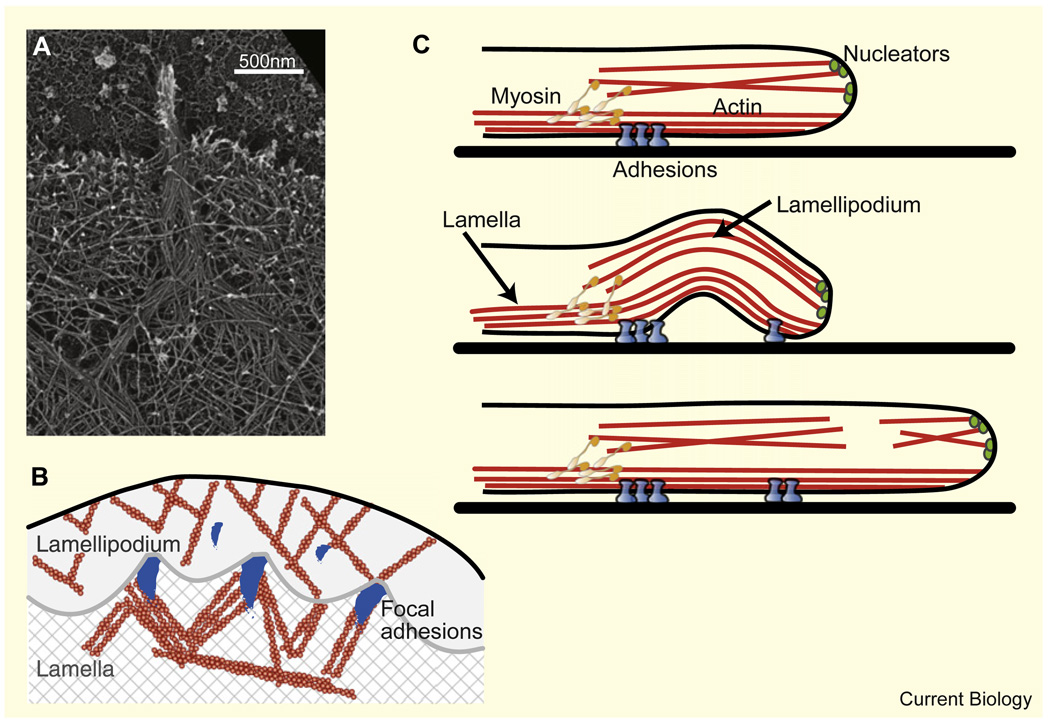
Cell shape is largely determined by the cooperative dynamics of the actomyosin cytoskeleton, adhesions and the cell membrane within the motile appendages at the cell periphery, so the fine-scale geometry of these appendages plays an important role in cell-shape determination. One of the better understood cytoskeletal structures is the lamellipodium [15], a broad and flat network of actin filaments (Figure 3A). The lamellipodium is usually many microns in length and width, but only ~0.1–0.2 µm high [16]. Within the lamellipodium the actin cytoskeleton forms a treadmilling dendritic array [17,18]: nascent filaments nucleate from Arp2/3 complexes at the side of existing filaments and elongate until growth is terminated by capping proteins. ADF/cofilin action coupled to ATP hydrolysis facilitates actin filament disassembly, and actin monomer diffusion — coupled with reactions with profilin — recycles the monomers to the leading edge. The front-to-rear length of the treadmilling lamellipodial actin network is governed by the dynamics of this biochemical cycle in which actin is being continuously converted from monomer to polymer and back again [19,20].

Figure 3. Dynamic actin structures at the cell periphery.

(A) Platinum replica electron micrograph of the leading edge of a cultured B16F1 mouse melanoma cell showing a branched network of actin filaments in the lamellipodium and parallel bundles of actin filaments in the filopodium. Filopodial filaments begin in the lamellipodium and converge to form a bundle (copyright Tatyana Svitkina, courtesy of the Biology Image Library: http://biologyimagelibrary.com/imageID=48811). (B) Schematic depiction of the boundary between a fibroblast’s lamellipodium and lamella as observed in [33]. The boundary is demarcated by periodically spaced focal adhesions and attains a characteristic concave arc shape between them. Nascent focal adhesions appear in the lamellipodium ahead of the boundary. (C) Suggested leading edge dynamics of a motile fibroblast [34]. The lamellipodium sits on top of the lamella (upper panel). Myosin motors pull on the lamellipodial network causing it to buckle and retract (middle panel). Consequently, the lamellipodium breaks, and then resumes growth at the leading edge, resulting in protrusion (lower panel).

The actin filaments in the lamellipodium are oriented with their barbed ends toward the leading edge [17], and this arrangement is crucial for maintaining lamellipodial structure. This preferred filament orientation could arise, according to 2D theoretical models, from suppression of capping at the very leading edge; filaments growing away from the leading edge are rapidly capped, while forward-growing filaments are protected and ‘win’ resources such as Arp2/3 [21,22]. This, of course, requires actin nucleators to localize to the leading edge. One attractive possibility is that myosin motors transport these nucleators in the direction in which barbed ends point [23], providing a positive feedback loop that can maintain both barbed ends and nucleators at the front of the cell.

Recent simulations of dendritic actin arrays demonstrated that the mechanics of the flexible filaments and the membrane ensure that locally the lamellipodial leading edge is almost straight [24]. Another study [25], however, suggests that if activators of actin polymerization, such as the GTPase Cdc42 and phosphatidylinositol (4,5) bisphosphate (PIP₂), which diffuse in the membrane, are incorporated into the picture, then a positive feedback between actin growth, membrane curvature and activator density could lead to a locally wavy leading edge and even instabilities — precursors of filopodial protrusions. One recent study [26] reports observations of such non-random undulating leading edge dynamics and suggests that the shape fluctuations result from more complex self-organizing oscillatory dynamics involving GTPases, in which RhoA is activated during protrusion, while Rac1 and Cdc42 are activated with a delay of ~40 seconds behind the leading edge, reinforcing protrusion transiently through control of adhesion dynamics. The recently discovered actin polymerization waves, emerging from yet another set of mechanochemical interactions [27,28], could also lead to local undulations of the cell’s leading edge.

Why is the lamellipodium flat? Perhaps the simplest idea to explain the thinness of the lamellipodium is that some molecular complex spans the lamellipodium and, in a way, ‘staples’ the dorsal surface to the ventral one [7]; however, there is no evidence for the existence of such a complex. A different model suggests that myosin-powered contraction contributes to lamellipodial flatness by pulling the lamellipodial network toward the substrate and thus restricting its height [29]. Alternatively, actin-filament growth may be confined to the proximity of the ventral surface either because of inhibition by factors in the dorsal membrane or due to the need for activation in close contact with adhesion complexes at the ventral surface. Finally, an elegant biophysical model [30] proposes a positive feedback loop in which polymerizing barbed ends push and curve the leading edge membrane. Hypothetical membrane-associated actin-nucleation complexes could have curved membrane domains that preferentially target them to membrane regions with high curvature. These nucleation complexes will therefore concentrate at the curved leading edge and focus polymerization in the forward direction there. This proposed feedback process could also explain the preferential orientation of filaments with their barbed ends directed toward the leading edge.

Curiously, when Arp2/3 complexes are activated every-where in the cell (and not just at the leading edge) the actin network swells up [31].

The protrusive appendages in many cells consist of two overlapping but molecularly and functionally distinct actin networks – the lamellipodium and the lamella [32]. The lamellipodium assembles at the leading edge but then disassembles within a few microns. It is coupled to a second network, the lamella, where myosin contraction is integrated with substrate adhesion. Interesting shapes and dynamics associated with the interaction between these two networks can be gleaned from two recent studies. Alexandrova et al. [33] observed a boundary, demarcated by periodically spaced focal adhesions, between the lamellipodium and the lamella (Figure 3B). The boundary attained a characteristic concave arc shape between focal adhesions, as if the rapid retrograde flow of the lamellipodial actin network, created by polymerization at the membrane, breaks against the adhesions, which act like jetties, and arches between them. Interestingly, nascent focal adhesions appeared in the lamellipodium ahead of the boundary, and within seconds, the boundary advanced locally towards these new adhesions, concurrent with local protrusion of the lamellipodial leading edge. Giannone et al. [34], on the other hand, collected data suggesting that the lamellipodial actin network lies above the lamellar network (Figure 3C) and that myosin clusters periodically pull the lamellipodium rearward relative to the lamella, which leads to buckling upward of the whole leading edge. The resulting breaking and re-growth of the lamellipodium lead to cycles of protrusion–retraction, harkening back to the classic descriptions of protrusion–retraction cycles in the early Abercrombie studies [35].

In many cases, the lamellipodial leading edge is interspersed with filopodia — bundles of actin filaments that are tightly packed together and protrude forward (Figure 3A). Current evidence shows that lamellipodial filaments can bend together and zipper into such parallel bundles [36]. What regulates the number and length of bundled filaments and their spacing along the leading edge? Recent experiments [37] and modeling [38,39] shed some light on possible answers, suggesting, for example, that the number of bundled filaments could be a compromise between the delivery of necessary proteins to the filopodial tip and mechanical stability of the filopodia: it is harder to supply proteins for thicker bundles but thinner bundles could buckle. Another study [40] suggests that competition between the bending and adhesion energies of filaments plays an important role in filopodia formation, by demonstrating that the spacing and thickness of filopodia-like structures in vitro is largely determined by two parameters — the length of the filaments and the lamellipodial mesh size, which determines the distance between filaments. Longer filaments that are closer together are easier to bend into a parallel bundle and thus can form a filopodium.

The Simplest Motile Cell – A Fish Keratocyte

Keratocytes are an ideal model system for investigating the mechanisms of cell-shape determination because they maintain nearly constant cell shape, speed, and direction over many cell lengths [41]. Keratocytes assume a stereotypical shape with a broad flat lamellipodium characterized by rapid actin dynamics and turnover [15]. The microscopic actin-growth dynamics predict a locally straight boundary along the cell’s leading edge [24], but additional ingredients are required in order to understand how the characteristic fan-shaped lamellipodium (Figure 1B and Figure 2C) evolves and how the cell boundary curves on cellular length scales. As mentioned earlier, the GRE model (Figure 2A) describes the kinematics of keratocyte shape, but does not explain what determines cell shape in the first place or how the molecular dynamics generate the graded extension rates responsible for maintaining cellular geometry. Two observations — that cell area is constant [42], and that the density of filamentous actin along the leading edge is graded [43] — led to a proposed mechanism of keratocyte shape regulation [42] (Figure 2C). This mechanism is predicated on previous observations that the lamellipodial actin network treadmills, with net assembly at the leading edge and net disassembly toward the rear [15]. Polymerizing actin filaments push the cell membrane from within, generating tension which rapidly equilibrates across the fluid membrane. At the center of the leading edge, where actin-filament density is high, the membrane resistance per filament is small, allowing filaments to grow rapidly and generate protrusion. As filament density gradually decreases toward the cell sides, the load force per filament due to membrane tension increases. As a result, local protrusion rates decrease smoothly from the center toward the sides of the leading edge. Assuming that protrusion is locally perpendicular to the cell boundary, this implies that the sides of the leading edge lag behind the center, causing the leading edge to become curved as observed (Figure 1B and Figure 2C). Finally, actin polymerization is stalled at the far sides of the cell, which therefore neither protrude nor retract. At the rear of the cell, where the actin network disassembles, membrane tension, assisted by myosin contraction, crushes the weakened network and moves actin debris forward, thereby retracting the cell rear (Figure 2C).

Overall, the picture is very simple (Figure 2C): actin-network treadmilling drives from within the forward protrusion of an inextensible membrane bag. This basic mechanism appears to be sufficient to explain the persistent and coordinated movement of keratocytes without incorporating signaling molecules or microtubules, suggesting that, at least in keratocytes, these elements are dispensable or redundant; indeed, microtubules are not necessary for keratocyte movement [41]. The model highlights the important global regulatory role of membrane tension in cell shape: local actin assembly at the leading edge and disassembly at the cell rear are both modulated and coupled by forces imposed on the actin network by the membrane.

The graded distribution of actin filament density is crucial for generating graded protrusion along the leading edge in this model. An attractive hypothesis is that this spatial grading results from a self-organization process [43,44]. Along the leading edge, growing filaments compete for resources (the molecular identity of which is unknown, but Arp2/3 and/or VASP may be involved) to branch out nascent filaments, while existing filaments get capped and lag behind the protruding edge. At the rear corners of the cell, the density of actin filaments is reduced, perhaps by the large adhesion complexes there that appear to compete with actin-polymerization processes for some molecular resource, the identity of which is again unknown, although VASP is a likely candidate [43] (Figure 2C). Filaments at the center of the leading edge can out-compete filaments at the sides because they are not inhibited by the adhesions at the sides, so the actin density peaks at the center. Together these processes can yield an inverted parabolic actin-filament distribution, as observed experimentally [42,43].

Myosin does not seem to be crucial for movement; keratocytes continue to move after myosin inhibition, albeit more slowly and with less regular shapes [42]. However, the myosin molecules that are swept to the rear as the cell moves forward do contribute to the motility process. Myosin contracts the actin network weakened by depolymerization, probably contributing to the process of pulling the cell body forward [45] and to pulling the cell sides inward, thereby containing their spread, as well as contributing to actin-network disassembly, leading to faster actin turnover. In addition, without myosin stationary keratocytes cannot polarize and start moving [46–48].

An adhesion module must act together with the minimal ‘actin treadmill in the membrane bag’ module to translate actin treadmilling into forward translocation of the cell. Adhesion complexes form at the very leading edge and remain nearly stationary with respect to the substrate as the cell moves forward. In many cases, it appears that adhesion is graded — stronger at the front, and weaker at the rear [49,50]. How this graded adhesion is generated and regulated is unclear. One attractive hypothesis [49,50] is that rapid assembly of integrin, talin, vinculin and other adhesion molecules takes place at the front where nascent actin network forms, followed by slower aging of the adhesion complexes, which leads to weakening of adhesions as they approach the cell rear.

Cell area was found to be intrinsic to each cell and constant through time [42]. It remains unclear what determines cell area and the manner by which it is regulated. The simplest explanation would be that cell area is determined by the amount of available plasma membrane, which can be regulated mostly by exchange with intracellular membrane sources [51]. Adhesions and myosin may play a role in supplementing membrane area regulation and controlling cell size. For example, data in fibroblasts suggest that cell size can be determined by a balance between actin outward growth and myosin-powered centripetal actin flow [52–55]. Yet another possibility is that the number of adhesion molecules involved in cell attachment is limiting [56]. Observations in fibroblasts suggest a model in which a certain number of adhesion molecules per unit area are needed to support motility, so cell area is proportional to the number of adhesion molecules at the ventral surface. New molecules are added to the ventral surface at a rate proportional to cell mass, while retraction removes molecules from the ventral surface (with a mean rate proportional to cell area), a fraction of which is lost and the rest are recycled. This model correctly predicts that cell area is proportional to cell mass [56]. Note that this model works equally well if, instead of adhesion molecules, another actin accessory protein, such as Arp2/3, is the limiting factor.

Fibroblasts and Cell Shape

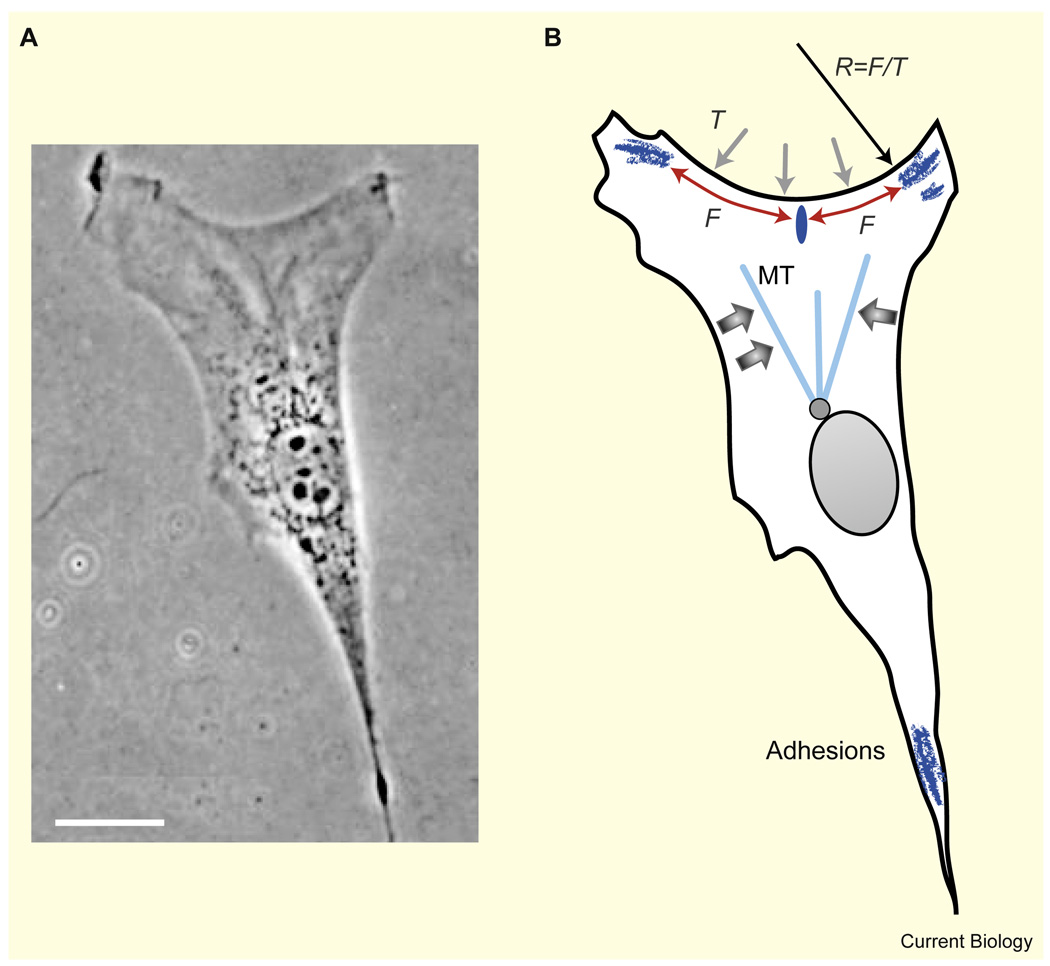
As indicated by the geometric model of Satulovsky et al. [14], the characteristic keratocyte shape can be ‘converted’ into a fibroblast shape (Figure 1C and Figure 4) by simply decreasing the lateral coherence of the protrusion activity and introducing focal adhesions along the cell boundary. Indeed, fibroblasts often have discrete mature adhesion sites at their outer edge [57]. Protrusive activity between the adhesions is slow, and these sites are connected by actin fibers, which mainly outline the cellular periphery in a sequence of inward-curved circular arcs [58,59] (Figure 4); similar arcs and fibers overhang non-adhesive regions when cells are planted on Y-shaped adhesive islands [60]. The first elegant explanation for the shape and radius of these concave arcs [59] was based on a balance between elastic line tension in the actin fibers, F, and surface tension, T, of the cell membrane/actin cortex (Figure 4), described by Laplace law: T = F/R. Thus, the edges between adhesions have to be circular, with a radius R = F/T. If line tension of actin fibers is primarily generated by myosin contraction, then inhibition of myosin is expected to lead to a decrease in line tension, resulting in increased curvature of the boundary. This prediction compares well with experiments which show that the cell boundary can be well fit with a sequence of circular arcs, the radii of which decreases when myosin is inhibited [60]. A more advanced theory explains the detailed arc shape by deformations of the actin gel modeled as a contractile cable network [58]. One of the predictions of this theory — that the arc radius is proportional to the distance between adhesions — was confirmed by experiments in which fibroblasts were plated on a lattice of fibronectin dots [58].

Figure 4. Fibroblast shape.

(A) Phase contrast image (adapted from [9]) and (B) scheme of a migrating fibroblast. Bar, 20 µm. The cell has adhesion sites at the outer edge corners. These sites are connected by actin fibers, which form inward-curved circular arcs. The shape of these arcs is determined by a balance between elastic line tension in the actin fibers, F, and surface tension, T. A weak adhesion formed along the middle of the arc (dark ellipse) does not mature because it is pulled apart by canceling forces, whereas the adhesions in the corners mature since they are pulled inward. The microtubules (MT) could possibly be focused in the forward direction by forces due to myosin contraction (wide arrows).

Fibroblast shape depends on the location of the discrete adhesion sites, but at the same time, the generation of these adhesions depends on cell shape [57,61,62]. This dependence is exemplified by experiments in which cells were plated on polygonal adhesive islands [63]: focal adhesions connected by stress fibers developed at the corners of these islands. One possible explanation is that adhesion maturation is triggered and maintained by force [64]. At the corners, stress fibers from both sides pull the adhesion inward, so these forces add and cause adhesion maturation [65]. Along the smooth parts of the cell boundary, the stress fiber forces pulling on an adhesion site act in opposite directions and cancel each other out, so adhesions disassemble (Figure 4).

This discussion points out that perhaps the main reason for the different shape of keratocytes and fibroblasts is the nature of adhesions in these cells. In keratocytes, discrete strong adhesions play a minor role, whereas in fibroblasts their role is significant, disrupting the coherent protrusion of the actin network. This hypothesis, if true, predicts that temporal variation of the relative magnitude of protrusion and contraction and/or adhesion activities in the same cell would correlate with shape changes. Notably, fibroblasts can assume two interconvertible morphologies — a triangular tailed shape, and a tailless form that resembles a half-moon-shaped keratocyte [66] — whereas keratocytes can occasionally develop a transient tail and assume a triangular form [67].

Related to this hypothesis, Paul et al. [68] developed an adhesion–contraction model of the lamellipodial network (complementing the actin–membrane model of Keren et al. [42]), which is described as a flat contractile cable network adhering to the substrate at the periphery. In the model, the peripheral adhesions are assumed to break when stressed above a threshold. In addition, there are internal contractile forces pulling the cell body forward, toward the leading edge. Interestingly, when one starts with an ellipsoidal cell with a broad leading edge and narrow sides, the adhesions at the broad rear edge break, sharp rear corners emerge, and the cell assumes the characteristic crescent keratocyte-like shape. On the other hand, if one considers an ellipsoidal cell with a narrow leading edge and broad sides, then the adhesions at the rear halves of the sides break, but the adhesions at the very rear survive, and a triangular tailed fibroblast-like shape emerges, with concave sides. These studies hint again that the extent of lateral spread of actin protrusive activity at the cell front coupled with global retraction (governed by myosin and/or membrane tension) and force-dependent adhesion dynamics may control the vast diversity of motile cell shapes.

Shape Regulators: Biochemical Pathways and Microtubules

The mechanics of the actin–myosin–adhesion–membrane system discussed so far are fairly complex, yet they are only part of the picture. Motile cells are not simply mechanical machines, they are mechanochemical systems and there are multiple feedbacks and crosstalk between biochemical pathways and mechanical modules [4,69,70]. We briefly discuss some relevant biochemical and cytoskeletal regulators [4,15,71] in Box 1 (see also Figure 5). In particular, there is a tight relationship between cellular geometry and biochemical pathways [72,73]: activation and distribution of signaling molecules strongly depend on cell shape; in turn, these molecular distributions affect cytoskeletal dynamics and, ultimately, cell shape. One of the reasons for this dependence is that signaling molecules are often activated at the plasma membrane, and then diffuse and get de-activated in the cytoplasm, leading to a cell-shape-dependent gradient in the distribution of these activated signaling molecules. An open question regarding signaling reaction–diffusion systems that is most relevant for cell-shape dynamics is whether these systems support stable spatial molecular distributions that scale with cell size in a specific dynamic geometry [74], or Turing-like patterns that have intrinsic spatial scales [75].

Some shape-related regulatory pathways

Actin accessory proteins

Treadmilling of the actin network and ultimately cell shape and speed are regulated by actin accessory proteins. A small subset of these includes: the branching regulator Arp2/3; capping protein; ADF/cofilin, which accelerates actin network disassembly; profilin, which enhances polymerization [15]; VASP, which helps to focus polymerization to the leading edge [43]; and coronin and cortactin, which regulate the lamellipodial network architecture [95].

Adhesion molecules

Treadmilling of adhesion molecules — sequential activation and binding of integrins followed by clustering, association with talin, vinculin and other adhesion molecules, myosin-force-mediated maturation, and then detachment and recycling — is another important factor in cell-shape regulation and motility [96].

Membrane transport

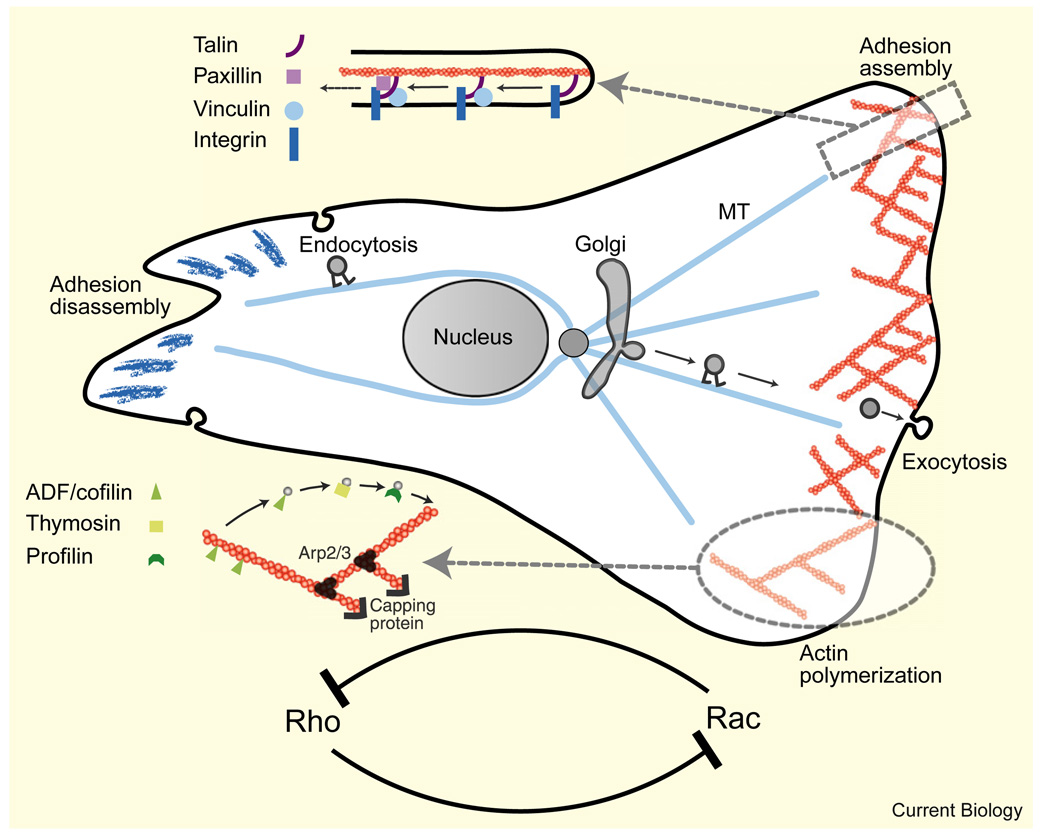
The mechanisms of forward translocation of the plasma membrane in motile cells are largely unclear. In some cell types, rapid diffusion of lipid molecules within the lipid bilayer may be sufficient for forward translocation of the membrane. However, in most cell types membrane translocation and recycling probably occur primarily by spatially segregated exocytosis/endocytosis [97,98] (Figure 5), regulated by microtubule-motor transport.

Rho family GTPases

A crucial feature of motile cells is their polarity — protruding front, retracting rear and quiescent sides. It is likely that in keratocytes mechanics alone are sufficient for maintaining cell polarity [47,48], but in fibroblasts [4], Dictyostelium [99,100] and neutrophils [11] polarization depends on the activity of Rho-family proteins Rac, Rho and Cdc42 (Figure 5). Many groups have reported intricate pathways that amount to an antagonism between Rac/Cdc42 and Rho [101]. This mutual inhibition of Rac/Cdc42 and Rho can lead to a bistable system, which, in the presence of rapid diffusion of inactive Rho GTPases in the cytosol, supports a stable spatial segregation of Rho proteins in polarized cells [74]. Indeed, epithelial cells and neuronal growth cones are characterized by increased concentration of Rac1 and Cdc42 activity towards the lamellipodial membrane protrusion, while RhoA activity is elevated both at the leading protruding and the rear retracting boundaries [102]. Rho GTPases regulate the activity of numerous proteins that affect the cytoskeleton, forming a link to the mechanical module [103]. To name but a few pathways, Rac stimulates branching and polymerization of actin filaments via the Arp2/3 complex, inhibits capping of actin filaments via PIP₂ and stimulates LIM kinase, which inactivates cofilin. Rho, on the other hand, stimulates myosin light chain phosphorylation via its downstream target Rho kinase, thereby increasing contractility, and promotes actin bundling by activating the formin mDia1 [104]. Thus, the self-polarizing Rac/Rho reaction–diffusion system can stably maintain protrusive activity at the front and contractile action at the rear thereby regulating cell shape. In addition to this system, some pathways, such as the phosphatidylinositol 3-kinase/PTEN system [105], can be ‘gradient amplifiers’, enhancing the spatial Rac/Rho segregation.

Figure 5. Regulation modules governing cell shape and movement (only a few modules and respective molecules are shown).

Details of actin and adhesion accessory proteins involved in treadmilling of the actin meshwork and adhesion complexes are shown schematically. The microtubule system promotes assembly of the lamellipodial actin network at the front, myosin contraction at the middle, and adhesion disassembly at the tail by serving as tracks for polarized, motor-mediated transport of regulatory proteins. Antagonistic interactions between the Rho GTPases coupled with diffusion lead to chemical polarization in the cell, which is an important part of the mechanochemical shaping mechanism.

Microtubules play an important role in cell polarity and motility in many cell types [76] (Figure 5); a number of studies suggest that microtubule lengths and densities are the main parameters regulating the length of some motile cells [54]. One of the main respective mechanisms is the antagonism between microtubules and actomyosin contractility [77]. This antagonism can be a result of several issues: the mechanical properties of microtubules, which are stiff compressed struts that resist myosin-powered contraction [78]; the role of microtubules as tracks on which kinesins deliver regulators of actomyosin dynamics to cell edges [71]; finally, the interaction of microtubules with, and the depletion of, molecular activators of actomyosin contractility [79]. The actomyosin activity feeds back to microtubules: the transient binding of microtubules to the actin network, which flows centripetally inward, restricts microtubule expansion [80]. Microtubules can interconnect with cell shape in a number of other ways as well. It is possible that microtubule plus ends are reeled into the cell’s leading edge by dynein motors localized there, thus orienting the microtubule-organizing center and Golgi apparatus toward the leading edge [81]. In turn, microtubule- mediated delivery of Golgi-derived vesicles to the leading edge provides membrane and associated proteins needed for forward protrusion [82] (Figure 5). A few other mechanochemical ‘microtubule–actin–myosin–adhesion modules’ are described in [71].

Shape and Movement in a 3D Environment

The discussion above has focused on cells crawling on 2D surfaces. While this provides important insights into the molecular basis of cell shape and movement, our ultimate goal is to understand how cells migrate through tissue in vivo. A central question — whether motile structures such as the lamellipodium and filopodium observed in 2D also exist in 3D — does not yet have a definitive answer, but it is likely that cells in vivo employ similar structures [83,84]. Notable fine-scale actin structures found in vivo are invadopodia and podosomes that protrude from the ventral surface of the flat pseudopodia of cancer cells, invading and degrading the basement membrane covering blood vessels [85,86]. Podosomes have a characteristic ring-like morphology with a core consisting of numerous small actin ‘dots’ surrounded by a vinculin-rich structure, while invadopodia are finger-like projections that extend deep into the extracellular matrix. Both structures are dependent on actin dynamics involving the N-WASP–Arp2/3–cortactin–dynamin machinery, resembling in this respect lamellipodia and filopodia. However, podosomes and invadopodia have a number of unique characteristics, including co-localization of focal adhesion proteins and actin, dependence on Src kinase signaling and enrichment in matrix-degrading proteases. A recent combined modeling and experimental study suggests that the size of invadopodia is determined by a peculiar stochastic dynamic instability process (not unlike that which occurs in microtubules), in which invadopodia start growing with constant rates and retreat with rates dependent on the properties of the extracellular matrix [87]. The molecular mechanisms behind this process remain largely unknown.

On larger scales, there are also significant differences in overall cell morphology and movement between 2D and 3D environments. While the rear (cell body and tail) and leading (lamellipodial) zones of cells in 2D and 3D look rather similar, the intermediate zones (lamella) are very different. The lamella in 3D consists of ramified cylindrical protrusions, while in 2D it spreads wide in close apposition to the substratum [88]. Adhesion complexes, which are primarily localized to the cell periphery in cells crawling on 2D substrates, are found along the entire length of the cell in 3D [89]. These differences in shape correlate with different movement strategies [89]. Cells moving in a 3D environment are generally faster, more dependent on myosin contraction for rapid migration, and, unlike in 2D, inefficient tail retraction does not hinder leading edge protrusion. A plausible explanation for these differences is related to the changes in the topology of the substrate contact area and inmembrane geometry. In 2D, the lamellipodium and lamella spread far and wide, so the membrane is stretched and tense. The membrane tension can then assist in rear retraction, making this process less dependent on myosin contraction [42]. At the same time, if the cell rear gets stuck, membrane tension hinders protrusion of the leading edge of the cell [67]. In 3D, the membrane area is not the limiting factor, so the rear does not restrain the front. A cell can move faster in this case, but it must rely primarily on myosin contraction to pull up the rear since the reduced membrane tension is less effective in retraction.

The characteristics of 3D environments can be variable: the extracellular matrix can be dense and rigid, or loose and soft, or somewhere between these extremes. Some cells are able to transition between smoother, mesenchymal translocation when moving through dense tissue to a more convulsive, amoeboid motility when crawling through softer tissue [84,90]. The former mode involves making protrusions, adhering to the extracellular matrix fibers, and pulling up the cell body using actin–myosin contraction and is largely similar to 2D migration. However, there is at least one important difference: when the rigid pores in the tissue are significantly smaller than the cell’s nucleus size, the cell deploys matrix metalloproteinases to cleave the matrix fibrils [91]. Interestingly, this matrix breakdown is localized several microns behind the leading edge [92]. Matrix breakdown is the limiting step in this type of migration [91], so perhaps cells switch to amoeboid motility when the nucleus can squeeze through the malleable pores. This way of migration relies on pushing, rather than pulling the cell body, probably by generating a hydrostatic pressure behind the nucleus with the help of myosin contraction, and the resulting cytoplasmic streaming carrying the cell body forward [84,90]. Recent advances in understanding the blebbing phenomenon [93], in which myosin contraction generates hydrostatic pressures that squeeze the cytoplasm through poroelastic cytoskeleton and force the membrane to bulge in regions where the membrane and cytoskeleton adhere weakly, could be very relevant for elucidating the 3D amoeboid movements.

Conclusions

Cell shape and motility emerge from the interplay between several components, most notably the cytoskeleton, the cell membrane, and cell–substrate adhesions. We know a fair deal about the characteristics of each of these components separately; moreover, some general principles regarding the behavior of the system as a whole are beginning to unfold. Geometric theories [13,14] illustrate the dynamic relationship between the kinetics of the cell’s boundary and cell shape, and emphasize important parameters in cell-shape determination. Studies on fish keratocytes — likely the simplest model system for cellular motility — suggest a minimal motility module consisting of a treadmilling actin network within an inextensible membrane bag [42]. It is clear that this mechanical system is neither rigid nor unique: cells have numerous feedbacks and redundant mechanisms (myosin-powered inward flow of actin, force-and-geometry-dependent adhesions, reaction– diffusion biochemical regulators, microtubule-mediated pathways), so they are able to compensate and substitute for missing modules. Recent studies are beginning to shed light on the intricacies of the spatio-temporal coordination between these modules in the motility process (reviewed in [4,8,15,71]).

The brilliant idea of D’Arcy Thomson [12] — that mechanics is a fundamental determinant of biological form — provides a unifying thesis; the challenge is to understand how behavior at the cellular level arises from the local dynamics. Painstaking combined efforts of experimentalists and theorists will help to untangle the molecular modules and the mechanical/biochemical feedbacks of the cell’s motility machinery. One cannot expect a ‘one size fits all’ model explaining the shapes of all motile cell types, but hopefully a finite number of quantitative principles will emerge and these will help us predict form and movement from molecular mechanics and biochemical interactions.