Abstract
Most models of protein evolution are based upon proteins that form relatively rigid 3D structures. A significant fraction of proteins, the so-called disordered proteins, do not form rigid 3D structures and sample a broad conformational ensemble. Disordered proteins do not typically maintain long-range interactions, so the constraints on their evolution should be different than ordered proteins. To test this hypothesis, we developed and compared models of evolution for disordered and ordered proteins. Substitution matrices were constructed using the sequences of putative homologs for sets of experimentally characterized disordered and ordered proteins. Separate matrices, at three levels of sequence similarity (>85%, 85–60%, and 60–40%), were inferred for each type of protein structure. The substitution matrices for disordered and ordered proteins differed significantly at each level of sequence similarity. The disordered matrices reflected a greater likelihood of evolutionary changes, relative to the ordered matrices, and these changes involved nonconservative substitutions. Glutamic acid and asparagine were interesting exceptions to this result. Important differences between the substitutions that are accepted in disordered proteins relative to ordered proteins were also identified. In general, disordered proteins have fewer evolutionary constraints than ordered proteins. However, some residues like tryptophan and tyrosine are highly conserved in disordered proteins. This is due to their important role in forming protein–protein interfaces. Finally, the amino acid frequencies for disordered proteins, computed during the development of the matrices, were compared with amino acid frequencies for different categories of secondary structure in ordered proteins. The highest correlations were observed between the amino acid frequencies in disordered proteins and the solvent-exposed loops and turns of ordered proteins, supporting an emerging structural model for disordered proteins.
Keywords: evolution, protein structure, intrinsically disordered protein, substitution matrix
Introduction
Biologists infer models of evolution for DNA and protein sequences to try and identify the acceptable pathways for change in these molecules. Identifying these pathways can lead to an understanding of the evolutionary processes responsible for the observed differences among homologous sequences. Considerable work has been done developing models of evolution for both DNA and protein sequences and recently in combining models of protein substitutions with models of DNA substitutions (Thorne et al. 1991; Goldman et al. 1998; Lio and Goldman 1998; Thorne 2000; Yang et al. 2000; Posada and Crandall 2001; Whelan and Goldman 2001; Kosiol et al. 2007; Anisimova and Kosiol 2009). For these combined models to be useful, they must accurately reflect the patterns of change in both the DNA and protein sequences.
Empirical models of protein evolution can be used to infer the relative frequencies of amino acid substitutions for proteins. While these amino acid substitution matrices have been used to improve database queries, sequence alignments and phylogenetic inference, they are also very valuable for investigating the processes by which protein sequences evolve. The models originally developed by Dayhoff et al. (1978) were based on a limited number of proteins with known 3D structures. These initial models were followed by a succession of models using data sets of increasing sizes, algorithms of increasing complexity and assumptions of different physical and evolutionary constraints (Dayhoff et al. 1978; Gonnet et al. 1992; Henikoff S and Henikoff JG 1992; Jones et al. 1992; Kosiol et al. 2007). Some models are based upon the average evolutionary patterns of many proteins, whereas others are based upon the evolutionary patterns of specific protein structures (Jones et al. 1994).
There are clear indications that the process of protein evolution is not simply additive over time. For instance, amino acid substitution matrices extrapolated from shorter to longer divergence times are different from matrices developed using sequences with different percent identity levels (Benner et al. 1994). In the short term, protein evolution is constrained by the genetic code. Over the long term, protein evolution is constrained by the physical characteristics of the amino acids and their interactions with one another. This latter constraint is so important that simultaneous substitutions may occur in the DNA to avoid an amino acid substitution that disrupts the structure and function of the protein (Kosiol et al. 2007).
Several groups have shown that models of protein sequence evolution can be improved when various types of protein structure are considered (Benner 1989; Thorne et al. 1996; Goldman et al. 1998; Dean et al. 2002). These studies have identified differences in the frequencies of amino acid substitutions for alpha helices, beta sheets, coils and turns, as well as differences that depend on whether the amino acids are located on the surface (hydrophilic) or the interior (hydrophobic) of folded proteins. These results indicate that structure is an important constraint on protein evolution. However, these studies are incomplete because an important category of protein structure has been overlooked.
The existence of two distinct categories of protein tertiary structure is now well established (Wright and Dyson 1999; Uversky et al. 2000; Dunker et al. 2002; Tompa 2002; Uversky 2002). The category that has held the most attention in the past 60 years is ordered proteins. Ordered proteins form conformational ensembles that experience small fluctuations in the average positions of backbone atoms. These are the proteins whose structures are most easily determined by X-ray crystallography and nuclear magnetic resonance spectroscopy. These are also the proteins that formed the basis for modeling protein evolution, either explicitly, such as in the models of Dayhoff et al. (1978) and Goldman et al. (1998) or implicitly in models that regularly exclude regions with ambiguous alignments (Henikoff S and Henikoff JG 1992; Kosiol et al. 2007). It is well known among structural biologists that these regions of ambiguity are often not ordered.
It is now widely accepted that there is a second category of functional proteins that do not adopt compact rigid structures. These proteins form dynamic conformational ensembles that experience large fluctuations in the average positions of their amino acids (Wright and Dyson 1999; Uversky et al. 2000; Dunker et al. 2002; Tompa 2002; Uversky 2002; Daughdrill et al. 2005; Dyson and Wright 2005). These (intrinsically) disordered proteins have a significantly different average amino acid composition than ordered proteins with fewer nonpolar and more charged amino acids (Uversky et al. 2000; Williams et al. 2001; Lise and Jones 2005). Some disordered proteins are characterized by low sequence complexity, often due to repeat sequences (Romero et al. 2001; Tompa 2003).
Much of the increased interest in disordered proteins comes from their distribution across the tree of life, with increasing frequency in bacterial to archaeal to eukaryal genomes (Dunker et al. 2000; Ward et al. 2004), and to their prevalence in biological processes related to cancer and other diseases (Iakoucheva et al. 2002; Dunker and Uversky 2008; Uversky et al. 2008). Disordered proteins have several specific molecular functions related to their inherent flexibility; these functions include molecular recognition, protein modification, molecular assembly and entropic tethering (Uversky et al. 2000; Dunker et al. 2002; Tompa 2002; Vucetic et al. 2007; Xie, Vucetic, Iakoucheva, Oldfield, Dunker, Obradovic, and Uversky 2007; Xie, Vucetic, Iakoucheva, Oldfield, Dunker, Uversky, and Obradovic 2007).
Evolutionary studies of disordered proteins indicate that they generally evolve at a significantly faster rate than ordered proteins. This faster rate includes changes that result in amino acid substitutions, repeat expansions, and insertions and deletions (Huntley and Golding 2000; Brown et al. 2002; Tompa 2003; Lin et al. 2007). Several studies of individual protein families indicate that the functions of these disordered regions are maintained even in the face of this rapid evolution (Daughdrill et al. 2007; Denning and Rexach 2007; Ayme-Southgate et al. 2008).
Because disordered proteins evolve faster than ordered proteins, it might be expected that the pattern of amino acid substitutions would also be different. Previous work by Radivojac et al. (2002) has shown that substitution matrices based upon families of disordered proteins are different from other matrices and are better able to detect and discriminate related disordered proteins whose average sequence identity among family members is below 50%. This suggests that the long-term constraints on disordered proteins are significantly different from ordered proteins. It is assumed these differences are related to differences in the structure and function of disordered versus ordered proteins.
To extend our understanding of how patterns of substitutions differ between ordered and disordered proteins, we have developed empirical models of protein evolution for families of well-characterized proteins of these two types. The models were developed separately for different degrees of divergence among sequences of each type so that differences between the models over evolution could be detected. Comparisons between the models indicate expected and unexpected differences in the patterns of evolution between ordered and disordered proteins.
Materials and Methods
Data Sources
Experimentally Characterized Proteins.
The disordered protein sequences were taken from a curated database of experimentally determined disordered proteins, DisProt 3.6 (Vucetic et al. 2005). There were 287 disordered sequences with a total of 40,770 residues. Each disordered sequence was ≥30 residues in length. The disordered sequences had a mean length of 142 residues and a median of 86 residues. The longest disordered sequence was of 2,174 residues. The ordered protein sequences were taken from PDB Select 25, a nonredundant subset of the Protein Data Bank (PDB). This data set was chosen because all proteins share ≤25% sequence identity (Boberg et al. 1992; Berman et al. 2000). The sequences were selected from structures that were determined by X-ray crystallography and had strong indications of order, with a resolution ≤2Å, an R factor ≤20%, and no missing backbone or side chain atoms (Smith et al. 2003). The proteins in this data set are ≥80 residues in length and contained no nonstandard residues. There were 289 ordered sequences with a total of 67,548 residues. The ordered sequences had a mean length of 289 residues and a median of 193 residues. The longest ordered sequence was 907 residues. The proteins are listed in supplementary table S1 (Supplementary Material online).
Families of Related Sequences.
Putative homologs of the experimentally characterized disordered and ordered proteins were identified by performing a basic alignment search tool (BLAST) search with each ordered and disordered sequence against GenBank release 159 (Altschul et al. 1997; Benson et al. 2008). To ensure quality matches, the maximum allowed e value was 0.0001, and the minimum match length was at least 35% of the length of the query sequence. Match sequences were cropped to the region corresponding to the start and end of the query. Sequences identified as hypothetical, patented, or predicted were removed from the alignments. Only one sequence in a group of sequences with 100% identity was retained so that all sequences in a family were unique.
During this analysis, it was determined that families of proteins from the Human Immunodeficiency Virus, and some other viruses, contained large numbers of similar sequences having a disproportionate effect on the results. Many papers submitting sequences of these viruses obtained them from an individual organism (see for instance [Huet et al. 1989; Herring et al. 2001]). In order to reduce any undue influence from these families, only one randomly chosen sequence from each referenced paper was included. Unreferenced sequences were not included. The sequences whose families were culled in this way included DP00048, DP00148, DP00160, and DP00424 for the disordered set and 1mml, 1idaa, and 1svb for the ordered set.
Procedure for Developing Matrices
To demonstrate different levels of evolutionary divergence, substitution matrices were developed for three percent identity levels, defined as 85% to <100%, 60–85%, and 40–60% identity (table 1). The number of gaps of any length in the alignments was minimized to reduce ambiguity while still maintaining enough data for meaningful comparisons. This was achieved by specifying no gaps for matrices with 85% minimum percent identity and no more than four gaps for the 60% and 40% matrices. The maximum number of gaps was set to 4 because it was the lowest number that included the majority of alignments in the 60% and 40% percent identity levels.
Table 1.
Criteria Used to Develop Matrices.
| Matrix Label (D/O) | Minimum % Identity | Maximum % Identity | Maximum No. of Gaps | Starting Matrix | No. of Realignments (D/O) |
| D85/O85 | 85 | <100 | 0 | BLOSUM62 | 3/3 |
| D60/O60 | 60 | 85 | 4 | First 85%, zero gaps | 4/3 |
| D40/O40 | 40 | 60 | 4 | First 60%, four gaps | 3/3 |
NOTE.—D, disorder; O, order.
Alignments for Counting Substitutions.
Amino acid substitution frequencies were inferred from sequence alignments. Sets of pairwise alignments were created (fig. 1) such that each sequence of a family was aligned with every other sequence in that family using the Needleman–Wunsch algorithm as implemented by The European Molecular Biology Open Software Suite (EMBOSS)’ needle but modified to perform pairwise comparisons on a group of sequences loaded from a single file (Needleman and Wunsch 1970; Rice et al. 2000). The gap-opening penalty was 10 and the gap-extension penalty was 0.5. The substitution matrix that was used to initially align the sequences is shown in table 1. The substitution matrix inferred from these alignments was then used to realign the sequences (fig. 1). This realignment cycle was done for each matrix class and percent identity level until the difference between successive matrices had no individual log odds value changing by more than 1 and there were fewer than 10 log odds values that differed in subsequent iterations. Table 1 shows the numbers of cycles required for each matrix.
FIG. 1.
Iterative procedure used for constructing substitution matrices.
Pairwise alignments were included in counts for a substitution matrix based on two criteria, the percent identity and the number of gaps in the alignment. The process of including an alignment has three steps: 1) Pairwise alignments were performed between a putative family member and a sequence from the experimentally characterized set. If this alignment met the criteria for minimum percent identity and maximum number of gaps, then it was included in the count for a substitution matrix. 2) A family member included at this level was then used to recruit new family members based on pairwise alignments that met the criteria for minimum percent identity. Alignments among these new recruits were included in the count for a substitution matrix when their pairwise alignments with other recruits at the same level also met the criteria for minimum percent identity. 3) New family members identified in step 2 were then used to recruit the next level of family members based on pairwise alignments that met the criteria for minimum percent identity. This last step was repeated until no more alignments were added. At each new level, pairwise alignments between recruits that met the criteria for minimum percent identity were not included if their pairwise alignment with at least one established family member did not meet the criteria for minimum percent identify. Otherwise, sequences with very low percent identities in alignments with the sequence from the experimentally characterized set would be included. Alignments that did not meet the criteria for minimum percent identity were not included, even if these alignments were between established family members.
Calculating Substitution Matrices
Scaling by Family Size.
The amino acid substitutions and matches of all included alignments from each family were tallied and scaled according to family size. Large families have a disproportionate influence on substitution matrices because they increase the number of alignments, and thus the number of counted substitutions, at a rate of n × (n − 1)/2. Ideally, we would like to offset this effect by scaling the increase in number of alignments from a quadratic to a linear function. This was not possible because the system was developed such that the number of sequences did not directly determine the number of alignments. Therefore, the total number of substitutions each family contributed was scaled instead. In the scaling, it is assumed that the substitutions are increasing quadratically and then they are mapped to a linear function. Let y be the total number of substitutions for a family; the scaled number of substitutions would be x when solving the equation y = x × (x − 1)/2. The matrix of scaled substitution counts for that family can then be calculated by multiplying the matrix of raw substitution counts by x/y.
Calculating the Log Odds.
The log odds for the substitution matrices were calculated using the matrix of scaled substitution counts, C. To calculate amino acid frequencies, C was mirrored and values off of the diagonal were halved. Then, the sum of substitution counts of each column was divided by the total substitution counts in C to get the amino acid frequency pi. To calculate the substitution frequencies qij, each value of C was divided by the total number of substitutions. The observed frequency of substitution qij is divided by the expected frequency pipj to get the odds ratio of that substitution. The log odds value sij of the odds ratio is 2 × log2 of the odds ratio. In the 85% matrices, some of the amino acid substitutions had no counts. This prevented us from calculating their true log odds values, as the log of 0 is infinity. In order to approximate the values for these substitutions, a value that was half of the lowest existing count was used instead. This approximation gave an appropriately lower frequency for that substitution and worked well for scaled substitution counts.
Special treatment was also given to the X (any residue), B (N or D), and Z (Q or E) ambiguity codes. These ambiguity codes are present in a few of the sequences and are included in many substitution matrices. Substitution values between standard residues and the ambiguity codes B and Z were an average of the values for substitutions between their constituent residues and that standard residue. Values of X in the 85%, 60%, and 40% identity class matrices were replaced by the X values in the EMBOSS substitution matrices, EBLOSUM85, EBLOSUM60, and EBLOSUM40, respectively (Rice et al. 2000).
Comparing Matrices Using the Sum of Off-Diagonal Matrix Values
In order to compare the disordered and ordered matrices calculated at a similar percent identity level, the sum of the off-diagonal values in the substitution matrix was computed. The off-diagonal sum of a substitution matrix's log odds values gives an idea of how unlikely substitutions are overall, separated from the context of the amino acid frequencies. More negative sums indicate substitutions are more unlikely overall for that matrix. A jackknife procedure was used to estimate the variance of this statistic: substitution matrices were calculated leaving out the substitution counts for one family at a time. The statistical difference between the off-diagonal values for disorder and order was then determined using Welch's t-test.
Results
Constructing Amino acid Substitution Matrices
In order to develop accurate models of protein evolution, consideration must be given to various types of protein structure. In this study, amino acid substitution matrices were developed for two categories of protein structures: 1) ordered proteins and domains, which form compact globular structures, and 2) disordered proteins and domains, which form an ensemble of rapidly interconverting structures. These substitution matrices indicate the relative frequencies of amino acid changes in these two categories of proteins. In order to describe the effect of evolution occurring on multiple timescales, matrices were developed for each protein class at three levels of percent identity, 40%, 60%, and 85%. Alignments were included in the development of a matrix based on these percent identities and the maximum number of gapped regions (table 1). The initial alignments were performed with the matrices listed in table 1 and then realigned for the given number of times for disorder (D) and order (O).
To construct substitution matrices, experimentally characterized proteins were used to identify families of homologous proteins and domains. Initially, approximately 290 protein families were used for each structural category. Ultimately, some families were excluded because of the criteria used for performing sequence alignments. For alignments between 85% and 100%, no gaps were allowed in the alignment in order to eliminate the possibility of misaligned residues. At the lower percent identity levels, up to four gapped regions of any length were allowed because this was the lowest number of gapped regions that included the majority of alignments. This criterion was also designed to minimize the chance of aligning residues that are not related by evolutionary descent. Requiring a small number of gapped regions reduced the number of alignments at each level, especially in the disordered proteins (table 2), because disordered proteins have more indels than ordered proteins at each percent identity level (data not shown).
Table 2.
Number of Families, Sequences, and Alignments Used to Develop Each Matrix.
| Matrix, No. of Gaps | Families | Sequences | Total Alignments | Included Alignments | % Alignments Excluded |
| D85, 0 | 213 | 3,127 | 76,840 | 29,259 | 61.922 |
| O85, 0 | 213 | 3,408 | 68,397 | 41,551 | 39.250 |
| D60, 4 | 207 | 18,883 | 750,526 | 662,599 | 11.715 |
| O60, 4 | 224 | 27,316 | 3,483,138 | 3,327,744 | 4.461 |
| D40, 4 | 182 | 31,361 | 2,417,993 | 1,738,606 | 28.097 |
| O40, 4 | 242 | 52,527 | 8,548,724 | 5,949,331 | 30.407 |
NOTE.—D, disorder; O, order.
Analysis of Amino acid Frequencies in the Data set.
To construct amino acid substitution matrices, the frequencies of each amino acid in the sequences used for alignments is determined (pi). Figure 2 shows the amino acid frequencies for each of the six matrices. The frequencies presented in figure 2 were scaled to account for the different sizes of protein families by transforming the substitution counts from a quadratic to a linear function (see Materials and Methods). All residue types, except glycine (G) and asparagine (N), have similar frequencies across each of the percent identity ranges for both the ordered and disordered proteins. Glycine and asparagine show significantly higher frequencies in the disordered protein matrices, at the 40% and 60% identities, relative to 85%. Therefore, at the lower percent identity levels, the new sequences that are included in the alignment tend to have more glycines and asparagines. The lack of glycines in D85 may be due to the propensity for glycines in disordered proteins to be found in indels (data not shown) and the selection of alignments that do not have gaps for the D85 matrix. This is not the case for asparagines, however, which are rarely found in indels in disordered proteins (data not shown). This strongly suggests that as disordered proteins evolve away from a common ancestor, their sequences tend to accumulate these residue types. For glycine, we can infer that this is because of selection for flexibility, but it is unclear what advantage this provides. A structural basis for the accumulation of asparagines during evolution is less clear. However, it is noted that asparagines are sites for glycosylation and these posttranslational modifications tend to occur in disordered regions (Xie, Vucetic, Iakoucheva, Oldfield, Dunker, Obradovic, and Uversky 2007).
FIG. 2.
Amino acid frequencies (pi) of residues in each matrix. The axis is sorted by average frequency of the residues in the D matrices. Shades of red are D matrices; shades of blue are O matrices. Bars indicate ±0.2%, which is within rounding error and slightly greater than the maximum standard deviation. D, disorder; O, order.
Previous studies have shown that there is a large difference in the amino acid composition of ordered and disordered proteins, reflected primarily by fewer nonpolar amino acids and more charged and polar amino acids in disordered proteins relative to ordered proteins (Romero et al. 2001; Radivojac et al. 2007). This conclusion is largely reflected in the data shown in figure 2. There are, however, small differences between our results and previous results that are probably due to using information from aligned homologs, versus experimentally characterized proteins, to determine amino acid frequencies. Amino acids found more frequently in ordered proteins than disordered proteins are considered order promoting, whereas those that are more frequent in disordered proteins are considered disorder promoting. Based upon residue frequencies in DisProt 3.4, Radivojac et al. (2007) concluded that the order-promoting residues are C, W, Y, I, F, V and L, the disorder-promoting residues are M, K, R, S, Q, P and E, whereas H, T, N, D, A and G are neutral.
Identifying Substitution Probabilities.
The next step in calculating a substitution matrix is to count the number of times a pair of amino acids align together among all the pairwise alignments. These values are then converted to the probabilities of finding the two amino acids aligned (pij). The sum of the pij’s, where i and j are not the same residue, yields the mutation rate for the matrix (table 3, column 2). The ranges of percent identity included in each matrix provided an upper and lower bound on the frequency of substitutions (i.e., the range of substitution frequencies for 85% was >0 to 0.15, 60% was >0.15 to 0.4, and 40% was >0.4 to 0.6), and the mutation rate reflects the average frequency of substitutions for that matrix. Note that the 60% identity matrices had the greatest difference in average frequency of substitutions, and the ordered matrix had the greater number of substitutions. The mutation rates were similar between the ordered and disordered matrices at the other two levels of similarity.
Table 3.
Summary Statistics for the Six Substitution Matrices.
| Matrix | Mutation Rate | Expected Value | Off-Diagonal Sum | Diagonal Sum |
| D85 | 0.063 | −8.14 | −1909 ± 7 | 177 ± 0.2 |
| O85 | 0.060 | −8.28 | −1797 ± 4 | 176 ± 0.2 |
| D60 | 0.253 | −2.66 | −623 ± 2 | 167 ± 0.2 |
| O60 | 0.299 | −2.45 | −607 ± 2 | 163 ± 0.1 |
| D40 | 0.478 | −0.50 | −97 ± 2 | 144 ± 0.2 |
| O40 | 0.495 | −0.45 | −179 ± 1 | 141 ± 0.1 |
NOTE.—The off-diagonal and diagonal sums are the average (±the standard error of the mean) of the jackknife replicates for each matrix. D, disorder; O, order.
Substitution Matrices.
The final step in calculating a substitution matrix is to convert the frequencies of substitutions to log odds [2log2(qij/pipj)]. This method normalizes the frequency of substitutions by the frequencies of the residues being substituted. Negative values indicate that substitutions are occurring less often than would be expected if two amino acids substituted at random, and positive values indicate that substitutions are occurring more often than expected. A value of zero indicates that substitutions between two amino acids are occurring at a rate expected by the frequencies of the two amino acids in the data set from which the matrix was derived. Substitutions are rare, so the values along the diagonal, which reflect the probability that a site has not undergone a substitution, are always positive. As the level of divergence increases, these diagonal values decrease because there has been more time for a substitution to arise. The expected values in table 3 (column 3) represent the expected log odds score between two randomly chosen amino acids (Altschul 1991). Because substitutions are the least frequent in the 85% matrices, these matrices have the smallest expected values reflecting the small probability of seeing substitutions. Some substitutions were never seen, such as between lysine (K) and tyrosine (Y) in D85, yielding extremely negative values. On the other hand, substitutions are so common at 40% similarity that the expected value approaches what is expected simply due to the amino acid frequencies. At this level of sequence divergence, substitutions that occur more often than expected by chance probably reflect persistent back substitutions among amino acids with similar biochemical properties.
Figure 3A shows one-half of the symmetric substitution matrices for D40 (lower) and O40 (upper). The matrices are shaded to provide a quick visual reference of which amino acid substitutions are more or less likely. It is clear that the overall pattern of substitutions appears to be the same between the two structural types for many of the amino acid pairs. For instance, order-promoting amino acids are more likely to substitute with other order-promoting amino acids (shaded in dark green), and disorder-promoting amino acids are more likely to substitute with other disorder-promoting amino acids (shaded in white). Substitutions between order-promoting and disorder-promoting amino acids are less likely to occur for both matrices. There are some interesting exceptions to this observation. First, cysteine (C) has a far greater probability of substituting in disordered proteins than in ordered proteins. This is expected given the importance of C in forming disulfide bridges in ordered proteins and the lack of a similar function in disordered proteins. Second, and more unexpected, is the conserved nature of glutamic acid (E) especially relative to the less conserved, but biochemically similar, aspartic acid (D).
FIG. 3.
(A) Substitution matrices for ordered (O40, upper) and disordered (D40, lower) proteins at 40–60% sequence identity. Color shading indicates probability of substitutions being greater than expected by chance (blue) or less than expected (red). (B) Matrix showing the difference between D40 and O40. Color shading indicates greater frequency of substitutions in disorder (blue) or greater frequency in order (red). In all matrices, residues are ordered from most order promoting (green) to most disorder promoting (white) as shown in (Radivojac et al. 2007). D, disorder; O, order.
There is also a difference between the matrices in the degree of substitutions. Figure 3B shows the difference between the disordered and ordered matrices. Blue shading in this matrix indicates that substitutions are more common in disordered proteins versus ordered. This matrix clearly highlights the less conserved nature of C and the more conserved nature of E in disordered proteins. It also shows that although substitutions between order- and disorder-promoting amino acids are not as common as would be expected by chance, disordered proteins are more likely than ordered proteins to undergo these types of substitution. All the matrices can be found at http://people.ibest.uidaho.edu/∼celesteb/Matrices/.
Evolutionary Differences between Ordered and Disordered Proteins
Comparison of Ordered and Disordered Substitution Matrices.
In order to test for significant differences between the ordered and disordered substitution matrices at each percent identity level, a jackknife procedure was used to calculate the variance of the means of the off-diagonal and diagonal sums. This procedure removes one family from the data set of aligned sequences and recalculates the substitution matrix. Table 3 (columns 4 and 5) shows the average sum and standard error of the mean for the off-diagonal or diagonal cells from the jackknife replicates for each matrix. The sums are significantly different between the ordered or disordered matrix for a particular percent identity (P << 0.0001) using a two-sided t-test with unequal variances.
Within each percent identity class, both the sums of the off-diagonal and of the diagonal are significantly different between the ordered and disordered substitution matrices, indicating that ordered and disordered proteins have different patterns of substitutions that are accepted by evolution, as well as different patterns of conservation. Note, however, that the difference between the off-diagonal sums of D60 and O60 are the smallest and the difference in mutation rate is the largest. We suspect that if the mutation rates had been more equal, the difference in off-diagonal sums between D60 and O60 would have been even smaller and possibly not significant.
One of the surprising results from this analysis is that as the percent identity of the matrices decreased, the difference between the off-diagonal sums for the ordered and disordered matrices changed sign (table 3, column 4). The sum of the off-diagonal elements of D85 was more negative than O85, the sums of D60 and O60 are about equal, and D40 is less negative than O40. This indicates that as disordered proteins diverge, their substitutions approach what would be expected by random substitutions among the amino acids faster than ordered proteins. This means that when an amino acid changes in a disordered protein, it has more options. This is consistent with what is known about the structures of disordered proteins. Their ensembles are dominated by local interactions, and they have very few, if any, long-range interactions. Local interactions largely depend on the ability of an amino acid to occupy different regions of the Ramachandran map and this ability is fairly uniform for most amino acids. Notable exceptions include glycine and proline.
Evolutionary Conservation of Disordered and Ordered Proteins.
Interestingly, the disordered matrices show consistently higher values for the diagonal sums, or the log odds of not substituting, implying greater conservation. Consistently higher levels of conservation in disordered versus ordered proteins were not expected and prompted a closer look at our evolutionary models. Because the log odds values in the matrices are influenced by the amino acid frequencies, the matrices of qij’s were investigated more closely to determine which substitutions are acceptable. For each column of the qij matrix (representing each amino acid), the values were divided by their row totals to create a matrix showing the probability of a substitution between i and j. In other words, if a site in the alignment is amino acid i, what is the probability that the same site in a homologous sequence is amino acid j. In the resulting matrix, the residue-normalized values off the diagonal indicate how often one amino acid substitutes for another (pij), and the residue-normalized values along the diagonal indicate how often an amino acid is conserved (pii). The diagonal values were then used to investigate the difference in amino acid conservation between disordered and ordered proteins.
Figure 4A shows the differences in amino acid conservation between the D40 and O40 matrices by comparing their diagonal probabilities, pii. Values >0 indicate that an amino acid is more conserved in D40 than in O40. It is not surprising that cysteine (C) is more conserved in ordered proteins than in disordered proteins because it often forms long-range covalent bonds that stabilize the folded protein. It was surprising to find that several amino acids, including glutamic acid (E) and asparagine (N), were more conserved in disordered proteins than in ordered proteins. Because C is more frequent in ordered proteins, and E and N are more frequent in disordered proteins at this percent identity, we checked to see if there was a correlation between the probability that an amino acid is conserved and the frequency of each amino acid (fig. 4B). Excluding glycine (G), which is a clear outlier in this graph, there is no correlation between pii and pi for either the disordered or ordered matrices.
FIG. 4.
Residues that are most conserved are different between disordered and ordered proteins, and conservation is not determined by frequency. (A) Differences between the probability that an amino acid is conserved at a site (pii) for disorder and order at 40–60% identity for each of the 20 amino acids (i). Error bars indicate one standard deviation. (B) Scatter plot of the frequencies of each amino acid versus pii for disorder (filled diamonds) and order (open squares) at 40–60% identity.
Relationship between Amino acid Frequencies in Disordered Proteins and Secondary Structure Categories in Ordered Proteins.
Ordered proteins are composed of four types of secondary structure: helix, sheet, turn, and coil. These four categories of secondary structure have different amino acid frequencies within the ordered proteins as well as different distributions of phi and psi dihedral angles. Disordered proteins do not form tertiary structures, but a number of studies have shown the presence of different levels of transient secondary structure. In recent structural studies, realistic ensembles of disordered proteins were generated using a database of phi and psi dihedral angles assembled from the coil and turn regions of high-resolution X-ray structures of ordered proteins (Bernado et al. 2005; Jha et al. 2005). Ensembles generated by this method were used to predict residual dipolar couplings and small-angle X-ray scattering data for chemically denatured proteins and at least two intrinsically disordered proteins with high accuracy. Due to the success of this approach, we anticipated that the amino acid composition of disordered proteins might be most similar to the coil and turn regions of ordered proteins.
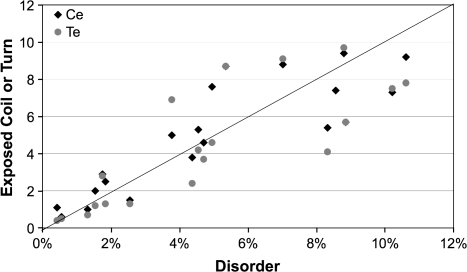
To investigate this possibility, the amino acid frequencies for the D85 matrix were compared with the frequencies identified by Goldman et al. (Goldman et al. 1998) for their eight structural classes of ordered proteins, buried or exposed alpha helices, beta sheets, turns (including bends) and coils. Table 4 shows that the amino acid frequencies for D85 are most highly correlated with those for the solvent-exposed coils and turns of ordered proteins. Figure 5 shows the correlation plot for the frequencies of individual amino acids from the solvent-exposed coils and turns of ordered proteins versus the amino acid frequencies from the D85 matrix. This strong correlation is important because it suggests that the evolution of coils and turns, which are the most structurally dynamic regions of ordered proteins, is most similar to the evolution of disordered proteins. If this is correct, it supports the assumption that the structural ensembles are similar.
Table 4.
Correlations between Amino acid Composition of Disordered Proteins and Different Classes of Secondary Structure in Ordered Proteins.
| Exposed Residues |
Buried Residues |
||||||||
| Helix | Sheet | Turn | Coil | Helix | Sheet | Turn | Coil | D85 | |
| Exposed | |||||||||
| Helix | 1 | 0.53 | 0.44 | 0.61 | 0.12 | −0.23 | −0.04 | −0.18 | 0.64 |
| Sheet | 2.6 | 1 | 0.38 | 0.71 | −0.04 | −0.08 | 0.01 | 0.10 | 0.49 |
| Turn | 2.1 | 1.8 | 1 | 0.81 | −0.10 | −0.28 | 0.67 | 0.35 | 0.74 |
| Coil | 3.3 | 4.3* | 5.7* | 1 | −0.11 | −0.33 | 0.30 | 0.22 | 0.85 |
| Buried | |||||||||
| Helix | 0.5 | −0.2 | −0.4 | −0.5 | 1 | 0.80 | 0.33 | 0.62 | 0.08 |
| Sheet | −1.0 | −0.4 | −1.2 | −1.5 | 5.7* | 1 | 0.28 | 0.70 | −0.20 |
| Turn | −0.2 | 0.0 | 3.8 | 1.3 | 1.5 | 1.2 | 1 | 0.76 | 0.32 |
| Coil | −0.8 | 0.4 | 1.6 | 1.0 | 3.4 | 4.1* | 4.9* | 1 | 0.22 |
| D85 | 3.5 | 2.4 | 4.6* | 6.9* | 0.3 | −0.9 | 1.4 | 0.9 | 1 |
NOTE.—The t scores for each correlation are shown, and asterisks indicate significance at P <0.05 using the Holm–Bonferroni correction. D, disorder. Information for disordered proteins is based upon the >85% similarity matrix and for ordered proteins is from Goldman, et al. 1998.
FIG. 5.
Frequencies of amino acids in disordered proteins are most similar to the frequencies of amino acids in the exposed coils and turns of ordered proteins. The line indicates a one-to-one correspondence between frequency in order and disorder. (Information for disordered proteins is based upon the >85% similarity matrix and for ordered proteins is from Goldman et al. 1998.)
Evolution of Disordered Proteins Appears to be More Neutral Than Ordered Proteins.
Previous studies have indicated that disordered proteins are evolving more rapidly than ordered proteins but a comparison has not been made between disordered proteins and the individual secondary structure classes of ordered proteins. Figure 6 shows a scatter plot of the pii values for the eight secondary structure matrices developed by Goldman et al. (1998) and the D85 matrix developed in this study. The plot is ordered based upon increasing pii values of the D85 matrix. Lines between data points from the same matrix are added for clarity. From this figure, it is clear that the buried residues from ordered proteins are the most conserved and the disordered residues are the least conserved, even at 85–100% identity. Each amino acid in disordered proteins is less conserved than it's counterpart in ordered proteins except tryptophan in exposed turns and coils and glycine in exposed helices. This result suggests that the evolution of disordered proteins is more neutral or less prone to purifying selection than ordered proteins.
FIG. 6.
Scatter plot of the residue-normalized diagonal values, pii, for the eight secondary structure matrices and D85. The plot is ordered based upon increasing pii of the D85 matrix. Lines between data points from the same matrix are added for clarity. (Information for disordered proteins is based upon the >85% similarity matrix and for ordered proteins is from Goldman et al. 1998.). D, disorder; O, order.
To address this question, a direct comparison was made between the different substitution matrices for ordered and disordered proteins developed in this study. To do this, each of the percent identity matrices was extrapolated to a PAM250 distance matrix, using the program DARWIN (Gonnet et al. 2000; http://www.cbrg.ethz.ch/biorecipes/mathematical/Dayhoff; http://www.cbrg.ethz.ch/darwin). First, a PAM1 mutation matrix was calculated for each substitution matrix. Then the PAM1 matrix was multiplied by itself 250 times, and the log odds values of the substitutions were calculated from this mutation matrix. Table 5 (columns 2 and 3) shows the sum of the cells for each of the PAM250 matrices. When the sum becomes more positive, substitutions occur at a level that is similar to the relative frequencies of the amino acids. Table 5 shows that the disordered sum changes more than the ordered sum; it starts out slightly lower than order in the 85% range and ends up significantly higher in the 60% and 40% ranges. Indeed, the sum for the extrapolated D40 matrix is slightly positive, suggesting that at this level, substitutions are occurring more often than expected by chance.
Table 5.
Sum of Log Odds Values for PAM250 Extrapolation Matrices and Difference from the GCM.
| % Identity Level | D Sum | O Sum | Δ GCM D | Δ GCM O |
| 85 | −351 | −402 | 1,089 | 1,084 |
| 60 | −90 | −326 | 735 | 991 |
| 40 | 31 | −201 | 635 | 820 |
NOTE.—GCM, genetic code matrix; D, disorder; O, order.
To test our models of evolution against neutral evolution, the PAM250 extrapolations were compared with the genetic code matrix (GCM) from Benner et al. (1994). This matrix is a PAM250 extrapolation of a PAM1 mutation matrix made assuming that the only constraint on amino acid divergence is the genetic code, thus representing a neutral model of evolution. The last two columns of table 5 show the absolute sum of the difference between the PAM250 extrapolations and the GCM; a smaller sum indicates the matrix is closer to the GCM because there is less difference in the log odds values overall. Taken together, the log odds sums from the PAM250 extrapolations and the log odds differences between the PAM250 matrices and the GCM indicate that the evolution of disordered proteins is more neutral than ordered proteins, confirming our earlier work (Brown et al. 2002; Daughdrill et al. 2007). One obvious physical characteristic to attribute the lack of amino acid conservation for disordered proteins is the absence of a structure that is stabilized by interactions between amino acids that are far apart in the sequence. The absence of this physical constraint permits a greater level of sequence variation.
Discussion
To compare the evolution of disordered and ordered proteins, substitution matrices were calculated from pairwise alignments for three levels of percent identity, at 85% to <100%, 60–85%, and 40–60%. Relatively small sets of well-characterized disordered and ordered proteins were used to represent the overall characteristics of the two structural classes. Separate matrices were not calculated for different structural subclasses in either the ordered or disordered set, so these matrices are an average over all subclasses. These average models are being used because the small size of the disorder data set used in this study precludes any rigorous delineation into specific structural or functional categories. Additionally, there is currently no reliable scheme for identifying structural families of disordered proteins, and indeed, it may not be possible to group some disordered proteins into separate functional classes like linker type and binding type because of their multifunctional nature. Therefore, the matrices presented here should be viewed as overall models of protein evolution for ordered and disordered proteins, comparable to the PAM; Jones, Taylor, and Thorton; BLOSUM; and Gonnet matrices (Dayhoff et al. 1978; Gonnet et al. 1992; Henikoff S and Henikoff JG 1992; Jones et al. 1992). These earlier matrices also provide overall models of protein evolution that average evolution over the various structural and functional subclasses. Because these matrices are still widely used, we are confident that the approach of averaging the data sets is robust.
As mentioned above, there is not a reliable structural classification scheme that encompasses disordered proteins. Although many studies have improved our ability to detect unstructured regions in database queries, they have not provided a systematic description of the various structural ensembles that are populated by different functional classes of disordered proteins (Vucetic et al. 2003; Ward et al. 2004; Schlessinger et al. 2007; Schlessinger et al. 2009). According to the classification scheme proposed by Dunker et al. (2002), disordered proteins can be grouped into 34 functional subclasses. Upon close inspection, many of these 34 functional subclasses fall into one of two structural classes. There are disordered proteins that function primarily as entropic tethers or linkers (linker type), and there are disordered proteins that fold in the presence of other protein partners (binding type). It is possible that the substitution matrices developed for this study would show distinct differences between these two classes.
Previous studies have shown that binding-type disordered proteins, also termed molecular recognition elements, have a frequency of aromatic residues similar to the value observed for ordered proteins, and their proline content is almost 50% greater than the value observed for ordered proteins (Oldfield et al. 2005; Mohan et al. 2006). The increased content of aromatic residues, and even the nonpolar proline, is important because it is expected that these residues will form the interface with protein-binding partners. This expectation was verified in a detailed analysis of binding-type protein structures (Gunasekaran et al. 2004). In this study, it was shown that the composition of the molecular interfaces that form between disordered and ordered proteins are dominated by contacts between hydrophobic residues. The authors speculate that the greater occurrence of hydrophobic contacts at the interface combined with the fact that hydrophobic residues occur less frequently in disordered proteins means that these residues should be conserved. Figure 6 shows very clearly which nonpolar residues fall into this conserved category. These residues are F, L, Y, W, and P, which all have pii values greater than 0.9. While P occurs at a relatively high frequency in disordered proteins and F, L, Y, and W occur at lower frequencies (see fig. 2), their high levels of conservation indicate they are important for function.
Previous studies have also shown that linker-type sequences have few evolutionary constraints (Brown et al. 2002; Daughdrill et al. 2007), and one might expect that binding-type sequences would have more evolutionary constraints. Based on the analysis presented above, this appears to be the case. However, the following example demonstrates how difficult it is to make even this simple generalization. The transactivation domain from the tumor suppressor protein p53 is a binding-type disordered domain approximately 90 residues long. It contains at least 20 well-characterized binding sites for other proteins and numerous sites for posttranslational modifications (Appella and Anderson 2001). Two of the well-characterized binding sites are for the ubiquitin ligase, MDM2, and the 70-kDa subunit of replication protein A, RPA70 (Kussie et al. 1996; Abramova et al. 1997; Bode and Dong 2004; Bochkareva et al. 2005; Vise et al. 2005). When bound to MDM2, p53 becomes ubiquinated and targeted for proteosome-mediated degradation. When bound to RPA70, p53 may be stabilized and available to amplify the cellular response to DNA damage. The expectation is that the MDM2 and RPA70 binding sites will be conserved between homologs of the p53 transactivation domain (p53TAD). However, inspection of figure 7 shows that this is not the case. In figure 7, a protein sequence alignment is shown for p53TAD from seven mammalian homologs. The orange bar indicates the location of the MDM2 binding site, and the green bar indicates the location of the RPA70 binding site. Both binding sites form amphipathic helices in the bound state (Kussie et al. 1996; Bochkareva et al. 2005). Figure 7 shows that the MDM2 binding site is highly conserved and the RPA70 binding site is less conserved. The protein sequences for MDM2 and RPA70 from the same species are highly conserved, so this difference may not be due to differences in variability of the binding proteins themselves. This is just one example, but it indicates the difficulty with making any generalizations about the evolution of different functional categories of disordered proteins without additional structural data.
FIG. 7.
Protein sequence alignment of the disordered p53 transactivation domain for seven closely related family members. The orange bar shows the position of the amphipathic helix that forms when p53 binds to the ubiquitin ligase, MDM2. The green bar shows the position of the amphipathic helix that forms when p53 binds to RPA70.
Recently, an attempt was made to improve the alignment of disordered protein sequences using a substitution matrix that was based on a curated set of disordered proteins (Radivojac et al. 2002). Similar to the current study, BLAST was used to find homologs of disordered proteins. The minimum and maximum observed sequence identities between any two aligned sequences were 10% and 99.53%, respectively. Therefore, a broad range of sequence evolution was used to infer a single matrix. This substitution matrix showed a marked improvement in the detection and discrimination of related disordered proteins whose average sequence identity with other family members was less than 50%. Their results indicate that optimizing gap penalties could be used to make further improvements for disordered protein sequence alignments.
In the current study, substitution matrices were not constructed for the purpose of improving sequence alignments and instead were used to make direct comparisons between models of evolution developed for ordered proteins, which form fixed 3D structures, and disordered proteins, which sample a broad conformational ensemble. In this context, our work represents a significant advance over previous studies because the substitution matrices for ordered and disordered proteins can be compared directly and over different evolutionary times. We show that disordered proteins are more similar to neutrally evolving proteins by comparison to a matrix based upon the genetic code, and this similarity increases over greater levels of divergence. Additionally, the data presented in figure 4A show the clear differences in the conservation of certain amino acids in disordered and ordered proteins. It was surprising to see that E and N are more conserved in disordered proteins, whereas D is more conserved in ordered proteins. This was consistent with the analysis of amino acid frequencies for ordered and disordered proteins at different percent identity levels. This analysis revealed that as disordered proteins evolve away from a common ancestor, their sequences tend to accumulate G and N. We speculate that the accumulation of G is due to selection for flexibility and the accumulation of N is related to its role as a common site for glycosylation. It is also worth noting that E has a higher helical propensity than D and therefore, its conservation could be related to its occurrence at helical binding interfaces. Taken together, the data indicate that the evolution of disordered proteins is driven by their structure and function just as the evolution of ordered proteins.
Supplementary Material
Supplementary table S1 is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Supplementary Material
Acknowledgments
Research was performed at the University of Idaho. C.J.B. and A.K.J. were funded by the National Institutes of Health (P20RR16448). G.W.D. is funded by the American Cancer Society (RSG-07-289-01-GMC) and the National Science Foundation (0744839). Bioinformatics facilities were supported by P20RR16448 and P20RR016454.
References
- Abramova NA, Russell J, Botchan M, Li R. Interaction between replication protein A and p53 is disrupted after UV damage in a DNA repair-dependent manner. Proc Natl Acad Sci USA. 1997;94:7186–7191. doi: 10.1073/pnas.94.14.7186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S, Madden T, Schaffer A, Zhang J, Zhang Z, Miller W, Lipman D. Gapped BLAST and PSI-BLAST: a new generation of protein database search tools. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul SF. Amino acid substitution matrices from an information theoretic perspective. J Mol Biol. 1991;219:555–565. doi: 10.1016/0022-2836(91)90193-A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anisimova M, Kosiol C. Investigating protein-coding sequence evolution with probabilistic codon substitution models. Mol Biol Evol. 2009;26:255–271. doi: 10.1093/molbev/msn232. [DOI] [PubMed] [Google Scholar]
- Appella E, Anderson CW. Post-translational modifications and activation of p53 by genotoxic stresses. Eur J Biochem. 2001;268:2764–2772. doi: 10.1046/j.1432-1327.2001.02225.x. [DOI] [PubMed] [Google Scholar]
- Ayme-Southgate AJ, Southgate RJ, Philipp RA, Sotka EE, Kramp C. The myofibrillar protein, projectin, is highly conserved across insect evolution except for its PEVK domain. J Mol Evol. 2008;67:653–669. doi: 10.1007/s00239-008-9177-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benner SA. Patterns of divergence in homologous proteins as indicators of tertiary and quaternary structure. Adv Enzyme Regul. 1989;28:219–236. doi: 10.1016/0065-2571(89)90073-3. [DOI] [PubMed] [Google Scholar]
- Benner SA, Cohen MA, Gonnet GH. Amino acid substitution during functionally constrained divergent evolution of protein sequences. Protein Eng. 1994;7:1323–1332. doi: 10.1093/protein/7.11.1323. [DOI] [PubMed] [Google Scholar]
- Benson DA, Karsch-Mizrachi I, Lipman DJ, Ostell J, Wheeler DL. GenBank. Nucleic Acids Res. 2008;36:D25–D30. doi: 10.1093/nar/gkm929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernado P, Blanchard L, Timmins P, Marion D, Ruigrok RW, Blackledge M. A structural model for unfolded proteins from residual dipolar couplings and small-angle x-ray scattering. Proc Natl Acad Sci USA. 2005;102:17002–17007. doi: 10.1073/pnas.0506202102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boberg J, Salakoski T, Vihinen M. Selection of a representative set of structures from Brookhaven Protein Data Bank. Proteins. 1992;14:265–276. doi: 10.1002/prot.340140212. [DOI] [PubMed] [Google Scholar]
- Bochkareva E, Kaustov L, Ayed A, et al. (11 co-authors) Single-stranded DNA mimicry in the p53 transactivation domain interaction with replication protein A. Proc Natl Acad Sci USA. 2005;102:15412–15417. doi: 10.1073/pnas.0504614102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bode AM, Dong Z. Post-translational modification of p53 in tumorigenesis. Nat Rev Cancer. 2004;4:793–805. doi: 10.1038/nrc1455. [DOI] [PubMed] [Google Scholar]
- Brown CJ, Takayama S, Campen AM, Vise P, Marshall TW, Oldfield CJ, Williams CJ, Dunker AK. Evolutionary rate heterogeneity in proteins with long disordered regions. J Mol Evol. 2002;55:104–110. doi: 10.1007/s00239-001-2309-6. [DOI] [PubMed] [Google Scholar]
- Daughdrill GW, Narayanaswami P, Gilmore SH, Belczyk A, Brown CJ. Dynamic behavior of an intrinsically unstructured linker domain is conserved in the face of negligible amino acid sequence conservation. J Mol Evol. 2007;65:277–288. doi: 10.1007/s00239-007-9011-2. [DOI] [PubMed] [Google Scholar]
- Daughdrill GW, Pielak GJ, Uversky VN, Cortese MS, Dunker AK. Natively disordered proteins. In: Buchner J, Kiefhaber T, editors. Protein folding handbook. Darmstadt (Germany): WILEY-VCH; 2005. pp. 275–357. [Google Scholar]
- Dayhoff MO, Schwartz RM, Orcutt BC. A model of evolutionary change in proteins. In: Dayhoff MO, editor. Atlas of Protein Sequence and Structure. Washington, DC: Natl. Biomed. Res. Found; 1978. vol. 5, suppl. 3. pp. 345–352. [Google Scholar]
- Dean AM, Neuhauser C, Grenier E, Golding GB. The pattern of amino acid replacements in alpha/beta-barrels. Mol Biol Evol. 2002;19:1846–1864. doi: 10.1093/oxfordjournals.molbev.a004009. [DOI] [PubMed] [Google Scholar]
- Denning DP, Rexach MF. Rapid evolution exposes the boundaries of domain structure and function in natively unfolded FG nucleoporins. Mol Cell Proteomics. 2007;6:272–282. doi: 10.1074/mcp.M600309-MCP200. [DOI] [PubMed] [Google Scholar]
- Dunker AK, Brown CJ, Lawson JD, Iakoucheva LM, Obradovic Z. Intrinsic disorder and protein function. Biochemistry. 2002;41:6573–6582. doi: 10.1021/bi012159+. [DOI] [PubMed] [Google Scholar]
- Dunker AK, Obradovic Z, Romero P, Garner EC, Brown CJ. Intrinsic protein disorder in complete genomes. Genome Inform Ser Workshop Genome Inform. 2000;11:161–171. [PubMed] [Google Scholar]
- Dunker AK, Uversky VN. Signal transduction via unstructured protein conduits. Nat Chem Biol. 2008;4:229–230. doi: 10.1038/nchembio0408-229. [DOI] [PubMed] [Google Scholar]
- Dyson HJ, Wright PE. Intrinsically unstructured proteins and their functions. Nat Rev Mol Cell Biol. 2005;6:197–208. doi: 10.1038/nrm1589. [DOI] [PubMed] [Google Scholar]
- Goldman N, Thorne JL, Jones DT. Assessing the impact of secondary structure and solvent accessibility on protein evolution. Genetics. 1998;149:445–458. doi: 10.1093/genetics/149.1.445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonnet GH, Cohen MA, Benner SA. Exhaustive matching of the entire protein sequence database. Science. 1992;256:1443–1445. doi: 10.1126/science.1604319. [DOI] [PubMed] [Google Scholar]
- Gonnet GH, Hallett MT, Korostensky C, Bernardin L. Darwin v. 2.0: an interpreted computer language for the biosciences. Bioinformatics. 2000;16:101–103. doi: 10.1093/bioinformatics/16.2.101. [DOI] [PubMed] [Google Scholar]
- Gunasekaran K, Tsai CJ, Nussinov R. Analysis of ordered and disordered protein complexes reveals structural features discriminating between stable and unstable monomers. J Mol Biol. 2004;341:1327–1341. doi: 10.1016/j.jmb.2004.07.002. [DOI] [PubMed] [Google Scholar]
- Henikoff S, Henikoff JG. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci USA. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herring C, Quinn G, Bower R, et al. (13 co-authors) Mapping full-length porcine endogenous retroviruses in a large white pig. J Virol. 2001;75:12252–12265. doi: 10.1128/JVI.75.24.12252-12265.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huet T, Dazza MC, Brun-Vezinet F, Roelants GE, Wain-Hobson S. A highly defective HIV-1 strain isolated from a healthy Gabonese individual presenting an atypical western blot. AIDS. 1989;3:707–715. doi: 10.1097/00002030-198911000-00004. [DOI] [PubMed] [Google Scholar]
- Huntley M, Golding GB. Evolution of simple sequence in proteins. J Mol Evol. 2000;51:131–140. doi: 10.1007/s002390010073. [DOI] [PubMed] [Google Scholar]
- Iakoucheva LM, Brown CJ, Lawson JD, Obradovic Z, Dunker AK. Intrinsic disorder in cell-signaling and cancer-associated proteins. J Mol Biol. 2002;323:573–584. doi: 10.1016/s0022-2836(02)00969-5. [DOI] [PubMed] [Google Scholar]
- Jha AK, Colubri A, Freed KF, Sosnick TR. Statistical coil model of the unfolded state: resolving the reconciliation problem. Proc Natl Acad Sci USA. 2005;102:13099–13104. doi: 10.1073/pnas.0506078102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT, Taylor WR, Thornton JM. The rapid generation of mutation data matrices from protein sequences. Comput Appl Biosci. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- Jones DT, Taylor WR, Thornton JM. A mutation data matrix for transmembrane proteins. FEBS Lett. 1994;339:269–275. doi: 10.1016/0014-5793(94)80429-x. [DOI] [PubMed] [Google Scholar]
- Kosiol C, Holmes I, Goldman N. An empirical codon model for protein sequence evolution. Mol Biol Evol. 2007;24:1464–1479. doi: 10.1093/molbev/msm064. [DOI] [PubMed] [Google Scholar]
- Kussie PH, Gorina S, Marechal V, Elenbaas B, Moreau J, Levine AJ, Pavletich NP. Structure of the MDM2 oncoprotein bound to the p53 tumor suppressor transactivation domain. Science. 1996;274:948–953. doi: 10.1126/science.274.5289.948. [DOI] [PubMed] [Google Scholar]
- Lin YS, Hsu WL, Hwang JK, Li WH. Proportion of solvent-exposed amino acids in a protein and rate of protein evolution. Mol Biol Evol. 2007;24:1005–1011. doi: 10.1093/molbev/msm019. [DOI] [PubMed] [Google Scholar]
- Lio P, Goldman N. Models of molecular evolution and phylogeny. Genome Res. 1998;8:1233–1244. doi: 10.1101/gr.8.12.1233. [DOI] [PubMed] [Google Scholar]
- Lise S, Jones DT. Sequence patterns associated with disordered regions in proteins. Proteins. 2005;58:144–150. doi: 10.1002/prot.20279. [DOI] [PubMed] [Google Scholar]
- Mohan A, Oldfield CJ, Radivojac P, Vacic V, Cortese MS, Dunker AK, Uversky VN. Analysis of molecular recognition features (MoRFs) J Mol Biol. 2006;362:1043–1059. doi: 10.1016/j.jmb.2006.07.087. [DOI] [PubMed] [Google Scholar]
- Needleman SB, Wunsch CD. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J Mol Biol. 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- Oldfield CJ, Cheng Y, Cortese MS, Romero P, Uversky VN, Dunker AK. Coupled folding and binding with alpha-helix-forming molecular recognition elements. Biochemistry. 2005;44:12454–12470. doi: 10.1021/bi050736e. [DOI] [PubMed] [Google Scholar]
- Posada D, Crandall KA. Selecting the best-fit model of nucleotide substitution. Syst Biol. 2001;50:580–601. [PubMed] [Google Scholar]
- Radivojac P, Iakoucheva LM, Oldfield CJ, Obradovic Z, Uversky VN, Dunker AK. Intrinsic disorder and functional proteomics. Biophys J. 2007;92:1439–1456. doi: 10.1529/biophysj.106.094045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radivojac P, Obradovic Z, Brown CJ, Dunker AK. Improving sequence alignments for intrinsically disordered proteins. Pac Symp Biocomput. 2002;2002:589–600. [PubMed] [Google Scholar]
- Rice P, Longden I, Bleasby A. EMBOSS: the European Molecular Biology Open Software Suite. Trends Genet. 2000;16:276–277. doi: 10.1016/s0168-9525(00)02024-2. [DOI] [PubMed] [Google Scholar]
- Romero P, Obradovic Z, Li X, Garner EC, Brown CJ, Dunker AK. Sequence complexity of disordered protein. Proteins. 2001;42:38–49. doi: 10.1002/1097-0134(20010101)42:1<38::aid-prot50>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Schlessinger A, Punta M, Rost B. Natively unstructured regions in proteins identified from contact predictions. Bioinformatics. 2007;23:2376–2384. doi: 10.1093/bioinformatics/btm349. [DOI] [PubMed] [Google Scholar]
- Schlessinger A, Punta M, Yachdav G, Kajan L, Rost B. Improved disorder prediction by combination of orthogonal approaches. PLoS One. 2009;4:e4433. doi: 10.1371/journal.pone.0004433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith DK, Radivojac P, Obradovic Z, Dunker AK, Zhu G. Improved amino acid flexibility parameters. Protein Sci. 2003;12:1060–1072. doi: 10.1110/ps.0236203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorne JL. Models of protein sequence evolution and their applications. Curr Opin Genet Dev. 2000;10:602–605. doi: 10.1016/s0959-437x(00)00142-8. [DOI] [PubMed] [Google Scholar]
- Thorne JL, Goldman N, Jones DT. Combining protein evolution and secondary structure. Mol Biol Evol. 1996;13:666–673. doi: 10.1093/oxfordjournals.molbev.a025627. [DOI] [PubMed] [Google Scholar]
- Thorne JL, Kishino H, Felsenstein J. An evolutionary model for maximum likelihood alignment of DNA sequences. J Mol Evol. 1991;33:114–124. doi: 10.1007/BF02193625. [DOI] [PubMed] [Google Scholar]
- Tompa P. Intrinsically unstructured proteins. Trends Biochem Sci. 2002;27:527–533. doi: 10.1016/s0968-0004(02)02169-2. [DOI] [PubMed] [Google Scholar]
- Tompa P. Intrinsically unstructured proteins evolve by repeat expansion. Bioessays. 2003;25:847–855. doi: 10.1002/bies.10324. [DOI] [PubMed] [Google Scholar]
- Uversky VN. Natively unfolded proteins: a point where biology waits for physics. Protein Sci. 2002;11:739–756. doi: 10.1110/ps.4210102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uversky VN, Gillespie JR, Fink AL. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins. 2000;41:415–427. doi: 10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- Uversky VN, Oldfield CJ, Dunker AK. Intrinsically disordered proteins in human diseases: introducing the D2 concept. Annu Rev Biophys. 2008;37:215–246. doi: 10.1146/annurev.biophys.37.032807.125924. [DOI] [PubMed] [Google Scholar]
- Vise PD, Baral B, Latos AJ, Daughdrill GW. NMR chemical shift and relaxation measurements provide evidence for the coupled folding and binding of the p53 transactivation domain. Nucleic Acids Res. 2005;33:2061–2077. doi: 10.1093/nar/gki336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vucetic S, Brown CJ, Dunker AK, Obradovic Z. Flavors of protein disorder. Proteins: Structure, Function, Genetics. 2003;52:573–584. doi: 10.1002/prot.10437. [DOI] [PubMed] [Google Scholar]
- Vucetic S, Obradovic Z, Vacic V, et al. (12 co-authors) DisProt: a database of protein disorder. Bioinformatics. 2005;21:137–140. doi: 10.1093/bioinformatics/bth476. [DOI] [PubMed] [Google Scholar]
- Vucetic S, Xie H, Iakoucheva LM, Oldfield CJ, Dunker AK, Obradovic Z, Uversky VN. Functional anthology of intrinsic disorder. 2. Cellular components, domains, technical terms, developmental processes, and coding sequence diversities correlated with long disordered regions. J Proteome Res. 2007;6:1899–1916. doi: 10.1021/pr060393m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward JJ, Sodhi JS, McGuffin LJ, Buxton BF, Jones DT. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J Mol Biol. 2004;337:635–645. doi: 10.1016/j.jmb.2004.02.002. [DOI] [PubMed] [Google Scholar]
- Whelan S, Goldman N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol Biol Evol. 2001;18:691–699. doi: 10.1093/oxfordjournals.molbev.a003851. [DOI] [PubMed] [Google Scholar]
- Williams RM, Obradovic Z, Mathura V, Braun W, Garner EC, Young J, Takayama S, Brown CJ, Dunker AK. The protein non-folding problem: amino acid determinants of intrinsic order and disorder. Pac Symp Biocomput. 2001;6:89–100. doi: 10.1142/9789814447362_0010. [DOI] [PubMed] [Google Scholar]
- Wright PE, Dyson HJ. Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J Mol Biol. 1999;293:321–331. doi: 10.1006/jmbi.1999.3110. [DOI] [PubMed] [Google Scholar]
- Xie H, Vucetic S, Iakoucheva LM, Oldfield CJ, Dunker AK, Obradovic Z, Uversky VN. Functional anthology of intrinsic disorder. 3. Ligands, post-translational modifications, and diseases associated with intrinsically disordered proteins. J Proteome Res. 2007;6:1917–1932. doi: 10.1021/pr060394e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie H, Vucetic S, Iakoucheva LM, Oldfield CJ, Dunker AK, Uversky VN, Obradovic Z. Functional anthology of intrinsic disorder. 1. Biological processes and functions of proteins with long disordered regions. J Proteome Res. 2007;6:1882–1898. doi: 10.1021/pr060392u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z, Nielsen R, Goldman N, Pedersen AM. Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics. 2000;155:431–449. doi: 10.1093/genetics/155.1.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.