Skip to main content
NCBI home page
Genetics logoLink to Genetics
. 2010 Feb;184(2):439–453. doi: 10.1534/genetics.109.110833

Ploidy and the Evolution of Endosperm of Flowering Plants

Aurélie Cailleau 1,1, Pierre-Olivier Cheptou 1, Thomas Lenormand 1
PMCID: PMC2828724  PMID: 19933875

Abstract

In angiosperms, spermatozoa go by pair in each pollen grain and fertilize, in addition to the egg cell, one of its sister cells, called the central cell. This “double fertilization” leads to the embryo on the one hand and to its nutritive tissue, the endosperm, on the other hand. In addition, in most flowering plants, the endosperm is triploid because of a doubled maternal genetic contribution in the central cell. Most of the hypotheses trying to explain these eccentricities rest on the assumption of a male/female conflict over seed resource allocation. We investigate an alternative hypothesis on the basis of the masking of deleterious alleles. Using analytical methods, we show that a doubled maternal contribution and double fertilization tend to be favored in a wide range of conditions when deleterious mutations alter the function of the endosperm. Furthermore, we show that these conditions vary depending on whether these traits are under male or female control, which allows us to describe a new type of male/female conflict.

FEMALES provision their offspring with resources. These resources can be accumulated before fertilization. When some of the gametes are not fertilized, this strategy is extremely wasteful. In a number of species, females have evolved conditional strategies avoiding this problem—in particular by providing most resources after fertilization [i.e., to diploid offspring instead of haploid gametes (Westoby and Rice 1982; Baroux et al. 2002)]. This postfertilization provisioning occurs, for instance, in viviparous animals, such as mammals, some reptiles (De Fraipont et al. 1996), some sharks (Wourms 1993), some scorpions (Brown and Formanowicz 1996), and velvet worms (Tutt et al. 2002). In plants, resource provisioning to offspring can also occur before or after fertilization.

The life cycle of plants typically alternates a sporophytic stage (2n) and a gametophytic stage (n) that are both multicellular. A newly formed sporophyte (the diploid zygote) will typically use the resources accumulated in tissues derived from the female haploid gametophyte and not in tissues derived from the diploid sporophyte. For instance, in ferns and mosses, the new embryo develops “parasitically” on the free gametophyte. In gymnosperms, the embryo acquires its resource from a nonfree female gametophyte (it is encapsulated within sporophytic tissues). In some of them (cycads and ginkgoes) the resource is fully accumulated before fertilization, while in some others (Pinaceae) the resource accumulates both before and after fertilization (Friedman 2001b). The former situation is comparable to what happens in many fish while the latter is comparable to what happens in many bird species (egg formation before fertilization and incubation after fertilization). In angiosperms, resource provisioning to the seed really starts after fertilization (Friedman 2001b), a situation comparable to placental mammals (Figure 1).

Figure 1.—

Figure 1.—

Open in a new tab

Timing of resource accumulation in the seed. All the resources are allocated before fertilization in cycads and ginkgoes. Resources are allocated both before and after fertilization in conifers and all the resources are allocated after fertilization in angiosperms.

Compared to other seed plants, the case of angiosperms is complicated by the occurrence of a “double fertilization” (Nawaschin 1898; Guignard 1899): two identical (mitotically derived) spermatozoa from a single pollen grain fertilize in parallel two cells of the female gametophyte. The fertilization of the egg cell produces the embryo. The fertilization of the central cell produces the endosperm, a specific organ that serves as an interface for resource transfer between the diploid mother and its offspring (like the placenta in mammals). This tissue can either be transitory or serve as a storage tissue in the seed. In this article, we study the evolution of this nutritive tissue. More specifically, we focus on the evolution of its genetic constitution.

The diversity of endosperms reflects directly the diversity of female gametophytes (Friedman et al. 2008). In some angiosperms [Austrobaileyales (Friedman et al. 2003), Oenothera (Maheshwari 1963), and Nympheales (Williams and Friedman 2002)], the female gametophyte is made of four haploid cells that are mitotically derived from a single spore. One of them is the central cell and contains one maternal contribution (1m). This type of gametophyte is referred to as “Oenothera.” After double fertilization (which adds one paternal contribution, 1p), the central cell becomes a diploid endosperm (1m:1p). This endosperm is genetically identical to the embryo. In other angiosperms, the female gametophyte is eight-nucleated, but seven-celled because the central cell remains binucleate (2m). This type of gametophyte is referred to as “Polygonum.” Double fertilization again carries one paternal contribution (1p). Thus, the central cell becomes a triploid endosperm (2m:1p). Other types of female gametophytes can be found sporadically among angiosperms. They are characterized by an increased number of maternal contributions in the central cell and/or by polyspory. These types are derived from the Polygonum type and we do not consider them further. As already mentioned, in gymnosperms and ferns the embryo feeds directly on the haploid female gametophyte (1m:0p), which can be considered as the ancestral state of the nutritive tissue.

In this article, we focus on the evolution of double fertilization (DF) (0p → 1p) and maternal contribution doubling (MCD) (1m → 2m) from this 1m:0p ancestral state. In principle, two scenarios can be considered (Figure 2). In the first scenario, DF evolves before MCD (1m:0p → 1m:1p → 2m:1p). In the second, MCD evolves first and DF second (1m:0p → 2m:0p → 2m:1p). The latter scenario involves an additional step (secondary loss of the second maternal contribution, 2m:1p → 1m:1p) to account for the occurrence of 1m:1p endosperms in Nympheales (Nuphar, Nymphea, Cabomba) and the Illiciales-Trimeniaceae-Austrobaileyaceae clade (Schisandra, Illicium). It is therefore less parsimonious. For this reason, we consider only the first scenario (1m:0p → 1m:1p → 2m:1p) in this article.

Figure 2.—

Figure 2.—

Open in a new tab

Possible scenarios for the evolution of the genetic makeup of the embryo nutritive tissue, modified from Friedman and Ryerson (2009). In the left scenario, there are one 1m:0p → 1m:1p transition and two 1m:1p → 2m:1p transitions and thus three steps. In the right scenario, there are one 1m:0p → 2m:0p transition, one 2m:0p → 2m:1p transition, and two 2m:1p → 1m:1p transitions and thus four steps. In addition, the latter scenario involves a 2m:0p state that has never been observed in any taxa.

Three main theories have been proposed to explain the evolution of DF and MCD. They all rely on the fact that some resources are accumulated to the seed after fertilization. The first theory proposes that postfertilization resource allocation triggers a genetic conflict over resource allocation among parents and/or offspring. Indeed, an antagonistic coevolution can occur between the male, the female, and/or the embryos when their optimal seed sizes differ, to take control over resource allocation (Trivers 1974; Haig 2000). Because the endosperm plays a pivotal role in the control of resource allocation, DF and MCD are considered in this theory to be adaptations allowing the father and the mother to take and take back the control over resource allocation, respectively (Charnov 1979; Westoby and Rice 1982; Queller 1983; Willson and Burley 1983; Law and Cannings 1984; Bulmer 1986; Shaanker et al. 1988; Haig and Westoby 1989; Friedman 1995; Shaanker and Ganeshaiah 1997; Hardling and Nilsson 1999, 2001). These “allocation conflict theories” include the kinship theory of genomic imprinting (Haig 2000, 2004; De Jong et al. 2005) and have received the most extensive theoretical development.

A second theory (hereafter metabolic theory) proposes that DF and MCD evolve because of the metabolic properties of polyploid tissues (Stebbins 1976; Donoghue and Scheiner 1992). More specifically, the idea is that DF and MCD increase the endosperm ploidy level, which enhances its postfertilization metabolic efficiency (increased transcription rate, increased cell size, and resource storage). The problem with this view is that endomitosis would achieve the same effect and is very common at the beginning of gametophyte/endosperm development in both angiosperm and gymnosperm (Friedman 2001a,b): DF and MCD seem unnecessary to increase ploidy in the endosperm in the first place. Moreover, this theory does not account for the presence of a male nucleus specifically (Willson and Burley 1983).

A third theory proposes that DF and MCD evolve because of the genetic properties of polyploid tissues (Brink and Cooper 1940). More specifically, the idea is that DF combines two different genomes (maternal and paternal) in the nutritive tissue, which masks the effect of recessive deleterious mutations and thus enhances the postfertilization metabolic efficiency of the nutritive tissue. Following Friedman et al. (2008), we refer to this theory as the “heterozygosity theory.” The heterozygosity theory explanation for endosperm's genetic evolution seems close to explanations for ploidy evolution. Several models have been worked out to understand the effect of the masking of deleterious mutations in the evolution of ploidy levels (Perrot et al. 1991; Bengtsson 1992; Otto and Goldstein 1992). These models have shown that masking protects diploid individuals from the effect of recessive deleterious mutations, but that it also reduces the elimination of these mutations from the population, creating genetic association favorable to haploidy (Otto and Goldstein 1992). The problem of the evolution of the genetic constitution of the endosperm is, however, not directly comparable to the problem of life cycles evolution. First, the phenotype under selection (e.g., resource in the seed) is at least partly determined by the genotype of the nutritive tissue (the gametophyte or the endosperm), which can differ from the genotype of the diploid embryo. Second, double fertilization is not symmetrical with respect to sexes: it masks maternal alleles but reveals paternal alleles in the endosperm. Third, double fertilization can be under pollen and/or female gametophyte control, while the timing of meiosis in life cycle evolution is controlled by the diploid stage. In fact, no formal model has been created to explore specifically the heterozygosity theory. The aim of this article is to develop such models.

We build two models to study the evolution of DF and MCD. More explicitly, we study the evolution of a modifier locus that changes their probability of occurrence. We show that masking deleterious mutations can favor both DF and MCD. However, unlike models for the evolution of ploidy, we find conditions where DF evolves in opposite directions depending on the sex where the modifier is expressed. In different conditions, the same scheme occurs for MCD. This situation reveals that male/female conflict extends well beyond the problem of resource allocation to embryos: a conflict can also occur over the genetic constitution of embryos' nutritive tissues.

MODEL

We analyze the evolution of DF and MCD in two distinct deterministic models. Both involve two linked diallelic loci. The first one (the viability locus) is subject to deleterious mutations and determines the survival of the embryo while the other one (the modifier locus) controls the probability of DF or MCD.

Life cycle:

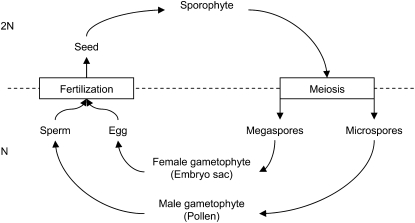
To build each model, we first write exact recursions of the frequency of the different haploid genotypes. We follow the different events in the life cycle over one generation, which alternates a gametophytic haploid with a sporophytic diploid stage (Figure 3). We start at the gametophytic stage. The male gametophyte (pollen) contains two identical sperm cells (they are mitotically derived). The female gametophyte (embryo sac) contains also a given number of genetically identical cells, among which are the egg cell and the central cell. First, fertilization occurs in a panmictic way (pairing one pollen grain with one embryo sac). The genetic constitution of the endosperm is determined at this stage, but differently in the different models (see below). Second, the nutritive tissue and the embryo develop (seed formation). Selection occurs among seeds in the population, on the basis of the genotype of their nutritive tissue. Third, the surviving embryos become hermaphroditic sporophytes and produce haploid spores through meiosis (where the two loci recombine at a rate R). Finally, the spores undergo mutation and each produces a new gametophyte through mitosis. To describe the different events in this life cycle, we introduce several parameters, specific to each locus. We present each locus in turn.

Figure 3.—

Figure 3.—

Open in a new tab

Life cycle. The sporophyte is born from the fertilization of a male gamete and a female gamete. These gametes are produced by the male and female gametophytes (the pollen and the embryo sac, respectively). In the sporophyte's sexual organs, meiosis produces spores that develop in new gametophytes.

Viability locus:

The first locus is expressed in the embryo's nutritive tissue (we refer to this tissue as the endosperm) where it potentially affects any function (e.g., the accumulation or the transfer of resources to the embryo or the protection of the embryo). This function, in turn, determines the survival of the embryo. We model this directly by assigning different viabilities to embryos associated to different endosperm genotypes. We consider that recurrent deleterious mutations occur at a rate μ at the viability locus. We denote Pa the frequency of a (the deleterious allele) and PA the frequency of A (the wild-type allele). The embryos associated to a nutritive tissue that carries only the wild-type allele (A, AA, AAA) have a survival of 1. Those associated to a nutritive tissue that carries only the deleterious allele (a, aa, aaa) have a survival of 1 − s. The embryos associated to a heterozygous nutritive tissue have survival 1 − hs, 1 − h1s, and 1 − h2s for Aa, aaA, and AAa genotypes, respectively. The parameters h, h1, and h2 are the coefficients of dominance of a on A. We consider h1 ≥ h2 (a alleles are more exposed in aaA endosperms than in aAA endosperms). Because we assume that Wa = Waa = Waaa and WA = WAA = WAAA, our model excludes potential effects of gene copy number (i.e., dosage effects in “metabolic theory”). Because we do not introduce any competition between embryos or endosperms produced by the same sporophyte (the viability of a given embryo depends only on the genotype at the viability locus of its own endosperm), our model excludes any effect involved in the allocation conflict theories. In fact, our model can be understood as if there was a single female gametophyte produced by each sporophyte. Thus, by construction, our model focuses exclusively on the heterozygosity theory.

Modifier locus:

The second locus controls the genetic constitution of the nutritive tissue. More specifically, it controls the rate of double fertilization (i.e., 1m:0p vs. 1m:1p, in the DF model) or the rate of doubling of maternal contribution (i.e., 1m:1p vs. 2m:1p, in the MCD model). We consider two alleles M and m with frequency PM and Pm, respectively. In each model, the modifier locus is expressed in the pollen (paternal control), the embryo sac (maternal control), or both (biparental control). In the first two cases, the expression of the modifier locus is haploid. In these cases, we denote νM or νm the probability of double fertilization (or maternal contribution doubling) when the gametophyte controlling the trait carries the M or the m allele, respectively. In the biparental case, we assume that the modifier effect is additive (i.e., the probabilities of DF and MCD are νM, (νM + νm)/2, and νm when the embryo is MM, Mm, and mm, respectively). To give a concrete example, in a DF model with a paternal control of the modifier locus, the mating between AM male gametophytes (pollen) and am female gametophytes will produce a proportion νM of embryos whose nutritive tissue is 1m:1p (Aa, with fitness 1 − hs) and a proportion 1 − νM embryos whose nutritive tissue is 1m:0p (a, with fitness 1 − s). Tables 1 and 2 summarize all these notations. Without loss of generality, we discuss the fate of modifier alleles that increase the probabilities of DF and MCD (νm > νM).

TABLE 1.

Genotypic control of selection

Endosperm ploidy level Endosperm genotype (m:p) Embryo's W Model
n (1m:0p) A: ∅ 1 DF
n (1m:0p) a: ∅ 1 − s DF
2n (1m:1p) A: A 1 DF, MCD
2n (1m:1p) A: a 1 − hs DF, MCD
2n (1m:1p) a: a 1 − s DF, MCD
3n (2m:1p) AA: A 1 MCD
3n (2m:1p) AA: a 1 − h2s MCD
3n (2m:1p) aa: A 1 − h1s MCD
3n (2m:1p) aa: a 1 − s MCD
Open in a new tab

We assume h2 < h and h2 < h1, 0 ≤ h ≤ 1, 0 ≤ s ≤ 1.

TABLE 2.

Genotypic control of the genetic makeup of the endosperm

Probability of
Control Modifier locus genotype DF: double fertilization (= proportion of 1m:1p endosperms) MCD: doubling (= proportion of 1m:2p endosperms)
Biparental MM νM = ν νM = ν
Mm (νM + νm)/2 = ν + δν/2 (νM + νm)/2 = ν + δν/2
mm νm = ν + δν νm = ν + δν
Uniparental M νM = ν νM = ν
m νm = ν + δν νM = ν + δν
Open in a new tab

Recursion equations:

The recursion equations describing the dynamics of the model are given in appendix a for the case of the evolution of DF with a paternal control. These recursions can be written for the frequency of the four haplotypes (paM, pAm, pAM, and pam). Equivalently, they can be expressed for the allele frequencies (pm and pa) and linkage disequilibrium (Cam = pAM pam − paM pAm = pam − pa pm). In this case, we define Cam such that it is positive when the modifier allele (m) is positively associated to the deleterious allele at the viability locus (a). To fully understand the model, we also describe the population during the diploid phase. In diploids, several genetic associations CU,V analogous to Cam can be defined (as in, e.g., Barton and Turelli 1991), where U denotes a set of alleles on the maternally inherited chromosome and V a set of alleles in the paternally inherited chromosome. In our case, we have two biallelic loci and we have therefore 11 associations: Inline graphic. For instance, the Ca,m association measures the fact that the presence of the a allele on the maternally inherited chromosome covaries with the presence of the m allele on the paternally inherited chromosome.

ANALYSIS

We analyze DF and MCD models with two complementary methods: quasi-linkage equilibrium, (QLE) and stability analysis (see, e.g., Otto and Day 2007). In these two methods, we assume that the frequency of deleterious mutations pa is close to its equilibrium value (noted Inline graphic) and small (which entails that Cam is also small). This assumption requires that μ ≪ s. This is the only common assumption to the two approaches. In the QLE approach, we also assume that s is small, R is large, and the modifier has a weak effect. In the stability analysis, the only additional assumption to μ ≪ s is that the modifier frequency is small. To easily define the orders of magnitude, we use a small parameter ξ as a scaling throughout.

The QLE analysis assumes that linkage disequilibrium equilibrates much faster than allele frequencies, so that it can be considered to always be at a “quasi-equilibrium.” This approach works best if the modifier effect is small and the recombination rate large (that is why we consider νM = ν and νm = ν + δν, where δν is proportional to ξ; in the case of a modifier with a specifically maternal or paternal effect, we write δν,∅ and δ∅,ν instead of δν, respectively). With this approach, we focus on convergence stability. We perform the stability analysis to assess the robustness of this QLE analysis and to investigate what is going on for low recombination rate. This method considers the fate of the modifier introduced at a low frequency in a population at equilibrium at the viability locus. We first start by studying the DF model.

Mutation–selection at the viability locus in the DF model:

To start, it is important to understand what is going on at the viability locus alone. According to the assumptions given above for the QLE approach, the change over one generation (noted with Δ) of the frequency of the deleterious allele at the viability locus is

graphic file with name M3.gif (1)

and thus, at equilibrium (Δpa = 0), the frequency of the a allele (noted with an asterisk) depends on the rate of double fertilization (ν):

graphic file with name M4.gif (2)

The same equations are obtained under the assumption of the stability analysis, except that the orders of the two equations are Inline graphic and Inline graphic, respectively. With complete double fertilization (ν = 1), the endosperm is diploid and we retrieve the equilibrium frequency of a deleterious mutation under diploid selection (μ/hs). However, with no double fertilization (ν = 0), Inline graphic: the efficiency of selection is halved compared to the classic haploid selection situation (μ/s). Indeed, half the alleles (the paternal ones) are not exposed to selection since they are in the embryo, but not in the endosperm. Interestingly, this result points out that having a haploid endosperm is not equivalent to haploidy. Note that the equilibrium described above is a good approximation only if h > s when ν is close to 1. A more complicated approximation can be found for small values of h and 1 − ν (see Chasnov 2000 for a similar treatment), but, as explained below, a better approximation is not necessary to accurately predict how DF and MCD evolve in our models.

QLE analysis of the DF model:

We compute the overall frequency change at the modifier locus Inline graphic as a sum of two terms. The first, Inline graphic, is proportional to pm(1 − pm) and corresponds to direct selection. The second, Inline graphic, is proportional to Cam and corresponds to indirect selection. Under the QLE assumptions given above, we obtain at leading orders

graphic file with name M11.gif (3)

We study these terms separately for two reasons. First they represent qualitatively different processes. Second, their relative magnitude varies in different ways throughout the parameter range (e.g., we expect indirect selection to become increasingly important as R decreases and direct selection to vanish when h becomes close to Inline graphic), and it is therefore quantitatively useful to combine their leading orders.

Direct selection:

The sign of Inline graphic is given by the sign of Inline graphic. When mutations are recessive (Inline graphic), direct selection favors the evolution of DF. In fact, h can be understood as the “exposition” (to selection) of the a allele in a 1m:1p seed, while Inline graphic can be understood as its exposition in a 1m:0p seed. Indeed, as said before, only half the a alleles (the maternally inherited ones) are exposed to selection in 1m:0p endosperms. Direct selection simply tends to minimize the exposition of the deleterious alleles. This effect is quite different from the “masking effect” described in models of ploidy evolution (Otto and Goldstein 1992). In these models, exposition of the deleterious alleles is always greater with haploidy (Aa individuals have a better survival than haploid a individuals as long as h < 1), but this is compensated by the fact that a diploid individual has twice the chance to carry a deleterious mutation (it has two alleles). As a consequence, diploidy is favored by direct selection when exposition (h) is at least halved to compensate for this doubled risk of inheriting a deleterious mutation (i.e., when h < Inline graphic). In contrast, in our model, all individuals have the same risk to carry a deleterious mutation (all embryos are diploid), but the exposition of the deleterious alleles is greater with 1m:0p only if Inline graphic (because only half the alleles, the maternal ones, are exposed to selection without DF).

Indirect selection:

The sign of Inline graphic directly depends on the sign of the linkage disequilibrium Cam. To evaluate indirect selection more precisely, it is useful to express the value of Cam in terms of the model's parameters. Under the QLE assumptions, Cam reaches a pseudoequilibrium value (Inline graphic) that is obtained by solving ΔCam = 0, yielding

graphic file with name M21.gif (4)

where K = 1 − R, R, and Inline graphic for maternal, paternal, or biparental expression of the modifier locus, respectively. Thus, the sign of Inline graphic depends entirely on the sign of K − h, that is, of 1 − R − h, R − h, and Inline graphic, for maternal, paternal, and biparental expression of the modifier locus, respectively. This result can be interpreted by following step by step how the linkage disequilibrium is built through selection and meiosis.

Building of genetic associations by selection:

A lower exposition of deleterious alleles is immediately beneficial to an individual but leads to their accumulation. More specifically, in diploid embryos, deleterious mutations tend to become associated to modifier alleles that minimize exposition. A paternally acting modifier exposes the deleterious allele carried on the paternal chromosome (exposition is increased from 0 to h in the case of DF), which enhances the purge of these paternally inherited chromosomes. As a consequence, a paternally acting modifier tends to become associated to less loaded paternal chromosomes (Inline graphic, where the prime indicates that the association is measured after selection):

graphic file with name M26.gif (5)

On the contrary, a paternally acting modifier always reduces the exposition of the deleterious alleles carried on the maternal chromosome (from 1 to h when there is DF), which reduces purging on these chromosomes and generates more loaded maternal chromosomes (Inline graphic):

graphic file with name M28.gif (6)

The exact opposite occurs for a maternally acting modifier (Inline graphic and Inline graphic):

graphic file with name M31.gif (7)
graphic file with name M32.gif (8)

All of these effects occur when the modifier has an effect in both male and female gametophytes (i.e., in the biparental case).

Effect of meiosis:

The haploid linkage disequilibrium after meiosis (Inline graphic) results from the diploid associations as

graphic file with name M34.gif (9)

(Barton and Turelli 1991); i.e., the diploid cis-associations are carried over at a rate 1 − R while the diploid trans-associations are transformed into Cam at a rate R. In particular, as the recombination rate becomes lower, cis-associations contribute more to generating Cam. Combining Equations 5–9, one easily retrieves Equation 4. For example, with a paternally acting modifier, the cis-association C∅,am is proportional to −h, while the trans-association Ca,m is proportional to 1 − h. Because recombination breaks up cis-associations and transforms trans-associations into haploid cis-associations (Equation 9), the modifier stays overall associated to purged genomes (and favored by indirect selection) when (1 − h)R − h(1 − R) < 0, i.e., when R < h (Equation 4, Figure 4A). In the case of a maternally acting modifier, the roles of cis- and trans-associations (and thus the effect of recombination) are reversed. The modifier stays overall associated to purged genomes when (1 − h)(1 − R) − hR < 0, i.e., when 1 − R < h (Equation 4, Figure 4B). In the biparental case, the four associations Inline graphic play a role and the effect of recombination cancels out. The modifier stays overall associated to purged genomes when (1 − R)(1 − h) − hR + R(1 − h) − h(1 − R) < 0, i.e., when Inline graphic (Equation 4).

Figure 4.—

Figure 4.—

Open in a new tab

Illustration of the QLE analysis of the DF and MCD models. The direction of selection at the modifier locus is indicated for different h (x-axis) and R (y-axis) values. In A and B (DF model), 1m:1p is favored in the shaded area whereas 1m:0p is favored in the open area. In C and D (MCD model), 2m:1p is favored in the shaded area whereas 1m:1p is favored in the open area. A, C and B, D illustrate paternal and maternal expression of the modifier locus, respectively. In all panels, the dashed area corresponds to a negative linkage disequilibrium (the modifier is associated to the purged chromosome). Direct selection favors DF on the left-hand side of the dashed line (which is Inline graphic, A and B), whereas it favors MCD on the right-hand side of the dashed line (which is h = hm = 0.3, C and D). The QLE approximation becomes inaccurate when R is very low (the points represent critical h values obtained directly from exact simulations). Parameter values are s = 5 × 10−2, μ = 10−3, υ = 0.1, δυ = 0.01, h1 = 0.2, and h2 = 0.4.

Overall selection on the modifier:

To obtain the selection coefficient on the modifier [defined as Inline graphic], we replace Cam by Inline graphic in Equation 3, yielding

graphic file with name M40.gif (10)

The sign of sm depends on the term within the brackets. In Figure 4, we illustrate the conditions where sm is positive. When Inline graphic, |Cam| is low: indirect selection is negligible and the sign of sm is given by Inline graphic − h. In this case two equilibria (ν = 0 and ν = 1) exist, and DF is favored when Inline graphic. When R is lower, indirect selection can counterbalance direct selection. With a paternally acting modifier, DF is favored from h = 0 up to Inline graphic, where

graphic file with name M45.gif (11)

On the contrary, with a maternally acting modifier, DF is favored from h = 0 up to Inline graphic. In other words, DF is favored for Inline graphic when Inline graphic. Otherwise (Inline graphic), DF is favored for a range of h values wider than 0 < Inline graphic with a paternal expression of the modifier locus and for a range of h values narrower than 0 < Inline graphic with a maternal expression of the modifier locus. Note that in both the maternal and the paternal case, an intermediate unstable equilibrium (ν different from zero or one) exists in a very small portion of the parameter space when h is between Inline graphic and Inline graphic, where

graphic file with name M54.gif (12)

In this region, the evolutionary outcome depends on initial conditions. Above Inline graphic, DF is disfavored. DF is selected in different conditions depending on whether the modifier locus is paternally or maternally expressed (Inline graphic); it is a case of male/female conflict. With a biparentally expressed modifier, direct and indirect selection has always opposite signs, but indirect selection is never strong enough to counterbalance direct selection. Thus, the critical value of h below which DF is favored is Inline graphic regardless of other parameter values.

Stability analysis of the DF model:

To check the QLE analysis for small R values, we perform a stability analysis. To do so, we consider a population where M is fixed (pAm = pam = 0) and at mutation–selection equilibrium at the viability locus (Inline graphic, Equation 2). We then compute the frequency change of a rare modifier allele introduced in this population. Technically, we linearize the exact recursions on the Am and am haplotypes, assuming they are rare. We then find the dominant eigenvalue of the transition matrix corresponding to these two equations, yielding

graphic file with name M59.gif (13)

where K1 and K2 depend on whether the modifier is maternally, paternally, or biparentally expressed. Their values are given in Table 3. Assuming that mutations are rare, the rate of DF will evolve through successive fixations in the direction predicted by the sign of Inline graphic. The results of the stability analysis are qualitatively comparable to those of QLE. The critical value of h below which DF is favored predicted by this analysis is close to the critical value predicted under QLE assumptions (Inline graphic, Inline graphic). In fact, the absolute difference between the critical h values predicted by the two approaches is Inline graphic, which is negligible when R is large, as expected. In the stability analysis, as in the QLE, an intermediate unstable equilibrium exists in a small portion of the parameter space. In this region, both full and no DF are locally convergent stable states (the outcome depends on initial conditions). The area of this region is very small, ∼s/32 (if one considers that the parameter space is Inline graphic and Inline graphic). This small region is illustrated in Figure 5. In a slightly larger region of the parameter space around the latter, a single convergent stable state is present, but is not stable faced with mutations of large effects. In all cases, the results between QLE and stability analysis are very comparable and qualitatively identical. We now switch to the MCD model.

TABLE 3.

Values of K1 and K2 in the stability analysis for each model

Maternally acting modifier Paternally acting modifier Biparentally acting modifier
DF
    K1 Inline graphic Inline graphic Inline graphic
    K2 h Inline graphic Inline graphic
MCD
    K1 Inline graphic Inline graphic 0
    K2 Inline graphic Inline graphic 0
Open in a new tab

Figure 5.—

Figure 5.—

Open in a new tab

Illustration of the stability analysis of DF and MCD models. The direction of selection at the modifier locus is indicated for different dominance (h, x-axis) and recombination values (R, y-axis). In A and B (DF model), 1m:1p is favored in the area with dark shading [that corresponds to the pairwise invasibility plot (PIP) a], whereas 1m:0p is favored in the open area (that corresponds to PIP e). The areas with intermediate shading correspond to b, c, and d, that is, to cases where (b) DF is only convergent stable, (c) an intermediary, unstable equilibrium exists, and (d) DF is not convergent stable. In C and D (MCD model), 2m:1p is favored in the shaded area whereas 1m:1p is favored in the open area. We can see that the intermediate cases are indistinguishable for the MCD model. The parameters values are h1 = 0.2, h2 = 0.4, μ = 10−3, and s = 10−1.

MCD model analysis:

We analyze this model in the same way as the DF model, using the same assumptions.

Mutation–selection at the viability locus:

The mutation–selection equilibrium at the viability locus is

graphic file with name M76.gif (14)

where hm = (h1 + h2)/2. This value is comparable to the equilibrium frequency in the DF model (Equation 2). Indeed, in the DF model, the exposition of the a allele ranges from h (full DF) to Inline graphic (no DF). Similarly, in the MCD model, the exposition of the a allele ranges from hm (full MCD) to h (no MCD).

Frequency change at the modifer locus:

The frequency change at the modifier locus is determined by direct and indirect selection, as in Equation 3:

graphic file with name M78.gif (15)

The sign of direct selection is given by the sign of h − hm; i.e., direct selection favors the state where the average exposition of deleterious alleles is maximal. This term favors MCD when hm < h. The sign of indirect selection depends directly on the sign of Cam, whose QLE value has the same form as in Equation 4,

graphic file with name M79.gif (16)

where K = 0, Inline graphic, and Inline graphic for biparental, paternal, and maternal expression of the modifier locus, respectively. In the very likely situation where h1 > h2, K is positive for a maternally expressed modifier and negative for a paternally expressed one. Because the sign of Cam depends entirely on the sign of K + h − hm, it is therefore more easily positive with a maternal expression of the modifier locus. The way cis- and trans-associations are built by selection is qualitatively the same as in the DF model:

graphic file with name M82.gif (17)
graphic file with name M83.gif (18)
graphic file with name M84.gif (19)
graphic file with name M85.gif (20)

An important difference between DF and MCD is that MCD can increase or decrease the exposition of maternally inherited deleterious alleles (depending on the value of h1, the exposition of the a allele in aaA endosperms) and can increase or decrease the exposition of paternally inherited deleterious alleles (depending on the value of h2, the exposition of the a allele in AAa endosperms). For instance, a paternally acting modifier increasing MCD decreases the exposition of the deleterious allele carried on the paternal chromosome from h to h1, if h > h1, but increases it if h < h1. In the first case, the paternally acting modifier tends to become associated to more loaded paternal chromosomes (Inline graphic > 0), while in the second case it tends to become associated to less loaded chromosomes (Inline graphic < 0). Combining Equations 17–20 with Equation 9, one easily retrieves the value of Inline graphic. With uniparental expression of the modifier locus, three configurations can occur. In the case where h2 < h < h1, the situation is “reversed” compared to what happens in the DF model, because in these conditions MCD increases the maternal allele's exposition and decreases the paternal allele's one. For instance, for a paternally acting modifier, the cis-association C∅,am is proportional to h − h2 (positive), while the trans-association Ca,m is proportional to h − h1 (negative). The modifier stays overall associated to purged genomes when (h − h2)(1 − R) − (h − h1)R < 0, i.e., when R < (h − h2)/(2h − h1 − h2) (Figure 4C). For a maternally acting modifier, the modifier stays overall associated to purged genomes when (h − h1)(1 − R) − (h − h2)R < 0, i.e., when R < (h − h1)/(2h − h1 − h2) (Figure 4D). In the case of biparental expression of the modifier locus, the effect of recombination cancels out as in the DF model, and the modifier stays overall associated to purged genomes when hm > h. In the second case, where h2 < h1 < h, both maternal and paternal alleles have a better exposition at the 2m:1p state. The haploid linkage disequilibrium Cam is always negative. On the contrary, in the third case, where h < h2 < h1, both maternal and paternal alleles have a better exposition at the 1m:1p state and Cam is always positive.

Overall selection on the modifier:

The selection coefficient at the modifier locus at QLE is of the same form as Equation 10:

graphic file with name M89.gif (21)

In Figure 4, we illustrate the conditions where sm is positive. As in the DF model, there is in most cases only one convergent stable state (either full or no MCD). However, in a region of the parameter space full and no MCD may be both convergent stable states and their domain of attraction is determined by an unstable intermediate equilibrium. As in the DF model, this region is, however, very small. When R = Inline graphic, the sign of sm simply depends on the sign of h − hm. When R is smaller, indirect selection can counterbalance direct selection: with a paternally acting modifier, MCD is favored from h = 1 down to Inline graphic, where

graphic file with name M92.gif (22)

which is narrower than from h = 1 down to h = hm. On the contrary, with a maternally acting modifier, MCD is favored from h = 1 to Inline graphic, which is wider than from h = 1 to h = hm. Like DF, MCD may be selected or counterselected depending on whether the modifier locus is paternally or maternally expressed. When the recombination rate is low, there is a male/female conflict regarding MCD evolution. With a biparentally expressed modifier, indirect selection is never strong enough to oppose direct selection: MCD is favored when hm < h.

Stability analysis:

We make a stability analysis as for the DF model. The dominant eigenvalue of the matrix is

graphic file with name M94.gif (23)

where Inline graphic and where K1 and K2 depend on whether the modifier is maternally, paternally, or biparentally expressed. Their values are given in Table 3. The direction of selection is illustrated in Figure 4. As in the DF model, the QLE and the stability analysis yield comparable results. The absolute difference between the critical h values predicted by the two approaches is Inline graphic, which is negligible when R is large, as expected. As in the DF model, there is also a small region of the parameter space with an intermediate unstable equilibrium, but it is so small that it can hardly be seen in Figure 5.

Combining the evolution of DF and MCD:

So far, we have described the conditions favoring DF and MCD independently. We now consider how these conditions combine to give an overall picture of the evolution of the different types of endosperms (1m:0p, 1m:1p, and 2m:1p). There are a large number of possibilities depending on the relative values of h1, h2, and h. Considering that h2 < h < h1 [as one would expect following the classical metabolic theory of dominance (Kacser and Burns 1981)] and that Inline graphic, we can delineate seven cases. They are illustrated in Figure 6. However, all seven cases are not equally plausible. In particular, h is very likely to be Inline graphic since the deleterious mutations have always been found to be recessive on average in various diploid taxa (see, e.g., García-Dorado and Caballero 2000; Vassilieva et al. 2000; Szafraniec et al. 2003). With this additional condition, only six cases are possible (all but case 7 in Figure 6). With a high recombination rate (i.e., from the conditions where a male/female conflict occurs), only two evolutionary outcomes are possible: 1m:1p if h < hm and 2m:1p if h > hm (cases 1 and 2 in Figure 6). For lower recombination rates, four other possibilities can also occur, including the 1m:0p case (see cases 3–6 in Figure 6).

Figure 6.—

Figure 6.—

Open in a new tab

Combined evolution of DF and MCD. The different possible scenarios for the combined evolution of DF and MCD are shown when Inline graphic. (h1 = 0.6 and h2 = 0.2 in this example, yielding hm = 0.4). The solid lines indicate the critical maternal and paternal h values for DF model. The dashed lines indicate the critical maternal and paternal h values for MCD model. In area 1, DF is favored, and MCD is not (1m:1p is thus expected to evolve). In area 2, both DF and MCD are favored (2m:1p evolves). In area 3, DF is favored and MCD is favored only if under maternal control (thus either 1m:1p or 2m:1p may evolve depending on which sex predominantly controls MCD). In area 4, DF is favored only if under paternal control, and MCD is not favored (thus either 1m:0p or 1m:1p may evolve). In area 5 DF is favored only if under paternal control, while MCD is favored only if under maternal control, and thus 1m:0p, 1m:1p, or 2m:1p may be favored. In area 6 DF is favored only if under paternal control and MCD is always favored (either 1m:1p or 2m:1p may evolve). Eventually, in area 7 neither DF nor MCD is favored, and 1m:0p evolves. The figure is drawn using the results of the stability analysis and with μ = 10−3, s = 10−1, νM = 0.1, and νm = 0.1.

Robustness of the results:

These two-locus models are simplified ways to investigate the effect of masking on DF and MCD evolutions. Integrating the overall selection coefficient over a full genome with many viability loci might be achieved by summing the frequency change of the modifier caused independently by each of them (see, e.g., Otto 2003). This approach is, however, complicated by three factors. First, one would have to integrate over an explicit genetic map (to account for different R values). Second, different loci may exhibit different parameter values (h, h1, h2, s, μ) and the distributions of these parameter values are not well known (including possible correlations between those parameters, for instance, s and h). Third, selective interactions may occur among viability loci and our models do not explore these effects. Finally, we do not incorporate departure from random mating that might affect the conclusions. Future work is required to account for these complications.

DISCUSSION

In this article we modeled the masking of deleterious mutations in the endosperm and its influence on the evolution of DF and MCD. More specifically, we followed the fate of alleles modifying the probability of occurrence of DF or MCD at a modifier locus with a sex-limited expression. In our models, a second locus is expressed in the endosperm and controls the amount of resources available to the embryo. At this locus, deleterious alleles diminish the ability to accumulate resources, and the seeds inheriting this allele have therefore a lower survival rate. In these models, there is no resource reallocation between the different embryos produced by the same mother plant. Thus, all of our results are unrelated to theories based on competition between embryos or kin selection and are attributable only to masking and its possible side effects.

Our work is the first formal demonstration that the masking of deleterious mutations is sufficient for DF and MCD to evolve. In fact, two different effects combine in this theory: first, a direct effect of masking, which depends only on the dominance level of deleterious mutations, and second, an indirect and side effect of masking, proportional to linkage disequilibrium, the value of which depends on whether the expression of the modifier locus is paternal or maternal. The latter effect depends mainly on the values of dominance (h1, h2, and h) and recombination rate. When the recombination rate is high, the indirect effect is always negligible and evolution favors the state with highest masking. Contrary to what is suggested in the literature (Willson and Burley 1983), the 1m:1p state is not necessarily the situation with the strongest masking: for instance, masking can be stronger in 2m:1p than in 1m:1p, when hm < h. When recombination is low, the indirect effect can become predominant and the outcome depends on whether DF or MCD are paternally, maternally, or biparentally controlled.

A new type of male/female conflict:

Our results indicate that for low recombination rates, there is a male/female conflict for the genetic constitution of the endosperm. This male/female conflict results from the fact that increasing the exposition of alleles inherited from a given parent diminishes the exposition of alleles inherited from the other one. In the case of paternal expression of the modifier locus, indirect selection increases the range of h values where DF evolves, while it reduces the range of hm values where MCD evolves. Exactly the opposite occurs with maternal expression of the modifier locus. With biparental expression of the modifier locus, the indirect effect is always negligible even when recombination is low. For instance, with Inline graphic and h = 0.5, a paternal but not a maternal DF allele would spread (see Figures 4 and 5). Similarly, with Inline graphic and h = hm, a maternal but not a paternal MCD allele would spread (see Figures 4 and 5).

Evolutions of DF and MCD:

Both 2m:1p and 1m:1p endosperms can be found in angiosperms. How can such a diversity be explained? Deleterious mutations tend to be recessive in diploids, with average h ranging between 0.1 and 0.4 depending on the studies (see, e.g., García-Dorado and Caballero 2000; Vassilieva et al. 2000; Szafraniec et al. 2003). As a consequence, we would expect that paternally expressed genes favoring DF should always spread or be maintained. This is at least the case for the genes that determine the occurrence of two mitotically derived spermatozoa, since this characteristic, which is a necessary condition for DF evolution, is maintained in all angiosperms (but intriguingly also in gymnosperms). We would also expect that maternally expressed genes favoring DF should spread provided that the average recombination rate is not too low. In other words, for low recombination rates, we do not expect DF to be systematically maintained (depending on which sex controls the trait, see Figure 6). Among angiosperms with postfertilization resource allocation by the female sporophyte, few have lost DF or at least a functional endosperm, the only ones being Podostemaceae and Trapaceae (Chopra and Sachar 1963). These species exhibit high selfing rates (Haig 1988). Including selfing effects in our models will be the purpose of a future study. The Orchidaceae is the other important group where DF occurs but no functional endosperm is present (Chopra and Sachar 1963). In this group, however, there are virtually no resources allocated by the female sporophyte to the seed: the seedlings acquire resources through mycorrhiza. Thus, the degeneration of endosperm in orchids may be unrelated to DF or MCD evolution.

Compared to diploids, little is known about the typical dominance of deleterious mutations in triploids (i.e., the dominance h1 of the aaA genotype and the dominance h2 of the AAa genotype). It seems, however, likely the average dominance in triploids is close to that in diploids [i.e., (h1 + h2)/2 = hm ≈ h], so that we would expect to be often close to the situation where there is a male/female conflict over the evolution of MCD. In these conditions, we would expect to find both types of endosperm (1m:1p and 2m:1p, see Figure 6). Consistent with this prediction, some angiosperms [in Nympheaceae, Hydatellaceae, Cabombaceae, Illiciaceae, Schisandraceae, Austrobaileyaceae, and Oenothera (Maheshwari 1963; Friedman 2001a; Williams and Friedman 2002; Friedman and Ryerson 2009)] have a 1m:1p endosperm (DF, no MCD) and others a 2m:1p endosperm (other groups, both DF and MCD evolved).

DF and diploidy:

It is worth comparing our models of DF evolution with models for the evolution of diploid life cycles (in particular, the model of Otto and Goldstein 1992, which is referred to hereafter as OG92 and is reinvestigated in appendix b). Following the OG92 model, the evolution toward diploid life cycles (2N) requires deleterious mutations to be recessive and recombination to be “sufficiently large.” In fact, these conditions are close to the conditions favoring DF when the expression of the modifier locus is maternal. We can compare these conditions in Figure 7: all other parameter values being equal, the range of R and h values in which DF evolves is slightly wider, but comparable with the range of R and h values favoring 2N. In the two models (DF and OG92), the selection coefficient acting on the modifier can be decomposed into two terms, a direct and an indirect effect that are, superficially at least, comparable. In both models, direct selection favors diploidy when Inline graphic, but for different reasons. In the OG92 model, the exposition of the deleterious alleles is always higher with 1N (full exposition) than with 2N (exposition at a level h). In the DF model, only maternal alleles are exposed. Thus, the average exposition is greater with “haploidy” (1m:0p) only if Inline graphic. As we have already mentioned, this is compensated by the fact that, unlike in the DF model, 2N individuals have twice the chance to carry a deleterious mutation compared to 1N individuals. A second important difference is that, in the DF but not in the OG92 model, the direction and strength of indirect selection differ for paternally or maternally expressed modifiers. In the OG92 model, cis-associations between 2N modifier and deleterious mutations are always positive (in other words, modifiers of haploidy are found more often on purged chromosomes). In contrast, because of the asymmetry inherent to the DF model, where haploidy necessarily concerns maternally inherited alleles at the viability locus, purging of deleterious alleles causes positive cis-association only with maternally expressed modifiers. In other words, maternally acting modifiers of haploidy are found more often on purged chromosomes, while paternally acting modifiers of haploidy are found more often on nonpurged chromosomes. Overall, 2N and OG92 models are in fact quite different, in terms of both direct and indirect selection. In terms of parameter range, DF is necessarily favored if 2N is favored (the reverse is not true). This is consistent with the view that angiosperms have both evolved DF and the shortest haploid phase.

Figure 7.—

Figure 7.—

Open in a new tab

Comparison of the conditions for the evolution of diploidy and DF. The overlap of the conditions of h and R is shown, where diploidy (2N) is favored by the conditions of h and R where DF is favored. Indeed, 2N is favored on the left of the dashed line, while DF is favored on the left of the solid lines (the left solid line corresponds to the case of a maternal expression of the modifier locus and the right solid line corresponds to the case of a paternal expression of the modifier locus). The figure is drawn using the results of the stability analysis and with s = 10−1, μ = 10−3, νM = 0.1, and νm = 0.1.

DF and imprinting:

Our model of DF evolution can also be closely compared to some models of imprinting evolution (Spencer and Williams 1997). Indeed, the evolution toward imprinting in animals can be viewed, at the level of a locus, as a transition from a diploid (1m:1p) to a functionally haploid state (0m:1p for maternal imprinting or 1m:0p for paternal imprinting). In the absence of double fertilization, only the maternally inherited haploid genome is expressed in the endosperm. This situation is therefore similar to a genomewide paternal imprint. More specifically, Spencer and Williams (1997) consider a two-locus model in which the primary locus determines embryo survival and is exposed to deleterious mutations and the second, a modifier locus, is maternally expressed (e.g., during female meiosis) and determines whether the maternal copy of the primary locus is imprinted or not in the embryo. This model would be comparable to a DF model with a paternal expression of the modifier locus. Indeed, in both cases the modifier is cis-acting, meaning that the allele causing silencing is on the same chromosome as the silenced allele (we define the trans-acting modifier as the reverse situation, where the allele causing silencing is not on the same chromosome as the silenced allele). In the DF model with paternal expression, the silenced allele is paternal (as in all DF models) and the control is also paternal. In the Spencer and Williams (1997) model, the silenced allele is maternal and the modifier is also controlled maternally. The comparison of our model with this model of imprinting highlights an important and possibly general feature of models for the evolution of gene expression. More than a maternal vs. paternal effect, the crucial issue is whether the modifier is cis- or trans-acting. It is much more difficult to evolve a cis- than a trans-acting silencing allele because indirect selection always benefits a modifier associated to purged chromosomes. In fact, for any given locus controlling the expression of genes exposed to deleterious mutations, there is a potential for conflict between its alleles. This conflict can occur if the modifier alleles do not have an additive effect (such as when there is a sex-limited expression of the modifier, but the phenomenon may be much more general).

Kin conflict vs. heterozygosity theory:

A widespread view is that DF and MCD evolved in response to a kin conflict over resource allocation (Queller 1984; Dominguez 1995; Friedman 1995; Shaanker and Ganeshaiah 1997; Hardling and Nilsson 1999). This theory relies strongly on the idea that embryos compete for maternal resources. In fact, this theory is appealing because it claims to explain quite generally the evolution of traits involved in postfertilization resource allocation in both plants (DF, MCD, and imprinting) and animals (imprinting). It is, however, mostly supported from observations related to imprinting (see, e.g., Dominguez 1995). The central argument is that the male/female conflict theory predicts a male–female coevolution, which can be detected by distinctive adaptations and counteradaptations. There is, for instance, the well-known case of imprinting of the fetal growth factor Igf2 and its inhibitor Igf2r. Similarly, DF and MCD are viewed as steps in this male/female conflict in plants. There are two problems with this argument. First, what is interpreted here as the signature of a male/female conflict does not necessarily support the kin conflict theory since any theory involving an escalation would be consistent with this interpretation. For instance, our model shows that a male/female conflict can occur over the genetic constitution of the endosperm even in the absence of problems of resource allocation among kin. Second, under a conflict theory, we would expect to see, at least in some cases, an escalation of adaptations and counteradaptations. This is clearly not the case for the evolution of the ploidy of the endosperm: no plants exhibit, for instance, 2m:2p or 3m:2p endosperms, while nothing seems to limit a priori such escalation (contrary to the Igf2 and Igf2r system where the escalation is maximal: the expression of these genes is totally suppressed when inherited maternally or paternally, respectively). Our models show that, depending on parameter values, DF and MCD may be stable states (advantageous for both males and females), which might in fact more closely reflect the data. Thus, the available evidence does not critically favor one theory over the other. More specific tests would be required to discriminate between them.

Combining theories:

The masking effects generated by DF and MCD could interfere with resource allocation to the seed. Willson and Burley (1983) proposed that DF, by masking deleterious mutations in the endosperm, should increase resource allocation to the associated seed (and favor the transmission of paternally inherited alleles). They viewed MCD as a return to a state closer to 1m:0p, which, by exposing deleterious mutations in the endosperm, should decrease resource allocation to the associated seed (and favor the transmission of maternally inherited alleles). This view attempts to bridge the different theories by linking heterosis in the endosperm with the amount of resource allocation to the seed. It may provide a mechanism explaining how DF and MCD could play a role in a male/female conflict over resource allocation. The first part of this argument holds, but could be stated more precisely. Provided Inline graphic, DF increases transitorily the mean fitness in a 1m:0p population. (It is, however, not true at equilibrium where the load is higher in a 1m:1p population if Inline graphic.) Similarly, the second part of the argument can hold, but only under specific conditions. MCD transitorily decreases the mean fitness in a 1m:1p population only if h < hm. This latter condition may, however, not be systematically verified. Overall, combining these two theories would require including them in a proper model, to investigate the conditions where they predict different and distinguishable outcomes. In any case, it seems necessary to include the impact of deleterious mutations because they necessarily occur and because they can produce similar patterns of genetic conflict.

Alternative nutritive tissues:

Accumulating resources directly from an embryonic tissue (like cotyledons) or from a maternal or sporophytic tissue (like the seed coat) could be considered as an alternative to double fertilization. These tissues become predominant in the mature seed in some angiosperms, but the endosperm nearly always subsists, at least transitorily or as an interface. We may wonder why the endosperm is nearly always maintained in such cases. We can tentatively suggest two hypotheses. First, the endosperm can develop immediately after fertilization, while the development of a nutritive embryonic tissue would be constrained by the necessary steps of embryo development. Second, a sporophytic maternal tissue (1m1m′:0p) would confer a similar direct effect of masking but would lead to a very inefficient purge of deleterious mutations because it dissociates the genotype of the embryo from the phenotype on which selection occurs. Indeed, a deleterious m′ allele would decrease the survival of embryos not carrying the mutation, while a deleterious p allele would not be purged (because it is not expressed in a 1m1m′:0p perisperm) although it is transmitted to the next generation. Thus, one can see that selection should be more efficient in purging deleterious mutations with a 1m:1p than with a 1m1m′:0p nutritive tissue.

In some angiosperms, endosperms derived from polysporic gametophytes are alternatives to 1m:1p or 2m:1p endosperms. In a tetrasporic or a bisporic gametophyte, the endosperm can be made of m, m′, and p contributions (Friedman et al. 2008). As with the perisperm, polyspory dissociates the genotype of the embryo from the phenotype on which selection occurs, so that purging would be less efficient with polyspory. However, compared with a monosporic endosperm (2m:1p) where the two maternal alleles are mitotically derived, a polysporic endosperm (1m1m′:1p, for instance) is unlikely to carry two deleterious maternal alleles, and aaA endosperms would be comparatively less frequent with polyspory. For this reason, masking of deleterious alleles would be more efficient with polyspory. A further development of our theory should therefore include a model to evaluate how these antagonistic direct (masking) and indirect (purging) effects combine and to predict conditions when polyspory should evolve.

Conclusion:

Double fertilization and maternal contribution doubling can both evolve because of the masking/exposition of deleterious mutations. This theory is consistent with the pattern seen in seed plants as well as with the theory of kin conflict. Interestingly, our model also predicts that conflicting selection pressures for DF and MCD may occur in male and female gametophytes. The effect of deleterious mutations cannot therefore be neglected in a comprehensive theory of DF and MCD evolution.

Acknowledgments

We thank E. Imbert for stimulating discussions and Dan Schoen, an anonymous reviewer, and Evolutionary Genetics and Ecology Group students, in particular, F. Débarre, for useful comments on the manuscript. This work was supported by a starting grant from the European Research Council to T.L. A.C. benefited from a fellowship from the French Ministry of Research.

APPENDIX A: RECURSIONS

The exact recursions of gamete frequencies (respectively, AM, aM, AM′, and aM′) are for the example of the DF model with a paternal expression of the modifier locus,

graphic file with name M106.gif (A1)
graphic file with name M107.gif (A2)
graphic file with name M108.gif (A3)
graphic file with name M109.gif (A4)

where

graphic file with name M110.gif (A5)

APPENDIX B: QLE ANALYSIS OF THE OTTO AND GOLDSTEIN (1992) MODEL

Whatever the expression of the modifier locus (uniparental or biparental expression), the selection coefficient of diploidy (2N), calculated with QLE assumptions, is

graphic file with name M111.gif (B1)

The eigenvalue is given in their original article. [All parameters are used equivalently except d11 = νM, d12 = (νM + νM)/2, and d22 = νm.]

References

  1. Baroux, C., C. Spillane and U. Grossniklaus, 2002. Evolutionary origins of the endosperm in flowering plants. Genome Biol. 3 1026.1021–1026.1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barton, N. H., and M. Turelli, 1991. Natural and sexual selection on many loci. Genetics 127 229–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bengtsson, B. O., 1992. Deleterious mutations and the origin of the meiotic ploidy cycle. Genetics 131 741–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brink, R. A., and D. C. Cooper, 1940. Double fertilization and development of the seed in angiosperms. Bot. Gaz. 102 1–25. [Google Scholar]
  5. Brown, C. A., and D. R. Formanowicz, 1996. Reproductive investment in two species of scorpion, Vaejovis waueri (Vaejovidae) and Diplocentrus linda (Diplocentridae), from West Texas. Ann. Entomol. Soc. Am. 89 41–46. [Google Scholar]
  6. Bulmer, M., 1986. Genetic models of endosperm evolution in higher plants, pp. 743–763 in Evolutionary Process and Theory, edited by S. Karlin and E. Nevo. Academic Press, New York.
  7. Charnov, E. L., 1979. Simultaneous hermaphroditism and sexual selection. Proc. Natl. Acad. Sci. USA 76 2480–2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Chasnov, J. R., 2000. Mutation selection balance, dominance and the maintenance of sex. Genetics 156 1419–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chopra, R., and R. Sachar, 1963. Endosperm, pp. 135–170 in New Advances in the Embryology of Endosperm, edited by P. Maheshwari. International Society of Plant Morphologists, Delhi, India.
  10. De Fraipont, M., J. Clobert and R. Barbault, 1996. The evolution of oviparity with egg guarding and viviparity in lizards and snakes: a phylogenetic analysis. Evolution 50 391–400. [DOI] [PubMed] [Google Scholar]
  11. De Jong, T. J., H. Van Dijk and P. G. L. Klinkhamer, 2005. Hamilton's rule, imprinting and parent-offspring conflict over seed mass in partially selfing plants. J. Evol. Biol. 18 676–682. [DOI] [PubMed] [Google Scholar]
  12. Dominguez, C. A., 1995. Genetic conflicts-of-interest in plants. Trends Ecol. Evol. 10 412–416. [DOI] [PubMed] [Google Scholar]
  13. Donoghue, M. J., and S. M. Scheiner, 1992. The evolution of endosperm: a phylogenetic account, pp. 356–389 in In Ecology and Evolution of Plant Reproduction: New Approaches, edited by R. Wyatt. Chapman & Hall, New York.
  14. Friedman, W. E., 1995. Organismal duplication, inclusive fitness theory, and altruism—understanding the evolution of endosperm and the angiosperm reproductive syndrome. Proc. Natl. Acad. Sci. USA 92 3913–3917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Friedman, W. E., 2001. a Comparative embryology of basal angiosperms. Curr. Opin. Plant Biol. 4 14–20. [DOI] [PubMed] [Google Scholar]
  16. Friedman, W. E., 2001. b Developmental and evolutionary hypotheses for the origin of double fertilization and endosperm. C. R. Acad. Sci. Ser. III Sci. Vie. Life Sci. 324 559–567. [DOI] [PubMed] [Google Scholar]
  17. Friedman, W. E., and K. C. Ryerson, 2009. Reconstructing the ancestral female gametophyte of angiosperms: insights from Amborella and other ancient lineages of flowering plants. Am. J. Bot. 96 129–143. [DOI] [PubMed] [Google Scholar]
  18. Friedman, W. E., W. N. Gallup and J. H. Williams, 2003. Female gametophyte development in Kadsura: implications for Schisandraceae, Austrobaileyales, and the early evolution of flowering plants. Int. J. Plant Sci. 164 S293–S305. [Google Scholar]
  19. Friedman, W. E., E. N. Madrid and J. H. Williams, 2008. Origin of the fittest and survival of the fittest: relating female gametophyte development to endosperm genetics. Int. J. Plant Sci. 169 79–92. [Google Scholar]
  20. García-Dorado, A., and A. Caballero, 2000. On the average coefficient of dominance of deleterious spontaneous mutations. Genetics 155 1991–2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Guignard, L., 1899. Sur les anthérozoïdes et la double copulation sexuelle chez les végétaux angiospermes. C. R. Acad. Sci. Paris 128 864–871. [DOI] [PubMed] [Google Scholar]
  22. Haig, D., 2000. The kinship theory of genomic imprinting. Annu. Rev. Ecol. Syst. 31 9–32. [Google Scholar]
  23. Haig, D., 2004. Genomic imprinting and kinship: How good is the evidence? Annu. Rev. Genet. 38 553–585. [DOI] [PubMed] [Google Scholar]
  24. Haig, D., and M. Westoby, 1988. Inclusive fitness, seed resource and maternal care, pp. 60–79 in Plant Reproductive Ecology: Patterns and Strategies, edited by J. L. Doust and L. L. Doust. Oxford University Press, Oxford.
  25. Haig, D., and M. Westoby, 1989. Parent-specific gene-expression and the triploid endosperm. Am. Nat. 134 147–155. [Google Scholar]
  26. Hardling, R., and P. Nilsson, 1999. Parent-offspring and sexual conflicts in the evolution of angiosperm seeds. Oikos 84 27–34. [Google Scholar]
  27. Hardling, R., and P. Nilsson, 2001. A model of triploid endosperm evolution driven by parent-offspring conflict. Oikos 92 417–423. [Google Scholar]
  28. Kacser, H., and J. A. Burns, 1981. The molecular-basis of dominance. Genetics 97 639–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Law, R., and C. Cannings, 1984. Genetic analysis of conflicts arising during development of seeds in the Angiospermophyta. Proc. R. Soc. Lond. Ser. B Biol. Sci. 221 53–70. [Google Scholar]
  30. Maheshwari, P., 1963. Recent Advances in the Embryology of Angiosperms. Ed. International Society of Plant Morphologists, University of Delhi, Delhi, India.
  31. Nawaschin, S. G., 1898. Resultate einer Revision der Befruchtungsvorgänge bei Lilium Martagon und Fritillaria tenella. Bull. Acad. Sci. St. Petersburg 9 377–382. [Google Scholar]
  32. Otto, S. P., 2003. The advantages of segregation and the evolution of sex. Genetics 164 1099–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Otto, S. P., and T. Day, 2007. A Biologist's Guide to Mathematical Modeling in Ecology and Evolution. Princeton University Press, Princeton, NJ.
  34. Otto, S. P., and D. B. Goldstein, 1992. Recombination and the evolution of diploidy. Genetics 131 745–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Perrot, V., S. Richerd and M. Valero, 1991. Transition from haploidy to diploidy. Nature 351 315–317. [DOI] [PubMed] [Google Scholar]
  36. Queller, D. C., 1983. Kin selection and conflict in seed maturation. J. Theor. Biol. 100 153–172. [Google Scholar]
  37. Queller, D. C., 1984. Models of kin selection on seed provisioning. Heredity 53 151–165. [Google Scholar]
  38. Shaanker, R. U., and K. N. Ganeshaiah, 1997. Conflict between parent and offspring in plants: predictions, processes and evolutionary consequences. Curr. Sci. 72 932–939. [Google Scholar]
  39. Shaanker, R. U., K. N. Ganeshaiah and K. S. Bawa, 1988. Parent-offspring conflict, sibling rivalry, and brood size patterns in plants. Annu. Rev. Ecol. Syst. 19 177–205. [Google Scholar]
  40. Spencer, H. G., and J. M. Williams, 1997. The evolution of genomic imprinting: two modifier-locus models. Theor. Popul. Biol. 51 23–35. [DOI] [PubMed] [Google Scholar]
  41. Stebbins, G. L., 1976. Seeds, seedlings, and the origin of angiosperms, pp. 300–311 in Origin and Early Evolution of Angiosperms, edited by C. B. Beck. Columbia University Press, New York.
  42. Szafraniec, K., D. M. Wloch, P. Sliwa, R. H. Borts and R. Korona, 2003. Small fitness effects and weak genetic interactions between deleterious mutations in heterozygous loci of the yeast Saccharomyces cerevisiae. Genet. Res. 82 19–31. [DOI] [PubMed] [Google Scholar]
  43. Trivers, R. L., 1974. Parent-offspring conflict. Am. Zool. 14 249–264. [Google Scholar]
  44. Tutt, K., C. H. Daugherty and G. W. Gibbs, 2002. Differential life-history characteristics of male and female Peripatoides novaezealandiae (Onychophora: Peripatopsidae). J. Zool. 258 257–267. [Google Scholar]
  45. Vassilieva, L. L., A. M. Hook and M. Lynch, 2000. The fitness effects of spontaneous mutations in Caenorhabditis elegans. Evolution 54 1234–1246. [DOI] [PubMed] [Google Scholar]
  46. Westoby, M., and B. Rice, 1982. Evolution of the seed plants and inclusive fitness of plant-tissues. Evolution 36 713–724. [DOI] [PubMed] [Google Scholar]
  47. Williams, J. H., and W. E. Friedman, 2002. Identification of diploid endosperm in an early angiosperm lineage. Nature 415 522–526. [DOI] [PubMed] [Google Scholar]
  48. Willson, M., and N. Burley, 1983. Sporogenesis and double fertilization, pp. 75–93 in Mate Choice in Plants: Tactics, Mechanisms, and Consequences, edited by R. May. Princeton University Press, Princeton, NJ.
  49. Wourms, J. P., 1993. Maximization of evolutionary trends for placental viviparity in the spadenose shark, Scoliodon-laticaudus. Environ. Biol. Fishes 38 269–294. [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES