Fast multiple alignment of ungapped DNA sequences using information theory and a relaxation method

Abstract

An information theory based multiple alignment (“Malign”) method was used to align the DNA binding sequences of the OxyR and Fis proteins, whose sequence conservation is so spread out that it is difficult to identify the sites. In the algorithm described here, the information content of the sequences is used as a unique global criterion for the quality of the alignment. The algorithm uses look-up tables to avoid recalculating computationally expensive functions such as the logarithm. Because there are no arbitrary constants and because the results are reported in absolute units (bits), the best alignment can be chosen without ambiguity. Starting from randomly selected alignments, a hill-climbing algorithm can track through the immense space of sⁿ combinations where s is the number of sequences and n is the number of positions possible for each sequence. Instead of producing a single alignment, the algorithm is fast enough that one can afford to use many start points and to classify the solutions. Good convergence is indicated by the presence of a single well-populated solution class having higher information content than other classes. The existence of several distinct classes for the Fis protein indicates that those binding sites have self-similar features.

INTRODUCTION

To study the statistics of bases in binding sites, not only do we need the sequences and an appropriate measure of the property we are interested in, but we also must have the sequences aligned against one another. Much attention has been paid to the alignment of one sequence against another [22] but the alignment of more than two sequences is hindered by the exponential nature of the problem. With a typical binding site having only 20 sequences available, each allowed to move back and forth over 10 positions, we find ourselves exploring a space of 10²⁰ possible alignments.¹ With exceptional cases, such as splice junctions [19], one could have 10¹⁰⁰⁰⁰ alignments.

It is impractical to thoroughly search this space for “the best alignment”, so perhaps we can find a set of reasonable alignments. The algorithm developed in this paper allows one to explore a reasonable portion of the space of possible alignments. The method does not allow for gaps in the sequence because it is designed to align a set of sequences that contain a DNA (or RNA) binding site. It was successfully used to align binding sequences of the OxyR protein [21] and used to determine that an alignment of Fis binding sites was optimal.²

METHODS

This method uses a set of nucleic-acid sequences with an initially arbitrary alignment. A window, window_left to window_right is chosen relative to a base assigned coordinate 0. For example, the window consisting of positions −10 to +10 is shown by the *’s in the alignment below:

The algorithm also uses a global measure of how good the sequence alignment is within the window. For this purpose we chose the information measure R_sequence [13, 2, 23], which represents the total sequence conservation in the window. Unlike other measures, R_sequence has the advantage that the alignment results are consistent with further information analysis [7] and with a two-state thermodynamic model for the binding process [10]. We will describe the algorithm by a series of improvements on a basic method.

Some useful definitions are:

• step: to move one sequence left or right.

• shuffle: a set of steps of one sequence from window_left to window_right.

• pass: a set of shuffles over all sequences.

• run (or alignment): a set of passes starting from different initial alignments.

In the simplest algorithm, we perform these operations at each step:

1. Tabulate the number of bases b ∈ {A,C,G,T} at each position l within the window. Call this table n(b, l).

2. Determine the number of bases at each position,

   $$n(l)=\sum _{b=A}^{T}n(b,l)$$ (1)

   and then create a table of frequencies:

   $$f(b,l)=\frac{n(b,l)}{n(l)}.$$ (2)

3. We now evaluate the uncertainty [16, 17, 18] of each base within this window:

   $$Hs(l)=-\sum _{b=A}^{T}f(b,l){log}_{2}f(b,l)(\text{bits}\text{per}\text{base}).$$ (3)

4. The information in the sequences is

   $$R_{\mathit{sequence}}(l)=2-(Hs(l)+e(n(l)))(\text{bits}\text{per}\text{base}),$$ (4)

   where e(n(l)) is a small sample correction for Hs(l) [13].

5. Our goal is to maximize the information from the entire window:

   $$R_{\mathit{sequence}}=\sum _l{R}_{\mathit{sequence}}(l)(\text{bits}\text{per}\text{site}).$$ (5)

   R_sequence is a global measure because it is calculated uniformly from all the sequences at once.

6. In a single shuffle, a sequence is moved left by a predetermined parameter “shift left”, evaluated, and then moved one position to the right, evaluated, and so forth until it has arrived at “shift right”. The position that gives the highest information content, R_sequence, is chosen as the new alignment for that sequence. Conflicts are resolved by pseudo-random choice.

7. We then perform a series of passes through the sequences. A pass consists of shuffling the first sequence back and forth to maximize R_sequence, then the second sequence is shuffled, and so forth through the entire set of sequences. The algorithm halts when an entire pass has been completed with no change to any alignment, the change in R_sequence is less than a given tolerance or, to avoid infinite cycling, when an arbitrary limit of passes has been reached.

The algorithm as it stands is slow because each evaluation requires a large amount of tabulation, and the calculation of many additions, divisions, multiplications and logarithms. We now show how the speed of the algorithm can be drastically increased, so that it becomes a practical tool. First, for simplicity, we will assume that n(l) = n, a constant. (In our current implementation, the ends of the sequences are not allowed to slide into the window.) Second, any constant quantity, such as the value 2 and e(n(l)) in equation (4), can be removed. So, instead of maximizing the information R_sequence, we minimize the total uncertainty:

$$H=\sum _l\sum _{b=A}^T-f(b,l){log}_{2}f(b,l)$$ (6)

(The method is therefore curiously related to maximum entropy procedures. In biological systems the entropy is minimized by evolutionary selective pressure [8].) Third, since there are only n sequences, we can make up a table for values of partial uncertainties

$$\mathit{flogf}(i)=-f{log}_{2}f$$ (7)

for f = i/n over the range i = 0 … n. Even with many sequences it is not expensive to store this table. flogf (0) = 0 since lim_{f → 0} f log₂ f = 0. This table is constructed after n has been determined, but before the alignment passes are performed, so it eliminates all the divisions, multiplications and logarithms from the main loop. Now only table lookups and additions are needed to do a shuffle.

The algorithm can be improved further by reducing the computation at each step. At this point to do each step we:

1. remove a sequence from the n(b, l) table by subtracting 1 from the appropriate entries. Call the table for the n − 1 other sequences n′(b, l).

2. add the sequence back to n′(b, l) in all positions determined by “shift left” to “shift right” to regenerate n(b, l).

3. Use the f log f table to find the alignment that gives the minimum H:

   $$H=\sum _l\sum _b\mathit{flogf}(n(b,l)).$$ (8)

This algorithm requires changing n(b, l) for every step of the shuffle. We can avoid this by computing a table of differences of f log f before we begin the run:

$$\mathit{dflogf}(i)=\left[-\frac{i+1}{n}{log}_2\frac{i+1}{n}\right]-\left[-\frac{i}{n}{log}_2\frac{i}{n}\right]$$ (9)

over the range i = 0… n − 1. Suppose that a new alignment of the sequence will place base d at position l of the window. Then the uncertainty at position l will be

$$H(l)=\mathit{flogf}(n^{\prime }(d,l)+1)+\sum _{b,b\ne d}\mathit{flogf}(n^{\prime }(b,l)).$$ (10)

But since

$$\mathit{dflogf}(n^{\prime }(d,l))=\mathit{flogf}(n^{\prime }(d,l)+1)-\mathit{flogf}(n^{\prime }(d,l)),$$ (11)

equation (10) becomes

$$H(l)=\mathit{dflogf}(n^{\prime }(d,l))+\sum _b\mathit{flogf}(n^{\prime }(b,l))$$ (12)

so

$$H=\sum _l\mathit{dflogf}(n^{\prime }(d,l))+\sum _l\sum _b\mathit{flogf}(n^{\prime }(b,l)).$$ (13)

The second term is a constant which does not need to be calculated during a shuffle because n′(b, l) is a constant that does not change during a shuffle. So by precalculating differences of the evaluation function, one can evaluate an aligned set of sequences using only table lookups and a sum. Each sequence is only removed from n(b, l) once and restored in a different position only after the new alignment has been found. (If the sequence is not shifted, then the original n(b, l) need not be changed at all.)

The overall shuffle algorithm is now:

1. Remove a sequence from the n(b, l) table to create n′(b, l);

2. For each sequence shift, (shift ∈ shift_left … shift_right) find the sum of the increments in H that would accumulate over the bases in the window:

   $$dH=\sum _{l={\text{window}}_{\text{left}}}^{{\text{window}}_{\text{right}}}\mathit{dflogf}[n^{\prime }(\mathit{sequence}(l+\text{shift}),l)].$$ (14)

3. Choose the alignment shift that gives the smallest dH. Call this dH_minimum.

4. Adjust the overall uncertainty H by

   $$H_{\text{new}}=H_{\text{old}}+{dH}_{\text{minimum}}-{dH}_{\text{old}}$$ (15)

   The value of dH_old for the alignment without any shift is conveniently found by using an “if shift = 0” statement in the shuffle loop that determines dH_minimum.

5. Add the sequence back into the n′(b, l) table at the best shift to create the new n(b, l).

An alignment is uniquely identified by the vector consisting of the n shifts. When a new alignment is found at the end of a run, its vector is placed into a list of vectors and when an alignment is found that is already in the list, only the total number of times it has appeared needs to be recorded.

The alignment vector (4,2,3) is equivalent to (0, −2, −1) because each sequence is shifted by −4, so vectors can be normalized by subtracting the first shuffle element from all elements. (This is not yet implemented in Malign version 2.38.)

The final sets of alignments are sorted by their information contents and reported as vectors. A second program, Malin, allows one to convert various alignments into Delila instructions [14] so that the sequences can be further manipulated and viewed with the sequence logo technique [12].

PROGRAMS

The Malign multiple alignment program was written in Pascal [6] and can be automatically converted to C. It is available as part of the Delila system [14, 15] by anonymous ftp to ftp.ncifcrf.gov in pub/delila/malign.p or via the World Wide Web site http://www-lmmb.ncifcrf.gov/~toms.

RESULTS

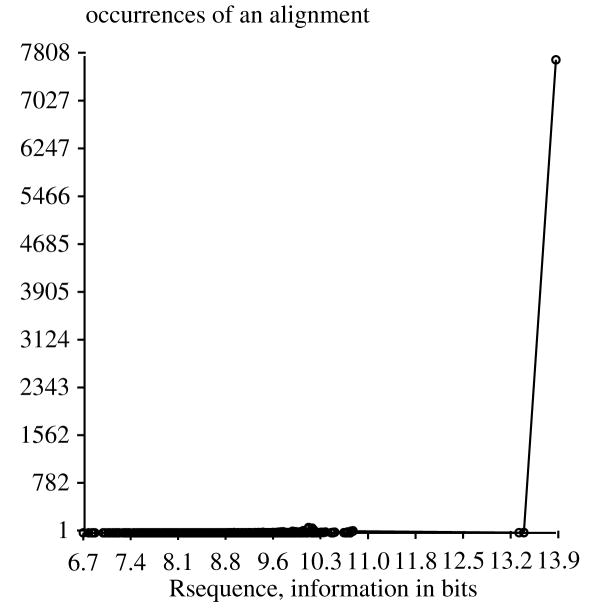
We aligned 16 randomly generated sequences that bind to OxyR [21], using a window of 35 bases from −17 to +17. The shifting parameters were set to the range −100 to +100 so that the Malign program would shift each sequence to its limit (without introducing gaps). For 1000 alignments there is a single well-populated best alignment, separated from all other alignments by more than 3 bits. For 10000 alignments the same well-populated best alignment at R_sequence = 13.9 bits was found, but three new alignments were found near 13.4 bits. Fig. 1 shows the distribution of R_sequence values. (Because alignment vectors are not yet normalized, this is only an approximate distribution. However in the distribution there are only 140 duplicated values for OxyR and none for Fis.)

Figure 1.

Distribution of 10000 alignments of 16 OxyR binding sites.

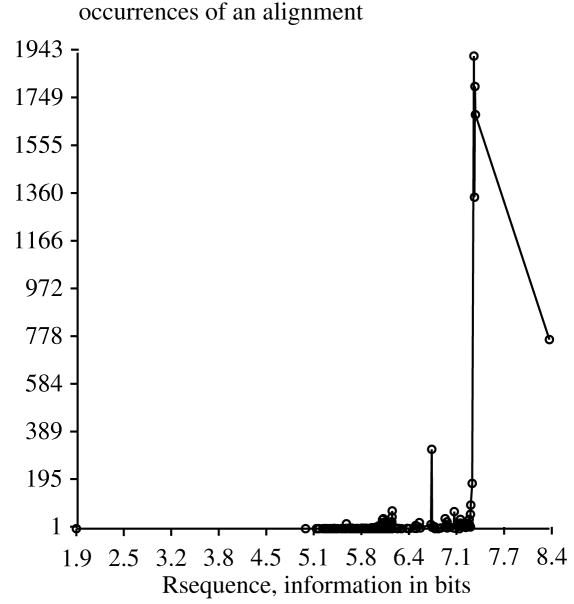
We collected 44 binding sites of the Fis protein [3, 4] from Escherichia coli and Salmonella typhimurium (manuscript in preparation) and we wanted to know whether the sites were aligned correctly. A window of 21 bases, from −10 to +10, covers the Fis sites. Since several of the Fis sites are spaced only 7 bases apart, we allowed shifting of each sequence only from −6 to +6. The total number of possible alignments in this space is 44¹³ = 2.3×10²¹. 1000 alignments took 103 seconds on a Sun SPARCstation 20/61. 10000 alignments took 1023 seconds, and gave almost identical results. Another 10000 alignments starting with a different random number seed took 1014 seconds, and again gave almost identical results. Fig. 2 shows the distribution of R_sequence values. There is a well-populated best alignment, a gap of about 1 bit and then a series of worse alignments. The next best alignments are more populated than the best alignment, but this means that they are easier to find, not that they are necessarily better. Despite our naive attempt to prevent the program from finding the nearby sites, the range −6 to +6 still allowed Malign to find alignments that include those sites. The striking difference between the distributions for Fis and OxyR can be explained by proposing that Fis sites have a self-similar structure, while OxyR sites do not, in contrast to the previous report [21]. The self-similarity of Fis sites gives spacings of 7 and 11 bases, as will be described elsewhere (P. N. Hengen et al., manuscript in preparation). Inspection of the alignment vectors revealed the nature of the three peaks. The lowest peak represents shifts of ±6 and ±5. For example, 1702 alignments occurred with an R_sequence of 7.4 bits and the following relative aligned bases:

Figure 2.

Distribution of 10000 alignments of 44 Fis binding sites.

Many of these combinations would be equivalent to spacings of sites exactly 11 base pairs apart. (There are 92 alignments in the vector because both the sequences and their complements were used. They are listed as pairs of numbers which is why each number is followed by its negative.) The highest peak contained ±5 and ±2 (spacing of 7) and the middle peak appears to contain a combination of these.

DISCUSSION

Although the order of the algorithm is proportional to the number of sequences (n), the width of the window (w = window_right − window_left + 1), and the extent of the shuffle (s = shift_right − shift_left + 1), this is not a major hindrance because the algorithm converges quickly. This allows many of the sⁿ possible alignments to be tried as starting points, and allows the program to find a distribution of alignments, each a local minimum in the n dimensional alignment space defined by the alignment vectors.

The Malign program has several advantageous features:

1. It is able to try many combinations because it is fast.

2. Confidence in an alignment grows when it is found many times.

3. Although sequence alignments are discrete, they can be almost uniquely identified by their information content since the information measure is continuous.

4. The program is most useful in cases where a clear consensus sequence could not be determined. In retrospect we can understand why this happened for OxyR. The OxyR binding sites are spread out over 4 major and 3 minor grooves of B-form DNA and so have low information content per position on the average (0.4 bits/base), although the total is around 14 bits. This made alignment of synthetic random sequences difficult by hand but straightforward with Malign. Fis binding sites are smaller but their low information content of 8 bits has prevented determination of a consistent consensus [3, 4]. Forming a consensus requires altering the frequencies of bases from low values to zero and from high values to 50 or 100 percent, and this destroys the sensitivity that is maintained by Malign.

5. Because many alignments can be tried, the program provides a sensitive way to detect repetitious structures in a set of sequences.

Each step and the sums in the step are amenable to parallel processing, as is computation of the precalculated tables.

Multiple alignment with gaps [2, 23] is a difficult problem which we are often able to avoid because DNA-protein contacts are to a first approximation rigid. However cases of flexibility are known, such as the variable distance between procaryotic promoter −35 and −10 regions [5] and a few cases of altered spacing in CRP sites [1]. Ideally we would like to eliminate the arbitrary “gap penalties” used in many methods [22] because unlike the uncertainty, which corresponds to the entropy of the sequences [9], gap penalties have no obvious physical basis and the penalties might vary from position to position in a sequence. To devise a gap-penalty free algorithm we must first determine how to handle the gaps: should they be treated as characters or not? If one treats them as characters then the alignment will expand indefinitely because insertion of columns of blank characters would increase the information content. On the other hand, if one simply accepts the blanks and only calculates on the sequences, then one is reducing the variability of the patterns and so perhaps artificially raising the information content [13]. A simple solution is to calculate the additional uncertainty at each position using gaps and non-gaps as the symbols, since this has the property of not contributing to the total if gaps or non-gaps predominate. This method of counting gaps at each position seems to suggest that gaps could leap from one site to another irrespective of the surrounding sequence, and so it may not be reasonable. Alternatively, one may compute a penalty in bits for each sequence containing a given number of gaps by computing the logarithm of the total possible number of gap and non-gap arrangements, which would be a binomial. The overall penalty could be taken as the average over all sequences in the entire set. This method has the advantage of directly counting the number of ways a sequence recognizing molecule could be stretched to fit the binding site, but it appears to be sensitive to the size of the alignment window. Finally, the gaps could be treated in the computation as a set of bases with equal probabilities (or probabilities from the genome of the organism). It is not yet clear which, if any, method is correct in a philosophical sense. In addition to these subtle issues there are also technical difficulties, one of which is how to introduce the many possible combinations of gaps and non-gaps without requiring impossibly large computations. It is likely that dynamic programming methods could be used for this process.