Abstract
Different chemical and mutational processes within genomes give rise to sequences with different compositions and perhaps different capacities for evolution. The evolution of functional RNAs may occur on a “neutral network” in which sequences with any given function can easily mutate to sequences with any other. This neutral network hypothesis is more likely if there is a particular region of composition that contains sequences that are functional in general, and if many different functions are possible within this preferred region of composition. We show that sequence preferences in active sites recovered by in vitro selection combine with biophysical folding rules to support the neutral network hypothesis. These simple active-site specifications and folding preferences obtained by artificial selection experiments recapture the previously observed purine bias and specific spread along the GC axis of naturally occurring aptamers and ribozymes isolated from organisms, although other types of RNAs, such as miRNA precursors and spliceosomal RNAs, that act primarily through complementarity to other amino acids do not share these preferences. These universal evolved sequence features are therefore intrinsic in RNA molecules that bind small-molecule targets or catalyze reactions.
Keywords: SELEX, in vitro selection, nucleotide composition, self-organization
INTRODUCTION
Studies of RNA have long provided a fruitful paradigm for the evolution of complex traits (Eigen and Schuster 1977; Fontana and Schuster 1998), in part because the RNA molecule itself embodies both genotype and phenotype. Experimental studies of the evolution of functional RNAs through in vitro selection (Ellington and Szostak 1990; Robertson and Joyce 1990; Tuerk and Gold 1990) to recapture known activities (Salehi-Ashtiani and Szostak 2001) or enhance new activities (Lehman and Joyce 1993; Johnston et al. 2001) have demonstrated that many RNA sequences have the capacity to acquire new functions with only small changes in the primary sequence. It is even possible to traverse the path from one arbitrarily chosen functional RNA molecule to another by single mutations that preserve function right up to the “intersection sequence” that links the neutral networks of sequences that embody each function (Schultes and Bartel 2000; Held et al. 2003).
A second tradition in studies of RNA evolution examines compositional biases, primarily in naturally occurring RNAs in cells. Many functional RNA molecules show a preference for purines (Elson and Chargaff 1955; Lao and Forsdyke 2000), and there is far more variation along the GC axis (i.e., the axis where the compositions of G and C are the same, as well as of A and U) than along the two other orthogonal axes of composition (Schultes et al. 1997, 1999; Smit et al. 2006). These patterns are replicated in both ribosomal RNA subunits from all three domains of life, although these key features may be due to self-organization of RNA during secondary structure assembly rather than due to selection for specific compositions (Smit et al. 2006). Interestingly, RNAs can be artificially selected for functions using as few as three of the four standard nucleotides (Rogers and Joyce 1999) or as few as two nonstandard nucleotides (Reader and Joyce 2002), albeit with reduced efficiency. Within genomes, it is known that different mutational patterns can have large impacts on overall composition (Sueoka 1962, 1988). However, no large-scale comparison of naturally selected RNAs (from modern organisms) to artificially selected RNAs (from in vitro selection in the laboratory) has yet been performed. Such a comparison is essential for understanding whether the preferences found in RNAs within organisms are accidents of biology or universal features of functional RNAs.
In the current study, we have taken artificially selected RNAs from the literature and determined their distributions within composition space using computational techniques that we previously used to show that the hammerhead ribozyme and the isoleucine aptamer have different regions of preferred composition (Knight et al. 2005). However, with a sample size of two sites, we were unable in that previous work to draw general conclusions about the preferred compositions of artificially selected RNAs. Comparing the distributions of artificially selected RNAs to those of naturally occurring RNAs from cells provides important insights into explaining observed compositional biases, designing efficient in vitro selection experiments, and furthering our understanding of RNA evolution.
RESULTS
To compare the distributions of naturally and artificially selected RNAs, we plotted their nucleotide compositions using a 3D projection that preserves all the information about the nucleotide composition (Schultes et al. 1997; Knight et al. 2005; see also Materials and Methods). Specifically, we define three orthogonal axes for pairwise combinations of nucleotides, so that all possible sequences lie within a tetrahedron where the vertices represent 100% composition of each of the 4 nucleotides (nt). We can then plot the location of each sequence within this space, and define regions of composition space where particular kinds of RNAs appear or, in the case of classes of RNAs containing specific motifs, are likely to be found.
Artificially selected and naturally occurring RNAs have similar compositional preferences
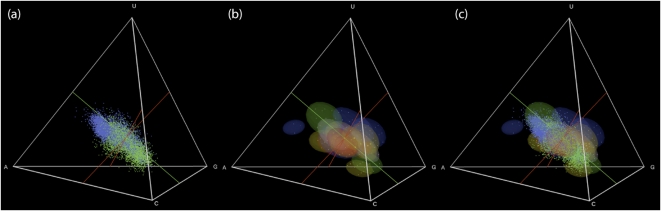
The regions of composition space occupied by naturally occurring aptamers and ribozymes from cells, obtained from Rfam release 9.1 (Gardner et al. 2009), match the regions that our calculations predict to have high probabilities of containing artificially selected aptamer and ribozyme motifs (Fig. 1; for details, see Materials and Methods). In both cases, the distributions are significantly biased toward purines (P < 10−6, t-test) and more spread out along the GC axis than along the other axes (P < 0.001, Monte Carlo). Overall, the probability that the two distributions match as well as they do by chance is P ≈ 0.001 (Monte Carlo). This result shows that the distribution of natural aptamers and ribozymes is likely governed by intrinsic properties of functional RNA that are recaptured in artificial selection experiments in the laboratory. Interestingly, miRNA precursors and guide RNAs (spliceosomal RNAs and snoRNAs) do not share these biases (Fig. 3, see below). These structural identities are therefore characteristic of RNAs that perform catalytic and binding tasks, rather than RNAs that act primarily through complementarity to other sequences.
FIGURE 1.
Striking similarities between distributions of (a) natural aptamers (green) and ribozymes (blue), and (b) artificial aptamers and ribozymes colored by function (nucleotide binding, red; antibiotic binding, blue; amino acid binding, yellow; self-cleaving ribozyme, gray; other, green); (c) the superposition of the two. Results for artificial sequences shown here and in Figure 2 are for 100-nt sequences; sequence length had little effect (Fig. 7). Summing the individual motif probabilities, rather than calculating motif overlaps, gave similar results (Fig. 8).
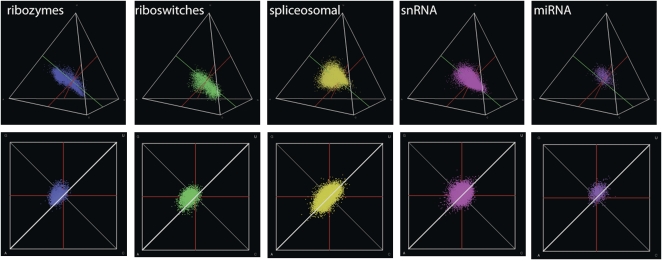
FIGURE 3.
miRNA precursors and guide RNAs (spliceosomal and snRNAs, whose functionality is governed by complementarity to a target) do not follow the same compositional distribution as do RNAs that are themselves functional (i.e., aptamers and ribozymes). Only natural ribozymes and aptamers (riboswitches) follow the patterns shown by the high-probability regions of the artificially selected motifs.
Differential effects of sequence and folding
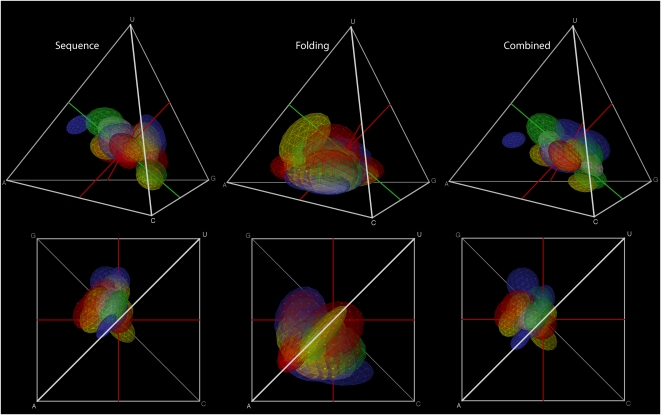
To isolate the source of the observed compositional biases, we separated the effects of active-site composition and of folding on the overall abundance of each motif (Fig. 2). Specifically, at each location in composition space, we calculated the probability of observing a sequence compatible with all the active-site elements (stems and unpaired regions, in the correct order), and then summarized the results for each motif as an ellipsoid as in Figure 1b (Fig. 2, left panels; see Materials and Methods for more details on this calculation and the other calculations in this section). We then calculated the probability that, once generated, the sequences with each composition would fold into the correct structure by testing whether the minimum free energy structure produced by RNAfold contained all the base pairs required by the motif and also left unpaired all the bases that the motif specified as unpaired. We used a binary measure (compatible/incompatible) for each sequence rather than summarizing probabilities from partition function folding because the latter is considerably slower, and small-scale initial tests indicated that the results were comparable (data not shown). The ellipsoid for each motif summarizing where the sequences compatible with the motif, once generated, are most likely to fold is shown in the middle panels of Figure 2. The overall probability that a sequence compatible with active site motifs identified by in vitro selection will occur is highest in moderately purine rich regions of composition space, especially for sequences that are more biased toward G than toward A. However, the probability that a compatible sequence, once generated, will fold into the motif correctly is highest in sequences that are biased toward A, perhaps because of the unique contribution of A to base stacking (Gutell et al. 2000). The combination of these two factors explains the overall compositional bias in the region in which randomly generated sequences are most likely to be functional, and suggests that the biases stem from rules of RNA self-assembly (Schultes et al. 1999) rather than selection (Lao and Forsdyke 2000). Note that part of the contribution to self-assembly is that the sequences contain regions compatible with stems, which we count under the “sequence requirements” rather than the “folding requirements” in this study. Because our artificial RNAs have never been inside a cell and are independently folded through computer simulation, specific biological features or intermolecular interactions cannot explain the compositional preferences.
FIGURE 2.
Separate components of active-site composition and folding preferences. (Left) Active-site sequence requirements; (middle) folding; (right) combined. Although more of the effect comes from the active-site requirements than from folding, the effects of folding shift the overall position of the distribution.
Effect of RNA function
We found no association between particular functions and location in composition space: four general categories of motifs (amino acid aptamers, antibiotic aptamers, self-cleaving ribozymes, and miscellaneous other motifs) did not occupy statistically distinct regions of sequence space. A label permutation test (see Materials and Methods) showed no overall clustering of the means of these distributions relative to chance expectations (P > 0.05). These results suggest that there are not specific regions of composition space that are especially enriched for individual RNA functions. Instead, there are overall compositional preferences that all functional RNAs share. However, it is not simply the case that all biological RNAs automatically follow these same preferences. Figure 3 presents plots of several different kinds of biological RNAs. Although naturally occurring RNAs that are aptamers (e.g., in riboswitches) or ribozymes follow the patterns observed for artificially selected RNAs; other types of RNAs that are functionally important, such as miRNAs, snRNAs, and snoRNAs, do not. These latter RNAs, which function primarily by complementarity to another nucleic acid target, follow their own characteristic distributions of composition that are markedly different and may be related to their different modes of action.
DISCUSSION
Previous work on the subtle interplay between sequence composition and molecular function (Schultes et al. 1997; Knight et al. 2005) has been extensive and informative, but limited either in the number of functions studied or the range of compositions examined. The availability of a principled method for estimating the probabilities of each active site, and the application of this method to a large number of motifs throughout the full range of sequence composition, has allowed for the first time the identification of general biases due to active site preferences and to folding that hold across many motifs. The new approaches for assessing the probability that a given sequence contains the elements required for a specific molecular function allow us to place guaranteed upper bounds on the results we obtained.
Our results have broad implications for evolution both in the RNA World and in the laboratory today: they suggest that the purine bias is universal to all functional RNAs, not just to biological ones, and explain the empirically observed ease of evolution from one active site to another. The implications for searches for functional RNAs in genomes and for the design of pools for in vitro selection are that introducing generalized purine biases may be useful. For genome searches, introducing compositional preferences that include covariation in compositions across homologous sequences could provide more power than existing approaches based on GC content or homology alone. For SELEX pools, purine biases could potentially improve the overall probability of function from 0.00093 for unbiased sequences to 0.0014 at an approximately optimal composition of 30% A, 15% C, 30% G, and 25% U; a 50% increase in overall probability of function. In contrast, tuning the composition of random-sequence pools for specific activities (Kim et al. 2007) may not provide an additional advantage over tuning the pools for activity overall. This interpenetration of regions where function is abundant suggests that there are many pathways and many chemistries by which an RNA World (Gilbert 1986) could have started: that is, evolution of one functional RNA would automatically predispose to the production of others.
Although the final bridge (the probability that a motif that is predicted to fold correctly has biochemical activity, as validated by laboratory experiments) remains to be crossed, the fact that independent simulated folding of RNAs containing small active-site motifs recaptures universal features of aptamers and ribozymes in organisms indicates that the physical models underlying predictions of RNA secondary structure (Jaeger et al. 1989) are reasonable approximations to the truth and can inform us about universal principles of self-assembly of RNA active sites.
MATERIALS AND METHODS
Methods overview
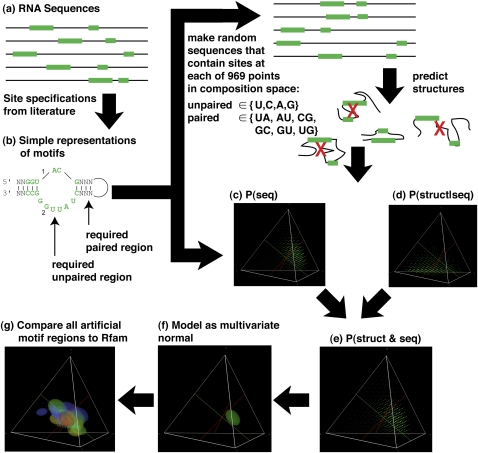
To determine the optimal regions of composition space for occurrence of functional RNAs, we performed the following procedure: for each sequence composition, we calculated the probability of sequences matching a given active site, estimated the probability of correct folding given that the sequence elements were found, then multiplied these two probabilities to obtain the joint probability of the sequence elements and the correct secondary structure (Fig. 4; Knight et al. 2005). We collected from the literature active-site specifications for 23 non-redundant RNA motifs isolated by in vitro selection (Table 1; Ellington and Szostak 1990; Robertson and Joyce 1990; Tuerk and Gold 1990). Even though the probability of occurrence of small motifs can be calculated exactly using finite-state automata (Lladser et al. 2008), the actual motifs are sufficiently large to require approximations (Kennedy et al. 2008). Although the Poisson approximation gives results that match empirical data well over many orders of magnitude (Knight et al. 2005; Kennedy et al. 2008), it does not provide a guaranteed bound on the estimates. We therefore considered an approximation that does provide a guaranteed upper bound, which also gives negligible average error (<1% over several thousand simulated motifs) (Fig. 5). We calculated (by computationally predicting the structure of each RNA) the conditional probability of correct structure given that the sequence elements were found by sampling from the distribution of sequences that contained the active-site specifications, including base pairing, at each of 969 points of composition (multiples of 5% of each of the 4 nt containing at least 5% of each of the 4 nt, e.g., 80% A, 10% G, 5%C, and 5% U). We then compared the regions at which each artificially selected motif was likely to be found, was likely to fold correctly, and we compared the joint probability of both to the corresponding regions for other artificially selected motifs, and to naturally occurring functional RNAs from cells.
FIGURE 4.
Overall workflow. (a) Motifs were identified from sequences in the literature. (b) We included all motifs where both a secondary structure diagram and a multiple sequence alignment of the corresponding sequences were available to us. We used RNAfold to predict the folding of the sequences corresponding to each motif, and excluded motifs where none of the sequences for that motif folded into a secondary structure compatible with the published secondary structure diagram (four of 33 motifs examined overall). (c) For each location in sequence space where the frequencies of each nucleotide were an even multiple of 5% (e.g., 55% A, 15% C, 20% A, 10% U), we calculated the probability of each motif using the new upper-bound method (see Materials and Methods). (d) At the same locations, we also calculated the conditional probability of folding correctly, given that the motif was present, by sampling 10,000 sequences drawn from the distribution of sequences containing the motif, folding each sequence with RNAfold, and calculating the fraction of sequences for which the calculated minimum free energy structure was compatible with the motif. (e) Finally, we multiplied these two probabilities together to obtain the joint probability that a randomly chosen sequence of a given length and composition both contains the sequence elements required for the motif and folds correctly. We repeated this procedure for each of the 969 5% interior composition intervals in the space of possible compositions (i.e., compositions that have at least 5% of each base and an even multiple of 5% of all bases). (f) We then modeled the probability distribution of each motif as a multivariate normal distribution, showing ellipsoids at 1 standard deviation from the mean. Superimposing all these ellipsoids allowed us to determine the regions at which each function, or combination of functions, was most likely to occur. (g) Finally, we downloaded biological aptamer and ribozyme sequences from Rfam, plotted their compositions (so that each point corresponds to an individual aptamer or ribozyme sequence), and superimposed them on the distribution of artificial motifs.
TABLE 1.
RNA motifs from SELEX and their structures
FIGURE 5.
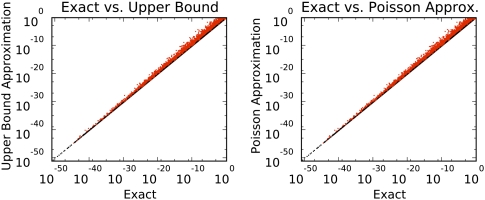
Fit between exact and upper-bound calculations. Red points indicate conditions that failed inclusion criteria (i.e., probability of an individual module >0.01, or probability over all modules >0.001: these criteria were set such that all examined motifs were included). The same motifs were used for both sets of calculations, so the graphs are nearly identical. Correlations and relative errors are as follows. Upper-Bound: r2 = 0.998, r2 for filtered points only = 0.999999, mean relative error = 12.9, mean filtered relative error = 0.0093. Poisson: r2 = 0.997, r2 filtered = 0.999999, mean relative error = 12.8, mean filtered relative error = 0.00076. For numerical stability we approximated 1 − e−x by its second-order Taylor series when 0 < x <10−8. Thus the two methods perform similarly and provide excellent agreement with exact calculations over the range of motifs examined.
Probabilistic model
Our probabilistic model for the composition of a random sequence of n nucleotides assumes that the RNA bases occur with frequencies pA, pC, pG, pU ≥ 0 (pA + pC + pG + pU = 1), and that matches with a base at a given position are independent from matches at the other positions. This is reasonable for sequences from in vitro selection because extensive effort is expended, ensuring that the coupling efficiencies are equal during chemical synthesis, so that the base at each position does not affect the probability of seeing each of the four bases at the next position.
Poisson versus upper-bound approximation
For a given motif m let W be the number of matches with this motif in a random sequence of length n. Define l as the length of the shortest random sequence in which m has a strictly positive probability of occurring, and let p be the probability that there is a match in a random sequence of length l. If l is well-defined (i.e., it does not depend on the values assigned to the degenerate bases nor the correlations both within and across modules) and N denotes all the different positions in which the motif could be matched in a random sequence of length n, then P[W ≥ 1] ≈ 1 − e−pN, due to the Poisson approximation heuristic (Knight et al. 2005). General error-bounds for this approximation are known only for motifs consisting of a single module as long as no version of the motif is a proper sub-word of another version of it (Roquain and Schbath 2007); in particular, bounds for the error are unknown for motifs with two or more modules with unbounded gaps. However, due to Markov's inequality (Durrett 2004), for an arbitrary motif m we have P[W ≥ 1] ≤ E(W), where E(W) denotes the expected value of W. But, due to the stationarity of our probabilistic model and the linearity of the expectation operator, E(W) = Np, and hence P[W ≥ 1] ≤ Np. We will refer to Np as the Upper-Bound approximation. Notice that
 |
where t is a variable of integration ranging from 0 to 1 (i.e., it has no biological interpretation). As a result, (1 − e−pN) ≤ Np and the difference between the Poisson and the Upper-Bound approximation is at most (Np)2/2, which is negligible when Np is small. Furthermore, because Np is a guaranteed upper-bound for the probability of interest, the approximation P[W ≥ 1] ≈ Np seems more suitable when very small values of Np are considered (for which numerical instability may become an issue).
Comparison of Poisson and upper-bound approximations
Motifs were generated randomly as follows. Each parameter was chosen uniformly from the following distributions: background sequence composition, all compositions with 5%–85% of any given base; length of each module, 1–20; number of correlated base pairs, 0 to half the sequence length; degenerate bases, 0–4. All calculations assumed that degenerate positions could be filled by any one of the four bases.
The exact probability of occurrence of each motif in a specified random background was calculated using a deterministic finite automaton (Lladser et al. 2008). This probability was then approximated using the Poisson method (Knight et al. 2005) and the Upper-Bound approximation described above. Poisson and Upper-Bound approximations were compared with the exact probabilities by calculating the average relative error and coefficient of determination of the log-scaled data using PyCogent (Fig. 5; Knight et al. 2007).
Folding calculations
The folding calculations reported in this paper required considerable computational resources. We performed folding experiments for 23 motifs using RNAfold in the Vienna Package (Hofacker et al. 1994). For each motif we folded 38,760,000 molecules, which means that we folded a total of ∼1.3 × 109 molecules, or about 1.3 × 1011 nucleotides. Approximately 10,000 CPU hours were needed for these computational foldings. The computational folding runs were performed on clusters provided by the Shared Hierarchical Academic Research Computing Network (SHARCNET; https://www.sharcnet.ca/my/front/).
We used the GridBASE framework (De Sterck et al. 2007, 2008) for distributing the folding tasks over a collection of clusters, and for organizing the tasks and their input and output. GridBASE is a framework for database-driven grid computing, and was developed to make it easy to grid-enable a certain class of (task-farmable) applications. Industry-strength database technology plays a key role in the design of the framework. The database is used as a scalable, reliable, and remotely accessible component both for storing and organizing the configuration information of the grid, and for managing information related to the grid users and the jobs and tasks they submit for execution.
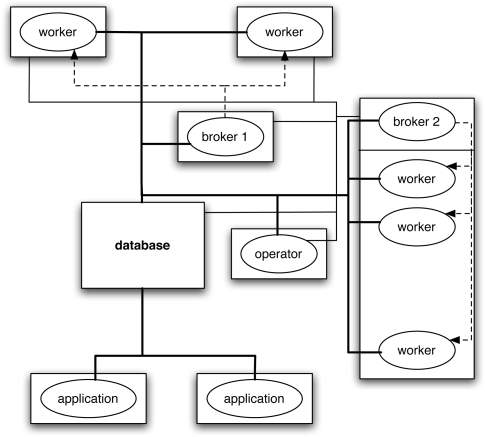
Other system components are worker nodes, a simple resource broker, a grid operator console, and application clients (see Fig. 6). The broker matches available workers with unprocessed tasks, and the workers then pull the tasks from the database superqueue. This mechanism offers decoupling in space, as components may be distributed over geographically distributed machines, and decoupling in time, as tasks may wait in the database until workers become available. In analogy with electrical power grids, a clear distinction is made in our design between the role played by grid users on the one hand, who develop and submit application code but are otherwise mostly isolated from resource deployment and selection, and the role played by the grid operator on the other hand, who is responsible for providing computing resources and assuring system availability and maintenance. Application code can be written in any language, and simple workflow support is provided. Code delivery and input and output file delivery also occur via the database component. Our approach is based on decentralization and implemented in Java, leading to a lightweight, portable, and scalable grid computing solution that is especially suited for parallel bioinformatics. GridBASE can be downloaded from http://www.math.uwaterloo.ca/groups/SSC/software/gridbase/index.shtml.
FIGURE 6.
GridBASE deployment diagram. Rectangular boxes represent different machines. The thick solid lines represent connections to the database. The thin solid lines represent direct control interactions initiated by the operator component. The dashed lines represent notification of workers by their associated brokers (multiple brokers may be employed, for instance, to handle firewall restrictions).
Association between motif function and spatial location
The test statistic used was the average difference between the means of the centroids of the ellipsoids for each pair of functional categories. The association between each motif and its function was randomized and the test statistic was measured. This procedure was repeated 10,000 times, and the P-value reported is the proportion of times that the test statistic of the randomized associations exceeded the test statistic of the correctly labeled motifs. This test thus indicates whether functions are more localized than we would expect by chance.
Association between the spatial location of real aptamers/ribozymes and the ellipsoids representing artificially selected motifs
The test statistic was the fraction of aptamers/ribozymes taken from the Rfam database that are within at least a single one-standard-deviation ellipsoid of any of the artificially selected motifs. Random sequences equal to the number of Rfam aptamers/ribozymes were generated from equal base frequencies with sequence lengths drawn from the distribution of actual Rfam sequences. This procedure was repeated 10,000 times. The P-value reported is the proportion of times that the number of points from the null model that were within at least one ellipsoid exceeded the number of real Rfam sequences that were within at least one ellipsoid. This gives an indication of whether actual sequences overlap the high-probability region of artificially selected motifs more than would be expected for random sequences with the same lengths.
Functional overlap
For each functional category, the top 5% of points in composition space with the highest probability for any motif having that function were selected. The number of points in composition space that occurred in the top 5% of zero to five of the functional categories was recorded. By chance, we would expect any given point to occur in n functional categories according to a binomial distribution with parameters n = 5, P = 0.05. The P-value reported compares these two models using a χ2 goodness-of-fit test. This gives an indication of whether the high-probability regions of different functions overlap more than we would expect by chance.
Purine bias
The mean of the centroids of all motifs was projected onto the AG/CU axis and tested for purine bias using a one-sample t-test. The same test was performed for purine bias among Rfam aptamers/ribozymes.
Spread along GC axis
The test statistic was: Var(GC axis)/max[Var(GU axis), Var(GA axis)]. A set of points with the same number of sequences as the Rfam ribozyme/aptamers was created using a composition the same as that of the average Rfam ribozyme/aptamer and a sequence length drawn from the same length distribution as the Rfam sequences. This was repeated 10,000 times. The reported P-value is the proportion of times that the test statistic of the random sequences was greater than that of the real Rfam sequences, and thus gives an indication of whether the excess spread along the GC axis as compared to the two axes orthogonal to it is greater than we would expect by chance.
Overlap of Rfam sequences and artificially selected motifs
The high-probability regions corresponding to the one-standard-deviation ellipsoids that were fit to the probability distributions of each motif and the three-standard-deviation ellipsoid that was fit to the Rfam aptamers/ribozymes were tested for significant overlap.
First, a randomly placed ellipsoid with the same volume as the ellipsoid fit to the Rfam sequences was produced using the following procedure.
A covariance matrix was generated by sampling standard deviations for the x-, y-, and z-axis uniformly on [0,0.5] and sampling correlation coefficients for each pair of axes uniformly on [−1,1]. These values were converted into variance and covariance, respectively, to create a covariance matrix. The matrix was scaled by the cube root of the desired volume divided by the current volume of the one-standard-deviation ellipsoid so that the resulting one-standard-deviation ellipsoid had the desired volume. A random mean was selected within the simplex, and the ellipsoid was tested for whether it extended outside the simplex by using the inverse of the square root of the covariance matrix as a linear transformation applied to each of the bounding planes of the simplex after they had been shifted so that the ellipsoid was centered at the origin; if the transformed planes intersected a sphere with radius 1 centered at the origin then the covariance matrix was rejected and the procedure was repeated.
The volume shared between the randomly generated ellipsoid and the set of ellipsoids of all motifs was calculated by sampling 50,000 points within the simplex and multiplying the proportion of these points that were shared by the volume of the simplex tetrahedron. This procedure was repeated 10,000 times. The P-value reported is the proportion of times that the estimated shared volume between the motif ellipsoids and the random ellipsoid with the same volume as the Rfam ellipsoid exceeded the shared volume associated with the actual Rfam ellipsoid. This gives an indication of how likely it is that we would see the observed amount of overlap between real and artificial sequences in composition space if the ellipsoids had been randomly distributed in the simplex (see, also, Figs. 7, 8).
FIGURE 7.
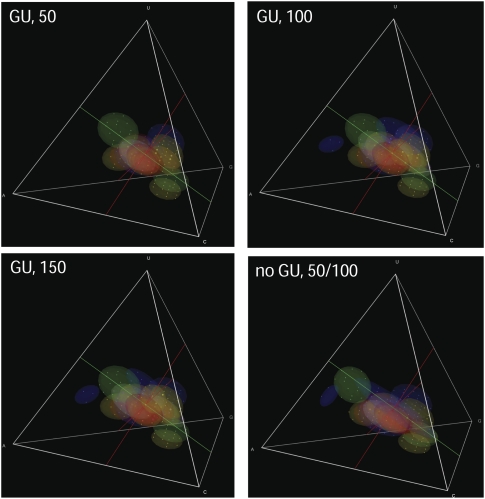
Effects of sequence length and GU base pairs on abundance. Varying the sequence length from 50 to 150 bases and keeping or omitting GU base pairs had little effect on compositional preferences, except that some motifs were unable to fold without GU pairs and others were unable to fit into the shorter sequence lengths (50, 100, and 150 base sequences with GU pairs; 50 or 100 base sequences as needed to contain the motif without GU pairs).
FIGURE 8.
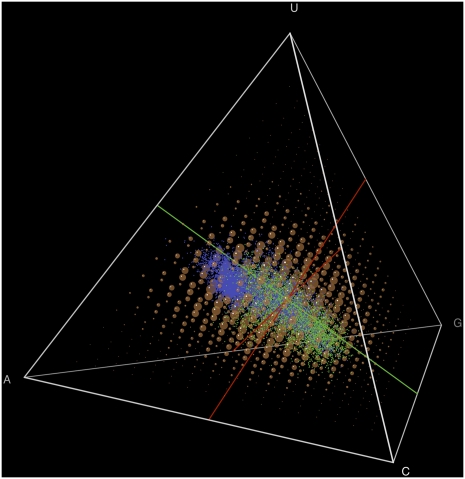
Summing the probabilities across motifs provides results similar to examining motif overlap. Brown points have radii proportional to the sum of probabilities of any motif: compare to Figure 1.
SUPPLEMENTAL MATERIAL
Supplemental material can be found at http://bayes.colorado.edu/SupplementaryMaterial/Kennedy09RNA/.
ACKNOWLEDGMENTS
This work was supported in part by NASA Astrobiology Grant NNX08AP60G to R.K.; NIH R01 GM 48080 and its biocomplexity supplement to M.Y.; NSF DMS-0805950 to M.E.Ll.; by NSERC of Canada; by the facilities of the Shared Hierarchical Academic Research Computing Network (SHARCNET); and by a SHARCNET fellowship. R.K. was supported in part by an Astronaut Foundation Scholarship. We thank Gerald Joyce, Niles Lehman, Erik Schultes, Catherine Lozupone, Jens Reeder, and Justin Kuczynski for comments on the manuscript. R.K. performed the bulk of the research, including implementing the statistical methods. M.E.Ll. derived the new approximations. Z.W. and C.Z. developed large-scale simulation code and ran computations on SHARCNET. M.E.Ll., M.Y., H.D.S., and R.K. directed the research and wrote the manuscript and supplementary materials. The authors declare no competing financial interests.
Footnotes
Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.1923210.
REFERENCES
- Bourdeau V, Ferbeyre G, Pageau M, Paquin B, Cedergren R. The distribution of RNA motifs in natural sequences. Nucleic Acids Res. 1999;27:4457–4467. doi: 10.1093/nar/27.22.4457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JH, Szostak JW. Isolation of high-affinity GTP aptamers from partially structured RNA libraries. Proc Natl Acad Sci. 2002;99:11616–11621. doi: 10.1073/pnas.182095699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Sterck H, Zhang C, Papo A. Database-driven grid computing with GridBASE. IEEE International Symposium on Bioinformatics and Life Science Computing (BLSC07), AINAW-07; IEEE Computer Society; Washington, DC. 2007. pp. 696–701. [Google Scholar]
- De Sterck H, Papo A, Zhang C, Hamady M, Knight R. Database-driven grid computing and distributed web applications: A comparison. In: Zomaya A, Taibi E-G, editors. Grids for bioinformatics and computational biology. Wiley Interscience; New York: 2008. pp. 247–266. [Google Scholar]
- Durrett R. Probability theory and examples. 3rd ed. Duxbury Press; Pacific Grove, CA: 2004. [Google Scholar]
- Eigen M, Schuster P. The hypercycle. A principle of natural self-organization. Part A: Emergence of the hypercycle. Naturwissenschaften. 1977;64:541–565. doi: 10.1007/BF00450633. [DOI] [PubMed] [Google Scholar]
- Ellington AD, Szostak JW. In vitro selection of RNA molecules that bind specific ligands. Nature. 1990;346:818–822. doi: 10.1038/346818a0. [DOI] [PubMed] [Google Scholar]
- Elson D, Chargaff E. Evidence of common regularities in the composition of pentose nucleic acids. Biochim Biophys Acta. 1955;17:367–376. doi: 10.1016/0006-3002(55)90385-1. [DOI] [PubMed] [Google Scholar]
- Famulok M. Molecular recognition of amino acids by RNA-aptamers: An L-citrulline binding RNA motif and its evolution into an L-arginine binder. J Am Chem Soc. 1994;116:1698–1706. [Google Scholar]
- Fontana W, Schuster P. Continuity in evolution: On the nature of transitions. Science. 1998;280:1451–1455. doi: 10.1126/science.280.5368.1451. [DOI] [PubMed] [Google Scholar]
- Gardner PP, Daub J, Tate JG, Nawrocki EP, Kolbe DL, Lindgreen S, Wilkinson AC, Finn RD, Griffiths-Jones S, Eddy SR, et al. Rfam: Updates to the RNA families database. Nucleic Acids Res. 2009;37:D136–D140. doi: 10.1093/nar/gkn766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert W. Origin of fife: The RNA world. Nature. 1986;319:618. [Google Scholar]
- Gutell RR, Cannone JJ, Shang Z, Du Y, Serra MJ. A story: Unpaired adenosine bases in ribosomal RNAs. J Mol Biol. 2000;304:335–354. doi: 10.1006/jmbi.2000.4172. [DOI] [PubMed] [Google Scholar]
- Held DM, Greathouse ST, Agrawal A, Burke DH. Evolutionary landscapes for the acquisition of new ligand recognition by RNA aptamers. J Mol Evol. 2003;57:299–308. doi: 10.1007/s00239-003-2481-y. [DOI] [PubMed] [Google Scholar]
- Hofacker I, Fontana W, Stadler PF, Bonhoeffer LS, Tacker M, Schuster P. Fast folding and comparison of RNA secondary structures. Monatsh Chem. 1994;125:167–188. [Google Scholar]
- Huang Z, Szostak JW. Evolution of aptamers with a new specificity and new secondary structures from an ATP aptamer. RNA. 2003;9:1456–1463. doi: 10.1261/rna.5990203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Illangasekare M, Kovalchuke O, Yarus M. Essential structures of a self-aminoacylating RNA. J Mol Biol. 1997;274:519–529. doi: 10.1006/jmbi.1997.1414. [DOI] [PubMed] [Google Scholar]
- Jaeger JA, Turner DH, Zuker M. Improved predictions of secondary structures for RNA. Proc Natl Acad Sci. 1989;86:7706–7710. doi: 10.1073/pnas.86.20.7706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston WK, Unrau PJ, Lawrence MS, Glasner ME, Bartel DP. RNA-catalyzed RNA polymerization: Accurate and general RNA-templated primer extension. Science. 2001;292:1319–1325. doi: 10.1126/science.1060786. [DOI] [PubMed] [Google Scholar]
- Kennedy R, Lladser ME, Yarus M, Knight R. Information, probability, and the abundance of the simplest RNA active sites. Front Biosci. 2008;13:6060–6071. doi: 10.2741/3137. [DOI] [PubMed] [Google Scholar]
- Kim N, Gan HH, Schlick T. A computational proposal for designing structured RNA pools for in vitro selection of RNAs. RNA. 2007;13:478–492. doi: 10.1261/rna.374907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight R, De Sterck H, Markel R, Smit S, Oshmyansky A, Yarus M. Abundance of correctly folded RNA motifs in sequence space, calculated on computational grids. Nucleic Acids Res. 2005;33:5924–5935. doi: 10.1093/nar/gki886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight R, Maxwell P, Birmingham A, Carnes J, Caporaso JG, Easton BC, Eaton M, Hamady M, Lindsay H, Liu Z, et al. PyCogent: A toolkit for making sense from sequence. Genome Biol. 2007;8:R171. doi: 10.1186/gb-2007-8-8-r171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lao PJ, Forsdyke DR. Thermophilic bacteria strictly obey Szybalski's transcription direction rule and politely purine-load RNAs with both adenine and guanine. Genome Res. 2000;10:228–236. doi: 10.1101/gr.10.2.228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laserson U, Gan HH, Schlick T. Predicting candidate genomic sequences that correspond to synthetic functional RNA motifs. Nucleic Acids Res. 2005;33:6057–6069. doi: 10.1093/nar/gki911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazarev D, Puskarz I, Breaker RR. Substrate specificity and reaction kinetics of an X-motif ribozyme. RNA. 2003;9:688–697. doi: 10.1261/rna.2600503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legiewicz M, Yarus M. A more complex isoleucine aptamer with a cognate triplet. J Biol Chem. 2005;280:19815–19822. doi: 10.1074/jbc.M502329200. [DOI] [PubMed] [Google Scholar]
- Lehman N, Joyce GF. Evolution in vitro of an RNA enzyme with altered metal dependence. Nature. 1993;361:182–185. doi: 10.1038/361182a0. [DOI] [PubMed] [Google Scholar]
- Lladser ME, Betterton MD, Knight R. Multiple pattern matching: A Markov chain approach. J Math Biol. 2008;56:51–92. doi: 10.1007/s00285-007-0109-3. [DOI] [PubMed] [Google Scholar]
- Majerfeld I, Yarus M. A diminutive and specific RNA binding site for L-tryptophan. Nucleic Acids Res. 2005;33:5482–5493. doi: 10.1093/nar/gki861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majerfeld I, Puthenvedu D, Yarus M. RNA affinity for molecular L-histidine; genetic code origins. J Mol Evol. 2005;61:226–235. doi: 10.1007/s00239-004-0360-9. [DOI] [PubMed] [Google Scholar]
- Reader JS, Joyce GF. A ribozyme composed of only two different nucleotides. Nature. 2002;420:841–844. doi: 10.1038/nature01185. [DOI] [PubMed] [Google Scholar]
- Robertson DL, Joyce GF. Selection in vitro of an RNA enzyme that specifically cleaves single-stranded DNA. Nature. 1990;344:467–468. doi: 10.1038/344467a0. [DOI] [PubMed] [Google Scholar]
- Rogers J, Joyce GF. A ribozyme that lacks cytidine. Nature. 1999;402:323–325. doi: 10.1038/46335. [DOI] [PubMed] [Google Scholar]
- Roquain E, Schbath S. Improved compound poisson approximation for the number of occurrences of any rare word family in a stationary Markov chain. Adv Appl Probab. 2007;39:128–140. [Google Scholar]
- Salehi-Ashtiani K, Szostak JW. In vitro evolution suggests multiple origins for the hammerhead ribozyme. Nature. 2001;414:82–84. doi: 10.1038/35102081. [DOI] [PubMed] [Google Scholar]
- Sazani PL, Larralde R, Szostak JW. A small aptamer with strong and specific recognition of the triphosphate of ATP. J Am Chem Soc. 2004;126:8370–8371. doi: 10.1021/ja049171k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultes EA, Bartel DP. One sequence, two ribozymes: Implications for the emergence of new ribozyme folds. Science. 2000;289:448–452. doi: 10.1126/science.289.5478.448. [DOI] [PubMed] [Google Scholar]
- Schultes E, Hraber PT, LaBean TH. Global similarities in nucleotide base composition among disparate functional classes of single-stranded RNA imply adaptive evolutionary convergence. RNA. 1997;3:792–806. [PMC free article] [PubMed] [Google Scholar]
- Schultes EA, Hraber PT, LaBean TH. Estimating the contributions of selection and self-organization in RNA secondary structure. J Mol Evol. 1999;49:76–83. doi: 10.1007/pl00006536. [DOI] [PubMed] [Google Scholar]
- Smit S, Yarus M, Knight R. Natural selection is not required to explain universal compositional patterns in rRNA secondary structure categories. RNA. 2006;12:1–14. doi: 10.1261/rna.2183806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sueoka N. On the genetic basis of variation and heterogeneity of DNA base composition. Proc Natl Acad Sci. 1962;48:582–592. doi: 10.1073/pnas.48.4.582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sueoka N. Directional mutation pressure and neutral molecular evolution. Proc Natl Acad Sci. 1988;85:2653–2657. doi: 10.1073/pnas.85.8.2653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuerk C, Gold L. Systematic evolution of ligands by exponential enrichment: RNA ligands to bacteriophage T4 DNA polymerase. Science. 1990;249:505–510. doi: 10.1126/science.2200121. [DOI] [PubMed] [Google Scholar]