Physical Model of Cellular Symmetry Breaking

Abstract

Cells can polarize in response to external signals, such as chemical gradients, cell–cell contacts, and electromagnetic fields. However, cells can also polarize in the absence of an external cue. For example, a motile cell, which initially has a more or less round shape, can lose its symmetry spontaneously even in a homogeneous environment and start moving in random directions. One of the principal determinants of cell polarity is the cortical actin network that underlies the plasma membrane. Tension in this network generated by myosin motors can be relaxed by rupture of the shell, leading to polarization. In this article, we discuss how simplified model systems can help us to understand the physics that underlie the mechanics of symmetry breaking.

Mechanical instabilities in animal cells can lead to symmetry breaking. Simplified experimental systems and models of cell polarization close to an instability threshold explains how.

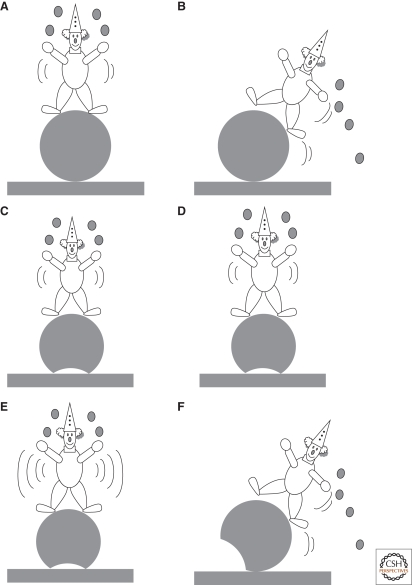
Symmetry breaking in physics is an old well-known concept. It is based on energy considerations: A symmetrical system can lose its symmetry if an asymmetrical state has a lower energy. The initial symmetrical state can be either unstable or metastable. In the latter case, there is an energy barrier to be overcome before symmetry breaking occurs. An external trigger can drive the system from its symmetrical to its asymmetrical state, but simple noise can also do so if its amplitude is sufficiently high. A simple example is a clown balancing on a ball: When the clown is standing on top of the ball, the system has a cylindrical symmetry (Fig. 1A). However, this state is unstable: The slightest perturbation will cause the clown to fall down in some direction, breaking the cylindrical symmetry (Fig. 1B). Imagine now that the ball is slightly flat on its base, giving more stability to the clown. Such a state is metastable: The clown can make small excursions safely (Fig. 1C,D), but if he moves too much (i.e., generates too much “noise”), he will fall down in this case also (Fig. 1E,F).

Figure 1.

Illustration of symmetry breaking with a clown standing on a balloon. In (A), the clown is in unstable equilibrium and the situation is symmetrical. However, any movement will make him fall down and the system (clown + balloon) then loses its symmetry. (B) If the balloon is slightly flat on its base (C–F), then the system is metastable, i.e., a slight perturbation of the clown will not break the symmetry (C, D), whereas a larger perturbation will destabilize the clown (F).

Symmetry breaking is ubiquitous in physics, and can lead to phase transitions or pattern formation. It is also an important theme in cell biology, in which polarization is crucial for proper functioning of the cell. Cell polarization typically occurs in response to certain external or internal triggers. A well-known example is chemotaxis, in which a chemical gradient leads to polarization and directed movement of bacterium cells. Polarization also occurs during cytokinesis, in which intracellular stimuli triggered by the mitotic spindle determine the position of the cleavage furrow (Burgess and Chang 2005). Interestingly, cells conserve the ability to polarize even in the absence of an asymmetric signal (Devreotes and Zigmond 1988). For example, chemotactic cells that are presented a uniform concentration of chemoattractant polarize and move in random directions. Another example is blebbing, the spontaneous appearance of bare membrane bulges in some cells.

Symmetry breaking in biological systems is a complex phenomenon, because biological systems are always out of equilibrium. Hence, symmetry breaking is not just a transition to a state of lower potential energy. Instead, active, dynamic processes must be considered that feed energy into the system. A biochemical explanation for symmetry breaking was given by Alan Turing. In a seminal paper in 1952 (Turing 1952), he showed that patterns can be generated by simple chemical reactions if the reactants have different diffusion rates. To make this clear, he considered the hypothetical situation in which the morphology of a cell (or cell clump) is determined by two chemical substances (called morphogens). These morphogens also control their own production rate: One enhances morphogen production (the activator) and the other inhibits morphogen production (the inhibitor). It was shown that a spatially homogeneous distribution of morphogens is unstable if the activator diffuses more slowly than the inhibitor. In this case, small stochastic concentration fluctuations are amplified, leading to a chemical instability (“a Turing instability”) and the formation of concentration gradients (or patterns). Reaction–diffusion models of the Turing type have been widely explored to explain polarization and biological development (Gierer and Meinhardt 1972; Sohrmann and Peter 2003; Wedlich-Soldner and Li 2003).

Although reaction–diffusion models have proven to be very successful, there is increasing evidence that cell polarization is not only a matter of biochemistry; mechanical aspects play an important role too. Recent work suggests that spontaneous polarization can also be driven by a mechanical instability of the actomyosin cortex of cells. In the remainder of this review, we focus on such mechanical instabilities.

THE ACTIN CORTEX AND POLARIZATION

A key role in animal cell polarization is played by the cortical actin network. This is a thin shell of cross-linked actin filaments, myosin motors, and actin-binding proteins between 100 nm and 1 µm thick, that underlies and supports the plasma membrane (Fig. 2). The spatial organization and dynamics of the actin cortex are only beginning to be resolved. The myosin motors that are present in the cortex generate contractile forces that result in a tensile stress in the actin network (Dai et al. 1999). A stress is a force per unit area whereas a tension is a force per unit length. Thus, the tension in the cortex is roughly equal to the stress multiplied by the thickness of the cortex. In fact, the exact tension is given by the integral of the stress over the cortex thickness. Because of these stresses, the cell cortex is metastable: The elastic energy that is stored in the stressed actin shell can be released by rupture of the network or by detachment of the membrane from the cortex, as seen in fibroblasts and lymphoblasts (Paluch et al. 2005). Expansion of the relaxed region because of pulling forces from the adjacent regions can lead to large cortical organizations known as cortical flows (Bray and White 1988; Munro et al. 2004) or to the growth of membrane protrusions called blebs (Keller et al. 2002; Charras et al. 2005; Paluch et al. 2005).

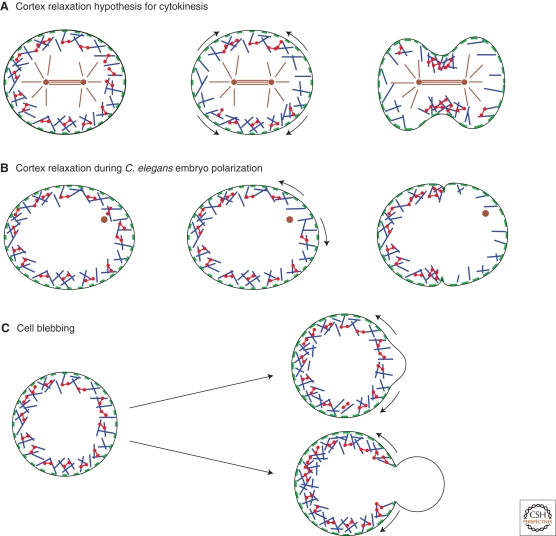
Figure 2.

Scheme for different cases of cortex relaxation in cellular events. (Blue rods) actin filaments, (red dumbbells) myosin fibers, (green patches) membrane attachments, (brown rods) microtubules, (brown dots) centrosomes. Curved arrows indicate the direction of cortex flows. (A) At the onset of cytokinesis, spindle microtubules have been proposed to cause cortex relaxation at the poles of the cell. The relaxed regions expand, leading to cleavage furrow formation. (B) In the Caenorhabditis elegans embryo, shortly after meiosis II, the sperm centrosome triggers cortex relaxation. The cortex then flows away from the relaxed region, leading to polarity protein segregation and pseudocleavage furrow formation. (C) Blebs form at sites of local detachment of the membrane from the cortex (top) or at sites of local cortex rupture (bottom). Cortex detachment from the membrane is sometimes followed by local cortex disassembly at the base of the bleb. Note that under certain conditions, multiple blebs can form. (© Paluch et al. 2006. Originally published in The Journal of Cell Biology. doi: 10.1083/jcb.200607159.)

Cells can use this instability of the actin-myosin cortex by biasing it with intracellular or extracellular cues. For example, flows of the actomyosin cortex have been observed in various cell lines at the onset of cytokinesis, in which they presumably contribute to formation of the cleavage furrow (Fig. 2A) (Cao and Wang 1990; DeBiasio et al. 1996). One possible mechanism that has been proposed to cause these cortical flows is a local relaxation of the cortex at the cell poles by astral microtubules (Bray and White 1988). Another process that is thought to depend on local cortex relaxation is the polarization of the one-cell C. elegans embryo. Here, the sperm provides the external cue: After fertilization, the point of sperm entry defines where cortical contractility locally relaxes (Cowan and Hyman 2004). As during cytokinesis, actin and myosin flow away from the relaxed region, transporting polarity proteins and shaping the pseudocleavage furrow (Fig. 2B) (Munro et al. 2004). Polarization by cortex relaxation may also, in some cells, precede cell migration (Paluch et al. 2006; Yoshida and Soldati 2006).

In the examples mentioned above, cortex instabilities and polarization are triggered by a spatial cue that presumably relaxes the cortex locally. However, the cortical tension can also relax spontaneously. This is observed, for example, in blebbing cells, where spontaneous rupture or detachment from the membrane leads to the expulsion of membrane bulges in the weakened regions, driven by the pressure generated by contraction of the actomyosin cortex (Fig. 2C) (Jungbluth et al. 1994; Keller et al. 2002; Paluch et al. 2005; Charras et al. 2005; Sheetz et al. 2006). Interestingly, blebbing cells can form one single large bleb (Paluch et al. 2005; Yoshida and Soldati 2006) or multiple smaller blebs over the cell surface (Cunningham 1995; Charras et al. 2005) (Fig. 3E,F) (see the following).

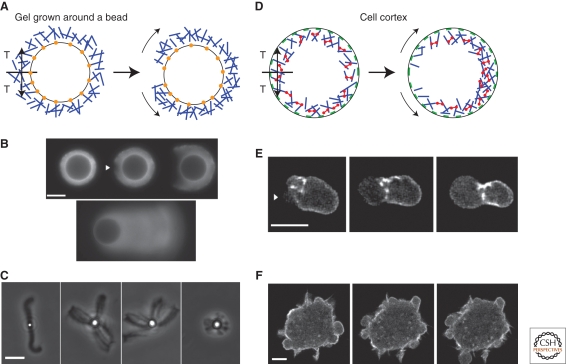
Figure 3.

Analogy of the tension state in an actin gel growing from a bead surface and in the cell cortex. (A–C) Growing from a bead surface. (D–F) in the cell cortex. (A and D) Schematic view of the symmetry breaking of an actin gel growing from the surface of a bead (A) or the breakage of the cell cortex (D). (Blue rods) actin filaments, (red dumbbells) myosin fibers, (green patches) membrane attachments, (orange dots) actin polymerization activators. In both cases, a tension (T) builds up because of polymerization in curved geometry for the gel on the bead and because of the presence of myosin motors in the cortex. Rupture of the gel leads to actin shell or cortical movement (curved arrows). (B) Time lapse of a symmetry-breaking event (arrowhead) preceding the actin-based movement of a bead (epifluorescence microscopy with actin-AlexaFluor594). The first three images were taken 21, 24, and 40 minutes after the start of incubation, respectively. The last image shows the comet that develops eventually. (Images are reprinted from van der Gucht et al. 2005.) (C) Phase-contrast images of beads of different diameters (1 µm for the left image and 2.8 µm for the three other images) at low gelsolin concentration. (Images were provided by M. Courtois, Institut Curie, Paris, France.) (E) Time lapse of cortex breakage (arrowhead) and bleb growth in an L929 fibroblast fragment expressing actin-GFP. Fluorescence images are projections from a three-dimension reconstruction (time between images is 20 seconds). (Images are reprinted from Paluch et al. 2005.) (F) Time lapse of a cell displaying multiple blebs. Confocal images of an L929 fibroblast expressing actin-GFP were taken at 0, 25, and 35 seconds. (Images were provided by J.-Y. Tinevez and E. Paluch, Max Planck Institute of Molecular Cell Biology and Genetics, Dresden, Germany.) Bars (B and C), 10 µm; (E and F), 5 µm. (© Paluch et al. 2006. Originally published in The Journal of Cell Biology. doi: 10.1083/jcb.200607159.)

BUILD-UP AND RELEASE OF TENSION IN ACTIN CORTICES GROWN AROUND BEADS

A much simpler system for studying cortex symmetry breaking consists of actin gel layers growing around beads that are coated with an activator of actin polymerization and placed in a medium that reconstitutes actin assembly (Bernheim-Groswasser et al. 2002; van der Gucht et al. 2005). Such beads have been used widely in the last 10 years as a model system for studying actin-based movement of intracellular objects and lamellipodium extension (van der Gucht et al. 2005; Mogilner 2006). Actin polymerization is activated at the surface of the bead, resulting in the growth of an actin gel around the bead. During gel growth, new monomers are incorporated at the bead surface underneath the pre-existing gel, which is thus pushed outward and stretched because of the curved surface (Noireaux et al. 2000). As a consequence, stresses build up and the actin shell is under tension (Fig. 3B). Initially, the shell grows homogeneously around the bead, but after some time the shell breaks spontaneously: A notch appears at the external surface of the actin gel (arrowhead in Fig. 3A), which grows inward and expands laterally with a velocity of a few micrometers per minute. After several minutes, the hole is big enough for the bead to escape from the gel, and the bead starts to move, trailing an actin comet (Fig. 3B). This symmetry breaking can also be triggered by a local disruption of the actin gel. Altogether, these observations strongly suggest that symmetry breaking is driven by the release of elastic energy (Noireaux et al. 2000; Bernheim-Groswasser et al. 2002) stored in the actin gel.

MODELING OF ACTIN SHELL GROWTH AND RUPTURE AROUND BEADS

Let us consider the growth of a homogeneous crosslinked actin gel around a bead in more detail. Polymerization occurs at the surface of the bead (where filaments are nucleated), whereas depolymerization occurs at the pointed ends that are assumed to be mostly situated near the exterior of the gel (Noireaux et al. 2000; Sekimoto et al. 2004). Thus, the growth velocity of the gel can be described as follows:

(1)

where k_on^b and k_off^p are the rate constants for monomer addition at the inner surface (barbed ends) and monomer loss at the outer surface (pointed ends), respectively; C_a is the concentration of monomeric (G-)actin available for polymerization; and a = 2.7 nm is the gained filament length per monomer (Holmes et al. 1990). Note that we neglect here depolymerization at the barbed end and polymerization at the pointed end. The rate parameters k_on^b and k_off^p depend on the stress in the gel, because forces pushing or pulling on a filament can change the rate constants (Hill and Kirschner 1982). However, in the early stages of gel growth, the stresses in the gel are still small, and the rate constants are approximately equal to those of free barbed and pointed ends. Experimentally, the optimum initial polymerization rate v_p⁰ is 0.6 µm/min, in accordance with an estimate of equation (1) using reported values for the rate constants (Pollard 1986): k_on^b = 12 µM⁻¹ s⁻¹, k_off^p = 0.8 s⁻¹, and C_a = 0.6 µM (close to the critical concentration of pointed ends, because all barbed ends are capped). Note that k_on^b, k_off^p, and thus v_p⁰, depend on the concentrations of the various actin binding proteins (van der Gucht et al. 2005).

As the gel grows thicker, the tensile stress in the gel also becomes higher. Assuming that the actin layer can be considered as an isotropic, linearly elastic gel, the tangential stress can be evaluated as (Noireaux et al. 2000)

(2)

in which E is the elastic modulus of the gel and R the radius of the bead. If the tensile stress becomes too high, the gel may rupture spontaneously. As suggested by Griffith (Griffith 1920), rupture of a gel starts at the weakest spot in the gel, that is at a defect or flaw. The resistance of a material to fracture can be estimated by considering (1) the energy that is needed for breaking bonds to make this defect larger and (2) the elastic energy that is released when the defect grows. As shown in van der Gucht et al. 2005, spontaneous fracture occurs as soon as the stress exceeds a critical value σ^f ≈ (EΓ/d)^1/2, which corresponds to a critical gel thickness

(3)

Here, Γ is the fracture energy per unit area, which depends on the density and the strength of the crosslinks in the gel, and d is the typical size of the defects in the gel. As soon as the gel reaches this critical thickness, it becomes unstable and ruptures spontaneously. The value of the critical thickness and the time needed for symmetry breaking depend on the radius and on the presence of actin-binding proteins and crosslinkers that affect the growth rate and the gel properties (van der Gucht et al. 2005).

The spontaneous fracture mechanism sketched previously occurs only under appropriate conditions, when the concentrations of the various actin-binding proteins are in the proper range. If this is not so, the symmetry breaking process is delayed. The gel thickness first reaches a stable value and it may take very (sometimes infinitely) long before gel rupture occurs. The occurrence of a steady gel thickness is caused by the influence of the stress on the polymerization rate. As the gel grows thicker, the polymerization rate is reduced and at some point it may become equal to the rate of depolymerization at the external surface. If that happens, the thickness reaches a steady-state value. Assuming that only the polymerization rate is affected by the stress, the following equation has been derived for the steady-state gel thickness (Noireaux et al. 2000):

(4)

in which is a measure for the energy of the polymerization process, and ξ is the mesh size of the actin network. For very large beads, the gel may become so thick that diffusion of actin monomers through the gel becomes the growth-limiting factor (Paluch et al. 2006).

It is clear that if h_s < h_f, the gel will stop growing before the critical thickness for fracture is reached. The gel is now in a metastable state: It is stable toward small fluctuations (because the stress is below the threshold), but large fluctuations can still lead to gel rupture, in analogy with our clown (Fig. 1C–F). The delay in symmetry breaking is because of an energy barrier that must be overcome. The height of the barrier is related to the difference between h_f and h_s. Such a nucleation mechanism process is also characterized by a much larger variation in symmetry breaking rates among different beads (van der Gucht et al. 2005). As discussed in Sekimoto et al. 2004, symmetry breaking could be enhanced in this case if the depolymerization rate is also affected by the stresses in the gel.

COMPARISON OF SYMMETRY BREAKING IN CELLS AND AROUND BEADS

At a microscopic scale, the actin gels around the bead and the cell cortex appear to differ in several ways: The origin of the tension is different in the two systems and the orientation of the actin filaments and the direction of network growth are different as well. Yet, at a mesoscopic scale, the two networks are very similar: Both are crosslinked actin meshworks where stresses develop tangentially to the actin layer (Fig. 3A,D). In both cases, relaxation of these stresses by rupture lead to polarization. Such a rupture occurs spontaneously if the stress exceeds a critical threshold (this corresponds to the unstable situation of the clown on a spherical ball), or it is delayed by an energy barrier (corresponding to the metastable situation of the clown on a flattened ball).

This implies that symmetry breaking can be enhanced either by lowering the threshold (the strength of the network) or by increasing the global tension (the driving force). Observations of symmetry breaking in both the bead system and the cell cortex support this idea.

In both systems, the instability threshold can be lowered by lowering the density of crosslinkers in the actin gel, like filamin or α-actinin, which leads to a softer and weaker network. Indeed, depletion of filamin or degradation of α-actinin in cells enhances blebbing, probably because of cortical breakage, or at least a local release in the cortical tension (Cunningham 1995; Miyoshi et al. 1996). Conversely, shell breakage in the bead system is slowed down by the presence of filamin or α-actinin (van der Gucht et al. 2005). In both systems, actin gel rupture is thus facilitated by the depletion of crosslinkers.

The driving force for cortex breakage in cells can be enhanced by increasing the activity of myosin II, leading to an increased contractility of the cortex and a larger cortical tension. Indeed, blebbing in cells is enhanced when the global contractility of the cortex is increased (Sahai and Marshall 2003) and, conversely, blebbing is reduced when contractility is decreased (Mills et al. 1998). In the bead system, the tension is related to the thickness of the gel layer. Hence, the analogous effect of decreased contractility (leading to a lower tension) in the bead system is a decrease in gel thickness. This can be achieved, for example, by adding ADF (actin depolymerizing factor)/cofilin, which enhances depolymerization of filaments in the outer regions of the actin gel. Indeed, at high ADF/cofilin concentrations, the gel thickness remains small and no symmetry breaking is observed, indicating that the threshold tension for gel rupture can never be reached (van der Gucht et al. 2005).

A growing actin shell in spherical geometry can break spontaneously and form a propelling comet at the opposite side of the breakage point, although the original breakage and therefore direction of the comet is random. If gel growth stops before the instability threshold is reached, then symmetry breaking can still be triggered by an external perturbation, for example by a local disruption of the actin network by photo-damage (van der Gucht et al. 2005). Likewise, a local alteration of the actin cortex in cells, either by locally applying drugs that affect actin or by increasing the local stress mechanically, induces cortex rupture and bleb formation (Paluch et al. 2005).

We can compare the forces necessary for shell breakage around beads and for cortex breakage in cells. The stresses in the gel around beads can be estimated from the elastic modulus of the actin gel and the thickness of the gel (Noireaux et al. 2000). This gives a value of 10³–10⁴ Pa for the critical tensile stress for gel rupture (van der Gucht et al. 2005). The cell cortical tension has been estimated in different cell types and is on the order of 10⁻³ N/m for Dictyostelium discoideum (Pasternak et al. 1989; Dai et al. 1999), lymphocytes (Pasternak and Elson 1985), or fibroblasts (Matzke et al. 2001), whereas it is about 20–30 times smaller for neutrophils (Evans and Yeung 1989). This gives, with a cortical thickness of a few hundred nanometers, a value of 10³–10⁴ Pa for the tensile stress in the cortex, very similar to the stress in the bead system. Interestingly, in Dictyostelium discoideum, deletion of either myosin II or of two myosin I, leads to a decrease of the tension by about 50%, suggesting that most of the cortex tension is because of myosin motors (Dai et al. 1999). Note that the cortical tension in these cells is very close to the threshold for cortex breakage, as breakage can be induced by applying pressures as small as 100 Pa, which is only 10% of the cortical stress (Paluch et al. 2005). However, in the case of C. elegans zygote, spontaneous symmetry breaking has never been observed: Polarization always requires a cue from sperm entry. This indicates that the symmetric state in this case is far from the threshold. This could be because, for example, of a specific acto-myosin organization, to a high degree of crosslinking, or to rapid acto-myosin dynamics that would allow for effective reparation of the cortex.

SYMMETRY CAN BREAK FROM ONE POINT OR FROM MULTIPLE POINTS

Cortex instabilities can occur at multiple sites along the cell periphery, leading to multiple blebs, or it can be a single event leading to a global polarization of the cell (as during polarization of the C. elegans embryo or the formation of large blebs) (Fig. 3E,F). Similarly, the gel growing around a bead can rupture once, leading to the formation of a single comet tail, or it can break at multiple sites, leading to several comets (Fig. 3B,C). The factors that determine whether a rupture leads to a global or to a local symmetry breaking are not well understood, but an analogy with the break-up of a liquid film on a surface by a nucleation and growth mechanism may provide insight. If nucleation of dry zones is fast compared with their growth, then dewetting will start independently from many different locations. In contrast, if nucleation is slow, then dewetting will start from one single hole that expands. Similarly, if nucleation of new holes in the stressed actin shell is fast compared with growth of existing holes, then the actin network is likely to break at multiple sites. In contrast, if nucleation is slow compared with growth of a hole, then the formation of a single hole will probably lead to global polarization. Indeed, multiple comet tails around beads are observed when gel growth proceeds slowly (e.g., at low gelsolin concentration) (J.v.d.G. unpublished results) and there is more time for new holes to appear in the gel. The biochemical factors that regulate the nucleation and growth rates of holes in the cell cortex remain to be explored, but we can nevertheless speculate about factors that affect these rates. The nucleation rate in cells depends on how far the cortical tension is from the instability threshold. Obviously, in cases in which spontaneous nucleation of instabilities does not occur but needs to be induced, there is usually only one rupture. In blebbing cells, on the other hand, nucleation is faster and blebs form spontaneously and rapidly. Multiple blebs tend to form when cells adhere to the substrate (Cunningham 1995; Sahai and Marshall 2003), whereas one single, large bleb is rather formed when cells are in suspension (Paluch et al. 2005). This might indicate that adhesion to the substrate could restrict membrane extension, and thus bleb growth.

The understanding of symmetry breaking in biomimetic systems can provide essential insight into spontaneous cortex rupture in cells. Therefore, reconstituting a cortex inside a liposome (Pontani et al. 2009) provides an interesting artificial system that paves the way to a controlled study of symmetry breaking mechanisms in cells.

STRESS-INDUCED POLARIZATION IN OTHER SYSTEMS

The concept of polarization driven by a global driving force that can locally exceed a mechanical threshold is not restricted to actin gels under tension, but can be applied more generally. For example, in plant cells, fungi, or bacteria, the force that drives cell deformation and growth comes from the internal osmotic pressure, whereas the mechanical strength that resists deformation is provided by the cell wall. Because the pressure in the cell is homogeneous, the polarized growth of walled cells requires an inhomogeneous extensibility of the cell wall (Cosgrove 2005). For example, root hairs and pollen tubes in plants, and buds in budding yeast are all initiated as small bulges growing at the cell periphery in regions where the cell wall is locally softened (Harold 2002). To achieve such a local wall softening, a cell needs to direct vesicles that contain cell-wall-loosening enzymes to specific sites at the cell periphery. This directed transport requires a polarized cytoskeleton, which may, in turn, be achieved by a biochemical instability (Wedlich-Soldner and Li 2003). Similarly, neuritogenesis starts by the growth of small buds at the initially spherical neuron surface. Buds are thought to result from pushing forces exerted by microtubules at spots where the actin network underlying the membrane is locally relaxed (Da Silva and Dotti 2002). This relaxation could be tension-driven, because the implication of the Rho/ROCK pathway, which activates myosin II, has been reported (Da Silva et al. 2003). It could also result from some other kind of instability triggered by external signals (Da Silva and Dotti 2002).

On a larger scale, a mechanical instability has been proposed to explain the shape and size oscillations observed during regeneration of fresh-water polyp Hydra Vulgaris. At the initial stages, Hydra cells form a hollow sphere consisting of a cell bilayer. This sphere inflates by uptake of fluid and builds up pressure because of stretching of the cells, analogous to the accumulation of stress in the actin gel growing around a bead. It has been proposed that this stress is released by rupture of the cell layer, followed by rapid shrinkage of the cell wall and reswelling, thus generating an oscillation mechanism (Fütterer et al. 2003). Interestingly, it has been suggested in a recent paper (Soriano et al. 2009) that Hydra symmetry breaking is a combination of a mechanical and a biochemical (Turing) instability: Mechanical stresses in the cell aggregate affect the diffusion rates of proteins and thereby provide the biochemical conditions necessary for a Turing instability.

CONCLUSION

Cell polarization is a complex process that involves many factors, including the cytoskeleton, soluble cytoplasmic proteins, and intra- and extracellular signals. The fact that cells can polarize even without external cues implies that they are operating close to an instability threshold. This increases their sensitivity to small stimuli, but also makes them sensitive to fluctuations. The nature of the symmetry-breaking instability can be mechanical, based on a release of stored elastic energy, or biochemical, based on reaction-diffusion processes. This suggests that cells could have redundant mechanisms for their polarization that can be triggered by different signals. It is very likely, however, that the two types of instabilities are strongly intertwined. In the case of Hydra, for example, biochemical instability seems to be triggered by a mechanical instability that precedes it. Conversely, it is well possible that in other cells a Turing-instability can lead to local cortex relaxations, and thus precede a mechanical instability.

Note that mechanical aspects play an important role in polarization, as illustrated in a recent study of symmetry breaking of fresh-water polyp Hydra vulgaris, in which Turing instability has been proposed to result from mechanical stresses (Soriano et al. 2009).