Abstract
Much recent evidence suggests that bone cells sense their mechanical environment via interstitial fluid flow. In this review, we summarize theoretical and experimental approaches to quantify fluid and solute transport in bone, starting with the early investigations of fluid shear stress applied to bone cells. The pathways of bone interstitial fluid and solute movement are high-lighted based on recent theoretical models, as well as a new generation of tracer experiments that have clarified and refined the structure and function of the osteocyte pericellular matrix. Then we trace how the fluid-flow models for mechanotransduction have evolved as new ultrastructural features of the osteocyte lacunar-canalicular porosity have been identified and how more recent in vitro fluid-flow and cell-stretch experiments have helped elucidate at the molecular level the possible pathways for cellular excitation in bone.
Keywords: interstitial fluid, fluid flow, osteocyte, lacunar-canalicular porosity, lacuna, canaliculi
1. INTRODUCTION
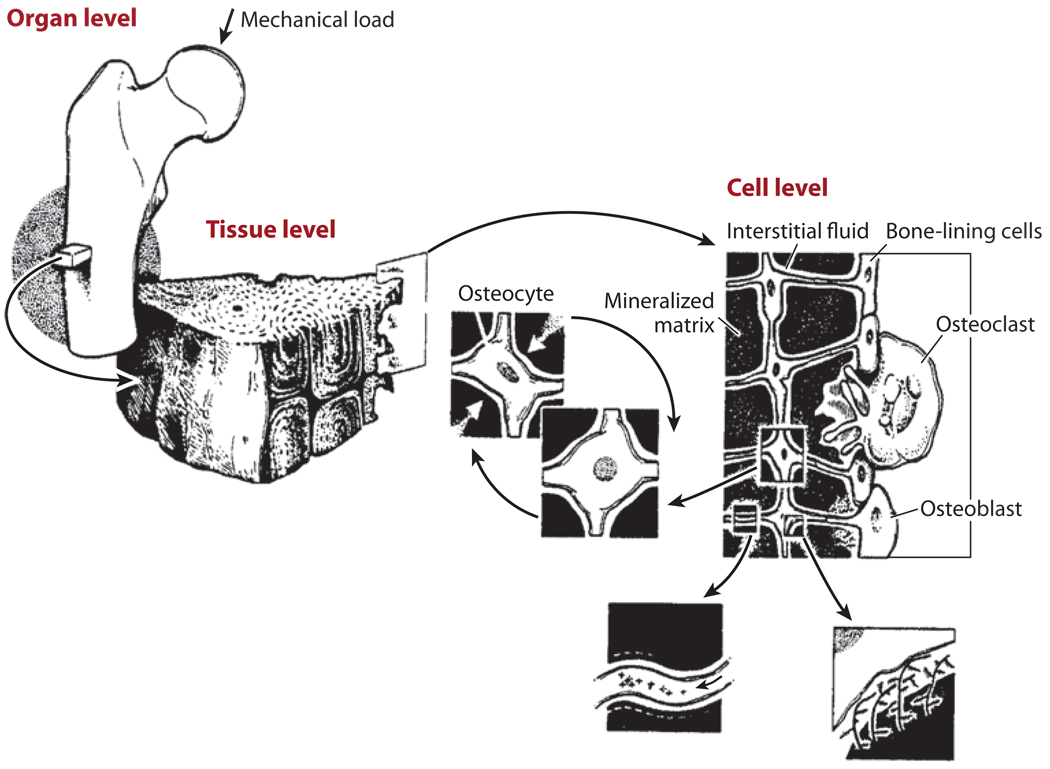
Bone is a dynamic and complex cellular structure that adapts to accommodate changes in its functional environment. Exercise can increase bone mass, whereas reduced loading (such as bed rest or exposure to a microgravity environment) can induce bone loss. Although it is well accepted that mechanical signals are critical to maintain an adequate skeleton, the mechanism by which bone cells sense their mechanical environment and initiate the deposition or resorption of bone tissue has not been ascertained completely. Much recent evidence points to cellular excitation due to interstitial fluid flow, as we outline in this review (Figure 1).
Figure 1.
Mechanical loading applied at the whole bone level is transmitted through the bone tissue to the cellular level and causes movement of the interstitial fluid surrounding osteocytes in the mineralized matrix. The osteocytes are distributed throughout bone tissue and connect to each other and to bone-lining cells and osteoblasts on the bone surfaces. Figure adapted from Rubin et al. 1990. Reprinted with permission from Elsevier.
In their pioneering paper, Piekarski & Munro (1977) first proposed that fluid flows in the lacunar-canalicular system of bones in response to mechanical loading. This and many subsequent papers over the next two decades were primarily concerned with the nutritional aspects of how the cells that lived within the calcified bone matrix, osteocytes, received their nutrients and disposed of the waste products of their metabolism. The basic mystery of how these bone cells sensed their mechanical loading and converted these signals into a biochemical response was unresolved. Cowin et al. (1991) present an excellent summary on the differing views of bone mechanotransduction in the early 1990s. The hypothesis that had gained the widest following was that it resulted from strain-generated potentials (SGPs) arising from load-induced fluid flow through a connected system of micropores in the collagen-apatite porosity (Salzstein & Pollack 1987, Salzstein et al. 1987, Starkebaum et al. 1979). This fluid pathway contradicted the nutritional pathway proposed by Piekarski & Munro (1977), and the predicted pore size did not agree with some early tracer studies that showed that solutes as small as 2 nm did not penetrate the mineralized matrix (Tanaka & Sakano 1985). Clouding the issue were tracer studies with larger molecules such as ferritin (12 nm) that showed partial rings or halos surrounding osteonal canals (Montgomery et al. 1988). The first fluid-flow studies on bone cells in culture were performed by Reich et al. (1990) and Reich & Frangos (1991), who demonstrated that osteoblasts exposed to fluid shear stress (FSS) elicited similar responses as endothelial cells at the same FSS levels. The physiological relevance of these cell-culture experiments was difficult to evaluate at the time because it seemed counterintuitive that the small fluid movements in bone due to mechanical loading could generate FSS anywhere near those levels seen in blood vessels.
Three papers appearing in the mid-1990s provided a turning point in the various controversies summarized above (Cowin et al. 1995, Klein-Nulend et al. 1995, Weinbaum et al. 1994). Weinbaum et al. (1994) introduced the hypothesis that FSS acting on the osteocyte processes residing in the lacunar-canalicular porosity was the initiating signal for cellular excitation and developed a detailed hierarchical model predicting that the FSS on these cellular processes due to flow induced by physiological loading was nearly the same as that observed on endothelial cells in the vascular system. A central tenet of this new hypothesis was that the pericellular space surrounding the osteocyte processes was filled with an extracellular matrix that sieved molecules the size of albumin (7-nm diameter) or larger. Cowin et al. (1995) proposed that the lacunar-canalicular porosity (not the micropores in the collagen-apatite porosity) was the site of the SGP and that the electrokinetic behavior resulted from the flow through the charged matrix surrounding the cell processes. Klein-Nulend et al. (1995) were the first to demonstrate the sensitivity of osteocytes to FSS at the levels predicted by Weinbaum et al. (1994).
In this review we emphasize the major developments that have followed since the appearance of these three paradigm-shifting papers. In particular, we trace how the fluid-flow models for mechanotransduction have changed as new ultrastructural features of the lacunar-canalicular porosity have been identified, how the structure and function of the osteocyte pericellular matrix have been clarified and refined through a new generation of tracer experiments, and how recent in vitro fluid-flow and cell-stretch experiments have helped elucidate at the molecular level the possible pathways for cellular excitation.
2. HIERARCHICAL STRUCTURE OF BONE AND ITS POROSITIES
Bone cells are distributed throughout bone tissue and are connected to one another through the bone porosities. Osteoblasts, which produce bone matrix, are found on bone surfaces along with bone-lining cells. Osteocytes lie in lacunae in the mineralized bone matrix; their long, slender cell processes reside in small channels called canaliculi and connect to each other and to bone surface cells via gap junctions, forming an interconnected network.
Cortical bone tissue contains the following porosities (Figure 1 and Figure 2): (a) the vascular porosity, which consists of primary or secondary osteonal lumens and Volkmann (transverse) canals and contains blood vessels, nerves, and interstitial fluid (on the order of 20–40 µm); (b) the lacunar-canalicular porosity, which contains osteocytes bathed in interstitial fluid (annular fluid space in canaliculi on the order of 100 nm); a pericellular matrix surrounds the osteocyte processes in the canaliculi (fiber matrix pore size on the order of 10 nm; see Section 4); and (c) the collagen-apatite porosity, which surrounds the collagen and the crystallites of the mineral apatite. Historically, the collagen-apatite porosity was thought to form a connected system of small pores, but many studies demonstrate that the water in this porosity is bound and the pores do not form an interconnected porosity (e.g.,Wang et al. 2004, Nyman et al. 2006).
Figure 2.
Osteocytes are housed in lacunae; their cell processes connect with one another through canaliculi. During cyclic mechanical loading, interstitial fluid from the canaliculi flows into and out of the vascular porosity surrounding bone capillaries. Figure adapted and used with permission from Kelly PJ. 1983. Pathways of transport in bone. In Handbook of Physiology: The Cardiovascular System. Peripheral Circulation and Organ Blood Flow, ed. JT Shephard, FM Abboud, sect. 2, pt. 1, chapt. 12, pp. 371–96. Bethesda, MD: Am. Physiol. Soc.
Cancellous bone also has three levels of porosity, with the largest porosity being the space surrounding the trabeculae instead of the vascular (Haversian/Volkmann canals) porosity that exists in cortical bone. Some animal species (e.g., rats) mostly do not have secondary osteons; however, the same basic structure exists: vascular porosity, lacunar-canalicular porosity, and collagen-apatite porosity.
3. STRAIN-GENERATED POTENTIALS AND THE FLUID-SHEAR-STRESS HYPOTHESIS
As first proposed by Piekarski & Munro (1977), the small deformations of bone due to mechanical loading cause fluid movement in the lacunar-canalicular porosity. This fluid movement was proposed to be the primary mechanism delivering nutrients to the osteocytes and removing waste products. Pollack and coworkers presented an alternate view of this pathway. These investigators measured the SGP across osteons in bone specimens subjected to four-point bending (Starkebaum et al. 1979) and then developed a theoretical model based on streaming potentials to predict the observed potential distribution (Pollack et al. 1984, Salzstein et al. 1987). Their model assumed that the collagen-apatite porosity was filled with a connected system of small pores (described in Section 2), and fitting their measured data to their theory predicted an effective pore size of 16-nm radius in this porosity. In marked contrast, Tanaka & Sakano (1985) and Ayasaka et al. (1992) showed that a solute as small as microperoxidase (2-nm diameter) could not enter the mineralized matrix. More recent studies (Knothe Tate et al. 1998b,Wang et al. 2004) have convincingly demonstrated that the mineralized matrix is nearly impermeable to small solutes and that the likely pathway for the streaming potentials is the pericellular matrix surrounding the osteocyte process as first proposed by Cowin et al. (1995).
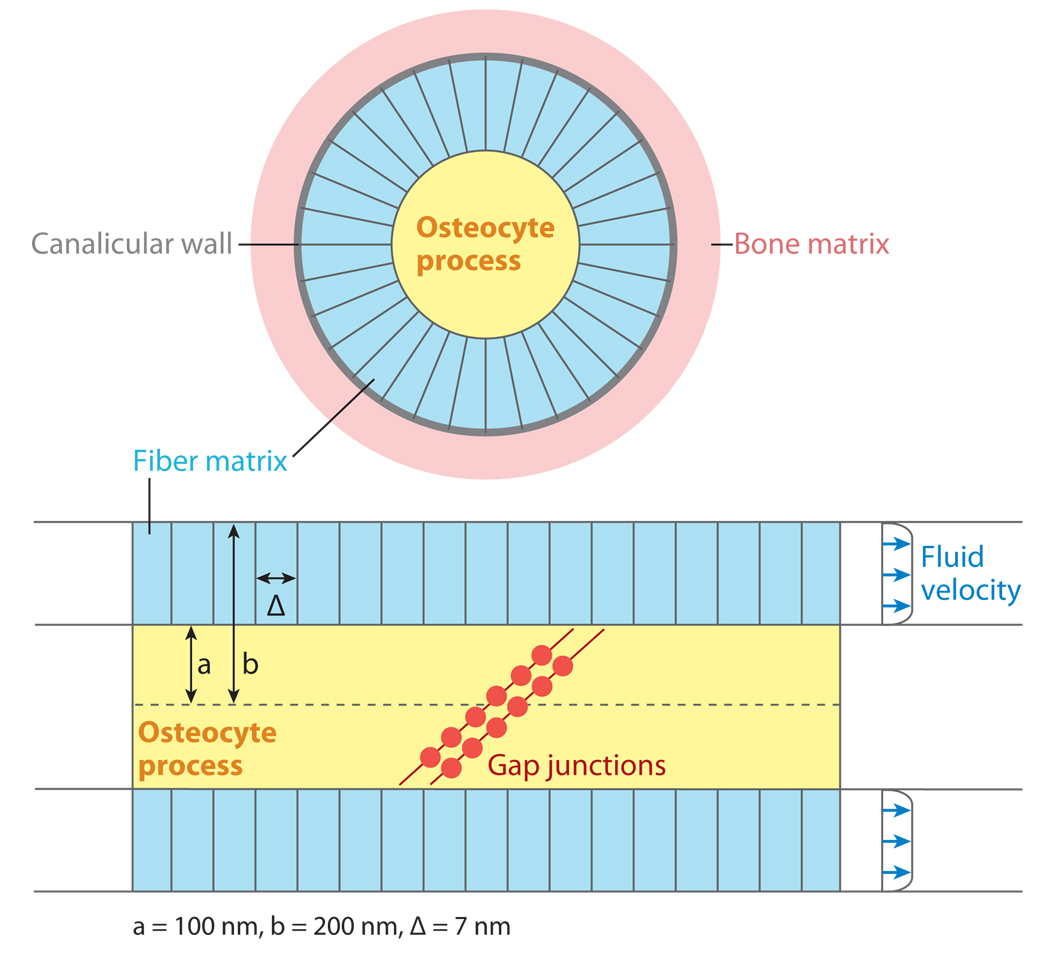
Weinbaum et al. (1994) first attempted to model the hierarchical structure of bone, including the pericellular matrix that surrounds the osteocyte processes in their canaliculi. Although Kufahl & Saha (1990) had proposed a model to study the stress-induced flow between lacunae in an osteon, the ultrastructural details of the flow in the canaliculi were missing because the model treated canaliculi as simple cylindrical tubes. Weinbaum et al. (1994) proposed an FSS hypothesis to explain how bone cells detected mechanical loading and developed an idealized mathematical model for the flow through the pericellular matrix surrounding an osteocyte process in its canaliculus (Figure 3). The flow in the porous pericellular matrix was described by a Brinkman equation, and the flow in the larger tissue space was described by Biot theory. The model remarkably and nonintuitively predicted that, despite the small deformations of whole bone tissue and the small dimensions of the pericellular annulus (typically 0.1 µm), the FSS on the membranes of the osteocyte processes (8 to 30 dyn cm−2 for physiological loading magnitudes applied at 1 Hz) was roughly the same as for the vascular endothelium in capillaries (Weinbaum et al. 1994).
Figure 3.
Schematic illustration of an osteocyte process and canaliculus, showing a cross-section view (top) and a longitudinal segment (bottom) with the ends of two cell processes connecting via gap junctions. The fluid annulus surrounding the osteocyte is filled with a pericellular matrix with pore size ∆. Figure adapted from Weinbaum et al. 1994. Reprinted with permission from Elsevier.
Weinbaum et al.’s (1994) fluid-flow model was then extended to predict the SGP across the entire bone tissue and also in the vicinity of osteonal canals using the theory developed by Petrov et al. (1989) and Zeng et al. (1994) for the flow in individual osteons. As noted earlier, Cowin et al. (1995) made the case that the canaliculi are the site of the SGPs and showed that the streaming potentials measured by Starkebaum et al. (1979) can be predicted if one considers the currents in the Debye layer along the walls of the fluid annulus and along the fibers of the osteocyte pericellular matrix. This new view was now compatible with early tracer experiments for small solutes and the model proposed by Piekarski & Munro for fluid flow in the lacunar-canalicular porosity. Cowin et al.’s (1995) theory for the SGP was subsequently combined with electrical cable theory for the ionic current through the gap junctions of the connected cell network to predict the voltage difference across the membranes of the osteocyte processes (Zhang et al. 1997, 1998a) and the possible opening of voltage-gated ion channels in the process membrane. The potential differences predicted were too small for this to occur, but the basic idea that ion channels can open and depolarize the cell is strongly suggested by the latest theory for integrin-based, flow-induced, strain-activated ion channels (Wang et al. 2007), as summarized in Section 8.
4. BONE’S INTERSTITIAL FLUID PATHWAYS
4.1. Importance of Vascular Pore Space in Bone Interstitial Fluid Flow
The detailed SGPs measured by Starkebaum et al. (1979) demonstrated that local spatial voltage gradients near osteonal canals (the vascular canals) are 10 to 30 times greater than the spatial gradients across the whole bone specimen. This nonuniform distribution of microscopic SGP gradients (and the corresponding nonuniform pressure gradients and interstitial fluid flow) is incompatible with theoretical models that assume a spatially homogeneous lacunar-canalicular porosity that neglects the osteonal canals of the vascular porosity. The experiments of Starkebaum et al. (1979) and Otter et al. (1994) suggest that fluid-flow models should consider the heterogeneous microstructure of bone and that the assumption that bone fluid relaxes across the entire bone-specimen thickness via the lacunar-canalicular porosity only is incorrect.
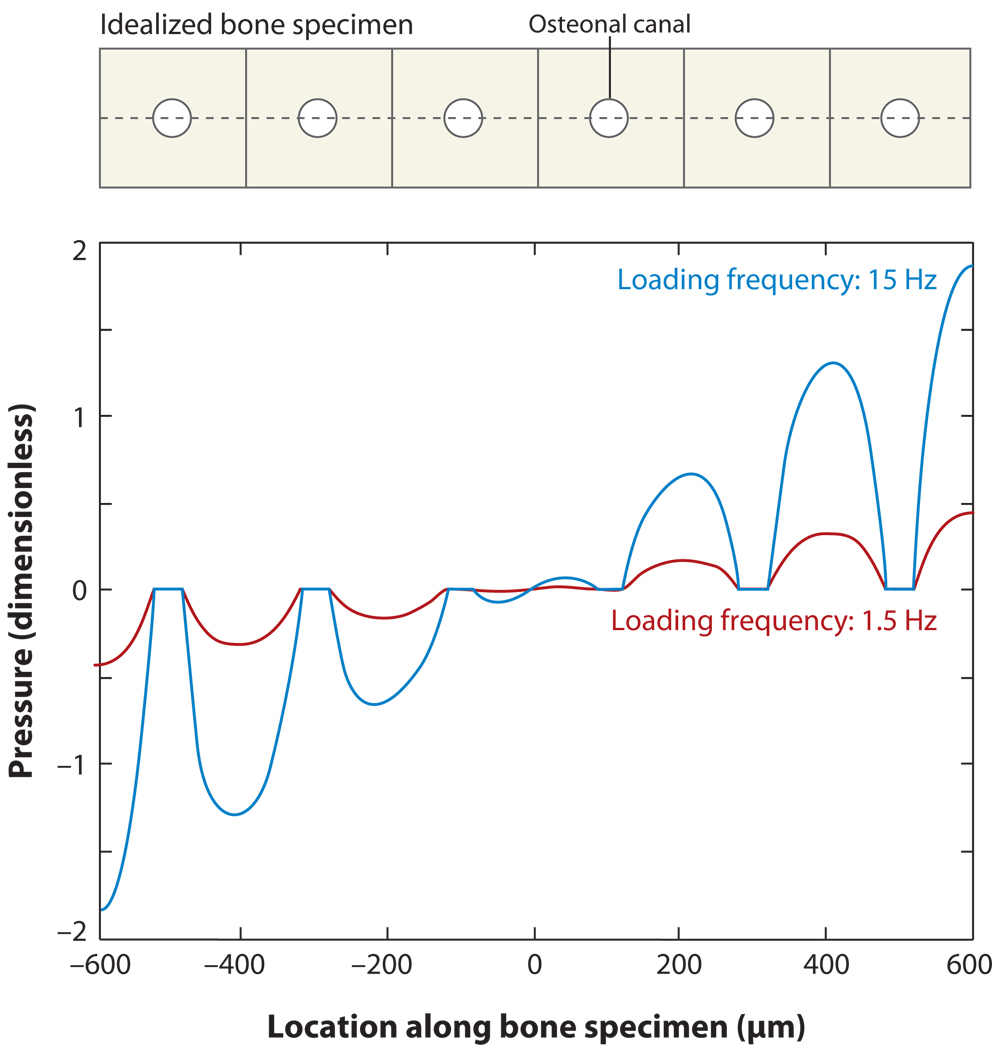
Prior to 1999, most bone fluid-flow models featured single osteons (Petrov et al. 1989, Pollack et al. 1984, Zeng et al. 1994) or homogeneous sections of bone tissue (Salzstein & Pollack 1987, Weinbaum et al. 1994). Although some models attempted to include the lacunar-canalicular network as well as the osteonal structure in a section of bone tissue (Harrigan & Hamilton 1993, Kufahl & Saha 1990, Mak et al. 1997), they did not predict the pressure profiles observed by Starkebaum et al. (1979), showing both mean and detailed pressure gradients around each vascular canal, as well as across the entire bone specimen. Wang et al. (1999) first presented this more detailed model, which also considered the permeability of the osteon cement line for the first time (Figure 4). The most important prediction of this more sophisticated model is the clear demonstration that the primary relaxation of the excess bone fluid pressure occurs via the vascular canals and not between the outer surfaces of the bone specimen as had been assumed previously. This prediction explained Otter et al.’s (1994) experiments in which the relaxation time for the excess pore pressure due to mechanical loading did not depend on the thickness of the cortical bone specimens, but seemed to correlate with the distance between the vascular canals. Whether the bone has secondary osteons or primary vascular canals, the relaxation of the excess bone fluid pressure occurs primarily as a result of fluid from the lacunar-canalicular system emptying into the vascular pores.
Figure 4.
Pressure distribution across a portion of an idealized bone specimen of thickness 1.2 mm (shown on top), mimicking Starkebaum et al.’s (1979) bending experiments. The circles represent osteonal canals, and the cusps around the canals demonstrate higher pressure gradients near the vascular pores, which are further amplified at higher loading frequencies. Figure adapted from Wang et al. 1999. Reprinted with permission from Elsevier.
Besides explaining Otter et al.’s (1994) observations, Wang et al.’s (1999) bone fluid model also sheds some light on a possible amplification mechanism in the transduction of mechanical signals to bone cells. This study indicates that the local pressure gradients near the vascular canals are significantly amplified at higher loading frequencies. These amplified pressure gradients would drive the interstitial fluid to flow over the cell processes at a higher velocity, inducing larger hydrodynamic forces and causing the cells to have a higher sensitivity to high-frequency loading. Higher pressure gradients would also produce larger fluid displacements during cyclic loading and thus greater mixing of solutes per loading cycle, as discussed below.
4.2. Contribution of Bone Microstructure to Bone Permeability
Several experimental studies have measured the hydraulic permeability of cortical and cancellous bone (Grimm & Williams 1997, Kohles et al. 2001, Li et al. 1987, Lim & Hong 2000, Nauman et al. 1999, Rouhana et al. 1981). The values of permeability reported represent the permeability through lumped porosities; none of the techniques differentiates between the permeability of the lacunar-canalicular porosity and the vascular porosity or intertrabecular porosity. The characteristic lineal dimension of the vascular porosity and intertrabecular porosity is two to three orders of magnitude larger than that of the lacunar-canalicular porosity (Cowin 1999), and thus these porosities act as low-pressure reservoirs that interstitial fluid from the lacunar-canalicular porosity can flow into and out of as shown by Wang et al. (1999). Most estimates of the vascular permeability suggest that it is at least three or four orders of magnitude larger than the estimates of the lacunar-canalicular permeability (Zhang et al. 1998b). Experimental measurement of the hydraulic permeability of the fluid space surrounding the osteocytes is difficult because the vascular porosity is intermingled with the lacunar-canalicular porosity, and it is difficult to apply traditional permeability measurement methods at the length scale of the lacunar-canalicular porosity (on the order of 100 nm) (Knothe Tate 2001, Sander & Nauman 2003). A promising new technique for measuring diffusive permeability in real time is the approach developed by Wang et al. (2005) that combines fluorescence recovery after photobleaching with confocal microscopy to measure the time-dependent filling of individual lacunae after photobleaching. These experiments have led to the important prediction that the pericellular matrix surrounding the osteocyte processes sieves molecules of the same size as the glycocalyx on endothelial cells, in which the cutoff is close to the effective diameter of albumin (7 nm). Su et al. (2006) extended this approach to evaluate molecular transport with and without applied loading in an ex vivo mouse femur. Performing similar measurements in vivo would provide the first direct measurements of flow velocities in the lacunar-canalicular porosity.
A number of studies have used poroelastic finite-element models to quantify macroscopic bone fluid flow in response to mechanical loading (e.g., Fornells et al. 2007, Gururaja et al. 2005, Manfredini et al. 1999, Smit et al. 2002, Steck et al. 2003). Whereas many models lump the vascular porosity and the lacunar-canalicular porosity together, Smit et al. (2002) estimated isotropic poroelastic parameters for the two porosity levels using composite modeling and SGP data from Otter et al. (1992). Steck et al. (2003) applied anisotropic permeability for the lacunar-canalicular porosity using rough estimates derived from the literature. A complete anisotropic poroelastic parameter data set was recently reported based on a micromechanical analysis (Yoon & Cowin 2008). Other recent work has attempted to quantify the three-dimensional architecture of the osteocyte lacunar-canalicular porosity to better estimate bone permeability in three orthogonal directions (Beno et al. 2006).
Recent studies have also used confocal microscopy to characterize the microstructure of the lacunar-canalicular porosity to better quantify the interstitial fluid pathway. Three-dimensional measurements of the osteocyte lacunar shape (McCreadie et al. 2004) as well as the number of canaliculi per osteocyte have recently been reported (Beno et al. 2005, Sugawara et al. 2005). Sugawara et al. (2005) also quantified the total length of the canaliculi per cubic micrometer in embryonic chick bone, and Beno et al. (2005) quantified the three-dimensional canalicular distribution in rat bone in three orthogonal directions and used these measurements to estimate the anisotropy of the lacunar-canalicular porosity.
4.3. Tracer Studies to Delineate Transport Properties of the Osteocyte Pericellular Matrix
Another experimental approach to quantify bone interstitial fluid pathways involves the vascular injection of tracers of different sizes to track where the tracers travel in the bone porosities.Tracers such as horseradish peroxidase (Doty & Schofield 1972), microperoxidase (Ayasaka et al. 1992, Knothe Tate et al. 1998b, Tanaka & Sakano 1985), ferritin (Ciani et al. 2005, Dillaman 1984, Montgomery et al. 1988, Qin et al. 1999, Wang et al. 2004), and procion red and reactive red (Knothe Tate et al. 1998a, Wang et al. 2004) have been used to track fluid movement in the absence of applied external loading. Investigators have also used tracer methods to experimentally confirm the existence of stress-induced transport within bone tissue (Knothe Tate & Knothe 2000, Knothe Tate et al. 2000, Mak et al. 2000, Tami et al. 2003).
In vivo tracer studies have demonstrated that vascular pressure is capable of driving the flow of interstitial fluid in the bone porosities even in the absence of externally applied mechanical loading. Tracers injected into the blood circulation have been found to leak out of the capillaries and move into the lacunar-canalicular porosity (Dillaman 1984, Knothe Tate et al. 1998b, Montgomery et al. 1988, Qin et al. 1999, Tami et al. 2003, Wang et al. 2004). Other evidence of vascular pressure-driven interstitial fluid flow is the measurement of SGPs induced by the pulsatile medullary pressures within the marrow cavity (Otter et al. 1994). However, these potentials are an order of magnitude lower than those due to mechanical loading (Brookes & Revell 1998) (see sidebar).
Although many tracer experiments have been performed, the results from some of these studies have been contradictory. We summarize results below for studies using large, medium, and small tracers.
4.3.1. Large tracers
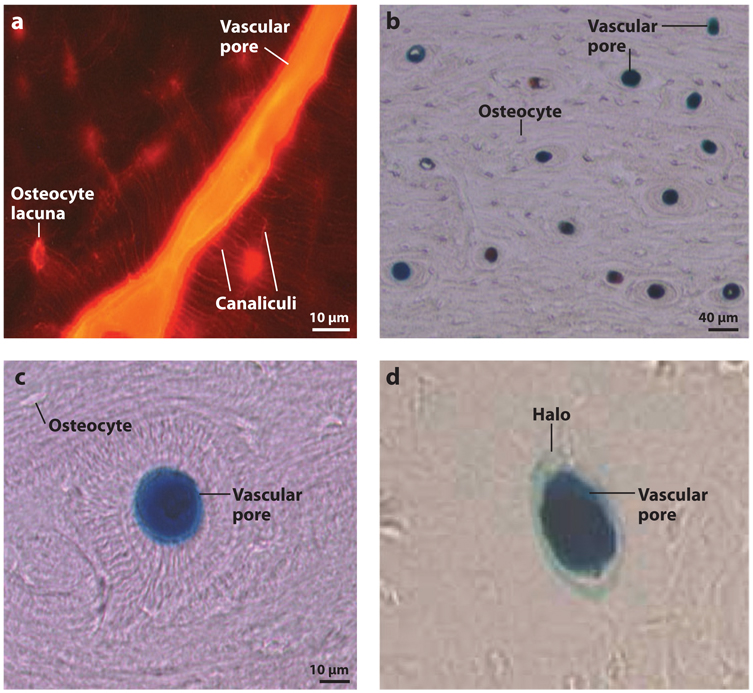
Studies with ferritin (~12-nm diameter) in 2-day-old chick embryo show continuous halo-shaped labeling around primary osteons 5 min after injection of the tracer (Dillaman 1984). A model by Keanini et al. (1995) suggested that the halos are a convective front of the tracer that passes through the unmineralized collagen-proteoglycan matrix. Because 2-day-old chick bone is incompletely mineralized, the presence of halos suggests that unmineralized bone contains continuous pores that are larger than 12 nm. Ferritin injected into mature dogs (Montgomery et al. 1988) and goats (Qin et al. 1999) also surprisingly showed halos surrounding the osteonal canals, an observation that was seen with no other tracer. This unusual result was recently explained by Wang et al. (2004) and Ciani et al. (2005), who demonstrated that such halos were likely an artifact of histological processing and could be eliminated by shortened fixation methods. These studies found that ferritin was confined exclusively to the vascular canals and blood vessels and did not enter the lacunar-canalicular porosity (Figure 5).
Figure 5.
Tracer labeling in the rat tibia mid-diaphysis. (a) Reactive red (~1-nm diameter) labeling shows vascular pore, osteocyte lacunae, and canaliculi staining. (b,c) Ferritin (~12-nm diameter) was found in vascular pores without labeling the surrounding osteocyte lacunae. Figure adapted from Wang et al. 2004. (d ) By varying the histological processing methods, ferritin halos surrounding vascular pores can be produced. Figure adapted from Ciani et al. 2005. Reprinted with permission from Elsevier.
4.3.2. Medium tracers
A medium-sized tracer, horseradish peroxidase (~6-nm diameter), has also been shown to be confined to the lacunar-canalicular system (Doty & Schofield 1972, Knothe Tate et al. 1998b, Wang et al. 2004), indicating that molecules of at least 6 nm can penetrate the pericellular matrix surrounding the osteocyte processes.
4.3.3. Small tracers
Microperoxidase (~2-nm diameter) was found to penetrate only the un-mineralized matrix surrounding lacunae and the borders of canaliculi but was absent from the mineralized region in 5-day-old rats (Tanaka & Sakano 1985). In older rats, microperoxidase also did not penetrate the mineralized matrix (Ayasaka et al. 1992, Wang et al. 2004). Although there has been a report that another small-sized tracer, procion red (~1-nm diameter), can penetrate the collagen-apatite porosity (Tami et al. 2003), most studies demonstrate that tracers of this size do not penetrate the mineralized matrix (e.g., Knothe Tate et al. 1998b, Wang et al. 2004) (Figure 5).
Collectively, these results indicate that, although small tracers (<6 nm) readily pass through the lacunar-canalicular porosity in the absence of mechanical loading, there appears to be an upper limit or cutoff size between horseradish peroxidase (40,000 Da, ~6 nm) and ferritin (440,000 Da, ~12 nm) for molecular movement from bone capillaries to osteocyte lacunae. This range of pore size contains the most likely fiber spacing (~7 nm), which Weinbaum et al. (1994) first proposed for the size of the molecular sieve in the lacunar-canalicular annular space. This size sieve was originally suggested because it is well recognized that bone capillaries are quite permeable to albumin, and one would want to have a reflection coefficient close to 1.0 to prevent major leakage of this important plasma protein, which is the body’s primary regulator of oncotic pressure. Finally, because halo labeling has not been found with any other tracer, we believe that ferritin labeling should not be used to explain interstitial fluid movement in bone; no other tracers demonstrate a centrifugal bulk movement of bone interstitial fluid due to hydrostatic pressure, as has been widely interpreted from the earlier ferritin results (Hillsley & Frangos 1994, Keanini et al. 1995, Mak et al. 1997, Winet 2003).
4.4. Solute Transport in the Lacunar-Canalicular Porosity Under Cyclic Mechanical Loading
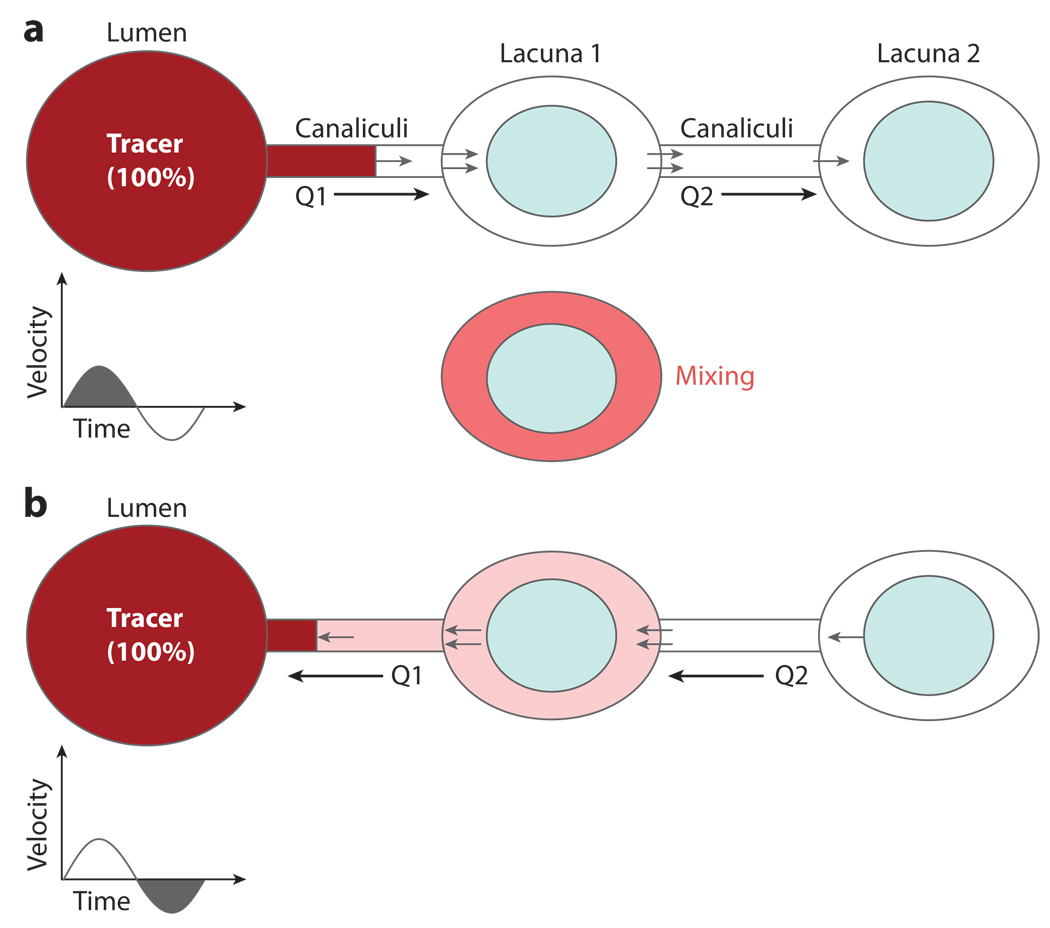
As proposed by Piekarski & Munro (1977) and later studied by Kufahl & Saha (1990) and Knothe Tate et al. (1998a), diffusion between the blood vessels and osteocytes may be insufficient for osteocytes to obtain nutrients and dispose of waste products appropriately so that stress-induced fluid flow in the lacunar-canalicular system is needed to enhance transport between the blood supply and bone cells. However, bone is usually subjected to cyclic loading owing to locomotion, and one is confronted with a basic paradox: How can net molecular transport occur when there is no net fluid transport in cyclically loaded bone? A similar paradox is encountered during breathing, in which the alveoli function as exchange reservoirs for mixing. Where are the mixing chambers in bone tissue? Wang et al. (2000) have provided a plausible explanation for this mystery (Figure 6). Instead of alveolar sacs, the numerous osteocyte lacunae serve as mixing chambers. Because the distance between lacunae is roughly 30 µm, solutes must have a diffusion coefficient of at least 10−5 cm2 s−1 to diffuse this distance at a loading frequency of 1 Hz, which is typical of locomotion (Wang et al. 2001). Gaseous molecules could do this, but most hydrophilic molecules could not. However, enhanced molecular transport could occur during cyclic loading if there were a convective flux of sufficient magnitude to allow the solute to travel to the next osteocyte lacunar space before flow reversal occurs. Many canaliculi feed each lacuna, in which the thickness dimension of the lacunar space surrounding the osteocyte cell body is ~1 µm. Thus, diffusional mixing is very rapid, and the solute concentration that leaves the lacuna can differ significantly from that which enters (Figure 6). It is this concentration difference between the inward and outward lacunar flow that is vital for net solute transport through the lacunar-canalicular porosity during cyclic loading. Model predictions indicate that tracer transport increases with higher loading magnitude and higher permeability and decreases with increasing loading frequency (Wang et al. 2000).
Figure 6.
Schematic of Wang et al.’s (2000) proposed mixing model. (a) For cyclic loading, if the fluid displacement is large enough to pass from the vascular lumen (the tracer source) through the canaliculi to the first osteocyte lacuna, an instant mixing process occurs in the lacuna. (b) Upon the reversal of cyclic loading, even though the fluid returns to the vascular pore, net solute transport to the lacuna occurs. Figure from Wang et al. 2000 with kind permission from Springer Science + Business Media.
EFFECT OF MEDULLARY PRESSURE AND VENOUS STASIS ON BONE FLUID FLOW
Increased interstitial fluid flow induced by increased intramedullary pressure has been proposed to account for the adaptive bone response found with compromised venous circulation or venous stasis (Bergula et al. 1999, Hillsley & Frangos 1994, Kelly & Bronk 1990, Welch et al. 1993). To investigate the shear stresses acting on bone cells owing to the blood circulation–driven interstitial fluid flow, Wang et al. (2003) used a poroelastic model in which the interstitial fluid flow in an osteon was driven by the pulsatile extravascular pressure in the vascular lumen as well as by the applied cyclic mechanical loading. The results showed that under normal conditions, the pulsatile extravascular pressure in the vascular lumen due to cardiac contraction and skeletal muscle contraction induced peak shear stresses on the osteocyte cell processes that were two orders of magnitude lower than those induced by physiological mechanical loading. In venous stasis, the induced peak shear stress was reduced further compared to normal conditions because, although the mean intramedullary pressure was increased, the amplitude of its pulsatile component was decreased. These results suggest that interstitial fluid flow is unlikely to cause the bone formation observed in venous stasis. However, the mean interstitial fluid pressure increases during venous stasis, which may pressurize the outer surface of a long bone (the periosteum) and thus play a role in periosteal bone formation. In contrast to these results, a recent study demonstrated increased interstitial flow when the femoral vein was ligated in a mouse model (Stevens et al. 2006). An interesting model that uses intramedullary pressure oscillations to increase bone mass (Qin et al. 2002, 2003) is described in Section 10.
5. EFFECT OF FLOW AND STRETCH IN BONE CELL–CULTURE STUDIES
The sensitivity of bone cell populations to fluid flow has been widely demonstrated in cell cultures within flow chambers. The early studies of Reich et al. (1990) and Reich & Frangos (1991) indicated that osteoblasts in culture responded to FSS much like endothelial cells in the activation of cyclic AMP and prostaglandin E2 (PGE2) release. These studies did not receive appropriate recognition at first because it seemed highly implausible that a stiff tissue such as bone could produce an FSS that was comparable with the FSS in the vascular system. Weinbaum et al.’s (1994) nonintuitive prediction that this was indeed the case (for reasons discussed in Section 3) led to a plethora of new experiments that exposed bone cells to fluid shear within flow chambers.
Most of the in vitro bone fluid-flow studies were performed on cultured osteoblasts until van der Plas & Nijweide (1992) were able to extract osteocytes from live bone tissue and grow them in culture; an osteocyte-like cell line (MLO-Y4) was established later (Bonewald 1999). Both osteoblasts and osteocytes respond to steady and pulsed fluid flow with a rapid increase in nitric oxide production (Johnson et al. 1996, Klein-Nulend et al. 1995, McAllister & Frangos 1999). Pulsed fluid flow applied to osteocyte cultures causes the release of PGE2 and PGI2, with the response dependent on the presence of an intact actin cytoskeleton (Ajubi et al. 1996). Fluid flow increases intracellular calcium in bone cells (Chen et al. 2000, Donahue et al. 2001, Hung et al. 1995, Williams et al. 1994), and both Ca2+ influx and actin filaments mediate the PGE2 response of osteocytes to pulsed fluid flow in vitro (Ajubi et al. 1999). Cultured osteocytes appear to be more sensitive to fluid flow than osteoblasts (Ajubi et al. 1996, Westbroek et al. 2000), possibly because of cytoskeletal differences, with osteocyte structure largely dependent on actin (McGarry et al. 2005, Tanaka-Kamioka et al. 1998). Recent studies also demonstrate that exposing osteocytes to FSS causes ATP release (Genetos et al. 2007), inhibits osteocyte apoptosis (Bakker et al. 2004), and inhibits osteoclast formation (Kim et al. 2006, Tan et al. 2007).
In vitro studies using oscillating fluid flow to more realistically model the cyclic loading of bone in vivo have found that bone cells must have sufficient nutrient supply and waste removal to be responsive to the oscillating flow (Haut Donahue et al. 2003, Jacobs et al. 1998). Several additional efforts are underway to develop bone culture systems that better mimic the in vivo bone fluid system. Some groups have grown bone cells in three-dimensional matrices to better simulate the fluid-flow conditions that occur in vivo (e.g., Mauney et al. 2004, Tanaka et al. 2005). In addition, new micropatterning techniques have made it possible to seed bone cells in individual wells in a manner that allows them to form an interconnected network with narrow channels that simulate canaliculi in vivo (Guo et al. 2006, You et al. 2008). Such a network is clearly a more realistic model of the lacunar-canalicular system, and future studies analyzing the effects of FSS on osteocytes grown in these connected networks will help to identify the cellular pathways in mechanotransduction.
Several studies demonstrate that bone cells are more responsive to fluid flow than to mechanical strain (Owan et al. 1997, Smalt et al. 1997, You et al. 2000). Particularly significant, You et al. (2000) both established the threshold response for the release of Ca2+ when bone cells were grown on stretchable substrates and compared this response with the FSS response of osteoblastic and osteocytic (MLO-Y4) cells using techniques that clearly distinguished the effects of FSS and stretch. These studies strongly suggested that in culture substrate strains appeared to be far less important than FSS in cellular excitation. In general, no biochemical responses were observed for cellular-level strains less than 0.5% (5000 microstrain) (You et al. 2000). Although the findings from bone cell–culture studies have been widely interpreted to strongly confirm the FSS hypothesis, more recent theoretical models suggest that, for osteocytes in vivo, the drag force on the osteocyte process is much greater than the FSS on the process (You et al. 2001) (see Section 6).
6. STRAIN-AMPLIFICATION HYPOTHESIS
A fundamental paradox in comparing the mechanical stimulation of bone cells in vivo and in vitro is that tissue-level strains caused by locomotion seldom exceed 0.2% (2000 microstrain) (Burr et al. 1996, Fritton & Rubin 2001, Fritton et al. 2000), yet the in vitro experiments with bone cells discussed in Section 5 indicate that cellular-level strains greater than 0.5% (5000 microstrain) are required to elicit intracellular signaling. Such large strains may cause bone tissue damage. This key observation suggests that whole tissue strains need to be substantially amplified to elicit a cellular biochemical response.
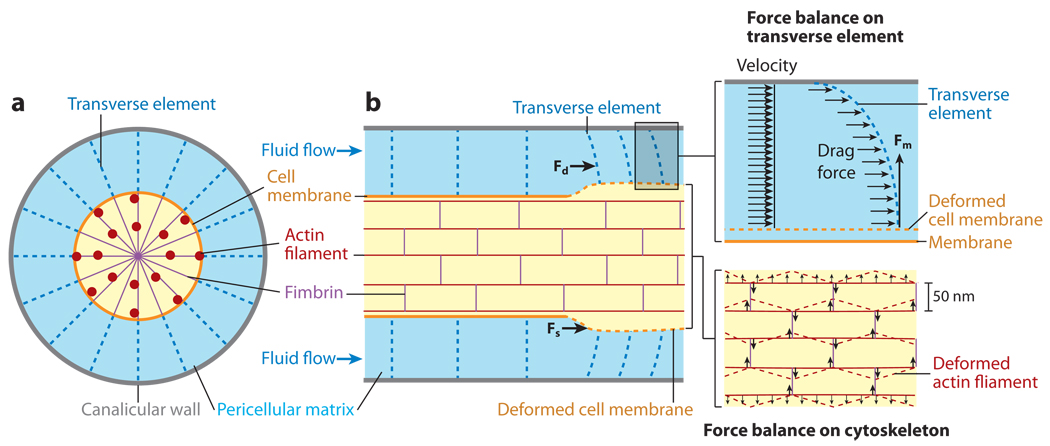
To resolve this mystery, investigators suggested (Cowin & Weinbaum 1998) and developed (You et al. 2001) a new strain-amplification model for the mechanical stimulation of the osteocyte process. Largely from intuitive arguments, it was hypothesized that the cell process was similar to a suspended cable that was attached by tethering elements to adhesion proteins lining the canalicular wall. The tethering fibers were proposed to be proteoglycans that spanned the fluid annulus and attached at binding sites to the membrane of the osteocyte process (Figure 7). The glycosaminoglycan fibers that formed the molecular sieve for the tracer molecules described in Section 4 were also assumed to be attached to these tethering elements, and when the bone tissue was deformed, the fluid passing through the osteocyte pericellular matrix would create a hydrodynamic drag on the matrix. This drag would put the tethering elements in tension, thereby producing a radial (hoop) strain on both the process membrane and its underlying central actin filament bundle (Figure 7).
Figure 7.
You et al.’s (2001) strain-amplification model illustrating the osteocyte process in cross section (a) and longitudinal section (b). Actin filaments span the process, which is attached to the canalicular wall via transverse elements. Applied loading results in interstitial fluid flow through the pericellular matrix, producing a drag force on the tethering fibers. Figure reprinted from You et al. 2001, with permission from Elsevier.
The predictions of this exploratory quantitative model demonstrated a cellular-level strain amplification of 10 to 100, depending on loading magnitude and frequency, and cellular strains of up to 5% for physiological loading at 1 Hz. The model not only confirmed the quantitative feasibility of the strain-amplification mechanism, but also showed that the drag on the pericellular matrix fibers per unit process length was 20 times greater than the FSS over the same process length, strongly suggesting that Weinbaum et al.’s (1994) FSS mechanism and the observations in the numerous cell-culture experiments described in Section 5 were not correctly interpreted. Weinbaum et al.’s fluid-flow model was valid; however, the activating mechanical signal was not FSS but, according to the new hypothesis, the flow-induced drag on the tethering fibers, which far exceeded the FSS on the cell process membrane. The simplified model for the elastic modulus of the actin filament bundle in the osteocyte process also predicted that this structure was 200 times stiffer than the measured modulus of osteoblast cell bodies (Shin & Athanasiou 1999).
7. ULTRASTRUCTURAL STUDIES OF THE OSTEOCYTE PERICELLULAR MATRIX AND CELL PROCESSES
The strain-amplification hypothesis stimulated a search for new fixation techniques in which key structural elements in the osteocyte pericellular matrix could be observed and details of the cytoskeletal structure of the central actin filament bundle in the cell process ascertained. Previous ultrastructural studies that removed chicken osteocyte membranes and examined their internal cytoskeleton using electron microscopy (EM) (Tanaka-Kamioka et al. 1998) revealed a cell process with a highly organized fimbrin cross-linked actin filament bundle running the entire length of the process and a cell body with a more diffuse actin organization. This qualitatively confirmed earlier EM studies on the actin organization of osteocytes in bone tissue (Holtrop 1975, King & Holtrop 1975, Shapiro et al. 1995), but the resolution of the latter was poor and the pericellular matrix was marginally preserved. Using new oxygen-based fixation techniques, improved EM images of both the central actin filament bundle and the pericellular matrix in cortical tibia of adult mouse were obtained (You et al. 2004). These images revealed a central actin filament bundle with typically 20 F-actin filaments arranged in a hexagonal array (Figure 8) with a spacing similar to the actin filament bundles in intestinal microvilli and stereocilia, structures known to be fimbrin cross-linked (Weinbaum et al. 2001).
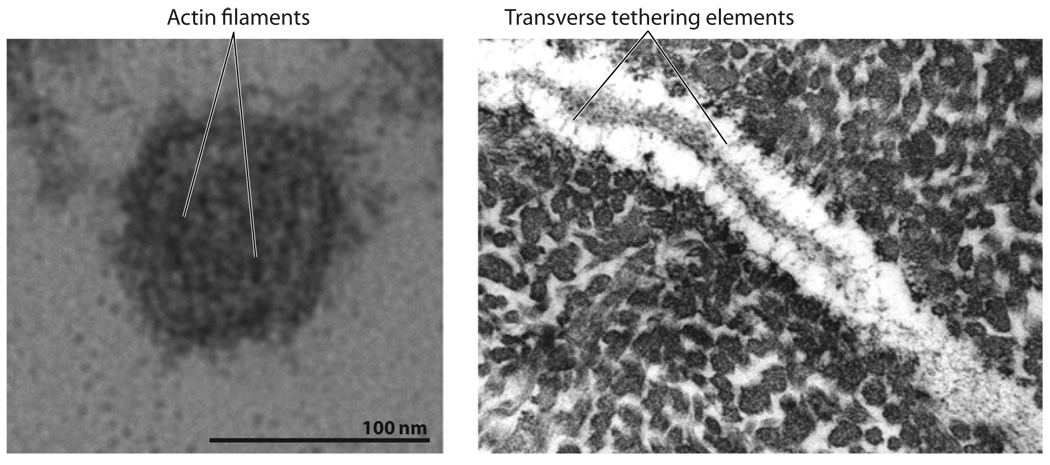
Figure 8.
(Left panel) Electron microscopy (EM) of a cross section of osteocyte process from mouse bone showing the central actin filament bundle. (Right panel) EM of a longitudinal section of osteocyte process from mouse bone showing tethering fibers. Figure taken from You et al. 2004 with permission.
You et al.’s (2004) most important observation was the identification of the tethering elements that had been hypothesized in their theoretical model paper (You et al. 2001) (Figure 7). They also demonstrated that the pericellular matrix filled the entire cross section of the fluid annulus. Unfortunately, the fixation procedures that most clearly preserve the pericellular matrix do not clearly show the central actin filament bundle and process membrane, so the linkage of the two cannot be easily discerned. However, other EM studies on intestinal microvilli, which have a central actin filament bundle that is similar to osteocyte processes, have provided the key structural details on this linkage (Matsudaira & Burgess 1982, Mooseker & Tilney 1975). These microvilli studies provide a detailed picture of the cross-filaments, which attach the central filament bundle to proteins in the encircling membrane and the hexagonal cross-linked structure of the central actin bundle (Volkmann et al. 2001).
8. REFINED MODELS FOR STRAIN AMPLIFICATION AND INTEGRIN-BASED MECHANOTRANSDUCTION
You et al.’s (2001) relatively crude model assumed a simplified radial arrangement of actin filaments in the central actin filament bundle (Figure 7) and greatly simplified the structural details in the cross-linking of the filaments. Using You et al.’s (2004) detailed ultrastructural measurements, Han et al. (2004) constructed a refined elastohydrodynamic model for the flow-induced strain amplification of the osteocyte processes (Figure 9).
Figure 9.
Schematic of Han et al.’s (2004) strain-amplification model, illustrating greatly refined actin filament and cross-filament arrangements. (a) Cross section of osteocyte process. (b) Fimbrin cross-linking arrangement. (c) Longitudinal section of osteocyte process. (d ) Double helix of cross-filaments. Figure taken from Han et al. 2004, Proc. Natl. Acad. Sci. USA 101:16689–94. Copyright (2004) National Academy of Sciences, U.S.A.
Han et al.’s (2004) results demonstrate that for physiological loading at 1Hz (walking frequency) with a 20-MPa load (0.1% or 1000 microstrain tissue strain), the cellular-level strain is 0.5% or just sufficient to elicit intracellular signaling. This prediction is of special interest in that it is close to the threshold loading required for the maintenance of bone mass with 100 cycles of loading daily at 1 Hz (Rubin & Lanyon 1985). Tissue loadings of <20 MPa can also produce strains that exceed the 0.5% cellular-level threshold for activation, but only at higher frequencies. Han et al. (2004) also found that the theoretical model predictions for the effective Young’s modulus of the actin filament bundle, based on its measured value for a single actin filament, are 600 times that measured for the cell body or three times that predicted by You et al. (2001).
The foregoing results are primarily pertinent to in vivo loading, but how do they apply to cultured bone cells in flow chambers, which do not have tethering fibers but in all likelihood have integrins that attach their dendritic processes to their substrate? This question—and the fact that none of the likely molecules in the tethering complex modeled by You et al. (2001) and Han et al. (2004) (CD44, proteoglycans, hyaluronic acid) is a known initiator of intracellular signaling—motivated an investigation into integrin-based focal adhesion complexes on the den-dritic processes of osteocytes in vivo because such complexes have been implicated as important mechanical transducer sites in many other cells.
Wang et al. (2007) proposed a model that presents a new paradigm for the initiation of integrin-based intracellular signaling (Figure 10). The model differs from Han et al.’s (2004) model (Figure 9) in the presence of rigid integrin attachments at the apex of local conical protuberances. The conical protuberance, found in Wang et al.’s (2007) EM studies, is a striking canalicular feature that had been previously ignored: There are infrequent, discrete structures protruding from the canalicular wall that completely cross the pericellular space and make direct contact with the membrane of the osteocyte process (Figure 10). Because these projections appear the same in both longitudinal and transverse sections, they are conical in shape. These direct contacts are absent from the cell body because the pericellular space is much wider (~1 µm). Immunohistochemical analysis revealed punctate staining of αVβ3 integrins confined to the cell process and β1 integrins concentrated on the cell body but absent from the processes (McNamara et al. 2006). Finally, tethering fibers were seen in the same cross-sectional plane as the conical projections (Figure 10). In the model (Wang et al. 2007), the tethering complex at the membrane surface is linked to the central actin filament bundle by cross-linking molecules. The actin filaments can slide axially relative to one another, as clearly demonstrated in stereocilia. This motion of the actin filaments and the flexibility of the tethering elements allow local stress concentrations and large axial strains to build up in the vicinity of the more rigid integrin attachment sites when there is interstitial fluid flow through the pericellular matrix.
Figure 10.
(a) Electron micrographs illustrating the canalicular protrusions and transverse tethering elements of the osteocyte process. (b) Schematic of Wang et al.’s (2007) integrin-based strain-amplification model. The conical canalicular protrusions can be seen both in cross section (left) and longitudinal section (right). Figure adapted from Wang et al. 2007, Proc. Natl. Acad. Sci. USA 104:15941–46. Copyright (2007) National Academy of Sciences, U.S.A.
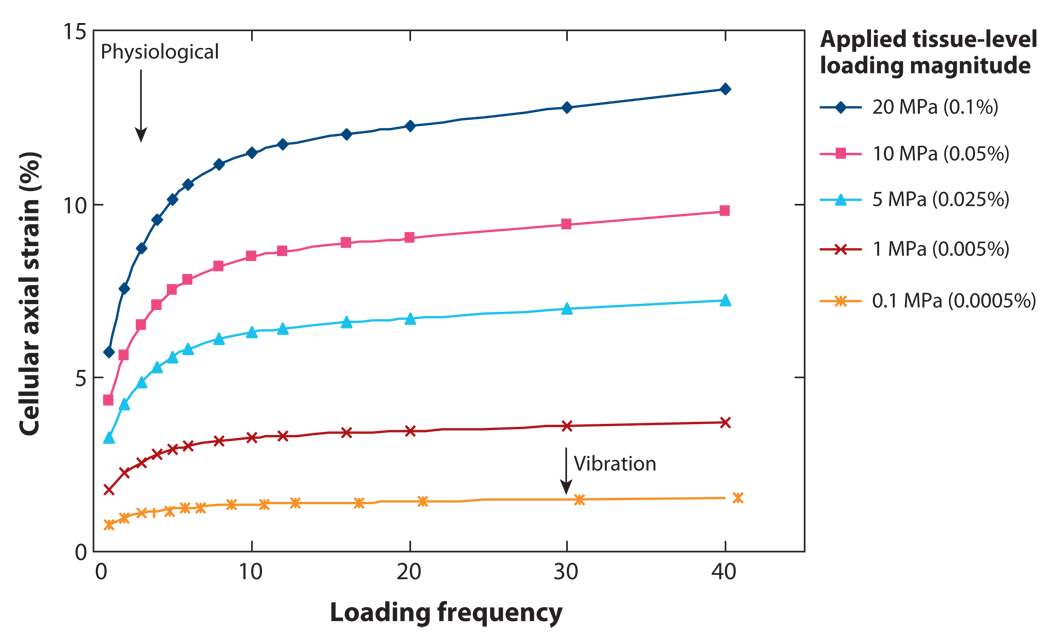
Wang et al.’s (2007) elastohydrodynamic model for integrin-based signaling leads to greatly amplified axial strains in the osteocyte membrane in the vicinity of the integrin attachment site (Figure 11). These strains are nearly6%for a 20-MPa (0.1% or 1000 microstrain) tissue loading at 1 Hz, more than 10 times the hoop strain predicted by Han et al. (2004) at the same tissue loading. Strains of this order are sufficient to open stretch-activated ion channels and initiate electrical signaling, a behavior that has been extensively studied for hair cells in the inner ear in which tip links open stretch-activated Ca2+ channels in the membrane of stereocilia (Hudspeth et al. 2000). This possibility could prove to be an important new area of research in bone mechanotransduction.
Figure 11.
Cellular axial strains as a function of applied tissue-level strains and loading frequency. Physiological loading is marked as loading at 1 Hz, the approximate frequency of walking. Vibration loading applied by a low-magnitude oscillating platform is also indicated. For vibration loading shown by Rubin et al. (2004) to inhibit bone loss in humans, the osteocyte axial strain is predicted to be greater than the 0.5% strain (5000 microstrain) required to elicit intracellular signaling in vitro. Figure adapted from Wang et al. 2007, Proc. Natl. Acad. Sci. USA 104:15941–46. Copyright (2007) National Academy of Sciences, U.S.A.
Perhaps the most important prediction in Wang et al. (2007) is the magnitude of the forces on the integrin attachments. Because the apex of the conical projection is only 10 nm, it is possible that only a single integrin resides at this point of contact. If so, this would be the first prediction of the force on an individual integrin in vivo. Forces have been measured on large focal adhesion complexes involving complexes of talin, vinculin, and paxillin, but these are large integrin aggregates associated with the termini of actin stress fibers at basal attachment sites to fibronectin and collagen substrates in fibroblasts and endothelial cells. The predicted flow-induced force was 10 pN for a 20-MPa load at 1 Hz and 1 pN for a 0.1-MPa load at 20 Hz (Wang et al. 2007). This prediction has important implications because forces of this magnitude have been shown to initiate Ca2+ signaling when applied to dendritic processes of bone cells in vitro but not when applied to the cell body (D.C. Spray, personal communication).
9. RELATIONSHIP BETWEEN MODEL FINDINGS AND IN VITRO FLUID-FLOW EXPERIMENTS: WHAT PORTION OF THE CELL IS STIMULATED?
A fundamental unanswered question is which part of the osteocyte acts as the mechanical sensor, and is it the same in vivo and in vitro? Intuitively, one anticipates that the elastic modulus for the osteocyte process would be much stiffer than the cell body because there is a highly organized central actin filament bundle that is cross-linked by fimbrin (Han et al. 2004, Tanaka-Kamioka et al. 1998), whereas the actin filament structure in the cell body is much more loosely cross-linked by α-actinin. A uniform FSS in a flow chamber is thus far more likely to deform a soft cell body than a much stiffer cell process. In marked contrast, FSS in vivo is much more likely to stimulate the osteocyte processes, as demonstrated by models that predict this shear stress to be at least two orders of magnitude larger than on the cell body because the pericellular space in the lacuna is much wider than the narrow annulus surrounding the cell process in the canaliculus (Anderson et al. 2005, Weinbaum et al. 1994). As discussed in Section 4, the osteocyte lacunae are largely mixing chambers with low flow and low FSS. Furthermore, cells in culture do not have the tethering elements observed by You et al. (2004), which are the key structural elements in the strain-amplification models. The common feature is that bone cells in vivo and in vitro do have integrin attachments, and if signaling is initiated though integrins, Wang et al.’s (2007) model could provide a crucial link if the signaling is initiated in the cell processes. The critical experiment that needs to be performed to resolve this issue would be to apply a localized, quantifiable, hydrodynamic force on the cell processes in vitro that is of the same magnitude as the tensile force on the integrins in vivo predicted by Wang et al. (2007).
Recent experiments provide important clues as to how FSS might be communicated to the cytoskeleton. Reilly et al. (2003) demonstrated that the enzymatic removal of the pericellular matrix of MLO-Y4 cells entirely abolished a fourfold increase in PGE2 release in response to FSS, but intracellular Ca2+ was unaffected, suggesting that integrin-associated stretch-activated channels in the cell processes were affected, but that there was little change in the deformation of the cell body in which intracellular Ca2+ is stored. Such behavior is consistent with the hypothesis that, in the osteocyte process membrane, integrins colocalize with channels that permit the passage of ATP and/or PGE2. Although the molecular identification of these channels has been controversial, suggested candidates include connexin 43 hemichannels, pannexins, and P2 receptors (Cherian et al. 2005, Genetos et al. 2007, Li et al. 2005, Spray et al. 2006). Another important recent discovery is Vatsa et al.’s (2008) observation that labeling of paxillin, a molecule associated with integrin complexes, is only found on cell bodies in vivo and is absent from dendritic processes. This is strong evidence suggesting that the punctate integrin attachments observed by Wang et al. (2007) and McNamara et al. (2006) along the cell process are distinct from the focal adhesion complexes that have been extensively studied in the past. This possibility is also suggested by the fact that the attachments are along the side of an actin filament bundle and not the anchoring termini of stress fibers. Nicolella et al. (2006) have suggested that stress concentrations can also build up in regions of high curvature in the lacunae and that this could be communicated via integrins to the cell body. Although possible, this is unlikely because the deformations would be greatly attenuated by the thick (1-µm) pericellular matrix layer that surrounds the cell body.
Other recent work provides evidence that primary cilia projecting from the surface of cultured bone cells translate fluid flow into cellular responses independently of Ca2+ flux and stretch-activated ion channels (Malone et al. 2007). Efforts underway to apply FSS to osteocytes in culture in a manner that isolates the response of the cell processes and the cell body and investigates the contribution of primary cilia will help identify which part of the cell is the mechanical sensor.
10. LINKING FLUID FLOW TO IN VIVO BONE ADAPTATION
Although it is widely believed that interstitial fluid flow effectively stimulates bone cells in vivo, little work has been done to directly link this flow to the in vivo adaptive effects of applied mechanical loading. Many studies have demonstrated that osteocytes respond to mechanical loading in vivo (e.g., Dodd et al. 1999, Dodds et al. 1993, Forwood et al. 1998, Gluhak-Heinrich et al. 2003, Lean et al. 1995, Pead et al. 1988, Robling et al. 2008, Rubin et al. 1999, Skerry et al. 1989), yet none provides a direct link between osteocyte stimulation and fluid flow. In studies using animal models to demonstrate bone formation in response to applied loading, interstitial fluid flow is frequently mentioned as playing a role in the adaptive process, but again, no direct connections have been made. Some in vivo mechanical loading studies have attempted to link fluid flow to bone formation via strain gradients that could cause fluid movement (e.g., Gross et al. 1997, Judex et al. 1997), whereas others have used network models to explain how the fluid-flow stimulus could result in new bone formation demonstrated in vivo (Gross et al. 2004; Mi et al. 2005a,b). The enhanced tracer movement due to applied loading that has been demonstrated in a rat loading model that increases bone mass also does not provide direct evidence that load-induced interstitial flow stimulates bone cells as part of the adaptation process (Knothe Tate et al. 1998b, 2000).
A few recent in vivo models have tried to isolate the effects of fluid flow as a mechanical stimulus. Qin et al. (2003) applied a sinusoidal intramedullary pressure to the isolated avian ulna without otherwise deforming the bone tissue. The model demonstrates increased bone formation in response to the applied pressure, although a limitation is that the model is invasive, and the ends of the diaphysis of the ulna are capped internally. This approach has recently been extended to a rat model (Frangos et al. 2007). Another recent in vivo model that attempts to isolate the effects of fluid flow applies noninvasive loading to the mouse knee joint, producing low strains in the diaphysis of the femur as well as a rise in intramedullary pressure (Zhang et al. 2007). This model produces bone formation in the femur (Zhang et al. 2006a) and tibia (Zhang et al. 2006b), and a similar model using the mouse elbow produced bone formation in the ulna (Yokota & Tanaka 2005). In these models, the applied lateral joint loadings, which were applied for a very short period, do not appear to be physiological and could possibly trigger a response unrelated to fluid flow owing to the method of load application. Continued investigations into further establishing direct links between osteocyte stimulation and in vivo bone adaptation are necessary to confirm the role of interstitial fluid flow in bone’s mechanotransduction mechanism.
11. UNRESOLVED ISSUES AND FUTURE DIRECTIONS
Although much has been discovered regarding loading-induced interstitial fluid flow and its probable role in bone’s mechanotransduction mechanism, several unresolved issues remain that should guide future work. As outlined in Section 10, a direct link between interstitial fluid flow and bone adaptation needs to be more completely established. It is also necessary to determine the role the structural differences in the osteocyte processes and cell body play in the transmission of flow-induced mechanical forces and in the initiation of intracellular signaling. Because existing in vitro studies do not reproduce the fluid-flow environment of the osteocyte in its in vivo lacunar-canalicular environment, they do not distinguish between signaling that originates in the cell process and signaling that originates in the cell body. Work should be continued to create in vitro fluid-flow environments that better simulate in vivo loading. Loading systems should be created that distinguish the effects of fluid flow acting on the osteocyte body as well as hydrodynamic forces acting on the cell processes. If integrins play a pivotal role in the initiation of signaling, as recently suggested, there may be a close link between in vitro and in vivo studies because cell processes are attached to their substrate in culture by integrins. Confirmation of the colocalization of integrins with the protrusions connecting the osteocyte process to the canalicular wall is necessary, as is the determination of whether primary cilia play a role in mechanosensation. Identification of the membrane channels that exist in osteocytes and their localization as well as the sequence of signaling molecule release (e.g., does PGE2 release precede or follow ATP release?) will also help to further elucidate the mechanotransduction mechanism.
As outlined in this review, recent tracer and confocal microscopy studies have helped to quantify the transport parameters defining the osteocyte pericellular space in the lacunar-canalicular porosity and the three-dimensional microstructure of this porosity. In addition, improved EM techniques have led to a new generation of models that more accurately describe how loading-induced flow is communicated as a mechanical signal to the cell cytoskeleton. However, important questions remain, such as what is the three-dimensional heterogeneity of the lacunar-canalicular porosity examined at high resolution across an entire bone sample? To what extent are the lacunar-canalicular porosity and interstitial fluid flow altered in diseases such as osteoporosis? Which are more important for mechanotransduction in the osteocyte process, radial (hoop) strains or axial strains? In addition, in vivo measurement of fluid flow in the lacunar-canalicular porosity using a fluorescence recovery after photobleaching technique or by isolating bone samples containing only the lacunar-canalicular porosity is necessary to better quantify bone permeability. Such measurements will help to validate theoretical and finite-element models created to quantify bone interstitial fluid movement in response to mechanical loading.
Addressing these issues will increase our understanding of the role interstitial fluid flow plays in the mechanism by which bone tissue detects mechanical loading and organizes the necessary readjustment or maintenance of tissue for normal bone function. This understanding is vital for the effective development of strategies to prevent and treat the problems of bone loss, as well as to build effective bone tissue replacements.
SUMMARY POINTS
The lacunar-canalicular porosity surrounding the osteocytes and their cell processes forms an extensive interconnected fluid pathway. When bone is subjected to cyclic mechanical loading, interstitial fluid drains from the lacunar-canalicular system into and out of the low-pressure vascular porosity that surrounds the bone capillaries.
The pericellular matrix surrounding the osteocyte process plays a central role in determining the size of solutes that can pass through the lacunar-canalicular system. Tracer studies suggest a molecular sieve that is greater than horseradish peroxidase (6 nm), less than ferritin (12 nm), and probably close to the size of albumin (7 nm).
The collagen-apatite porosity is impermeable to solutes at least as small as reactive red (1 nm), strongly suggesting that SGPs result from fluid flow in the lacunar-canalicular porosity, not the collagen-apatite porosity.
The osteocyte lacunae in bone play a central role in the transport of tracers and nutrition during cyclic mechanical loading by serving as mixing reservoirs that allow for net solute transport without any net fluid transport, much like alveoli in the lung.
A fundamental paradox in bone tissue is that tissue-level strains, which rarely exceed 0.2% in vivo, are too small to initiate intracellular signaling in vitro, whereas the strains necessary to elicit biochemical responses (>0.5%) may cause bone tissue damage.
Recent ultrastructural studies demonstrate that osteocyte processes are tethered to their canalicular walls by transverse elements that span the pericellular space. Fluid flow through the lacunar-canalicular porosity creates a tension on the tethering elements that can amplify whole-tissue strains by a factor of 10–100 depending on loading frequency, producing strains large enough to elicit biochemical responses in vitro.
Osteocyte processes also appear to be attached at discrete sites along the canalicular wall at the apex of conical projections. These attachments, which appear to be focal adhesions containing at most a few β3 integrins, produce local stress concentrations with local axial strains that are an order of magnitude larger than hoop strains in the osteocyte process, strains that may be large enough to open stretch-activated channels.
Most current flow chambers do not replicate the FSS generated by in vivo mechanical loading. In vivo the FSS on the osteocyte processes is more than two orders of magnitude greater than on the cell body in its lacuna, whereas in culture this shear stress is the same. Because the osteocyte processes are two to three orders of magnitude stiffer than the cell body, the intracellular Ca2+ responses observed in vitro owing to FSS most likely result from the deformation of the much softer cell body. Further investigation into the role integrins and primary cilia play in bone mechanotransduction via interstitial fluid flow should be undertaken.
ACKNOWLEDGMENTS
This work was supported by NIH/NIAMS grants AR052866 (S.P.F.) and AR46899 (S.W.). The authors thank Dr. Stephen C. Cowin for his comments on the final draft of this manuscript.
Glossary
- Interstitial fluid
extravascular fluid external to osteocytes in the lacunar-canalicular porosity and bone capillaries in the vascular porosity
- Osteocyte
bone cell derived from an osteoblast; forms an interconnected network with other osteocytes throughout bone tissue
- Mechanotransduction
the mechanism by which mechanical signals are transmitted to bone cells to adequately maintain bone tissue
- SGP
strain-generated potential
- Mineralized matrix
the portion of bone tissue that contains only the collagen-apatite porosity
- Osteoblast
bone-forming cell found on bone surfaces
- FSS
fluid shear stress
- Lacunar-canalicular porosity
the space in the lacunae and canaliculi; contains osteocytes and interstitial fluid
- Pericellular matrix
a fiber matrix that surrounds the osteocyte and fills the annular fluid space in the canaliculi
- Canaliculi
small channels in the mineralized matrix that contain the osteocyte cell processes
- Vascular porosity
the space in the vascular canals found throughout mineralized bone matrix; contains bone capillaries, nerves, and interstitial fluid
- Lacuna
cavity in the mineralized matrix that houses the osteocyte cell body
- EM
electron microscopy
Footnotes
DISCLOSURE STATEMENT
The authors are not aware of any biases that might be perceived as affecting the objectivity of this review.
Contributor Information
Susannah P. Fritton, Email: fritton@ccny.cuny.edu.
Sheldon Weinbaum, Email: weinbaum@ccny.cuny.edu.
LITERATURE CITED
- Ajubi NE, Klein-Nulend J, Alblas MJ, Burger EH, Nijweide PJ. Signal transduction pathways involved in fluid flow-induced PGE2 production by cultured osteocytes. Am. J. Physiol. 1999;276:E171–E178. doi: 10.1152/ajpendo.1999.276.1.E171. [DOI] [PubMed] [Google Scholar]
- Ajubi NE, Klein-Nulend J, Nijweide PJ, Vrijheid-Lammers T, Alblas MJ, Burger EH. Pulsating fluid flow increases prostaglandin production by cultured chicken osteocytes—a cytoskeleton-dependent process. Biochem. Biophys. Res. Commun. 1996;225:62–68. doi: 10.1006/bbrc.1996.1131. [DOI] [PubMed] [Google Scholar]
- Anderson EJ, Kaliyamoorthy S, Iwan J, Alexander D, Knothe Tate ML. Nano-microscale models of periosteocytic flow show differences in stresses imparted to cell body and processes. Ann. Biomed. Eng. 2005;33:52–62. doi: 10.1007/s10439-005-8962-y. [DOI] [PubMed] [Google Scholar]
- Ayasaka N, Kondo T, Goto T, Kido MA, Nagata E, Tanaka T. Differences in the transport systems between cementocytes and osteocytes in rats using microperoxidase as a tracer. Arch. Oral Biol. 1992;37:363–369. doi: 10.1016/0003-9969(92)90019-5. [DOI] [PubMed] [Google Scholar]
- Bakker A, Klein-Nulend J, Burger E. Shear stress inhibits while disuse promotes osteocyte apoptosis. Biochem. Biophys. Res. Commun. 2004;320:1163–1168. doi: 10.1016/j.bbrc.2004.06.056. [DOI] [PubMed] [Google Scholar]
- Beno T, Ciani C, Doty S, Fritton SP. Structural measurements of osteocyte lacunae and canaliculi using confocal microscopy; Proc. 2005 Summer Bioeng. Conf; 2005. Abstract No. 92348. [Google Scholar]
- Beno T, Yoon Y-J, Cowin SC, Fritton SP. Estimation of bone permeability using accurate microstructural measurements. J. Biomech. 2006;39:2378–2387. doi: 10.1016/j.jbiomech.2005.08.005. [DOI] [PubMed] [Google Scholar]
- Bergula AP, Huang W, Frangos JA. Femoral vein ligation increases bone mass in the hindlimb suspended rat. Bone. 1999;24:171–177. doi: 10.1016/s8756-3282(98)00165-3. [DOI] [PubMed] [Google Scholar]
- Bonewald LF. Establishment and characterization of an osteocyte-like cell line, MLO-Y4. J. Bone Miner. Metab. 1999;17:61–65. doi: 10.1007/s007740050066. [DOI] [PubMed] [Google Scholar]
- Burr DB, Milgrom C, Fyhrie D, Forwood M, Nyska M, et al. In vivo measurement of human tibial strains during vigorous activity. Bone. 1996;18:405–410. doi: 10.1016/8756-3282(96)00028-2. [DOI] [PubMed] [Google Scholar]
- Brookes M, Revell WJ. The Blood Supply of Bone: Scientific Aspects. London: Springer-Verlag; 1998. [Google Scholar]
- Chen NX, Ryder KD, Pavalko FM, Turner CH, Burr DB, et al. Ca2+ regulates fluid shear-induced cytoskeletal reorganization and gene expression in osteoblasts. Am. J. Physiol. Cell Physiol. 2000;278:C989–C997. doi: 10.1152/ajpcell.2000.278.5.C989. [DOI] [PubMed] [Google Scholar]
- Cherian PP, Siller-Jackson AJ, Gu S, Wang X, Bonewald LF, et al. Mechanical strain opens connexin 43 hemichannels in osteocytes: a novel mechanism for the release of prostaglandin. Mol. Biol. Cell. 2005;16:3100–3106. doi: 10.1091/mbc.E04-10-0912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciani C, Doty SB, Fritton SP. Mapping bone interstitial fluid movement: displacement of ferritin tracer during histological processing. Bone. 2005;37:379–387. doi: 10.1016/j.bone.2005.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowin SC. Bone poroelasticity. J. Biomech. 1999;32:217–238. doi: 10.1016/s0021-9290(98)00161-4. [DOI] [PubMed] [Google Scholar]
- Cowin SC, Moss-Salentijn L, Moss ML. Candidates for the mechanosensory system in bone. J. Biomech. Eng. 1991;113:191–197. doi: 10.1115/1.2891234. [DOI] [PubMed] [Google Scholar]
- Cowin SC, Weinbaum S. Strain amplification in the bone mechanosensory system. Am. J. Med. Sci. 1998;316:184–188. doi: 10.1097/00000441-199809000-00006. [DOI] [PubMed] [Google Scholar]
- Cowin SC, Weinbaum S, Zeng Y. A case for bone canaliculi as the anatomical site of strain generated potentials. J. Biomech. 1995;28:1281–1296. doi: 10.1016/0021-9290(95)00058-p. [DOI] [PubMed] [Google Scholar]
- Dillaman RM. Movement of ferritin in the 2-day-old chick femur. Anat. Rec. 1984;209:445–453. doi: 10.1002/ar.1092090404. [DOI] [PubMed] [Google Scholar]
- Dodd JS, Raleigh JA, Gross TS. Osteocyte hypoxia: a novel mechanotransduction pathway. Am. J. Physiol. 1999;277:C598–C602. doi: 10.1152/ajpcell.1999.277.3.C598. [DOI] [PubMed] [Google Scholar]
- Dodds RA, Ali N, Pead MJ, Lanyon LE. Early loading-related changes in the activity of glucose 6-phosphate dehydrogenase and alkaline phosphatase in osteocytes and periosteal osteoblasts in rat fibulae in vivo. J. Bone Miner. Res. 1993;8:261–267. doi: 10.1002/jbmr.5650080303. [DOI] [PubMed] [Google Scholar]
- Donahue SW, Jacobs CR, Donahue HJ. Flow-induced calcium oscillations in rat osteoblasts are age, loading frequency, and shear stress dependent. Am. J. Physiol. Cell Physiol. 2001;281:C1635–C1641. doi: 10.1152/ajpcell.2001.281.5.C1635. [DOI] [PubMed] [Google Scholar]
- Doty SB, Schofield BH. Metabolic and structural changes within osteocytes of rat bone. In: Talmage RV, Munson PL, editors. Calcium, Parathyroid Hormone and the Calcitonins. Amsterdam: Elsevier; 1972. pp. 353–364. [Google Scholar]
- Fornells P, Garcia-Aznar JM, Doblare M. Afinite element dual porosity approach to model deformation-induced fluid flow in cortical bone. Ann. Biomed. Eng. 2007;35:1687–1698. doi: 10.1007/s10439-007-9351-5. [DOI] [PubMed] [Google Scholar]
- Forwood MR, Kelly WL, Worth NF. Localisation of prostaglandin endoperoxideHsynthase (PGHS)-1 and PGHS-2 in bone following mechanical loading in vivo. Anat. Rec. 1998;252:580–586. doi: 10.1002/(SICI)1097-0185(199812)252:4<580::AID-AR8>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- Frangos JA, Meays DR, Gaskill DF, Stevens HY. Pulsatile pressure loading of rodent femur using a fully implantable device. Trans. Orthop. Res. Soc. 2007;32:1387. [Google Scholar]
- Fritton SP, McLeod KJ, Rubin CT. Quantifying the strain history of bone: spatial uniformity and self-similarity of low magnitude strains. J. Biomech. 2000;33:317–325. doi: 10.1016/s0021-9290(99)00210-9. [DOI] [PubMed] [Google Scholar]
- Fritton SP, Rubin CT. In vivo measurement of bone deformations using strain gages. In: Cowin SC, editor. Bone Mechanics Handbook. Boca Raton, FL: CRC; 2001. pp. 8.1–8.41. [Google Scholar]
- Genetos DC, Kephart CJ, Zhang Y, Yellowley CE, Donahue HJ. Oscillating fluid flow activation of gap junction hemichannels induces ATP release from MLO-Y4 osteocytes. J. Cell Physiol. 2007;212:207–214. doi: 10.1002/jcp.21021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gluhak-Heinrich J, Ye L, Bonewald LF, Feng JQ, MacDougall M, et al. Mechanical loading stimulates dentin matrix protein 1 (DMP1) expression in osteocytes in vivo. J. Bone Miner. Res. 2003;18:807–817. doi: 10.1359/jbmr.2003.18.5.807. [DOI] [PubMed] [Google Scholar]
- Grimm MJ, Williams JL. Measurements of permeability in the human calcaneal trabecular bone. J. Biomech. 1997;30:743–745. doi: 10.1016/s0021-9290(97)00016-x. [DOI] [PubMed] [Google Scholar]
- Guo XE, Takai E, Jiang X, Xu Q, Whitesides GM, et al. Intracellular calcium waves in bone cell networks under single cell nanoindentation. Mol. Cell Biomech. 2006;3:95–107. [PubMed] [Google Scholar]
- Gross TS, Edwards JL, McLeod KJ, Rubin CT. Strain gradients correlate with sites of periosteal bone formation. J. Bone Miner. Res. 1997;12:982–988. doi: 10.1359/jbmr.1997.12.6.982. [DOI] [PubMed] [Google Scholar]
- Gross TS, Poliachik SL, Ausk BJ, Sanford DA, Becker BA, Srinivasan S. Why rest stimulates bone formation: a hypothesis based on complex adaptive phenomenon. Exerc. Sport Sci. Rev. 2004;32:9–13. doi: 10.1097/00003677-200401000-00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gururaja S, Kim HJ, Swan CC, Brand RA, Lakes RS. Modeling deformation-induced fluid flow in cortical bone’s canalicular-lacunar system. Ann. Biomed. Eng. 2005;33:7–25. doi: 10.1007/s10439-005-8959-6. [DOI] [PubMed] [Google Scholar]
- Han Y, Cowin SC, Schaffler MB, Weinbaum S. Mechanotransduction and strain amplification in osteocyte cell processes. Proc. Natl. Acad. Sci. USA. 2004;101:16689–16694. doi: 10.1073/pnas.0407429101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrigan TP, Hamilton JJ. Bone strain sensation via transmembrane potential changes in surface osteoblasts: loading rate and microstructural implications. J. Biomech. 1993;26:183–200. doi: 10.1016/0021-9290(93)90048-j. [DOI] [PubMed] [Google Scholar]
- Haut Donahue TL, Haut TR, Yellowley CE, Donahue HJ, Jacobs CR. Mechanosensitivity of bone cells to oscillating fluid flow induced shear stress may be modulated by chemotransport. J. Biomech. 2003;36:1363–1371. doi: 10.1016/s0021-9290(03)00118-0. [DOI] [PubMed] [Google Scholar]
- Hillsley MV, Frangos JA. Bone tissue engineering: the role of interstitial fluid flow. Biotech. Bioeng. 1994;43:573–581. doi: 10.1002/bit.260430706. [DOI] [PubMed] [Google Scholar]
- Holtrop ME. The ultrastructure of bone. Ann. Clin. Lab. Sci. 1975;5:264–271. [PubMed] [Google Scholar]
- Hudspeth AJ, Choe Y, Mehta AD, Martin P. Putting ion channels to work: mechanoelectrical transduction, adaptation, and amplification by hair cells. Proc. Natl. Acad. Sci. USA. 2000;97:11765–11772. doi: 10.1073/pnas.97.22.11765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hung CT, Pollack SR, Reilly TM, Brighton CT. Real-time calcium response of cultured bone cells to fluid flow. Clin. Orthop. 1995;313:256–269. [PubMed] [Google Scholar]
- Jacobs CR, Yellowley CE, Davis BR, Zhou Z, Cimbala JM, Donahue HJ. Differential effect of steady versus oscillating flow on bone cells. J. Biomech. 1998;31:969–976. doi: 10.1016/s0021-9290(98)00114-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DL, McAllister TN, Frangos JA. Fluid flow stimulates rapid and continuous release of nitric oxide in osteoblasts. Am. J. Physiol. 1996;271:E205–E208. doi: 10.1152/ajpendo.1996.271.1.E205. [DOI] [PubMed] [Google Scholar]
- Judex S, Gross TS, Zernicke RF. Strain gradients correlate with sites of exercise-induced bone-forming surfaces in the adult skeleton. J. Bone Miner. Res. 1997;12:1737–1745. doi: 10.1359/jbmr.1997.12.10.1737. [DOI] [PubMed] [Google Scholar]
- Keanini RG, Roer RD, Dillaman RM. A theoretical model of circulatory interstitial fluid flow and species transport within porous cortical bone. J. Biomech. 1995;28:901–914. doi: 10.1016/0021-9290(94)00157-y. [DOI] [PubMed] [Google Scholar]
- Kelly PJ. Pathways of transport in bone. In: Shephard JT, Abboud FM, editors. Handbook of Physiology: The Cardiovascular System. Peripheral Circulation and Organ Blood Flow. Bethesda, MD: Am. Physiol. Soc; 1983. pp. 371–396. [Google Scholar]
- Kelly PJ, Bronk JT. Venous pressure and bone formation. Microvasc. Res. 1990;39:364–375. doi: 10.1016/0026-2862(90)90049-w. [DOI] [PubMed] [Google Scholar]
- Kim CH, You L, Yellowley CE, Jacobs CR. Oscillatory fluid flow-induced shear stress decreases osteoclastogenesis through RANKL and OPG signaling. Bone. 2006;39:1043–1047. doi: 10.1016/j.bone.2006.05.017. [DOI] [PubMed] [Google Scholar]
- King GJ, Holtrop ME. Actin-like filaments in bone cells of cultured mouse calvaria as demonstrated by binding to heavy meromyosin. J. Cell Biol. 1975;66:445–451. doi: 10.1083/jcb.66.2.445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein-Nulend J, van Der Plas A, Semeins CM, Ajubi NE, Frangos JA, et al. Sensitivity of osteocytes to biomechanical stress in vitro. FASEB J. 1995;9:441–445. doi: 10.1096/fasebj.9.5.7896017. [DOI] [PubMed] [Google Scholar]
- Knothe Tate ML. Interstitial fluid flow. In: Cowin SC, editor. Bone Mechanics Handbook. Boca Raton, FL: CRC; 2001. pp. 22.1–22.29. [Google Scholar]
- Knothe Tate ML, Knothe U. An ex vivo model to study transport processes and fluid flow in loaded bone. J. Biomech. 2000;33:247–254. doi: 10.1016/s0021-9290(99)00143-8. [DOI] [PubMed] [Google Scholar]
- Knothe Tate ML, Knothe U, Niederer P. Experimental elucidation of mechanical load-induced fluid flow and its potential role in bone metabolism and functional adaptation. Am. J. Med. Sci. 1998a;316:189–195. doi: 10.1097/00000441-199809000-00007. [DOI] [PubMed] [Google Scholar]
- KnotheTate ML, Niederer P, Knothe U. In vivo tracer transport through the lacunocanalicular system of rat bone in an environment devoid of mechanical loading. Bone. 1998b;22:107–117. doi: 10.1016/s8756-3282(97)00234-2. [DOI] [PubMed] [Google Scholar]
- Knothe Tate ML, Steck R, Forwood MR, Niederer P. In vivo demonstration of load-induced fluid flow in the rat tibia and its potential implications for processes associated with functional adaptation. J. Exp. Biol. 2000;203:2737–2745. doi: 10.1242/jeb.203.18.2737. [DOI] [PubMed] [Google Scholar]
- Kohles SS, Roberts JB, Upton ML, Wilson CG, Bonassar LJ, Schlichting AL. Direct perfusion measurements of cancellous bone anisotropic permeability. J. Biomech. 2001;34:1197–1202. doi: 10.1016/s0021-9290(01)00082-3. [DOI] [PubMed] [Google Scholar]
- Kufahl RH, Saha S. A theoretical model for stress-generated fluid flow in the canaliculi-lacunae network in bone tissue. J. Biomech. 1990;23:171–180. doi: 10.1016/0021-9290(90)90350-c. [DOI] [PubMed] [Google Scholar]
- Lean JM, Jagger CJ, Chambers TJ, Chow JW. Increased insulin-like growth factor I mRNA expression in rat osteocytes in response to mechanical stimulation. Am. J. Physiol. 1995;268:E318–E327. doi: 10.1152/ajpendo.1995.268.2.E318. [DOI] [PubMed] [Google Scholar]
- Li G, Bronk JT, An K, Kelly PJ. Permeability of cortical bone of canine tibiae. Microvasc. Res. 1987;34:302–310. doi: 10.1016/0026-2862(87)90063-x. [DOI] [PubMed] [Google Scholar]
- Li J, Liu D, Ke HZ, Duncan RL, Turner CH. The P2X7 nucleotide receptor mediates skeletal mechanotransduction. J. Biol. Chem. 2005;280:42952–42959. doi: 10.1074/jbc.M506415200. [DOI] [PubMed] [Google Scholar]
- Lim T-H, Hong J. Poroelastic properties of bovine vertebral trabecular bone. J. Orthop. Res. 2000;18:671–677. doi: 10.1002/jor.1100180421. [DOI] [PubMed] [Google Scholar]
- Mak AFT, Qin L, Hung LK, Cheng CW, Tin CF. A histomorphometric observation of flows in cortical bone under dynamic loading. Microvasc. Res. 2000;59:290–300. doi: 10.1006/mvre.1999.2215. [DOI] [PubMed] [Google Scholar]
- Mak AT, Huang DT, Zhang JD, Tong P. Deformation-induced hierarchical flows and drag forces in bone canaliculi and matrix microporosity. J. Biomech. 1997;30:11–18. doi: 10.1016/s0021-9290(96)00121-2. [DOI] [PubMed] [Google Scholar]
- Malone AM, Anderson CT, Tummala P, Kwon RY, Johnston TR, et al. Primary cilia mediate mechanosensing in bone cells by a calcium-independent mechanism. Proc. Natl. Acad. Sci.USA. 2007;104:13325–13330. doi: 10.1073/pnas.0700636104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manfredini P, Cocchetti G, Maier G, Redaelli A, Montevecchi FM. Poroelastic finite element analysis of a bone specimen under cyclic loading. J. Biomech. 1999;32:135–144. doi: 10.1016/s0021-9290(98)00162-6. [DOI] [PubMed] [Google Scholar]
- Matsudaira PT, Burgess DR. Organization of the cross-filaments in intestinal microvilli. J. Cell Biol. 1982;92:657–664. doi: 10.1083/jcb.92.3.657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauney JR, Sjostorm S, Blumberg J, Horan R, O’Leary JP, et al. Mechanical stimulation promotes osteogenic differentiation of human bone marrow stromal cells on 3-D partially demineralized bone scaffolds in vitro. Calcif. Tissue Int. 2004;74:458–468. doi: 10.1007/s00223-003-0104-7. [DOI] [PubMed] [Google Scholar]
- McAllister TN, Frangos JA. Steady and transient fluid shear stress stimulate NO release in osteoblasts through distinct biochemical pathways. J. Bone Miner. Res. 1999;14:930–936. doi: 10.1359/jbmr.1999.14.6.930. [DOI] [PubMed] [Google Scholar]
- McCreadie BR, Hollister SJ, Schaffler MB, Goldstein SA. Osteocyte lacuna size and shape in women with and without osteoporotic fracture. J. Biomech. 2004;37:563–572. doi: 10.1016/S0021-9290(03)00287-2. [DOI] [PubMed] [Google Scholar]
- McGarry JG, Klein-Nulend J, Prendergast PJ. The effect of cytoskeletal disruption on pulsatile fluid flow-induced nitric oxide and prostaglandin E2 release in osteocytes and osteoblasts. Biochem. Biophys. Res. Commun. 2005;330:341–348. doi: 10.1016/j.bbrc.2005.02.175. [DOI] [PubMed] [Google Scholar]
- McNamara LM, Majeska RJ, Weinbaum S, Friedrich V, Schaffler MB. Attachment of osteocyte cell processes to the bone matrix. Trans. Orthop. Res. Soc. 2006;31:393. doi: 10.1002/ar.20869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mi LY, Basu M, Fritton SP, Cowin SC. Analysis of avian bone response to mechanical loading. Part two: development of a computational connected cellular network to study bone intercellular communication. Biomech. Model Mechanobiol. 2005a;4:132–146. doi: 10.1007/s10237-004-0066-3. [DOI] [PubMed] [Google Scholar]
- Mi LY, Fritton SP, Basu M, Cowin SC. Analysis of avian bone response to mechanical loading. Part one: distribution of bone fluid shear stress induced by bending and axial loading. Biomech. Model Mechanobiol. 2005b;4:118–131. doi: 10.1007/s10237-004-0065-4. [DOI] [PubMed] [Google Scholar]
- Montgomery RJ, Sutker BD, Bronk JT, Smith SR, Kelly PJ. Interstitial fluid flow in cortical bone. Microvasc. Res. 1988;35:295–307. doi: 10.1016/0026-2862(88)90084-2. [DOI] [PubMed] [Google Scholar]
- Mooseker MS, Tilney LG. Organization of an actin filament-membrane complex: filament polarity and membrane attachment in the microvilli of intestinal epithelial cells. J. Cell Biol. 1975;67:725–743. doi: 10.1083/jcb.67.3.725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nauman EA, Fong KE, Keaveny TM. Dependence of intertrabecular permeability on flow direction and anatomic site. Ann. Biomed. Eng. 1999;27:517–524. doi: 10.1114/1.195. [DOI] [PubMed] [Google Scholar]
- Nicolella DP, Moravits DE, Gale AM, Bonewald LF, Lankford J. Osteocyte lacunae tissue strain in cortical bone. J. Biomech. 2006;39:1735–1743. doi: 10.1016/j.jbiomech.2005.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyman JS, Roy A, Shen X, Acuna RL, Tyler JH, Wang X. The influence of water removal on the strength and toughness of cortical bone. J. Biomech. 2006;39:931–938. doi: 10.1016/j.jbiomech.2005.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otter MW, MacGinitie LA, Seiz KG, Johnson MW, Dell RB, Cochran GVB. Dependence of streaming potential frequency response on sample thickness: implications for fluid flow through bone microstructure. Biomemetics. 1994;2:57–75. [Google Scholar]
- Otter MW, Palmieri VR, Wu DD, Seiz KG, MacGinitie LA, Cochran GV. A comparative analysis of streaming potentials in vivo and in vitro. J. Orthop. Res. 1992;10:710–719. doi: 10.1002/jor.1100100513. [DOI] [PubMed] [Google Scholar]
- Owan I, Burr DB, Turner CH, Qiu J, Tu Y, Onyia JE, Duncan RL. Mechanotransduction in bone: osteoblasts are more responsive to fluid forces than mechanical strain. Am. J. Physiol. 1997;273:C810–C815. doi: 10.1152/ajpcell.1997.273.3.C810. [DOI] [PubMed] [Google Scholar]
- Pead MJ, Suswillo R, Skerry TM, Vedi S, Lanyon LE. Increased 3H-uridine levels in osteocytes following a single short period of dynamic bone loading in vivo. Calcif. Tissue Int. 1988;43:92–96. doi: 10.1007/BF02555153. [DOI] [PubMed] [Google Scholar]
- Petrov N, Pollack SR, Blagoeva R. A discrete model for streaming potentials in a single osteon. J. Biomech. 1989;22:517–521. doi: 10.1016/0021-9290(89)90002-x. [DOI] [PubMed] [Google Scholar]
- Piekarski K, Munro M. Transport mechanism operating between blood supply and osteocytes in long bones. Nature. 1977;269:80–82. doi: 10.1038/269080a0. [DOI] [PubMed] [Google Scholar]
- Pollack SR, Petrov N, Saltzstein R, Brankov G, Blagoeva R. Ananatomical model for streaming potentials in osteons. J. Biomech. 1984;17:627–636. doi: 10.1016/0021-9290(84)90094-0. [DOI] [PubMed] [Google Scholar]
- Qin L, Mak ATF, Cheng CW, Hung LK, Chan KM. Histomorphological study on pattern of fluid movement in cortical bone in goats. Anat. Rec. 1999;255:380–387. doi: 10.1002/(SICI)1097-0185(19990801)255:4<380::AID-AR3>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- Qin YX, Kaplan T, Saldanha A, Rubin C. Fluid pressure gradients, arising from oscillations in intramedullary pressure, is correlated with the formation of bone and inhibition of intracortical porosity. J. Biomech. 2003;36:1427–1437. doi: 10.1016/s0021-9290(03)00127-1. [DOI] [PubMed] [Google Scholar]
- Qin YX, Lin W, Rubin C. The pathway of bone fluid flow as defined by in vivo intramedullary pressure and streaming potential measurements. Ann. Biomed. Eng. 2002;30:693–702. doi: 10.1114/1.1483863. [DOI] [PubMed] [Google Scholar]
- Reich KM, Frangos JA. Effect of flow on prostaglandin E2 and inositol trisphosphate levels in osteoblasts. Am. J. Physiol. 1991;261:C428–C432. doi: 10.1152/ajpcell.1991.261.3.C428. [DOI] [PubMed] [Google Scholar]
- Reich KM, Gay CV, Frangos JA. Fluid shear stress as a mediator of osteoblast cyclic adenosine monophosphate production. J. Cell Phys. 1990;143:100–104. doi: 10.1002/jcp.1041430113. [DOI] [PubMed] [Google Scholar]
- Reilly GC, Haut TR, Yellowley CE, Donahue HJ, Jacobs CR. Fluid flow induced PGE2 release by bone cells is reduced by glycocalyx degradation whereas calcium signals are not. Biorheology. 2003;40:591–603. [PubMed] [Google Scholar]
- Robling AG, Niziolek PJ, Baldridge LA, Condon KW, Allen MR, et al. Mechanical stimulation of bone in vivo reduces osteocyte expression of sost/sclerostin. J. Biol. Chem. 2008;283:5866–5875. doi: 10.1074/jbc.M705092200. [DOI] [PubMed] [Google Scholar]
- Rouhana SW, Johnson MW, Chakkalakal DA, Harper RA. Permeability of the osteocyte lacunocanalicular compact bone. Joint ASME-ASCE Conf. Biomech. Symp. AMD. 1981;43:169–172. [Google Scholar]
- Rubin CT, Lanyon LE. Regulation of bone mass by mechanical strain magnitude. Calcif. Tissue Int. 1985;37:411–417. doi: 10.1007/BF02553711. [DOI] [PubMed] [Google Scholar]
- Rubin CT, McLeod KJ, Bain SD. Functional strains and cortical bone adaptation: epigenetic assurance of skeletal integrity. J. Biomech. 1990;23(Suppl 1):43–54. doi: 10.1016/0021-9290(90)90040-a. [DOI] [PubMed] [Google Scholar]
- Rubin C, Recker R, Cullen D, Ryaby J, McCabe J, McLeod K. Prevention of postmenopausal bone loss by a low-magnitude, high-frequency mechanical stimuli: a clinical trial assessing compliance, efficacy, and safety. J. Bone Miner. Res. 2004;19:343–351. doi: 10.1359/JBMR.0301251. [DOI] [PubMed] [Google Scholar]
- Rubin C, Sun YQ, Hadjiargyrou M, McLeod K. Increased expression of matrix metalloproteinase-1 in osteocytes precedes bone resorption as stimulated by disuse: evidence for autoregulation of the cell’s mechanical environment? J. Orthop. Res. 1999;17:354–361. doi: 10.1002/jor.1100170309. [DOI] [PubMed] [Google Scholar]
- Salzstein RA, Pollack SR. Electromechanical potentials in cortical bone, II. Experimental analysis. J. Biomech. 1987;20:271–280. doi: 10.1016/0021-9290(87)90294-6. [DOI] [PubMed] [Google Scholar]
- Salzstein RA, Pollack SR, Mak AFT, Petrov N. Electromechanical potentials in cortical bone, I. A continuum approach. J. Biomech. 1987;20:261–270. doi: 10.1016/0021-9290(87)90293-4. [DOI] [PubMed] [Google Scholar]
- Sander EA, Nauman EA. Permeability of musculoskeletal tissues and scaffolding materials: experimental results and theoretical predictions. Crit. Rev. Biomed. Eng. 2003;31:1–26. doi: 10.1615/critrevbiomedeng.v31.i12.10. [DOI] [PubMed] [Google Scholar]
- Shapiro F, Cahill C, Malatantis G, Nayak RC. Transmission electron microscopic demonstration of vimentin in rat osteoblast and osteocyte cell bodies and processes using the immunogold technique. Anat. Rec. 1995;241:39–48. doi: 10.1002/ar.1092410107. [DOI] [PubMed] [Google Scholar]
- Shin D, Athanasiou K. Cytoindentation for obtaining cell biomechanical properties. J. Orthop. Res. 1999;17:880–890. doi: 10.1002/jor.1100170613. [DOI] [PubMed] [Google Scholar]
- Skerry TM, Bitensky L, Chayen J, Lanyon LE. Early strain-related changes in enzyme activity in osteocytes following bone loading in vivo. J. Bone Miner. Res. 1989;4:783–788. doi: 10.1002/jbmr.5650040519. [DOI] [PubMed] [Google Scholar]
- Smalt R, Mitchell FT, Howard RL, Chambers TJ. Induction of NO and prostaglandin E2 in osteoblasts by wall-shear stress but not mechanical strain. Am. J. Physiol. 1997;273:E751–E758. doi: 10.1152/ajpendo.1997.273.4.E751. [DOI] [PubMed] [Google Scholar]
- Smit TH, Huyghe JM, Cowin SC. Estimation of the poroelastic parameters of cortical bone. J. Biomech. 2002;35:829–835. doi: 10.1016/s0021-9290(02)00021-0. [DOI] [PubMed] [Google Scholar]
- Spray DC, Ye ZC, Ransom BR. Functional connexin “hemichannels”: a critical appraisal. Glia. 2006;54:758–773. doi: 10.1002/glia.20429. [DOI] [PubMed] [Google Scholar]
- Starkebaum W, Pollack SR, Korostoff E. Microelectrode studies of stress-generated potentials in four-point bending of bone. J. Biomed. Mater. Res. 1979;13:729–751. doi: 10.1002/jbm.820130506. [DOI] [PubMed] [Google Scholar]
- Steck R, Niederer P, Knothe Tate ML. A finite element analysis for the prediction of load-induced fluid flow and mechanochemical transduction in bone. J. Theor. Biol. 2003;220:249–259. doi: 10.1006/jtbi.2003.3163. [DOI] [PubMed] [Google Scholar]
- Stevens HY, Meays DR, Frangos JA. Pressure gradients and transport in the murine femur upon hindlimb suspension. Bone. 2006;39:565–572. doi: 10.1016/j.bone.2006.03.007. [DOI] [PubMed] [Google Scholar]
- Su M, Jiang H, Zhang P, Liu Y, Wang E, et al. Knee-loading modality drives molecular transport in mouse femur. Ann. Biomed. Eng. 2006;34:1600–1606. doi: 10.1007/s10439-006-9171-z. [DOI] [PubMed] [Google Scholar]
- Sugawara Y, Kamioka H, Honjo T, Tezuka K, Takano-Yamamoto T. Three-dimensional reconstruction of chick calvarial osteocytes and their cell processes using confocal microscopy. Bone. 2005;36:877–883. doi: 10.1016/j.bone.2004.10.008. [DOI] [PubMed] [Google Scholar]
- Tami AE, Schaffler MB, Knothe Tate ML. Probing the tissue to subcellular level structure underlying bone’s molecular sieving function. Biorheology. 2003;40:577–590. [PubMed] [Google Scholar]
- Tan SD, de Vries TJ, Kuijpers-Jagtman AM, Semeins CM, Everts V, Klein-Nulend J. Osteocytes subjected to fluid flow inhibit osteoclast formation and bone resorption. Bone. 2007;41:745–751. doi: 10.1016/j.bone.2007.07.019. [DOI] [PubMed] [Google Scholar]
- Tanaka SM, Sun HB, Roeder RK, Burr DB, Turner CH, Yokota H. Osteoblast responses one hour after load-induced fluid flow in a three-dimensional porous matrix. Calcif. Tissue Int. 2005;76:261–271. doi: 10.1007/s00223-004-0238-2. [DOI] [PubMed] [Google Scholar]
- Tanaka T, Sakano A. Differences in permeability of microperoxidase and horseradish peroxidase into the alveolar bone of developing rats. J. Dent. Res. 1985;64:870–876. doi: 10.1177/00220345850640060201. [DOI] [PubMed] [Google Scholar]
- Tanaka-Kamioka K, Kamioka H, Ris H, Lim SS. Osteocyte shape is dependent on actin filaments and osteocyte processes are unique actin-rich projections. J. Bone Miner. Res. 1998;13:1555–1568. doi: 10.1359/jbmr.1998.13.10.1555. [DOI] [PubMed] [Google Scholar]
- van Der Plas A, Nijweide PJ. Isolation and purification of osteocytes. J. Bone Miner. Res. 1992;7:389–396. doi: 10.1002/jbmr.5650070406. [DOI] [PubMed] [Google Scholar]
- Vatsa A, Semeins CM, Smit TH, Klein-Nulend J. Paxillin localisation in osteocytes: Is it determined by the direction of loading? Biochem. Biophys. Res. Commun. 2008 doi: 10.1016/j.bbrc.2007.12.174. In press. [DOI] [PubMed] [Google Scholar]
- Volkmann N, DeRosier D, Matsudaira P, Hanein D. An atomic model of actin filaments cross-linked by fimbrin and its implications for bundle assembly and function. J. Cell Biol. 2001;153:947–956. doi: 10.1083/jcb.153.5.947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Ciani C, Doty SB, Fritton SP. Delineating bone’s interstitial fluid pathway in vivo. Bone. 2004;34:499–509. doi: 10.1016/j.bone.2003.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Cowin SC, Weinbaum S, Fritton SP. Modeling tracer transport in an osteon under cyclic loading. Ann. Biomed. Eng. 2000;28:1200–1209. doi: 10.1114/1.1317531. [DOI] [PubMed] [Google Scholar]
- Wang L, Cowin SC, Weinbaum S, Fritton SP. In response to ‘Mixing mechanisms and net solute transport in bone’ by ML Knothe Tate. Ann. Biomed. Eng. 2001;29:812–816. doi: 10.1114/1.1397788. [DOI] [PubMed] [Google Scholar]
- Wang L, Fritton SP, Cowin SC, Weinbaum S. Fluid pressure relaxation depends upon osteonal microstructure: modeling an oscillatory bending experiment. J. Biomech. 1999;32:663–672. doi: 10.1016/s0021-9290(99)00059-7. [DOI] [PubMed] [Google Scholar]
- Wang L, Fritton SP, Weinbaum S, Cowin SC. On bone adaptation due to venous stasis. J. Biomech. 2003;36:1439–1451. doi: 10.1016/s0021-9290(03)00241-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Wang Y, Han Y, Henderson SC, Majeska RJ, et al. In situ measurement of solute transport in the bone lacunar-canalicular system. Proc. Natl. Acad. Sci. USA. 2005;102:11911–11916. doi: 10.1073/pnas.0505193102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, McNamara LM, Schaffler MB, Weinbaum S. A model for the role of integrins in flow induced mechanotransduction in osteocytes. Proc. Natl. Acad. Sci. USA. 2007;104:15941–15946. doi: 10.1073/pnas.0707246104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinbaum S, Cowin SC, Zeng Y. Amodel for the excitation of osteocytes by mechanical loading-induced bone fluid shear stresses. J. Biomech. 1994;27:339–360. doi: 10.1016/0021-9290(94)90010-8. [DOI] [PubMed] [Google Scholar]
- Weinbaum S, Guo P, You L. A new view of mechanotransduction and strain amplification in cells with microvilli and cell processes. Biorheology. 2001;38:119–142. [PubMed] [Google Scholar]
- Welch RD, Johnston CE, Waldron MJ, Poteet B. Bone changes associated with intraosseous hypertension in the caprine tibia. J. Bone Joint. Surg. Am. 1993;75:53–60. doi: 10.2106/00004623-199301000-00008. [DOI] [PubMed] [Google Scholar]
- Westbroek I, Ajubi NE, Alblas MJ, Semeins CM, Klein-Nulend J, et al. Differential stimulation of prostaglandin G/H synthase-2 in osteocytes and other osteogenic cells by pulsating fluid flow. Biochem. Biophys. Res. Commun. 2000;268:414–419. doi: 10.1006/bbrc.2000.2154. [DOI] [PubMed] [Google Scholar]
- Williams JL, Iannotti JP, Ham A, Bleuit J, Chen JH. Effects of fluid shear stress on bone cells. Biorheology. 1994;31:163–170. doi: 10.3233/bir-1994-31204. [DOI] [PubMed] [Google Scholar]
- Winet H. A bone fluid flow hypothesis for muscle pump-driven capillary filtration: II. Proposed role for exercise in erodible scaffold implant incorporation. Eur. Cell Mater. 2003;6:1–10. doi: 10.22203/ecm.v006a01. [DOI] [PubMed] [Google Scholar]
- Yokota H, Tanaka SM. Osteogenic potentials with joint-loading modality. J. Bone Miner.Metab. 2005;23:302–308. doi: 10.1007/s00774-005-0603-x. [DOI] [PubMed] [Google Scholar]
- Yoon YJ, Cowin SC. An estimate of anisotropic poroelastic constants of an osteon. Biomech. Model Mechanobiol. 2008;7:13–26. doi: 10.1007/s10237-006-0071-9. [DOI] [PubMed] [Google Scholar]
- You L, Cowin SC, Schaffler MB, Weinbaum S. A model for strain amplification in the actin cytoskeleton of osteocytes due to fluid drag on pericellular matrix. J. Biomech. 2001;34:1375–1386. doi: 10.1016/s0021-9290(01)00107-5. [DOI] [PubMed] [Google Scholar]
- You L, Temiyasathit S, Tao E, Prinz F, Jacobs CR. 3D microfluidic approach to mechanical stimulation of osteocyte processes. Cell. Mol. Bioeng. 2008;1:103–107. [Google Scholar]
- You LD, Weinbaum S, Cowin SC, Schaffler MB. Ultrastructure of the osteocyte process and its peri-cellular matrix. Anat. Rec. 2004;278:A505–A513. doi: 10.1002/ar.a.20050. [DOI] [PubMed] [Google Scholar]
- You J, Yellowley CE, Donahue HJ, Zhang Y, Chen Q, Jacobs CR. Substrate deformation levels associated with routine physical activity are less stimulatory to bone cells relative to loading-induced oscillatory fluid flow. J. Biomech. Eng. 2000;122:387–393. doi: 10.1115/1.1287161. [DOI] [PubMed] [Google Scholar]
- Zeng Y, Cowin SC, Weinbaum S. A fiber matrix model for fluid flow and streaming potentials in the canaliculi of an osteon. Ann. Biomed. Eng. 1994;22:280–292. doi: 10.1007/BF02368235. [DOI] [PubMed] [Google Scholar]
- Zhang D, Cowin SC, Weinbaum S. Electrical signal transmission and gap junction regulation in a bone cell network: a cable model for an osteon. Ann. Biomed. Eng. 1997;25:357–374. doi: 10.1007/BF02648049. [DOI] [PubMed] [Google Scholar]
- Zhang D, Weinbaum S, Cowin SC. Electrical signal transmission in a bone cell network: the influence of a discrete gap junction. Ann. Biomed. Eng. 1998a;26:644–659. doi: 10.1114/1.123. [DOI] [PubMed] [Google Scholar]
- Zhang D, Weinbaum S, Cowin SC. Estimates of the peak pressures in bone pore water. J. Biomech. Eng. 1998b;120:697–703. doi: 10.1115/1.2834881. [DOI] [PubMed] [Google Scholar]
- Zhang P, Su M, Liu Y, Hsu A, Yokota H. Knee loading dynamically alters intramedullary pressure in mouse femora. Bone. 2007;40:538–543. doi: 10.1016/j.bone.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang P, Su M, Tanaka SM, Yokota H. Knee loading stimulates cortical bone formation in murine femurs. BMC Musculoskelet. Disord. 2006a;7:73. doi: 10.1186/1471-2474-7-73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang P, Tanaka SM, Jiang H, Su M, Yokota H. Diaphyseal bone formation in murine tibiae in response to knee loading. J. Appl. Physiol. 2006b;100:1452–1459. doi: 10.1152/japplphysiol.00997.2005. [DOI] [PubMed] [Google Scholar]