Abstract
Although humans have a large repertoire of potential movements, gait patterns tend to be stereotypical and appear to be selected according to optimality principles such as minimal energy. When applied to dynamic musculoskeletal models such optimality principles might be used to predict how a patient’s gait adapts to mechanical interventions such as prosthetic devices or surgery. In this paper we study the effects of different performance criteria on predicted gait patterns using a 2D musculoskeletal model. The associated optimal control problem for a family of different cost functions was solved utilizing the direct collocation method. It was found that fatigue-like cost functions produced realistic gait, with stance phase knee flexion, as opposed to energy-related cost functions which avoided knee flexion during the stance phase. We conclude that fatigue minimization may be one of the primary optimality principles governing human gait.
Keywords: gait, simulation, musculoskeletal modeling, optimal control
1. INTRODUCTION
Dynamic simulation of human gait is a well established research technique but has been mainly applied to track observed human movements (Zajac et al., 2003). Predictive simulations of gait, on the other hand, are based solely on an assumed optimality criterion, e.g. minimal energy, which is used to solve an optimal control problem. Such simulations can help uncover underlying principles of neuromuscular coordination and have potential applications in predicting patient responses to surgical interventions (e.g. a tendon transfer procedure), in the design of prosthetic and orthotic devices, or in the reconstruction of gait for dinosaurs (Sellers and Manning, 2007). Predictive simulation has not yet found widespread application because of its high computational cost (Anderson and Pandy, 2001). In addition, there is no generally accepted optimality criterion for human gait. Previous studies have only used a single optimality criterion and it is not clear how the choice of optimality criterion affects the results.
Energy consumption appears to play a role in the selection of overall gait characteristics, such as step length and cadence, as corroborated by many experimental studies (e.g. Bertram and Ruina, 2001; Ralston, 1976). This, however, does not necessarily imply that minimal energy also governs detailed features of gait such as joint angles and muscle recruitment. Other criteria such as muscle fatigue or peak joint loads, might play a role.
In particular, the knee flexion observed in the weight acceptance phase of normal gait raises questions as it requires the activation of the large Quadriceps to prevent knee collapse and may, therefore, be inconsistent with minimal energy criteria. Indeed, stance phase knee flexion appears to be absent in several energy-based predictive gait simulations (Sellers et al., 2005; Nagano et al., 2005).
In this context, the objective of this paper is to shed some light into the effects of the cost function choice on the predicted kinematics and muscle recruitment patterns of gait. A series of predictive simulations of gait are performed utilizing a family of cost functions representative of a large range of performance criteria traditionally adopted in the literature.
2. METHODS
2.1. Musculoskeletal Model
The musculoskeletal dynamics model (Gerritsen et al., 1998; Hardin et al., 2004) consists of seven body segments (trunk, thighs, shanks, and feet) and has nine kinematic degrees of freedom. Eight muscle groups are included in each lower extremity: Iliopsoas, Glutei, Hamstrings, Rectus Femoris, Vasti, Gastrocnemius, Soleus, and Tibialis Anterior. Each muscle is represented by a 3-element Hill-type model, using the equations from McLean et al. (2003) and muscle properties from Gerritsen et al. (1998). This model has 50 state variables in the state vector x: f = 9 generalized coordinates in q, f = 9 generalized velocities in q̇, m = 16 muscle contractile element (CE) lengths in lce, and m = 16 muscle activations in a, where . The differential equations describing the dynamics of the musculoskeletal system read as
| (1a) |
| (1b) |
| (1c) |
| (1d) |
where I denotes the identity matrix, Eq. 1b contains the equations of motion which were generated by SD/Fast (Parametric Technology Corp., Needham, MA), Eq. 1c describes the muscle contraction dynamics, and Eq. 1d describes the muscle activation dynamics in which u are the m = 16 neural excitations to the muscles. The muscle force is a function of muscle CE length and pose of the skeletal model in q via the series elastic properties as fm = fm(q, lce).
2.2. Ground Contact Model
The interaction between feet and ground is modeled by means of 10 spring-damper elements uniformly distributed along each foot sole. The vertical force for each contact element j, was modeled as
| (2) |
where δj is the ground penetration of element j, a is a vertical stiffness parameter set to a = 5.0e7 Nm−3, and b is a vertical damping parameter set to b = 1.0 m−1s. These parameter values are consistent with dynamic force-deformation tests from Aerts and de Clercq (1993).
The horizontal force at contact element j was modeled by an approximation of Coulomb friction (van den Bogert et al., 1989) using a logistic function:
| (3) |
where fy,j is the vertical force at contact element j, vs,j is the sliding velocity at element j, and vc is a scaling factor set to vc = 0.05 ms−1. The friction coefficient μ was 1.0. The logistic approximation is necessary to ensure differentiability, where a lower scaling factor vc implies a better approximation of true Coulomb friction.
2.3. Problem Formulation
The general optimal control problem for gait consists of searching for time histories of controls u(t) and states x(t) that minimize a scalar, integral cost function
| (4) |
where T is the gait cycle period. The solution must satisfy the differential equations describing the dynamics of the musculoskeletal system
| (5) |
represented by Eqs. 1, and the additional inequality constraints typically given by bounds on the neural excitations
| (6) |
and on the states
| (7) |
A periodic gait at an average locomotion speed vw is ensured by
| (8a) |
| (8b) |
where x̄ contains all the states excepting the horizontal position of the model, xh. In the optimizations performed in this study, vw is prescribed as a task constraint while T is allowed to be optimized. Bilateral symmetry was imposed so that only half a gait cycle needed to be simulated.
2.4. Solution Method
The optimal neuromuscular control problem for gait presented in the previous section was transformed into a parameter optimization utilizing direct collocation (Betts, 2001). Direct collocation (DC) has been extensively used for trajectory optimization in aeronautics and aerospace engineering (Betts, 1998) and was used because of its potential advantages over the traditional shooting method for predictive simulation of gait (Anderson and Pandy, 2001). DC allows the addition of task constraints such as periodicity of gait and is often computationally more efficient than shooting methods (Betts, 1998).
The states x(t) as well as the controls u(t), i.e. neural excitations, were discretized by means of a 50 node temporal grid for half a gait cycle. The dynamical constraints, Eq. 5, were transformed into a large set of algebraic constraints using the Euler discretization scheme (Betts, 2001). For details on the formulation of the problem using direct collocation, please, refer to the Appendix. The SNOPT code for Matlab (Tomlab Optimization Inc., Pullman, WA) was used to solve the resulting nonlinear programming problem. SNOPT is a sequential quadratic programming (SQP) algorithm for solving large-scale, sparse nonlinear programming problems (Gill et al., 2002).
2.5. Cost Functions and Simulations
The following family of cost functions was used to investigate the effects of different performance criteria on predicted gait patterns. The latter is quantified by integrals of weighted muscle activations to a power p as
| (9) |
where m is the number of muscle groups, a is the muscle activation, and p and ωi are the exponent of a and weighting factors, respectively. Two different sets of weighting factors ωi, i = 1 … m, and four different values for the exponent p, p = 1, 2, 3 and 10, were combined, leading to a total of 8 different cost functions investigated, Jk with k = 1 … 8, as specified in Table I.
TABLE I.
Specification of the cost functions for predictive simulations of gait characterized by the combination of weight factors ωi and exponent p in Eq. 9.
| p = 1 | p = 2 | p = 3 | p = 10 | |
|---|---|---|---|---|
| ωi = 1, i = 1 … m | J1 | J2 | J3 | J4 |
| ωi = Vi, i = 1 … m | J5 | J6 | J7 | J8 |
Equation 9 covers a wide range of cost functions traditionally used to locally solve the muscle force-sharing problem (Crowninshield and Brand, 1981; Glitsch and Baumann, 1997; Thelen and Anderson, 2006). For instance, the muscle volume scaling, Vi, was adopted by Happee and Helm (1995) and by Thelen and Anderson (2006), and the exponents p = 1 to 3 have been commonly used to solve the muscle force-sharing problem (Pedotti et al., 1978; Crowninshield and Brand, 1981; Glitsch and Baumann, 1997; Thelen et al., 2003). The high exponent p = 10 strongly penalizes large muscle activations and approximates a minmax optimization (Rasmussen et al., 2001). Indeed, in the limit, for p → ∞, only the maximal activation matters and the problem becomes equivalent to a minmax optimization.
The eight different cost functions were classified either as “effort” or “fatigue”-like. Although this classification is imperfect, there is a rationale behind it. Muscle fatigue (inverse of muscle endurance) is related to the percentage of the total muscle fibers activated, i.e. muscle activation, and there is experimental evidence that this relation is approximately cubic (Crowninshield and Brand, 1981). Furthermore, the endurance of the whole muscle system is determined solely by the maximally fatigued muscle, so that a minmax optimization problem arises as discussed in the previous paragraph. On the contrary, muscle effort, a surrogate to muscle energy expenditure, is correlated to the volume of activated muscle tissue and depends more linearly, or less nonlinearly, on muscle activation (Minetti and Alexander, 1997; Umberger et al., 2003; Bhargava et al., 2004). Thus, cost functions presenting muscle volume weighting and lower exponents (J1, J5, J6 and J7) were classified as effort-like, while cost functions without muscle volume weighting and higher exponents (J2, J3, J4 and J8) were classified as fatigue-like. The differences between these two groups will become more evident in the light of the simulation results.
For the predictive simulations using J2, with p = 2 and ωi = 1, the solution of a tracking optimization of normative data from Winter (1991) was used as initial guess. This tracking simulation was able to approximate the reference ground reaction forces and kinematics from Winter (1991) well within one standard deviation. In order to decrease the probability of finding local minima as a consequence of utilizing a gradient-based optimization method, for each one of the other cost functions, two simulations were performed, using two different previous solutions as initial guess, the solution from the tracking optimization and the solution for J2. A walking speed of 1.1 m/s was prescribed for all predictive simulations.
3. RESULTS
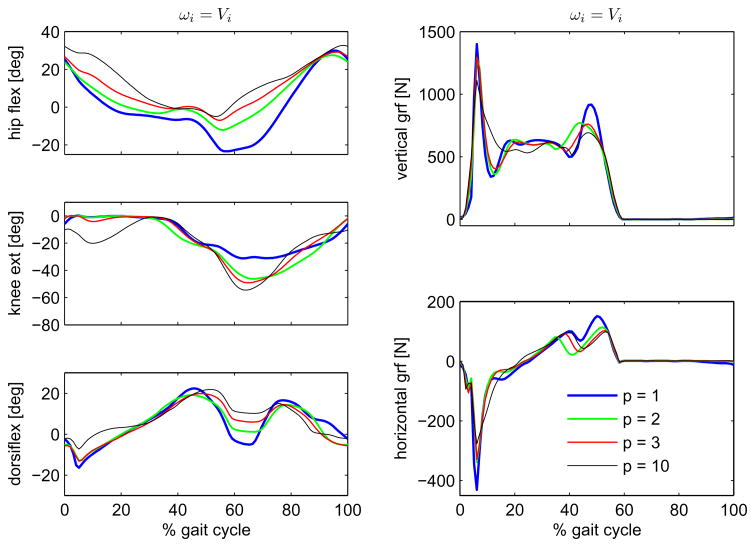
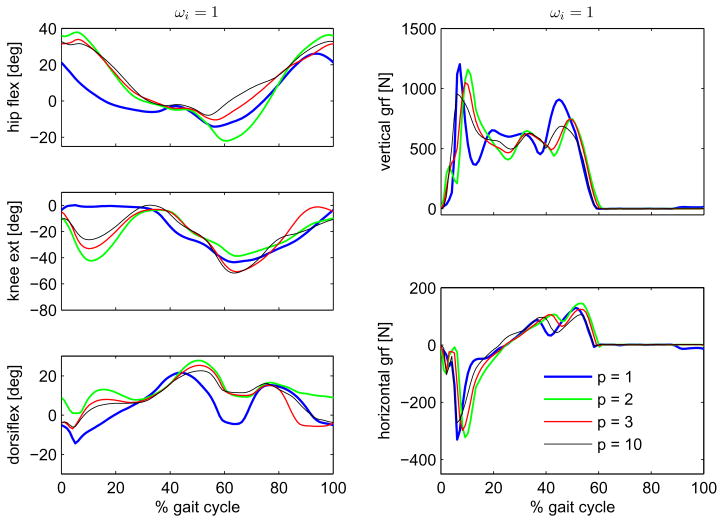
Figures 1 and 2 show the results for the simulations using the muscle volume-based weighting factors, ωi = Vi, corresponding to cost functions J5, J6, J7 and J8, and for the simulations using a unitary weighting factors, ωi = 1, corresponding to cost functions J1, J2, J3 and J4 in Table I, respectively. A comparison of the predicted kinematics on the left and of the ground contact forces on the right are shown for the four different exponents p (1, 2, 3 and 10) in the cost function, Eq. 9. As explained in the previous section, for each cost function, two optimizations using two different initial guesses were performed. The two initial guesses led to virtually the same solutions for three (J2, J3 and J7) of seven cost functions. In contrast, they led to clearly different solutions for the remaining four cost functions (J1, J4, J5 and J8). In the cases in which the two simulations converged to different solutions only the solutions with the lowest cost function values were further considered. The other solutions were disregarded as local minima.
FIG. 1.
Comparison of hip, knee and ankle angles on the left, and of vertical and horizontal ground contact forces on the right, obtained through predictive simulations using the family of cost functions in Eq. 9 with muscle volume-based weighting factors, ωi = Vi.
FIG. 2.
Comparison of hip, knee and ankle angles on the left, and of vertical and horizontal ground contact forces on the right, obtained through predictive simulations using the family of cost functions in Eq. 9 with unitary weighting factors, ωi = 1.
Predicted motion and ground contact forces using the cost functions specified by Eq. 9 all reproduce salient features of normal gait, Fig. 3. Nevertheless, closer inspection reveals some interesting deviations from normal gait. Regardless of the weighting factors, an exponent p = 1 led to a very reduced knee flexion during stance while an exponent p = 10 led to a normal ~ 20° knee flexion pattern. In contrast, the exponents p = 2 and p = 3 led either to a reduced knee flexion with the muscle volume-based weighting factors, or to a large knee flexion in the optimizations without volume weighting in the cost function. The solutions that did not flex the knee in stance also had high peak ground reaction force at impact.
FIG. 3.
Stick figure of predicted gait patterns with p = 2 and ωi = Vi (top), and p = 3 and ωi = 1 (bottom). Note the difference in knee flexion during stance.
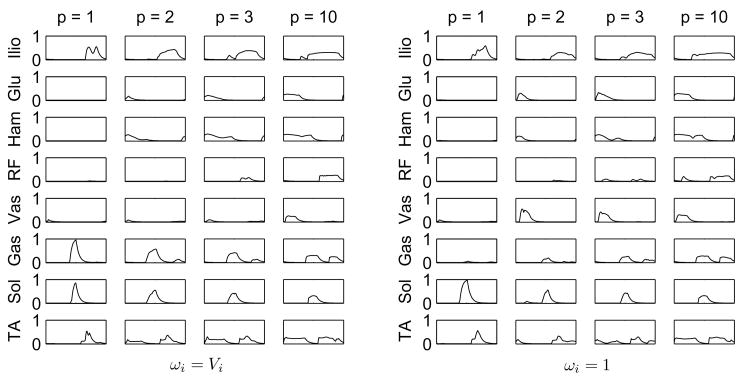
The cost functions also caused differences in predicted muscle activation patterns, Fig. 4. Lower exponents p led to the recruitment of a few muscles, which are highly activated, while higher exponents favored a more uniform distribution of muscle activations. Notice that the use of muscle volume-based weighting factors favors activation of smaller muscles such as the Gastrocnemius and inhibits the activation of larger muscle groups as the Vasti. The latter difference in the results is significant up to the exponent p = 3, while the exponent p = 10 leads to very similar results regardless of weighting factors. There was a strong correlation between the activation of Vasti and knee flexion in stance, see Table II and Figs. 1 and 2.
FIG. 4.
Comparison of muscle activations predicted through the predictive simulations using the family of cost functions in Eq. 9 with the muscle volume-based weighting factors, ωi = Vi, on the left and unitary weighting factors, ωi = 1, on the right.
TABLE II.
Correlation between knee flexion in stance and maximal activation of the Vasti for various combinations of exponents p and weights ωi in the optimization objective (Eq. 9).
| p = 1 | p = 2 | p = 3 | p = 10 | |
|---|---|---|---|---|
| ωi = 1, i = 1 … m | 1°/0.10 | 42°/0.55 | 33°/0.42 | 260.30 |
| ωi = Vi, i = 1 … m | 1°/0.10 | 1°/0.08 | 4°/0.10 | 20°/0.26 |
4. DISCUSSION
Different performance criteria led to substantially distinct gait predictions, Figs. 1–3, showing the importance of the choice of an appropriate cost function. Perhaps the most remarkable differences occur in knee flexion angle during initial and mid-stance. Cost functions J2, J3, J4 and J8 led to a maximal knee flexion of 20° or higher in mid-stance, while cost functions J1, J5, J6 and J7 led to a straight-legged pattern, with only very slight knee flexion. As explained in Section 2.5, these two groups of cost functions can be related to muscle fatigue and effort, respectively.
Muscle fatigue depends on the percentage of muscle fibers activated, and this dependency is approximately cubic. Furthermore, the endurance (the inverse of fatigue) of the body equals the endurance of the maximally fatigued muscle, so that maximization of endurance (or minimization of fatigue) is achieved by fatigue minimization of the maximally fatigued muscle (minmax problem). Therefore, cost functions without muscle-volume scaling and high values of p (J2, J3, J4 and J8), which penalize the higher muscle activations, relate to muscle fatigue. For very large exponents p, e.g. p = 10, the scaling factor becomes unimportant because only the muscle with the highest activation contributes to the cost function, and the problem approximates a minimization of maximal muscle activation. In fact, cost function J4 (ωi = 1) and J8 (ωi = Vi) led to very similar kinematics and muscle coordination (Figs. 1–3). On the contrary, muscle effort, considered here as a surrogate to muscle energy expenditure, depends on the percentage of muscle volume activated, and its dependency on muscle activation is less nonlinear. Thus, cost functions with muscle-volume scaling and lower values of p (J1, J5, J6 and J7) can be interpreted as being more related to muscle effort or energy consumption than to fatigue.
The “effort” cost functions led to straight-leg patterns, with reduced knee flexion during initial and mid-stance in contrast to the “fatigue” cost functions, which predicted knee flexion of 20° or higher during mid-stance. Figure 4 shows that the “effort” cost functions caused a gait pattern that avoids using the large Vasti muscle group, which then requires the elimination of knee flexion in stance, in turn causing high impact forces. This mechanism is illustrated by the strong correlation between maximal knee flexion in stance and Vasti activation level shown in Tab. II. The “fatigue” cost functions tended to produce more realistic movements and ground reaction forces, refer to Fig. 3, especially at high exponents. At high exponents, only the muscle with the largest activation matters, and the volume weighting no longer makes a difference. These findings suggest that minmax criteria, as proposed by Rasmussen et al. (2001) should be seriously considered for gait prediction. This result is opposite to the findings of Anderson and Pandy (2001), where energy minimization produced realistic movements. That optimization, however, was unable to predict walking patterns without stance phase knee flexion, because initial conditions were fixed and defined based on human data at the beginning of single stance, with substantial initial knee flexion.
Thus, while energy minimization appears to be an important performance criterion in experimental studies, e.g. Bertram and Ruina (2001), other criteria such as fatigue avoidance or reduction of peak joint forces, might play an important role even during normal walking. This may explain why a straight-legged stance phase is rarely seen in humans in spite of the fact that flexing the knee seems to increase energy consumption. Inspection of previous minimal-energy gait simulation results reported in the literature (Sellers et al., 2005; Nagano et al., 2005) also reveals the prediction of a straight-legged pattern in stance, corroborating this conclusion.
Confronted with the necessity of performing several predictive optimizations of gait, we used direct collocation (DC) as an alternative to the shooting method for solving the optimal control problem for gait. Direct collocation has been extensively used for trajectory optimization in aeronautics and aerospace engineering (Betts, 1998) and was used for human pedaling simulation by Kaplan and Heegaard (2001) and in the solution of optimal kicking motion by Stelzer and von Stryk (2006). DC performed well in our application, typically solving the gait optimization problem in 35 minutes, which compares favorably to the thousands of hours required with traditional shooting methods for predictive optimization (Anderson and Pandy, 2001), although model complexity was certainly a confounding factor. Furthermore, close inspection of our results reveal perfectly periodic solutions, which was not achieved by Anderson and Pandy (2001). The performance of DC is mainly due to the implicit solution of the differential equations, which avoids the need for time consuming explicit forward integration. We have verified that our DC solution with 50 time points was identical to a traditional forward integration driven by the optimal controls, which required 3000 integration steps.
This study questions the notion that energy-based criteria are predominant during normal gait, and shows the necessity of further experimental and computational investigations on appropriate optimality criteria for human movement. Establishing realistic optimality-criteria is essential to the success of predictive simulations in clinical applications such as the computer-aided design of surgical interventions, prostheses, and other mechanical interventions which aim to improve human gait.
Acknowledgments
This study is supported by the NIH grant R01 EB006735 and NSF grant BES 0302259.
APPENDIX
Direct collocation uses a temporal discretization of the state and control time histories. Because walking is symmetric, only half a gait cycle needs to be considered to fully characterize the entire walking cycle. The time interval for half a gait cycle was divided into n equally spaced nodes:
| (A-1) |
The states x(t) and the controls, i.e. the neural excitations u(t), were accordingly discretized and collected in a vector containing all unknowns:
| (A-2) |
where xk = x(tk) and uk = u(tk). Note that χ contains also the duration of half a gait cycle T/2. Values of the controls and states at the nth node are not included because the motion is periodic, so that states and neural excitations in one half of the body at the end of the half gait cycle coincide with the ones in the other half of the body at the beginning of the gait cycle, or and , where and contain appropriate “mirroring” permutations of the elements of xk and uk, respectively, and where the horizontal position xh is shifted by vwT/2 as .
In this paper we use the Euler discretization scheme (Betts, 2001) which transforms the system differential equations, Eq. 5, into algebraic constraints called defects Δk as
| (A-3a) |
| (A-3b) |
where fk = f (xk, uk, tk), Δt = tk − tk−1, and is an appropriate permutation of fk as done for x*. Periodicity constraints, Eqs. 8, are implicitly included in Eq. A-3b. All algebraic constraints in Eqs. A-3 are collected in a vector of constraints
| (A-4) |
The lower and upper bounds on the neural excitations, Eq. 6, on the states, Eq. 7, and on the duration of half a gait cycle are replaced by bounds on the optimization variables as
| (A-5) |
The cost function was computed using the trapezoidal quadrature rule to estimate the integral in Eq. 9. The discretized version of Eq. 9 is a simple function of system states allowing for the computation of analytical gradient and a sparse Hessian, which reduces computation time. The constraints Jacobian matrix is also sparse with a known structure and was calculated through finite-difference approximations.
All simulations in this paper were performed using 50 nodes for half a gait cycle, based on preliminary work showing that a 50 node solution had all relevant details of gait and was indistinguishable from a 400-node solution in simulations tracking the normative gait data from Winter (1991). The average computation time required per predictive simulation in this study was approximately 35 minutes. Occasional divergence of the SQP algorithm was observed, probably due to the high nonlinearity of the contact model. Simply restarting the optimization from the failure point was usually successful.
Successful optimization requires initial guesses for the neural excitation and state histories that are sufficiently dynamically consistent. We used the following three-step approach. First, the system was forward integrated using a variable step differential equation solver using freely chosen initial conditions for the states and arbitrary time histories of the neural excitations. This leads to time histories of the states and controls that are dynamically consistent, but do not satisfy periodicity constraints. The second step uses this as initial guess for a tracking optimization using DC, where the periodicity constraints in Eq. A-3b are deactivated but added to the cost function as a weighted penalty term. This optimization guides the solution to the neighborhood of the target data while simultaneously reducing the violation of the periodicity constraints. The third and last step consists of using this solution as initial guess for the regular optimization, where both Eq. A-3a and Eq. A-3b are activated. This is now possible because the violation of all dynamics constraints was sufficiently reduced in the previous steps. Generating an initial guess this way was computationally intensive (about 6 hours), but we note that this needs to be done only once for a model. Subsequent DC optimizations, after changing the cost function or model parameters, can start with a previous DC result.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Parts of this work were first presented in January 2008 at the Workshop 3 - Biomechanics and Neural Control - Muscle, Limb and Brain, Mathematical Biosciences Institute, Columbus, OH.
References
- 1.Aerts P, de Clercq D. Deformation characteristics of the heel region of the shod foot during a simulated heel strike: the effect of varying midsole hardness. Journal of Sports Sciences. 1993;11:449–461. doi: 10.1080/02640419308730011. [DOI] [PubMed] [Google Scholar]
- 2.Anderson FC, Pandy MG. Dynamic optimization of human walking. Journal of Biomechanical Engineering. 2001;123:381–390. doi: 10.1115/1.1392310. [DOI] [PubMed] [Google Scholar]
- 3.Bertram JEA, Ruina A. Multiple walking speed-frequency relations are predicted by constrained optimization. Journal of Theoretical Biology. 2001;209:445–453. doi: 10.1006/jtbi.2001.2279. [DOI] [PubMed] [Google Scholar]
- 4.Betts JT. Survey of numerical methods for trajectory optimization. Journal of Guidance, Control, and Dynamics. 1998;21:193–207. [Google Scholar]
- 5.Betts JT. Practical Methods for Optimal Control Using Nonlinear Programming. SIAM; 2001. [Google Scholar]
- 6.Bhargava LJ, Pandy MG, Anderson FC. A phenomenological model for estimating metabolic energy consumption in muscle contraction. Journal of Biomechanics. 2004;37:81–88. doi: 10.1016/s0021-9290(03)00239-2. [DOI] [PubMed] [Google Scholar]
- 7.Crowninshield RD, Brand RA. Physiologically based criterion of muscle force prediction in locomotion. Journal of Biomechanics. 1981;14:793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
- 8.Delp SL, Loan JP. A computational framework for simulating and analyzing human and animal movement. IEEE Computing in Science and Engineering. 2000;2:46–55. [Google Scholar]
- 9.Gerritsen KGM, van den Bogert AJ, Hulliger M, Zernicke RF. Intrinsic muscle properties facilitate locomotor control – a computer simulation study. Motor Control. 1998;2:206–220. doi: 10.1123/mcj.2.3.206. [DOI] [PubMed] [Google Scholar]
- 10.Gill P, Murray W, Saunders MA. SNOPT: an SQP algorithm for large-scale constrained optimization. SIAM Journal on Optimization. 2002;12:979–1006. [Google Scholar]
- 11.Glitsch U, Baumann W. The three-dimensional determination of internal loads in the lower extremity. Journal of Biomechanics. 1997;30:1123–1131. doi: 10.1016/s0021-9290(97)00089-4. [DOI] [PubMed] [Google Scholar]
- 12.Happee R, van der Helm FCT. The control of shoulder muscles during goal directed movements, an inverse dynamic analysis. Journal of Biomechanics. 1995;28:1179–1191. doi: 10.1016/0021-9290(94)00181-3. [DOI] [PubMed] [Google Scholar]
- 13.Hardin EC, Su A, van den Bogert AJ. Foot and ankle forces during an automobile collision: the influence of muscles. Journal of Biomechanics. 2004;37:637–44. doi: 10.1016/j.jbiomech.2003.09.030. [DOI] [PubMed] [Google Scholar]
- 14.Kaplan ML. Ph.D. Thesis. Stanford University; 2000. E3cient optimal control of large-scale biomechanical systems. [Google Scholar]
- 15.Kaplan ML, Heegaard JH. Predictive algorithms for neuromuscular control of human locomotion. Journal of Biomechanics. 2001;34:1077–1083. doi: 10.1016/s0021-9290(01)00057-4. [DOI] [PubMed] [Google Scholar]
- 16.McLean SG, Su A, van den Bogert AJ. Development and validation of a 3-D model to predict knee joint loading during dynamic movement. Journal of Biomechanical Engineering. 2003;125:864–874. doi: 10.1115/1.1634282. [DOI] [PubMed] [Google Scholar]
- 17.Minetti AE, Alexander RMcN. A theory of metabolic cost for bipedal gaits. Journal of Theoretical Biology. 1997;186:467–476. doi: 10.1006/jtbi.1997.0407. [DOI] [PubMed] [Google Scholar]
- 18.Nagano A, Umberger BR, Marzke MW, Gerritsen KGM. Neuromuscu-loskeletal computer modeling and simulation of upright, straight-legged, bipedal locomotion of Australopithecus Afarensis (A.L. 288–1) American Journal of Physical Anthropology. 2005;126:2–13. doi: 10.1002/ajpa.10408. [DOI] [PubMed] [Google Scholar]
- 19.Pedotti A, Krishnan VV, Stark L. Optimization of muscle-force sequencing in human locomotion. Mathematical Biosciences. 1978;38:57–76. [Google Scholar]
- 20.Ralston HJ. Energetics of human walking. In: Herman RM, et al., editors. Neural Control of Locomotion. Plenum Press; 1976. [Google Scholar]
- 21.Rasmussen J, Damsgaard M, Voigt M. Muscle recruitment by min/max criterion – a comparative numerical study. Journal of Biomechanics. 2001;34:409–415. doi: 10.1016/s0021-9290(00)00191-3. [DOI] [PubMed] [Google Scholar]
- 22.Sellers WI, Cain GM, Wang W, Crompton RH. Stride lengths, speed and energy costs in walking of Autralopithecus afarensis: using evolutionary robotics to predict locomotion of early human ancestors. Journal of the Royal Society Interface. 2005;2:431–441. doi: 10.1098/rsif.2005.0060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sellers WI, Manning PL. Estimating dinosaur maximum running speeds using evolutionary robotics. Proceedings of the Royal Society B. 2007;274:2711–2716. doi: 10.1098/rspb.2007.0846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stelzer M, von Stryk O. Efficient forward dynamics simulation and optimization of human body dynamics. Journal of Applied Mathematics and Mechanics (ZAMM) 2006;10:828–840. [Google Scholar]
- 25.Thelen DG, Anderson FC, Delp SL. Generating dynamic simulations of movement using computed muscle control. Journal of Biomechanics. 2003;36:321–328. doi: 10.1016/s0021-9290(02)00432-3. [DOI] [PubMed] [Google Scholar]
- 26.Thelen DG, Anderson FC. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. Journal of Biomechanics. 2006;39:1107–1115. doi: 10.1016/j.jbiomech.2005.02.010. [DOI] [PubMed] [Google Scholar]
- 27.Umberger BR, Gerritsen KGM, Martin PE. A model of human muscle energy expenditure. Computer Methods in Biomechanics & Biomedical Engineering. 2003;6:99–111. doi: 10.1080/1025584031000091678. [DOI] [PubMed] [Google Scholar]
- 28.van den Bogert AJ, Schamhardt HC, Crowe A. Simulation of quadrupedal locomotion using a rigid body model. Journal of Biomechanics. 1989;22:33–41. doi: 10.1016/0021-9290(89)90182-6. [DOI] [PubMed] [Google Scholar]
- 29.Winter DA. The biomechanics and motor control of human gait: normal, elderly and pathological. 2 University of Waterloo Press; Waterloo: 1991. [Google Scholar]
- 30.Zajac FE, Neptune RR, Kautz SA. Biomechanics and muscle coordination of human walking part II: lessons from dynamical simulations and clinical implications. Gait and Posture. 2003;17:1–17. doi: 10.1016/s0966-6362(02)00069-3. [DOI] [PubMed] [Google Scholar]