Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Jan 20.
Published in final edited form as: Int J Comput Biol Drug Des. 2009 Oct 3;2(2):115–133. doi: 10.1504/IJCBDD.2009.028820

Automatic inference of multicellular regulatory networks using informative priors

Xiaoyun Sun 1, Pengyu Hong 2,✉
PMCID: PMC3024031  NIHMSID: NIHMS261797  PMID: 20090166

Abstract

To fully understand the mechanisms governing animal development, computational models and algorithms are needed to enable quantitative studies of the underlying regulatory networks. We developed a mathematical model based on dynamic Bayesian networks to model multicellular regulatory networks that govern cell differentiation processes. A machine-learning method was developed to automatically infer such a model from heterogeneous data. We show that the model inference procedure can be greatly improved by incorporating interaction data across species. The proposed approach was applied to C. elegans vulval induction to reconstruct a model capable of simulating C. elegans vulval induction under 73 different genetic conditions.

Keywords: multicellular regulatory network, DBN, dynamic Bayesian network, animal development

1 Introduction

Genes and their products dynamically interact with each other at multiple levels to form complex networks that regulate how individual cells respond to environmental cues and how cells coordinate with each other via intercellular signalling to execute developmental programmes. Understanding how genes/proteins regulate each other to generate functions at tissue level or a higher level can provide insights into drug therapy design, tissue engineering and regenerative medicine (Hanahan and Weinberg, 2000; Noble, 2002; Davidson et al., 2003; Giurumescu and Asthagiri, 2008). A huge amount of heterogeneous biological data has been generated to study the underlying regulatory mechanisms. To fully understand the function and dysfunction of organisms, a Systems Biology approach is needed to reconstruct and study such biological networks (Ideker et al., 2001a; Kitano, 2002; Barabasi and Oltvai, 2004; Werner, 2005; Zhong and Sternberg, 2007). Nevertheless, it remains a great challenge to integrate those diverse biological data sets to advance our understanding of network functions at systems-level and generate testable hypotheses (Ideker et al., 2001a, 2001b; Kitano, 2002; Ge et al., 2003; Barabasi and Oltvai, 2004; Aderem, 2005; Kirschner, 2005; Klipp et al., 2005; Papin et al., 2005; Joyce and Palsson, 2006; Quackenbush, 2006; Albert, 2007; Bruggeman and Westerhoff, 2007; Christensen et al., 2007; Wingender et al., 2007).

Approaches to modelling cellular regulatory networks in the context of multicellular systems are emerging (Davidson et al., 2002; Noble, 2002; Werner, 2003; Fisher et al., 2005; Werner, 2005; Sun and Hong, 2007). We recently took a machine-learning approach and developed a methodology to infer multicellular regulatory networks by integrating heterogeneous biological data (Sun and Hong, 2007). Our multicellular regulatory network model is based on Dynamic Bayesian Networks (DBN) (Dean and Kanazawa, 1989; Murphy, 2002) – one type of statistical graphic models. Our approach was novel on several fronts.

First, our model introduced control nodes to quantitatively model non-deterministic interventions, such as reduce-function mutation, gain-function mutation, RNA interference, chemical treatment, and so on. This was an important improvement over previous studies using graphic models (Pearl, 2000; Pe’er, 2005) that only dealt with deterministic interventions (e.g., gene knockout) and deterministically assigned a value to the intervened variables. Different from deterministic interventions that allow us to deterministically set the state of a gene/protein, the effects of non-deterministic interventions are not fixed. For example, knocking down a gene by RNAi will stochastically (but often not completely) silence the expression of that gene. Ignoring this fact may greatly affect network inference results and lead to inaccurate understanding of the underlying biology.

Second, we applied the parameter tying technique (Tonomura et al., 1995; Nathan et al., 1996; Simonin et al., 1996) to enforce the genetic identicalness of cells in the model. Basically, all cell modules in a multicellular regulatory model share the same structure and the same parameter set. The overall states of different cells can be different and are combinatorially decided by the states of their own network components. This technique effectively reduces the number of free parameters in a model and increases its robustness.

Third, we developed a new machine-learning method to automatically infer multicellular regulatory networks by integrating heterogeneous biological data. Our method was based on Markov Chain Monte Carlo and was capable of dealing with incomplete data. Owing to technical difficulties and cost concerns, a typical biological data sample only provides observations of a portion of network components. That is the information about the remaining network components is missing in this sample. For example, gene expression data does not directly provide information about protein activities. In the machine-learning community, this type of data is said to be incomplete or partially observed. It should be noted that incomplete data is pervasive in biological and biomedical research. Our model deals with the incomplete data problem by treating the observed and unobserved network components as observed and hidden variables, respectively.

Finally, we applied our method to study C. elegans vulval induction and inferred a model that contains six interacting cell modules. Each cell consists of 20 network components. The model was capable of correctly simulating vulval induction under 36 different genetic conditions. As far as we know, the model was the first to demonstrate the stochastic control mechanisms deployed in cell differentiation, which are among the main factors underlying fate-commitment variability observed experimentally (i.e., one cell adopts different fates under the same genetic background and developmental context). In addition, several hypothetical causal relationships between network components were proposed in the model, which could serve as guidance for designing future experiments.

C. elegans vulval development is a paradigmatic example of animal organogenesis (Sternberg, 2005). It represents a striking case of tissue remodelling as the results of cell–cell interactions. It is a representative case for studying the complex interactions among pathways, especially the antagonism between the EGFR and Notch signalling pathways. During C. elegans vulval induction (Figure 1(a)), each of the six multi-potent Vulval Precursor Cells (VPCs) is capable of committing to one of three fates termed 1°, 2° and 3°. The precise formation of VPC fate pattern is controlled by a long-range gradient inductive signal to VPCs from an anchor cell and a short-range lateral signal between neighbouring VPCs (Sternberg and Horvitz, 1989; Sternberg, 2004). A strong enough inductive signal can activate the EGFR pathway in a VPC (Figure 1(b))

Figure 1.

Figure 1

Open in a new tab

C. elegans vulval induction: (a) during the L3 stage of worm development, an inductive signal from the Anchor Cell (AC) and the lateral signals among the six multipotent VPCs (named P3.p, P4.p, P5.p, P6.p, P7.p, and P8.p) collaboratively specify each VPC to adopt one of the three fates termed 1°, 2°, or 3°. In wildtype C. elegans, VPCs form a precise formation of the 3°-3°-2°-1°-2°-3° pattern. The thickness of arrows indicates the strength of the signals and (b) the diagrammatic model of the cellular regulatory network controlling the fate of one VPC. Arrow represents activation. Bar represents repression. See text for details

  1. to promote 1°-specific genes

  2. inhibit its LIN-12/Notch pathway and 3°-specific genes

  3. send out a lateral signal.

The LIN-12/Notch pathway in a VPC can be activated by a strong enough lateral signal to promote 2°-specific genes and down-regulate EGFR signalling (Figure 1(b)).

C. elegans vulval development has attracted sufficient general research interest systematically generate extensive experimental data in the last few decades. However, its underlying mechanism is still not fully understood, which makes it an ideal test-bed for research on modelling and inferring multicellular regulatory networks. On the basis of the existing cellular molecular knowledge about vulval development, Fisher et al. (2005, 2007) manually constructed formal models for C. elegans vulval induction. Their latest model (Fisher et al., 2007) contains 11 different network components: let-23 (the EGF receptor, i.e., the inductive signal receptor), lin-3 (the inductive signal), sem-5 (the Grb2-like adaptor), let-60 (the RAS GTP-binding protein), lst genes, lin-12 (the Notch receptor), mpk-1 (the MAP kinase), lin-15, fate 1°, fate 2°, and fate 3°. This model was capable of simulating vulval inductions under 48 genetic conditions. Nevertheless, the formal models are deterministic and hence are not able to deal with the biological variances observed in experiments (i.e., worms with the same genetic background may show different VPC fate-commitment patterns).

Our multicellular regulatory network model and automatic model inference method offer great advantages over previous approaches. However, our inference method needs to search a huge model space when the number of network components is large (the size of the model space is super-exponential to the number of network components). In this work, interaction data across species is used to generate an informative prior about the model structure that helps reduce computational time and infer better models. In addition, we report an expanded vulval induction model that contains 27 network components and is capable of simulating vulval induction results under 73 different genetic conditions.

2 Methods

2.1 Multicellular regulatory network model

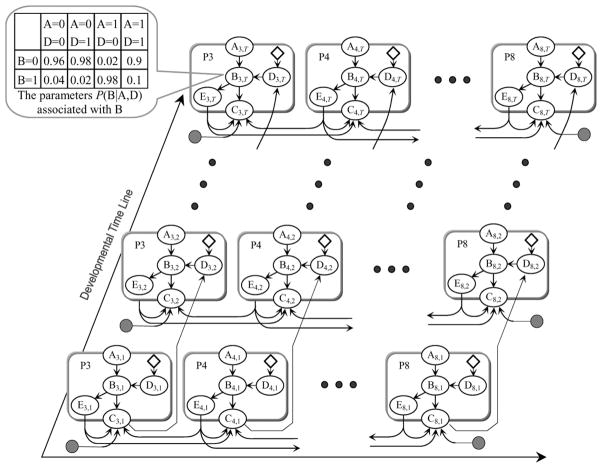
A simple example is shown in Figure 2 to demonstrate the idea of our multicellular regulatory model. Basically, each cell in the network is represented by a cell module. Network components in a cell module are represented as nodes. The temporal causal relationships between network components are represented as links between nodes. Each node is associated with a set of local parameters that quantitatively encode the relationship between it and its parent nodes. For example, in Figure 2, the parameters of node B3,T (the table in Figure 2) specify how its state (inactive = 0 and active = 1) is probabilistically regulated by the states of two other network components A3,T and D3,T. In this case, as indicated by the parameters, A3,T is an activator of B3,T, and D3,T is a repressor of B3,T. The nodes of the same molecule but in different cell modules share the same parameter set. Some nodes are control nodes indicating the genetic backgrounds (e.g., loss-function mutation, gain-function mutation, etc.) of their children nodes. The detailed mathematical formulation of this multicellular regulatory network was described in Sun and Hong (2007).

Figure 2.

Figure 2

Open in a new tab

A simple multicellular regulatory model is unrolled along the developmental time line to have T time slices. It consists of six identical cell modules (P3-8) in rounded rectangles. Each cell module contains five nodes representing five cellular network components (A, B, C, D, E). The subscription index of a node denotes the cell ID and the time slice. Nodes E represent the lateral signal among cells. Nodes C represent the receptor of the lateral signal E. To ensure that all cells are structurally and parametrically identical, dumb nodes (in gray) are introduced as additional lateral signals to P3 and P8. The values of dumb nodes are always set to 0 (i.e., no lateral signal). The control nodes (in diamond shape) are used to indicate the genetic states of their children nodes

To simulate the developmental process, we first unroll a multicellular regulatory network to have T time-slices (e.g., Figure 2). By doing so, we discretise the continuous developmental process into T steps. The value of T depends on the developmental process under investigation. It can either be based on the existing biological knowledge or be set empirically. Some network components are completely decided by out-of-system factors and should be preset based on the existing biological knowledge. For example, the control nodes should be set to reflect the desired genetic backgrounds (e.g., wild-type, loss-function mutation, reduce-function mutation, gain-function mutation, etc.). In C. elegans vulval development, the inductive signal level received by each VPC depends on how far away it is from the anchor cell. The states of the rest network components are then sampled based on their parameters, the structure of the model, and the states of their parents. For example, in Figure 2, if A3,T = 0 and D3,T = 1, the state of B3,T is more likely to be 0 (with a probability of 0.98) than 1 (with a probability of 0.02). Upon finishing the simulation, the fate of a cell can be decided by the states of its fate markers. For example, we decided that a VPC committed to fate 1° if its fate 1° marker was the only marker stabilised at its highest level.

2.2 Inferring multicellular regulatory models

Our previous method (Algorithm 1) for inferring multicellular regulatory models (Sun and Hong, 2007) was based on the Metropolis-Hastings algorithm (Hastings, 1970). Mathematically, let a model be denoted as M = < G, Θ > where G and Θ are the structure and parameter set of the model, respectively. The algorithm starts with an initial model M1 and then repeats the following steps until converge:

Algorithm 1.

Learning multicellular regulatory network

  1. Initialise the model M1 with the structure G1

  2. Estimate the parameter set Θ1 of M1 given its structure G1 and the training data O

  3. Estimate the likelihood of the training data P(O|M1)

  4. for k = 1, 2, …, until converge

    • (d.1)

      Randomly select a structure G′ from N(Gk) that is the neighbourhood of Gk and contains the structures differing from Gk by only one edge

    • (d.2)

      Estimate the parameter set Θ′ of M′ given G′ and O

    • (d.3)

      Estimate the likelihood P(O|M′)

    • (d.4)

      Compute ratio R=P(O∣M′)P(G′)P(O∣Mk)P(Gk)∣N(Gk)∣∣N(G′)∣

    • (d.5)

      Accept M′ with the probability of min(1, R). If accepted, let Mk+1 = M′, otherwise Mk+1 = Mk

  5. Return Mk+1

Open in a new tab

  1. samples a new structure G′ in the neighbourhood of the current structure

  2. estimates the parameters Θ′ associated with the new structure G′ using the training data O

  3. estimates the likelihood P(O|M′) of the training data O given the new model M′

  4. accepts the new model M′ based on the Metropolis-Hastings ratio R.

Since the model space to be searched is huge, we need to make use of biological knowledge and some heuristics to reduce the computational complexity. For example, when modelling C. elegans vulval induction (Sun and Hong, 2007), we used a strong prior that assumed LET-60 (RAS), LIN-45 (RAF), MEK-2 (MAPKK), and MPK-1 (MAPK) to form a canonical linear RTK/Ras/MAPK signalling pathway known to be conserved across many species. In addition, we limited the maximum number of the parents of any node to 3. However, the power of this approach was very limited. In the following section, we propose a better approach to derive and use informative structure priors.

2.3 Deriving and using informative structure prior

Promising results have been reported in several studies that interactions in one species of interest can be inferred from interactions in other species (Matthews et al., 2001; Ge et al., 2003; Rhodes et al., 2005; Gandhi et al., 2006; Hirsh and Sharan, 2007). It was also shown that using informative structure priors could significantly improve the results and speed of model inference methods (Le Phillip et al., 2004; Bernard and Hartemink, 2005; Chen et al., 2006; Geier et al., 2007; Mukherjee and Speed, 2007). This inspired us to make use of interaction data across species to construct informative priors for inferring multicellular regulatory networks. We applied this idea to reconstruct the multicellular regulatory network underlying C. elegans vulval induction.

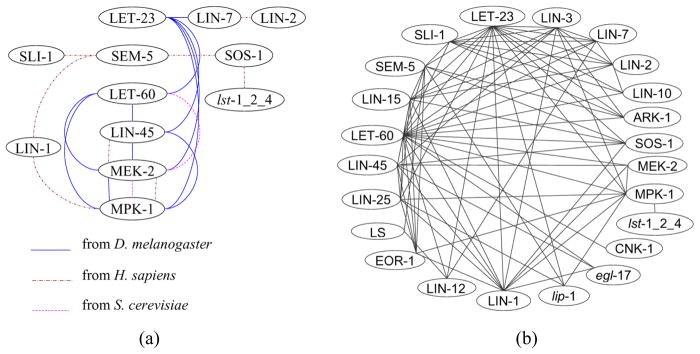
We downloaded the interaction data from NCBI as of 12/01/2007. The data set includes interaction data from BIND (Bader et al., 2003), BioGrid (Stark et al., 2006), and HPRD (Peri et al., 2003). It contains 6846, 32180, 61086, 134163 interactions in C. elegans, D. melanogaster, H. sapiens, and S. cerevisiae, respectively. We supplemented this dataset with genetic interaction data obtained from WormBase (www.wormbase.org). In this project, we were only interested in only the following genes (or gene groups) and proteins, for which we have collected training data from literature: LIN-3 (inductive signal), LIN-2, LIN-7, LIN-10, LET-23, SLI-1, LIN-15, SEM-5, ARK-1, SOS-1, LET-60, CNK-1, LIN-45, MEK-2, MPK-1, LIN-1, LIN-25, EOR-1, lip-1, egl-17 (fate 1° marker), LIN-12, lst-1_2_4 (gene group of lst-1, lst-2, and lst-4), dpy-23_lst-3 (gene group of dpy-23 and lst-3), LS (lateral signal ligands), fate 2° marker, and fate 3° marker. Using the NCBI Homologue database, we mapped the interactions between the homologues of the above-mentioned C. elegans genes in D. melanogaster, H. sapiens, and S. cerevisiae to C. elegans. The results are summarised in Figure 3 and the details are provided in the Supplementary Materials. As shown in Figure 3(a), the relationships among LET-60, LIN-45, MEK-2, and MPK-1 are indeed evolutionally conserved.

Figure 3.

Figure 3

Open in a new tab

(a) The interaction map derived from the interaction data of D. melanogaster, H. sapiens, and S. cerevisiae. There are 21 interactions in total and (b) the map derived from the interaction data of C. elegans. There are 85 interactions in the map. Node LS denotes the ligand set (apx-1, dsl-1, and lag-2) of the Notch receptor, and node lst-1_2_4 denotes the gene group consisted of lst-1, lst-2 and lst-4. A link is added between a group node X and another node Y if there is at least one interaction between Y and one of members in X (see online version for colours)

We used the following ad hoc method to assign weights to the potential links between network components. Initially, the weight of every link was set to one. Using Table 1, we added additional points to each link depending on the types of the related interactions reported in literature. Basically, higher points were given to physical interactions than genetic interactions within the same species. Interactions in C. elegans were given higher points than the same type of interactions in other species. The structure prior P(G) was designed as cϕδw(G), where c is a normalisation constant, ϕ is empirically set as 0.8, δ represents the total number of parameters in G to penalise complex models, and w(G) is the total link weight of G that takes into account the experimentally observed interactions between network components. It should be noted that the weights were assigned without considering the potential directionality of the relationships. The model inference algorithm will decide the directionality. To use the prior P(G), we made an important improvement to step (d.1) of Algorithm 1. The modified version samples a new structure G′ from N(Gk) based on P(G) so that a structure with a higher prior probability is more likely to be chosen.

Table 1.

Weight table

Interaction type Point added
Physical interaction in C. elegans 3
Genetic interaction in C. elegans 1.5
Physical interaction in other species 2
Genetic interaction in other species 1
Open in a new tab

3 Results

3.1 Training data

Sun and Hong (2007) have previously collected a set of training data, which mainly consisted of phenotypic data samples and a few qualitative descriptions of temporal gene expression patterns, from Sternberg and Horvitz (1989), Beitel et al. (1990), Simske et al. (1996), Berset et al. (2001), and Yoo et al. (2004). In this work, we expanded the training data to include some observations reported by Tuck and Greenwald (1995), Lackner and Kim (1998), Chang et al. (2000), Hopper et al. (2000), Yoon et al. (2000), Howard and Sundaram (2002) and Rocheleau et al. (2005). The newly collected data was processed in the same described in Sun and Hong (2007). Basically, the phenotypic observations were converted into the states of fate markers, and the genetic mutations were converted into the states of the control nodes. The complete details about the training data are provided in the Supplementary Materials.

3.2 A multicellular regulatory network for C. elegans vulval induction

The usage of the informative prior derived from the interaction data significantly improved the computational results. Compared with our previous method without using such an informative prior, the computational time was reduced by more than 200-fold using our current implementation. One of the most likely models inferred by this improved method is shown in Figure 4. Compared to the model reported by Sun and Hong (2007), this model contains seven new network components (SLI-1, ARK-1, SOS-1, CNK-1, LIN-25, EOR-1, and LIN-1) and is capable of simulating vulval induction under 73 genetic conditions (see Supplementary Materials for the complete set of simulation results), which represent a more than 100% increase in the model’s capability. Similar to the old model, the new model uses a deterministic node (Sum_LS) to integrate lateral signals so as to reduce the model complexity. In addition, dpy-23 and lst-3 were still grouped together as dpy-23_lst-3, and lst-1, lst-2 and lst-4 were grouped as lst-1_2_4 because no further evidence allowed us to infer more specific information about them.

Figure 4.

Figure 4

Open in a new tab

The structure of one of the best vulval induction multicellular regulatory models. Only one cell module is shown. Solid edges are intra-slice links, and dashed edges are inter-slice links. L_LS is the lateral signal from the left neighbouring VPC, i.e., the LS node in the left VPC module. R_LS is the lateral signal from the right neighbouring VPC, i.e., the LS node in the right VPC module. Sum_LS is the signal integration node. dpy-23_lst-3 denotes the gene group of dpy-23 and lst-3, lst-1_2_4 denotes the gene group of lst-1, lst-2 and lst-4. The marker gene of fate 1° is egl-17. Nodes 2° and 3° represent gene groups specific to fates 2° and 3°, respectively

The new model also helped advance our understanding about C. elegans vulval induction. For example, we previously reported that there were six equally possible linear sub-paths formed by LIN-2, LIN-7, and LIN-10. Anyone of LIN-2, LIN-7, and LIN-10 can be a parent node of LET-23. The new results showed that the structure LIN-10 → LIN-2 → LIN-7 → LET-23 was dominantly preferred, which truly reflected the interaction order among LIN-2, LIN-7, LIN-10, and LET-23 (Kaech et al., 1998). This result could be mainly due to the observations of the following physical interaction pairs: LIN-10 ↔ LIN-2 in C. elegans, LIN-2 ↔ LIN-7 in C. elegans, LIN-7 ↔ LET-23 in C. elegans, Egfr (homologue of let-23) ↔ veli (homologue of lin-7) in D. melanogaster, and LIN7C (homologue of lin-7) ↔ CASK (homologue of lin-2) in H. sapiens. In another example, the old model reported that lst-1_2_4 feedbacks into MEK-2. The new model suggests that lst-1_2_4 feedbacks into MPK-1. This result could be mainly because C. elegans LST-1 and MPK-1 were detected to interact with each other in yeast two-hybrid experiment (Li et al., 2004). The new model inference process also changed the negative feedback point of lip-1 into the EGFR signalling to be at LIN-25 – a transcription factor. Finally, the new model encodes the collaboration of LIN-1 (a transcription factor with an Ets-domain) and LIN-25 in regulating genes specific to fate 1°.

4 Discussion

Phenotypic data is still the major information source used by us to infer the multicellular regulatory network governing C. elegans vulval induction. For example, the following links in our new model were not observed in the interaction data: CNK1 → LIN-45, dpy-23_lst-3 → LET-60, LIN-25 → egl-17, EOR-1 → egl-17, egl-17 → LIN-12, LIN-12 → lst-1_2_4 and LIN-12 → dpy-23_lst-3. They were derived mainly from the phenotypic data. These links may represent functional interactions that could be useful for designing future experiments.

Not every physical interaction appeared in our new model. For example, SEM-5 was reported to physically interact with SOS-1 and SLI-1 in yeast two-hybrid experiments. However, neither of these two interaction pairs appeared in the new model. This result may be due to the following three reasons. First, those interactions could be false-positives. Huang et al. (2007) estimated that a non-trivial portion of experimentally observed interactions could be false positives. Second, these interactions are not functional in the context of vulval induction so that they are not supported by our training data. Finally, our model inference procedure searches for models that can not only explain the training data but also should be as simple as possible. Adding SOS-1 and SLI-1 as the parents of SEM-5 will certainly increase the complexity of the model, and hence were not adopted.

Although the expanded model is capable of simulating certain fate-commitment variations (i.e., phenotypic penetrance), we have not fully addressed this problem yet. Many labs have independently reported that the same genetic background could result in different degree of penetrance. For example, Berset et al. (2001) reported that the average number of induced VPCs is 2.4 under a double mutation background of let-23 reduction-function mutation and lip-1 loss-function mutation. This clearly suggests that some worms under this genetic condition have three or more induced VPCs and others have two or less induced VPCs. Since it was very difficult to convert this kind of data to a form that could be computed by our method, we either avoided using this kind of samples or rounded them towards the closest reasonable fate-commitment patterns (e.g., we rounded average 2.9 induced VPCs towards three induced VPCs). Phenotypic penetrance is not only very complicated but also extremely important for understanding the underlying biology. It indicates that the underlying multicellular regulatory mechanism is much more intricate than what we know about the system and existing computational models.

Supplementary Material

Acknowledgments

This work is partially supported by an NIH grant to PH.

Biographies

Xiaoyun Sun is a PhD student in Computer Science at Brandeis University.

Pengyu Hong is an Assistant Professor of Computer Science at Brandeis University. He received his BS and MS in Computer Science from Tsinghua University and his PhD in Computer Science from University of Illinois at Urbana-Champaign. He was a post-doc fellow at the Department of Statistics at Harvard University from 2002 to 2004, and continued his post-doc training at the Department of Statistics at Stanford University in 2005. He started the Computational Systems Biology lab at Brandeis in 2005. His research includes high-content image analysis and automatic inference of biological networks governing signal transduction and animal development.

Contributor Information

Xiaoyun Sun, Email: xsun@brandeis.edu, Department of Computer Science, Brandeis University, Waltham, MA 02454, USA.

Pengyu Hong, Email: hongpeng@brandeis.edu, Department of Computer Science, National Center for Behavioral Genomics, Brandeis University, Waltham, MA 02454, USA.

References

  1. Aderem A. Systems biology: its practice and challenges. Cell. 2005;121(4):511–513. doi: 10.1016/j.cell.2005.04.020. [DOI] [PubMed] [Google Scholar]
  2. Albert R. Network inference, analysis, and modeling in systems biology. Plant Cell. 2007;19(11):3327–3338. doi: 10.1105/tpc.107.054700. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bader GD, Betel D, Hogue CW. BIND: the biomolecular interaction network database. Nucleic Acids Res. 2003;31(1):248–250. doi: 10.1093/nar/gkg056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Barabasi AL, Oltvai ZN. Network biology: understanding the cell’s functional organization. Nat Rev Genet. 2004;5(2):101–113. doi: 10.1038/nrg1272. [DOI] [PubMed] [Google Scholar]
  5. Beitel GJ, Clark SG, Horvitz HR. Caenorhabditis elegans ras gene let-60 acts as a switch in the pathway of vulval induction. Nature. 1990;348(6301):503–509. doi: 10.1038/348503a0. [DOI] [PubMed] [Google Scholar]
  6. Bernard A, Hartemink AJ. Informative structure priors: joint learning of dynamic regulatory networks from multiple types of data. Pac Symp Biocomput. 2005:459–570. [PubMed] [Google Scholar]
  7. Berset T, Hoier EF, Battu G, Canevascini S, Hajnal A. Notch inhibition of RAS signaling through MAP kinase phosphatase LIP-1 during C. elegans vulval development. Science. 2001;291(5506):1055–1058. doi: 10.1126/science.1055642. [DOI] [PubMed] [Google Scholar]
  8. Bruggeman FJ, Westerhoff HV. The nature of systems biology. Trends Microbiol. 2007;15(1):45–50. doi: 10.1016/j.tim.2006.11.003. [DOI] [PubMed] [Google Scholar]
  9. Chang C, Hopper NA, Sternberg PW. Caenorhabditis elegans SOS-1 is necessary for multiple RAS-mediated developmental signals. Embo J. 2000;19(13):3283–3294. doi: 10.1093/emboj/19.13.3283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chen XW, Anantha G, Wang X. An effective structure learning method for constructing gene networks. Bioinformatics. 2006;22(11):1367–1374. doi: 10.1093/bioinformatics/btl090. [DOI] [PubMed] [Google Scholar]
  11. Christensen C, Thakar J, Albert R. Systems-level insights into cellular regulation: inferring, analysing, and modelling intracellular networks. IET Syst Biol. 2007;1(2):61–77. doi: 10.1049/iet-syb:20060071. [DOI] [PubMed] [Google Scholar]
  12. Davidson EH, McClay DR, Hood L. Regulatory gene networks and the properties of the developmental process. Proc Natl Acad Sci USA. 2003;100(4):1475–1480. doi: 10.1073/pnas.0437746100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Davidson EH, Rast JP, Oliveri P, Ransick A, Calestani C, Yuh CH, Minokawa T, Amore G, Hinman V, Arenas-Mena C, Otim O, Brown CT, Livi CB, Lee PY, Revilla R, Rust AG, Pan Z, Schilstra MJ, Clarke PJ, Arnone MI, Rowen L, Cameron RA, McClay DR, Hood L, Bolouri H. A genomic regulatory network for development. Science. 2002;295(5560):1669–1678. doi: 10.1126/science.1069883. [DOI] [PubMed] [Google Scholar]
  14. Dean T, Kanazawa K. A model for reasoning about persistence and causation. Computational Intelligence. 1989;5(3):142–150. [Google Scholar]
  15. Fisher J, Piterman N, Hajnal A, Henzinger TA. Predictive modeling of signaling crosstalk during C. elegans vulval development. PLoS Comput Biol. 2007;3(5):e92. doi: 10.1371/journal.pcbi.0030092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fisher J, Piterman N, Hubbard EJ, Stern MJ, Harel D. Computational insights into Caenorhabditis elegans vulval development. Proc Natl Acad Sci USA. 2005;102(6):1951–1956. doi: 10.1073/pnas.0409433102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gandhi TK, Zhong J, Mathivanan S, Karthick L, Chandrika KN, Mohan SS, Sharma S, Pinkert S, Nagaraju S, Periaswamy B, Mishra G, Nandakumar K, Shen B, Deshpande N, Nayak R, Sarker M, Boeke JD, Parmigiani G, Schultz J, Bader JS, Pandey A. Analysis of the human protein interactome and comparison with yeast, worm and fly interaction datasets. Nat Genet. 2006;38(3):285–293. doi: 10.1038/ng1747. [DOI] [PubMed] [Google Scholar]
  18. Ge H, Walhout AJ, Vidal M. Integrating ‘omic’ information: a bridge between genomics and systems biology. Trends Genet. 2003;19(10):551–560. doi: 10.1016/j.tig.2003.08.009. [DOI] [PubMed] [Google Scholar]
  19. Geier F, Timmer J, Fleck C. Reconstructing gene-regulatory networks from time series, knock-out data, and prior knowledge. BMC Syst Biol. 2007;1:11. doi: 10.1186/1752-0509-1-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Giurumescu CA, Asthagiri AR. Signal processing during developmental multicellular patterning. Biotechnol Prog. 2008;24(1):80–88. doi: 10.1021/bp070127t. [DOI] [PubMed] [Google Scholar]
  21. Hanahan D, Weinberg RA. The hallmarks of cancer. Cell. 2000;100(1):57–70. doi: 10.1016/s0092-8674(00)81683-9. [DOI] [PubMed] [Google Scholar]
  22. Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
  23. Hirsh E, Sharan R. Identification of conserved protein complexes based on a model of protein network evolution. Bioinformatics. 2007;23(2):e170–e176. doi: 10.1093/bioinformatics/btl295. [DOI] [PubMed] [Google Scholar]
  24. Hopper NA, Lee J, Sternberg PW. ARK-1 inhibits EGFR signaling in C. elegans. Mol Cell. 2000;6(1):65–75. [PubMed] [Google Scholar]
  25. Howard RM, Sundaram MV. C. elegans EOR-1/PLZF and EOR-2 positively regulate Ras and Wnt signaling and function redundantly with LIN-25 and the SUR-2 Mediator component. Genes Dev. 2002;16(14):1815–1827. doi: 10.1101/gad.998402. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Huang H, Jedynak BM, Bader JS. Where have all the interactions gone? Estimating the coverage of two-hybrid protein interaction maps. PLoS Comput Biol. 2007;3(11):e214. doi: 10.1371/journal.pcbi.0030214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ideker T, Galitski T, Hood L. A new approach to decoding life: systems biology. Annu Rev Genomics Hum Genet. 2001a;2:343–372. doi: 10.1146/annurev.genom.2.1.343. [DOI] [PubMed] [Google Scholar]
  28. Ideker T, Thorsson V, Ranish JA, Christmas R, Buhler J, Eng JK, Bumgarner R, Goodlett DR, Aebersold R, Hood L. Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science. 2001b;292(5518):929–934. doi: 10.1126/science.292.5518.929. [DOI] [PubMed] [Google Scholar]
  29. Joyce AR, Palsson BO. The model organism as a system: integrating ‘omics’ data sets. Nat Rev Mol Cell Biol. 2006;7(3):198–210. doi: 10.1038/nrm1857. [DOI] [PubMed] [Google Scholar]
  30. Kaech SM, Whitfield CW, Kim SK. The LIN-2/LIN-7/LIN-10 complex mediates basolateral membrane localization of the C. elegans EGF receptor LET-23 in vulval epithelial cells. Cell. 1998;94(6):761–771. doi: 10.1016/s0092-8674(00)81735-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Kirschner MW. The meaning of systems biology. Cell. 2005;121(4):503–504. doi: 10.1016/j.cell.2005.05.005. [DOI] [PubMed] [Google Scholar]
  32. Kitano H. Systems biology: a brief overview. Science. 2002;295(5560):1662–1664. doi: 10.1126/science.1069492. [DOI] [PubMed] [Google Scholar]
  33. Klipp E, Herwig R, Kowald A, Wierling C, Lehrach H. Systems Biology in Practice: Concepts, Implementation and Application. Wiley-VCH; 2005. [Google Scholar]
  34. Lackner MR, Kim SK. Genetic analysis of the Caenorhabditis elegans MAP kinase gene mpk-1. Genetics. 1998;150(1):103–117. doi: 10.1093/genetics/150.1.103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Le Phillip P, Bahl A, Ungar LH. Using prior knowledge to improve genetic network reconstruction from microarray data. In Silico Biol. 2004;4(3):335–353. [PubMed] [Google Scholar]
  36. Li S, Armstrong CM, Bertin N, Ge H, Milstein S, Boxem M, Vidalain PO, Han JD, Chesneau A, Hao T, Goldberg DS, Li N, Martinez M, Rual JF, Lamesch P, Xu L, Tewari M, Wong SL, Zhang LV, Berriz GF, Jacotot L, Vaglio P, Reboul J, Hirozane-Kishikawa T, Li Q, Gabel HW, Elewa A, Baumgartner B, Rose DJ, Yu H, Bosak S, Sequerra R, Fraser A, Mango SE, Saxton WM, Strome S, Van Den Heuvel S, Piano F, Vandenhaute J, Sardet C, Gerstein M, Doucette-Stamm L, Gunsalus KC, Harper JW, Cusick ME, Roth FP, Hill DE, Vidal M. A map of the interactome network of the metazoan C. elegans. Science. 2004;303(5657):540–543. doi: 10.1126/science.1091403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Matthews LR, Vaglio P, Reboul J, Ge H, Davis BP, Garrels J, Vincent S, Vidal M. Identification of potential interaction networks using sequence-based searches for conserved protein-protein interactions or ‘interologs’. Genome Res. 2001;11(12):2120–2126. doi: 10.1101/gr.205301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mukherjee S, Speed TP. Markov Chain Monte Carlo for Structural Inference with Prior Information. University of California; Berkeley: 2007. [Google Scholar]
  39. Murphy KP. Dynamic Bayesian Networks: Representation, Inference and Learning. Computer Science, University of California; Berkeley: 2002. [Google Scholar]
  40. Nathan KS, Subrahmonia J, Perrone MP. Parameter tying in writer-dependent recognition of on-line handwriting. Proceedings of the 13th International Conference on Pattern Recognition; Vienna, Austria. 1996. [Google Scholar]
  41. Noble D. Modeling the heart – from genes to cells to the whole organ. Science. 2002;295(5560):1678–1682. doi: 10.1126/science.1069881. [DOI] [PubMed] [Google Scholar]
  42. Papin JA, Hunter T, Palsson BO, Subramaniam S. Reconstruction of cellular signalling networks and analysis of their properties. Nat Rev Mol Cell Biol. 2005;6(2):99–111. doi: 10.1038/nrm1570. [DOI] [PubMed] [Google Scholar]
  43. Pe’er D. Bayesian network analysis of signaling networks: a primer. Sci STKE. 2005;2005(281):l4. doi: 10.1126/stke.2812005pl4. [DOI] [PubMed] [Google Scholar]
  44. Pearl J. Causality: Models, Reasoning, and Inference. Cambridge University Press; 2000. [Google Scholar]
  45. Peri S, Navarro JD, Amanchy R, Kristiansen TZ, Jonnalagadda CK, Surendranath V, Niranjan V, Muthusamy B, Gandhi TK, Gronborg M, Ibarrola N, Deshpande N, Shanker K, Shivashankar HN, Rashmi BP, Ramya MA, Zhao Z, Chandrika KN, Padma N, Harsha HC, Yatish AJ, Kavitha MP, Menezes M, Choudhury DR, Suresh S, Ghosh N, Saravana R, Chandran S, Krishna S, Joy M, Anand SK, Madavan V, Joseph A, Wong GW, Schiemann WP, Constantinescu SN, Huang L, Khosravi-Far R, Steen H, Tewari M, Ghaffari S, Blobe GC, Dang CV, Garcia JG, Pevsner J, Jensen ON, Roepstorff P, Deshpande KS, Chinnaiyan AM, Hamosh A, Chakravarti A, Pandey A. Development of human protein reference database as an initial platform for approaching systems biology in humans. Genome Res. 2003;13(10):2363–2371. doi: 10.1101/gr.1680803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Quackenbush J. From ‘omes to biology’. Anim Genet. 2006;37(Suppl 1):48–56. doi: 10.1111/j.1365-2052.2006.01476.x. [DOI] [PubMed] [Google Scholar]
  47. Rhodes DR, Tomlins SA, Varambally S, Mahavisno V, Barrette T, Kalyana-Sundaram S, Ghosh D, Pandey A, Chinnaiyan AM. Probabilistic model of the human protein-protein interaction network. Nat Biotechnol. 2005;23(8):951–959. doi: 10.1038/nbt1103. [DOI] [PubMed] [Google Scholar]
  48. Rocheleau CE, Ronnlund A, Tuck S, Sundaram MV. Caenorhabditis elegans CNK-1 promotes Raf activation but is not essential for Ras/Raf signaling. Proc Natl Acad Sci USA. 2005;102(33):11757–11762. doi: 10.1073/pnas.0500937102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Simonin J, Bodin S, Jouvet D, Bartkova K. Parameter tying for flexible speech recognition. International Conference on Spoken Language Processing; Philadelphia, PA. 1996. pp. 1089–1092. [Google Scholar]
  50. Simske JS, Kaech SM, Harp SA, Kim SK. LET-23 receptor localization by the cell junction protein LIN-7 during C. elegans vulval induction. Cell. 1996;85(2):195–204. doi: 10.1016/s0092-8674(00)81096-x. [DOI] [PubMed] [Google Scholar]
  51. Stark C, Breitkreutz BJ, Reguly T, Boucher L, Breitkreutz A, Tyers M. BioGRID: a general repository for interaction datasets. Nucleic Acids Res. 2006;34(Database Issue):D535–D539. doi: 10.1093/nar/gkj109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Sternberg PW. Developmental biology. A pattern of precision. Science. 2004;303(5658):637–638. doi: 10.1126/science.1094409. [DOI] [PubMed] [Google Scholar]
  53. Sternberg PW. Vulval Development, WormBook: The Online Review of C. elegans Biology. 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Sternberg PW, Horvitz HR. The combined action of two intercellular signaling pathways specifies three cell fates during vulval induction in C. elegans. Cell. 1989;58(4):679–693. doi: 10.1016/0092-8674(89)90103-7. [DOI] [PubMed] [Google Scholar]
  55. Sun X, Hong P. Computational modeling of Caenorhabditis elegans vulval induction. Bioinformatics. 2007;23(13):i499–i507. doi: 10.1093/bioinformatics/btm214. [DOI] [PubMed] [Google Scholar]
  56. Tonomura M, Kosaka T, Matsunaga S. Speaker adaptation based on transfer vector field smoothing using maximum a posteriori probability estimation. International Conference on Acoustics, Speech, and Signal Processing.1995. [Google Scholar]
  57. Tuck S, Greenwald I. lin-25, a gene required for vulval induction in Caenorhabditis elegans. Genes Dev. 1995;9(3):341–357. doi: 10.1101/gad.9.3.341. [DOI] [PubMed] [Google Scholar]
  58. Werner E. In silico multicellular systems biology and minimal genomes. Drug Discov Today. 2003;8(24):1121–1127. doi: 10.1016/s1359-6446(03)02918-0. [DOI] [PubMed] [Google Scholar]
  59. Werner E. Meeting report: the future and limits of systems biology. Sci STKE. 2005;2005(278):pe16. doi: 10.1126/stke.2782005pe16. [DOI] [PubMed] [Google Scholar]
  60. Wingender E, Crass T, Hogan JD, Kel AE, Kel-Margoulis OV, Potapov AP. Integrative content-driven concepts for bioinformatics ‘beyond the cell’. J Biosci. 2007;32(1):169–180. doi: 10.1007/s12038-007-0015-2. [DOI] [PubMed] [Google Scholar]
  61. Yoo AS, Bais C, Greenwald I. Crosstalk between the EGFR and LIN-12/Notch pathways in C. elegans vulval development. Science. 2004;303(5658):663–666. doi: 10.1126/science.1091639. [DOI] [PubMed] [Google Scholar]
  62. Yoon CH, Chang C, Hopper NA, Lesa GM, Sternberg PW. Requirements of multiple domains of SLI-1, a Caenorhabditis elegans homologue of c-Cbl, and an inhibitory tyrosine in LET-23 in regulating vulval differentiation. Mol Biol Cell. 2000;11(11):4019–4031. doi: 10.1091/mbc.11.11.4019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Zhong W, Sternberg PW. Automated data integration for developmental biological research. Development. 2007;134(18):3227–3238. doi: 10.1242/dev.001073. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NIHMS261797-supplement-supplement_1.pdf (116.1KB, pdf)

RESOURCES