What’s New in Trial Design: Propensity Scores, Equivalence, and Non-Inferiority

Abstract:

Recent modifications to traditional clinical research designs include propensity scores, equivalence, and non-inferiority trials, as well as greater use of pooled endpoints for primary outcome measures. Each of these innovations offers benefits, but they have been misused. Propensity score techniques can account for imbalance in treatment group allocation to provide more accurate estimates of benefit or risk. Unlike clinical trials, they typically represent real world, everyday practice and so their findings may in fact be less biased. Equivalence and non-inferiority designs can tailor clinical trials to address clinically meaningful questions: Is a proposed new technique at least as good as current treatment? Pooled endpoints can summarize a range of beneficial outcomes as well as reduce the required sample size. A clearer understanding of bias and confounding, and the interpretation of the 95% confidence interval of the estimated treatment effect are central to proper use of these techniques.

Clinical studies can be used to identify potentially useful or unsafe interventions. They may also identify ineffective (compared with placebo) or equivalent (compared with an established treatment) interventions. Each of these aims has special considerations for trial design and interpretation.

Most clinical trials aim to demonstrate efficacy of an active intervention when compared with placebo, or one active intervention over another. These are the familiar superiority trials (1,2). Safety is more difficult to prove, because adverse effects are generally rare, and large numbers of subjects and specific data collection are required to detect them. Furthermore, those at highest risk of adverse effects are typically excluded from randomized clinical trials (3). Clinical trials are thus likely to miss some important adverse effects (3). Large observational cohort studies and case-control studies, ideally with multivariate adjustment, are better options (3,4). One recent modification to this is use of propensity scores, aiming to balance baseline risk to detect a specific treatment effect (5–7). There has also been innovation in clinical trial design to include equivalence and non-inferiority trials (8–12) (Table 1). Each of these study designs can provide particular advantages for the researcher and clinician, in terms of timeliness and efficiency, and more specific information provided to assist in clinical decision-making and patient care. But the design and interpretation of such studies need careful consideration because they can be misleading (10–13).

Table 1.

Increase in the number of surgical studies using novel designs.

	2000	2004	2008
Propensity score	0	5	53
Equivalence trial	6	13	23
Noninferiority trial	0	2	9

Medline was searched in each year, using terms “surgery” and each of the designs.

Randomized trials use the play of chance to assign patients to the groups being compared (1,2,14,15). This process is designed to prevent systematic differences between groups. Overt, spurious, and hidden explanations for differences between groups can lead to an apparent effect that is not real (4,16,17), resulting in the adoption of unhelpful, expensive, or harmful therapies.

Small randomized trials account for many sources of bias, but may not avoid confounding. Larger numbers are required before random imbalance of potentially confounding factors, “covariates", are minimized. Here both known and unknown factors will be balanced, particularly if a large sample size is used. There are several methods available to account for confounding (15); the most widely known is regression modeling but the propensity score approach is being increasingly used (5–7).

PROPENSITY SCORE TECHNIQUES

Multivariate regression analysis identifies significant covariates, which can be adjusted to more precisely estimate the likely effect of the variable (intervention) of interest. Propensity scores address this issue in a different way: A logistic regression model is used to predict, backwards, the baseline variables that are associated with the group (intervention) of interest (5).

The propensity score describes the probability that each subject would be in the intervention group or comparison group, based on an analysis of baseline covariates. If all subjects with a similar treatment probability are batched, then the selection of the actual intervention group approaches that of random allocation—that is, propensity scoring attempts to recreate a random decision process. It is therefore a quasi-randomization technique, and is an efficient and recommended method of analyzing large databases.

Databases, registries, and other observational cohort studies, despite being derived in a non-randomized way, have the advantage of more truly representing everyday practice better than trial settings. One of the earliest examples of a propensity score technique was confirmation of the superiority of surgical intervention over medical therapy for coronary artery disease using Coronary Artery Surgery Study data in 1987 (18).

Calculation of the propensity score begins with selection of the baseline variables to be included in the model. As with other multivariate techniques, the selection and inclusion of the variables should be based on biologic plausibility and clinical judgment as to what is rational and practical in the decision-making and other processes used to determine whether or not a treatment is used. Logistic regression is then used to identify which of these variables are significantly associated with the treatment group. The propensity score is the conditional probability that this occurred, given all the measured covariates.

Groups of subjects with similar propensity scores can then be expected to have near-equivalent baseline risk. Subjects can be matched into quintiles of similar scores ("propensity matching") or the final group effect can be adjusted using the propensity score. The former is generally preferred (5,7). Examples of both approaches used to analyze the potential adverse effects of aprotinin in cardiac surgery have been published recently (19,20). Propensity score techniques can be used to investigate efficacy and/ or safety. But it is the latter for which they have the greatest value, because large datasets in routine clinical settings, including high-risk, elderly, and complex patients, can be included. These groups are often excluded in clinical trials (3).

It must be appreciated, however, that like regression modeling, propensity scores cannot alleviate all bias and confounding (2,17). For example, in recent studies of aprotinin that used propensity scores (19,20), it was clearly apparent that high risk patients were more likely to receive aprotinin, as well as being more likely to have postoperative complications. This is called confounding by indication. It is difficult to determine whether or not a propensity score has sufficiently accounted for such imbalance.

A group from the Cleveland Clinic analyzed their unit’s database of 32,298 cardiac surgical patients over a 13-year period up to 2006 to ascertain the risks of platelet transfusion (21). Simple univariate comparisons demonstrated that patients who received platelet transfusions had worse outcomes. This suggests a direct adverse effect of platelets, but this finding can also be explained by the higher risk settings in which platelet transfusion is used: emergency surgery, more complex surgery, co-existent sepsis, renal failure, and long bypass runs. They therefore used multivariate regression to adjust for such imbalance, and subsequently demonstrated that platelet transfusion was not significantly associated with in-hospital mortality: odds ration (OR) .74 (95% Confidence Interval (CI): .58–.95), p = .017. The authors then additionally tested their findings with propensity scores. Among 2774 propensity matched-pairs, platelet transfusion was associated with comparable or reduced morbidity for most individual morbidity and mortality endpoints. They thus concluded there was no evidence that platelet transfusion had worse outcomes after cardiac surgery.

SUPERIORITY, EQUIVALENCE, AND NON-INFERIORITY TRIALS

Most clinical trials aim to establish the superiority of one intervention over another. In other words, to assess whether the null hypothesis should be accepted or rejected. But how should a non-significant result be interpreted? It is a common error to conclude this indicates therapeutic equivalence (9–11). The correct conclusion and interpretation from such a study is that there is no evidence of difference between interventions, not that there is evidence of no difference.

Placebo-controlled trials can be unethical if an existing treatment is known to be effective. The ability to demonstrate a difference between two active groups, as opposed to an active group compared with placebo, is lessened because the effect size will be smaller. There is then a need to a have a larger sample size to maintain study power. One way to reduce this requirement is to focus on equivalence or non-inferiority rather than superiority, particularly if this is in fact what is of interest to the clinician. The study can then be designed as a one-sided trial and the necessary sample size will be less (9). The testing of a new drug or intervention to specifically show comparable efficacy may justify its introduction into clinical practice if there are potential other benefits such as lower cost, safety, or convenience. It is for these reasons that equivalence and non-inferiority trials are becoming increasingly popular in clinical research.

The first step is to determine what difference between groups could be considered small, or not clinically important. This is best dictated by expert clinical judgment but the assumptions will be more strongly substantiated if this can be referenced to published outcome data. The chosen effect size is defined as the pre-specified delta, Δ. If the difference between groups is less than the delta boundary then the groups are deemed to be equivalent. Or more precisely, if the 95% CI of the treatment difference excludes the delta value, then it can be concluded that the groups are equivalent (9–11). In a non-inferiority trial, if the upper bound of the 95% CI of the estimated treatment difference lies below the non-inferiority margin, it can be concluded that the new treatment is non-inferior to the standard treatment.

The choice of boundaries for equivalence must be critically reviewed, because it is on this basis that the interpretation of the results and conclusions are made. Relative differences of, say, up to 20% (odds or risk ratio of 1.2) are commonly used.

A recent trial comparing two fibrinolytic drugs, tenecteplase and alteplase, is a good example of an equivalence trial (22). The study was designed to show the equivalence of single-bolus tenecteplase and standard alteplase treatment in acute myocardial infarction (MI), using random allocation of 16,949 patients presenting with MI within 6 hours. The primary outcome was equivalence in all-cause mortality at 30 days; equivalence was defined as a mortality difference, or delta, of less than 1%. The eventual mortality rates were almost identical for the two groups: 6.18% and 6.15%, with an absolute difference of .03 (95% CI: −.55–.61), test of equivalence p = .006. Because the 95% one-sided upper boundary of the absolute difference in 30-day mortality was .61%, less than the pre-specified delta of 1%, it fulfilled the pre-specified criteria of equivalence. The authors noted that adverse event rates were generally lower for tenecteplase, and ease of administration favored this drug. They concluded that both drugs were equivalent, but that other considerations might favor tenecteplase in this setting. This is a clinically useful and practical finding.

Two antiplatelet drugs, tirofiban and abciximab, were tested for equivalence in 692 patients undergoing percutaneous coronary intervention (23). The authors chose a rate of ST-segment resolution of 10% for their definition of equivalence. The procedure was successful in 96.7% of the abciximab group and in 96.6% of the tirofiban group (p = .94). Complete ST-segment resolution was obtained in 67.1% of the tirofiban and 70.5% of the abciximab group, with a 95% CI for the difference of ?10.4 to +3.6. Because the 95% CI extends beyond the predefined delta of ±10%, the authors concluded that the study failed to demonstrate equivalence of these two drugs in this setting.

Non-inferiority trials aim to demonstrate comparable or better efficacy (8,9,11). As for equivalence trials, the key step is to nominate a clinically important excess adverse outcome rate above, which defines the criteria for inferiority of the new treatment. In addition, consideration of superiority can be incorporated in the study design, ideally using pre-specified secondary endpoints and/or supplementary cost analyses (9,11).

Serruys et al. (24) did a randomized trial comparing percutaneous coronary intervention with CABG in 1800 patients with triple-vessel or left main coronary artery disease. A non-inferiority design was used to compare the two groups, with the primary endpoint being major cardiac or cerebrovascular events (death, stroke, MI, or repeat revascularization) up to 12 months after treatment. Their non-inferiority delta value was 6.6%, derived from objective historical data. In the 12-month follow-up period they found significantly higher rates of major adverse events in the percutaneous coronary intervention group, 18% vs. 12% (p = .002), largely due to an increased rate of repeat revascularization. The 95% CI of the difference ranged up to 8.3%, exceeding their pre-specified boundary for non-inferiority. They therefore concluded that coronary artery bypass graft (CABG) should remain the standard of care for patients with extensive coronary artery disease.

Greilich et al. (25) used a non-inferiority design to compare epsilon aminocaproic acid with aprotinin and placebo in uncomplicated CABG surgery. Their outcomes of interest were fibrinolysis and blood loss. They set their non-inferiority margins at 30% for peak d-dimer formation (difference of 250 μg/L) and 350 mL for 24-hour chest tube drainage. Focusing on the two active drug groups, the 95% CI of the difference in peak d-dimer formation (–203–195 μg/L) and 24-hour blood loss (–90–230 mL) were within their predetermined non-inferiority margins, satisfying the criteria for non-inferiority. In view of the added cost, risk of re-exposure anaphylaxis, and other safety concerns for aprotinin, it is clear that epsilon aminocaproic acid should be recommended in preference to aprotinin in this setting.

INTERPRETING NEGATIVE TRIALS AND BORDERLINE P-VALUES

Many “negative” trials are underpowered and may have missed a clinically important difference between groups (26,27). It should not be concluded that such treatment groups are equivalent. A key consideration is the width of the 95% CI, a measure of the precision, or certainty, of the estimated treatment effect. If either of the 95% confidence limits includes a value that would be considered clinically important, then uncertainty remains and a larger more definitive study will be needed before reliable conclusions can be made.

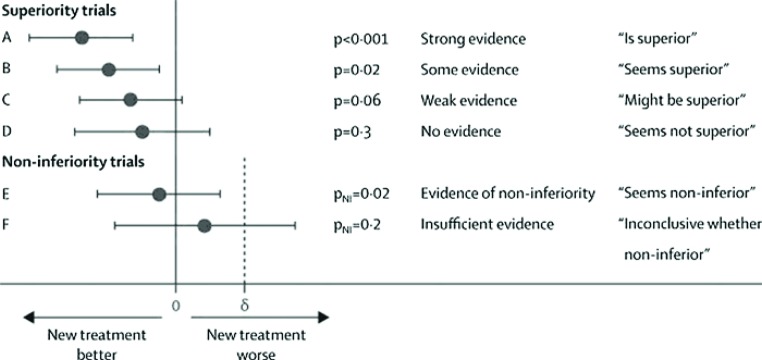
A recent Lancet editorial has made some suggestions on how to translate various statistical findings into simple English (see Figure 1) (27). The interpretation of p -values, and more particularly the 95% CI, derived from non-inferiority or equivalence trials can be particularly challenging (27). If the 95% CI for the treatment difference ex cludes the pre-specified non-inferiority delta margin then a conclusion of inferiority can be made. The authors recommend that the phrase “seems to have similar efficacy to the standard treatment” be used to describe this finding. However, if the 95% CI includes both zero (no difference) and delta (inferiority), then there is insufficient evidence either to claim non-inferiority or to conclude that the new treatment is inferior. Thus the trial is inconclusive—the groups should not be interpreted as “equivalent.”

Figure 1.

Six scenarios describing results of a clinical trial comparing two treatment groups. Each displays estimated treatment difference and its 95% CI, p-value, strength of evidence, and suggested phraseology to use in conclusions. For non-inferiority scenarios, non-inferiority margin delta (?) is shown, and pNI is the p-value for the test of non-inferiority. Reproduced with permission from The Lancet 2009;373:1926–8 (27).

DEFINING THE PRIMARY ENDPOINT

Many trials use a composite, or pooled, endpoint to define the primary outcome of the study (28–30). This is because effective interventions are likely to reduce several morbid endpoints, often via a single mechanism. For example, antithrombotic treatments may reduce non-fatal MI, non-fatal stroke, chronic heart failure, and thrombotic deaths. The pooled endpoint will have a higher incidence than each of the composites and this reduces the sample size requirement for the trial.

Pooled endpoints have an inherent assumption that each component of the endpoint has a similar burden on health (28–32). This is not often the case. Endpoints of least importance to patients, such as subclinical MI as opposed to stroke or death, typically contribute most to trial events (30). A recent systematic review found that in about half the trials reviewed there were large or moderate gradients in both importance to patients and magnitude of effect across components. The most serious and highly-rated events typically occurred least often, so that they provided the least information (numerical value) to the pooled end-point. This may result in misleading impressions of the true clinical value of the new treatment.

Cardiovascular trials commonly use major adverse cardiac events (MACE) as a pooled primary endpoint (29). But there is no standard definition for MACE. A review on the use of MACE as a pooled endpoint in stent trials found substantial variability in the study-specific individual outcomes used to define it (29). Most included MI, stroke and death; many included revascularizations; some included cardiac arrest, heart failure, or bleeding complications. Combining efficacy and safety components is particularly problematic. Each of these issues can lead to substantially different results and conclusions. Risks may outweigh benefits of a new treatment. Perhaps the best and most recent example is the POISE trial (33), which identified a significant reduction in perioperative MI but at a cost of excess death and stroke. There was also more hypotension and bradycardia.

Critical review of the frequency of each of the components of the pooled endpoint, and whether the treatment effect seems to be consistent for each of these, is strongly recommended (28–32). If large variations exist between components then the value of the pooled endpoint is diminished. Study designs using pooled endpoints should provide separate safety and effectiveness outcomes, and construct separate pooled endpoints to match these different clinical goals (29).

CONCLUSIONS

Innovations and developments in clinical study design can optimize the information available for clinicians. Propensity score techniques provide additional methods to account for imbalance in treatment group allocation, and hopefully lead to more accurate estimates of benefit or risk. Unlike clinical trials, the study data typically represent real world, everyday practice and so their findings may in fact be less biased. They are particularly useful when assessing safety.

Equivalence and non-inferiority designs can tailor clinical trials to address clinically meaningful questions: Is a proposed new technique at least as good as current treatment? They are best used when comparing two active interventions, particularly when one may be a cheaper or safer alternative. Training and experience in clinical trial design and interpretation, as with surgical or perfusion techniques, can improve how we gain new knowledge and apply interventions to improve patient care.