Abstract
The biomechanical influence of thoraco-lumbo-sacral bracing, a commonly employed treatment in scoliosis, is still not fully understood. The aim of this study was to compare the immediate corrections generated by different virtual braces using a patient-specific finite element model (FEM) and to analyze the most influential design factors. The 3D geometry of three patients presenting different types of curves was acquired with a multi-view X-ray technique and surface topography. A personalized FEM of the patients’ trunk and a parametric model of a virtual custom-fit brace were then created. The installation of the braces on the patients was simulated. The influence of 15 design factors on the 3D correction generated by the brace was evaluated following a design of experiments simulation protocol allowing computing the main and two-way interaction effects of the design factors. A total of 12,288 different braces were tested. Results showed a great variability of the braces effectiveness. Of the 15 design factors investigated, according to the 2 modalities chosen for each one, the 5 most influential design factors were the position of the brace opening (posterior vs. anterior), the strap tension, the trochanter extension side, the lordosis design and the rigid shell shape. The position of the brace opening modified the correction mechanism. The trochanter extension position influenced the efficiency of the thoracic and lumbar pads by modifying their lever arm. Increasing the strap tension improved corrections of coronal curves. The lordosis design had an influence in the sagittal plane but not in the coronal plane. This study could help to better understand the brace biomechanics and to rationalize and optimize their design.
Keywords: Scoliosis, Brace, Finite element model, Design, Optimization
Introduction
Scoliosis is a three-dimensional deformity of the spine and of the rib cage. For moderate deformities, bracing is the most common treatment. However, its efficiency in preventing the progression of scoliotic deformities is still controversial [14, 17, 19, 20, 29]. Many questions remain about what could be the best brace design. For instance it is unclear where the pads and openings should be positioned and how they should be shaped. Rigo [28] found significant variability in the brace designs that were recommended by 21 brace specialists for the same patient (right thoracic curve scoliosis with a minor lumbar curve). There was no consensus about whether the thoracic pad should be positioned below, at or above the apical rib, the optimal shape of the pads, the inclusion of an anterior derotational thoracic pad and the shape of the pelvis section (side of trochanteric extension and location of pads). Van Rhijn [32] compared the immediate effect of lumbar and thoracic braces on coronal curves and found that lumbar braces, relative to thoracic braces, significantly improved the correction of the lumbar curve and allowed spontaneous correction in the thoracic curve through improved balance of the spine. To our knowledge, this study was the only one that compared the efficiency of different brace designs on the same given patient.
A numerical model-based analysis of brace biomechanics overcomes the experimental limitation of multiple radiographic exposures required to test the effect of multiple brace designs on the same patient. A common method is to generate a finite element model (FEM) of a patient’s trunk and to simulate brace treatment by applying the forces exerted by the brace on the FEM [1, 13, 21, 26, 33]. Andriacchi [1] simulated the Milwaukee brace immediate effect and concluded that it was efficient in correcting coronal curves. Wynarsky [33] and Gignac [13] tried to find the optimal location and amplitude of the corrective forces generated by a brace; however, the method has several limitations. The corrective forces applied on the trunk FEM were not necessarily balanced and equilibrium was obtained using restrictive boundary conditions. Furthermore, the optimization process cannot include many brace design parameters, such as the strap tension, the rigid shell geometry, or the pads’ shape. In our previous studies (Perie [25] and Clin [8]), we presented a new method wherein a single brace with all its components (rigid shell, pads, openings, straps, foam layer) was explicitly modeled for one patient. Its installation was simulated using a contact interface between the patient’s trunk and brace models. The method is a more realistic representation of the actual procedure of fitting a brace onto a patient’s torso.
This study uses the previously developed simulation process to test multiple brace designs on given patients and to compare their immediate corrections of the 3D scoliotic deformities. The aim was to detect the most influential brace design factors and to quantify their influence on the immediate 3D corrections.
Methods
Simulation of the brace installation
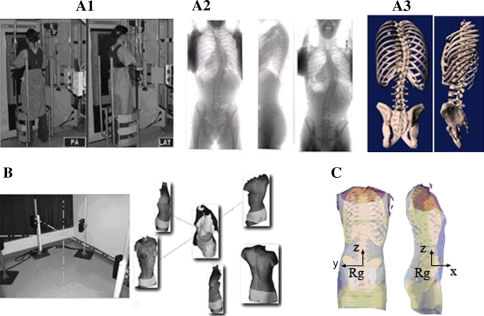
The geometry of the spine, rib cage and pelvis of three scoliotic patients [thoracic and lumbar Cobb: P1 (38°, 23°); P2 (36°, 16°); P3 (20°, 33°)] was reconstructed in 3D using a multi-view radiographic self-calibration technique [4, 7, 15, 16] (Figs. 1a, 2). The accuracy of this reconstruction method was 3.3 mm on average (SD 3.8 mm) [9]. In addition the external trunk surface of the patient was digitized using a 3D range-sensing technique (3-dimensional Capturor, Inspeck Inc., Montreal, Quebec, Canada) [22–24] (Fig. 1b). Using fiducial radiopaque landmarks visible on both the X-rays and the trunk surface, the internal and external geometries were then superimposed using a point-to-point least square algorithm (Fig. 1c) [12]. A global coordinate system Rg, with the origin at the center of the first sacral vertebra S1, was associated with this geometry such that the z-axis was directed vertically upwards, x-axis was postero-anterior and the y-axis was lateral (oriented from right to left).
Fig. 1.
Acquisition of the internal geometry using the multi-view radiographic reconstruction technique. a1 Postero-anterior (PA) and lateral acquisition. a2 PA, lateral, and PA with an incidence of 20° radiographs. a3 3D reconstruction. b Acquisition of the external geometry using the range sensor topography technique. c Superimposition of the two geometries (Rg global reference system)
Fig. 2.
Postero-anterior and lateral radiographs of the patients
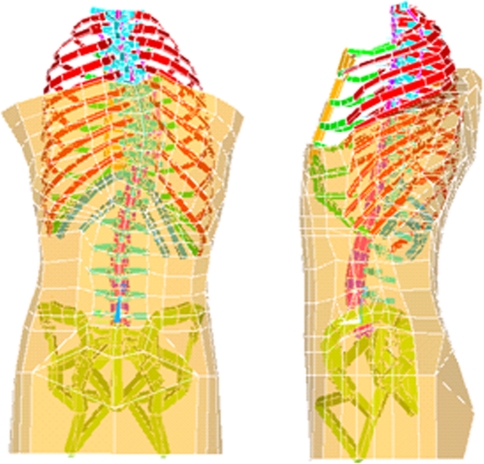
Based on this geometry, a personalized finite element model (FEM) of the patient’s torso was built [3, 26] (Fig. 3) using Ansys 11.0 FE package (Ansys Inc., Canonsburg, PA, USA). In brief, the thoracic and lumbar vertebrae, intervertebral discs, ribs, sternum, rib cartilages and abdominal cavity were represented by 3D elastic beam elements, the zygapophyseal joints by shells and surface-to-surface contact elements, the vertebral and intercostal ligaments by tension-only spring elements and the external soft tissues by hexahedral elements. Mechanical properties of all the components of the model were taken from experimental and published data [3, 25, 26]. The influence of the spine flexibility (“stiff” and “flexible” spines) was tested (intervertebral disc stiffness multiplied and divided by 2, respectively) [27].
Fig. 3.
Trunk FEM of the patient P2 (intercostal ligaments and abdominal beams are not shown for clarity)
A custom-fit geometrical brace model was created over the already generated FEM of the patient’s trunk (Fig. 4a–c). It included the external rigid shell, the foam layer, the openings and the pads. The external rigid shell was modeled by 4-node quadrilateral shell elements. The foam layer and the pads were modeled by 8-node hexahedral elements. The material of the rigid shell was polyethylene (E = 1,500 Mpa, ν = 0.3), that of the foam layer was soft polyethylene foam (E = 1 MPa, ν = 0.3) and that of the pads was stiff polyethylene foam (E = 10 MPa, ν = 0.3) [25, 30]. A surface-to-surface contact interface was created between the interior of the brace model and the exterior of the trunk model.
Fig. 4.
a Generative curves; b geometrical model of the brace; c finite element model of the brace; d FEM Brace installed on the patient
Boundary conditions were applied on the trunk model to mimic an in-brace patient. The pelvis was fixed in space and translation of the first thoracic vertebra in the transverse plane (x and y directions) was blocked.
Brace installation on the patient was simulated. The simulation process was divided into two steps: (1) the brace was opened by applying displacements on four nodes and was positioned on the patient; (2) forces representing strap tensions were applied on the nodes corresponding to the strap fixations. At the end of the simulation, the virtual brace was consequently installed on the patient (Fig. 4d).
On completion of the simulation, corrections in 3D clinical indices (Cobb angles, kyphosis, lordosis, rib hump, apical axial rotation) were computed [8, 13, 26].
Design of experiments
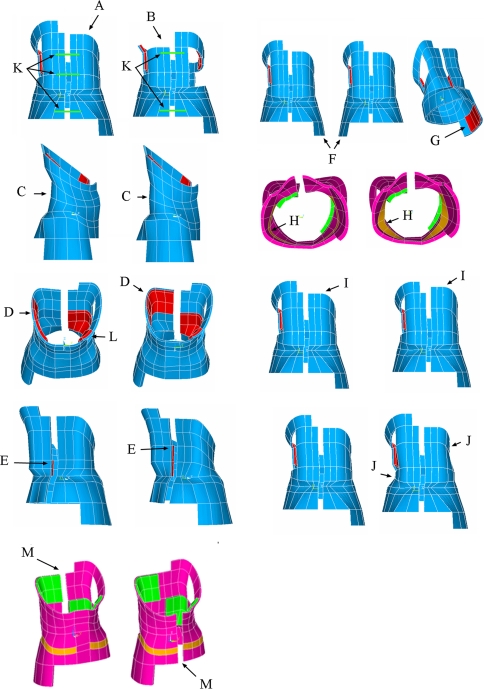
For each patient, with either the flexible or stiff spine model, a Box, Hunter and Hunter fractional design of experiments [5] was used to evaluate the effects of 15 brace design factors: strap number and tension, type of brace, thoracic pad position in the transverse and vertical planes, lumbar, anterior thoracic and trochanteric pads presence, iliac crest roll design, lordosis design, height of lumbar pad, rigid shell symmetry, trochanteric extension side, brace size and opening position. Each factor had two modalities. Table 1 lists the two modalities that were tested for each of the 15 factors illustrated in Fig. 5. The modalities for each design factor were chosen based on previous published studies [10, 18, 28] and according to the recommendations of orthotists.
Table 1.
Brace design factors tested with the design of experiments
| Design factor | Modality 1 | Modality 2 | Ref. (Fig. 5) |
|---|---|---|---|
| 1: Brace type | Thoracic brace | Lumbar brace | A, B |
| 2: Number of straps | 2 | 3 | K |
| 3: Strap tension | 20 N | 60 N | |
| 4: Sagittal profile | Follows the sagittal curves | Sagittal curves reduced | C |
| 5: Thoracic pad position | Lateral | Posterior | D |
| 6: Thoracic pad upper limit | Rib of the thoracic apex | Two ribs above | I |
| 7: Anterior derotational thoracic pad | Absent | Present | L |
| 8: Lumbar pad | Absent | Present | E |
| 9: Upper limit of the lumbar pad | Lumbar curve apex vertebra | Two vertebrae above | E |
| 10: Trochanter extension side | Right | Left | F |
| 11: Trochanter pad | Absent | Present | G |
| 12: Iliac crest roll presence | Absent | Present | H |
| 13: Rigid shell symmetry | Symmetric | Asymmetric [10% reduction of (coronal plane) thoracic and lumbar parts] | J |
| 14: Brace size | 5% too tight | 5% too large | |
| 15: Brace opening position | Posterior | Anterior | M |
Fig. 5.
Brace design factors: A and B Brace type; C lordosis design; D thoracic pad position; E lumbar pad height; F trochanter extension side; G trochanter pad; H iliac crest roll design; I thoracic pad height; J shell symmetry; K number of straps; L counter-thoracic pad; M opening position
Using the fractional design of experiments, for each patient, with either the flexible or stiff spine model, 2,048 (2(15−4)) virtual braces were tested (total of 12,288: 3 patients × 2 flexibility models × 2048 braces). It allowed evaluating the main and two-way interaction effects of the tested design factors on the 3D corrections generated by the brace. For example, the main effect of the strap tension on the correction of the thoracic curve Cobb angle is the mean change of correction (for all the tested braces) of the thoracic curve Cobb angle when the strap tension increases from 20 to 60 N. The interaction effect of the strap tension and the brace type on the correction of the thoracic curve Cobb angle is the difference of effect of the strap tension on the correction of the thoracic curve Cobb angle between the lumbar braces and the thoracic braces. Likewise for every design factor, the main effect and its interaction with the remaining factors were evaluated.
Results
The immediate correction in all the tested braces was quite variable, especially when the thoracic and lumbar Cobb angles, the kyphosis and the lordosis parameters were considered (Table 2). For instance, for P1 with a flexible spine, the thoracic Cobb in-brace varied between 6° and 54°. There was little correction on average in the transverse plane (axial rotation and rib hump). Relatively more correction in the coronal plane was obtained for the flexible spine as compared to the stiff spine model. For instance, the mean in-brace thoracic Cobb angle for P1 was 24° with a flexible spine and 31° with a stiff spine.
Table 2.
Geometrical indices of the models before and after the simulation of the brace installation
| Index | Initial | In brace | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flexible spine | Stiff spine | |||||||||||||
| Posterior opening | Anterior opening | Posterior opening | Anterior opening | |||||||||||
| Mean | Max | Min | Mean | Max | Min | Mean | Max | Min | Mean | Max | Min | |||
| P1 | Thoracic Cobb | 37 | 24 | 35 | 6 | 29 | 54 | 17 | 31 | 36 | 23 | 33 | 39 | 26 |
| Lumbar Cobb | 23 | 13 | 20 | 1 | 16 | 24 | 9 | 19 | 22 | 14 | 20 | 24 | 17 | |
| Kyphosis | 18 | 13 | 23 | 0 | 14 | 25 | 1 | 15 | 21 | 4 | 15 | 22 | 9 | |
| Lordosis | 25 | 21 | 27 | 7 | 21 | 28 | 11 | 23 | 26 | 17 | 23 | 27 | 19 | |
| Rib hump | 17 | 16 | 26 | 11 | 16 | 32 | 11 | 16 | 23 | 12 | 15 | 27 | 11 | |
| Axial rotation | 22 | 22 | 32 | 15 | 21 | 35 | 14 | 22 | 28 | 18 | 21 | 29 | 12 | |
| P2 | Thoracic Cobb | 39 | 29 | 40 | 14 | 28 | 36 | 17 | 36 | 40 | 30 | 35 | 38 | 31 |
| Lumbar Cobb | 17 | 11 | 17 | 2 | 11 | 16 | 4 | 15 | 17 | 12 | 15 | 17 | 13 | |
| Kyphosis | 9 | 7 | 16 | 0 | 5 | 15 | 0 | 7 | 12 | 0 | 6 | 11 | 0 | |
| Lordosis | 35 | 33 | 38 | 25 | 32 | 37 | 25 | 34 | 36 | 30 | 33 | 36 | 30 | |
| Rib hump | 22 | 24 | 33 | 18 | 20 | 33 | 14 | 25 | 33 | 19 | 22 | 27 | 17 | |
| Axial rotation | 13 | 12 | 17 | 9 | 9 | 19 | 5 | 13 | 17 | 10 | 11 | 15 | 7 | |
| P3 | Thoracic Cobb | 20 | 12 | 23 | 0 | 15 | 28 | 4 | 17 | 21 | 10 | 19 | 22 | 14 |
| Lumbar Cobb | 30 | 22 | 30 | 9 | 25 | 32 | 18 | 28 | 31 | 23 | 29 | 31 | 25 | |
| Kyphosis | 53 | 48 | 54 | 37 | 49 | 58 | 42 | 51 | 55 | 44 | 51 | 56 | 47 | |
| Lordosis | 37 | 34 | 38 | 27 | 35 | 41 | 28 | 36 | 38 | 32 | 36 | 39 | 33 | |
| Rib hump | 9 | 8 | 11 | 6 | 9 | 15 | 6 | 9 | 11 | 7 | 9 | 11 | 7 | |
| Axial rotation | 11 | 11 | 14 | 9 | 11 | 18 | 9 | 11 | 13 | 9 | 11 | 12 | 9 | |
All values are in degrees
An interaction was found between the position of the brace opening (anterior or posterior) and the other design factors, which revealed that the effect of the design factors was quite different if the opening was anterior or posterior. For instance, in case of P1, when a brace with a posterior opening was used, the four influential parameters that impacted most thoracic Cobb angle were strap tension, trochanter extension side, brace symmetry and the number of straps. For the same case, when a brace with an anterior opening was used, the four influential parameters were the brace type, brace symmetry, trochanter extension side and brace size.
For both types of brace openings (anterior and posterior), the main effects on the 3D geometrical indices of the most influential brace design factors are presented in Table 3. As an example, in the case of P1, when a brace with a posterior opening was used, changing the position of the trochanter extension from right to left increased the in-brace thoracic Cobb angle by 5° (first row, second factor in Table 3). For the same case, when a brace with an anterior opening was used, an increase of 3.6° was obtained (seventh row, third factor in Table 3). Results of only the flexible spine models are listed in Table 3. For the stiff spine models, although the most influential design factors were identical for all indices, the resulting effects were weaker due to smaller corrections.
Table 3.
Effects of the most influential design factors
| Opening position | Index (°) | First factor | Second factor | Third factor | Fourth factor | Fifth factor | |
|---|---|---|---|---|---|---|---|
| P1 | Posterior | Thoracic Cobb | Strap tension | Troch. ext. side | Brace symmetry | Strap number | Brace size |
| −5.2 | 5.0 | −3.9 | −2.5 | 2.0 | |||
| Lumbar Cobb | Strap tension | Brace type | Brace symmetry | Strap number | Troch. ext. side | ||
| −4.9 | −3.4 | −2.8 | −2.1 | 1.4 | |||
| Kyphosis | Lordosis design | Strap tension | Thor. pad position | Brace symmetry | Lumbar pad | ||
| −5.9 | −4.7 | −2.9 | 2.8 | 2.6 | |||
| Lordosis | Lordosis design | Strap tension | Brace symmetry | Thor. pad position | Lumbar pad | ||
| −5.7 | −2.5 | 1.8 | −1.6 | 1.5 | |||
| Rib hump | Brace type | Thor. pad position | Brace size | Strap tension | Counter-thor. pad | ||
| −3.7 | −1.5 | −1.2 | 0.6 | −0.5 | |||
| Axial rotation | Brace type | Brace size | Thor. pad position | Troch. ext. side | Brace symmetry | ||
| −4.2 | −1.5 | −1.4 | −0.8 | 0.5 | |||
| Anterior | Thoracic Cobb | Brace type | Brace symmetry | Troch. ext. side | Brace size | Strap tension | |
| 4.6 | −3.6 | 3.6 | 2.9 | −2.0 | |||
| Lumbar Cobb | Brace symmetry | Brace size | Strap tension | Troch. ext. side | Thor. pad position | ||
| −3.2 | 2.2 | −2.1 | 1.1 | 1.1 | |||
| Kyphosis | Lordosis design | Lumbar pad | Thor. pad position | Strap tension | Brace symmetry | ||
| −4.6 | 2.6 | −1.8 | −1.7 | 1.5 | |||
| Lordosis | Lordosis design | Strap tension | Brace symmetry | Lumbar pad | Thor. pad position | ||
| −4.6 | −2.1 | 1.6 | 1.6 | −1.0 | |||
| Rib hump | Brace size | Lordosis design | Troch. ext. side | Brace type | Strap tension | ||
| 2.7 | −1.1 | 0.9 | −0.8 | 0.8 | |||
| Axial rotation | Brace size | Lordosis design | Strap tension | Brace type | Troch. ext. side | ||
| 2.6 | −1.3 | 0.9 | −0.8 | 0.7 | |||
| P2 | Posterior | Thoracic Cobb | Troch. ext. side | Brace symmetry | Brace size | Thor. pad height | Brace type |
| 4.2 | −4.0 | 2.9 | −1.4 | −1.3 | |||
| Lumbar Cobb | Brace type | Brace symmetry | Troch. ext. side | Thor. pad height | Brace size | ||
| −2.3 | −2.2 | 1.6 | −1.2 | 1.2 | |||
| Kyphosis | Lordosis design | Strap tension | Brace size | Brace symmetry | Thor. pad height | ||
| −3.8 | −3.4 | −2.2 | 1.7 | 1.3 | |||
| Lordosis | Lordosis design | Strap tension | Brace type | Brace symmetry | Thor. pad position | ||
| −3.5 | −2.0 | 1.6 | 1.2 | −0.9 | |||
| Rib hump | Brace type | Brace size | Strap tension | Thor. pad position | Thor. pad height | ||
| −2.6 | −1.9 | 0.9 | −0.8 | 0.5 | |||
| Axial rotation | Brace type | Brace size | Thor. pad position | Brace symmetry | Lumbar pad | ||
| −1.2 | −1.1 | −0.5 | −0.4 | −0.3 | |||
| Anterior | Thoracic Cobb | Troch. ext. side | Brace symmetry | Brace size | Strap tension | Thor. pad height | |
| 4.4 | −2.9 | 2.2 | −2.0 | −0.9 | |||
| Lumbar Cobb | Brace symmetry | Brace type | Strap tension | Troch. ext. side | Thor. pad height | ||
| −2.3 | −1.9 | −1.8 | 1.6 | −0.9 | |||
| Kyphosis | Lordosis design | Brace symmetry | Lumbar pad | Strap tension | Brace size | ||
| −5.0 | 1.9 | 1.9 | −1.2 | 1.2 | |||
| Lordosis | Lordosis design | Strap tension | Brace symmetry | Lumbar pad | Thor. pad position | ||
| −3.6 | −1.4 | 1.4 | 1.2 | −0.8 | |||
| Rib hump | Thor. pad position | Brace symmetry | Troch. ext. side | Lordosis design | Brace type | ||
| −0.9 | 0.9 | 0.6 | −0.5 | −0.3 | |||
| Axial rotation | Lordosis design | Strap tension | Brace symmetry | Thor. pad position | Thor. pad height | ||
| −0.5 | −0.5 | 0.4 | −0.4 | −0.3 | |||
| P3 | Posterior | Thoracic Cobb | Strap tension | Troch. ext. side | Brace size | Strap number | Brace symmetry |
| −7.5 | 3.3 | −3.0 | −2.4 | −2.3 | |||
| Lumbar Cobb | Strap tension | Brace symmetry | Troch. ext. side | Strap number | Brace type | ||
| −5.9 | −2.9 | 2.4 | −2.2 | −1.7 | |||
| Kyphosis | Lordosis design | Strap tension | Lumbar pad | Thor. pad position | Strap number | ||
| −3.8 | −3.8 | 1.7 | −1.5 | −1.4 | |||
| Lordosis | Lordosis design | Strap tension | Thor. pad position | Brace symmetry | Lumbar pad | ||
| −3.8 | −2.0 | −1.0 | 0.9 | 0.9 | |||
| Rib hump | Troch. ext. side | Brace symmetry | Strap tension | Thor. pad position | Counter-thor. pad | ||
| 0.9 | −0.8 | −0.8 | 0.5 | 0.3 | |||
| Axial rotation | Troch. ext. side | Strap tension | Brace type | Brace symmetry | Thor. pad position | ||
| −0.8 | 0.6 | 0.6 | 0.6 | −0.2 | |||
| Anterior | Thoracic Cobb | Brace type | Strap tension | Brace symmetry | Thor. pad height | Iliac crest roll | |
| 2.5 | −2.5 | −2.4 | 0.8 | −0.4 | |||
| Lumbar Cobb | Strap tension | Troch. ext. side | Lumbar pad | Lordosis design | Counter-thor. pad | ||
| −2.4 | 2.4 | −0.5 | 0.4 | 0.4 | |||
| Kyphosis | Brace type | Lumbar pad | Brace size | Thor. pad position | Lumb. pad height | ||
| 2.0 | 1.9 | 1.1 | −1.0 | −0.9 | |||
| Lordosis | Lumbar pad | Brace type | Brace symmetry | Strap tension | Thor. pad position | ||
| 1.4 | 1.4 | 1.2 | −1.2 | −0.9 | |||
| Rib hump | Strap tension | Troch. ext. side | Brace symmetry | Thor. pad position | Strap number | ||
| −0.6 | 0.5 | −0.4 | 0.4 | −0.2 | |||
| Axial rotation | Strap tension | Brace size | Brace symmetry | Brace type | Thor. pad height | ||
| 0.5 | 0.5 | 0.4 | 0.3 | 0.3 |
Flexible spine models, all values are in degrees. Example: for P1, using brace with a posterior opening, changing the position of the trochanter extension from right to left increased the in-brace thoracic Cobb angle by 5° (first row, second factor), increasing the strap tension from 20 to 60 N decreased the in-brace thoracic Cobb angle by 5.2° (first row, first factor)
Increasing strap tension and using three straps instead of two gave a better correction in the coronal plane (Table 3). Introducing an asymmetry relative to the sagittal plane in the rigid shell also gave better correction. The ‘lumbar brace’ type improved the correction of the lumbar curve relatively to the ‘thoracic brace’. The trochanter extension side had an important effect on the coronal curves. Positioning it on the right (side of the thoracic curve for the patients in this study) improved the correction of both the thoracic and lumbar Cobb angles. Figure 6 shows the spinal shape of the patients in the coronal plane before the brace installation and the same after two different braces installation, both of which were identical except for the trochanter extension side. When the trochanter extension side was on the right, the brace pushed the spine more to the left. For patients P1 and P3, even if it increased the reduction of the thoracic and lumbar Cobb angles, it also aggravated the decompensation of the trunk to the left.
Fig. 6.
Effect of the position of the trochanter extension side on the spine shape of the three patients P1, P2, P3 in the coronal plane (postero-anterior view) (blue diamond spinal shape without brace, red square in brace with the trochanter extension on the right side, green triangle in brace with the trochanter extension on the left side)
In the sagittal plane, the most influential factor was the lordosis design. When the sagittal curve of the brace rigid shell was reduced, it decreased both the lordosis and the kyphosis (for instance 5° on average for P1 with a flexible spine) (Table 3). However, it did not generate a significant reduction of the coronal curves. An increase of the strap tension reduced the sagittal curves while an asymmetry in the rigid shell increased them. The presence of the lumbar pad, positioned posteriorly, had a lordotic effect. When the thoracic pad was positioned posteriorly rather than laterally, aside from decreasing the kyphosis and lordosis, it also reduced rib hump and apical axial rotation. No distinct tendency for the other design factors was observed in the transverse plane (rib hump and vertebral axial rotation).
Discussion
Simulating brace treatment allowed testing a large number of virtual braces (12,288). Such numerical simulations allow the comparison of immediate in-brace corrections obtained using different brace designs for the same patient. It also provides a versatile tool to examine the impact of varying specific design parameters and the relative interaction between them. Such comparisons and evaluations on patients are very difficult to do with real braces.
The trochanter extension side significantly impacted the correction of the coronal curves and the global coronal balance of the trunk; mechanically, it acts as a lever arm. If positioned on the right side, it enhances the action of the right thoracic pad and the trunk is pushed globally to the left. If positioned on the left side, it enhances the action of the left lumbar pad but the effect is less because the lever arm is shorter (see Fig. 6). The brace lordosis design influenced the sagittal curves. The trunk shape tended to conform to the brace shape. When the thoracic pad was placed in a more posterior position, it pushed the right rib hump forward, which reduced the transverse plane deformity (vertebral axial rotation, rib hump) but also induced a reduction in the kyphosis. Aubin et al. [2] also observed this effect. In a similar way, the presence of the posterior lumbar pad, that pushes the abdomen forward, had a lordotic effect. These results corroborate with empirical observations [6–8].
The thoracic and lumbar pads upper limit had limited effects of the scoliotic coronal curves, and the current study does not support the general recommendation of brace manufacturers to place the thoracic and lumbar pads below the curve apex [8]. No correlation was found between the reduction of the lordosis and the correction of the coronal curves, even if this is one of the principles of the Boston brace system [10]. The reduction of the lordotic profile of the brace had only a negative effect on sagittal curves (hypo-kyphosing and hypo-lordosing). An asymmetric rigid shell was more efficient in correcting the coronal curves than a symmetric one. A more thorough optimization study of the rigid shell shape could help better understand these results.
The interaction effect between the opening position and the other design factors reveals that braces like for instance the Boston brace (posterior opening) and the Chêneau brace (anterior opening) have quite different working mechanisms. It can be explained mechanically by the fact that the pressures exerted by the pads on the torso result from the tension applied to the straps. Changing the opening position and hence the straps’ location modifies the moment created by the strap force on the pads location, and consequently, it modifies the action of the pads on the torso. The optimal opening position could be an interesting future direction to investigate.
Fifteen design factors were examined to limit the already extensive number of simulations. Other design factors could also be considered, e.g., position of the lumbar pad in the transverse plane (posterior or postero-lateral position), the presence of an abdominal pad, the shape of the pads, and other configurations of openings. It should also be noted that the ranking of the design factors by their effects magnitude (Table 3) is dependant on the two modalities that were chosen for each factor in the design of experiments (Table 1). Other modalities could be investigated in the future. The present study, as it detected some of the key brace design parameters, could be the basis of an optimization process. It could notably help to choose the optimization variables. An objective function representing appropriately the orthotist definition of an efficient brace treatment should also be defined.
The present model has, as any numerical models, its limitations and the results should therefore be interpreted with caution. Given the boundary conditions, the pelvis was not allowed to tilt, which could have modified notably the effect of the brace lordosis design. The first thoracic vertebra was only free to move along the vertical axis and the effect of the brace on the patient decompensation could not be evaluated. The intervertebral discs and the ligaments were modeled as linear elastic. These limitations were more thoroughly discussed by Clin and Perie [8, 25, 26].
Only the passive action of the brace was simulated as no muscles were present in the model. It could be reasonable, however, to assume that the active action, if any, would be concomitant, complementary, to the passive action and that it would amplify the brace design factors’ effects generated by the passive action. For instance, it might be that greater strap tension increases the passive effect as studied here, and also increases the discomfort, thereby encouraging an ‘active’ response. More generally, to model the muscular contribution is complex and a great challenge to be undertaken in the future.
The present study focused on the immediate action of braces but the aim of brace treatment is to stop the progression of scoliotic deformities in a long-term perspective. It was, however, remarked that the immediate efficiency of a brace is a good predictor of the outcome of the treatment [6, 11, 31], which justifies to focus mainly on this immediate action.
Different studies were done to evaluate the brace model validity [8, 25, 26]. Perie [26] compared the spinal geometries obtained after simulation and in the real brace and found differences in Cobb angles inferior to 8°. Differences in positions of vertebrae in coronal and sagittal planes were inferior to 6 and 9.8 mm, respectively. The pressures exerted by the virtual brace on the patients’ torso FE models were also computed and compared to pressures measured experimentally. They were found to be in the same range (0–30 mm Hg). The validation process will however continue, by integrating personalized mechanical properties for instance.
The model used in this study is an improvement over the previous methods used to simulate brace treatment because the brace is explicitly modeled, all its components are included (pads, openings, foam layer, straps) and the simulation process represents adequately the installation of the brace on the patient (opening, positioning, tightening of straps) [8].
Conclusion
By using a finite element model to simulate brace treatment, it was possible to compare the efficiency of multiple brace designs on specific patients. Results showed great variability of the 3D corrections generated by the braces according to their design. The most influential design factors were identified. The importance of strap tension, trochanter extension side, rigid shell shape and lordosis design was notably detected. The position of the opening, posterior or anterior, changed the working mechanism of the brace. The present study provides a better understanding of brace biomechanics and gives insights for an objective assessment of the bracing treatment.
Acknowledgments
This study was funded by the Natural Sciences and Engineering Research Council of Canada.
Contributor Information
Julien Clin, Email: julien.clin@polymtl.ca.
Carl-Eric Aubin, Phone: +1-514-340-4711, FAX: +1-514-340-5867, Email: carl-eric.aubin@polymtl.ca.
References
- 1.Andriacchi TP, Schultz AB, Belytschko TB, Dewald R. Milwaukee brace correction of idiopathic scoliosis. A biomechanical analysis and a retrospective study. J Bone Jt Surg Am. 1976;58:806–815. [PubMed] [Google Scholar]
- 2.Aubin CE, Dansereau J, Guise JA, Labelle H. Rib cage-spine coupling patterns involved in brace treatment of adolescent idiopathic scoliosis. Spine. 1997;22:629–635. doi: 10.1097/00007632-199703150-00010. [DOI] [PubMed] [Google Scholar]
- 3.Aubin CE, Dansereau J, Guise JA, Labelle H. A study of biomechanical coupling between spine and rib cage in the treatment by orthosis of scoliosis. Ann Chir. 1996;50:641–650. [PubMed] [Google Scholar]
- 4.Aubin CE, Descrimes JL, Dansereau J, Skalli W, Lavaste F, Labelle H. Geometrical modeling of the spine and the thorax for the biomechanical analysis of scoliotic deformities using the finite element method. Ann Chir. 1995;49:749–761. [PubMed] [Google Scholar]
- 5.Box GEP, Hunter JS. The 2 k-p fractional factorial designs. Part I. Technometrics. 2000;42:28–47. doi: 10.2307/1271430. [DOI] [Google Scholar]
- 6.Castro FP., Jr Adolescent idiopathic scoliosis, bracing, and the Hueter-Volkmann principle. Spine J. 2003;3:180–185. doi: 10.1016/S1529-9430(02)00557-0. [DOI] [PubMed] [Google Scholar]
- 7.Cheriet F, Remaki L, Bellefleur C, Koller A, Labelle H, Dansereau J. A new X-ray calibration/reconstruction system for 3D clinical assessment of spinal deformities. Stud Health Technol Inform. 2002;91:257–261. [PubMed] [Google Scholar]
- 8.Clin J, Aubin CE, Labelle H. Virtual prototyping of a brace design for the correction of scoliotic deformities. Med Biol Eng Comput. 2007;45:467–473. doi: 10.1007/s11517-007-0171-4. [DOI] [PubMed] [Google Scholar]
- 9.Delorme S, Petit Y, Guise JA, Labelle H, Aubin CE, Dansereau J. Assessment of the 3-d reconstruction and high-resolution geometrical modeling of the human skeletal trunk from 2-D radiographic images. IEEE Trans Biomed Eng. 2003;50:989–998. doi: 10.1109/TBME.2003.814525. [DOI] [PubMed] [Google Scholar]
- 10.Emans JB (2003) Boston Brace. srs bracing manual (http://wwwsrsorg/professionals/bracing_manuals/)
- 11.Emans JB, Kaelin A, Bancel P, Hall JE, Miller ME. The Boston bracing system for idiopathic scoliosis. Follow-up results in 295 patients. Spine. 1986;11:792–801. doi: 10.1097/00007632-198610000-00009. [DOI] [PubMed] [Google Scholar]
- 12.Fortin D, Cheriet F, Beausejour M, Debanne P, Joncas J, Labelle H. A 3D visualization tool for the design and customization of spinal braces. Comput Med Imaging Graph. 2007;31:614–624. doi: 10.1016/j.compmedimag.2007.07.006. [DOI] [PubMed] [Google Scholar]
- 13.Gignac D, Aubin CE, Dansereau J, Labelle H. Optimization method for 3D bracing correction of scoliosis using a finite element model. Eur Spine J. 2000;9:185–190. doi: 10.1007/s005860000135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Goldberg CJ, Moore DP, Fogarty EE, Dowling FE. Adolescent idiopathic scoliosis: the effect of brace treatment on the incidence of surgery. Spine. 2001;26:42–47. doi: 10.1097/00007632-200101010-00009. [DOI] [PubMed] [Google Scholar]
- 15.Kadoury S, Cheriet F, Dansereau J, Labelle H. Three-dimensional reconstruction of the scoliotic spine and pelvis from uncalibrated biplanar X-ray images. J Spinal Disord Tech. 2007;20:160–167. doi: 10.1097/01.bsd.0000211259.28497.b8. [DOI] [PubMed] [Google Scholar]
- 16.Kadoury S, Cheriet F, Laporte C, Labelle H. A versatile 3D reconstruction system of the spine and pelvis for clinical assessment of spinal deformities. Med Biol Eng Comput. 2007;45:591–602. doi: 10.1007/s11517-007-0182-1. [DOI] [PubMed] [Google Scholar]
- 17.Lenssinck ML, Frijlink AC, Berger MY, Bierman-Zeinstra SM, Verkerk K, Verhagen AP. Effect of bracing and other conservative interventions in the treatment of idiopathic scoliosis in adolescents: a systematic review of clinical trials. Phys Ther. 2005;85:1329–1339. [PubMed] [Google Scholar]
- 18.Mac-Thiong JM, Petit Y, Aubin CE, Delorme S, Dansereau J, Labelle H. Biomechanical evaluation of the Boston brace system for the treatment of adolescent idiopathic scoliosis: relationship between strap tension and brace interface forces. Spine. 2004;29:26–32. doi: 10.1097/01.BRS.0000103943.25412.E9. [DOI] [PubMed] [Google Scholar]
- 19.Nachemson AL, Peterson LE. Effectiveness of treatment with a brace in girls who have adolescent idiopathic scoliosis. A prospective, controlled study based on data from the Brace Study of the Scoliosis Research Society. J Bone Jt Surg Am. 1995;77:815–822. doi: 10.2106/00004623-199506000-00001. [DOI] [PubMed] [Google Scholar]
- 20.Noonan KJ, Weinstein SL, Jacobson WC, Dolan LA. Use of the Milwaukee brace for progressive idiopathic scoliosis. J Bone Jt Surg Am. 1996;78:557–567. doi: 10.2106/00004623-199604000-00009. [DOI] [PubMed] [Google Scholar]
- 21.Patwardhan AG, Bunch WH, Meade KP, Vanderby R, Jr, Knight GW. A biomechanical analog of curve progression and orthotic stabilization in idiopathic scoliosis. J Biomech. 1986;19:103–117. doi: 10.1016/0021-9290(86)90141-7. [DOI] [PubMed] [Google Scholar]
- 22.Pazos V, Cheriet F, Danserau J, Ronsky J, Zernicke RF, Labelle H. Reliability of trunk shape measurements based on 3-D surface reconstructions. Eur Spine J. 2007;16:1882–1891. doi: 10.1007/s00586-007-0457-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pazos V, Cheriet F, Labelle H, Dansereau J. 3D reconstruction and analysis of the whole trunk surface for non-invasive follow-up of scoliotic deformities. Stud Health Technol Inform. 2002;91:296–299. [PubMed] [Google Scholar]
- 24.Pazos V, Cheriet F, Song L, Labelle H, Dansereau J. Accuracy assessment of human trunk surface 3D reconstructions from an optical digitising system. Med Biol Eng Comput. 2005;43:11–15. doi: 10.1007/BF02345117. [DOI] [PubMed] [Google Scholar]
- 25.Perie D, Aubin CE, Lacroix M, Lafon Y, Labelle H. Biomechanical modelling of orthotic treatment of the scoliotic spine including a detailed representation of the brace–torso interface. Med Biol Eng Comput. 2004;42:339–344. doi: 10.1007/BF02344709. [DOI] [PubMed] [Google Scholar]
- 26.Perie D, Aubin CE, Petit Y, Labelle H, Dansereau J. Personalized biomechanical simulations of orthotic treatment in idiopathic scoliosis. Clin Biomech (Bristol, Avon) 2004;19:190–195. doi: 10.1016/j.clinbiomech.2003.11.003. [DOI] [PubMed] [Google Scholar]
- 27.Petit Y, Aubin CE, Labelle H. Patient-specific mechanical properties of a flexible multi-body model of the scoliotic spine. Med Biol Eng Comput. 2004;42:55–60. doi: 10.1007/BF02351011. [DOI] [PubMed] [Google Scholar]
- 28.Rigo M, Negrini S, Weiss HR, Grivas TB, Maruyama T, Kotwicki T. SOSORT consensus paper on brace action: TLSO biomechanics of correction (investigating the rationale for force vector selection) Scoliosis. 2006;1:11. doi: 10.1186/1748-7161-1-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rowe DE, Bernstein SM, Riddick MF, Adler F, Emans JB, Gardner-Bonneau D. A meta-analysis of the efficacy of non-operative treatments for idiopathic scoliosis. J Bone Jt Surg Am. 1997;79:664–674. doi: 10.2106/00004623-199705000-00005. [DOI] [PubMed] [Google Scholar]
- 30.Sanders JE, Greve JM, Mitchell SB, Zachariah SG. Material properties of commonly used interface materials and their static coefficients of friction with skin and socks. J Rehabil Res Dev. 1998;35:161–176. [PubMed] [Google Scholar]
- 31.Upadhyay SS, Nelson IW, Ho EK, Hsu LC, Leong JC. New prognostic factors to predict the final outcome of brace treatment in adolescent idiopathic scoliosis. Spine. 1995;20:537–545. doi: 10.1097/00007632-199503010-00006. [DOI] [PubMed] [Google Scholar]
- 32.Rhijn LW, Veraart BE, Plasmans CM. Application of a lumbar brace for thoracic and double thoracic lumbar scoliosis: a comparative study. J Pediatr Orthop B. 2003;12:178–182. doi: 10.1097/00009957-200305000-00002. [DOI] [PubMed] [Google Scholar]
- 33.Wynarsky GT, Schultz AB. Optimization of skeletal configuration: studies of scoliosis correction biomechanics. J Biomech. 1991;24:721–732. doi: 10.1016/0021-9290(91)90336-L. [DOI] [PubMed] [Google Scholar]